From Wikipedia, the free encyclopedia
Protein design is the
rational design of new
protein molecules to design novel activity, behavior, or purpose, and to advance basic understanding of protein function
[1]. Proteins can be designed from scratch (
de novo design) or by making calculated variants of a known protein structure and its sequence (termed
protein redesign).
Rational protein design
approaches make protein-sequence predictions that will fold to specific
structures. These predicted sequences can then be validated
experimentally through methods such as
peptide synthesis,
site-directed mutagenesis, or
artificial gene synthesis.
Rational protein design dates back to the mid-1970s, although initial
protein design approaches were based mostly on sequence composition and
did not account for specific interactions between side-chains at the
atomic level.
[2] Recently, however, improvements in molecular force fields, protein design algorithms, and
structural bioinformatics, such as
libraries of amino acid conformations,
have enabled the development of advanced computational protein design
tools. These computational tools can make complex calculations on
protein energetics and flexibility, and perform searches over vast
configuration spaces,
which would be unfeasible to perform manually. Due to the development
of computational protein design programs, and important successes in the
field (see
examples below), rational protein design has become one of the most important tools in
protein engineering.
Overview and history
The goal in rational protein design is to predict
amino acid sequences that will
fold
to a specific protein structure. Although the number of possible
protein sequences is vast, growing exponentially with the size of the
protein chain, only a subset of them will fold reliably and quickly to
one
native state. Protein design involves identifying novel sequences within this subset. The native state of a protein is the conformational
free energy
minimum for the chain. Thus, protein design is the search for sequences
that have the chosen structure as a free energy minimum. In a sense, it
is the reverse of
protein structure prediction. In design, a
tertiary structure is specified, and a sequence that will fold to it is identified. Hence, it is also termed
inverse folding.
Protein design is then an optimization problem: using some scoring
criteria, an optimized sequence that will fold to the desired structure
is chosen.
When the first proteins were rationally designed during the 1970s and
1980s, the sequence for these was optimized manually based on analyses
of other known proteins, the sequence composition, amino acid charges,
and the geometry of the desired structure.
[2]
The first designed proteins are attributed to Bernd Gutte, who designed
a reduced version of a known catalyst, bovine ribonuclease, and
tertiary structures consisting of beta-sheets and alpha-helices,
including a binder of
DDT. Urry and colleagues later designed
elastin-like
fibrous
peptides based on rules on sequence composition. Richardson and
coworkers designed a 79-residue protein with no sequence homology to a
known protein.
[2] In the 1990s, the advent of powerful computers,
libraries of amino acid conformations, and force fields developed mainly for
molecular dynamics
simulations enabled the development of structure-based computational
protein design tools. Following the development of these computational
tools, great success has been achieved over the last 30 years in protein
design. The first protein successfully designed completely
de novo was done by
Stephen Mayo and coworkers in 1997,
[3] and, shortly after, in 1999
Peter S. Kim and coworkers designed dimers, trimers, and tetramers of unnatural right-handed
coiled coils.
[4][5] In 2003,
David Baker's laboratory designed a full protein to a fold never seen before in nature.
[6] Later, in 2008, Baker's group computationally designed enzymes for two different reactions.
[7]
In 2010, one of the most powerful broadly neutralizing antibodies was
isolated from patient serum using a computationally designed protein
probe.
[8] Due to these and other successes (e.g., see
examples below), protein design has become one of the most important tools available for
protein engineering. There is great hope that the design of new proteins, small and large, will have uses in
biomedicine and
bioengineering.
Underlying models of protein structure and function
Protein design programs use
computer models of the molecular forces that drive proteins in
in vivo
environments. In order to make the problem tractable, these forces are
simplified by protein design models. Although protein design programs
vary greatly, they have to address four main modeling questions: What is
the target structure of the design, what flexibility is allowed on the
target structure, which sequences are included in the search, and which
force field will be used to score sequences and structures.
Target structure
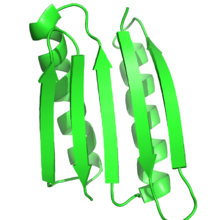
The
Top7 protein was one of the first proteins designed for a fold that had never been seen before in nature
[6]
Protein function is heavily dependent on protein structure, and
rational protein design uses this relationship to design function by
designing proteins that have a target structure or fold. Thus, by
definition, in rational protein design the target structure or ensemble
of structures must be known beforehand. This contrasts with other forms
of protein engineering, such as
directed evolution, where a variety of methods are used to find proteins that achieve a specific function, and with
protein structure prediction where the sequence is known, but the structure is unknown.
Most often, the target structure is based on a known structure of
another protein. However, novel folds not seen in nature have been made
increasingly possible. Peter S. Kim and coworkers designed trimers and
tetramers of unnatural coiled coils, which had not been seen before in
nature.
[4][5] The protein Top7, developed in
David Baker's lab, was designed completely using protein design algorithms, to a completely novel fold.
[6] More recently, Baker and coworkers developed a series of principles to design ideal
globular-protein structures based on
protein folding funnels
that bridge between secondary structure prediction and tertiary
structures. These principles, which build on both protein structure
prediction and protein design, were used to design five different novel
protein topologies.
[9]
Sequence space
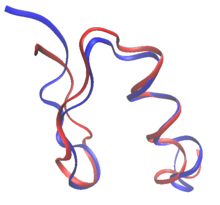
FSD-1 (shown in blue, PDB id: 1FSV) was the first
de novo computational design of a full protein.
[3]
The target fold was that of the zinc finger in residues 33–60 of the
structure of protein Zif268 (shown in red, PDB id: 1ZAA). The designed
sequence had very little sequence identity with any known protein
sequence.
In rational protein design, proteins can be redesigned from the
sequence and structure of a known protein, or completely from scratch in
de novo protein design. In protein redesign, most of the
residues in the sequence are maintained as their wild-type amino-acid
while a few are allowed to mutate. In
de novo design, the entire sequence is designed anew, based on no prior sequence.
Both
de novo designs and protein redesigns can establish rules on the
sequence space:
the specific amino acids that are allowed at each mutable residue
position. For example, the composition of the surface of the
RSC3 probe
to select HIV-broadly neutralizing antibodies was restricted based on
evolutionary data and charge balancing. Many of the earliest attempts on
protein design were heavily based on empiric
rules on the sequence space.
[2] Moreover, the
design of fibrous proteins usually follows strict rules on the sequence space.
Collagen-based designed proteins, for example, are often composed of Gly-Pro-X repeating patterns.
[2] The advent of computational techniques allows designing proteins with no human intervention in sequence selection.
[3]
Structural flexibility
Common protein design programs use rotamer libraries to simplify the
conformational space of protein side chains. This animation loops
through all the rotamers of the isoleucine amino acid based on the
Penultimate Rotamer Library.
[10]
In protein design, the target structure (or structures) of the
protein are known. However, a rational protein design approach must
model some
flexibility on the target structure in order to
increase the number of sequences that can be designed for that structure
and to minimize the chance of a sequence folding to a different
structure. For example, in a protein redesign of one small amino acid
(such as alanine) in the tightly packed core of a protein, very few
mutants would be predicted by a rational design approach to fold to the
target structure, if the surrounding side-chains are not allowed to be
repacked.
Thus, an essential parameter of any design process is the amount of
flexibility allowed for both the side-chains and the backbone. In the
simplest models, the protein backbone is kept rigid while some of the
protein side-chains are allowed to change conformations. However,
side-chains can have many degrees of freedom in their bond lengths, bond
angles, and
χ dihedral angles.
To simplify this space, protein design methods use rotamer libraries
that assume ideal values for bond lengths and bond angles, while
restricting
χ dihedral angles to a few oft-observed low-energy conformations termed
rotamers.
Rotamer libraries describe rotamers based on an analysis of many
protein structures. Backbone-independent rotamer libraries describe all
rotamers.
[10]
Backbone-dependent rotamer libraries, in contrast, describe the
rotamers as how likely they are to appear depending on the protein
backbone arrangement around the side chain.
[11]
The rotamers described by rotamer libraries are usually regions in
space. Most protein design programs use one conformation (e.g., the
modal value for rotamer dihedrals in space) or several points in the
region described by the rotamer; the
OSPREY protein design program, in contrast, models the entire continuous region.
[12]
Although rational protein design must preserve the general backbone
fold a protein, allowing some backbone flexibility can significantly
increase the number of sequences that fold to the structure while
maintaining the general fold of the protein.
[13]
Backbone flexibility is especially important in protein redesign
because sequence mutations often result in small changes to the backbone
structure. Moreover, backbone flexibility can be essential for more
advanced applications of protein design, such as binding prediction and
enzyme design. Some models of protein design backbone flexibility
include small and continuous global backbone movements, discrete
backbone samples around the target fold, backrub motions, and protein
loop flexibility.
[13][14]
Energy function
Comparison of various potential energy functions. The most accurate
energy are those that use quantum mechanical calculations, but these are
too slow for protein design. On the other extreme, heuristic energy
functions, are based on statistical terms and are very fast. In the
middle are molecular mechanics energy functions that are
physically-based but are not as computationally expensive as quantum
mechanical simulations.
[15]
Rational protein design techniques must be able to discriminate
sequences that will be stable under the target fold from those that
would prefer other low-energy competing states. Thus, protein design
requires accurate
energy functions
that can rank and score sequences by how well they fold to the target
structure. At the same time, however, these energy functions must
consider the computational
challenges
behind protein design. One of the most challenging requirements for
successful design is an energy function that is both accurate and simple
for computational calculations.
The most accurate energy functions are those based on quantum
mechanical simulations. However, such simulations are too slow and
typically impractical for protein design. Instead, many protein design
algorithms use either physics-based energy functions adapted from
molecular mechanics simulation programs,
knowledge based energy-functions, or a hybrid mix of both. The trend has been toward using more physics-based potential energy functions.
[15]
Physics-based energy functions, such as
AMBER and
CHARMM,
are typically derived from quantum mechanical simulations, and
experimental data from thermodynamics, crystallography, and
spectroscopy.
[16]
These energy functions typically simplify physical energy function and
make them pairwise decomposable, meaning that the total energy of a
protein conformation can be calculated by adding the pairwise energy
between each atom pair, which makes them attractive for optimization
algorithms. Physics-based energy functions typically model an
attractive-repulsive
Lennard-Jones term between atoms and a pairwise
electrostatics coulombic term
[17] between non-bonded atoms.
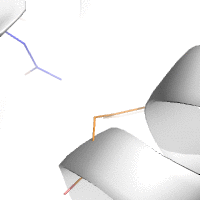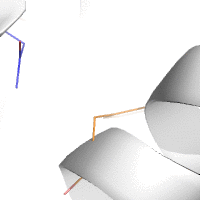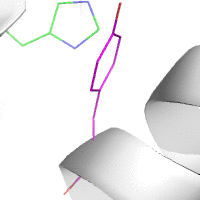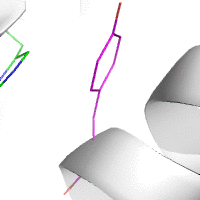
Water-mediated hydrogen bonds play a key role in protein–protein
binding. One such interaction is shown between residues D457, S365 in
the heavy chain of the HIV-broadly-neutralizing antibody VRC01 (green)
and residues N58 and Y59 in the HIV envelope protein GP120 (purple).
[18]
Statistical potentials, in contrast to physics-based potentials, have
the advantage of being fast to compute, of accounting implicitly of
complex effects and being less sensitive to small changes in the protein
structure.
[19] These energy functions are
based on deriving energy values from frequency of appearance on a structural database.
Protein design, however, has requirements that can sometimes be
limited in molecular mechanics force-fields. Molecular mechanics
force-fields, which have been used mostly in molecular dynamics
simulations, are optimized for the simulation of single sequences, but
protein design searches through many conformations of many sequences.
Thus, molecular mechanics force-fields must be tailored for protein
design. In practice, protein design energy functions often incorporate
both statistical terms and physics-based terms. For example, the Rosetta
energy function, one of the most-used energy functions, incorporates
physics-based energy terms originating in the CHARMM energy function,
and statistical energy terms, such as rotamer probability and
knowledge-based electrostatics. Typically, energy functions are highly
customized between laboratories, and specifically tailored for every
design.
[16]
Challenges for effective design energy functions
Water
makes up most of the molecules surrounding proteins and is the main
driver of protein structure. Thus, modeling the interaction between
water and protein is vital in protein design. The number of water
molecules that interact with a protein at any given time is huge and
each one has a large number of degrees of freedom and interaction
partners. Instead, protein design programs model most of such water
molecules as a continuum, modeling both the hydrophobic effect and
solvation polarization.
[16]
Individual water molecules can sometimes have a crucial structural
role in the core of proteins, and in protein–protein or protein–ligand
interactions. Failing to model such waters can result in mispredictions
of the optimal sequence of a protein–protein interface. As an
alternative, water molecules can be added to rotamers.
As an optimization problem
This animation illustrates the complexity of a protein design search,
which typically compares all the rotamer-conformations from all possible
mutations at all residues. In this example, the residues Phe36 and His
106 are allowed to mutate to, respectively, the amino acids Tyr and Asn.
Phe and Tyr have 4 rotamers each in the rotamer library, while Asn and
His have 7 and 8 rotamers, respectively, in the rotamer library (from
the Richardson's penultimate rotamer library
[10]).
The animation loops through all (4 + 4) x (7 + 8) = 120 possibilities.
The structure shown is that of myoglobin, PDB id: 1mbn.
The goal of protein design is to find a protein sequence that will
fold to a target structure. A protein design algorithm must, thus,
search all the conformations of each sequence, with respect to the
target fold, and rank sequences according to the lowest-energy
conformation of each one, as determined by the protein design energy
function. Thus, a typical input to the protein design algorithm is the
target fold, the sequence space, the structural flexibility, and the
energy function, while the output is one or more sequences that are
predicted to fold stably to the target structure.
The number of candidate protein sequences, however, grows
exponentially with the number of protein residues; for example, there
are 20
100 protein sequences of length 100. Furthermore, even if amino acid side-chain conformations are limited to a few rotamers (see
Structural flexibility),
this results in an exponential number of conformations for each
sequence. Thus, in our 100 residue protein, and assuming that each amino
acid has exactly 10 rotamers, a search algorithm that searches this
space will have to search over 200
100 protein conformations.
The most common energy functions can be decomposed into pairwise
terms between rotamers and amino acid types, which casts the problem as a
combinatorial one, and powerful optimization algorithms can be used to
solve it. In those cases, the total energy of each conformation
belonging to each sequence can be formulated as a sum of individual and
pairwise terms between residue positions. If a designer is interested
only in the best sequence, the protein design algorithm only requires
the lowest-energy conformation of the lowest-energy sequence. In these
cases, the amino acid identity of each rotamer can be ignored and all
rotamers belonging to different amino acids can be treated the same. Let
ri be a rotamer at residue position
i in the protein chain, and
E(r
i) the potential energy between the internal atoms of the rotamer. Let
E(
ri,
rj) be the potential energy between
ri and rotamer
rj at residue position
j. Then, we define the optimization problem as one of finding the conformation of minimum energy (
ET):
![\min E_{{T}}=\sum _{{i}}{\Big [}E_{i}(r_{i})+\sum _{{i\neq j}}E_{{ij}}(r_{i},r_{j}){\Big ]}\,](https://wikimedia.org/api/rest_v1/media/math/render/svg/3332d826843218136390cef20e4ee8e3694fc477)
|
|
(1)
|
The problem of minimizing
ET is an
NP-hard problem.
[14][20][21]
Even though the class of problems is NP-hard, in practice many
instances of protein design can be solved exactly or optimized
satisfactorily through heuristic methods.
Algorithms
Several
algorithms have been developed specifically for the protein design
problem. These algorithms can be divided into two broad classes: exact
algorithms, such as
dead-end elimination, that lack
runtime guarantees but guarantee the quality of the solution; and
heuristic
algorithms, such as Monte Carlo, that are faster than exact algorithms
but have no guarantees on the optimality of the results. Exact
algorithms guarantee that the optimization process produced the optimal
according to the protein design model. Thus, if the predictions of exact
algorithms fail when these are experimentally validated, then the
source of error can be attributed to the energy function, the allowed
flexibility, the sequence space or the target structure.
Some protein design algorithms are listed below. Although these
algorithms address only the most basic formulation of the protein design
problem, Equation (
1),
when the optimization goal changes because designers introduce
improvements and extensions to the protein design model, such as
improvements to the structural flexibility allowed (e.g., protein
backbone flexibility) or including sophisticated energy terms, many of
the extensions on protein design that improve modeling are built atop
these algorithms. For example, Rosetta Design incorporates sophisticated
energy terms, and backbone flexibility using Monte Carlo as the
underlying optimizing algorithm. OSPREY's algorithms build on the
dead-end elimination algorithm and A* to incorporate continuous backbone
and side-chain movements. Thus, these algorithms provide a good
perspective on the different kinds of algorithms available for protein
design.
With mathematical guarantees
Dead-end elimination
The dead-end elimination (DEE) algorithm reduces the search space of
the problem iteratively by removing rotamers that can be provably shown
to be not part of the global lowest energy conformation (GMEC). On each
iteration, the dead-end elimination algorithm compares all possible
pairs of rotamers at each residue position, and removes each rotamer
r′i that can be shown to always be of higher energy than another rotamer
ri and is thus not part of the GMEC:

Other powerful extensions to the dead-end elimination algorithm include the
pairs elimination criterion, and the
generalized dead-end elimination criterion. This algorithm has also been extended to handle continuous rotamers with provable guarantees.
Although the Dead-end elimination algorithm runs in polynomial time
on each iteration, it cannot guarantee convergence. If, after a certain
number of iterations, the dead-end elimination algorithm does not prune
any more rotamers, then either rotamers have to be merged or another
search algorithm must be used to search the remaining search space. In
such cases, the dead-end elimination acts as a pre-filtering algorithm
to reduce the search space, while other algorithms, such as A*, Monte
Carlo, Linear Programming, or FASTER are used to search the remaining
search space.
[14]
Branch and bound
The protein design conformational space can be represented as a
tree, where the protein residues are ordered in an arbitrary way, and the tree branches at each of the rotamers in a residue.
Branch and bound algorithms use this representation to efficiently explore the conformation tree: At each
branching, branch and bound algorithms
bound the conformation space and explore only the promising branches.
[14][23][24]
A popular search algorithm for protein design is the
A* search algorithm.
[14][24]
A* computes a lower-bound score on each partial tree path that lower
bounds (with guarantees) the energy of each of the expanded rotamers.
Each partial conformation is added to a priority queue and at each
iteration the partial path with the lowest lower bound is popped from
the queue and expanded. The algorithm stops once a full conformation has
been enumerated and guarantees that the conformation is the optimal.
The A* score
f in protein design consists of two parts,
f=g+h.
g is the exact energy of the rotamers that have already been assigned in the partial conformation.
h is a lower bound on the energy of the rotamers that have not yet been assigned. Each is designed as follows, where
d is the index of the last assigned residue in the partial conformation.

![h=\sum _{{j=d+1}}^{n}[\min _{{r_{j}}}(E(r_{j})+\sum _{{i=1}}^{d}E(r_{i},r_{j})+\sum _{{k=j+1}}^{n}\min _{{r_{k}}}E(r_{j},r_{k}))]](https://wikimedia.org/api/rest_v1/media/math/render/svg/e143d714d94f81766d65c1ab49da42eeeed08b4a)
Integer linear programming
The problem of optimizing
ET (Equation (
1)) can be easily formulated as an
integer linear program (ILP).
[25]
One of the most powerful formulations uses binary variables to
represent the presence of a rotamer and edges in the final solution, and
constraints the solution to have exactly one rotamer for each residue
and one pairwise interaction for each pair of residues:

s.t.



ILP solvers, such as
CPLEX, can compute the exact optimal solution for large instances of protein design problems. These solvers use a
linear programming relaxation of the problem, where
qi and
qij are allowed to take continuous values, in combination with a
branch and cut
algorithm to search only a small portion of the conformation space for
the optimal solution. ILP solvers have been shown to solve many
instances of the side-chain placement problem.
[25]
Message-passing based approximations to the linear programming dual
ILP solvers depend on linear programming (LP) algorithms, such as the
Simplex or
barrier-based
methods to perform the LP relaxation at each branch. These LP
algorithms were developed as general-purpose optimization methods and
are not optimized for the protein design problem (Equation (
1)). In consequence, the LP relaxation becomes the bottleneck of ILP solvers when the problem size is large.
[26] Recently, several alternatives based on
message-passing algorithms
have been designed specifically for the optimization of the LP
relaxation of the protein design problem. These algorithms can
approximate both the
dual or the
primal
instances of the integer programming, but in order to maintain
guarantees on optimality, they are most useful when used to approximate
the dual of the protein design problem, because approximating the dual
guarantees that no solutions are missed. Message-passing based
approximations include the
tree reweighted max-product message passing algorithm,
[27][28] and the
message passing linear programming algorithm.
[29]
Optimization algorithms without guarantees
Monte Carlo and simulated annealing
Monte
Carlo is one of the most widely used algorithms for protein design. In
its simplest form, a Monte Carlo algorithm selects a residue at random,
and in that residue a randomly chosen rotamer (of any amino acid) is
evaluated.
[21] The new energy of the protein,
Enew is compared against the old energy
Eold and the new rotamer is
accepted with a probability of:

where
β is the
Boltzmann constant and the temperature
T can be chosen such that in the initial rounds it is high and it is slowly
annealed to overcome local minima.
[12]
FASTER
The
FASTER algorithm uses a combination of deterministic and stochastic
criteria to optimize amino acid sequences. FASTER first uses DEE to
eliminate rotamers that are not part of the optimal solution. Then, a
series of iterative steps optimize the rotamer assignment.
[30][31]
Belief propagation
In
belief propagation for protein design, the algorithm exchanges messages that describe the
belief
that each residue has about the probability of each rotamer in
neighboring residues. The algorithm updates messages on every iteration
and iterates until convergence or until a fixed number of iterations.
Convergence is not guaranteed in protein design. The message
mi→ j(rj that a residue
i sends to every rotamer
(rj at neighboring residue
j is defined as:

Both max-product and sum-product belief propagation have been used to optimize protein design.
Applications and examples of designed proteins
Enzyme design
The design of new
enzymes
is a use of protein design with huge bioengineering and biomedical
applications. In general, designing a protein structure can be different
from designing an enzyme, because the design of enzymes must consider
many states involved in the
catalytic mechanism. However protein design is a prerequisite of
de novo
enzyme design because, at the very least, the design of catalysts
requires a scaffold in which the catalytic mechanism can be inserted.
[32]
Great progress in
de novo enzyme design, and redesign, was
made in the first decade of the 21st century. In three major studies,
David Baker and coworkers
de novo designed enzymes for the retro-
aldol reaction,
[33] a Kemp-elimination reaction,
[34] and for the
Diels-Alder reaction.
[35]
Furthermore, Stephen Mayo and coworkers developed an iterative method
to design the most efficient known enzyme for the Kemp-elimination
reaction.
[36] Also, in the laboratory of
Bruce Donald, computational protein design was used to switch the specificity of one of the
protein domains of the
nonribosomal peptide synthetase that produces
Gramicidin S, from its natural substrate
phenylalanine
to other noncognate substrates including charged amino acids; the
redesigned enzymes had activities close to those of the wild-type.
[37]
Design for affinity
Protein–protein interactions are involved in most biotic processes. Many of the hardest-to-treat diseases, such as
Alzheimer's, many forms of
cancer (e.g.,
TP53), and human immunodeficiency virus (
HIV)
infection involve protein–protein interactions. Thus, to treat such
diseases, it is desirable to design protein or protein-like therapeutics
that bind one of the partners of the interaction and, thus, disrupt the
disease-causing interaction. This requires designing
protein-therapeutics for
affinity toward its partner.
Protein–protein interactions can be designed using protein design
algorithms because the principles that rule protein stability also rule
protein–protein binding. Protein–protein interaction design, however,
presents challenges not commonly present in protein design. One of the
most important challenges is that, in general, the interfaces between
proteins are more polar than protein cores, and binding involves a
tradeoff between desolvation and hydrogen bond formation.
[38]
To overcome this challenge, Bruce Tidor and coworkers developed a
method to improve the affinity of antibodies by focusing on
electrostatic contributions. They found that, for the antibodies
designed in the study, reducing the desolvation costs of the residues in
the interface increased the affinity of the binding pair.
[38][39][40]
Scoring binding predictions
Protein
design energy functions must be adapted to score binding predictions
because binding involves a trade-off between the lowest-
energy conformations of the free proteins (
EP and
EL) and the lowest-energy conformation of the bound complex (
EPL):

.
The K* algorithm approximates the binding constant of the algorithm
by including conformational entropy into the free energy calculation.
The K* algorithm considers only the lowest-energy conformations of the
free and bound complexes (denoted by the sets
P,
L, and
PL) to approximate the partition functions of each complex:
[14]

Design for specificity
The
design of protein–protein interactions must be highly specific because
proteins can interact with a large number of proteins; successful design
requires selective binders. Thus, protein design algorithms must be
able to distinguish between on-target (or
positive design) and off-target binding (or
negative design).
[2][38] One of the most prominent examples of design for specificity is the design of specific
bZIP-binding
peptides by Amy Keating and coworkers for 19 out of the 20 bZIP
families; 8 of these peptides were specific for their intended partner
over competing peptides.
[38][41][42] Further, positive and negative design was also used by Anderson and
coworkers to predict mutations in the active site of a drug target that
conferred resistance to a new drug; positive design was used to maintain
wild-type activity, while negative design was used to disrupt binding
of the drug.
[43] Recent computational redesign by Costas Maranas and coworkers was also capable of experimentally switching the
cofactor specificity of
Candida boidinii xylose reductase from
NADPH to
NADH.
[44]
Protein resurfacing
Protein
resurfacing consists of designing a protein's surface while preserving
the overall fold, core, and boundary regions of the protein intact.
Protein resurfacing is especially useful to alter the binding of a
protein to other proteins. One of the most important applications of
protein resurfacing was the design of the RSC3 probe to select broadly
neutralizing HIV antibodies at the NIH Vaccine Research Center. First,
residues outside of the binding interface between the gp120 HIV envelope
protein and the formerly discovered b12-antibody were selected to be
designed. Then, the sequence spaced was selected based on evolutionary
information, solubility, similarity with the wild-type, and other
considerations. Then the RosettaDesign software was used to find optimal
sequences in the selected sequence space. RSC3 was later used to
discover the broadly neutralizing antibody VRC01 in the serum of a
long-term HIV-infected non-progressor individual.
[45]
Design of globular proteins
Globular proteins
are proteins that contain a hydrophobic core and a hydrophilic surface.
Globular proteins often assume a stable structure, unlike
fibrous proteins,
which have multiple conformations. The three-dimensional structure of
globular proteins is typically easier to determine through
X-ray crystallography and
nuclear magnetic resonance than both fibrous proteins and
membrane proteins,
which makes globular proteins more attractive for protein design than
the other types of proteins. Most successful protein designs have
involved globular proteins. Both
RSD-1, and
Top7 were
de novo
designs of globular proteins. Five more protein structures were
designed, synthesized, and verified in 2012 by the Baker group. These
new proteins serve no biotic function, but the structures are intended
to act as building-blocks that can be expanded to incorporate functional
active sites. The structures were found computationally by using new
heuristics based on analyzing the connecting loops between parts of the
sequence that specify secondary structures.
[46]
Design of transmembrane proteins
Membrane
proteins are inherently hard to design, in large part because it is
hard to validate the designs experimentally for several reasons.
Membrane proteins are hard to purify. Their structure is hard to
characterize because they adopt their native conformation only in the
presence of a membrane. Crystallization is inherently hard, and NMR
studies of membrane proteins can fail because of their size.
Design of fibrous proteins
Fibrous proteins, such as
elastin or
collagen,
typically have no one structure. However, such proteins likely lack
random folds, and instead have folds defined within an ensemble of
structures. This ensemble defines their behavior. Thus, in theory it is
possible to rationally design fibrous proteins by selecting a sequence
that will populate a specific ensemble.
Other applications
One of the most desirable uses for protein design is for
biosensors,
proteins that will sense the presence of specific compounds. Some
attempts in the design of biosensors include sensors for unnatural
molecules including
TNT.
[47] More recently, Kuhlman and coworkers designed a biosensor of the
PAK1.
[48]




![\min E_{{T}}=\sum _{{i}}{\Big [}E_{i}(r_{i})+\sum _{{i\neq j}}E_{{ij}}(r_{i},r_{j}){\Big ]}\,](https://wikimedia.org/api/rest_v1/media/math/render/svg/3332d826843218136390cef20e4ee8e3694fc477)






