Artificial life

From Wikipedia, the free encyclopedia

Artificial life (often abbreviated ALife or A-Life) is a field of study wherein researchers examine systems related to natural life, its processes, and its evolution, through the use of simulations with computer models, robotics, and biochemistry.^[1] The discipline was named by Christopher Langton, an American theoretical biologist, in 1986.^[2] There are three main kinds of alife,^[3] named for their approaches: soft,^[4] from software; hard,^[5] from hardware; and wet, from biochemistry. Artificial life researchers study traditional biology by trying to recreate aspects of biological phenomena.

A Braitenberg vehicle simulation, programmed in breve, an artificial life simulator

Overview

Artificial life studies the fundamental processes of living systems in artificial environments in order to gain a deeper understanding of the complex information processing that define such systems. These topics are broad, but often include evolutionary dynamics, emergent properties of collective systems, biomimicry, as well as related issues about the philosophy of the nature of life and the use of lifelike properties in artistic works.

Philosophy

The modeling philosophy of artificial life strongly differs from traditional modeling by studying not only "life-as-we-know-it" but also "life-as-it-might-be".^[8]

A traditional model of a biological system will focus on capturing its most important parameters. In contrast, an alife modeling approach will generally seek to decipher the most simple and general principles underlying life and implement them in a simulation. The simulation then offers the possibility to analyse new and different lifelike systems.

Vladimir Georgievich Red'ko proposed to generalize this distinction to the modeling of any process, leading to the more general distinction of "processes-as-we-know-them" and "processes-as-they-could-be".^[9]

At present, the commonly accepted definition of life does not consider any current alife simulations or software to be alive, and they do not constitute part of the evolutionary process of any ecosystem. However, different opinions about artificial life's potential have arisen:

• The strong alife (cf. Strong AI) position states that "life is a process which can be abstracted away from any particular medium" (John von Neumann)^{[citation needed]}. Notably, Tom Ray declared that his program Tierra is not simulating life in a computer but synthesizing it.^[10]
• The weak alife position denies the possibility of generating a "living process" outside of a chemical solution. Its researchers try instead to simulate life processes to understand the underlying mechanics of biological phenomena.

Organizations

Software-based ("soft")

Techniques

• Cellular automata were used in the early days of artificial life, and are still often used for ease of scalability and parallelization. Alife and cellular automata share a closely tied history.
• Artificial neural networks are sometimes used to model the brain of an agent. Although traditionally more of an artificial intelligence technique, neural nets can be important for simulating population dynamics of organisms that can learn. The symbiosis between learning and evolution is central to theories about the development of instincts in organisms with higher neurological complexity, as in, for instance, the Baldwin effect.

Notable simulators

This is a list of artificial life/digital organism simulators, organized by the method of creature definition.

Name	Driven By	Started	Ended
Avida	executable DNA	1993	ongoing
Neurokernel	Geppetto	2014	ongoing
Creatures	neural net/simulated biochemistry	1996-2001	Fandom still active to this day, some abortive attempts at new products
Critterding	neural net	2005	ongoing
Darwinbots	executable DNA	2003	ongoing
DigiHive	executable DNA	2006	2009
DOSE	executable DNA	2012	ongoing
EcoSim	Fuzzy Cognitive Map	2009	ongoing
Evolve 4.0	executable DNA	1996	Prior to Nov. 2014
Framsticks	executable DNA	1996	ongoing
Noble Ape	neural net	1996	ongoing
OpenWorm	Geppetto	2011	ongoing
Polyworld	neural net	1990	ongoing
Primordial Life	executable DNA	1994	2003
ScriptBots	executable DNA	2010	ongoing
TechnoSphere	modules	1995
Tierra	executable DNA	1991	2004
3D Virtual Creature Evolution	neural net	2008	NA

Program-based

Program-based simulations contain organisms with a complex DNA language, usually Turing complete. This language is more often in the form of a computer program than actual biological DNA. Assembly derivatives are the most common languages used. An organism "lives" when its code is executed, and there are usually various methods allowing self-replication. Mutations are generally implemented as random changes to the code. Use of cellular automata is common but not required. Another example could be an artificial intelligence and multi-agent system/program.

Module-based

Individual modules are added to a creature. These modules modify the creature's behaviors and characteristics either directly, by hard coding into the simulation (leg type A increases speed and metabolism), or indirectly, through the emergent interactions between a creature's modules (leg type A moves up and down with a frequency of X, which interacts with other legs to create motion). Generally these are simulators which emphasize user creation and accessibility over mutation and evolution.

Parameter-based

Organisms are generally constructed with pre-defined and fixed behaviors that are controlled by various parameters that mutate. That is, each organism contains a collection of numbers or other finite parameters. Each parameter controls one or several aspects of an organism in a well-defined way.

Neural net–based

These simulations have creatures that learn and grow using neural nets or a close derivative. Emphasis is often, although not always, more on learning than on natural selection.

Complex systems modelling

Mathematical models of complex systems are of three types: black-box (phenomenological), white-box (mechanistic, based on the first principles) and grey-box (mixtures of phenomenological and mechanistic models) ^[11][12]. In black-box models, the individual-based (mechanistic) mechanisms of a complex dynamic system remain hidden.

Mathematical models for complex systems

Black-box models are completely nonmechanistic. They are phenomenological and ignore a composition and internal structure of a complex system. We cannot investigate interactions of subsystems of such a non-transparent model. A white-box model of complex dynamic system has ‘transparent walls’ and directly shows underlying mechanisms. All events at micro-, meso- and macro-levels of a dynamic system are directly visible at all stages of its white-box model evolution. In most cases mathematical modelers use the heavy black-box mathematical methods, which cannot produce mechanistic models of complex dynamic systems. Grey-box models are intermediate and combine black-box and white-box approaches.

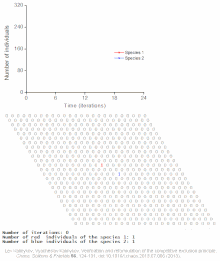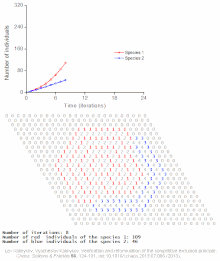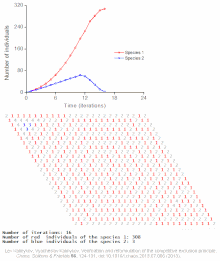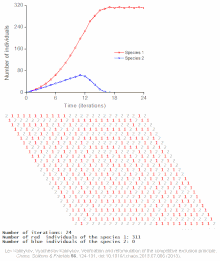
Logical deterministic individual-based cellular automata model of single species population growth

Creation of a white-box model of complex system is associated with the problem of the necessity of an a priori basic knowledge of the modeling subject. The deterministic logical cellular automata are necessary but not sufficient condition of a white-box model. The second necessary prerequisite of a white-box model is the presence of the physical ontology of the object under study. The white-box modeling represents an automatic hyper-logical inference from the first principles because it is completely based on the deterministic logic and axiomatic theory of the subject. The purpose of the white-box modeling is to derive from the basic axioms a more detailed, more concrete mechanistic knowledge about the dynamics of the object under study. The necessity to formulate an intrinsic axiomatic system of the subject before creating its white-box model distinguishes the cellular automata models of white-box type from cellular automata models based on arbitrary logical rules. If cellular automata rules have not been formulated from the first principles of the subject, then such a model may have a weak relevance to the real problem ^[12].

Logical deterministic individual-based cellular automata model of interspecific competition for a single limited resource

Hardware-based ("hard")

Hardware-based artificial life mainly consist of robots, that is, automatically guided machines able to do tasks on their own.

Biochemical-based ("wet")

Biochemical-based life is studied in the field of synthetic biology. It involves e.g. the creation of synthetic DNA. The term "wet" is an extension of the term "wetware".

Open problems

How does life arise from the nonliving?^[13][14]

• Generate a molecular proto-organism in vitro.
• Achieve the transition to life in an artificial chemistry in silico.
• Determine whether fundamentally novel living organizations can exist.
• Simulate a unicellular organism over its entire life cycle.
• Explain how rules and symbols are generated from physical dynamics in living systems.

What are the potentials and limits of living systems?

• Determine what is inevitable in the open-ended evolution of life.
• Determine minimal conditions for evolutionary transitions from specific to generic response systems.
• Create a formal framework for synthesizing dynamical hierarchies at all scales.
• Determine the predictability of evolutionary consequences of manipulating organisms and ecosystems.
• Develop a theory of information processing, information flow, and information generation for evolving systems.

How is life related to mind, machines, and culture?

• Demonstrate the emergence of intelligence and mind in an artificial living system.
• Evaluate the influence of machines on the next major evolutionary transition of life.
• Provide a quantitative model of the interplay between cultural and biological evolution.
• Establish ethical principles for artificial life.

Related subjects

1. Artificial intelligence has traditionally used a top down approach, while alife generally works from the bottom up.^[15]
2. Artificial chemistry started as a method within the alife community to abstract the processes of chemical reactions.
3. Evolutionary algorithms are a practical application of the weak alife principle applied to optimization problems. Many optimization algorithms have been crafted which borrow from or closely mirror alife techniques. The primary difference lies in explicitly defining the fitness of an agent by its ability to solve a problem, instead of its ability to find food, reproduce, or avoid death.^{[citation needed]} The following is a list of evolutionary algorithms closely related to and used in alife:
   • Ant colony optimization
   • Bacterial colony optimization
   • Genetic algorithm
   • Genetic programming
   • Swarm intelligence
4. Multi-agent system – A multi-agent system is a computerized system composed of multiple interacting intelligent agents within an environment.
5. Evolutionary art uses techniques and methods from artificial life to create new forms of art.
6. Evolutionary music uses similar techniques, but applied to music instead of visual art.
7. Abiogenesis and the origin of life sometimes employ alife methodologies as well.

Criticism

Alife has had a controversial history. John Maynard Smith criticized certain artificial life work in 1994 as "fact-free science".^[16]

Fuzzy logic

From Wikipedia, the free encyclopedia

Fuzzy logic is a form of many-valued logic in which the truth values of variables may be any real number between 0 and 1. It is employed to handle the concept of partial truth, where the truth value may range between completely true and completely false.^[1] By contrast, in Boolean logic, the truth values of variables may only be the integer values 0 or 1.

The term fuzzy logic was introduced with the 1965 proposal of fuzzy set theory by Lotfi Zadeh.^[2][3] Fuzzy logic had however been studied since the 1920s, as infinite-valued logic—notably by Łukasiewicz and Tarski.^[4]

Fuzzy logic has been applied to many fields, from control theory to artificial intelligence.

Overview

Classical logic only permits conclusions which are either true or false. However, there are also propositions with variable answers, such as one might find when asking a group of people to identify a color. In such instances, the truth appears as the result of reasoning from inexact or partial knowledge in which the sampled answers are mapped on a spectrum.^{[citation needed]}

Both degrees of truth and probabilities range between 0 and 1 and hence may seem similar at first, but fuzzy logic uses degrees of truth as a mathematical model of vagueness, while probability is a mathematical model of ignorance.^{[citation needed]}

Applying truth values

A basic application might characterize various sub-ranges of a continuous variable. For instance, a temperature measurement for anti-lock brakes might have several separate membership functions defining particular temperature ranges needed to control the brakes properly. Each function maps the same temperature value to a truth value in the 0 to 1 range. These truth values can then be used to determine how the brakes should be controlled.^{[citation needed]}

Linguistic variables

While variables in mathematics usually take numerical values, in fuzzy logic applications, non-numeric values are often used to facilitate the expression of rules and facts.^[5]

A linguistic variable such as age may accept values such as young and its antonym old. Because natural languages do not always contain enough value terms to express a fuzzy value scale, it is common practice to modify linguistic values with adjectives or adverbs. For example, we can use the hedges rather and somewhat to construct the additional values rather old or somewhat young.

Fuzzification operations can map mathematical input values into fuzzy membership functions. And the opposite de-fuzzifying operations can be used to map a fuzzy output membership functions into a "crisp" output value that can be then used for decision or control purposes.

Process

1. Fuzzify all input values into fuzzy membership functions.
2. Execute all applicable rules in the rulebase to compute the fuzzy output functions.
3. De-fuzzify the fuzzy output functions to get "crisp" output values.

Fuzzification

Fuzzy logic temperature

In this image, the meanings of the expressions cold, warm, and hot are represented by functions mapping a temperature scale. A point on that scale has three "truth values"—one for each of the three functions. The vertical line in the image represents a particular temperature that the three arrows (truth values) gauge. Since the red arrow points to zero, this temperature may be interpreted as "not hot". The orange arrow (pointing at 0.2) may describe it as "slightly warm" and the blue arrow (pointing at 0.8) "fairly cold".

Fuzzy sets are often defined as triangle or trapezoid-shaped curves, as each value will have a slope where the value is increasing, a peak where the value is equal to 1 (which can have a length of 0 or greater) and a slope where the value is decreasing.^{[citation needed]} They can also be defined using a sigmoid function.^[6] One common case is the standard logistic function defined as

${\displaystyle S(x)={\frac {1}{1+e^{-x}}}}$

which has the following symmetry property

$${\displaystyle S(x)+S(-x)=1}$$

From this it follows that

$${\displaystyle (S(x)+S(-x))\cdot (S(y)+S(-y))\cdot (S(z)+S(-z))=1}$$

Fuzzy logic operators

Fuzzy logic works with membership values in a way that mimics Boolean logic.^{[citation needed]}

To this end, replacements for basic operators AND, OR, NOT must be available. There are several ways to this. A common replacement is called the Zadeh operators:

Boolean	Fuzzy
AND(x,y)	MIN(x,y)
OR(x,y)	MAX(x,y)
NOT(x)	1 – x

For TRUE/1 and FALSE/0, the fuzzy expressions produce the same result as the Boolean expressions.

There are also other operators, more linguistic in nature, called hedges that can be applied. These are generally adverbs such as very, or somewhat, which modify the meaning of a set using a mathematical formula.

However, an arbitrary choice table does not always define a fuzzy logic function. In the paper,^[7] a criterion has been formulated to recognize whether a given choice table defines a fuzzy logic function and a simple algorithm of fuzzy logic function synthesis has been proposed based on introduced concepts of constituents of minimum and maximum. A fuzzy logic function represents a disjunction of constituents of minimum, where a constituent of minimum is a conjunction of variables of the current area greater than or equal to the function value in this area (to the right of the function value in the inequality, including the function value).

Another set of AND/OR operators is based on multiplication

x AND y = x*y
x OR y = 1-(1-x)*(1-y) = x+y-x*y

1-(1-x)*(1-y) comes from this:

x OR y = NOT( AND( NOT(x), NOT(y) ) )
x OR y = NOT( AND(1-x, 1-y) )
x OR y = NOT( (1-x)*(1-y) )
x OR y = 1-(1-x)*(1-y)

IF-THEN rules

IF-THEN rules map input or computed truth values to desired output truth values. Example:

IF temperature IS very cold THEN fan_speed is stopped
IF temperature IS cold THEN fan_speed is slow
IF temperature IS warm THEN fan_speed is moderate
IF temperature IS hot THEN fan_speed is high

Given a certain temperature, the fuzzy variable hot has a certain truth value, which is copied to the high variable.

Should an output variable occur in several THEN parts, then the values from the respective IF parts are combined using the OR operator.

Defuzzification

The goal is to get a continuous variable from fuzzy truth values.^{[citation needed]}
This would be easy if the output truth values were exactly those obtained from fuzzification of a given number. Since, however, all output truth values are computed independently, in most cases they do not represent such a set of numbers.^{[citation needed]} One has then to decide for a number that matches best the "intention" encoded in the truth value. For example, for several truth values of fan_speed, an actual speed must be found that best fits the computed truth values of the variables 'slow', 'medium' and so on.^{[citation needed]}

There is no single algorithm for this purpose.

A common algorithm is

1. For each truth value, cut the membership function at this value
2. Combine the resulting curves using the OR operator
3. Find the center-of-weight of the area under the curve
4. The x position of this center is then the final output.

Forming a consensus of inputs and fuzzy rules

Since the fuzzy system output is a consensus of all of the inputs and all of the rules, fuzzy logic systems can be well behaved when input values are not available or are not trustworthy. Weightings can be optionally added to each rule in the rulebase and weightings can be used to regulate the degree to which a rule affects the output values. These rule weightings can be based upon the priority, reliability or consistency of each rule. These rule weightings may be static or can be changed dynamically, even based upon the output from other rules.

Early applications

Many of the early successful applications of fuzzy logic were implemented in Japan. The first notable application was on the subway train in Sendai, in which fuzzy logic was able to improve the economy, comfort, and precision of the ride.^[8] It has also been used in recognition of hand written symbols in Sony pocket computers, flight aid for helicopters, controlling of subway systems in order to improve driving comfort, precision of halting, and power economy, improved fuel consumption for automobiles, single-button control for washing machines, automatic motor control for vacuum cleaners with recognition of surface condition and degree of soiling, and prediction systems for early recognition of earthquakes through the Institute of Seismology Bureau of Meteorology, Japan.^[9]

Logical analysis

In mathematical logic, there are several formal systems of "fuzzy logic", most of which are in the family of t-norm fuzzy logics.

Propositional fuzzy logics

The most important propositional fuzzy logics are:

• Monoidal t-norm-based propositional fuzzy logic MTL is an axiomatization of logic where conjunction is defined by a left continuous t-norm and implication is defined as the residuum of the t-norm. Its models correspond to MTL-algebras that are pre-linear commutative bounded integral residuated lattices.
• Basic propositional fuzzy logic BL is an extension of MTL logic where conjunction is defined by a continuous t-norm, and implication is also defined as the residuum of the t-norm. Its models correspond to BL-algebras.
• Łukasiewicz fuzzy logic is the extension of basic fuzzy logic BL where standard conjunction is the Łukasiewicz t-norm. It has the axioms of basic fuzzy logic plus an axiom of double negation, and its models correspond to MV-algebras.
• Gödel fuzzy logic is the extension of basic fuzzy logic BL where conjunction is Gödel t-norm. It has the axioms of BL plus an axiom of idempotence of conjunction, and its models are called G-algebras.
• Product fuzzy logic is the extension of basic fuzzy logic BL where conjunction is product t-norm. It has the axioms of BL plus another axiom for cancellativity of conjunction, and its models are called product algebras.
• Fuzzy logic with evaluated syntax (sometimes also called Pavelka's logic), denoted by EVŁ, is a further generalization of mathematical fuzzy logic. While the above kinds of fuzzy logic have traditional syntax and many-valued semantics, in EVŁ is evaluated also syntax. This means that each formula has an evaluation. Axiomatization of EVŁ stems from Łukasziewicz fuzzy logic. A generalization of classical Gödel completeness theorem is provable in EVŁ.

Predicate fuzzy logics

These extend the above-mentioned fuzzy logics by adding universal and existential quantifiers in a manner similar to the way that predicate logic is created from propositional logic. The semantics of the universal (resp. existential) quantifier in t-norm fuzzy logics is the infimum (resp. supremum) of the truth degrees of the instances of the quantified subformula.

Decidability issues for fuzzy logic

The notions of a "decidable subset" and "recursively enumerable subset" are basic ones for classical mathematics and classical logic. Thus the question of a suitable extension of them to fuzzy set theory is a crucial one. A first proposal in such a direction was made by E.S. Santos by the notions of fuzzy Turing machine, Markov normal fuzzy algorithm and fuzzy program (see Santos 1970). Successively, L. Biacino and G. Gerla argued that the proposed definitions are rather questionable. For example, in ^[10] one shows that the fuzzy Turing machines are not adequate for fuzzy language theory since there are natural fuzzy languages intuitively computable that cannot be recognized by a fuzzy Turing Machine. Then, they proposed the following definitions. Denote by Ü the set of rational numbers in [0,1]. Then a fuzzy subset s : S ${\displaystyle \rightarrow }$[0,1] of a set S is recursively enumerable if a recursive map h : S×N ${\displaystyle \rightarrow }$Ü exists such that, for every x in S, the function h(x,n) is increasing with respect to n and s(x) = lim h(x,n). We say that s is decidable if both s and its complement –s are recursively enumerable. An extension of such a theory to the general case of the L-subsets is possible (see Gerla 2006). The proposed definitions are well related with fuzzy logic. Indeed, the following theorem holds true (provided that the deduction apparatus of the considered fuzzy logic satisfies some obvious effectiveness property).

Any "axiomatizable" fuzzy theory is recursively enumerable. In particular, the fuzzy set of logically true formulas is recursively enumerable in spite of the fact that the crisp set of valid formulas is not recursively enumerable, in general. Moreover, any axiomatizable and complete theory is decidable.

It is an open question to give supports for a "Church thesis" for fuzzy mathematics, the proposed notion of recursive enumerability for fuzzy subsets is the adequate one. In order to solve this, an extension of the notions of fuzzy grammar and fuzzy Turing machine are necessary. Another open question is to start from this notion to find an extension of Gödel's theorems to fuzzy logic.

Fuzzy databases

Once fuzzy relations are defined, it is possible to develop fuzzy relational databases. The first fuzzy relational database, FRDB, appeared in Maria Zemankova's dissertation (1983). Later, some other models arose like the Buckles-Petry model, the Prade-Testemale Model, the Umano-Fukami model or the GEFRED model by J.M. Medina, M.A. Vila et al.

Fuzzy querying languages have been defined, such as the SQLf by P. Bosc et al. and the FSQL by J. Galindo et al. These languages define some structures in order to include fuzzy aspects in the SQL statements, like fuzzy conditions, fuzzy comparators, fuzzy constants, fuzzy constraints, fuzzy thresholds, linguistic labels etc.

Comparison to probability

Fuzzy logic and probability address different forms of uncertainty. While both fuzzy logic and probability theory can represent degrees of certain kinds of subjective belief, fuzzy set theory uses the concept of fuzzy set membership, i.e., how much an observation is within a vaguely defined set, and probability theory uses the concept of subjective probability, i.e., likelihood of some event or condition. The concept of fuzzy sets was developed in the mid-twentieth century at Berkeley ^[11] as a response to the lacking of probability theory for jointly modelling uncertainty and vagueness.^[12]

Bart Kosko claims in Fuzziness vs. Probability that probability theory is a subtheory of fuzzy logic, as questions of degrees of belief in mutually-exclusive set membership in probability theory can be represented as certain cases of non-mutually-exclusive graded membership in fuzzy theory. In that context, he also derives Bayes' theorem from the concept of fuzzy subsethood. Lotfi A. Zadeh argues that fuzzy logic is different in character from probability, and is not a replacement for it. He fuzzified probability to fuzzy probability and also generalized it to possibility theory.

More generally, fuzzy logic is one of many different extensions to classical logic intended to deal with issues of uncertainty outside of the scope of classical logic, the inapplicability of probability theory in many domains, and the paradoxes of Dempster-Shafer theory.

Relation to ecorithms

Computational theorist Leslie Valiant uses the term ecorithms to describe how many less exact systems and techniques like fuzzy logic (and "less robust" logic) can be applied to learning algorithms. Valiant essentially redefines machine learning as evolutionary. In general use, ecorithms are algorithms that learn from their more complex environments (hence eco-) to generalize, approximate and simplify solution logic. Like fuzzy logic, they are methods used to overcome continuous variables or systems too complex to completely enumerate or understand discretely or exactly. ^[14] Ecorithms and fuzzy logic also have the common property of dealing with possibilities more than probabilities, although feedback and feed forward, basically stochastic weights, are a feature of both when dealing with, for example, dynamical systems.

Compensatory fuzzy logic

Compensatory fuzzy logic (CFL) is a branch of fuzzy logic with modified rules for conjunction and disjunction. When the truth value of one component of a conjunction or disjunction is increased or decreased, the other component is decreased or increased to compensate. This increase or decrease in truth value may be offset by the increase or decrease in another component. An offset may be blocked when certain thresholds are met. Proponents claim that CFL allows for better computational semantic behaviors and mimic natural language.

Compensatory Fuzzy Logic consists of four continuous operators: conjunction (c); disjunction (d); fuzzy strict order (or); and negation (n). The conjunction is the geometric mean and its dual as conjunctive and disjunctive operators.^[17]

IEEE STANDARD 1855–2016 – IEEE Standard for Fuzzy Markup Language

The IEEE 1855, the IEEE STANDARD 1855–2016, is about a specification language named Fuzzy Markup Language (FML)^[18] developed by the IEEE Standards Association. FML allows modelling a fuzzy logic system in a human-readable and hardware independent way. FML is based on eXtensible Markup Language (XML). The designers of fuzzy systems with FML have a unified and high-level methodology for describing interoperable fuzzy systems. IEEE STANDARD 1855–2016 uses the W3C XML Schema definition language to define the syntax and semantics of the FML programs.

Prior to the introduction of FML, fuzzy logic practitioners could exchange information about their fuzzy algorithms by  adding to their software functions the ability to read, correctly parse, and store the results of their work in a  form compatible with the Fuzzy Control Language (FCL) described and specified by Part 7 of IEC 61131.^[19][20]

Machines Who Think

Recent commentary about the 25th anniversary edition of Machines Who Think.

"Over the course of the last half-century, a number of books have sought to explain AI to a larger audience and many more devoted to writing the formal history of AI. It is a tribute to her powers of observation and her conversational style that none has really proven more successful than Pamela McCorduck's Machines Who Think now approaching the quarter century mark. Currently, it is the first source cited on the AI Topics web site on the history of AI. Based on extensive interviews with many of the early key players, it managed to forge the template for most subsequent histories, in the sense of providing them both the time line and the larger frame tale."

AI Magazine, Winter 2004 "In summary, if you are interested in the story of how the pioneers of AI approached the problem of getting a machine to think like a human, a story told with verve, wit, intelligence and perception, there is no better place to go than this book."

Nature "The enormous, if stealthy, influence of AI bears out many of the wonders foretold 25 years ago in Machines Who Think, Pamela McCorduck's groundbreaking survey of the history and prospects of the field…. [T]aken together, the original and the afterword form a rich and fascinating history." –Scientific American, May 2004Machines Who Think was conceived as a history of artificial intelligence, beginning with the first dreams of the classical Greek poets (and the nightmares of the Hebrew prophets), up through its realization as twentieth-century science.

The interviews with AI's pioneer scientists took place when the field was young and generally unknown. They were nearly all in robust middle age, with a few decades of fertile research behind them, and luckily, more to come. Thus their explanations of what they thought they were doing were spontaneous, provisional, and often full of glorious fun. Tapes and transcriptions of these interviews, along with supporting material and working drafts of the manuscript, can be found in the Pamela McCorduck Collection at the Carnegie Mellon University Library Archives. If you believe (and I do) that artificial intelligence is not only one of the most audacious of scientific undertakings, but also one of the most important, these interviews are a significant record of the original visionaries, whose intellectual verve set the tone for the field for years to come. That verve–that arrogance, some people thought–also set teeth on edge, as I've pointed out.

Practicing scientists, more interested in what will happen than what once did, are apt to forget their field's history. The new is infinitely seductive. But an interesting characteristic of AI research is how often good ideas were proposed, tried, then dropped, as the technology of the moment failed to allow a good idea to flourish. Then technology would catch up, and a whole new set of possibilities would emerge; another generation would rediscover a good idea, and the dance would begin once more. Meanwhile, new ideas have come up alongside the old: far from "the failure" its critics love to claim, the field thrives and already permeates everyday life.

But above all, the history of AI is a splendid tale in its own right–the search for intelligence outside the human cranium. It entailed defining just what "intellience" might be (disputed territory even yet) and which Other, among several candidates, might exhibit it. The field called up serious ethical and moral questions, and still does. It all happens to be one of the best tales of our times.

From the new foreword:"Machines Who Think has its own modest history that may be worth telling. In the early summer of 1974, John McCarthy made an emergency landing in his small plane in Alaska, at a place called (roughly translated) the Pass of Much Caribou Dung, so remote a spot he could not radio for help."

From the 30,000-word afterword, that summarizes the field since the original was published:

"In the late 1970s and early 1980s, artificial intelligence moved from the fringes to become a celebrity science. Seen in the downtown clubs, boldface in the gossip columns, stalked by paparazzi, it was swept up in a notorious publicity and commercial frenzy."

The new edition also has two separate time-lines, one tracing the evolution of AI in its narrowest sense, and a second one taking a much broader view of intellectual history, and placing AI in the context of all human information gathering, organizing, propagation, and discovery, a central place for AI that has only become apparent with the development of the second generation World Wide Web, which will depend deeply on AI techniques for finding, shaping and inventing knowledge.

Herb Simon himself urged me to re-publish. "Pamela," he wrote in email a few months before he died. "Do consider what might be done about bringing Machines Who Think back into print. More machines are thinking every day, and I would expect that every one of them would want to buy a copy. Soccer robots alone should account for a first printing."

FAQ answered by Pamela McCorduck: Q: How long has the human race dreamed about thinking machines?A: Since at least the time of classical Greece, when Homer's Iliad tells us about robots that are made by the Greek god Hephaestos, also known, in Roman mythology, as Vulcan. Some of these robots are human-like, and some of them are just machines–for example, golden tripods that serve food and wine at banquets. At about the same time, the Chinese were also telling tales of human-like machines that could think. It's also important to remember that this is the time in human history when the Second Commandment was codified, prohibiting the making of graven images, which in reality forbids humans to take on the creative privileges of divinities. In my book, I describe each attitude: I call one the Hellenic point of view, meaning out of Greece, and generally welcoming the idea of thinking machines. The other I call the Hebraic, which finds the whole idea of thinking machines wicked, even blasphemous. These two attitudes are very much alive today. The history of thinking machines is extremely rich: every century has its version. The 19th century was particularly fertile: Frankenstein and the Tales of E. T. A. Hoffman were published, and the fake chess machine called "The Turk" was on exhibit. Q: What's the difference between all those tall tales and what you're writing about?A: They were exactly that–tall tales. However, by the middle of the 20th century, a small group of farsighted scientists understood that the computer would allow them to actually realize this longstanding dream of a thinking machine.  Q: What does it mean that a machine beat Garry Kasparov, the world's chess champion?A: It's a tremendous achievement for human scientists to design a machine smart enough to beat not only the reigning chess champion, but also a man said to be the best chess champion ever. Kasparov, for his part, claims that these programs are making him a better chess player. Q: And what about the recent wins by IBM's program Watson at the guessing game, Jeopardy?This was spectacular. Watson had to understand natural language—in this case, English—to the point where it (yes, everyone on the Jeopardy program was referring to it as "he," but I'll continue to say "it") could outguess two of the best human players ever. To play Jeopardy, you must be able to crack riddles, puns, puzzles, and interpret ambiguous statements. Watson is a tremendous achievement. Q: Does this mean that machines are smarter than we are?A: Machines have been "smarter" than us in many ways for a while. Chess and Jeopardy are the best-known achievements, but many artificially intelligent programs have been at work for more than two decades in finance, in many sciences, such as molecular biology and high-energy physics, and in manufacturing and business processes all over the world. We've lately seen a program that has mastered the discovery process in a large, complex legal case, using a small fraction of the time, an even smaller fraction of costs—and it's more accurate. So if you include arithmetic, machines have been "smarter" than us for more than a century. People no longer feel threatened by machines that can add, subtract, and remember faster and better than we can, but machines that can manipulate and even interpret symbols better than we can give us pause. Q: Those are very narrow domains. Do general-purpose intelligent machines as smart as humans exist?A: Not yet. But scientists are trying to figure out how to design a machine that exhibits general intelligence, even if that means sacrificing a bit of specialized intelligence. Q: If the human chess champion has finally been defeated, and the best human Jeopardy players went down, what's the next big goal? A: It took fifty years between the time scientists first proposed the goal of a machine that could be the world's chess champion, and when that goal was reached. It took another fourteen years for Watson to emerge as the Jeopardy champion. In the late 1990s, a major new goal was set. In fifty years, AI should field a robot team of soccer players to compete with and defeat the human team of champions at the World's Cup. In the interim, more modestly accomplished soccer robots are teaching scientists a great deal about physical coordination in the real world, pattern recognition, teamwork, and real-time tactics and strategy under stress. Scientists from all over the world are fielding teams right now–one of the most obvious signs of how international artificial intelligence research has become. Q: Artificial intelligence–is it real?A: It's real. For more than two decades, your credit card company has employed various kinds of artificial intelligence programs to tell whether or not the transaction coming in from your card is typical for you, or whether it's outside your usual pattern. Outside the pattern, a warning flag goes up. The transaction might even be rejected. This isn't usually an easy, automatic judgment–many factors are weighed as the program is deciding. In fact, finance might be one of the biggest present-day users of AI. Utility companies employ AI programs to figure out whether small problems have the potential to be big ones, and if so, how to fix the small problem. Many medical devices now employ AI to diagnose and manage the course of therapy. Construction companies use AI to figure out schedules and manage risks. The U.S. armed forces uses all sorts of AI programs–to manage battles, to detect real threats out of possible noise, and so on. Though these programs are usually smarter than humans could be, they aren't perfect. Sometimes, like humans, they fail. Q: What so-called smart computers do–is that really thinking?A: No, if you insist that thinking can only take place inside the human cranium. But yes, if you believe that making difficult judgments, the kind usually left to experts, choosing among plausible alternatives, and acting on those choices, is thinking. That's what artificial intelligences do right now. Along with most people in AI, I consider what artificial intelligences do as a form of thinking, though I agree that these programs don't think just like human beings do, for the most part. I'm not sure that's even desirable. Why would we want AIs if all we want is human-level intelligence? There are plenty of humans on the planet. The field's big project is to make intelligences that exceed our own. As these programs come into our lives in more ways, we'll need programs that can explain their reasoning to us before we accept their decisions. Q: But doesn't that mean our own machines will replace us?A: This continues to be debated both inside and outside the field. Some people fear this–that smart machines will eventually get smart enough to come in and occupy our ecological niche, and that will be that. So long, human race. Some people think that the likeliest scenario is that smart machines will help humans become smarter, the way Garry Kasparov feels that smart chess-playing machines have made him a better player. Some people think that smart machines won't have any desire to occupy our particular niche: instead, being smarter than we are, they'll lift the burden of managing the planet off our shoulders, and leave us to do the things we do best–a rather pleasant prospect. But a few years ago, Bill Joy, an eminent computer scientist who helped found Sun Microsystems, was worried enough to write an article that calls for a halt in AI and some other kinds of research. He's far from the first, by the way. Most of the arguments against halting suggest that the benefits will outweigh the dangers. But nobody believes that there's no chance of danger. I should add that forbidding AI research is pretty hopeless. Research isn't being done on some mountaintop in secret. It's being done all over the planet. Suppose a group of nations (or firms, or universities) decided to stop doing AI research. Would that stop other researchers elsewhere? No, the perceived advantage of continuing this research would make at least a small group continue. The abstainers would be forced to continue themselves for their own protection. Q: Aren't you yourself worried?A: I agree that the dangerous scenarios are entirely plausible. I explore that further in my book. But I also believe that the chance is worth taking. The benefits could be tremendous. Let's take some examples. Scientists are at work right now on robots that will help the elderly stay independently in their own homes longer than otherwise. I think that's terrific. At the 2003 Superbowl (and presumably at the 2004 Superbowl too) a kind of artificial intelligence called "smart dust"–smart sensors a millimeter by a millimeter–was deployed to sense and report on unusual activity, looking for terrorists. Scientists are also at work on a machine that can detect the difference between a natural disease outbreak and a bio-terror attack. Unfortunately, these are issues we must address for the foreseeable future. We've recently had a lot of bad news about cheating going on in the financial sector. At least one part of that sector, the National Association of Security Dealers, uses AI to monitor the activities of its traders, looking not only at the trading patterns of individual traders, but at articles in newspapers and other possible influences. Q: Whoa! Isn't that a big invasion of privacy? In fact, didn't we hear that AI was going to be used for the government's Total Information Awareness project? That makes me very uncomfortable. A: Americans cherish their privacy, and so they should. American ideas about privacy have evolved legally and socially over a long period. Moreover, Americans aren't the only ones with such concerns–the European Union is even stricter about the use of personal information than the U.S. But the European Union also understands that the best defense against terrorism is to be able to detect patterns of behavior that might alert law enforcement officers to potential terrorism before it happens. Like the privacy you give up for the convenience of using a credit card, it's a trade-off. I think that trade-off should be publicly debated, with all the gravity it deserves. Q: Shouldn't we just say no to intelligent machines? Aren't the risks too scary?A: The risks are scary; the risks are real; but I don't think we should say no. In my book, I go further. I don't think we can say no. Here's what I mean: one of the best things humans have ever done for themselves was to collect, organize, and distribute information in the form of libraries and encyclopedias. We have always honored that effort, because we understand that no human can carry everything worth knowing inside a single head. The World Wide Web is this generation's new giant encyclopedia, and the Semantic Web, which is the next generation Web, will have intelligence built in. It will be as if everybody with access to a computer can have the world's smartest reference librarian at their fingertips, ready to help find exactly what you need, no matter how ill-formed your question is. And it will be able to offer some assurance that the information you are getting is reliable–the present World Wide Web cannot do that. In other words, intelligent machines seem to be part of a long human impulse to educate ourselves better and better, to make life better for each of us. Q: What's ahead as AI succeeds even more?A: Many of us already deal with limited AI in our daily lives–credit cards, search engines like Google, automated voice instructions from our GPS devices to help us drive to our destinations; we order prescriptions over the phone from semi-intelligent voice machines. But visionary projects are underway to make–hey, read my book! Q: Would you consider yourself an AI optimist?On the whole, yes, though I'm not nearly as certain that AI will succeed on the time scale that some observers, such as Ray Kurzweil, believe. However, I'm re-thinking my skepticism as programs like Watson exceed my expectations. I've always thought that significant AI would come to us, but not in a rush. Now I'm not so sure—it might be sooner than I expected. Maybe much sooner. My book talks about my experience with intelligent robots at a meeting in the summer of 2003. Some people have said I was too critical, too negative about that. But in March 2004, DARPA staged a race for autonomous vehicles over a 30-mile desert course. The best vehicle (Carnegie-Mellon's entry) did just over 7 miles before it quit. Some vehicles didn't even get started. The following year, however, the winning intelligent, autonomous car did its entire course without mishap, and it had a few others in the rearguard doing just fine too. These DARPA competitions have continued with ever more difficult problems posed and solved. But we still have a way to go, and no wonder. In just a few decades, we're trying to mimic and even surpass millions of years of natural evolution. Q: How do you feel about what's called "the singularity"? A: Oh, boy. I've long felt that "the singularity"—the moment when machine intelligence exceeds human intelligence—was so far off (if it happened at all) that anything I could say about it could only be hot air. With AI climbing the learning curve as fast as it has been lately, I've needed to revisit that stance. For now, I still maintain that if and when it happens, humans then and there will have the best opinions on how to confront this unprecedented event. We also need to question whether this singularity will arrive, as most proponents seem to think, in the form of a homogenous membrane, spreading all over the planet all at once. It makes more sense to me that it will arrive in fits and starts, and will sometimes be self-contradictory—which would raise other kinds of problems for us, and for it. I wouldn't be astonished if, at that point, we turn to our own smart machines for advice on what the best next move is for the human race.

Computational cognition

From Wikipedia, the free encyclopedia

Computational cognition (sometimes referred to as computational cognitive science or computational psychology) is the study of the computational basis of learning and inference by mathematical modeling, computer simulation, and behavioral experiments. In psychology, it is an approach which develops computational models based on experimental results. It seeks to understand the basis behind the human method of processing of information. Early on computational cognitive scientists sought to bring back and create a scientific form of Brentano’s psychology.^[1]

Artificial intelligence

There are two main purposes for the productions of artificial intelligence: to produce intelligent behaviors regardless of the quality of the results, and to model after intelligent behaviors found in nature.^[2] In the beginning of its existence, there was no need for artificial intelligence to emulate the same behavior as human cognition. Until 1960s, economist Herbert Simon and Allen Newell attempted to formalize human problem-solving skills by using the results of psychological studies to develop programs that implement the same problem-solving techniques as people would. Their works laid the foundation for symbolic AI and computational cognition, and even some advancements for cognitive science and cognitive psychology.^[3]
The field of symbolic AI is based on the physical symbol systems hypothesis by Simon and Newell, which states that expressing aspects of cognitive intelligence can be achieved through the manipulation of symbols.^[4] However, John McCarthy focused more on the initial purpose of artificial intelligence, which is to breakdown the essence of logical and abstract reasoning regardless of whether or not human employs the same mechanism.^[2]

Over the next decades, the progress made in artificial intelligence started to be focused more on developing logic-based and knowledge-based programs, veering away from the original purpose of symbolic AI. Researchers started to believe that artificial intelligence may never be able to imitate some intricate processes of human cognition like perception or learning. A chief failing of AI is not being able to achieve a complete likeness to human cognition due to the lack of emotion and the impossibility of implementing it into an AI. ^[5]They began to take a “sub-symbolic” approach to create intelligence without specifically representing that knowledge. This movement led to the emerging discipline of computational modeling, connectionism, and computational intelligence.^[4]

Computational modeling

As it contributes more to the understanding of human cognition than artificial intelligence, computational cognitive modeling emerged from the need to define various cognition functionalities (like motivation, emotion, or perception) by representing them in computational models of mechanisms and processes.^[6] Computational models study complex systems through the use of specific algorithms and extensive computational resources, or variables, to produce computer simulation.^[7] Simulation is achieved by adjusting the variables, changing one alone or even combining them together, to observe the effect on the outcomes. The results help experimenters make predictions about what would happen in the real system if those similar changes were to occur. ^[8]

When computational models attempt to mimic human cognitive functioning, all the details of the function must be known for them to transfer and display properly through the models, allowing researchers to thoroughly understand and test an existing theory because no variables are vague and all variables are modifiable. Consider a model of memory built by Atkinson and Shiffrin in 1968, it showed how rehearsal leads to long-term memory, where the information being rehearsed would be stored. Despite the advancement it made in revealing the function of memory, this model fails to provide answers to crucial questions like: how much information can be rehearsed at a time? How long does it take for information to transfer from rehearsal to long-term memory? Similarly, other computational models raise more questions about cognition than they answer, making their contributions much less significant for the understanding of human cognition than other cognitive approaches.^[9] An additional shortcoming of computational modeling is its reported lack of objectivity.^[10]

John Anderson in his ACT-R uses the functions of computational models and the findings of cognitive science. Adaptive Control of Thought-Rational is based on the theory that the brain consists of several modules which perform specialized functions separate of each other.^[9] The ACT-R model is classified as a symbolic approach to cognitive science.^[11]

Connectionist network

Another approach which deals more with the semantic content of cognitive science is connectionism or neural network modeling. Connectionism relies on the idea that the brain consists of simple units or nodes and the behavioral response comes primarily from the layers of connections between the nodes and not from the environmental stimulus itself.^[9]

Connectionist network differs from computational modeling specifically because of two functions: neural back-propagation and parallel-processing. Neural back-propagation is a method utilized by connectionist network to show evidence of learning. After a connectionist network produce a response, the stimulated results are compared to real-life situational results. The feedback provided by the backward propagation of errors would be used to improve accuracy for the network’s subsequent responses.^[12] The second function, parallel-processing, stemmed from the belief that knowledge and perception are not limited to specific modules but rather are distributed throughout the cognitive networks. The present of parallel distributed processing has been shown in psychological demonstrations like the Stroop effect, where the brain seems to be analyzing the perception of color and meaning of language at the same time.^[13] However, this theoretical approach has been continually disproved because the two cognitive functions for color-perception and word-forming are operating separately and simultaneously, not parallel of each other.^[14]

The field of cognition may have benefitted from the use of connectionist network but because of the completed system, setting up the neural network models can be quite a tedious task and the results may be less interpretable than the system they are trying to model. Therefore, the results can be used as evidence for broad theory of cognition without explaining the particular process happening within the cognitive function. Other disadvantages of connectionism lie in the research methods it employs or hypothesis it tests, which has been proven inaccurate or ineffective often, taking connectionist models further from an accurate representation of how the brain functions. These issues cause neural network models to be ineffective on studying higher forms of information-processing, and hinder connectionism from advancing the general understanding of human cognition.^[15]