Fusion power (updated)

From Wikipedia, the free encyclopedia

The Joint European Torus (JET) magnetic fusion experiment in 1991

Fusion power is a theoretical form of power generation in which energy will be generated by using nuclear fusion reactions to produce heat for electricity generation. In a fusion process, two lighter atomic nuclei combine to form a heavier nucleus, and at the same time, they release energy. This is the same process that powers stars like our Sun. Devices designed to harness this energy are known as fusion reactors. 

Fusion processes require fuel and a highly confined environment with a high temperature and pressure, to create a plasma in which fusion can occur. In stars, the most common fuel is hydrogen, and gravity creates the high temperature and confinement needed for fusion. Fusion reactors generally use hydrogen isotopes such as deuterium and tritium, which react more easily, and create a confined plasma of millions of degrees using inertial methods (laser) or magnetic methods (tokamak and similar), although many other concepts have been attempted. The major challenges in realising fusion power are to engineer a system that can confine the plasma long enough at high enough temperature and density, for a long term reaction to occur, and for the most common reactions, managing neutrons that are released during the reaction, which over time can degrade many common materials used within the reaction chamber. 

As a source of power, nuclear fusion is expected to have several theoretical advantages over fission. These include reduced radioactivity in operation and little nuclear waste, ample fuel supplies, and increased safety. However, controlled fusion has proven to be extremely difficult to produce in a practical and economical manner. Research into fusion reactors began in the 1940s, but to date, no design has produced more fusion power output than the electrical power input; therefore, all existing designs have had a negative power balance.

Over the years, fusion researchers have investigated various confinement concepts. The early emphasis was on three main systems: z-pinch, stellarator and magnetic mirror. The current leading designs are the tokamak and inertial confinement (ICF) by laser. Both designs are being built at very large scales, most notably the ITER tokamak in France, and the National Ignition Facility laser in the United States. Researchers are also studying other designs that may offer cheaper approaches. Among these alternatives there is increasing interest in magnetized target fusion and inertial electrostatic confinement.

Background

The Sun, like other stars, is a natural fusion reactor, where stellar nucleosynthesis transforms lighter elements into heavier elements with the release of energy.

 

Binding energy for different atomic nuclei. Iron-56 has the highest, making it the most stable. Nuclei to the left are likely to fuse; those to the right are likely to split.

Mechanism

Fusion reactions occur when two or more atomic nuclei come close enough for long enough that the nuclear force pulling them together exceeds the electrostatic force pushing them apart, fusing them into heavier nuclei. For nuclei lighter than iron-56, the reaction is exothermic, releasing energy. For nuclei heavier than iron-56, the reaction is endothermic, requiring an external source of energy. Hence, nuclei smaller than iron-56 are more likely to fuse while those heavier than iron-56 are more likely to break apart. 

The strong force acts only over short distances. The repulsive electrostatic force acts over longer distances. In order to undergo fusion, the fuel atoms need to be given enough energy to approach each other close enough for the strong force to become active. The amount of kinetic energy needed to bring the fuel atoms close enough is known as the "Coulomb barrier". Ways of providing this energy include speeding up atoms in a particle accelerator, or heating them to high temperatures. 

Once an atom is heated above its ionization energy, its electrons are stripped away (it is ionized), leaving just the bare nucleus (the ion). The result is a hot cloud of ions and the electrons formerly attached to them. This cloud is known as plasma. Because the charges are separated, plasmas are electrically conductive and magnetically controllable. Many fusion devices take advantage of this to control the particles as they are heated.

Cross Section

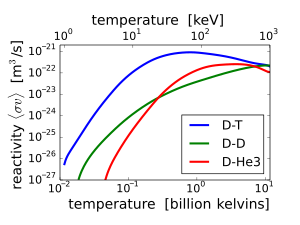
The fusion reaction rate increases rapidly with temperature until it maximizes and then gradually drops off. The deuterium-tritium fusion rate peaks at a lower temperature (about 70 keV, or 800 million kelvin) and at a higher value than other reactions commonly considered for fusion energy.

A reaction's cross section, denoted σ, is the measure of the probability that a fusion reaction will happen. This depends on the relative velocity of the two nuclei. Higher relative velocities generally increase the probability, but the probability begins to decrease again at very high energies. Cross sections for many fusion reactions were measured (mainly in the 1970s) using particle beams.

In a plasma, particle velocity can be characterized using a probability distribution. If the plasma is thermalized, the distribution looks like a bell curve, or maxwellian distribution. In this case, it is useful to use the average particle cross section over the velocity distribution. This is entered into the volumetric fusion rate:

${\displaystyle P_{\text{fusion}}=n_{A}n_{B}\langle \sigma v_{A,B}\rangle E_{\text{fusion}}}$

where:

• ${\displaystyle P_{\text{fusion}}}$ is the energy made by fusion, per time and volume
• n is the number density of species A or B, of the particles in the volume
• ${\displaystyle \langle \sigma v_{A,B}\rangle }$ is the cross section of that reaction, average over all the velocities of the two species v
• ${\displaystyle E_{\text{fusion}}}$ is the energy released by that fusion reaction.

Lawson Criterion

The Lawson Criterion shows how energy output varies with temperature, density, speed of collision, and fuel. This equation was central to John Lawson's analysis of fusion working with a hot plasma. Lawson assumed an energy balance, shown below.

${\displaystyle P_{\text{out}}=\eta _{\text{capture}}\left(P_{\text{fusion}}-P_{\text{conduction}}-P_{\text{radiation}}\right)}$

• η, efficiency
• ${\displaystyle P_{\text{conduction}}}$, conduction losses as energy laden mass leaves
• ${\displaystyle P_{\text{radiation}}}$, radiation losses as energy leaves as light
• ${\displaystyle P_{\text{out}}}$, net power from fusion
• ${\displaystyle P_{\text{fusion}}}$, is rate of energy generated by the fusion reactions.

Plasma clouds lose energy through conduction and radiation. Conduction occurs when ions, electrons or neutrals impact other substances, typically a surface of the device, and transfer a portion of their kinetic energy to the other atoms. Radiation is energy that leaves the cloud as light in the visible, UV, IR, or X-ray spectra. Radiation increases with temperature. Fusion power technologies must overcome these losses.

Triple product: density, temperature, time

The Lawson criterion argues that a machine holding a thermalized and quasi-neutral plasma has to meet basic criteria to overcome radiation losses, conduction losses and reach efficiency of 30 percent. This became known as the "triple product": the plasma density, temperature and confinement time. Attempts to increase the triple product led to targeting larger plants. Larger plants move structural materials further away from the centre of the plasma, which reduces conduction and radiation losses since more of the radiation is internally reflected. This emphasis on ${\displaystyle (nT\tau )}$ as a metric of success has impacted other considerations such as cost, size, complexity and efficiency. This has led to larger, more complicated and more expensive machines such as ITER and NIF.

Plasma behavior

Plasma is an ionized gas that conducts electricity. In bulk, it is modeled using magnetohydrodynamics, which is a combination of the Navier-Stokes equations governing fluids and Maxwell's equations governing how magnetic and electric fields behave. Fusion exploits several plasma properties, including:

• Self-organizing plasma conducts electric and magnetic fields. Its motions can generate fields that can in turn contain it.
• Diamagnetic plasma can generate its own internal magnetic field. This can reject an externally applied magnetic field, making it diamagnetic.
• Magnetic mirrors can reflect plasma when it moves from a low to high density field.

Energy capture

Multiple approaches have been proposed for energy capture. The simplest is to heat a fluid. Most designs concentrate on the D-T reaction, which releases much of its energy in a neutron. Electrically neutral, the neutron escapes the confinement. In most such designs, it is ultimately captured in a thick "blanket" of lithium surrounding the reactor core. When struck by a high-energy neutron, the lithium can produce tritium, which is then fed back into the reactor. The energy of this reaction also heats the blanket, which is then actively cooled with a working fluid and then that fluid is used to drive conventional turbomachinery. 

It has also been proposed to use the neutrons to breed additional fission fuel in a blanket of nuclear waste, a concept known as a fission-fusion hybrid. In these systems, the power output is enhanced by the fission events, and power is extracted using systems like those in conventional fission reactors.

Designs that use other fuels, notably the p-B reaction, release much more of their energy in the form of charged particles. In these cases, alternate power extraction systems based on the movement of these charges are possible. Direct energy conversion was developed at LLNL in the 1980s as a method to maintain a voltage using the fusion reaction products. This has demonstrated energy capture efficiency of 48 percent.

Approaches

Magnetic confinement

• Tokamak: the most well-developed and well-funded approach to fusion energy. This method races hot plasma around in a magnetically confined, donut-shaped ring, with an internal current. When completed, ITER will be the world's largest tokamak. As of April 2012 an estimated 215 experimental tokamaks were either planned, decommissioned or currently operating (35) worldwide.
• Spherical tokamak: also known as spherical torus. A variation on the tokamak with a spherical shape.
• Stellarator: Twisted rings of hot plasma. The stellarator attempts to create a natural twisted plasma path, using external magnets, while tokamaks create those magnetic fields using an internal current. Stellarators were developed by Lyman Spitzer in 1950 and have four designs: Torsatron, Heliotron, Heliac and Helias. One example is Wendelstein 7-X, a German fusion device that produced its first plasma on December 10, 2015. It is the world's largest stellarator, designed to investigate the suitability of this type of device for a power station.
• Levitated Dipole Experiment (LDX): These use a solid superconducting torus. This is magnetically levitated inside the reactor chamber. The superconductor forms an axisymmetric magnetic field that contains the plasma. The LDX was developed by MIT and Columbia University after 2000 by Jay Kesner and Michael E. Mauel.
• Magnetic mirror: Developed by Richard F. Post and teams at LLNL in the 1960s. Magnetic mirrors reflected hot plasma back and forth in a line. Variations included the Tandem Mirror, magnetic bottle and the biconic cusp. A series of well-funded, large, mirror machines were built by the US government in the 1970s and 1980s, principally at Lawrence Livermore National Laboratory.
• Bumpy torus: A number of magnetic mirrors are arranged end-to-end in a toroidal ring. Any fuel ions that leak out of one are confined in a neighboring mirror, permitting the plasma pressure to be raised arbitrarily high without loss. An experimental facility, the ELMO Bumpy Torus or EBT was built and tested at Oak Ridge National Laboratory in the 1970s.
• Field-reversed configuration: This device traps plasma in a self-organized quasi-stable structure; where the particle motion makes an internal magnetic field which then traps itself.
• Spheromak: Very similar to a field reversed configuration, a semi-stable plasma structure made by using the plasmas' own self-generated magnetic field. A spheromak has both a toroidal and poloidal fields, while a Field Reversed Configuration only has no toroidal field.
• Reversed field pinch: Here the plasma moves inside a ring. It has an internal magnetic field. Moving out from the center of this ring, the magnetic field reverses direction.

Inertial confinement

• Direct drive: In this technique, lasers directly blast a pellet of fuel. The goal is to ignite a fusion chain reaction. Ignition was first suggested by John Nuckolls, in 1972. Notable direct drive experiments have been conducted at the Laboratory for Laser Energetics, Laser Mégajoule and the GEKKO XII facilities. Good implosions require fuel pellets with close to a perfect shape in order to generate a symmetrical inward shock wave that produces the high-density plasma.
• Fast ignition: This method uses two laser blasts. The first blast compresses the fusion fuel, while the second high energy pulse ignites it. Experiments have been conducted at the Laboratory for Laser Energetics using the Omega and Omega EP systems and at the GEKKO XII laser at the Institute for Laser Engineering in Osaka Japan.
• Indirect drive: In this technique, lasers blasts a structure around the pellet of fuel. This structure is known as a Hohlraum. As it disintegrates the pellet is bathed in a more uniform x-ray light, creating better compression. The largest system using this method is the National Ignition Facility.
• Magneto-inertial fusion or Magnetized Liner Inertial Fusion: This combines a laser pulse with a magnetic pinch. The pinch community refers to it as magnetized liner Inertial fusion while the ICF community refers to it as magneto-inertial fusion.
• Heavy Ion Beams There are also proposals to do inertial confinement fusion with ion beams instead of laser beams. The main difference is the mass of the beam has momentum, whereas lasers do not.

Magnetic or electric pinches

• Z-Pinch: This method sends a strong current (in the z-direction) through the plasma. The current generates a magnetic field that squeezes the plasma to fusion conditions. Pinches were the first method for man-made controlled fusion. Some examples include the Dense plasma focus (DPF) and the Z machine at Sandia National Laboratories. In DPF the focus consists of two coaxial cylindrical electrodes made from copper or beryllium and housed in a vacuum chamber containing a low-pressure fusible gas. An electrical pulse is applied across the electrodes, heating the gas into a plasma. The current forms into a minuscule vortex along the axis of the machine, which then kinks into a cage of current with an associated magnetic field. The cage of current and magnetic-field-entrapped plasma is called a plasmoid. The acceleration of the electrons about the magnetic field lines heats the nuclei within the plasmoid to fusion temperatures.
• Theta-Pinch: This method sends a current inside a plasma, in the theta direction.
• Screw Pinch: This method combines a theta and z-pinch for improved stabilization.

Inertial electrostatic confinement

• Fusor: This method uses an electric field to heat ions to fusion conditions. The machine typically uses two spherical cages, a cathode inside the anode, inside a vacuum. These machines are not considered a viable approach to net power because of their high conduction and radiation losses. They are simple enough to build that amateurs have fused atoms using them.
• Polywell: This design attempts to combine magnetic confinement with electrostatic fields, to avoid the conduction losses generated by the cage.

Other

• Magnetized target fusion: This method confines hot plasma using a magnetic field and squeezes it using inertia. Examples include LANL FRX-L machine, General Fusion and the plasma liner experiment.
• Cluster Impact Fusion Microscopic droplets of heavy water are accelerated at great velocity into a target or into one another. Researchers at Brookhaven reported positive results which were later refuted by further experimentation. Fusion effects were actually produced because of contamination of the droplets.
• Uncontrolled: Fusion has been initiated by man, using uncontrolled fission explosions to ignite so-called Hydrogen Bombs. Early proposals for fusion power included using bombs to initiate reactions.
• Beam fusion: A beam of high energy particles can be fired at another beam or target and fusion will occur. This was used in the 1970s and 1980s to study the cross sections of high energy fusion reactions.
• Bubble fusion: This was a fusion reaction that was supposed to occur inside extraordinarily large collapsing gas bubbles, created during acoustic liquid cavitation. This approach was discredited.
• Cold fusion: This is a hypothetical type of nuclear reaction that would occur at, or near, room temperature. Cold fusion is discredited and gained a reputation as pathological science.
• Muon-catalyzed fusion: This approach replaces electrons in the plasma by muons - far more massive particles with the same electric charge. Their greater mass allows nuclei to get much closer and collide more easily, so it greatly reduces the kinetic energy (heat and pressure) required to initiate fusion. A problem is that muons require more energy to produce than can be obtained from muon-catalysed fusion, making this approach impractical for power generation.
• Space-Based Solar Power argues that a majority of available fusion fuels exists within the sphere of the Sun where it is gravitationally confined, and that a tractable way to accomplish large-scale fusion power is to build very large space-borne platforms that capture energy via photons rather than via a carnot cycle. The theoretical limit of producing power by such means is a type-2 civilization using a Dyson Sphere.

Common tools

Heating

Gas is heated to form a plasma hot enough to start fusion reactions. A number of heating schemes have been explored: Radiofrequency Heating A radio wave is applied to the plasma, causing it to oscillate. This is basically the same concept as a microwave oven. This is also known as electron cyclotron resonance heating or Dielectric heating.

Electrostatic Heating An electric field can do work on charged ions or electrons, heating them.

Neutral Beam Injection An external source of hydrogen is ionized and accelerated by an electric field to form a charged beam which is shone through a source of neutral hydrogen gas towards the plasma which itself is ionized and contained in the reactor by a magnetic field. Some of the intermediate hydrogen gas is accelerated towards the plasma by collisions with the charged beam while remaining neutral: this neutral beam is thus unaffected by the magnetic field and so shines through it into the plasma. Once inside the plasma the neutral beam transmits energy to the plasma by collisions as a result of which it becomes ionized and thus contained by the magnetic field thereby both heating and refuelling the reactor in one operation. The remainder of the charged beam is diverted by magnetic fields onto cooled beam dumps. 

Antiproton annihilation Theoretically a quantity of antiprotons injected into a mass of fusion fuel can induce thermonuclear reactions. This possibility as a method of spacecraft propulsion, known as Antimatter-catalyzed nuclear pulse propulsion, was investigated at Pennsylvania State University in connection with the proposed AIMStar project.

Measurement

Thomson Scattering Light scatters from plasma. This light can be detected and used to reconstruct the plasmas' behavior. This technique can be used to find its density and temperature. It is common in Inertial confinement fusion, Tokamaks and fusors. In ICF systems, this can be done by firing a second beam into a gold foil adjacent to the target. This makes x-rays that scatter or traverse the plasma. In Tokamaks, this can be done using mirrors and detectors to reflect light across a plane (two dimensions) or in a line (one dimension). 

Langmuir probe This is a metal object placed in a plasma. A potential is applied to it, giving it a positive or negative voltage against the surrounding plasma. The metal collects charged particles, drawing a current. As the voltage changes, the current changes. This makes a IV Curve. The IV-curve can be used to determine the local plasma density, potential and temperature.

Neutron detectors Deuterium or tritium fusion produces neutrons. Neutrons interact with surrounding matter in ways that can be detected. Several types of neutron detectors exist which can record the rate at which neutrons are produced during fusion reactions. They are an essential tool for demonstrating success. 

Flux loop A loop of wire is inserted into the magnetic field. As the field passes through the loop, a current is made. The current is measured and used to find the total magnetic flux through that loop. This has been used on the National Compact Stellarator Experiment, the polywell, and the LDX machines. 

X-ray detector All plasma loses energy by emitting light. This covers the whole spectrum: visible, IR, UV, and X-rays. This occurs anytime a particle changes speed, for any reason. If the reason is deflection by a magnetic field, the radiation is Cyclotron radiation at low speeds and Synchrotron radiation at high speeds. If the reason is deflection by another particle, plasma radiates X-rays, known as Bremsstrahlung radiation. X-rays are termed in both hard and soft, based on their energy.

Power production

It has been proposed that steam turbines be used to convert the heat from the fusion chamber into electricity. The heat is transferred into a working fluid that turns into steam, driving electric generators. 

Neutron blankets Deuterium and tritium fusion generates neutrons. This varies by technique (NIF has a record of 3E14 neutrons per second while a typical fusor produces 1E5–1E9 neutrons per second). It has been proposed to use these neutrons as a way to regenerate spent fission fuel  or as a way to breed tritium using a breeder blanket consisting of liquid lithium or, as in more recent reactor designs, a helium cooled pebble bed consisting of lithium bearing ceramic pebbles fabricated from materials such as Lithium titanate, lithium orthosilicate or mixtures of these phases.

Direct conversion This is a method where the kinetic energy of a particle is converted into voltage. It was first suggested by Richard F. Post in conjunction with magnetic mirrors, in the late sixties. It has also been suggested for Field-Reversed Configurations. The process takes the plasma, expands it, and converts a large fraction of the random energy of the fusion products into directed motion. The particles are then collected on electrodes at various large electrical potentials. This method has demonstrated an experimental efficiency of 48 percent.

Records

Fusion records have been set by a number of devices. Here are some:

Q

The ratio of energy extracted against the amount of energy supplied. This record is considered to be set by the Joint European Torus (JET) in 1997 when the device extracted 16 MW of power. However, this ratio can be seen three different ways.

• 0.69 is the actual point in time ratio between ”fusion power” and actual input power in the plasma (23 MW).
• 0.069 is the ratio between the “fusion” power and the power required to produce the 23MW input power (essentially it takes into account the efficiency of the NB system).
• 0.0069 is the ratio between the “fusion” power and the total peak power required for a JET pulse. This takes into account all the power from the grid plus the one from the two large JET flywheel generators.

Runtime

In Field Reversed Configurations, the longest run time is 300 ms, set by the Princeton Field Reversed Configuration in August 2016. However this involved no fusion.

Beta

The fusion power trends as the plasma confinement raised to the fourth power. Hence, getting a strong plasma trap is of real value to a fusion power plant. Plasma has a very good electrical conductivity. This opens the possibility of confining the plasma with magnetic field, generally known as magnetic confinement. The field puts a magnetic pressure on the plasma, which holds it in. A widely used measure of magnetic trapping in fusion is the beta ratio: 

${\displaystyle \beta ={\frac {p}{p_{mag}}}={\frac {nk_{B}T}{(B^{2}/2\mu _{0})}}}$ 

This is the ratio of the externally applied field to the internal pressure of the plasma. A value of 1 is ideal trapping. Some examples of beta values include:

1. The START machine: 0.32
2. The Levitated dipole experiment: 0.26
3. Spheromaks: ≈ 0.1, Maximum 0.2 based on Mercier limit.
4. The DIII-D machine: 0.126
5. The Gas Dynamic Trap a magnetic mirror: 0.6 for 5E-3 seconds.
6. The Sustained Spheromak Plasma Experiment at Los Alamos National labs < 0.05 for 4E-6 seconds.

Confinement

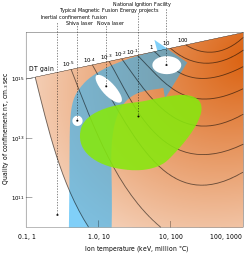
Parameter space occupied by inertial fusion energy and magnetic fusion energy devices as of the mid 1990s. The regime allowing thermonuclear ignition with high gain lies near the upper right corner of the plot.

Confinement refers to all the conditions necessary to keep a plasma dense and hot long enough to undergo fusion. Here are some general principles.

• Equilibrium: The forces acting on the plasma must be balanced for containment. One exception is inertial confinement, where the relevant physics must occur faster than the disassembly time.
• Stability: The plasma must be so constructed so that disturbances will not lead to the plasma disassembling.
• Transport or conduction: The loss of material must be sufficiently slow. The plasma carries off energy with it, so rapid loss of material will disrupt any machines power balance. Material can be lost by transport into different regions or conduction through a solid or liquid.

To produce self-sustaining fusion, the energy released by the reaction (or at least a fraction of it) must be used to heat new reactant nuclei and keep them hot long enough that they also undergo fusion reactions.

Unconfined

The first human-made, large-scale fusion reaction was the test of the hydrogen bomb, Ivy Mike, in 1952. As part of the PACER project, it was once proposed to use hydrogen bombs as a source of power by detonating them in underground caverns and then generating electricity from the heat produced, but such a power station is unlikely ever to be constructed.

Magnetic confinement

Magnetic Mirror One example of magnetic confinement is with the magnetic mirror effect. If a particle follows the field line and enters a region of higher field strength, the particles can be reflected. There are several devices that try to use this effect. The most famous was the magnetic mirror machines, which was a series of large, expensive devices built at the Lawrence Livermore National Laboratory from the 1960s to mid 1980s. Some other examples include the magnetic bottles and Biconic cusp. Because the mirror machines were straight, they had some advantages over a ring shape. First, mirrors were easier to construct and maintain and second direct conversion energy capture, was easier to implement. As the confinement achieved in experiments was poor, this approach was abandoned.

Magnetic Loops Another example of magnetic confinement is to bend the field lines back on themselves, either in circles or more commonly in nested toroidal surfaces. The most highly developed system of this type is the tokamak, with the stellarator being next most advanced, followed by the Reversed field pinch. Compact toroids, especially the Field-Reversed Configuration and the spheromak, attempt to combine the advantages of toroidal magnetic surfaces with those of a simply connected (non-toroidal) machine, resulting in a mechanically simpler and smaller confinement area.

Inertial confinement

Inertial confinement is the use of rapidly imploding shell to heat and confine plasma. The shell is imploded using a direct laser blast (direct drive) or a secondary x-ray blast (indirect drive) or heavy ion beams. Theoretically, fusion using lasers would be done using tiny pellets of fuel that explode several times a second. To induce the explosion, the pellet must be compressed to about 30 times solid density with energetic beams. If direct drive is used—the beams are focused directly on the pellet—it can in principle be very efficient, but in practice is difficult to obtain the needed uniformity. The alternative approach, indirect drive, uses beams to heat a shell, and then the shell radiates x-rays, which then implode the pellet. The beams are commonly laser beams, but heavy and light ion beams and electron beams have all been investigated.

Electrostatic confinement

There are also electrostatic confinement fusion devices. These devices confine ions using electrostatic fields. The best known is the Fusor. This device has a cathode inside an anode wire cage. Positive ions fly towards the negative inner cage, and are heated by the electric field in the process. If they miss the inner cage they can collide and fuse. Ions typically hit the cathode, however, creating prohibitory high conduction losses. Also, fusion rates in fusors are very low because of competing physical effects, such as energy loss in the form of light radiation. Designs have been proposed to avoid the problems associated with the cage, by generating the field using a non-neutral cloud. These include a plasma oscillating device, a magnetically-shielded-grid, a penning trap, the polywell, and the F1 cathode driver concept. The technology is relatively immature, however, and many scientific and engineering questions remain.

History of research

1920s

Research into nuclear fusion started in the early part of the 20th century. In 1920 the British physicist Francis William Aston discovered that the total mass equivalent of four hydrogen atoms (two protons and two neutrons) are heavier than the total mass of one helium atom (He-4), which implied that net energy can be released by combining hydrogen atoms together to form helium, and provided the first hints of a mechanism by which stars could produce energy in the quantities being measured. Through the 1920s, Arthur Stanley Eddington became a major proponent of the proton–proton chain reaction (PP reaction) as the primary system running the Sun.

1930s

Neutrons from fusion was first detected by staff members of Ernest Rutherfords' at the University of Cambridge, in 1933. The experiment was developed by Mark Oliphant and involved the acceleration of protons towards a target  at energies of up to 600,000 electron volts. In 1933, the Cavendish Laboratory received a gift from the American physical chemist Gilbert N. Lewis of a few drops of heavy water. The accelerator was used to fire heavy hydrogen nuclei deuterons at various targets. Working with Rutherford and others, Oliphant discovered the nuclei of Helium-3 (helions) and tritium (tritons).

A theory was verified by Hans Bethe in 1939 showing that beta decay and quantum tunneling in the Sun's core might convert one of the protons into a neutron and thereby producing deuterium rather than a diproton. The deuterium would then fuse through other reactions to further increase the energy output. For this work, Bethe won the Nobel Prize in Physics.

1940s

The first patent related to a fusion reactor was registered in 1946 by the United Kingdom Atomic Energy Authority. The inventors were Sir George Paget Thomson and Moses Blackman. This was the first detailed examination of the Z-pinch concept. Starting in 1947, two UK teams carried out small experiments based on this concept and began building a series of ever-larger experiments.

1950s

The first man-made device to achieve ignition was the detonation of this fusion device, codenamed Ivy Mike.

 

Early photo of plasma inside a pinch machine (imperial college 1950/1951)

The first successful man-made fusion device was the boosted fission weapon tested in 1951 in the Greenhouse Item test. This was followed by true fusion weapons in 1952's Ivy Mike, and the first practical examples in 1954's Castle Bravo. This was uncontrolled fusion. In these devices, the energy released by the fission explosion is used to compress and heat fusion fuel, starting a fusion reaction. Fusion releases neutrons. These neutrons hit the surrounding fission fuel, causing the atoms to split apart much faster than normal fission processes—almost instantly by comparison. This increases the effectiveness of bombs: normal fission weapons blow themselves apart before all their fuel is used; fusion/fission weapons do not have this practical upper limit. 

In 1949 an expatriate German, Ronald Richter, proposed the Huemul Project in Argentina, announcing positive results in 1951. These turned out to be fake, but it prompted considerable interest in the concept as a whole. In particular, it prompted Lyman Spitzer to begin considering ways to solve some of the more obvious problems involved in confining a hot plasma, and, unaware of the z-pinch efforts, he developed a new solution to the problem known as the stellarator. Spitzer applied to the US Atomic Energy Commission for funding to build a test device. During this period, James L. Tuck who had worked with the UK teams on z-pinch had been introducing the concept to his new coworkers at the Los Alamos National Laboratory (LANL). When he heard of Spitzer's pitch for funding, he applied to build a machine of his own, the Perhapsatron. 

Spitzer's idea won funding and he began work on the stellarator under the code name Project Matterhorn. His work led to the creation of the Princeton Plasma Physics Laboratory. Tuck returned to LANL and arranged local funding to build his machine. By this time, however, it was clear that all of the pinch machines were suffering from the same issues involving instability, and progress stalled. In 1953, Tuck and others suggested a number of solutions to the stability problems. This led to the design of a second series of pinch machines, led by the UK ZETA and Sceptre devices.

Spitzer had planned an aggressive development project of four machines, A, B, C, and D. A and B were small research devices, C would be the prototype of a power-producing machine, and D would be the prototype of a commercial device. A worked without issue, but even by the time B was being used it was clear the stellarator was also suffering from instabilities and plasma leakage. Progress on C slowed as attempts were made to correct for these problems.

By the mid-1950s it was clear that the simple theoretical tools being used to calculate the performance of all fusion machines were simply not predicting their actual behavior. Machines invariably leaked their plasma from their confinement area at rates far higher than predicted. In 1954, Edward Teller held a gathering of fusion researchers at the Princeton Gun Club, near the Project Matterhorn (now known as Project Sherwood) grounds. Teller started by pointing out the problems that everyone was having, and suggested that any system where the plasma was confined within concave fields was doomed to fail. Attendees remember him saying something to the effect that the fields were like rubber bands, and they would attempt to snap back to a straight configuration whenever the power was increased, ejecting the plasma. He went on to say that it appeared the only way to confine the plasma in a stable configuration would be to use convex fields, a "cusp" configuration.

When the meeting concluded, most of the researchers quickly turned out papers saying why Teller's concerns did not apply to their particular device. The pinch machines did not use magnetic fields in this way at all, while the mirror and stellarator seemed to have various ways out. This was soon followed by a paper by Martin David Kruskal and Martin Schwarzschild discussing pinch machines, however, which demonstrated instabilities in those devices were inherent to the design. 

The largest "classic" pinch device was the ZETA, including all of these suggested upgrades, starting operations in the UK in 1957. In early 1958, John Cockcroft announced that fusion had been achieved in the ZETA, an announcement that made headlines around the world. When physicists in the US expressed concerns about the claims they were initially dismissed. US experiments soon demonstrated the same neutrons, although temperature measurements suggested these could not be from fusion reactions. The neutrons seen in the UK were later demonstrated to be from different versions of the same instability processes that plagued earlier machines. Cockcroft was forced to retract the fusion claims, and the entire field was tainted for years. ZETA ended its experiments in 1968. 

The first experiment to achieve controlled thermonuclear fusion was accomplished using Scylla I at the Los Alamos National Laboratory in 1958. Scylla I was a θ-pinch machine, with a cylinder full of deuterium. Electric current shot down the sides of the cylinder. The current made magnetic fields that pinched the plasma, raising temperatures to 15 million degrees Celsius, for long enough that atoms fused and produce neutrons. The sherwood program sponsored a series of Scylla machines at Los Alamos. The program began with 5 researchers and 100,000 in US funding in January 1952. By 1965, a total of 21 million had been spent on the program and staffing never reached above 65. 

In 1950–1951 I.E. Tamm and A.D. Sakharov in the Soviet Union, first discussed a tokamak-like approach. Experimental research on those designs began in 1956 at the Kurchatov Institute in Moscow by a group of Soviet scientists led by Lev Artsimovich. The tokamak essentially combined a low-power pinch device with a low-power simple stellarator. The key was to combine the fields in such a way that the particles orbited within the reactor a particular number of times, today known as the "safety factor". The combination of these fields dramatically improved confinement times and densities, resulting in huge improvements over existing devices.

1960s

A key plasma physics text was published by Lyman Spitzer at Princeton in 1963. Spitzer took the ideal gas laws and adapted them to an ionized plasma, developing many of the fundamental equations used to model a plasma. 

Laser fusion was suggested in 1962 by scientists at Lawrence Livermore National Laboratory, shortly after the invention of the laser itself in 1960. At the time, Lasers were low power machines, but low-level research began as early as 1965. Laser fusion, formally known as inertial confinement fusion, involves imploding a target by using laser beams. There are two ways to do this: indirect drive and direct drive. In direct drive, the laser blasts a pellet of fuel. In indirect drive, the lasers blast a structure around the fuel. This makes x-rays that squeeze the fuel. Both methods compress the fuel so that fusion can take place.

At the 1964 World's Fair, the public was given its first demonstration of nuclear fusion. The device was a θ-pinch from General Electric. This was similar to the Scylla machine developed earlier at Los Alamos. 

The magnetic mirror was first published in 1967 by Richard F. Post and many others at the Lawrence Livermore National Laboratory. The mirror consisted of two large magnets arranged so they had strong fields within them, and a weaker, but connected, field between them. Plasma introduced in the area between the two magnets would "bounce back" from the stronger fields in the middle. 

The A.D. Sakharov group constructed the first tokamaks, the most successful being the T-3 and its larger version T-4. T-4 was tested in 1968 in Novosibirsk, producing the world's first quasistationary fusion reaction. When this were first announced, the international community was highly skeptical. A British team was invited to see T-3, however, and after measuring it in depth they released their results that confirmed the Soviet claims. A burst of activity followed as many planned devices were abandoned and new tokamaks were introduced in their place — the C model stellarator, then under construction after many redesigns, was quickly converted to the Symmetrical Tokamak. 

In his work with vacuum tubes, Philo Farnsworth observed that electric charge would accumulate in regions of the tube. Today, this effect is known as the Multipactor effect. Farnsworth reasoned that if ions were concentrated high enough they could collide and fuse. In 1962, he filed a patent on a design using a positive inner cage to concentrate plasma, in order to achieve nuclear fusion. During this time, Robert L. Hirsch joined the Farnsworth Television labs and began work on what became the fusor. Hirsch patented the design in 1966 and published the design in 1967.

1970s

Shiva laser, 1977, the largest ICF laser system built in the seventies

 

The Tandem Mirror Experiment (TMX) in 1979

In 1972, John Nuckolls outlined the idea of ignition. This is a fusion chain reaction. Hot helium made during fusion reheats the fuel and starts more reactions. John argued that ignition would require lasers of about 1 kJ. This turned out to be wrong. Nuckolls's paper started a major development effort. Several laser systems were built at LLNL. These included the argus, the Cyclops, the Janus, the long path, the Shiva laser and the Nova in 1984. This prompted the UK to build the Central Laser Facility in 1976.

During this time, great strides in understanding the tokamak system were made. A number of improvements to the design are now part of the "advanced tokamak" concept, which includes non-circular plasma, internal diverters and limiters, often superconducting magnets, and operate in the so-called "H-mode" island of increased stability. Two other designs have also become fairly well studied; the compact tokamak is wired with the magnets on the inside of the vacuum chamber, while the spherical tokamak reduces its cross section as much as possible.

In 1974 a study of the ZETA results demonstrated an interesting side-effect; after an experimental run ended, the plasma would enter a short period of stability. This led to the reversed field pinch concept, which has seen some level of development since. On May 1, 1974, the KMS fusion company (founded by Kip Siegel) achieves the world's first laser induced fusion in a deuterium-tritium pellet.

In the mid-1970s, Project PACER, carried out at Los Alamos National Laboratory (LANL) explored the possibility of a fusion power system that would involve exploding small hydrogen bombs (fusion bombs) inside an underground cavity. As an energy source, the system is the only fusion power system that could be demonstrated to work using existing technology. It would also require a large, continuous supply of nuclear bombs, however, making the economics of such a system rather questionable. 

In 1976, the two beam Argus laser becomes operational at livermore. In 1977, The 20 beam Shiva laser at Livermore is completed, capable of delivering 10.2 kilojoules of infrared energy on target. At a price of $25 million and a size approaching that of a football field, Shiva is the first of the megalasers. That same year, the JET project is approved by the European Commission and a site is selected.

1980s

Magnetic mirrors suffered from end losses, requiring high power, complex magnetic designs, such as the baseball coil pictured here.

 

The Novette target chamber (metal sphere with diagnostic devices protruding radially), which was reused from the Shiva project and two newly built laser chains visible in background.

 

Inertial confinement fusion implosion on the Nova laser during the 1980s was a key driver of fusion development.

As a result of advocacy, the cold war, and the 1970s energy crisis a massive magnetic mirror program was funded by the US federal government in the late 1970s and early 1980s. This program resulted in a series of large magnetic mirror devices including: 2X, Baseball I, Baseball II, the Tandem Mirror Experiment, the Tandem mirror experiment upgrade, the Mirror Fusion Test Facility and the MFTF-B. These machines were built and tested at Livermore from the late 1960s to the mid 1980s. A number of institutions collaborated on these machines, conducting experiments. These included the Institute for Advanced Study and the University of Wisconsin–Madison. The last machine, the Mirror Fusion Test Facility cost 372 million dollars and was, at that time, the most expensive project in Livermore history. It opened on February 21, 1986 and was promptly shut down. The reason given was to balance the United States federal budget. This program was supported from within the Carter and early Reagan administrations by Edwin E. Kintner, a US Navy captain, under Alvin Trivelpiece.

In Laser fusion progressed: in 1983, the NOVETTE laser was completed. The following December 1984, the ten beam NOVA laser was finished. Five years later, NOVA would produce a maximum of 120 kilojoules of infrared light, during a nanosecond pulse. Meanwhile, efforts focused on either fast delivery or beam smoothness. Both tried to deliver the energy uniformly to implode the target. One early problem was that the light in the infrared wavelength, lost lots of energy before hitting the fuel. Breakthroughs were made at the Laboratory for Laser Energetics at the University of Rochester. Rochester scientists used frequency-tripling crystals to transform the infrared laser beams into ultraviolet beams. In 1985, Donna Strickland and Gérard Mourou invented a method to amplify lasers pulses by "chirping". This method changes a single wavelength into a full spectrum. The system then amplifies the laser at each wavelength and then reconstitutes the beam into one color. Chirp pulsed amplification became instrumental in building the National Ignition Facility and the Omega EP system. Most research into ICF was towards weapons research, because the implosion is relevant to nuclear weapons. 

During this time Los Alamos National Laboratory constructed a series of laser facilities. This included Gemini (a two beam system), Helios (eight beams), Antares (24 beams) and Aurora (96 beams). The program ended in the early nineties with a cost on the order of one billion dollars.

In 1987, Akira Hasegawa  noticed that in a dipolar magnetic field, fluctuations tended to compress the plasma without energy loss. This effect was noticed in data taken by Voyager 2, when it encountered Uranus. This observation would become the basis for a fusion approach known as the Levitated dipole. 

In Tokamaks, the Tore Supra was under construction over the middle of the eighties (1983 to 1988). This was a Tokamak built in Cadarache, France. In 1983, the JET was completed and first plasmas achieved. In 1985, the Japanese tokamak, JT-60 was completed. In 1988, the T-15 a Soviet tokamak was completed. It was the first industrial fusion reactor to use superconducting magnets to control the plasma. These were Helium cooled. 

In 1989, Pons and Fleischmann submitted papers to the Journal of Electroanalytical Chemistry claiming that they had observed fusion in a room temperature device and disclosing their work in a press release. Some scientists reported excess heat, neutrons, tritium, helium and other nuclear effects in so-called cold fusion systems, which for a time gained interest as showing promise. Hopes fell when replication failures were weighed in view of several reasons cold fusion is not likely to occur, the discovery of possible sources of experimental error, and finally the discovery that Fleischmann and Pons had not actually detected nuclear reaction byproducts. By late 1989, most scientists considered cold fusion claims dead, and cold fusion subsequently gained a reputation as pathological science. However, a small community of researchers continues to investigate cold fusion claiming to replicate Fleishmann and Pons' results including nuclear reaction byproducts. Claims related to cold fusion are largely disbelieved in the mainstream scientific community. In 1989, the majority of a review panel organized by the US Department of Energy (DOE) found that the evidence for the discovery of a new nuclear process was not persuasive. A second DOE review, convened in 2004 to look at new research, reached conclusions similar to the first.

In 1984, Martin Peng of ORNL proposed an alternate arrangement of the magnet coils that would greatly reduce the aspect ratio while avoiding the erosion issues of the compact tokamak: a Spherical tokamak. Instead of wiring each magnet coil separately, he proposed using a single large conductor in the center, and wiring the magnets as half-rings off of this conductor. What was once a series of individual rings passing through the hole in the center of the reactor was reduced to a single post, allowing for aspect ratios as low as 1.2. The ST concept appeared to represent an enormous advance in tokamak design. However, it was being proposed during a period when US fusion research budgets were being dramatically scaled back. ORNL was provided with funds to develop a suitable central column built out of a high-strength copper alloy called "Glidcop". However, they were unable to secure funding to build a demonstration machine, "STX". Failing to build an ST at ORNL, Peng began a worldwide effort to interest other teams in the ST concept and get a test machine built. One way to do this quickly would be to convert a spheromak machine to the Spherical tokamak layout. Peng's advocacy also caught the interest of Derek Robinson, of the United Kingdom Atomic Energy Authority fusion center at Culham. Robinson was able to gather together a team and secure funding on the order of 100,000 pounds to build an experimental machine, the Small Tight Aspect Ratio Tokamak, or START. Several parts of the machine were recycled from earlier projects, while others were loaned from other labs, including a 40 keV neutral beam injector from ORNL. Construction of START began in 1990, it was assembled rapidly and started operation in January 1991.

1990s

Mockup of a gold-plated hohlraum designed for use in the National Ignition Facility

In 1991 the Preliminary Tritium Experiment at the Joint European Torus in England achieved the world's first controlled release of fusion power.

In 1992, a major article was published in Physics Today by Robert McCory at the Laboratory for laser energetics outlying the current state of ICF and advocating for a national ignition facility. This was followed up by a major review article, from John Lindl in 1995, advocating for NIF. During this time a number of ICF subsystems were developing, including target manufacturing, cryogenic handling systems, new laser designs (notably the NIKE laser at NRL) and improved diagnostics like time of flight analyzers and Thomson scattering. This work was done at the NOVA laser system, General Atomics, Laser Mégajoule and the GEKKO XII system in Japan. Through this work and lobbying by groups like the fusion power associates and John Sethian at NRL, a vote was made in congress, authorizing funding for the NIF project in the late nineties. 

In the early nineties, theory and experimental work regarding fusors and polywells was published. In response, Todd Rider at MIT developed general models of these devices. Rider argued that all plasma systems at thermodynamic equilibrium were fundamentally limited. In 1995, William Nevins published a criticism  arguing that the particles inside fusors and polywells would build up angular momentum, causing the dense core to degrade. 

In 1995, the University of Wisconsin–Madison built a large fusor, known as HOMER, which is still in operation. Meanwhile, Dr George H. Miley at Illinois, built a small fusor that has produced neutrons using deuterium gas  and discovered the "star mode" of fusor operation. The following year, the first "US-Japan Workshop on IEC Fusion", was conducted. At this time in Europe, an IEC device was developed as a commercial neutron source by Daimler-Chrysler and NSD Fusion.

In 1996, the Z-machine was upgraded and opened to the public by the US Army in August 1998 in Scientific American. The key attributes of Sandia's Z machine are its 18 million amperes and a discharge time of less than 100 nanoseconds. This generates a magnetic pulse, inside a large oil tank, this strikes an array of tungsten wires called a liner. Firing the Z-machine has become a way to test very high energy, high temperature (2 billion degrees) conditions. In 1996, the Tore Supra creates a plasma for two minutes with a current of almost 1 million amperes driven non-inductively by 2.3 MW of lower hybrid frequency waves. This is 280 MJ of injected and extracted energy. This result was possible because of the actively cooled plasma-facing components.

In 1997, JET produced a peak of 16.1MW of fusion power (65% of heat to plasma), with fusion power of over 10MW sustained for over 0.5 sec. Its successor, the International Thermonuclear Experimental Reactor (ITER), was officially announced as part of a seven-party consortium (six countries and the EU). ITER is designed to produce ten times more fusion power than the power put into the plasma. ITER is currently under construction in Cadarache, France.

In the late nineties, a team at Columbia University and MIT developed the Levitated dipole a fusion device which consisted of a superconducting electromagnet, floating in a saucer shaped vacuum chamber. Plasma swirled around this donut and fused along the center axis.

2000s

Starting in 1999, a growing number of amateurs have been able to fuse atoms using homemade fusors, shown here.

 

The Mega Ampere Spherical Tokamak became operational in the UK in 1999

In the March 8, 2002 issue of the peer-reviewed journal Science, Rusi P. Taleyarkhan and colleagues at the Oak Ridge National Laboratory (ORNL) reported that acoustic cavitation experiments conducted with deuterated acetone (C₃D₆O) showed measurements of tritium and neutron output consistent with the occurrence of fusion. Taleyarkhan was later found guilty of misconduct, the Office of Naval Research debarred him for 28 months from receiving Federal Funding, and his name was listed in the 'Excluded Parties List'.

"Fast ignition" was developed in the late nineties, and was part of a push by the Laboratory for Laser Energetics for building the Omega EP system. This system was finished in 2008. Fast ignition showed such dramatic power savings that ICF appears to be a useful technique for energy production. There are even proposals to build an experimental facility dedicated to the fast ignition approach, known as HiPER. 

In April 2005, a team from UCLA announced it had devised a way of producing fusion using a machine that "fits on a lab bench", using lithium tantalate to generate enough voltage to smash deuterium atoms together. The process, however, does not generate net power (see Pyroelectric fusion). Such a device would be useful in the same sort of roles as the fusor. In 2006, China's EAST test reactor is completed. This was the first tokamak to use superconducting magnets to generate both the toroidal and poloidal fields. 

In the early 2000s, Researchers at LANL reasoned that a plasma oscillating could be at local thermodynamic equilibrium. This prompted the POPS and Penning trap designs. At this time, researchers at MIT became interested in fusors for space propulsion and powering space vehicles. Specifically, researchers developed fusors with multiple inner cages. Greg Piefer graduated from Madison and founded Phoenix Nuclear Labs, a company that developed the fusor into a neutron source for the mass production of medical isotopes. Robert Bussard began speaking openly about the Polywell in 2006. He attempted to generate interest in the research, before his death. In 2008, Taylor Wilson achieved notoriety for achieving nuclear fusion at 14, with a homemade fusor.

In March 2009, a high-energy laser system, the National Ignition Facility (NIF), located at the Lawrence Livermore National Laboratory, became operational.

The early 2000s saw the founding of a number of privately backed fusion companies pursuing innovative approaches with the stated goal of developing commercially viable fusion power plants. Secretive startup Tri Alpha Energy, founded in 1998, began exploring a field-reversed configuration approach. In 2002, Canadian company General Fusion began proof-of-concept experiments based on a hybrid magneto-inertial approach called Magnetized Target Fusion. These companies are funded by private investors including Jeff Bezos (General Fusion) and Paul Allen (Tri Alpha Energy). Toward the end of the decade, UK-based fusion company Tokamak Energy started exploring spherical tokamak devices.

2010s

The preamplifiers of the National Ignition Facility. In 2012, the NIF achieved a 500-terawatt shot.

 

The Wendelstein7X under construction

 

Example of a stellarator design: A coil system (blue) surrounds plasma (yellow). A magnetic field line is highlighted in green on the yellow plasma surface.

NIF, the French Laser Mégajoule and the planned European Union High Power laser Energy Research (HiPER) facility continued researching inertial (laser) confinement. 

In 2010, NIF researchers conducted a series of "tuning" shots to determine the optimal target design and laser parameters for high-energy ignition experiments with fusion fuel. Firing tests were performed on October 31, 2010 and November 2, 2010. In early 2012, NIF director Mike Dunne expected the laser system to generate fusion with net energy gain by the end of 2012. However, that did not happen until August 2013. The facility reported that their next step involved improving the system to prevent the hohlraum from either breaking up asymmetrically or too soon.

A 2012 paper demonstrated that a dense plasma focus had achieved temperatures of 1.8 billion degrees Celsius, sufficient for boron fusion, and that fusion reactions were occurring primarily within the contained plasmoid, a necessary condition for net power.

In April 2014, Lawrence Livermore National Laboratory ended the Laser Inertial Fusion Energy (LIFE) program and redirected their efforts towards NIF. In August 2014, Phoenix Nuclear Labs announced the sale of a high-yield neutron generator that could sustain 5×10¹¹ deuterium fusion reactions per second over a 24-hour period.

In October 2014, Lockheed Martin's Skunk Works announced the development of a high beta fusion reactor, the Compact Fusion Reactor, intending on making a 100-megawatt prototype by 2017 and beginning regular operation by 2022. Although the original concept was to build a 20-ton, container-sized unit, the team later conceded that the minimum scale would be 2,000 tons.

In January 2015, the polywell was presented at Microsoft Research.

In August, 2015, MIT announced a tokamak it named ARC fusion reactor using rare-earth barium-copper oxide (REBCO) superconducting tapes to produce high-magnetic field coils that it claimed produce comparable magnetic field strength in a smaller configuration than other designs.

In October 2015, researchers at the Max Planck Institute of Plasma Physics completed building the largest stellarator to date, named Wendelstein 7-X. On December 10, they successfully produced the first helium plasma, and on February 3, 2016 produced the device's first hydrogen plasma. With plasma discharges lasting up to 30 minutes, Wendelstein 7-X is attempting to demonstrate the essential stellarator attribute: continuous operation of a high-temperature hydrogen plasma.

General Fusion developed its plasma injector technology and Tri Alpha Energy constructed and operated its C-2U device.

In 2017 Helion Energy's fifth-generation plasma machine went into operation, seeking to achieve plasma density of 20 Tesla and fusion temperatures. In 2018 General Fusion was developing a 70% scale demo system to be completed around 2023.

In 2018, energy corporation Eni announced a $50 million investment in the newly founded Commonwealth Fusion Systems, to attempt to commercialize ARC technology using a test reactor (SPARC) in collaboration with MIT.

Fuels

By firing particle beams at targets, many fusion reactions have been tested, while the fuels considered for power have all been light elements like the isotopes of hydrogen—protium, deuterium, and tritium. The deuterium and helium-3 reaction requires helium-3, an isotope of helium so scarce on Earth that it would have to be mined extraterrestrially or produced by other nuclear reactions. Finally, researchers hope to perform the protium and boron-11 reaction, because it does not directly produce neutrons, though side reactions can.

Deuterium, tritium

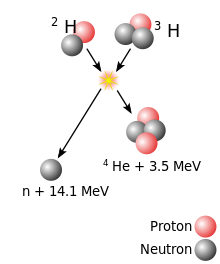
Diagram of the D-T reaction

The easiest nuclear reaction, at the lowest energy, is:

²
₁D
+ ³
₁T
→ ⁴
₂He
(3.5 MeV) + ¹
₀n
(14.1 MeV)

This reaction is common in research, industrial and military applications, usually as a convenient source of neutrons. Deuterium is a naturally occurring isotope of hydrogen and is commonly available. The large mass ratio of the hydrogen isotopes makes their separation easy compared to the difficult uranium enrichment process. Tritium is a natural isotope of hydrogen, but because it has a short half-life of 12.32 years, it is hard to find, store, produce, and is expensive. Consequently, the deuterium-tritium fuel cycle requires the breeding of tritium from lithium using one of the following reactions:

¹
₀n
+ ⁶
₃Li
→ ³
₁T
+ ⁴
₂He

¹
₀n
+ ⁷
₃Li
→ ³
₁T
+ ⁴
₂He
+ ¹
₀n

The reactant neutron is supplied by the D-T fusion reaction shown above, and the one that has the greatest yield of energy. The reaction with ⁶Li is exothermic, providing a small energy gain for the reactor. The reaction with ⁷Li is endothermic but does not consume the neutron. At least some neutron multiplication reactions are required to replace the neutrons lost to absorption by other elements. Leading candidate neutron multiplication materials are beryllium and lead however the ⁷Li reaction above also helps to keep the neutron population high. Natural lithium is mainly ⁷Li however this has a low tritium production cross section compared to ⁶Li so most reactor designs use breeder blankets with enriched ⁶Li. 

Several drawbacks are commonly attributed to D-T fusion power:

1. It produces substantial amounts of neutrons that result in the neutron activation of the reactor materials.
2. Only about 20% of the fusion energy yield appears in the form of charged particles with the remainder carried off by neutrons, which limits the extent to which direct energy conversion techniques might be applied.
3. It requires the handling of the radioisotope tritium. Similar to hydrogen, tritium is difficult to contain and may leak from reactors in some quantity. Some estimates suggest that this would represent a fairly large environmental release of radioactivity.

The neutron flux expected in a commercial D-T fusion reactor is about 100 times that of current fission power reactors, posing problems for material design. After a series of D-T tests at JET, the vacuum vessel was sufficiently radioactive that remote handling was required for the year following the tests.

In a production setting, the neutrons would be used to react with lithium in the context of a breeder blanket comprising lithium ceramic pebbles or liquid lithium, in order to create more tritium. This also deposits the energy of the neutrons in the lithium, which would then be transferred to drive electrical production. The lithium neutron absorption reaction protects the outer portions of the reactor from the neutron flux. Newer designs, the advanced tokamak in particular, also use lithium inside the reactor core as a key element of the design. The plasma interacts directly with the lithium, preventing a problem known as "recycling". The advantage of this design was demonstrated in the Lithium Tokamak Experiment.

Deuterium

Deuterium fusion cross section (in square meters) at different ion collision energies.

This is the second easiest fusion reaction, fusing two deuterium nuclei. The reaction has two branches that occur with nearly equal probability:

D + D	→ T	+ 1H
D + D	→ 3He	+ n

This reaction is also common in research. The optimum energy to initiate this reaction is 15 keV, only slightly higher than the optimum for the D-T reaction. The first branch does not produce neutrons, but it does produce tritium, so that a D-D reactor will not be completely tritium-free, even though it does not require an input of tritium or lithium. Unless the tritons can be quickly removed, most of the tritium produced would be burned before leaving the reactor, which would reduce the handling of tritium, but would produce more neutrons, some of which are very energetic. The neutron from the second branch has an energy of only 2.45 MeV (0.393 pJ), whereas the neutron from the D-T reaction has an energy of 14.1 MeV (2.26 pJ), resulting in a wider range of isotope production and material damage. When the tritons are removed quickly while allowing the ³He to react, the fuel cycle is called "tritium suppressed fusion" The removed tritium decays to ³He with a 12.5 year half life. By recycling the ³He produced from the decay of tritium back into the fusion reactor, the fusion reactor does not require materials resistant to fast 14.1 MeV (2.26 pJ) neutrons. 

Assuming complete tritium burn-up, the reduction in the fraction of fusion energy carried by neutrons would be only about 18%, so that the primary advantage of the D-D fuel cycle is that tritium breeding would not be required. Other advantages are independence from scarce lithium resources and a somewhat softer neutron spectrum. The disadvantage of D-D compared to D-T is that the energy confinement time (at a given pressure) must be 30 times longer and the power produced (at a given pressure and volume) would be 68 times less.

Assuming complete removal of tritium and recycling of ³He, only 6% of the fusion energy is carried by neutrons. The tritium-suppressed D-D fusion requires an energy confinement that is 10 times longer compared to D-T and a plasma temperature that is twice as high.

Deuterium, helium-3

A second-generation approach to controlled fusion power involves combining helium-3 (³He) and deuterium (²H):

D + 3He

→ 4He

+ 1H

This reaction produces a helium-4 nucleus (⁴He) and a high-energy proton. As with the p-¹¹B aneutronic fusion fuel cycle, most of the reaction energy is released as charged particles, reducing activation of the reactor housing and potentially allowing more efficient energy harvesting (via any of several speculative technologies). In practice, D-D side reactions produce a significant number of neutrons, resulting in p-¹¹B being the preferred cycle for aneutronic fusion.

Protium, boron-11

If aneutronic fusion is the goal, then the most promising candidate may be the hydrogen-1 (protium) and boron reaction, which releases alpha (helium) particles, but does not rely on neutron scattering for energy transfer.

¹H + ¹¹B → 3 ⁴He

Under reasonable assumptions, side reactions will result in about 0.1% of the fusion power being carried by neutrons. At 123 keV, the optimum temperature for this reaction is nearly ten times higher than that for the pure hydrogen reactions, the energy confinement must be 500 times better than that required for the D-T reaction, and the power density will be 2500 times lower than for D-T. 

Because the confinement properties of conventional approaches to fusion such as the tokamak and laser pellet fusion are marginal, most proposals for aneutronic fusion are based on radically different confinement concepts, such as the Polywell and the Dense Plasma Focus. Results have been extremely promising:

In the October 2013 edition of Nature Communications, a research team led by Christine Labaune at École Polytechnique in Palaiseau, France, reported a new record fusion rate: an estimated 80 million fusion reactions during the 1.5 nanoseconds that the laser fired, which is at least 100 times more than any previous proton-boron experiment.

Material selection

Considerations

Even on smaller plasma production scales, the material of the containment apparatus will be intensely blasted with matter and energy. Designs for plasma containment must consider:

• A heating and cooling cycle, up to a 10 MW/m² thermal load.
• Neutron radiation, which over time leads to neutron activation and embrittlement.
• High energy ions leaving at tens to hundreds of electronvolts.
• Alpha particles leaving at millions of electronvolts.
• Electrons leaving at high energy.
• Light radiation (IR, visible, UV, X-ray).

Depending on the approach, these effects may be higher or lower than typical fission reactors like the pressurized water reactor (PWR). One estimate put the radiation at 100 times that of a typical PWR. Materials need to be selected or developed that can withstand these basic conditions. Depending on the approach, however, there may be other considerations such as electrical conductivity, magnetic permeability and mechanical strength. There is also a need for materials whose primary components and impurities do not result in long-lived radioactive wastes.

Durability

For long term use, each atom in the wall is expected to be hit by a neutron and displaced about a hundred times before the material is replaced. High-energy neutrons will produce hydrogen and helium by way of various nuclear reactions that tends to form bubbles at grain boundaries and result in swelling, blistering or embrittlement.

Selection

One can choose either a low-Z material, such as graphite or beryllium, or a high-Z material, usually tungsten with molybdenum as a second choice. Use of liquid metals (lithium, gallium, tin) has also been proposed, e.g., by injection of 1–5 mm thick streams flowing at 10 m/s on solid substrates.

If graphite is used, the gross erosion rates due to physical and chemical sputtering would be many meters per year, so one must rely on redeposition of the sputtered material. The location of the redeposition will not exactly coincide with the location of the sputtering, so one is still left with erosion rates that may be prohibitive. An even larger problem is the tritium co-deposited with the redeposited graphite. The tritium inventory in graphite layers and dust in a reactor could quickly build up to many kilograms, representing a waste of resources and a serious radiological hazard in case of an accident. The consensus of the fusion community seems to be that graphite, although a very attractive material for fusion experiments, cannot be the primary plasma-facing material (PFM) in a commercial reactor. 

The sputtering rate of tungsten by the plasma fuel ions is orders of magnitude smaller than that of carbon, and tritium is much less incorporated into redeposited tungsten, making this a more attractive choice. On the other hand, tungsten impurities in a plasma are much more damaging than carbon impurities, and self-sputtering of tungsten can be high, so it will be necessary to ensure that the plasma in contact with the tungsten is not too hot (a few tens of eV rather than hundreds of eV). Tungsten also has disadvantages in terms of eddy currents and melting in off-normal events, as well as some radiological issues.

Safety and the environment

Accident potential

Unlike nuclear fission, fusion requires extremely precise and controlled temperature, pressure and magnetic field parameters for any net energy to be produced. If a reactor suffers damage or loses even a small degree of required control, fusion reactions and heat generation would rapidly cease. Additionally, fusion reactors contain only small amounts of fuel, enough to "burn" for minutes, or in some cases, microseconds. Unless they are actively refueled, the reactions will quickly end. Therefore, fusion reactors are considered immune from catastrophic meltdown.

For similar reasons, runaway reactions cannot occur in a fusion reactor. The plasma is burnt at optimal conditions, and any significant change will simply quench the reactions. The reaction process is so delicate that this level of safety is inherent. Although the plasma in a fusion power station is expected to have a volume of 1,000 cubic metres (35,000 cu ft) or more, the plasma density is low and typically contains only a few grams of fuel in use. If the fuel supply is closed, the reaction stops within seconds. In comparison, a fission reactor is typically loaded with enough fuel for several months or years, and no additional fuel is necessary to continue the reaction. It is this large amount of fuel that gives rise to the possibility of a meltdown; nothing like this exists in a fusion reactor.

In the magnetic approach, strong fields are developed in coils that are held in place mechanically by the reactor structure. Failure of this structure could release this tension and allow the magnet to "explode" outward. The severity of this event would be similar to any other industrial accident or an MRI machine quench/explosion, and could be effectively stopped with a containment building similar to those used in existing (fission) nuclear generators. The laser-driven inertial approach is generally lower-stress because of the increased size of the reaction chamber. Although failure of the reaction chamber is possible, simply stopping fuel delivery would prevent any sort of catastrophic failure.

Most reactor designs rely on liquid hydrogen as both a coolant and a method for converting stray neutrons from the reaction into tritium, which is fed back into the reactor as fuel. Hydrogen is highly flammable, and in the case of a fire it is possible that the hydrogen stored on-site could be burned up and escape. In this case, the tritium contents of the hydrogen would be released into the atmosphere, posing a radiation risk. Calculations suggest that at about 1 kilogram (2.2 lb), the total amount of tritium and other radioactive gases in a typical power station would be so small that they would have diluted to legally acceptable limits by the time they blew as far as the station's perimeter fence.

The likelihood of small industrial accidents, including the local release of radioactivity and injury to staff, cannot be estimated yet. These would include accidental releases of lithium or tritium or mishandling of decommissioned radioactive components of the reactor itself.

Magnet quench

A quench is an abnormal termination of magnet operation that occurs when part of the superconducting coil enters the normal (resistive) state. This can occur because the field inside the magnet is too large, the rate of change of field is too large (causing eddy currents and resultant heating in the copper support matrix), or a combination of the two. 

More rarely a defect in the magnet can cause a quench. When this happens, that particular spot is subject to rapid Joule heating from the enormous current, which raises the temperature of the surrounding regions. This pushes those regions into the normal state as well, which leads to more heating in a chain reaction. The entire magnet rapidly becomes normal (this can take several seconds, depending on the size of the superconducting coil). This is accompanied by a loud bang as the energy in the magnetic field is converted to heat, and rapid boil-off of the cryogenic fluid. The abrupt decrease of current can result in kilovolt inductive voltage spikes and arcing. Permanent damage to the magnet is rare, but components can be damaged by localized heating, high voltages, or large mechanical forces. 

In practice, magnets usually have safety devices to stop or limit the current when the beginning of a quench is detected. If a large magnet undergoes a quench, the inert vapor formed by the evaporating cryogenic fluid can present a significant asphyxiation hazard to operators by displacing breathable air. 

A large section of the superconducting magnets in CERN's Large Hadron Collider unexpectedly quenched during start-up operations in 2008, necessitating the replacement of a number of magnets. In order to mitigate against potentially destructive quenches, the superconducting magnets that form the LHC are equipped with fast-ramping heaters which are activated once a quench event is detected by the complex quench protection system. As the dipole bending magnets are connected in series, each power circuit includes 154 individual magnets, and should a quench event occur, the entire combined stored energy of these magnets must be dumped at once. This energy is transferred into dumps that are massive blocks of metal which heat up to several hundreds of degrees Celsius—because of resistive heating—in a matter of seconds. Although undesirable, a magnet quench is a "fairly routine event" during the operation of a particle accelerator.

Effluents

The natural product of the fusion reaction is a small amount of helium, which is completely harmless to life. Of more concern is tritium, which, like other isotopes of hydrogen, is difficult to retain completely. During normal operation, some amount of tritium will be continually released.

Although tritium is volatile and biologically active, the health risk posed by a release is much lower than that of most radioactive contaminants, because of tritium's short half-life (12.32 years) and very low decay energy (~14.95 keV), and because it does not bioaccumulate (instead being cycled out of the body as water, with a biological half-life of 7 to 14 days). Current ITER designs are investigating total containment facilities for any tritium.

Waste management

The large flux of high-energy neutrons in a reactor will make the structural materials radioactive. The radioactive inventory at shut-down may be comparable to that of a fission reactor, but there are important differences. 

The half-life of the radioisotopes produced by fusion tends to be less than those from fission, so that the inventory decreases more rapidly. Unlike fission reactors, whose waste remains radioactive for thousands of years, most of the radioactive material in a fusion reactor would be the reactor core itself, which would be dangerous for about 50 years, and low-level waste for another 100. Although this waste will be considerably more radioactive during those 50 years than fission waste, the very short half-life makes the process very attractive, as the waste management is fairly straightforward. By 500 years the material would have the same radiotoxicity as coal ash.

Additionally, the choice of materials used in a fusion reactor is less constrained than in a fission design, where many materials are required for their specific neutron cross-sections. This allows a fusion reactor to be designed using materials that are selected specifically to be "low activation", materials that do not easily become radioactive. Vanadium, for example, would become much less radioactive than stainless steel. Carbon fiber materials are also low-activation, as well as being strong and light, and are a promising area of study for laser-inertial reactors where a magnetic field is not required. 

In general terms, fusion reactors would create far less radioactive material than a fission reactor, the material it would create is less damaging biologically, and the radioactivity "burns off" within a time period that is well within existing engineering capabilities for safe long-term waste storage.

Nuclear proliferation

Although fusion power uses nuclear technology, the overlap with nuclear weapons would be limited. A huge amount of tritium could be produced by a fusion power station; tritium is used in the trigger of hydrogen bombs and in a modern boosted fission weapon, but it can also be produced by nuclear fission. The energetic neutrons from a fusion reactor could be used to breed weapons-grade plutonium or uranium for an atomic bomb (for example by transmutation of U²³⁸ to Pu²³⁹, or Th²³² to U²³³). 

A study conducted 2011 assessed the risk of three scenarios:

• Use in small-scale fusion station: As a result of much higher power consumption, heat dissipation and a more recognizable design compared to enrichment gas centrifuges this choice would be much easier to detect and therefore implausible.
• Modifications to produce weapon-usable material in a commercial facility: The production potential is significant. But no fertile or fissile substances necessary for the production of weapon-usable materials needs to be present at a civil fusion system at all. If not shielded, a detection of these materials can be done by their characteristic gamma radiation. The underlying redesign could be detected by regular design information verifications. In the (technically more feasible) case of solid breeder blanket modules, it would be necessary for incoming components to be inspected for the presence of fertile material, otherwise plutonium for several weapons could be produced each year.
• Prioritizing a fast production of weapon-grade material regardless of secrecy: The fastest way to produce weapon usable material was seen in modifying a prior civil fusion power station. Unlike in some nuclear power stations, there is no weapon compatible material during civil use. Even without the need for covert action this modification would still take about 2 months to start the production and at least an additional week to generate a significant amount for weapon production. This was seen as enough time to detect a military use and to react with diplomatic or military means. To stop the production, a military destruction of inevitable parts of the facility leaving out the reactor itself would be sufficient. This, together with the intrinsic safety of fusion power would only bear a low risk of radioactive contamination.

Another study concludes that "[..]large fusion reactors – even if not designed for fissile material breeding – could easily produce several hundred kg Pu per year with high weapon quality and very low source material requirements." It was emphasized that the implementation of features for intrinsic proliferation resistance might only be possible at this phase of research and development. The theoretical and computational tools needed for hydrogen bomb design are closely related to those needed for inertial confinement fusion, but have very little in common with the more scientifically developed magnetic confinement fusion.

Energy source

Large-scale reactors using neutronic fuels (e.g. ITER) and thermal power production (turbine based) are most comparable to fission power from an engineering and economics viewpoint. Both fission and fusion power stations involve a relatively compact heat source powering a conventional steam turbine-based power station, while producing enough neutron radiation to make activation of the station materials problematic. The main distinction is that fusion power produces no high-level radioactive waste (though activated station materials still need to be disposed of). There are some power station ideas that may significantly lower the cost or size of such stations; however, research in these areas is nowhere near as advanced as in tokamaks.

Fusion power commonly proposes the use of deuterium, an isotope of hydrogen, as fuel and in many current designs also use lithium. Assuming a fusion energy output equal to the 1995 global power output of about 100 EJ/yr (= 1 × 10²⁰ J/yr) and that this does not increase in the future, which is unlikely, then the known current lithium reserves would last 3000 years. Lithium from sea water would last 60 million years, however, and a more complicated fusion process using only deuterium would have fuel for 150 billion years. To put this in context, 150 billion years is close to 30 times the remaining lifespan of the sun, and more than 10 times the estimated age of the universe.

Economics

While fusion power is still in early stages of development, substantial sums have been and continue to be invested in research. In the EU almost €10 billion was spent on fusion research up to the end of the 1990s, and the new ITER reactor alone is budgeted at €6.6 billion total for the timeframe between 2008 and 2020.

It is estimated that up to the point of possible implementation of electricity generation by nuclear fusion, R&D will need further promotion totalling around €60–80 billion over a period of 50 years or so (of which €20–30 billion within the EU) based on a report from 2002. Nuclear fusion research receives €750 million (excluding ITER funding) from the European Union, compared with €810 million for sustainable energy research, putting research into fusion power well ahead of that of any single rivaling technology. Indeed, the size of the investments and time frame of the expected results mean that fusion research is almost exclusively publicly funded, while research in other forms of energy can be done by the private sector. In spite of that, a number of start-up companies active in the field of fusion power have managed to attract private money.

Advantages

Fusion power would provide more energy for a given weight of fuel than any fuel-consuming energy source currently in use, and the fuel itself (primarily deuterium) exists abundantly in the Earth's ocean: about 1 in 6500 hydrogen atoms in seawater is deuterium. Although this may seem a low proportion (about 0.015%), because nuclear fusion reactions are so much more energetic than chemical combustion and seawater is easier to access and more plentiful than fossil fuels, fusion could potentially supply the world's energy needs for millions of years.

Despite being technically non-renewable, fusion power (like fission power using breeder reactors and reprocessing) has many of the benefits of renewable energy sources (such as being a long-term energy supply and emitting no greenhouse gases or air pollution) as well as some of the benefits of the resource-limited energy sources as hydrocarbons and nuclear fission (without reprocessing). Like these currently dominant energy sources, fusion could provide very high power-generation density and uninterrupted power delivery (because it is not dependent on the weather, unlike wind and solar power). 

Another aspect of fusion energy is that the cost of production does not suffer from diseconomies of scale. The cost of water and wind energy, for example, goes up as the optimal locations are developed first, while further generators must be sited in less ideal conditions. With fusion energy the production cost will not increase much even if large numbers of stations are built, because the raw resource (seawater) is abundant and widespread.

Some problems that are expected to be an issue in this century, such as fresh water shortages, can alternatively be regarded as problems of energy supply. For example, in desalination stations, seawater can be purified through distillation or reverse osmosis. Nonetheless, these processes are energy intensive. Even if the first fusion stations are not competitive with alternative sources, fusion could still become competitive if large-scale desalination requires more power than the alternatives are able to provide.

A scenario has been presented of the effect of the commercialization of fusion power on the future of human civilization. ITER and later DEMO are envisioned to bring online the first commercial nuclear fusion energy reactor by 2050. Using this as the starting point and the history of the uptake of nuclear fission reactors as a guide, the scenario depicts a rapid take up of nuclear fusion energy starting after the middle of this century.

Fusion power could be used in interstellar space, where solar energy is not available.

Quantum dot

From Wikipedia, the free encyclopedia

Colloidal quantum dots irradiated with a UV light. Different sized quantum dots emit different color light due to quantum confinement.

Quantum dots (QD) are very small semiconductor particles, only several nanometres in size, so small that their optical and electronic properties differ from those of larger LED particles. They are a central theme in nanotechnology. Many types of quantum dot will emit light of specific frequencies if electricity or light is applied to them, and these frequencies can be precisely tuned by changing the dots' size, shape and material, giving rise to many applications. 

In the language of materials science, nanoscale semiconductor materials tightly confine either electrons or electron holes. Quantum dots are also sometimes referred to as artificial atoms, a term that emphasizes that a quantum dot is a single object with bound, discrete electronic states, as is the case with naturally occurring atoms or molecules.

Quantum dots exhibit properties that are intermediate between those of bulk semiconductors and those of discrete atoms or molecules. Their optoelectronic properties change as a function of both size and shape. Larger QDs (diameter of 5–6 nm, for example) emit longer wavelengths resulting in emission colors such as orange or red. Smaller QDs (diameter of 2–3 nm, for example) emit shorter wavelengths resulting in colors like blue and green, although the specific colors and sizes vary depending on the exact composition of the QD.

Because of their highly tunable properties, QDs are of wide interest. Potential applications include transistors, solar cells, LEDs, diode lasers and second-harmonic generation, quantum computing, and medical imaging. Additionally, their small size allows for QDs to be suspended in solution which leads to possible uses in inkjet printing and spin-coating. They have also been used in Langmuir-Blodgett thin-films. These processing techniques result in less expensive and less time-consuming methods of semiconductor fabrication.

Production

Quantum Dots with gradually stepping emission from violet to deep red

There are several ways to prepare quantum dots, the principal ones involving colloids.

Colloidal synthesis

Colloidal semiconductor nanocrystals are synthesized from solutions, much like traditional chemical processes. The main difference is the product neither precipitates as a bulk solid nor remains dissolved. Heating the solution at high temperature, the precursors decompose forming monomers which then nucleate and generate nanocrystals. Temperature is a critical factor in determining optimal conditions for the nanocrystal growth. It must be high enough to allow for rearrangement and annealing of atoms during the synthesis process while being low enough to promote crystal growth. The concentration of monomers is another critical factor that has to be stringently controlled during nanocrystal growth. The growth process of nanocrystals can occur in two different regimes, "focusing" and "defocusing". At high monomer concentrations, the critical size (the size where nanocrystals neither grow nor shrink) is relatively small, resulting in growth of nearly all particles. In this regime, smaller particles grow faster than large ones (since larger crystals need more atoms to grow than small crystals) resulting in "focusing" of the size distribution to yield nearly monodisperse particles. The size focusing is optimal when the monomer concentration is kept such that the average nanocrystal size present is always slightly larger than the critical size. Over time, the monomer concentration diminishes, the critical size becomes larger than the average size present, and the distribution "defocuses". 

Cadmium sulfide quantum dots on cells

There are colloidal methods to produce many different semiconductors. Typical dots are made of binary compounds such as lead sulfide, lead selenide, cadmium selenide, cadmium sulfide, cadmium telluride, indium arsenide, and indium phosphide. Dots may also be made from ternary compounds such as cadmium selenide sulfide. These quantum dots can contain as few as 100 to 100,000 atoms within the quantum dot volume, with a diameter of ≈10 to 50 atoms. This corresponds to about 2 to 10 nanometers, and at 10 nm in diameter, nearly 3 million quantum dots could be lined up end to end and fit within the width of a human thumb. 

Ideallized image of colloidal nanoparticle of lead sulfide (selenide) with complete passivation by oleic acid, oleyl amine and hydroxyl ligands (size ≈5nm)

Large batches of quantum dots may be synthesized via colloidal synthesis. Due to this scalability and the convenience of benchtop conditions, colloidal synthetic methods are promising for commercial applications. It is acknowledged^{[citation needed]} to be the least toxic of all the different forms of synthesis.

Plasma synthesis

Plasma synthesis has evolved to be one of the most popular gas-phase approaches for the production of quantum dots, especially those with covalent bonds. For example, silicon (Si) and germanium (Ge) quantum dots have been synthesized by using nonthermal plasma. The size, shape, surface and composition of quantum dots can all be controlled in nonthermal plasma. Doping that seems quite challenging for quantum dots has also been realized in plasma synthesis. Quantum dots synthesized by plasma are usually in the form of powder, for which surface modification may be carried out. This can lead to excellent dispersion of quantum dots in either organic solvents or water (i. e., colloidal quantum dots).

Fabrication

• Self-assembled quantum dots are typically between 5 and 50 nm in size. Quantum dots defined by lithographically patterned gate electrodes, or by etching on two-dimensional electron gasses in semiconductor heterostructures can have lateral dimensions between 20 and 100 nm.
• Some quantum dots are small regions of one material buried in another with a larger band gap. These can be so-called core–shell structures, e.g., with CdSe in the core and ZnS in the shell, or from special forms of silica called ormosil. Sub-monolayer shells can also be effective ways of passivating the quantum dots, such as PbS cores with sub-monolayer CdS shells.
• Quantum dots sometimes occur spontaneously in quantum well structures due to monolayer fluctuations in the well's thickness.
• Self-assembled quantum dots nucleate spontaneously under certain conditions during molecular beam epitaxy (MBE) and metallorganic vapor phase epitaxy (MOVPE), when a material is grown on a substrate to which it is not lattice matched. The resulting strain produces coherently strained islands on top of a two-dimensional wetting layer. This growth mode is known as Stranski–Krastanov growth. The islands can be subsequently buried to form the quantum dot. This fabrication method has potential for applications in quantum cryptography (i.e. single photon sources) and quantum computation. The main limitations of this method are the cost of fabrication and the lack of control over positioning of individual dots.
• Individual quantum dots can be created from two-dimensional electron or hole gases present in remotely doped quantum wells or semiconductor heterostructures called lateral quantum dots. The sample surface is coated with a thin layer of resist. A lateral pattern is then defined in the resist by electron beam lithography. This pattern can then be transferred to the electron or hole gas by etching, or by depositing metal electrodes (lift-off process) that allow the application of external voltages between the electron gas and the electrodes. Such quantum dots are mainly of interest for experiments and applications involving electron or hole transport, i.e., an electrical current.
• The energy spectrum of a quantum dot can be engineered by controlling the geometrical size, shape, and the strength of the confinement potential. Also, in contrast to atoms, it is relatively easy to connect quantum dots by tunnel barriers to conducting leads, which allows the application of the techniques of tunneling spectroscopy for their investigation.

The quantum dot absorption features correspond to transitions between discrete, three-dimensional particle in a box states of the electron and the hole, both confined to the same nanometer-size box.These discrete transitions are reminiscent of atomic spectra and have resulted in quantum dots also being called artificial atoms.

• Confinement in quantum dots can also arise from electrostatic potentials (generated by external electrodes, doping, strain, or impurities).
• Complementary metal-oxide-semiconductor (CMOS) technology can be employed to fabricate silicon quantum dots. Ultra small (L=20 nm, W=20 nm) CMOS transistors behave as single electron quantum dots when operated at cryogenic temperature over a range of −269 °C (4 K) to about −258 °C (15 K). The transistor displays Coulomb blockade due to progressive charging of electrons one by one. The number of electrons confined in the channel is driven by the gate voltage, starting from an occupation of zero electrons, and it can be set to 1 or many.

Viral assembly

Genetically engineered M13 bacteriophage viruses allow preparation of quantum dot biocomposite structures. It had previously been shown that genetically engineered viruses can recognize specific semiconductor surfaces through the method of selection by combinatorial phage display. Additionally, it is known that liquid crystalline structures of wild-type viruses (Fd, M13, and TMV) are adjustable by controlling the solution concentrations, solution ionic strength, and the external magnetic field applied to the solutions. Consequently, the specific recognition properties of the virus can be used to organize inorganic nanocrystals, forming ordered arrays over the length scale defined by liquid crystal formation. Using this information, Lee et al. (2000) were able to create self-assembled, highly oriented, self-supporting films from a phage and ZnS precursor solution. This system allowed them to vary both the length of bacteriophage and the type of inorganic material through genetic modification and selection.

Electrochemical assembly

Highly ordered arrays of quantum dots may also be self-assembled by electrochemical techniques. A template is created by causing an ionic reaction at an electrolyte-metal interface which results in the spontaneous assembly of nanostructures, including quantum dots, onto the metal which is then used as a mask for mesa-etching these nanostructures on a chosen substrate.

Bulk-manufacture

Quantum dot manufacturing relies on a process called "high temperature dual injection" which has been scaled by multiple companies for commercial applications that require large quantities (hundreds of kilograms to tonnes) of quantum dots. This reproducible production method can be applied to a wide range of quantum dot sizes and compositions.

The bonding in certain cadmium-free quantum dots, such as III-V-based quantum dots, is more covalent than that in II-VI materials, therefore it is more difficult to separate nanoparticle nucleation and growth via a high temperature dual injection synthesis. An alternative method of quantum dot synthesis, the “molecular seeding” process, provides a reproducible route to the production of high quality quantum dots in large volumes. The process utilises identical molecules of a molecular cluster compound as the nucleation sites for nanoparticle growth, thus avoiding the need for a high temperature injection step. Particle growth is maintained by the periodic addition of precursors at moderate temperatures until the desired particle size is reached. The molecular seeding process is not limited to the production of cadmium-free quantum dots; for example, the process can be used to synthesise kilogram batches of high quality II-VI quantum dots in just a few hours. 

Another approach for the mass production of colloidal quantum dots can be seen in the transfer of the well-known hot-injection methodology for the synthesis to a technical continuous flow system. The batch-to-batch variations arising from the needs during the mentioned methodology can be overcome by utilizing technical components for mixing and growth as well as transport and temperature adjustments. For the production of CdSe based semiconductor nanoparticles this method has been investigated and tuned to production amounts of kg per month. Since the use of technical components allows for easy interchange in regards of maximum through-put and size, it can be further enhanced to tens or even hundreds of kilograms.

In 2011 a consortium of U.S. and Dutch companies reported a "milestone" in high volume quantum dot manufacturing by applying the traditional high temperature dual injection method to a flow system.

On January 23, 2013 Dow entered into an exclusive licensing agreement with UK-based Nanoco for the use of their low-temperature molecular seeding method for bulk manufacture of cadmium-free quantum dots for electronic displays, and on September 24, 2014 Dow commenced work on the production facility in South Korea capable of producing sufficient quantum dots for "millions of cadmium-free televisions and other devices, such as tablets". Mass production is due to commence in mid-2015. On 24 March 2015 Dow announced a partnership deal with LG Electronics to develop the use of cadmium free quantum dots in displays.

Heavy-metal-free quantum dots

In many regions of the world there is now a restriction or ban on the use of heavy metals in many household goods, which means that most cadmium-based quantum dots are unusable for consumer-goods applications. 

For commercial viability, a range of restricted, heavy-metal-free quantum dots has been developed showing bright emissions in the visible and near infra-red region of the spectrum and have similar optical properties to those of CdSe quantum dots. Among these systems are InP/ZnS and CuInS/ZnS, for example.

Peptides are being researched as potential quantum dot material. Since peptides occur naturally in all organisms, such dots would likely be nontoxic and easily biodegraded.

Health and safety

Some quantum dots pose risks to human health and the environment under certain conditions. Notably, the studies on quantum dot toxicity are focused on cadmium containing particles and has yet to be demonstrated in animal models after physiologically relevant dosing. In vitro studies, based on cell cultures, on quantum dots (QD) toxicity suggests that their toxicity may derive from multiple factors including its physicochemical characteristics (size, shape, composition, surface functional groups, and surface charges) and environment. Assessing their potential toxicity is complex as these factors include properties such as QD size, charge, concentration, chemical composition, capping ligands, and also on their oxidative, mechanical and photolytic stability.

Many studies have focused on the mechanism of QD cytotoxicity using model cell cultures. It has been demonstrated that after exposure to ultraviolet radiation or oxidation by air, CdSe QDs release free cadmium ions causing cell death. Group II-VI QDs also have been reported to induce the formation of reactive oxygen species after exposure to light, which in turn can damage cellular components such as proteins, lipids and DNA. Some studies have also demonstrated that addition of a ZnS shell inhibit the process of reactive oxygen species in CdSe QDs. Another aspect of QD toxicity is the process of their size dependent intracellular pathways that concentrate these particles in cellular organelles that are inaccessible by metal ions, which may result in unique patterns of cytotoxicity compared to their constituent metal ions. The reports of QD localization in the cell nucleus present additional modes of toxicity because they may induce DNA mutation, which in turn will propagate through future generation of cells causing diseases. 

Although concentration of QDs in certain organelles have been reported in in vivo studies using animal models, no alterations in animal behavior, weight, hematological markers or organ damage has been found through either histological or biochemical analysis. These finding have led scientists to believe that intracellular dose is the most important deterring factor for QD toxicity. Therefore, factors determining the QD endocytosis that determine the effective intracellular concentration, such as QD size, shape and surface chemistry determine their toxicity. Excretion of QDs through urine in animal models also have demonstrated via injecting radio-labeled ZnS capped CdSe QDs where the ligand shell was labelled with ^99mTc. Though multiple other studies have concluded retention of QDs in cellular levels, exocytosis of QDs is still poorly studied in the literature. 

While significant research efforts have broadened the understanding of toxicity of QDs, there are large discrepancies in the literature and questions still remains to be answered. Diversity of this class material as compared to normal chemical substances makes the assessment of their toxicity very challenging. As their toxicity may also be dynamic depending on the environmental factors such as pH level, light exposure and cell type, traditional methods of assessing toxicity of chemicals such as LD₅₀ are not applicable for QDs. Therefore, researchers are focusing on introducing novel approaches and adapting existing methods to include this unique class of materials. Furthermore, novel strategies to engineer safer QDs are still under exploration by the scientific community. A recent novelty in the field is the discovery of carbon quantum dots, a new generation of optically-active nanoparticles potentially capable of replacing semiconductor QDs, but with the advantage of much lower toxicity.

Optical properties

Fluorescence spectra of CdTe quantum dots of various sizes. Different sized quantum dots emit different color light due to quantum confinement.

In semiconductors, light absorption generally leads to an electron being excited from the valence to the conduction band, leaving behind a hole. The electron and the hole can bind to each other to form an exciton. When this exciton recombines (i.e. the electron resumes its ground state), the exciton's energy can be emitted as light. This is called fluorescence. In a simplified model, the energy of the emitted photon can be understood as the sum of the band gap energy between the highest occupied level and the lowest unoccupied energy level, the confinement energies of the hole and the excited electron, and the bound energy of the exciton (the electron-hole pair): 

As the confinement energy depends on the quantum dot's size, both absorption onset and fluorescence emission can be tuned by changing the size of the quantum dot during its synthesis. The larger the dot, the redder (lower energy) its absorption onset and fluorescence spectrum. Conversely, smaller dots absorb and emit bluer (higher energy) light. Recent articles in Nanotechnology and in other journals have begun to suggest that the shape of the quantum dot may be a factor in the coloration as well, but as yet not enough information is available. Furthermore, it was shown that the lifetime of fluorescence is determined by the size of the quantum dot. Larger dots have more closely spaced energy levels in which the electron-hole pair can be trapped. Therefore, electron-hole pairs in larger dots live longer causing larger dots to show a longer lifetime. 

To improve fluorescence quantum yield, quantum dots can be made with "shells" of a larger bandgap semiconductor material around them. The improvement is suggested to be due to the reduced access of electron and hole to non-radiative surface recombination pathways in some cases, but also due to reduced Auger recombination in others.

Potential applications

Quantum dots are particularly promising for optical applications due to their high extinction coefficient. They operate like a single electron transistor and show the Coulomb blockade effect. Quantum dots have also been suggested as implementations of qubits for quantum information processing. 

Tuning the size of quantum dots is attractive for many potential applications. For instance, larger quantum dots have a greater spectrum-shift towards red compared to smaller dots, and exhibit less pronounced quantum properties. Conversely, the smaller particles allow one to take advantage of more subtle quantum effects. 

A device that produces visible light, through energy transfer from thin layers of quantum wells to crystals above the layers.

 

Being zero-dimensional, quantum dots have a sharper density of states than higher-dimensional structures. As a result, they have superior transport and optical properties. They have potential uses in diode lasers, amplifiers, and biological sensors. Quantum dots may be excited within a locally enhanced electromagnetic field produced by gold nanoparticles, which can then be observed from the surface plasmon resonance in the photoluminescent excitation spectrum of (CdSe)ZnS nanocrystals. High-quality quantum dots are well suited for optical encoding and multiplexing applications due to their broad excitation profiles and narrow/symmetric emission spectra. The new generations of quantum dots have far-reaching potential for the study of intracellular processes at the single-molecule level, high-resolution cellular imaging, long-term in vivo observation of cell trafficking, tumor targeting, and diagnostics. 

CdSe nanocrystals are efficient triplet photosensitizers. Laser excitation of small CdSe nanoparticles enables the extraction of the excited state energy from the Quantum Dots into bulk solution, thus opening the door to a wide range of potential applications such as photodynamic therapy, photovoltaic devices, molecular electronics, and catalysis.

Biology

In modern biological analysis, various kinds of organic dyes are used. However, as technology advances, greater flexibility in these dyes is sought. To this end, quantum dots have quickly filled in the role, being found to be superior to traditional organic dyes on several counts, one of the most immediately obvious being brightness (owing to the high extinction coefficient combined with a comparable quantum yield to fluorescent dyes) as well as their stability (allowing much less photobleaching). It has been estimated that quantum dots are 20 times brighter and 100 times more stable than traditional fluorescent reporters. For single-particle tracking, the irregular blinking of quantum dots is a minor drawback. However, there have been groups which have developed quantum dots which are essentially nonblinking and demonstrated their utility in single molecule tracking experiments.

The use of quantum dots for highly sensitive cellular imaging has seen major advances. The improved photostability of quantum dots, for example, allows the acquisition of many consecutive focal-plane images that can be reconstructed into a high-resolution three-dimensional image. Another application that takes advantage of the extraordinary photostability of quantum dot probes is the real-time tracking of molecules and cells over extended periods of time. Antibodies, streptavidin, peptides, DNA, nucleic acid aptamers, or small-molecule ligands  can be used to target quantum dots to specific proteins on cells. Researchers were able to observe quantum dots in lymph nodes of mice for more than 4 months.

 

Quantum dots can have antibacterial properties similar to nanoparticles and can kill bacteria in a dose-dependent manner. One mechanism by which quantum dots can kill bacteria is through impairing the functions of antioxidative system in the cells and down regulating the antioxidative genes. In addition, quantum dots can directly damage the cell wall. Quantum dots have been shown to be effective against both gram- positive and gram-negative bacteria.

Semiconductor quantum dots have also been employed for in vitro imaging of pre-labeled cells. The ability to image single-cell migration in real time is expected to be important to several research areas such as embryogenesis, cancer metastasis, stem cell therapeutics, and lymphocyte immunology. 

One application of quantum dots in biology is as donor fluorophores in Förster resonance energy transfer, where the large extinction coefficient and spectral purity of these fluorophores make them superior to molecular fluorophores It is also worth noting that the broad absorbance of QDs allows selective excitation of the QD donor and a minimum excitation of a dye acceptor in FRET-based studies. The applicability of the FRET model, which assumes that the Quantum Dot can be approximated as a point dipole, has recently been demonstrated.

The use of quantum dots for tumor targeting under in vivo conditions employ two targeting schemes: active targeting and passive targeting. In the case of active targeting, quantum dots are functionalized with tumor-specific binding sites to selectively bind to tumor cells. Passive targeting uses the enhanced permeation and retention of tumor cells for the delivery of quantum dot probes. Fast-growing tumor cells typically have more permeable membranes than healthy cells, allowing the leakage of small nanoparticles into the cell body. Moreover, tumor cells lack an effective lymphatic drainage system, which leads to subsequent nanoparticle-accumulation. 

Quantum dot probes exhibit in vivo toxicity. For example, CdSe nanocrystals are highly toxic to cultured cells under UV illumination, because the particles dissolve, in a process known as photolysis, to release toxic cadmium ions into the culture medium. In the absence of UV irradiation, however, quantum dots with a stable polymer coating have been found to be essentially nontoxic. Hydrogel encapsulation of quantum dots allows for quantum dots to be introduced into a stable aqueous solution, reducing the possibility of cadmium leakage.Then again, only little is known about the excretion process of quantum dots from living organisms.

In another potential application, quantum dots are being investigated as the inorganic fluorophore for intra-operative detection of tumors using fluorescence spectroscopy. 

Delivery of undamaged quantum dots to the cell cytoplasm has been a challenge with existing techniques. Vector-based methods have resulted in aggregation and endosomal sequestration of quantum dots while electroporation can damage the semi-conducting particles and aggregate delivered dots in the cytosol. Via cell squeezing, quantum dots can be efficiently delivered without inducing aggregation, trapping material in endosomes, or significant loss of cell viability. Moreover, it has shown that individual quantum dots delivered by this approach are detectable in the cell cytosol, thus illustrating the potential of this technique for single molecule tracking studies.

Photovoltaic devices

The tunable absorption spectrum and high extinction coefficients of quantum dots make them attractive for light harvesting technologies such as photovoltaics. Quantum dots may be able to increase the efficiency and reduce the cost of today's typical silicon photovoltaic cells. According to an experimental proof from 2004, quantum dots of lead selenide can produce more than one exciton from one high energy photon via the process of carrier multiplication or multiple exciton generation (MEG). This compares favorably to today's photovoltaic cells which can only manage one exciton per high-energy photon, with high kinetic energy carriers losing their energy as heat. Quantum dot photovoltaics would theoretically be cheaper to manufacture, as they can be made "using simple chemical reactions."

Quantum dot only solar cells

Aromatic self-assembled monolayers (SAMs) (e.g. 4-nitrobenzoic acid) can be used to improve the band alignment at electrodes for better efficiencies. This technique has provided a record power conversion efficiency (PCE) of 10.7%. The SAM is positioned between ZnO-PbS colloidal quantum dot (CQD) film junction to modify band alignment via the dipole moment of the constituent SAM molecule, and the band tuning may be modified via the density, dipole and the orientation of the SAM molecule.

Quantum dot in hybrid solar cells

Colloidal quantum dots are also used in inorganic/organic hybrid solar cells. These solar cells are attractive because of the potential for low-cost fabrication and relatively high efficiency. Incorporation of metal oxides, such as ZnO, TiO2, and Nb2O5 nanomaterials into organic photovoltaics have been commercialized using full roll-to-roll processing. A 13.2% power conversion efficiency is claimed in Si nanowire/PEDOT:PSS hybrid solar cells.

Quantum dot with nanowire in solar cells

Another potential use involves capped single-crystal ZnO nanowires with CdSe quantum dots, immersed in mercaptopropionic acid as hole transport medium in order to obtain a QD-sensitized solar cell. The morphology of the nanowires allowed the electrons to have a direct pathway to the photoanode. This form of solar cell exhibits 50–60% internal quantum efficiencies.

Nanowires with quantum dot coatings on silicon nanowires (SiNW) and carbon quantum dots. The use of SiNWs instead of planar silicon enhances the antiflection properties of Si. The SiNW exhibits a light-trapping effect due to light trapping in the SiNW. This use of SiNWs in conjunction with carbon quantum dots resulted in a solar cell that reached 9.10% PCE.

Graphene quantum dots have also been blended with organic electronic materials to improve efficiency and lower cost in photovoltaic devices and organic light emitting diodes (OLEDs) in compared to graphene sheets. These graphene quantum dots were functionalized with organic ligands that experience photoluminescence from UV-Vis absorption.

Light emitting diodes

Several methods are proposed for using quantum dots to improve existing light-emitting diode (LED) design, including "Quantum Dot Light Emitting Diode" (QD-LED or QLED) displays and "Quantum Dot White Light Emitting Diode" (QD-WLED) displays. Because Quantum dots naturally produce monochromatic light, they can be more efficient than light sources which must be color filtered. QD-LEDs can be fabricated on a silicon substrate, which allows them to be integrated onto standard silicon-based integrated circuits or microelectromechanical systems.

Quantum dot displays

Quantum dots are valued for displays because they emit light in very specific gaussian distributions. This can result in a display with visibly more accurate colors. 

A conventional color liquid crystal display (LCD) is usually backlit by fluorescent lamps (CCFLs) or conventional white LEDs that are color filtered to produce red, green, and blue pixels. Quantum dot displays use blue-emitting LEDs rather than white LEDs as the light sources. The converting part of the emitted light is converted into pure green and red light by the corresponding color quantum dots placed in front of the blue LED or using a quantum dot infused diffuser sheet in the backlight optical stack. Blank pixels are also used to allow the blue LED light to still generate blue hues. This type of white light as the backlight of an LCD panel allows for the best color gamut at lower cost than an RGB LED combination using three LEDs.

Another method by which quantum dot displays can be achieved is the electroluminescent (EL) or electro-emissive method. This involves embedding quantum dots in each individual pixel. These are then activated and controlled via an electric current application. Since this is often light emitting itself, the achievable colors may be limited in this method. Electro-emissive QD-LED TVs exist in laboratories only. 

The ability of QDs to precisely convert and tune a spectrum makes them attractive for LCD displays. Previous LCD displays can waste energy converting red-green poor, blue-yellow rich white light into a more balanced lighting. By using QDs, only the necessary colors for ideal images are contained in the screen. The result is a screen that is brighter, clearer, and more energy-efficient. The first commercial application of quantum dots was the Sony XBR X900A series of flat panel televisions released in 2013.

In June 2006, QD Vision announced technical success in making a proof-of-concept quantum dot display and show a bright emission in the visible and near infra-red region of the spectrum. A QD-LED integrated at a scanning microscopy tip was used to demonstrate fluorescence near-field scanning optical microscopy (NSOM) imaging.

Photodetector devices

Quantum dot photodetectors (QDPs) can be fabricated either via solution-processing, or from conventional single-crystalline semiconductors. Conventional single-crystalline semiconductor QDPs are precluded from integration with flexible organic electronics due to the incompatibility of their growth conditions with the process windows required by organic semiconductors. On the other hand, solution-processed QDPs can be readily integrated with an almost infinite variety of substrates, and also postprocessed atop other integrated circuits. Such colloidal QDPs have potential applications in surveillance, machine vision, industrial inspection, spectroscopy, and fluorescent biomedical imaging.

Photocatalysts

Quantum dots also function as photocatalysts for the light driven chemical conversion of water into hydrogen as a pathway to solar fuel. In photocatalysis, electron hole pairs formed in the dot under band gap excitation drive redox reactions in the surrounding liquid. Generally, the photocatalytic activity of the dots is related to the particle size and its degree of quantum confinement. This is because the band gap determines the chemical energy that is stored in the dot in the excited state. An obstacle for the use of quantum dots in photocatalysis is the presence of surfactants on the surface of the dots. These surfactants (or ligands) interfere with the chemical reactivity of the dots by slowing down mass transfer and electron transfer processes. Also, quantum dots made of metal chalcogenides are chemically unstable under oxidizing conditions and undergo photo corrosion reactions.

Theory

Quantum dots are theoretically described as a point like, or a zero dimensional (0D) entity. Most of their properties depend on the dimensions, shape and materials of which QDs are made. Generally QDs present different thermodynamic properties from the bulk materials of which they are made. One of these effects is the Melting-point depression. Optical properties of spherical metallic QDs are well described by the Mie scattering theory.

Quantum confinement in semiconductors

3D confined electron wave functions in a quantum dot. Here, rectangular and triangular-shaped quantum dots are shown. Energy states in rectangular dots are more s-type and p-type. However, in a triangular dot the wave functions are mixed due to confinement symmetry. (Click for animation)

In a semiconductor crystallite whose size is smaller than twice the size of its exciton Bohr radius, the excitons are squeezed, leading to quantum confinement. The energy levels can then be predicted using the particle in a box model in which the energies of states depend on the length of the box. Comparing the quantum dots size to the Bohr radius of the electron and hole wave functions, 3 regimes can be defined. A 'strong confinement regime' is defined as the quantum dots radius being smaller than both electron and hole Bohr radius, 'weak confinement' is given when the quantum dot is larger than both. For semiconductors in which electron and hole radii are markedly different, an 'intermediate confinement regime' exists, where the quantum dot's radius is larger than the Bohr radius of one charge carrier (typically the hole), but not the other charge carrier.

Splitting of energy levels for small quantum dots due to the quantum confinement effect. The horizontal axis is the radius, or the size, of the quantum dots and a_b* is the Exciton Bohr radius.

Band gap energy

The band gap can become smaller in the strong confinement regime as the energy levels split up. The Exciton Bohr radius can be expressed as:

${\displaystyle a_{b}^{*}=\varepsilon _{r}\left({\frac {m}{\mu }}\right)a_{b}}$

where a_b is the Bohr radius=0.053 nm, m is the mass, μ is the reduced mass, and ε_r is the size-dependent dielectric constant (Relative permittivity). This results in the increase in the total emission energy (the sum of the energy levels in the smaller band gaps in the strong confinement regime is larger than the energy levels in the band gaps of the original levels in the weak confinement regime) and the emission at various wavelengths. If the size distribution of QDs is not enough peaked, the convolution of multiple emission wavelengths is observed as a continuous spectra.

 

Confinement energy

 

The exciton entity can be modeled using the particle in the box. The electron and the hole can be seen as hydrogen in the Bohr model with the hydrogen nucleus replaced by the hole of positive charge and negative electron mass. Then the energy levels of the exciton can be represented as the solution to the particle in a box at the ground level (n = 1) with the mass replaced by the reduced mass. Thus by varying the size of the quantum dot, the confinement energy of the exciton can be controlled.

 

Bound exciton energy

 

There is Coulomb attraction between the negatively charged electron and the positively charged hole. The negative energy involved in the attraction is proportional to Rydberg's energy and inversely proportional to square of the size-dependent dielectric constant of the semiconductor. When the size of the semiconductor crystal is smaller than the Exciton Bohr radius, the Coulomb interaction must be modified to fit the situation.

Therefore, the sum of these energies can be represented as:

${\displaystyle {\begin{aligned}E_{\textrm {confinement}}&={\frac {\hbar ^{2}\pi ^{2}}{2a^{2}}}\left({\frac {1}{m_{e}}}+{\frac {1}{m_{h}}}\right)={\frac {\hbar ^{2}\pi ^{2}}{2\mu a^{2}}}\\E_{\textrm {exciton}}&=-{\frac {1}{\epsilon _{r}^{2}}}{\frac {\mu }{m_{e}}}R_{y}=-R_{y}^{*}\\E&=E_{\textrm {bandgap}}+E_{\textrm {confinement}}+E_{\textrm {exciton}}\\&=E_{\textrm {bandgap}}+{\frac {\hbar ^{2}\pi ^{2}}{2\mu a^{2}}}-R_{y}^{*}\end{aligned}}}$

where μ is the reduced mass, a is the radius of the quantum dot, m_e is the free electron mass, m_h is the hole mass, and ε_r is the size-dependent dielectric constant. 

Although the above equations were derived using simplifying assumptions, they imply that the electronic transitions of the quantum dots will depend on their size. These quantum confinement effects are apparent only below the critical size. Larger particles do not exhibit this effect. This effect of quantum confinement on the quantum dots has been repeatedly verified experimentally and is a key feature of many emerging electronic structures.

The Coulomb interaction between confined carriers can also be studied by numerical means when results unconstrained by asymptotic approximations are pursued.

Besides confinement in all three dimensions (i.e., a quantum dot), other quantum confined semiconductors include:

• Quantum wires, which confine electrons or holes in two spatial dimensions and allow free propagation in the third.
• Quantum wells, which confine electrons or holes in one dimension and allow free propagation in two dimensions.

Models

A variety of theoretical frameworks exist to model optical, electronic, and structural properties of quantum dots. These may be broadly divided into quantum mechanical, semiclassical, and classical.

Quantum mechanics

Quantum mechanical models and simulations of quantum dots often involve the interaction of electrons with a pseudopotential or random matrix.

Semiclassical

Semiclassical models of quantum dots frequently incorporate a chemical potential. For example, the thermodynamic chemical potential of an N-particle system is given by

${\displaystyle \mu (N)=E(N)-E(N-1)}$

whose energy terms may be obtained as solutions of the Schrödinger equation. The definition of capacitance,

${\displaystyle {1 \over C}\equiv {\Delta \,V \over \Delta \,Q}}$,

with the potential difference

${\displaystyle \Delta \,V={\Delta \,\mu \, \over e}={\mu (N+\Delta \,N)-\mu (N) \over e}}$

may be applied to a quantum dot with the addition or removal of individual electrons,

${\displaystyle \Delta \,N=1}$ and ${\displaystyle \Delta \,Q=e}$.

Then

${\displaystyle C(N)={e^{2} \over \mu (N+1)-\mu (N)}={e^{2} \over I(N)-A(N)}}$

is the "quantum capacitance" of a quantum dot, where we denoted by I(N) the ionization potential and by A(N) the electron affinity of the N-particle system.

Classical mechanics

Classical models of electrostatic properties of electrons in quantum dots are similar in nature to the Thomson problem of optimally distributing electrons on a unit sphere. 

The classical electrostatic treatment of electrons confined to spherical quantum dots is similar to their treatment in the Thomson, or plum pudding model, of the atom.

The classical treatment of both two-dimensional and three-dimensional quantum dots exhibit electron shell-filling behavior. A "periodic table of classical artificial atoms" has been described for two-dimensional quantum dots. As well, several connections have been reported between the three-dimensional Thomson problem and electron shell-filling patterns found in naturally-occurring atoms found throughout the periodic table. This latter work originated in classical electrostatic modeling of electrons in a spherical quantum dot represented by an ideal dielectric sphere.

History

The term “quantum dot” was coined in 1986. They were first discovered in a glass matrix and in colloidal solutions by Alexey Ekimov and Louis Brus.