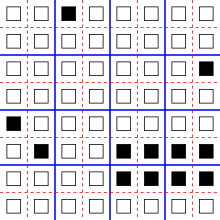
A
one-dimensional reversible cellular automaton with nine states. At each
step, each cell copies the shape from its left neighbor, and the color
from its right neighbor.
A reversible cellular automaton is a cellular automaton
in which every configuration has a unique predecessor. That is, it is a
regular grid of cells, each containing a state drawn from a finite set
of states, with a rule for updating all cells simultaneously based on
the states of their neighbors, such that the previous state of any cell
before an update can be determined uniquely from the updated states of
all the cells. The time-reversed dynamics
of a reversible cellular automaton can always be described by another
cellular automaton rule, possibly on a much larger neighborhood.
Several methods are known for defining cellular automata rules that are reversible; these include the block cellular automaton method, in which each update partitions the cells into blocks and applies an invertible function separately to each block, and the second-order cellular automaton
method, in which the update rule combines states from two previous
steps of the automaton. When an automaton is not defined by one of these
methods, but is instead given as a rule table, the problem of testing
whether it is reversible is solvable for block cellular automata and for
one-dimensional cellular automata, but is undecidable for other types of cellular automata.
Reversible cellular automata form a natural model of reversible computing, a technology that could lead to ultra-low-power computing devices. Quantum cellular automata, one way of performing computations using the principles of quantum mechanics, are often required to be reversible. Additionally, many problems in physical modeling, such as the motion of particles in an ideal gas or the Ising model of alignment of magnetic charges, are naturally reversible and can be simulated by reversible cellular automata.
Properties related to reversibility may also be used to study
cellular automata that are not reversible on their entire configuration
space, but that have a subset of the configuration space as an attractor that all initially random configurations converge towards. As Stephen Wolfram
writes, "once on an attractor, any system—even if it does not have
reversible underlying rules—must in some sense show approximate
reversibility."
Examples
One-dimensional automata
A cellular automaton is defined by its cells (often a one- or two-dimensional array), a finite set of values or states that can go into each cell, a neighborhood associating each cell with a finite set of nearby cells, and an update rule
according to which the values of all cells are updated, simultaneously,
as a function of the values of their neighboring cells.
The simplest possible cellular automata have a one-dimensional array of
cells, each of which can hold a binary value (either 0 or 1), with each
cell having a neighborhood consisting only of it and its two nearest
cells on either side; these are called the elementary cellular automata.
If the update rule for such an automaton causes each cell to always
remain in the same state, then the automaton is reversible: the previous
state of all cells can be recovered from their current states, because
for each cell the previous and current states are the same. Similarly,
if the update rule causes every cell to change its state from 0 to 1 and
vice versa, or if it causes a cell to copy the state from a fixed
neighboring cell, or if it causes it to copy a state and then reverse
its value, it is necessarily reversible. Toffoli & Margolus (1990)
call these types of reversible cellular automata, in which the state of
each cell depends only on the previous state of one neighboring cell,
"trivial". Despite its simplicity, the update rule that causes each cell
to copy the state of a neighboring cell is important in the theory of symbolic dynamics, where it is known as the shift map.
A little less trivially, suppose that the cells again form a one-dimensional array, but that each state is an ordered pair (l,r) consisting of a left part l and a right part r,
each drawn from a finite set of possible values. Define a transition
function that sets the left part of a cell to be the left part of its
left neighbor and the right part of a cell to be the right part of its
right neighbor. That is, if the left neighbor's state is (a,b) and the right neighbor's state is (c,d), the new state of a cell is the result of combining these states using a pairwise operation × defined by the equation (a,b) × (c,d) = (a,d).
An example of this construction is given in the illustration, in which
the left part is represented graphically as a shape and the right part
is represented as a color; in this example, each cell is updated with
the shape of its left neighbor and the color of its right neighbor. Then
this automaton is reversible: the values on the left side of each pair
migrate rightwards and the values on the right side migrate leftwards,
so the prior state of each cell can be recovered by looking for these
values in neighboring cells. The operation × used to combine pairs of states in this automaton forms an algebraic structure known as a rectangular band.
Multiplication of decimal numbers
by two or by five can be performed by a one-dimensional reversible
cellular automaton with ten states per cell (the ten decimal digits).
Each digit of the product depends only on a neighborhood of two digits
in the given number: the digit in the same position and the digit one
position to the right. More generally, multiplication or division of
doubly infinite digit sequences in any radix b, by a multiplier or divisor x all of whose prime factors are also prime factors of b,
is an operation that forms a cellular automaton because it depends only
on a bounded number of nearby digits, and is reversible because of the
existence of multiplicative inverses.
Multiplication by other values (for instance, multiplication of decimal
numbers by three) remains reversible, but does not define a cellular
automaton, because there is no fixed bound on the number of digits in
the initial value that are needed to determine a single digit in the
result.
There are no nontrivial reversible elementary cellular automata. However, a near-miss is provided by Rule 90 and other elementary cellular automata based on the exclusive or
function. In Rule 90, the state of each cell is the exclusive or of the
previous states of its two neighbors. This use of the exclusive or
makes the transition rule locally invertible, in the sense that any
contiguous subsequence of states can be generated by this rule. Rule 90
is not a reversible cellular automaton rule, because in Rule 90 every
assignment of states to the complete array of cells has exactly four
possible predecessors, whereas reversible rules are required to have
exactly one predecessor per configuration.
Critters
Gliders escape from a central random seed region in the Critters block cellular automaton rule.
Conway's Game of Life,
one of the most famous cellular automaton rules, is not reversible: for
instance, it has many patterns that die out completely, so the
configuration in which all cells are dead has many predecessors, and it
also has Garden of Eden patterns with no predecessors. However, another rule called "Critters" by its inventors, Tommaso Toffoli and Norman Margolus, is reversible and has similar dynamic behavior to Life.
The Critters rule is a block cellular automaton
in which, at each step, the cells of the automaton are partitioned into
2×2 blocks and each block is updated independently of the other blocks.
Its transition function flips the state of every cell in a block that
does not have exactly two live cells, and in addition rotates by 180°
blocks with exactly three live cells. Because this function is
invertible, the automaton defined by these rules is a reversible
cellular automaton.
When started with a smaller field of random cells centered within
a larger region of dead cells, many small patterns similar to Life's glider escape from the central random area and interact with each other. The Critters rule can also support more complex spaceships of varying speeds as well as oscillators with infinitely many different periods.
Constructions
Several general methods are known for constructing cellular automaton rules that are automatically reversible.
Block cellular automata
The
Margolus neighborhood for block cellular automata. The partition of the
cells alternates between the set of 2 × 2 blocks indicated by the solid
blue lines, and the set of blocks indicated by the dashed red lines.
A block cellular automaton
is an automaton at which, in each time step, the cells of the automaton
are partitioned into congruent subsets (called blocks), and the same
transformation is applied independently to each block. Typically, such
an automaton will use more than one partition into blocks, and will
rotate between these partitions at different time steps of the system.
In a frequently used form of this design, called the Margolus
neighborhood, the cells of the automaton form a square grid and are
partitioned into larger 2 × 2 square blocks at each step. The center of a
block at one time step becomes the corner of four blocks at the next
time step, and vice versa; in this way, the four cells in each 2 × 2
belong to four different 2 × 2 squares of the previous partition. The Critters rule discussed above is an example of this type of automaton.
Designing reversible rules for block cellular automata, and
determining whether a given rule is reversible, is easy: for a block
cellular automaton to be reversible it is necessary and sufficient that
the transformation applied to the individual blocks at each step of the
automaton is itself reversible. When a block cellular automaton is
reversible, the time-reversed version of its dynamics can also be
described as a block cellular automaton with the same block structure,
using a time-reversed sequence of partitions of cells into blocks, and
with the transition function for each block being the inverse function of the original rule.
Simulation of irreversible automata
Toffoli (1977) showed how to embed any irreversible d-dimensional cellular automaton rule into a reversible (d + 1)-dimensional rule. Each d-dimensional
slice of the new reversible rule simulates a single time step of the
original rule. In this way, Toffoli showed that many features of
irreversible cellular automata, such as the ability to simulate
arbitrary Turing machines, could also be extended to reversible cellular automata.
As Toffoli conjectured and Hertling (1998)
proved, the increase in dimension incurred by Toffoli's method is a
necessary payment for its generality: under mild assumptions (such as
the translation-invariance of the embedding), any embedding of a
cellular automaton that has a Garden of Eden into a reversible cellular automaton must increase the dimension.
Morita (1995)
describes another type of simulation that does not obey Hertling's
assumptions and does not change the dimension. Morita's method can
simulate the finite configurations of any irreversible automaton in
which there is a "quiescent" or "dead" state, such that if a cell and
all its neighbors are quiescent then the cell remains quiescent in the
next step. The simulation uses a reversible block cellular automaton of
the same dimension as the original irreversible automaton. The
information that would be destroyed by the irreversible steps of the
simulated automaton is instead sent away from the configuration into the
infinite quiescent region of the simulating automaton. This simulation
does not update all cells of the simulated automaton simultaneously;
rather, the time to simulate a single step is proportional to the size
of the configuration being simulated. Nevertheless, the simulation
accurately preserves the behavior of the simulated automaton, as if all
of its cells were being updated simultaneously. Using this method it is
possible to show that even one-dimensional reversible cellular automata
are capable of universal computation.
Second-order cellular automata
The past cells affecting the state of a cell at time t in a second-order cellular automaton
The
Rule 18 one-dimensional cellular automaton (left) and the second-order
cellular automaton derived from it (right). Each row of the image shows a
configuration of the automaton, with time running downwards.
The second-order cellular automaton technique is a method of transforming any cellular automaton into a reversible cellular automaton, invented by Edward Fredkin and first published by several other authors in 1984. In this technique, the state of each cell in the automaton at time t is a function both of its neighborhood at time t − 1 and of its own state at time t − 2. Specifically, the transition function of the automaton maps each neighborhood at time t − 1 to a permutation on the set of states, and then applies that permutation to the state at time t − 2.
The reverse dynamics of the automaton may be computed by mapping each
neighborhood to the inverse permutation and proceeding in the same way.
In the case of automata with binary-valued states (zero or one),
there are only two possible permutations on the states (the identity
permutation and the permutation that swaps the two states), which may
themselves be represented as the exclusive or
of a state with a binary value. In this way, any conventional
two-valued cellular automaton may be converted to a second-order
cellular automaton rule by using the conventional automaton's transition
function on the states at time t − 1, and then computing the exclusive or of these states with the states at time t − 2 to determine the states at time t.
However, the behavior of the reversible cellular automaton determined
in this way may not bear any resemblance to the behavior of the cellular
automaton from which it was defined.
Any second-order automaton may be transformed into a conventional
cellular automaton, in which the transition function depends only on
the single previous time step, by combining pairs of states from
consecutive time steps of the second-order automaton into single states
of a conventional cellular automaton.
Conserved landscape
A one-dimensional cellular automaton found by Patt (1971)
uses a neighborhood consisting of four contiguous cells. In this
automaton, a cell flips its state whenever it occupies the "?" position
in the pattern "0?10". No two such patterns can overlap, so the same
"landscape" surrounding the flipped cell continues to be present after
the transition. In the next step, the cell in the same "?" position will
flip again, back to its original state. Therefore, this automaton is
its own inverse, and is reversible. Patt performed a brute force search
of all two-state one-dimensional cellular automata with small
neighborhoods; this search led to the discovery of this automaton, and
showed that it was the simplest possible nontrivial one-dimensional
two-state reversible cellular automaton. There are no reversible
two-state automata with three-cell neighborhoods, and all two-state
reversible automata with four-cell neighborhoods are simple variants on
Patt's automaton.
Patt's automaton can be viewed in retrospect as an instance of
the "conserved landscape" technique for designing reversible cellular
automata. In this technique, a change to the state of a cell is
triggered by a pattern among a set of neighbors that do not themselves
change states. In this way, the existence of the same pattern can be
used to trigger the inverse change in the time-reversed dynamics of the
automaton. Patt's automaton has very simple dynamics (all cyclic
sequences of configurations have length two), but automata using the
same conserved landscape technique with more than one triggering pattern
are capable of more complex behavior. In particular they can simulate
any second-order cellular automaton.
The SALT model of Miller & Fredkin (2005)
is a special case of the conserved landscape technique. In this model,
the cells of an integer grid are split into even and odd subsets. In
each time step certain pairs of cells of one parity are swapped, based
on the configuration of nearby cells of the other parity. Rules using
this model can simulate the billiard ball computer,
or support long strings of live cells that can move at many different speeds or vibrate at many different frequencies.
Theory
A cellular automaton consists of an array of cells, each one of which has a finite number of possible states, together with a rule for updating all cells simultaneously based only on the states of neighboring cells. A configuration
of a cellular automaton is an assignment of a state to every cell of
the automaton; the update rule of a cellular automaton forms a function
from configurations to configurations, with the requirement that the
updated value of any cell depends only on some finite neighborhood of
the cell, and that the function is invariant under translations of the
input array.
With these definitions, a cellular automaton is reversible when
it satisfies any one of the following conditions, all of which are
mathematically equivalent to each other:
- Every configuration of the automaton has a unique predecessor that is mapped to it by the update rule.
- The update rule of the automaton is a bijection; that is, a function that is both one-to-one and onto.
- The update rule is an injective function, that is, there are no two configurations that both map to the same common configuration. This condition is obviously implied by the assumption that the update rule is a bijection. In the other direction, the Garden of Eden theorem for cellular automata implies that every injective update rule is bijective.
- The time-reversed dynamics of the automaton can be described by another cellular automaton. Clearly, for this to be possible, the update rule must be bijective. In the other direction, if the update rule is bijective, then it has an inverse function that is also bijective. This inverse function must be a cellular automaton rule. The proof of this fact uses the Curtis–Hedlund–Lyndon theorem, a topological characterization of cellular automata rules as the translation-invariant functions that are continuous with respect to the Cantor topology on the space of configurations.
- The update rule of the automaton is an automorphism of the shift dynamical system defined by the state space and the translations of the lattice of cells. That is, it is a homeomorphism that commutes with the shift map, as the Curtis–Hedlund–Lyndon theorem implies.
Di Gregorio & Trautteur (1975)
analyze several alternative definitions of reversibility for cellular
automata. Most of these turn out to be equivalent either to injectivity
or to surjectivity of the transition function of the automaton; however,
there is one more alternative that does not match either of these two
definitions. It applies to automata such as the Game of Life that have a
quiescent or dead state. In such an automaton, one can define a
configuration to be "finite" if it has only finitely many non-quiescent
cells, and one can consider the class of automata for which every finite
configuration has at least one finite predecessor. This class turns out
to be distinct from both the surjective and injective automata, and in
some subsequent research, automata with this property have been called invertible finite automata.
Testing reversibility
It was first shown by Amoroso & Patt (1972)
that the problem of testing reversibility of a given one-dimensional
cellular automaton has an algorithmic solution. Alternative algorithms
based on automata theory and de Bruijn graphs were given by Culik (1987) and Sutner (1991), respectively.
- Culik begins with the observation that a cellular automaton has an injective transition function if and only if the transition function is injective on the subsets of configurations that are periodic (repeating the same substring infinitely often in both directions). He defines a nondeterministic finite-state transducer that performs the transition rule of the automaton on periodic strings. This transducer works by remembering the neighborhood of the automaton at the start of the string and entering an accepting state when that neighborhood concatenated to the end of the input would cause its nondeterministically chosen transitions to be correct. Culik then swaps the input and output of the transducer. The transducer resulting from this swap simulates the inverse dynamics of the given automaton. Finally, Culik applies previously known algorithms to test whether the resulting swapped transducer maps each input to a single output.
- Sutner defines a directed graph (a type of de Bruijn graph) in which each vertex represents a pair of assignments of states for the cells in a contiguous sequence of cells. The length of this sequence is chosen to be one less than the neighborhood size of the automaton. An edge in Sutner's graph represents a pair of sequences of cells that overlap in all but one cell, so that the union of the sequences is a full neighborhood in the cellular automaton. Each such edge is directed from the overlapping subsequence on the left to the subsequence on the right. Edges are only included in the graph when they represent compatible state assignments on the overlapping parts of their cell sequences, and when the automaton rule (applied to the neighborhood determined by the potential edge) would give the same results for both assignments of states. By performing a linear-time strong connectivity analysis of this graph, it is possible to determine which of its vertices belong to cycles. The transition rule is non-injective if and only if this graph contains a directed cycle in which at least one vertex has two differing state assignments.
These methods take polynomial time, proportional to the square of the size of the state transition table of the input automaton. A related algorithm of Hillman (1991)
determines whether a given rule is surjective when applied to
finite-length arrays of cells with periodic boundary conditions, and if
so, for which lengths.
For a block cellular automaton, testing reversibility is also
easy: the automaton is reversible if and only if the transition function
on the blocks of the automaton is invertible, and in this case the
reverse automaton has the same block structure with the inverse
transition function.
However, for cellular automata with other neighborhoods in two or more dimensions, the problem of testing reversibility is undecidable,
meaning that there cannot exist an algorithm that always halts and
always correctly answers the problem. The proof of this fact by Kari (1990) is based on the previously known undecidability of tiling the plane by Wang tiles,
sets of square tiles with markings on their edges that constrain which
pairs of tiles can fit edge-to-edge. Kari defines a cellular automaton
from a set of Wang tiles, such that the automaton fails to be injective
if and only if the given tile set can tile the entire plane. His
construction uses the von Neumann neighborhood,
and cells with large numbers of states. In the same paper, Kari also
showed that it is undecidable to test whether a given cellular automaton
rule of two or more dimensions is surjective (that is, whether it has a
Garden of Eden).
Reverse neighborhood size
In a one-dimensional reversible cellular automaton with n states per cell, in which the neighborhood of a cell is an interval of m cells, the automaton representing the reverse dynamics has neighborhoods that consist of at most nm − 1 − m + 1 cells. This bound is known to be tight for m = 2: there exist n-state
reversible cellular automata with two-cell neighborhoods whose
time-reversed dynamics forms a cellular automaton with neighborhood size
exactly n − 1.
For any integer m there are only finitely many two-dimensional reversible m-state cellular automata with the von Neumann neighborhood. Therefore, there is a well-defined function f(m) such that all reverses of m-state cellular automata with the von Neumann neighborhood use a neighborhood with radius at most f(m): simply let f(m) be the maximum, among all of the finitely many reversible m-state
cellular automata, of the neighborhood size needed to represent the
time-reversed dynamics of the automaton. However, because of Kari's
undecidability result, there is no algorithm for computing f(m) and the values of this function must grow very quickly, more quickly than any computable function.
Wolfram's classification
A well-known classification of cellular automata by Stephen Wolfram
studies their behavior on random initial conditions. For a reversible
cellular automaton, if the initial configuration is chosen uniformly at
random among all possible configurations, then that same uniform
randomness continues to hold for all subsequent states. Thus it would
appear that most reversible cellular automata are of Wolfram's Class 3:
automata in which almost all initial configurations evolve
pseudo-randomly or chaotically. However, it is still possible to
distinguish among different reversible cellular automata by analyzing
the effect of local perturbations on the behavior of the automaton.
Making a change to the initial state of a reversible cellular automaton
may cause changes to later states to remain only within a bounded
region, to propagate irregularly but unboundedly, or to spread quickly,
and Wolfram (1984) lists one-dimensional reversible cellular automaton rules exhibiting all three of these types of behavior.
Later work by Wolfram identifies the one-dimensional Rule 37R
automaton as being particularly interesting in this respect. When run
on a finite array of cells with periodic boundary conditions, starting
from a small seed of random cells centered within a larger empty
neighborhood, it tends to fluctuate between ordered and chaotic states.
However, with the same initial conditions on an unbounded set of cells
its configurations tend to organize themselves into several types of
simple moving particles.
Abstract algebra
Another way to formalize reversible cellular automata involves abstract algebra, and this formalization has been useful in developing computerized searches for reversible cellular automaton rules. Boykett (2004) defines a semicentral bigroupoid to be an algebraic structure consisting of a set S of elements and two operations → and ← on pairs of elements, satisfying the two equational axioms:
- for all elements a, b, and c in S, (a → b) ← (b → c) = b, and
- for all elements a, b, and c in S, (a ← b) → (b ← c) = b.
For instance, this is true for the two operations in which operation → returns its right argument and operation ← returns its left argument.
As Boykett argues, any one-dimensional reversible cellular automaton is equivalent to an automaton in rectangular form,
in which the cells are offset a half unit at each time step, and in
which both the forward and reverse evolution of the automaton have
neighborhoods with just two cells, the cells a half unit away in each
direction. If a reversible automaton has neighborhoods larger than two
cells, it can be simulated by a reversible automaton with smaller
neighborhoods and more states per cell, in which each cell of the
simulating automaton simulates a contiguous block of cells in the
simulated automaton. The two axioms of a semicentral bigroupoid are
exactly the conditions required on the forward and reverse transition
functions of these two-cell neighborhoods to be the reverses of each
other. That is, every semicentral bigroupoid defines a reversible
cellular automaton in rectangular form, in which the transition function
of the automaton uses the → operation to combine the two cells of its neighborhood, and in which the ← operation
similarly defines the reverse dynamics of the automaton. Every
one-dimensional reversible cellular automaton is equivalent to one in
this form.
Boykett used this algebraic formulation as the basis for
algorithms that exhaustively list all possible inequivalent reversible
cellular automata.
Conservation laws
When
researchers design reversible cellular automata to simulate physical
systems, they typically incorporate into the design the conservation laws
of the system; for instance, a cellular automaton that simulates an
ideal gas should conserve the number of gas particles and their total momentum,
for otherwise it would not provide an accurate simulation. However,
there has also been some research on the conservation laws that
reversible cellular automata can have, independent of any intentional
design. The typical type of conserved quantity measured in these studies
takes the form of a sum, over all contiguous subsets of k
cells of the automaton, of some numerical function of the states of the
cells in each subset. Such a quantity is conserved if, whenever it
takes a finite value, that value automatically remains constant through
each time step of the automaton, and in this case it is called a kth-order invariant of the automaton.
For instance, recall the one-dimensional cellular automaton defined as an example from a rectangular band, in which the cell states are pairs of values (l,r) drawn from sets L and R
of left values and right values, the left value of each cell moves
rightwards at each time step, and the right value of each cell moves
leftwards. In this case, for each left or right value x of the band, one can define a conserved quantity, the total number of cells that have that value. If there are λ left values and ρ right values, then there are λ + ρ − 2
independent first-order-invariants, and any first-order invariant can
be represented as a linear combination of these fundamental ones. The
conserved quantities associated with left values flow uniformly to the
right at a constant rate: that is, if the number of left values equal to
x within some region C of the line takes a certain value at time 0, then it will take the same value for the shifted region C + t/2 at time t. Similarly, the conserved quantities associated with right values flow uniformly to the left.
Any one-dimensional reversible cellular automaton may be placed
into rectangular form, after which its transition rule may be factored
into the action of an idempotent
semicentral bigroupoid (a reversible rule for which regions of cells
with a single state value change only at their boundaries) together with
a permutation on the set of states. The first-order invariants for the idempotent lifting
of the automaton rule (the modified rule formed by omitting the
permutation) necessarily behave like the ones for a rectangular band:
they have a basis of invariants that flow either leftwards or rightwards
at a constant rate without interaction. The first-order invariants for
the overall automaton are then exactly the invariants for the idempotent
lifting that give equal weight to every pair of states that belong to
the same orbit
of the permutation. However, the permutation of states in the rule may
cause these invariants to behave differently from in the idempotent
lifting, flowing non-uniformly and with interactions.
In physical systems, Noether's theorem
provides an equivalence between conservation laws and symmetries of the
system. However, for cellular automata this theorem does not directly
apply, because instead of being governed by the energy
of the system the behavior of the automaton is encoded into its rules,
and the automaton is guaranteed to obey certain symmetries (translation
invariance in both space and time) regardless of any conservation laws
it might obey. Nevertheless, the conserved quantities of certain
reversible systems behave similarly to energy in some respects. For
instance, if different regions of the automaton have different average
values of some conserved quantity, the automaton's rules may cause this
quantity to dissipate, so that the distribution of the quantity is more
uniform in later states. Using these conserved quantities as a stand-in
for the energy of the system can allow it to be analyzed using methods
from classical physics.
Applications
Lattice gas automata
A lattice gas automaton is a cellular automaton designed to simulate the motion of particles in a fluid or an ideal gas. In such a system, gas particles move on straight lines with constant velocity, until undergoing elastic collision
with other particles. Lattice gas automata simplify these models by
only allowing a constant number of velocities (typically, only one speed
and either four or six directions of motion) and by simplifying the
types of collision that are possible.
Specifically, the HPP lattice gas model
consists of particles moving at unit velocity in the four axis-parallel
directions. When two particles meet on the same line in opposite
directions, they collide and are sent outwards from the collision point
on the perpendicular line. This system obeys the conservation laws of
physical gases, and produces simulations whose appearance resembles the
behavior of physical gases. However, it was found to obey unrealistic
additional conservation laws. For instance, the total momentum within
any single line is conserved. As well, the differences between
axis-parallel and non-axis-parallel directions in this model (its anisotropy) is undesirably high. The FHP lattice gas model
improves the HPP model by having particles moving in six different
directions, at 60 degree angles to each other, instead of only four
directions. In any head-on collision, the two outgoing particles are
deflected at 60 degree angles from the two incoming particles. Three-way
collisions are also possible in the FHP model and are handled in a way
that both preserves total momentum and avoids the unphysical added
conservation laws of the HPP model.
Because the motion of the particles in these systems is
reversible, they are typically implemented with reversible cellular
automata. In particular, both the HPP and FHP lattice gas automata can
be implemented with a two-state block cellular automaton using the
Margolus neighborhood.
Ising model
The Ising model is used to model the behavior of magnetic systems. It consists of an array of cells, the state of each of which represents a spin, either up or down.
The energy of the system is measured by a function that depends on the
number of neighboring pairs of cells that have the same spin as each
other. Therefore, if a cell has equal numbers of neighbors in the two
states, it may flip its own state without changing the total energy.
However, such a flip is energy-conserving only if no two adjacent cells
flip at the same time.
Cellular automaton models of this system divide the square
lattice into two alternating subsets, and perform updates on one of the
two subsets at a time. In each update, every cell that can flip does so.
This defines a reversible cellular automaton which can be used to
investigate the Ising model.[32]
Billiard ball computation and low-power computing
Fredkin & Toffoli (1982) proposed the billiard-ball computer as part of their investigations into reversible computing.
A billiard-ball computer consists of a system of synchronized particles
(the billiard balls) moving in tracks and guided by a fixed set of
obstacles. When the particles collide with each other or with the
obstacles, they undergo an elastic collision much as real billiard balls
would do. The input to the computer is encoded using the presence or
absence of particles on certain input tracks, and its output is
similarly encoded using the presence or absence of particles on output
tracks. The tracks themselves may be envisioned as wires, and the
particles as being Boolean signals transported on those wires. When a
particle hits an obstacle, it reflects from it. This reflection may be
interpreted as a change in direction of the wire the particle is
following. Two particles on different tracks may collide, forming a
logic gate at their collision point.
As Margolus (1984)
showed, billiard-ball computers may be simulated using a two-state
reversible block cellular automaton with the Margolus neighborhood. In
this automaton's update rule, blocks with exactly one live cell rotate
by 180°, blocks with two diagonally opposite live cells rotate by 90°,
and all other blocks remain unchanged. These rules cause isolated live
cells to behave like billiard balls, moving on diagonal trajectories.
Connected groups of more than one live cell behave instead like the
fixed obstacles of the billiard-ball computer. In an appendix, Margolus
also showed that a three-state second-order cellular automaton using the
two-dimensional Moore neighborhood could simulate billiard-ball computers.
One reason to study reversible universal models of computation such
as the billiard-ball model is that they could theoretically lead to
actual computer systems that consume very low quantities of energy.
According to Landauer's principle,
irreversible computational steps require a certain minimal amount of
energy per step, but reversible steps can be performed with an amount of
energy per step that is arbitrarily close to zero.
However, in order to perform computation using less energy than
Landauer's bound, it is not good enough for a cellular automaton to have
a transition function that is globally reversible: what is required is
that the local computation of the transition function also be done in a
reversible way. For instance, reversible block cellular automata are
always locally reversible: the behavior of each individual block
involves the application of an invertible function with finitely many
inputs and outputs. Toffoli & Margolus (1990) were the first to ask whether every reversible cellular automaton has a locally reversible update rule. Kari (1996) showed that for one- and two-dimensional automata the answer is positive, and Durand-Lose (2001)
showed that any reversible cellular automaton could be simulated by a
(possibly different) locally reversible cellular automaton. However, the
question of whether every reversible transition function is locally
reversible remains open for dimensions higher than two.
Synchronization
The rectilinear shapes generated by the Tron rule
The "Tron" rule of Toffoli and Margolus is a reversible block
cellular rule with the Margolus neighborhood. When a 2 × 2 block of
cells all have the same state, all cells of the block change state; in
all other cases, the cells of the block remain unchanged. As Toffoli and
Margolus argue, the evolution of patterns generated by this rule can be
used as a clock to synchronize any other rule on the Margolus
neighborhood. A cellular automaton synchronized in this way obeys the
same dynamics as the standard Margolus-neighborhood rule while running
on an asynchronous cellular automaton.
Encryption
Kari (1990) proposed using multidimensional reversible cellular automata as an encryption
system. In Kari's proposal, the cellular automaton rule would be the
encryption key. Encryption would be performed by running the rule
forward one step, and decryption would be performed by running it
backward one step. Kari suggests that a system such as this may be used
as a public-key cryptosystem.
In principle, an attacker could not algorithmically determine the
decryption key (the reverse rule) from a given encryption key (forward
rule) because of the undecidability of testing reversibility, so the
forward rule could be made public without compromising the security of
the system. However, Kari did not specify which types of reversible
cellular automaton should be used for such a system, or show how a
cryptosystem using this approach would be able to generate
encryption/decryption key pairs.
Chai, Cao & Zhou (2005)
have proposed an alternative encryption system. In their system, the
encryption key determines the local rule for each cell of a
one-dimensional cellular automaton. A second-order automaton based on
that rule is run for several rounds on an input to transform it into an
encrypted output. The reversibility property of the automaton ensures
that any encrypted message can be decrypted by running the same system
in reverse. In this system, keys must be kept secret, because the same
key is used both for encryption and decryption.
Quantum computing
Quantum cellular automata are arrays of automata whose states and state transitions obey the laws of quantum dynamics. Quantum cellular automata were suggested as a model of computation by Feynman (1982) and first formalized by Watrous (1995).
Several competing notions of these automata remain under research, many
of which require that the automata constructed in this way be
reversible.
Physical universality
Janzing (2010) asked whether it was possible for a cellular automaton to be physically universal,
meaning that, for any bounded region of the automaton's cells, it
should be possible to surround that region with cells whose states form
an appropriate support scaffolding that causes the automaton to
implement any arbitrary transformation on sets of states within the
region. Such an automaton must be reversible, or at least locally
injective, because automata without this property have Garden of Eden
patterns, and it is not possible to implement a transformation that
creates a Garden of Eden.
Schaeffer (2015)
constructed a reversible cellular automaton that is physically
universal in this sense. Schaeffer's automaton is a block cellular
automaton with two states and the Margolis neighborhood, closely related
to the automata for the billiard ball model and for the HPP lattice
gas. However, the billiard ball model is not physically universal, as it
can be used to construct impenetrable walls preventing the state within
some region from being read and transformed. In Schaeffer's model,
every pattern eventually decomposes into particles moving diagonally in
four directions. Thus, his automaton is not Turing complete.
However, Schaeffer showed that it is possible to surround any finite
configuration by scaffolding that decays more slowly than it. After the
configuration decomposes into particles, the scaffolding intercepts
those particles, and uses them as the input to a system of Boolean
circuits constructed within the scaffolding. These circuits can be used
to compute arbitrary functions of the initial configuration. The
scaffolding then translates the output of the circuits back into a
system of moving particles, which converge on the initial region and
collide with each other to build a copy of the transformed state. In
this way, Schaeffer's system can be used to apply any function to any
bounded region of the state space, showing that this automaton rule is
physically universal.