Phonon

From Wikipedia, the free encyclopedia

In physics, a phonon is a collective excitation in a periodic, elastic arrangement of atoms or molecules in condensed matter, like solids and some liquids. Often designated a quasiparticle, it represents an excited state in the quantum mechanical quantization of the modes of vibrations of elastic structures of interacting particles.

 

Phonons play a major role in many of the physical properties of condensed matter, like thermal conductivity and electrical conductivity. The study of phonons is an important part of condensed matter physics.

The concept of phonons was introduced in 1932 by Soviet physicist Igor Tamm. The name phonon comes from the Greek word φωνή (phonē), which translates to sound or voice because long-wavelength phonons give rise to sound. The name is based on the word photon.

Shorter-wavelength higher-frequency phonons are responsible for the majority of the thermal capacity of solids.

Definition

A phonon is the quantum mechanical description of an elementary vibrational motion in which a lattice of atoms or molecules uniformly oscillates at a single frequency. In classical mechanics this designates a normal mode of vibration. Normal modes are important because any arbitrary lattice vibration can be considered to be a superposition of these elementary vibration modes. While normal modes are wave-like phenomena in classical mechanics, phonons have particle-like properties too, in a way related to the wave–particle duality of quantum mechanics.

Lattice dynamics

The equations in this section do not use axioms of quantum mechanics but instead use relations for which there exists a direct correspondence in classical mechanics.

For example: a rigid regular, crystalline (not amorphous), lattice is composed of N particles. These particles may be atoms or molecules. N is a large number, say of the order of 10²³, or on the order of Avogadro's number for a typical sample of a solid. Since the lattice is rigid, the atoms must be exerting forces on one another to keep each atom near its equilibrium position. These forces may be Van der Waals forces, covalent bonds, electrostatic attractions, and others, all of which are ultimately due to the electric force. Magnetic and gravitational forces are generally negligible. The forces between each pair of atoms may be characterized by a potential energy function V that depends on the distance of separation of the atoms. The potential energy of the entire lattice is the sum of all pairwise potential energies multiplied by a factor of 1/2 to avoid double counting:

${\displaystyle {\frac {1}{2}}\sum _{i\neq j}V\left(r_{i}-r_{j}\right)}$

where r_i is the position of the ith atom, and V is the potential energy between two atoms. 

It is difficult to solve this many-body problem explicitly in either classical or quantum mechanics. In order to simplify the task, two important approximations are usually imposed. First, the sum is only performed over neighboring atoms. Although the electric forces in real solids extend to infinity, this approximation is still valid because the fields produced by distant atoms are effectively screened. Secondly, the potentials V are treated as harmonic potentials. This is permissible as long as the atoms remain close to their equilibrium positions. Formally, this is accomplished by Taylor expanding V about its equilibrium value to quadratic order, giving V proportional to the displacement x² and the elastic force simply proportional to x. The error in ignoring higher order terms remains small if x remains close to the equilibrium position. 

The resulting lattice may be visualized as a system of balls connected by springs. The following figure shows a cubic lattice, which is a good model for many types of crystalline solid. Other lattices include a linear chain, which is a very simple lattice which we will shortly use for modeling phonons.

The potential energy of the lattice may now be written as

${\displaystyle \sum _{\{ij\}(\mathrm {nn} )}{\tfrac {1}{2}}m\omega ^{2}\left(R_{i}-R_{j}\right)^{2}.}$

Here, ω is the natural frequency of the harmonic potentials, which are assumed to be the same since the lattice is regular. R_i is the position coordinate of the ith atom, which we now measure from its equilibrium position. The sum over nearest neighbors is denoted (nn).

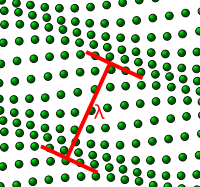
Lattice waves

Phonon propagating through a square lattice (atom displacements greatly exaggerated)

 

Due to the connections between atoms, the displacement of one or more atoms from their equilibrium positions gives rise to a set of vibration waves propagating through the lattice. One such wave is shown in the figure to the right. The amplitude of the wave is given by the displacements of the atoms from their equilibrium positions. The wavelength λ is marked. 

There is a minimum possible wavelength, given by twice the equilibrium separation a between atoms. Any wavelength shorter than this can be mapped onto a wavelength longer than 2a, due to the periodicity of the lattice. This can be thought as one consequence of Nyquist–Shannon sampling theorem, the lattice points are viewed as the "sampling points" of a continuous wave.

Not every possible lattice vibration has a well-defined wavelength and frequency. However, the normal modes do possess well-defined wavelengths and frequencies.

One-dimensional lattice

Animation showing the first 6 normal modes of a one-dimensional lattice: a linear chain of particles. The shortest wavelength is at top, with progressively longer wavelengths below. In the lowest lines the motion of the waves to the right can be seen.

 

In order to simplify the analysis needed for a 3-dimensional lattice of atoms, it is convenient to model a 1-dimensional lattice or linear chain. This model is complex enough to display the salient features of phonons.

Classical treatment

The forces between the atoms are assumed to be linear and nearest-neighbour, and they are represented by an elastic spring. Each atom is assumed to be a point particle and the nucleus and electrons move in step (adiabatic approximation): 

n − 1   n   n + 1   ←   a   →

···o++++++o++++++o++++++o++++++o++++++o++++++o++++++o++++++o++++++o···

→→ → →→→

u_{n − 1} u_n u_{n + 1}

where n labels the nth atom out of a total of N, a is the distance between atoms when the chain is in equilibrium, and u_n the displacement of the nth atom from its equilibrium position. 

If C is the elastic constant of the spring and m the mass of the atom, then the equation of motion of the nth atom is

${\displaystyle -2Cu_{n}+C\left(u_{n+1}+u_{n-1}\right)=m{\frac {d^{2}u_{n}}{dt^{2}}}.}$

This is a set of coupled equations. Since the solutions are expected to be oscillatory, new coordinates are defined by a discrete Fourier transform, in order to decouple them.

Put

${\displaystyle u_{n}=\sum _{Nak/2\pi =1}^{N}Q_{k}e^{ikna}}$

Here, na corresponds and devolves to the continuous variable x of scalar field theory. The Q_k are known as the normal coordinates, continuum field modes φ_k. Substitution into the equation of motion produces the following decoupled equations (this requires a significant manipulation using the orthonormality and completeness relations of the discrete Fourier transform

${\displaystyle 2C(\cos {ka-1})Q_{k}=m{\frac {d^{2}Q_{k}}{dt^{2}}}.}$

These are the equations for harmonic oscillators which have the solution

${\displaystyle Q_{k}=A_{k}e^{i\omega _{k}t};\qquad \omega _{k}={\sqrt {{\frac {2C}{m}}(1-\cos {ka})}}}$

Each normal coordinate Q_k represents an independent vibrational mode of the lattice with wavenumber k which is known as a normal mode. 

The second equation, for ω_k, is known as the dispersion relation between the angular frequency and the wavenumber. In the continuum limit, a→0, N→∞, with Na held fixed, u_n → φ(x), a scalar field, and ${\displaystyle \omega (k)\propto ka}$. This amounts to free scalar classical field theory.

Quantum treatment

A one-dimensional quantum mechanical harmonic chain consists of N identical atoms. This is the simplest quantum mechanical model of a lattice that allows phonons to arise from it. The formalism for this model is readily generalizable to two and three dimensions. 

In some contrast to the previous section, the positions of the masses are not denoted by u_i, but, instead, by x₁, x₂…, as measured from their equilibrium positions (i.e. x_i = 0 if particle i is at its equilibrium position.) In two or more dimensions, the x_i are vector quantities. The Hamiltonian for this system is

${\displaystyle {\mathcal {H}}=\sum _{i=1}^{N}{\frac {p_{i}^{2}}{2m}}+{\frac {1}{2}}m\omega ^{2}\sum _{\{ij\}(\mathrm {nn} )}\left(x_{i}-x_{j}\right)^{2}}$

where m is the mass of each atom (assuming it is equal for all), and x_i and p_i are the position and momentum operators, respectively, for the ith atom and the sum is made over the nearest neighbors (nn). However one expects that in a lattice there could also appear waves that behave like particles. It is customary to deal with waves in Fourier space which uses normal modes of the wavevector as variables instead coordinates of particles. The number of normal modes is same as the number of particles. However, the Fourier space is very useful given the periodicity of the system.

A set of N "normal coordinates" Q_k may be introduced, defined as the discrete Fourier transforms of the x_k and N "conjugate momenta" Π_k defined as the Fourier transforms of the p_k:

${\displaystyle {\begin{aligned}Q_{k}&={\frac {1}{\sqrt {N}}}\sum _{l}e^{ikal}x_{l}\\\Pi _{k}&={\frac {1}{\sqrt {N}}}\sum _{l}e^{-ikal}p_{l}.\end{aligned}}}$

The quantity k_n turns out to be the wavenumber of the phonon, i.e. 2π divided by the wavelength.

This choice retains the desired commutation relations in either real space or wavevector space

${\displaystyle {\begin{aligned}\left[x_{l},p_{m}\right]&=i\hbar \delta _{l,m}\\\left[Q_{k},\Pi _{k'}\right]&={\frac {1}{N}}\sum _{l,m}e^{ikal}e^{-ik'am}\left[x_{l},p_{m}\right]\\&={\frac {i\hbar }{N}}\sum _{l}e^{ial\left(k-k'\right)}=i\hbar \delta _{k,k'}\\\left[Q_{k},Q_{k'}\right]&=\left[\Pi _{k},\Pi _{k'}\right]=0\end{aligned}}}$

From the general result

${\displaystyle {\begin{aligned}\sum _{l}x_{l}x_{l+m}&={\frac {1}{N}}\sum _{kk'}Q_{k}Q_{k'}\sum _{l}e^{ial\left(k+k'\right)}e^{iamk'}=\sum _{k}Q_{k}Q_{-k}e^{iamk}\\\sum _{l}{p_{l}}^{2}&=\sum _{k}\Pi _{k}\Pi _{-k}\end{aligned}}}$

The potential energy term is

${\displaystyle {\tfrac {1}{2}}m\omega ^{2}\sum _{j}\left(x_{j}-x_{j+1}\right)^{2}={\tfrac {1}{2}}m\omega ^{2}\sum _{k}Q_{k}Q_{-k}(2-e^{ika}-e^{-ika})={\tfrac {1}{2}}\sum _{k}m{\omega _{k}}^{2}Q_{k}Q_{-k}}$

where

${\displaystyle \omega _{k}={\sqrt {2\omega ^{2}\left(1-\cos {ka}\right)}}=2\omega \left|\sin {\frac {ka}{2}}\right|}$

The Hamiltonian may be written in wavevector space as

${\displaystyle {\mathcal {H}}={\frac {1}{2m}}\sum _{k}\left(\Pi _{k}\Pi _{-k}+m^{2}\omega _{k}^{2}Q_{k}Q_{-k}\right)}$

The couplings between the position variables have been transformed away; if the Q and Π were Hermitian (which they are not), the transformed Hamiltonian would describe N uncoupled harmonic oscillators. 

The form of the quantization depends on the choice of boundary conditions; for simplicity, periodic boundary conditions are imposed, defining the (N + 1)th atom as equivalent to the first atom. Physically, this corresponds to joining the chain at its ends. The resulting quantization is

${\displaystyle k=k_{n}={\frac {2\pi n}{Na}}\quad {\mbox{for }}n=0,\pm 1,\pm 2,\ldots \pm {\frac {N}{2}}.\ }$

The upper bound to n comes from the minimum wavelength, which is twice the lattice spacing a, as discussed above. 

The harmonic oscillator eigenvalues or energy levels for the mode ω_k are:

${\displaystyle E_{n}=\left({\tfrac {1}{2}}+n\right)\hbar \omega _{k}\qquad n=0,1,2,3\ldots }$

The levels are evenly spaced at:

${\displaystyle {\tfrac {1}{2}}\hbar \omega ,\ {\tfrac {3}{2}}\hbar \omega ,\ {\tfrac {5}{2}}\hbar \omega \ \cdots }$

where 1/2ħω is the zero-point energy of a quantum harmonic oscillator.

An exact amount of energy ħω must be supplied to the harmonic oscillator lattice to push it to the next energy level. In comparison to the photon case when the electromagnetic field is quantized, the quantum of vibrational energy is called a phonon. 

All quantum systems show wavelike and particlelike properties simultaneously. The particle-like properties of the phonon are best understood using the methods of second quantization and operator techniques described later.

Three-dimensional lattice

This may be generalized to a three-dimensional lattice. The wavenumber k is replaced by a three-dimensional wavevector k. Furthermore, each k is now associated with three normal coordinates.

The new indices s = 1, 2, 3 label the polarization of the phonons. In the one-dimensional model, the atoms were restricted to moving along the line, so the phonons corresponded to longitudinal waves. In three dimensions, vibration is not restricted to the direction of propagation, and can also occur in the perpendicular planes, like transverse waves. This gives rise to the additional normal coordinates, which, as the form of the Hamiltonian indicates, we may view as independent species of phonons.

Dispersion relation

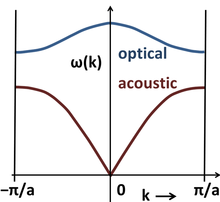
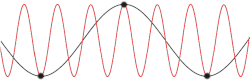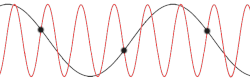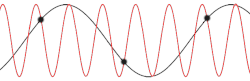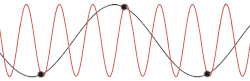
Dispersion curves in linear diatomic chain

 

Optical and acoustic vibrations in linear diatomic chain.

 

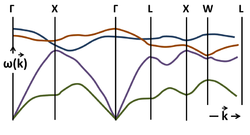
Dispersion relation ω = ω(k) for some waves corresponding to lattice vibrations in GaAs.

 

For a one-dimensional alternating array of two types of ion or atom of mass m₁, m₂ repeated periodically at a distance a, connected by springs of spring constant K, two modes of vibration result:

${\displaystyle \omega _{\pm }^{2}=K\left({\frac {1}{m_{1}}}+{\frac {1}{m_{2}}}\right)\pm K{\sqrt {\left({\frac {1}{m_{1}}}+{\frac {1}{m_{2}}}\right)^{2}-{\frac {4\sin ^{2}{\frac {ka}{2}}}{m_{1}m_{2}}}}},}$

where k is the wavevector of the vibration related to its wavelength by ${\displaystyle k={\frac {2\pi }{\lambda }}}$. 

The connection between frequency and wavevector, ω = ω(k), is known as a dispersion relation. The plus sign results in the so-called optical mode, and the minus sign to the acoustic mode. In the optical mode two adjacent different atoms move against each other, while in the acoustic mode they move together. 

The speed of propagation of an acoustic phonon, which is also the speed of sound in the lattice, is given by the slope of the acoustic dispersion relation, ∂ω_k/∂k (see group velocity.) At low values of k (i.e. long wavelengths), the dispersion relation is almost linear, and the speed of sound is approximately ωa, independent of the phonon frequency. As a result, packets of phonons with different (but long) wavelengths can propagate for large distances across the lattice without breaking apart. This is the reason that sound propagates through solids without significant distortion. This behavior fails at large values of k, i.e. short wavelengths, due to the microscopic details of the lattice.

For a crystal that has at least two atoms in its primitive cell, the dispersion relations exhibit two types of phonons, namely, optical and acoustic modes corresponding to the upper blue and lower red curve in the diagram, respectively. The vertical axis is the energy or frequency of phonon, while the horizontal axis is the wavevector. The boundaries at −π/a and π/a are those of the first Brillouin zone. A crystal with N ≥ 2 different atoms in the primitive cell exhibits three acoustic modes: one longitudinal acoustic mode and two transverse acoustic modes. The number of optical modes is 3N – 3. The lower figure shows the dispersion relations for several phonon modes in GaAs as a function of wavevector k in the principal directions of its Brillouin zone.

Many phonon dispersion curves have been measured by neutron scattering.

The physics of sound in fluids differs from the physics of sound in solids, although both are density waves: sound waves in fluids only have longitudinal components, whereas sound waves in solids have longitudinal and transverse components. This is because fluids can't support shear stresses (but see viscoelastic fluids, which only apply to high frequencies).

Interpretation of phonons using second quantization techniques

In fact, the above-derived Hamiltonian looks like the classical Hamiltonian function, but if it is interpreted as an operator, then it describes a quantum field theory of non-interacting bosons.

The energy spectrum of this Hamiltonian is easily obtained by the method of ladder operators, similar to the quantum harmonic oscillator problem. We introduce a set of ladder operators defined by:

${\displaystyle {\begin{alignedat}{2}b_{k}&={\frac {1}{\sqrt {2}}}\left({\frac {Q_{k}}{l_{k}}}+i{\frac {\Pi _{-k}}{\frac {\hbar }{l_{k}}}}\right),&\quad Q_{k}&=l_{k}{\frac {1}{\sqrt {2}}}\left({b_{k}}^{\dagger }+b_{-k}\right)\\{b_{k}}^{\dagger }&={\frac {1}{\sqrt {2}}}\left({\frac {Q_{-k}}{l_{k}}}-i{\frac {\Pi _{k}}{\frac {\hbar }{l_{k}}}}\right),&\quad \Pi _{k}&={\frac {\hbar }{l_{k}}}{\frac {i}{\sqrt {2}}}\left({b_{k}}^{\dagger }-b_{-k}\right)\\l_{k}&={\sqrt {\frac {\hbar }{m\omega _{k}}}}\end{alignedat}}}$

By direct insertion on the Hamiltonian, it is readily verified that

${\displaystyle {\mathcal {H}}=\sum _{k}\hbar \omega _{k}\left({b_{k}}^{\dagger }b_{k}+{\tfrac {1}{2}}\right),\quad \left[b_{k},{b_{k'}}^{\dagger }\right]=\delta _{k,k'},\quad {\Big [}b_{k},b_{k'}{\Big ]}=\left[{b_{k}}^{\dagger },{b_{k'}}^{\dagger }\right]=0.}$

As with the quantum harmonic oscillator, one can show that b_k^† and b_k respectively create and destroy one excitation of energy ħω_k. These excitations are phonons.

Two important properties of phonons may be deduced. Firstly, phonons are bosons, since any number of identical excitations can be created by repeated application of the creation operator b_k^†. Secondly, each phonon is a "collective mode" caused by the motion of every atom in the lattice. This may be seen from the fact that the ladder operators contain sums over the position and momentum operators of every atom.

It is not a priori obvious that these excitations generated by the b operators are literally waves of lattice displacement, but one may convince oneself of this by calculating the position–position correlation function. Let |k⟩ denote a state with a single quantum of mode k excited, i.e.

${\displaystyle |k\rangle =b_{k}^{\dagger }|0\rangle .}$

One can show that, for any two atoms j and l,

${\displaystyle \langle k|x_{j}(t)x_{l}(0)|k\rangle ={\frac {\hbar }{Nm\omega _{k}}}\cos {\big (}k(j-l)a-\omega _{k}t{\big )}+\langle 0|x_{j}(t)x_{l}(0)|0\rangle }$

which has the form of a lattice wave with frequency ω_k and wavenumber k.

In three dimensions the Hamiltonian has the form

${\displaystyle {\mathcal {H}}=\sum _{k}\sum _{s=1}^{3}\hbar \,\omega _{k,s}\left({b_{k,s}}^{\dagger }b_{k,s}+{\tfrac {1}{2}}\right).}$

Acoustic and optical phonons

Solids with more than one atom in the smallest unit cell, exhibit two types of phonons: acoustic phonons and optical phonons. 

Acoustic phonons are coherent movements of atoms of the lattice out of their equilibrium positions. If the displacement is in the direction of propagation, then in some areas the atoms will be closer, in others farther apart, as in a sound wave in air (hence the name acoustic). Displacement perpendicular to the propagation direction is comparable to waves on a string. If the wavelength of acoustic phonons goes to infinity, this corresponds to a simple displacement of the whole crystal, and this costs zero deformation energy. Acoustic phonons exhibit a linear relationship between frequency and phonon wavevector for long wavelengths. The frequencies of acoustic phonons tend to zero with longer wavelength. Longitudinal and transverse acoustic phonons are often abbreviated as LA and TA phonons, respectively. 

Optical phonons are out-of-phase movements of the atoms in the lattice, one atom moving to the left, and its neighbor to the right. This occurs if the lattice basis consists of two or more atoms. They are called optical because in ionic crystals, like sodium chloride, they are excited by infrared radiation. The electric field of the light will move every positive sodium ion in the direction of the field, and every negative chloride ion in the other direction, sending the crystal vibrating. 

Optical phonons have a non-zero frequency at the Brillouin zone center and show no dispersion near that long wavelength limit. This is because they correspond to a mode of vibration where positive and negative ions at adjacent lattice sites swing against each other, creating a time-varying electrical dipole moment. Optical phonons that interact in this way with light are called infrared active. Optical phonons that are Raman active can also interact indirectly with light, through Raman scattering. Optical phonons are often abbreviated as LO and TO phonons, for the longitudinal and transverse modes respectively; the splitting between LO and TO frequencies is often described accurately by the Lyddane–Sachs–Teller relation. 

When measuring optical phonon energy by experiment, optical phonon frequencies are sometimes given in spectroscopic wavenumber notation, where the symbol ω represents ordinary frequency (not angular frequency), and is expressed in units of cm⁻¹. The value is obtained by dividing the frequency by the speed of light in vacuum. In other words, the frequency in cm⁻¹ units corresponds to the inverse of the wavelength of a photon in vacuum, that has the same frequency as the measured phonon. The cm⁻¹ is a unit of energy used frequently in the dispersion relations of both acoustic and optical phonons, see units of energy for more details and uses.

Crystal momentum

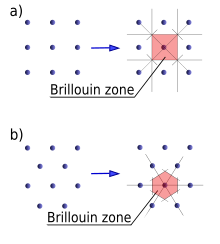
k-vectors exceeding the first Brillouin zone (red) do not carry any more information than their counterparts (black) in the first Brillouin zone.

 

By analogy to photons and matter waves, phonons have been treated with wavevector k as though it has a momentum ħk, however, this is not strictly correct, because ħk is not actually a physical momentum; it is called the crystal momentum or pseudomomentum. This is because k is only determined up to addition of constant vectors (the reciprocal lattice vectors and integer multiples thereof). For example, in the one-dimensional model, the normal coordinates Q and Π are defined so that

${\displaystyle Q_{k}{\stackrel {\mathrm {def} }{=}}Q_{k+K};\quad \Pi _{k}{\stackrel {\mathrm {def} }{=}}\Pi _{k+K}}$

where

${\displaystyle K={\frac {2n\pi }{a}}}$

for any integer n. A phonon with wavenumber k is thus equivalent to an infinite family of phonons with wavenumbers k ± 2π/a, k ± 4π/a, and so forth. Physically, the reciprocal lattice vectors act as additional chunks of momentum which the lattice can impart to the phonon. Bloch electrons obey a similar set of restrictions. 

Brillouin zones, (a) in a square lattice, and (b) in a hexagonal lattice

 

It is usually convenient to consider phonon wavevectors k which have the smallest magnitude |k| in their "family". The set of all such wavevectors defines the first Brillouin zone. Additional Brillouin zones may be defined as copies of the first zone, shifted by some reciprocal lattice vector.

Thermodynamics

The thermodynamic properties of a solid are directly related to its phonon structure. The entire set of all possible phonons that are described by the above phonon dispersion relations combine in what is known as the phonon density of states which determines the heat capacity of a crystal. 

At absolute zero temperature, a crystal lattice lies in its ground state, and contains no phonons. A lattice at a nonzero temperature has an energy that is not constant, but fluctuates randomly about some mean value. These energy fluctuations are caused by random lattice vibrations, which can be viewed as a gas of phonons. (The random motion of the atoms in the lattice is what we usually think of as heat.) Because these phonons are generated by the temperature of the lattice, they are sometimes designated thermal phonons.

Unlike the atoms which make up an ordinary gas, thermal phonons can be created and destroyed by random energy fluctuations. In the language of statistical mechanics this means that the chemical potential for adding a phonon is zero. This behavior is an extension of the harmonic potential, mentioned earlier, into the anharmonic regime. The behavior of thermal phonons is similar to the photon gas produced by an electromagnetic cavity, wherein photons may be emitted or absorbed by the cavity walls. This similarity is not coincidental, for it turns out that the electromagnetic field behaves like a set of harmonic oscillators; see Black-body radiation. Both gases obey the Bose–Einstein statistics: in thermal equilibrium and within the harmonic regime, the probability of finding phonons (or photons) in a given state with a given angular frequency is:

${\displaystyle n\left(\omega _{k,s}\right)={\frac {1}{\exp \left({\dfrac {\hbar \omega _{k,s}}{k_{\mathrm {B} }T}}\right)-1}}}$

where ω_k,s is the frequency of the phonons (or photons) in the state, k_B is Boltzmann's constant, and T is the temperature.

Heat flow in nanometer-wide gaps

The idea of quantum tunneling applied to phonons produces the idea of phonon tunneling, where across nanometer-wide gaps, heat can transfer between materials from phonon that "tunnel" between the two materials. The type of heat transfer works between distances too large for conduction to occur but too small for radiation to occur.

Operator formalism

The phonon Hamiltonian is given by

${\displaystyle {\mathcal {H}}={\tfrac {1}{2}}\sum _{\alpha }\left(p_{\alpha }^{2}+\omega _{\alpha }^{2}q_{\alpha }^{2}-{\tfrac {1}{2}}\hbar \omega _{\alpha }\right)}$

In terms of the operators, these are given by

${\displaystyle {\mathcal {H}}=\sum _{\alpha }\hbar \omega _{\alpha }{a_{\alpha }}^{\dagger }a_{\alpha }}$

Here, in expressing the Hamiltonian in operator formalism, we have not taken into account the 1/2ħω_q term, since if we take an infinite lattice or, for that matter a continuum, the 1/2ħω_q terms will add up giving an infinity. Hence, it is "renormalized" by putting the factor of 1/2ħω_q to 0 arguing that the difference in energy is what we measure and not the absolute value of it. Hence, the 1/2ħω_q factor is absent in the operator formalised expression for the Hamiltonian. 

The ground state also called the "vacuum state" is the state composed of no phonons. Hence, the energy of the ground state is 0. When, a system is in state |n₁n₂n₃…⟩, we say there are n_α phonons of type α. The n_α are called the occupation number of the phonons. Energy of a single phonon of type α being ħω_q, the total energy of a general phonon system is given by n₁ħω₁ + n₂ħω₂ +…. In other words, the phonons are non-interacting. The action of creation and annihilation operators are given by

${\displaystyle {a_{\alpha }}^{\dagger }{\Big |}n_{1}\ldots n_{\alpha -1}n_{\alpha }n_{\alpha +1}\ldots {\Big \rangle }={\sqrt {n_{\alpha }+1}}{\Big |}n_{1}\ldots ,n_{\alpha -1},(n_{\alpha }+1),n_{\alpha +1}\ldots {\Big \rangle }}$

and,

${\displaystyle a_{\alpha }{\Big |}n_{1}\ldots n_{\alpha -1}n_{\alpha }n_{\alpha +1}\ldots {\Big \rangle }={\sqrt {n_{\alpha }}}{\Big |}n_{1}\ldots ,n_{\alpha -1},(n_{\alpha }-1),n_{\alpha +1},\ldots {\Big \rangle }}$

i.e. a_α^† creates a phonon of type α while a_α annihilates. Hence, they are respectively the creation and annihilation operator for phonons. Analogous to the quantum harmonic oscillator case, we can define particle number operator as

${\displaystyle N=\sum _{\alpha }{a_{\alpha }}^{\dagger }a_{\alpha }.}$

The number operator commutes with a string of products of the creation and annihilation operators if, the number of a are equal to number of a^†.

Phonons are bosons, since |α,β⟩ = |β,α⟩ i.e. they are symmetric under exchange.

Nonlinearity

As well as photons, phonons can interact via parametric down conversion and form squeezed coherent states.

Predicted properties

Even though phonons are often used as a quasiparticle, some popular research has shown that phonons and rotons may indeed have some kind of mass and be affected by gravity as standard particles are. In particular, phonons are predicted to have a kind of negative mass and negative gravity. This can be shown in how phonons are known to travel faster in denser materials. Because the part of a material pointing towards a gravitational source is closer to the object, it becomes denser on that end. From this, it is predicted that phonons would deflect away as it detects the difference in densities, exhibiting the qualities of a negative gravitational field. Although the effect would be too small to measure, it is possible that future equipment could lead to successful results. 

Phonons have also been predicted play a key role in superconductivity in materials and the prediction of superconductive compounds.

High-temperature superconductivity

From Wikipedia, the free encyclopedia

A small sample of the high-temperature superconductor BSCCO-2223.

 

High-temperature superconductors (abbreviated high-T_c or HTS) are materials that behave as superconductors at unusually high temperatures. The first high-T_c superconductor was discovered in 1986 by IBM researchers Georg Bednorz and K. Alex Müller, who were awarded the 1987 Nobel Prize in Physics "for their important break-through in the discovery of superconductivity in ceramic materials".

Whereas "ordinary" or metallic superconductors usually have transition temperatures (temperatures below which they are superconductive) below 30 K (−243.2 °C) and must be cooled using liquid helium in order to achieve superconductivity, HTS have been observed with transition temperatures as high as 138 K (−135 °C), and can be cooled to superconductivity using liquid nitrogen. Until 2008, only certain compounds of copper and oxygen (so-called "cuprates") were known to have HTS properties, and the term high-temperature superconductor was used interchangeably with cuprate superconductor for compounds such as bismuth strontium calcium copper oxide (BSCCO) and yttrium barium copper oxide (YBCO). Several iron-based compounds (the iron pnictides) are now known to be superconducting at high temperatures.

In 2015, hydrogen sulfide (H₂S) under extremely high pressure (around 150 gigapascals) was found to undergo superconducting transition near 203 K (-70 °C), due the formation of H₃S, a new record high temperature superconductor.

History

The phenomenon of superconductivity was discovered by Kamerlingh Onnes in 1911, in metallic mercury below 4 K (−269.15 °C). Ever since, researchers have attempted to observe superconductivity at increasing temperatures with the goal of finding a room-temperature superconductor. By the late 1970s, superconductivity was observed in several metallic compounds (in particular Nb-based, such as NbTi, Nb₃Sn, and Nb₃Ge) at temperatures that were much higher than those for elemental metals and which could even exceed 20 K (−253.2 °C). In 1986, J. Georg Bednorz and K. Alex Müller, working at the IBM research lab near Zurich, Switzerland were exploring a new class of ceramics for superconductivity. Bednorz encountered a barium-doped compound of lanthanum and copper oxide whose resistance dropped to zero at a temperature around 35 K (−238.2 °C). Their results were soon confirmed by many groups, notably Paul Chu at the University of Houston and Shoji Tanaka at the University of Tokyo.

Shortly after, P. W. Anderson, at Princeton University came up with the first theoretical description of these materials, using the resonating valence bond theory, but a full understanding of these materials is still developing today. These superconductors are now known to possess a d-wave pair symmetry. The first proposal that high-temperature cuprate superconductivity involves d-wave pairing was made in 1987 by Bickers, Scalapino and Scalettar, followed by three subsequent theories in 1988 by Inui, Doniach, Hirschfeld and Ruckenstein, using spin-fluctuation theory, and by Gros, Poilblanc, Rice and Zhang, and by Kotliar and Liu identifying d-wave pairing as a natural consequence of the RVB theory. The confirmation of the d-wave nature of the cuprate superconductors was made by a variety of experiments, including the direct observation of the d-wave nodes in the excitation spectrum through Angle Resolved Photoemission Spectroscopy, the observation of a half-integer flux in tunneling experiments, and indirectly from the temperature dependence of the penetration depth, specific heat and thermal conductivity.

Until 2015 the superconductor with the highest transition temperature that had been confirmed by multiple independent research groups (a prerequisite to being called a discovery, verified by peer review) was mercury barium calcium copper oxide (HgBa₂Ca₂Cu₃O₈) at around 133 K.

After more than twenty years of intensive research, the origin of high-temperature superconductivity is still not clear, but it seems that instead of electron-phonon attraction mechanisms, as in conventional superconductivity, one is dealing with genuine electronic mechanisms (e.g. by antiferromagnetic correlations), and instead of conventional, purely s-wave pairing, more exotic pairing symmetries are thought to be involved (d-wave in the case of the cuprates; primarily extended s-wave, but occasionally d-wave, in the case of the iron-based superconductors). In 2014, evidence showing that fractional particles can happen in quasi two-dimensional magnetic materials, was found by EPFL scientists lending support for Anderson's theory of high-temperature superconductivity.

Crystal structures of high-temperature ceramic superconductors

The structure of high-T_c copper oxide or cuprate superconductors are often closely related to perovskite structure, and the structure of these compounds has been described as a distorted, oxygen deficient multi-layered perovskite structure. One of the properties of the crystal structure of oxide superconductors is an alternating multi-layer of CuO₂ planes with superconductivity taking place between these layers. The more layers of CuO₂, the higher T_c. This structure causes a large anisotropy in normal conducting and superconducting properties, since electrical currents are carried by holes induced in the oxygen sites of the CuO₂ sheets. The electrical conduction is highly anisotropic, with a much higher conductivity parallel to the CuO₂ plane than in the perpendicular direction. Generally, critical temperatures depend on the chemical compositions, cations substitutions and oxygen content. They can be classified as superstripes; i.e., particular realizations of superlattices at atomic limit made of superconducting atomic layers, wires, dots separated by spacer layers, that gives multiband and multigap superconductivity.

YBaCuO superconductors

YBCO unit cell

 

The first superconductor found with T_c > 77 K (liquid nitrogen boiling point) is yttrium barium copper oxide (YBa₂Cu₃O_7−x); the proportions of the three different metals in the YBa₂Cu₃O₇ superconductor are in the mole ratio of 1 to 2 to 3 for yttrium to barium to copper, respectively. Thus, this particular superconductor is often referred to as the 123 superconductor. 

The unit cell of YBa₂Cu₃O₇ consists of three pseudocubic elementary perovskite unit cells. Each perovskite unit cell contains a Y or Ba atom at the center: Ba in the bottom unit cell, Y in the middle one, and Ba in the top unit cell. Thus, Y and Ba are stacked in the sequence [Ba–Y–Ba] along the c-axis. All corner sites of the unit cell are occupied by Cu, which has two different coordinations, Cu(1) and Cu(2), with respect to oxygen. There are four possible crystallographic sites for oxygen: O(1), O(2), O(3) and O(4). The coordination polyhedra of Y and Ba with respect to oxygen are different. The tripling of the perovskite unit cell leads to nine oxygen atoms, whereas YBa₂Cu₃O₇ has seven oxygen atoms and, therefore, is referred to as an oxygen-deficient perovskite structure. The structure has a stacking of different layers: (CuO)(BaO)(CuO₂)(Y)(CuO₂)(BaO)(CuO). One of the key feature of the unit cell of YBa₂Cu₃O_7−x (YBCO) is the presence of two layers of CuO₂. The role of the Y plane is to serve as a spacer between two CuO₂ planes. In YBCO, the Cu–O chains are known to play an important role for superconductivity. T_c is maximal near 92 K when x ≈ 0.15 and the structure is orthorhombic. Superconductivity disappears at x ≈ 0.6, where the structural transformation of YBCO occurs from orthorhombic to tetragonal.

Bi-, Tl- and Hg-based high-T_c superconductors

The crystal structure of Bi-, Tl- and Hg-based high-T_c superconductors are very similar. Like YBCO, the perovskite-type feature and the presence of CuO₂ layers also exist in these superconductors. However, unlike YBCO, Cu–O chains are not present in these superconductors. The YBCO superconductor has an orthorhombic structure, whereas the other high-T_c superconductors have a tetragonal structure. 

The Bi–Sr–Ca–Cu–O system has three superconducting phases forming a homologous series as Bi₂Sr₂Ca_n−1Cu_nO_4+2n+x (n=1, 2 and 3). These three phases are Bi-2201, Bi-2212 and Bi-2223, having transition temperatures of 20, 85 and 110 K, respectively, where the numbering system represent number of atoms for Bi, Sr, Ca and Cu respectively. The two phases have a tetragonal structure which consists of two sheared crystallographic unit cells. The unit cell of these phases has double Bi–O planes which are stacked in a way that the Bi atom of one plane sits below the oxygen atom of the next consecutive plane. The Ca atom forms a layer within the interior of the CuO₂ layers in both Bi-2212 and Bi-2223; there is no Ca layer in the Bi-2201 phase. The three phases differ with each other in the number of CuO₂ planes; Bi-2201, Bi-2212 and Bi-2223 phases have one, two and three CuO₂ planes, respectively. The c axis lattice constants of these phases increases with the number of CuO₂ planes (see table below). The coordination of the Cu atom is different in the three phases. The Cu atom forms an octahedral coordination with respect to oxygen atoms in the 2201 phase, whereas in 2212, the Cu atom is surrounded by five oxygen atoms in a pyramidal arrangement. In the 2223 structure, Cu has two coordinations with respect to oxygen: one Cu atom is bonded with four oxygen atoms in square planar configuration and another Cu atom is coordinated with five oxygen atoms in a pyramidal arrangement.

Tl–Ba–Ca–Cu–O superconductor: The first series of the Tl-based superconductor containing one Tl–O layer has the general formula TlBa₂Ca_n-1Cu_nO_2n+3, whereas the second series containing two Tl–O layers has a formula of Tl₂Ba₂Ca_n-1Cu_nO_2n+4 with n =1, 2 and 3. In the structure of Tl₂Ba₂CuO₆ (Tl-2201), there is one CuO₂ layer with the stacking sequence (Tl–O) (Tl–O) (Ba–O) (Cu–O) (Ba–O) (Tl–O) (Tl–O). In Tl₂Ba₂CaCu₂O₈ (Tl-2212), there are two Cu–O layers with a Ca layer in between. Similar to the Tl₂Ba₂CuO₆ structure, Tl–O layers are present outside the Ba–O layers. In Tl₂Ba₂Ca₂Cu₃O₁₀ (Tl-2223), there are three CuO2 layers enclosing Ca layers between each of these. In Tl-based superconductors, T_c is found to increase with the increase in CuO₂ layers. However, the value of T_c decreases after four CuO₂ layers in TlBa₂Ca_n-1Cu_nO_2n+3, and in the Tl₂Ba₂Ca_n-1Cu_nO_2n+4 compound, it decreases after three CuO₂ layers.

Hg–Ba–Ca–Cu–O superconductor: The crystal structure of HgBa₂CuO₄ (Hg-1201), HgBa₂CaCu₂O₆ (Hg-1212) and HgBa₂Ca₂Cu₃O₈ (Hg-1223) is similar to that of Tl-1201, Tl-1212 and Tl-1223, with Hg in place of Tl. It is noteworthy that the T_c of the Hg compound (Hg-1201) containing one CuO₂ layer is much larger as compared to the one-CuO₂-layer compound of thallium (Tl-1201). In the Hg-based superconductor, T_c is also found to increase as the CuO₂ layer increases. For Hg-1201, Hg-1212 and Hg-1223, the values of T_c are 94, 128 and the record value at ambient pressure 134 K, respectively, as shown in table below. The observation that the T_c of Hg-1223 increases to 153 K under high pressure indicates that the T_c of this compound is very sensitive to the structure of the compound.

Critical temperature (T_c), crystal structure and lattice constants of some high-T_c superconductors

Formula	Notation	Tc (K)	No. of Cu-O planes in unit cell	Crystal structure
YBa2Cu3O7	123	92	2	Orthorhombic
Bi2Sr2CuO6	Bi-2201	20	1	Tetragonal
Bi2Sr2CaCu2O8	Bi-2212	85	2	Tetragonal
Bi2Sr2Ca2Cu3O10	Bi-2223	110	3	Tetragonal
Tl2Ba2CuO6	Tl-2201	80	1	Tetragonal
Tl2Ba2CaCu2O8	Tl-2212	108	2	Tetragonal
Tl2Ba2Ca2Cu3O10	Tl-2223	125	3	Tetragonal
TlBa2Ca3Cu4O11	Tl-1234	122	4	Tetragonal
HgBa2CuO4	Hg-1201	94	1	Tetragonal
HgBa2CaCu2O6	Hg-1212	128	2	Tetragonal
HgBa2Ca2Cu3O8	Hg-1223	134	3	Tetragonal

Preparation of high-T_c superconductors

The simplest method for preparing high-T_c superconductors is a solid-state thermochemical reaction involving mixing, calcination and sintering. The appropriate amounts of precursor powders, usually oxides and carbonates, are mixed thoroughly using a Ball mill. Solution chemistry processes such as coprecipitation, freeze-drying and sol-gel methods are alternative ways for preparing a homogeneous mixture. These powders are calcined in the temperature range from 800 °C to 950 °C for several hours. The powders are cooled, reground and calcined again. This process is repeated several times to get homogeneous material. The powders are subsequently compacted to pellets and sintered. The sintering environment such as temperature, annealing time, atmosphere and cooling rate play a very important role in getting good high-T_c superconducting materials. The YBa₂Cu₃O_7−x compound is prepared by calcination and sintering of a homogeneous mixture of Y₂O₃, BaCO₃ and CuO in the appropriate atomic ratio. Calcination is done at 900–950 °C, whereas sintering is done at 950 °C in an oxygen atmosphere. The oxygen stoichiometry in this material is very crucial for obtaining a superconducting YBa₂Cu₃O_7−x compound. At the time of sintering, the semiconducting tetragonal YBa₂Cu₃O₆ compound is formed, which, on slow cooling in oxygen atmosphere, turns into superconducting YBa₂Cu₃O_7−x. The uptake and loss of oxygen are reversible in YBa₂Cu₃O_7−x. A fully oxygenated orthorhombic YBa₂Cu₃O_7−x sample can be transformed into tetragonal YBa₂Cu₃O₆ by heating in a vacuum at temperature above 700 °C.

The preparation of Bi-, Tl- and Hg-based high-T_c superconductors is difficult compared to YBCO. Problems in these superconductors arise because of the existence of three or more phases having a similar layered structure. Thus, syntactic intergrowth and defects such as stacking faults occur during synthesis and it becomes difficult to isolate a single superconducting phase. For Bi–Sr–Ca–Cu–O, it is relatively simple to prepare the Bi-2212 (T_c ≈ 85 K) phase, whereas it is very difficult to prepare a single phase of Bi-2223 (T_c ≈ 110 K). The Bi-2212 phase appears only after few hours of sintering at 860–870 °C, but the larger fraction of the Bi-2223 phase is formed after a long reaction time of more than a week at 870 °C. Although the substitution of Pb in the Bi–Sr–Ca–Cu–O compound has been found to promote the growth of the high-T_c phase, a long sintering time is still required.

Properties

"High-temperature" has two common definitions in the context of superconductivity:

1. Above the temperature of 30 K that had historically been taken as the upper limit allowed by BCS theory (1957). This is also above the 1973 record of 23 K that had lasted until copper-oxide materials were discovered in 1986.
2. Having a transition temperature that is a larger fraction of the Fermi temperature than for conventional superconductors such as elemental mercury or lead. This definition encompasses a wider variety of unconventional superconductors and is used in the context of theoretical models.

The label high-T_c may be reserved by some authors for materials with critical temperature greater than the boiling point of liquid nitrogen (77 K or −196 °C). However, a number of materials – including the original discovery and recently discovered pnictide superconductors – had critical temperatures below 77 K but are commonly referred to in publication as being in the high-T_c class.

Technological applications could benefit from both the higher critical temperature being above the boiling point of liquid nitrogen and also the higher critical magnetic field (and critical current density) at which superconductivity is destroyed. In magnet applications, the high critical magnetic field may prove more valuable than the high T_c itself. Some cuprates have an upper critical field of about 100 tesla. However, cuprate materials are brittle ceramics which are expensive to manufacture and not easily turned into wires or other useful shapes. Also, high-temperature superconductors do not form large, continuous superconducting domains, but only clusters of microdomains within which superconductivity occurs. They are therefore unsuitable for applications requiring actual superconducted currents, such as magnets for magnetic resonance spectrometers.

After two decades of intense experimental and theoretical research, with over 100,000 published papers on the subject, several common features in the properties of high-temperature superconductors have been identified. As of 2011, no widely accepted theory explains their properties. Relative to conventional superconductors, such as elemental mercury or lead that are adequately explained by the BCS theory, cuprate superconductors (and other unconventional superconductors) remain distinctive. There also has been much debate as to high-temperature superconductivity coexisting with magnetic ordering in YBCO, iron-based superconductors, several ruthenocuprates and other exotic superconductors, and the search continues for other families of materials. HTS are Type-II superconductors, which allow magnetic fields to penetrate their interior in quantized units of flux, meaning that much higher magnetic fields are required to suppress superconductivity. The layered structure also gives a directional dependence to the magnetic field response.

Cuprates

Simplified doping dependent phase diagram of cuprate superconductors for both electron (n) and hole (p) doping. The phases shown are the antiferromagnetic (AF) phase close to zero doping, the superconducting phase around optimal doping, and the pseudogap phase. Doping ranges possible for some common compounds are also shown. After.

 

Cuprate superconductors are generally considered to be quasi-two-dimensional materials with their superconducting properties determined by electrons moving within weakly coupled copper-oxide (CuO₂) layers. Neighbouring layers containing ions such as lanthanum, barium, strontium, or other atoms act to stabilize the structure and dope electrons or holes onto the copper-oxide layers. The undoped "parent" or "mother" compounds are Mott insulators with long-range antiferromagnetic order at low enough temperature. Single band models are generally considered to be sufficient to describe the electronic properties. 

The cuprate superconductors adopt a perovskite structure. The copper-oxide planes are checkerboard lattices with squares of O²⁻ ions with a Cu²⁺ ion at the centre of each square. The unit cell is rotated by 45° from these squares. Chemical formulae of superconducting materials generally contain fractional numbers to describe the doping required for superconductivity. There are several families of cuprate superconductors and they can be categorized by the elements they contain and the number of adjacent copper-oxide layers in each superconducting block. For example, YBCO and BSCCO can alternatively be referred to as Y123 and Bi2201/Bi2212/Bi2223 depending on the number of layers in each superconducting block (n). The superconducting transition temperature has been found to peak at an optimal doping value (p=0.16) and an optimal number of layers in each superconducting block, typically n=3. 

Possible mechanisms for superconductivity in the cuprates are still the subject of considerable debate and further research. Certain aspects common to all materials have been identified. Similarities between the antiferromagnetic low-temperature state of the undoped materials and the superconducting state that emerges upon doping, primarily the d_x²-y² orbital state of the Cu²⁺ ions, suggest that electron-electron interactions are more significant than electron-phonon interactions in cuprates – making the superconductivity unconventional. Recent work on the Fermi surface has shown that nesting occurs at four points in the antiferromagnetic Brillouin zone where spin waves exist and that the superconducting energy gap is larger at these points. The weak isotope effects observed for most cuprates contrast with conventional superconductors that are well described by BCS theory.

Similarities and differences in the properties of hole-doped and electron doped cuprates:

• Presence of a pseudogap phase up to at least optimal doping.
• Different trends in the Uemura plot relating transition temperature to the superfluid density. The inverse square of the London penetration depth appears to be proportional to the critical temperature for a large number of underdoped cuprate superconductors, but the constant of proportionality is different for hole- and electron-doped cuprates. The linear trend implies that the physics of these materials is strongly two-dimensional.
• Universal hourglass-shaped feature in the spin excitations of cuprates measured using inelastic neutron diffraction.
• Nernst effect evident in both the superconducting and pseudogap phases.

Fig. 1. The Fermi surface of bi-layer BSCCO, calculated (left) and measured by ARPES (right). The dashed rectangle represents the first Brillouin zone.

 

The electronic structure of superconducting cuprates is highly anisotropic (see the crystal structure of YBCO or BSCCO). Therefore, the Fermi surface of HTSC is very close to the Fermi surface of the doped CuO₂ plane (or multi-planes, in case of multi-layer cuprates) and can be presented on the 2D reciprocal space (or momentum space) of the CuO₂ lattice. The typical Fermi surface within the first CuO₂ Brillouin zone is sketched in Fig. 1 (left). It can be derived from the band structure calculations or measured by angle resolved photoemission spectroscopy (ARPES). Fig. 1 (right) shows the Fermi surface of BSCCO measured by ARPES. In a wide range of charge carrier concentration (doping level), in which the hole-doped HTSC are superconducting, the Fermi surface is hole-like (i.e. open, as shown in Fig. 1). This results in an inherent in-plane anisotropy of the electronic properties of HTSC.

Iron-based superconductors

Simplified doping dependent phase diagrams of iron-based superconductors for both Ln-1111 and Ba-122 materials. The phases shown are the antiferromagnetic/spin density wave (AF/SDW) phase close to zero doping and the superconducting phase around optimal doping. The Ln-1111 phase diagrams for La and Sm were determined using muon spin spectroscopy, the phase diagram for Ce was determined using neutron diffraction. The Ba-122 phase diagram is based on.

 

Iron-based superconductors contain layers of iron and a pnictogen—such as arsenic or phosphorus—or a chalcogen. This is currently the family with the second highest critical temperature, behind the cuprates. Interest in their superconducting properties began in 2006 with the discovery of superconductivity in LaFePO at 4 K and gained much greater attention in 2008 after the analogous material LaFeAs(O,F) was found to superconduct at up to 43 K under pressure. The highest critical temperatures in the iron-based superconductor family exist in thin films of FeSe, where a critical temperature in excess of 100 K was reported in 2014.

Since the original discoveries several families of iron-based superconductors have emerged:

• LnFeAs(O,F) or LnFeAsO_1−x (Ln=lanthanide) with T_c up to 56 K, referred to as 1111 materials. A fluoride variant of these materials was subsequently found with similar T_c values.
• (Ba,K)Fe₂As₂ and related materials with pairs of iron-arsenide layers, referred to as 122 compounds. T_c values range up to 38 K. These materials also superconduct when iron is replaced with cobalt.
• LiFeAs and NaFeAs with T_c up to around 20 K. These materials superconduct close to stoichiometric composition and are referred to as 111 compounds.
• FeSe with small off-stoichiometry or tellurium doping.

Most undoped iron-based superconductors show a tetragonal-orthorhombic structural phase transition followed at lower temperature by magnetic ordering, similar to the cuprate superconductors. However, they are poor metals rather than Mott insulators and have five bands at the Fermi surface rather than one. The phase diagram emerging as the iron-arsenide layers are doped is remarkably similar, with the superconducting phase close to or overlapping the magnetic phase. Strong evidence that the T_c value varies with the As-Fe-As bond angles has already emerged and shows that the optimal T_c value is obtained with undistorted FeAs₄ tetrahedra. The symmetry of the pairing wavefunction is still widely debated, but an extended s-wave scenario is currently favored.

Hydrogen sulfide

At pressures above 90 GPa (Gigapascals), hydrogen sulfide becomes a metallic conductor of electricity. When cooled below a critical temperature this high-pressure phase exhibits superconductivity. The critical temperature increases with pressure, ranging from 23 K at 100 GPa to 150 K at 200 GPa. If hydrogen sulfide is pressurized at higher temperatures, then cooled, the critical temperature reaches 203 K (−70 °C), the highest accepted superconducting critical temperature as of 2015. It has been predicted that by substituting a small part of sulfur with phosphorus and using even higher pressures it may be possible to raise the critical temperature to above 273 K (0 °C) and achieve room-temperature superconductivity.

Other materials sometimes referred to as high-temperature superconductors

Magnesium diboride is occasionally referred to as a high-temperature superconductor because its T_c value of 39 K is above that historically expected for BCS superconductors. However, it is more generally regarded as the highest-T_c conventional superconductor, the increased T_c resulting from two separate bands being present at the Fermi level. 

Fulleride superconductors where alkali-metal atoms are intercalated into C₆₀ molecules show superconductivity at temperatures of up to 38 K for Cs₃C₆₀.

Some organic superconductors and heavy fermion compounds are considered to be high-temperature superconductors because of their high T_c values relative to their Fermi energy, despite the T_c values being lower than for many conventional superconductors. This description may relate better to common aspects of the superconducting mechanism than the superconducting properties.

Metallic hydrogen

Theoretical work by Neil Ashcroft in 1968 predicted that solid metallic hydrogen at extremely high pressure should become superconducting at approximately room-temperature because of its extremely high speed of sound and expected strong coupling between the conduction electrons and the lattice vibrations. As of 2016 this prediction is yet to be experimentally verified.

Magnetic properties

All known high-T_c superconductors are Type-II superconductors. In contrast to Type-I superconductors, which expel all magnetic fields due to the Meissner effect, Type-II superconductors allow magnetic fields to penetrate their interior in quantized units of flux, creating "holes" or "tubes" of normal metallic regions in the superconducting bulk called vortices. Consequently, high-T_c superconductors can sustain much higher magnetic fields.

Ongoing research

Superconductor timeline. BCS superconductors are displayed as green circles, cuprates as blue diamonds, and iron-based superconductors as yellow squares. (YBaCuO should be at 93K according to table below.)

 

The question of how superconductivity arises in high-temperature superconductors is one of the major unsolved problems of theoretical condensed matter physics. The mechanism that causes the electrons in these crystals to form pairs is not known. Despite intensive research and many promising leads, an explanation has so far eluded scientists. One reason for this is that the materials in question are generally very complex, multi-layered crystals (for example, BSCCO), making theoretical modelling difficult. 

Improving the quality and variety of samples also gives rise to considerable research, both with the aim of improved characterisation of the physical properties of existing compounds, and synthesizing new materials, often with the hope of increasing T_c. Technological research focuses on making HTS materials in sufficient quantities to make their use economically viable and optimizing their properties in relation to applications.

Possible mechanism

There have been two representative theories for high-temperature or unconventional superconductivity. Firstly, weak coupling theory suggests superconductivity emerges from antiferromagnetic spin fluctuations in a doped system. According to this theory, the pairing wave function of the cuprate HTS should have a d_x²-y² symmetry. Thus, determining whether the pairing wave function has d-wave symmetry is essential to test the spin fluctuation mechanism. That is, if the HTS order parameter (pairing wave function) does not have d-wave symmetry, then a pairing mechanism related to spin fluctuations can be ruled out. (Similar arguments can be made for iron-based superconductors but the different material properties allow a different pairing symmetry.) Secondly, there was the interlayer coupling model, according to which a layered structure consisting of BCS-type (s-wave symmetry) superconductors can enhance the superconductivity by itself. By introducing an additional tunnelling interaction between each layer, this model successfully explained the anisotropic symmetry of the order parameter as well as the emergence of the HTS. Thus, in order to solve this unsettled problem, there have been numerous experiments such as photoemission spectroscopy, NMR, specific heat measurements, etc. Up to date the results were ambiguous, some reports supported the d symmetry for the HTS whereas others supported the s symmetry. This muddy situation possibly originated from the indirect nature of the experimental evidence, as well as experimental issues such as sample quality, impurity scattering, twinning, etc. 

This summary makes an implicit assumption: superconductive properties can be treated by mean field theory. It also fails to mention that in addition to the superconductive gap, there is a second gap, the pseudogap. The cuprate layers are insulating, and the superconductors are doped with interlayer impurities to make them metallic. The superconductive transition temperature can be maximized by varying the dopant concentration. The simplest example is La(2)CuO(4), which consist of alternating CuO(2) and LaO layers which are insulating when pure. When 8% of the La is replaced by Sr, the latter act as dopants, contributing holes to the CuO(2) layers, and making the sample metallic. The Sr impurities also act as electronic bridges, enabling interlayer coupling. With this realistic picture of the electronic and atomic structure of high temperature superconductors, one can show from thousands of experiments that the basic pairing interaction is still interaction with phonons, just as in the old metallic superconductors with Cooper pairs. While the undoped materials are antiferromagnetic, even a few % impurity dopants introduce a smaller pseudogap in the CuO2 planes which is also caused by phonons (technically charge density waves). This gap decreases with increasing charge carriers, and as it nears the superconductive gap, the latter reaches its maximum. This picture has been extended to answer the most obvious question of high temperature superconductivity, why are the transition temperatures so high? The carriers follow zig-zag percolative paths, largely in metallic domains in the CuO(2) planes, until blocked by charge density wave domain walls, where they use dopant bridges to cross over to a metallic domain of an adjacent CuO(2) plane. This model of self-organized networks of percolative paths describes all known maximum transition temperatures with no adjustable parameters. The transition temperature maxima are reached when the host lattice has weak bond-bending forces, which produce strong electron-phonon interactions at the interlayer dopants.^[69]

Junction experiment supporting the d symmetry

The Meissner effect or a magnet levitating above a superconductor (cooled by liquid nitrogen)

 

An experiment based on flux quantization of a three-grain ring of YBa₂Cu₃O₇ (YBCO) was proposed to test the symmetry of the order parameter in the HTS. The symmetry of the order parameter could best be probed at the junction interface as the Cooper pairs tunnel across a Josephson junction or weak link. It was expected that a half-integer flux, that is, a spontaneous magnetization could only occur for a junction of d symmetry superconductors. But, even if the junction experiment is the strongest method to determine the symmetry of the HTS order parameter, the results have been ambiguous. J. R. Kirtley and C. C. Tsuei thought that the ambiguous results came from the defects inside the HTS, so that they designed an experiment where both clean limit (no defects) and dirty limit (maximal defects) were considered simultaneously. In the experiment, the spontaneous magnetization was clearly observed in YBCO, which supported the d symmetry of the order parameter in YBCO. But, since YBCO is orthorhombic, it might inherently have an admixture of s symmetry. So, by tuning their technique further, they found that there was an admixture of s symmetry in YBCO within about 3%. Also, they found that there was a pure d_x²-y² order parameter symmetry in the tetragonal Tl₂Ba₂CuO₆.

Qualitative explanation of the spin-fluctuation mechanism

Despite all these years, the mechanism of high-T_c superconductivity is still highly controversial, mostly due to the lack of exact theoretical computations on such strongly interacting electron systems. However, most rigorous theoretical calculations, including phenomenological and diagrammatic approaches, converge on magnetic fluctuations as the pairing mechanism for these systems. The qualitative explanation is as follows: 

In a superconductor, the flow of electrons cannot be resolved into individual electrons, but instead consists of many pairs of bound electrons, called Cooper pairs. In conventional superconductors, these pairs are formed when an electron moving through the material distorts the surrounding crystal lattice, which in turn attracts another electron and forms a bound pair. This is sometimes called the "water bed" effect. Each Cooper pair requires a certain minimum energy to be displaced, and if the thermal fluctuations in the crystal lattice are smaller than this energy the pair can flow without dissipating energy. This ability of the electrons to flow without resistance leads to superconductivity.

In a high-T_c superconductor, the mechanism is extremely similar to a conventional superconductor, except, in this case, phonons virtually play no role and their role is replaced by spin-density waves. Just as all known conventional superconductors are strong phonon systems, all known high-T_c superconductors are strong spin-density wave systems, within close vicinity of a magnetic transition to, for example, an antiferromagnet. When an electron moves in a high-T_c superconductor, its spin creates a spin-density wave around it. This spin-density wave in turn causes a nearby electron to fall into the spin depression created by the first electron (water-bed effect again). Hence, again, a Cooper pair is formed. When the system temperature is lowered, more spin density waves and Cooper pairs are created, eventually leading to superconductivity. Note that in high-T_c systems, as these systems are magnetic systems due to the Coulomb interaction, there is a strong Coulomb repulsion between electrons. This Coulomb repulsion prevents pairing of the Cooper pairs on the same lattice site. The pairing of the electrons occur at near-neighbor lattice sites as a result. This is the so-called d-wave pairing, where the pairing state has a node (zero) at the origin.

This summary assumes superconductive properties can be treated by mean field theory. It also fails to mention that in addition to the superconductive gap, there is a second gap, the pseudogap. The cuprate layers are insulating, and the superconductors are doped with interlayer impurities to make them metallic. The superconductive transition temperature can be maximized by varying the dopant concentration. The simplest example is La(2)CuO(4), which consist of alternating CuO(2) and LaO layers which are insulating when pure. When 8% of the La is replaced by Sr, the latter act as dopants, contributing holes to the CuO(2) layers, and making the sample metallic. The Sr impurities also act as electronic bridges, enabling interlayer coupling. With this realistic picture of the electronic and atomic structure of high temperature superconductors, one can show from thousands of experiments that the basic pairing interaction is still interaction with phonons, just as in the old metallic superconductors with Cooper pairs. While the undoped materials are antiferromagnetic, even a few % impurity dopants introduce a smaller pseudogap in the CuO2 planes which is also caused by phonons (technically charge density waves). This gap decreases with increasing charge carriers, and as it nears the superconductive gap, the latter reaches its maximum. This picture has been extended to answer the most obvious question of high temperature superconductivity, why are the transition temperatures so high? The carriers follow zig-zag percolative paths, largely in metallic domains in the CuO(2) planes, until blocked by charge density wave domain walls, where they use dopant bridges to cross over to a metallic domain of an adjacent CuO(2) plane. This model describes all known maximum transition temperatures with no adjustable parameters. The maxima are reached when the host lattice has weak bond-bending forces.

Examples

Examples of high-T_c cuprate superconductors include La_1.85Ba_0.15CuO₄, and YBCO (yttrium-barium-copper oxide), which is famous as the first material discovered to achieve superconductivity above the boiling point of liquid nitrogen. 

Transition temperatures of well-known superconductors (Boiling point of liquid nitrogen for comparison)

Transition temperature (in kelvins)	Transition temperature (in degrees Celsius)	Material	Class
203	−70	H2S (at 150 GPa pressure)	Hydrogen-based superconductor
195	−78	Sublimation point of dry ice
184	−89.2	Lowest temperature recorded on Earth
145	−128	Boiling point of tetrafluoromethane
133	−140	HgBa2Ca2Cu3Ox(HBCCO)	Copper-oxide superconductors
110	−163	Bi2Sr2Ca2Cu3O10(BSCCO)
93	−180	YBa2Cu3O7 (YBCO)
90	−183	Boiling point of liquid oxygen
77	−196	Boiling point of liquid nitrogen
55	−218	SmFeAs(O,F)	Iron-based superconductors
41	−232	CeFeAs(O,F)
26	−247	LaFeAs(O,F)
20	−253	Boiling point of liquid hydrogen
18	−255	Nb3Sn	Metallic low-temperature superconductors
10	−263	NbTi
9.2	−263.8	Nb
4.2	−268.8	Boiling point of liquid helium
4.2	−268.8	Hg (mercury)	Metallic low-temperature superconductors