A re-creation of the 1945 criticality accident using the Demon core: a plutonium pit is surrounded by blocks of neutron-reflective tungsten carbide.
The original experiment was designed to measure the radiation produced
when an extra block was added. The mass went supercritical when the
block was placed improperly by being dropped.
A critical mass is the smallest amount of fissile material needed for a sustained nuclear chain reaction. The critical mass of a fissionable material depends upon its nuclear properties (specifically, the nuclear fission cross-section), its density, its shape, its enrichment, its purity, its temperature, and its surroundings. The concept is important in nuclear weapon design.
Explanation of criticality
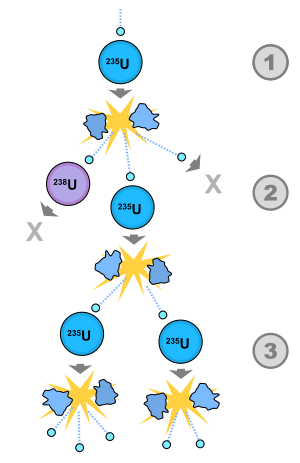
When a nuclear chain reaction in a mass of fissile material is self-sustaining, the mass is said to be in a critical state in which there is no increase or decrease in power, temperature, or neutron population.
A numerical measure of a critical mass is dependent on the effective neutron multiplication factor k,
the average number of neutrons released per fission event that go on to
cause another fission event rather than being absorbed or leaving the
material. When k = 1, the mass is critical, and the chain reaction is self-sustaining.
A subcritical mass is a mass of fissile material that does
not have the ability to sustain a fission chain reaction. A population
of neutrons introduced to a subcritical assembly will exponentially
decrease. In this case, k < 1. A
steady rate of spontaneous fissions causes a proportionally steady level
of neutron activity. The constant of proportionality increases as k increases.
A supercritical mass is one in which, once fission has
started, it will proceed at an increasing rate. The material may settle
into equilibrium (i.e. become critical again) at an elevated temperature/power level or destroy itself. In the case of supercriticality, k > 1.
Due to spontaneous fission a supercritical mass will undergo a chain reaction. For example, a spherical critical mass of pure uranium-235 will have a mass of 52 kg and will experience around 15 spontaneous fission events per second.
The probability that one such event will cause a chain reaction depends
on how much the mass exceeds the critical mass. If there is uranium-238 present, the rate of spontaneous fission will be much higher. Fission can also be initiated by neutrons produced by cosmic rays.
Changing the point of criticality
The
mass where criticality occurs may be changed by modifying certain
attributes such as fuel, shape, temperature, density and the
installation of a neutron-reflective substance. These attributes have
complex interactions and interdependencies. These examples only outline
the simplest ideal cases:
Varying the amount of fuel
It
is possible for a fuel assembly to be critical at near zero power. If
the perfect quantity of fuel were added to a slightly subcritical mass
to create an "exactly critical mass", fission would be self-sustaining
for only one neutron generation (fuel consumption then makes the
assembly subcritical again).
If the perfect quantity of fuel were added to a slightly
subcritical mass, to create a barely supercritical mass, the temperature
of the assembly would increase to an initial maximum (for example: 1 K
above the ambient temperature) and then decrease back to the ambient
temperature after a period of time, because fuel consumed during fission
brings the assembly back to subcriticality once again.
Changing the shape
A
mass may be exactly critical without being a perfect homogeneous
sphere. More closely refining the shape toward a perfect sphere will
make the mass supercritical. Conversely changing the shape to a less
perfect sphere will decrease its reactivity and make it subcritical.
Changing the temperature
A mass may be exactly critical at a particular temperature. Fission and absorption cross-sections
increase as the relative neutron velocity decreases. As fuel
temperature increases, neutrons of a given energy appear faster and thus
fission/absorption is less likely. This is not unrelated to Doppler broadening of the 238U
resonances but is common to all fuels/absorbers/configurations.
Neglecting the very important resonances, the total neutron
cross-section of every material exhibits an inverse relationship with
relative neutron velocity. Hot fuel is always less reactive than cold
fuel (over/under moderation in LWR is a different topic). Thermal
expansion associated with temperature increase also contributes a
negative coefficient of reactivity since fuel atoms are moving farther
apart. A mass that is exactly critical at room temperature would be
sub-critical in an environment anywhere above room temperature due to
thermal expansion alone.
Varying the density of the mass
The
higher the density, the lower the critical mass. The density of a
material at a constant temperature can be changed by varying the
pressure or tension or by changing crystal structure.
An ideal mass will become subcritical if allowed to expand or
conversely the same mass will become supercritical if compressed.
Changing the temperature may also change the density; however, the
effect on critical mass is then complicated by temperature effects (see
"Changing the temperature") and by whether the material expands or
contracts with increased temperature. Assuming the material expands with
temperature (enriched uranium-235
at room temperature for example), at an exactly critical state, it will
become subcritical if warmed to lower density or become supercritical
if cooled to higher density. Such a material is said to have a negative
temperature coefficient of reactivity to indicate that its reactivity
decreases when its temperature increases. Using such a material as fuel
means fission decreases as the fuel temperature increases.
Use of a neutron reflector
Surrounding a spherical critical mass with a neutron reflector further reduces the mass needed for criticality. A common material for a neutron reflector is beryllium metal. This reduces the number of neutrons which escape the fissile material, resulting in increased reactivity.
Use of a tamper
In
a bomb, a dense shell of material surrounding the fissile core will
contain, via inertia, the expanding fissioning material. This increases
the efficiency. A tamper also tends to act as a neutron reflector.
Because a bomb relies on fast neutrons (not ones moderated by reflection
with light elements, as in a reactor), the neutrons reflected by a
tamper are slowed by their collisions with the tamper nuclei, and
because it takes time for the reflected neutrons to return to the
fissile core, they take rather longer to be absorbed by a fissile
nucleus. But they do contribute to the reaction, and can decrease the
critical mass by a factor of four.
Also, if the tamper is (e.g. depleted) uranium, it can fission due to
the high energy neutrons generated by the primary explosion. This can
greatly increase yield, especially if even more neutrons are generated
by fusing hydrogen isotopes, in a so-called boosted configuration.
Critical size
The
critical size is the minimum size of a nuclear reactor core or nuclear
weapon that can be made for a specific geometrical arrangement and
material composition. The critical size must at least include enough
fissionable material to reach critical mass. If the size of the reactor
core is less than a certain minimum, too many fission neutrons escape
through its surface and the chain reaction is not sustained.
Critical mass of a bare sphere
Top: A sphere of fissile material is too small to allow the chain reaction to become self-sustaining as neutrons generated by fissions can too easily escape.
Middle: By increasing the mass of the sphere to a critical mass, the reaction can become self-sustaining.
Bottom: Surrounding the original sphere with a neutron reflector increases the efficiency of the reactions and also allows the reaction to become self-sustaining.
Middle: By increasing the mass of the sphere to a critical mass, the reaction can become self-sustaining.
Bottom: Surrounding the original sphere with a neutron reflector increases the efficiency of the reactions and also allows the reaction to become self-sustaining.
The shape with minimal critical mass and the smallest physical
dimensions is a sphere. Bare-sphere critical masses at normal density of
some actinides
are listed in the following table. Most information on bare sphere
masses is considered classified, since it is critical to nuclear weapons
design, but some documents have been declassified.
| Nuclide | Half life (y) |
Critical mass (kg) |
Diameter (cm) |
|---|---|---|---|
| uranium-233 | 159,200 | 15 | 11 |
| uranium-235 | 703,800,000 | 52 | 17 |
| neptunium-236 | 154,000 | 7 | 8.7 |
| neptunium-237 | 2,144,000 | 60 | 18 |
| plutonium-238 | 87.7 | 9.04–10.07 | 9.5–9.9 |
| plutonium-239 | 24,110 | 10 | 9.9 |
| plutonium-240 | 6561 | 40 | 15 |
| plutonium-241 | 14.3 | 12 | 10.5 |
| plutonium-242 | 375,000 | 75–100 | 19–21 |
| americium-241 | 432.2 | 55–77 | 20–23 |
| americium-242m | 141 | 9–14 | 11–13 |
| americium-243 | 7370 | 180–280 | 30–35 |
| curium-243 | 29.1 | 7.34–10 | 10–11 |
| curium-244 | 18.1 | 13.5–30 | 12.4–16 |
| curium-245 | 8500 | 9.41–12.3 | 11–12 |
| curium-246 | 4760 | 39–70.1 | 18–21 |
| curium-247 | 15,600,000 | 6.94–7.06 | 9.9 |
| berkelium-247 | 1380 | 75.7 | 11.8-12.2 |
| berkelium-249 | 330 days | 192 | 16.1-16.6 |
| californium-249 | 351 | 6 | 9 |
| californium-251 | 900 | 5.46 | 8.5 |
| californium-252 | 2.6 | 2.73 | 6.9 |
| einsteinium-254 | 275.7 days | 9.89 | 7.1 |
The critical mass for lower-grade uranium depends strongly on the grade: with 20% 235U it is over 400 kg; with 15% 235U, it is well over 600 kg.
The critical mass is inversely proportional to the square of the
density. If the density is 1% more and the mass 2% less, then the volume
is 3% less and the diameter 1% less. The probability for a neutron per
cm travelled to hit a nucleus is proportional to the density. It follows
that 1% greater density means that the distance travelled before
leaving the system is 1% less. This is something that must be taken into
consideration when attempting more precise estimates of critical masses
of plutonium isotopes than the approximate values given above, because
plutonium metal has a large number of different crystal phases which can
have widely varying densities.
Note that not all neutrons contribute to the chain reaction. Some escape and others undergo radiative capture.
Let q denote the probability that a given neutron induces fission in a nucleus. Consider only prompt neutrons, and let ν denote the number of prompt neutrons generated in a nuclear fission. For example, ν ≈ 2.5 for uranium-235. Then, criticality occurs when ν·q = 1. The dependence of this upon geometry, mass, and density appears through the factor q.
Given a total interaction cross section σ (typically measured in barns), the mean free path of a prompt neutron is where n is the nuclear number density. Most interactions are scattering events, so that a given neutron obeys a random walk
until it either escapes from the medium or causes a fission reaction.
So long as other loss mechanisms are not significant, then, the radius
of a spherical critical mass is rather roughly given by the product of
the mean free path and the square root of one plus the number of scattering events per fission event (call this s), since the net distance travelled in a random walk is proportional to the square root of the number of steps:
Note again, however, that this is only a rough estimate.
In terms of the total mass M, the nuclear mass m, the density ρ, and a fudge factor f which takes into account geometrical and other effects, criticality corresponds to
which clearly recovers the aforementioned result that critical mass depends inversely on the square of the density.
Alternatively, one may restate this more succinctly in terms of the areal density of mass, Σ:
where the factor f has been rewritten as f' to
account for the fact that the two values may differ depending upon
geometrical effects and how one defines Σ. For example, for a bare solid
sphere of 239Pu criticality is at 320 kg/m2, regardless of density, and for 235U at 550 kg/m2.
In any case, criticality then depends upon a typical neutron "seeing" an
amount of nuclei around it such that the areal density of nuclei
exceeds a certain threshold.
This is applied in implosion-type nuclear weapons where a
spherical mass of fissile material that is substantially less than a
critical mass is made supercritical by very rapidly increasing ρ (and
thus Σ as well) (see below). Indeed, sophisticated nuclear weapons
programs can make a functional device from less material than more
primitive weapons programs require.
Aside from the math, there is a simple physical analog that helps
explain this result. Consider diesel fumes belched from an exhaust
pipe. Initially the fumes appear black, then gradually you are able to
see through them without any trouble. This is not because the total
scattering cross section of all the soot particles has changed, but
because the soot has dispersed. If we consider a transparent cube of
length L on a side, filled with soot, then the optical depth of this medium is inversely proportional to the square of L,
and therefore proportional to the areal density of soot particles: we
can make it easier to see through the imaginary cube just by making the
cube larger.
Several uncertainties contribute to the determination of a
precise value for critical masses, including (1) detailed knowledge of
fission cross sections, (2) calculation of geometric effects. This
latter problem provided significant motivation for the development of
the Monte Carlo method in computational physics by Nicholas Metropolis and Stanislaw Ulam.
In fact, even for a homogeneous solid sphere, the exact calculation is
by no means trivial. Finally, note that the calculation can also be
performed by assuming a continuum approximation for the neutron
transport. This reduces it to a diffusion problem. However, as the
typical linear dimensions are not significantly larger than the mean
free path, such an approximation is only marginally applicable.
Finally, note that for some idealized geometries, the critical
mass might formally be infinite, and other parameters are used to
describe criticality. For example, consider an infinite sheet of
fissionable material. For any finite thickness, this corresponds to an
infinite mass. However, criticality is only achieved once the thickness
of this slab exceeds a critical value.
Criticality in nuclear weapon design
If two pieces of subcritical material are not brought together fast enough, nuclear predetonation (fizzle) can occur, whereby a very small explosion will blow the bulk of the material apart.
Until detonation is desired, a nuclear weapon
must be kept subcritical. In the case of a uranium bomb, this can be
achieved by keeping the fuel in a number of separate pieces, each below
the critical size
either because they are too small or unfavorably shaped. To produce
detonation, the pieces of uranium are brought together rapidly. In Little Boy, this was achieved by firing a piece of uranium (a 'doughnut') down a gun barrel onto another piece (a 'spike'). This design is referred to as a gun-type fission weapon.
A theoretical 100% pure 239Pu weapon could also be constructed as a gun-type weapon, like the Manhattan Project's proposed Thin Man design. In reality, this is impractical because even "weapons grade" 239Pu is contaminated with a small amount of 240Pu,
which has a strong propensity toward spontaneous fission. Because of
this, a reasonably sized gun-type weapon would suffer nuclear reaction (predetonation) before the masses of plutonium would be in a position for a full-fledged explosion to occur.
Instead, the plutonium is present as a subcritical sphere (or
other shape), which may or may not be hollow. Detonation is produced by
exploding a shaped charge surrounding the sphere, increasing the density (and collapsing the cavity, if present) to produce a prompt critical configuration. This is known as an implosion type weapon.
Prompt criticality
The event of fission must release, on the average, more than one free
neutron of the desired energy level in order to sustain a chain
reaction, and each must find other nuclei and cause them to fission.
Most of the neutrons released from a fission event come immediately from
that event, but a fraction of them come later, when the fission
products decay, which may be on the average from microseconds to minutes
later. This is fortunate for atomic power generation, for without this
delay "going critical" would always be an immediately catastrophic
event, as it is in a nuclear bomb where upwards of 80 generations of
chain reaction occur in less than a microsecond, far too fast for man,
or even machine, to react. Physicists recognize two points in the
gradual increase of neutron flux which are significant: critical, where
the chain reaction becomes self-sustaining thanks to the contributions
of both kinds of neutron generation, and prompt critical,
where the immediate "prompt" neutrons alone will sustain the reaction
without need for the decay neutrons. Nuclear power plants operate
between these two points of reactivity, while above the prompt critical point is the domain of nuclear weapons and some nuclear power accidents, such as the Chernobyl disaster.
A convenient unit for the measurement of the reactivity is that suggested by Louis Slotin: that of the dollar and cents.