Earth's rotation

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Earth%27s_rotation

 

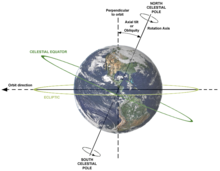
An animation of Earth's rotation around the planet's axis

 

This long-exposure photo of the northern night sky above the Nepali Himalayas shows the apparent paths of the stars as Earth rotates.

 

Earth's rotation imaged by DSCOVR EPIC on 29 May 2016, a few weeks before the solstice.

Earth's rotation is the rotation of Planet Earth around its own axis. Earth rotates eastward, in prograde motion. As viewed from the north pole star Polaris, Earth turns counterclockwise. 

The North Pole, also known as the Geographic North Pole or Terrestrial North Pole, is the point in the Northern Hemisphere where Earth's axis of rotation meets its surface. This point is distinct from Earth's North Magnetic Pole. The South Pole is the other point where Earth's axis of rotation intersects its surface, in Antarctica. 

Earth rotates once in about 24 hours with respect to the Sun, but once every 23 hours, 56 minutes, and 4 seconds with respect to other, distant, stars (see below). Earth's rotation is slowing slightly with time; thus, a day was shorter in the past. This is due to the tidal effects the Moon has on Earth's rotation. Atomic clocks show that a modern-day is longer by about 1.7 milliseconds than a century ago, slowly increasing the rate at which UTC is adjusted by leap seconds. Analysis of historical astronomical records shows a slowing trend of about 2.3 milliseconds per century since the 8th century BCE.

History

Among the ancient Greeks, several of the Pythagorean school believed in the rotation of Earth rather than the apparent diurnal rotation of the heavens. Perhaps the first was Philolaus (470–385 BCE), though his system was complicated, including a counter-earth rotating daily about a central fire.

A more conventional picture was that supported by Hicetas, Heraclides and Ecphantus in the fourth century BCE who assumed that Earth rotated but did not suggest that Earth revolved about the Sun. In the third century BCE, Aristarchus of Samos suggested the Sun's central place. 

However, Aristotle in the fourth century BCE criticized the ideas of Philolaus as being based on theory rather than observation. He established the idea of a sphere of fixed stars that rotated about Earth. This was accepted by most of those who came after, in particular Claudius Ptolemy (2nd century CE), who thought Earth would be devastated by gales if it rotated.

In 499 CE, the Indian astronomer Aryabhata wrote that the spherical Earth rotates about its axis daily, and that the apparent movement of the stars is a relative motion caused by the rotation of Earth. He provided the following analogy: "Just as a man in a boat going in one direction sees the stationary things on the bank as moving in the opposite direction, in the same way to a man at Lanka the fixed stars appear to be going westward."

In the 10th century, some Muslim astronomers accepted that Earth rotates around its axis. According to al-Biruni, Abu Sa'id al-Sijzi (d. circa 1020) invented an astrolabe called al-zūraqī based on the idea believed by some of his contemporaries "that the motion we see is due to the Earth's movement and not to that of the sky." The prevalence of this view is further confirmed by a reference from the 13th century which states: "According to the geometers [or engineers] (muhandisīn), the Earth is in constant circular motion, and what appears to be the motion of the heavens is actually due to the motion of the Earth and not the stars." Treatises were written to discuss its possibility, either as refutations or expressing doubts about Ptolemy's arguments against it. At the Maragha and Samarkand observatories, Earth's rotation was discussed by Tusi (b. 1201) and Qushji (b. 1403); the arguments and evidence they used resemble those used by Copernicus.

In medieval Europe, Thomas Aquinas accepted Aristotle's view and so, reluctantly, did John Buridan and Nicole Oresme in the fourteenth century. Not until Nicolaus Copernicus in 1543 adopted a heliocentric world system did the contemporary understanding of Earth's rotation begin to be established. Copernicus pointed out that if the movement of Earth is violent, then the movement of the stars must be very much more so. He acknowledged the contribution of the Pythagoreans and pointed to examples of relative motion. For Copernicus this was the first step in establishing the simpler pattern of planets circling a central Sun.

Tycho Brahe, who produced accurate observations on which Kepler based his laws, used Copernicus's work as the basis of a system assuming a stationary Earth. In 1600, William Gilbert strongly supported Earth's rotation in his treatise on Earth's magnetism and thereby influenced many of his contemporaries. Those like Gilbert who did not openly support or reject the motion of Earth about the Sun are often called "semi-Copernicans". A century after Copernicus, Riccioli disputed the model of a rotating Earth due to the lack of then-observable eastward deflections in falling bodies; such deflections would later be called the Coriolis effect. However, the contributions of Kepler, Galileo and Newton gathered support for the theory of the rotation of Earth.

Empirical tests

Earth's rotation implies that the Equator bulges and the geographical poles are flattened. In his Principia, Newton predicted this flattening would occur in the ratio of 1:230, and pointed to the pendulum measurements taken by Richer in 1673 as corroboration of the change in gravity, but initial measurements of meridian lengths by Picard and Cassini at the end of the 17th century suggested the opposite. However, measurements by Maupertuis and the French Geodesic Mission in the 1730s established the oblateness of Earth, thus confirming the positions of both Newton and Copernicus.

In Earth's rotating frame of reference, a freely moving body follows an apparent path that deviates from the one it would follow in a fixed frame of reference. Because of the Coriolis effect, falling bodies veer slightly eastward from the vertical plumb line below their point of release, and projectiles veer right in the Northern Hemisphere (and left in the Southern) from the direction in which they are shot. The Coriolis effect is mainly observable at a meteorological scale, where it is responsible for the opposite directions of cyclone rotation in the Northern and Southern hemispheres (anticlockwise and clockwise, respectively). 

Hooke, following a suggestion from Newton in 1679, tried unsuccessfully to verify the predicted eastward deviation of a body dropped from a height of 8.2 meters, but definitive results were obtained later, in the late 18th and early 19th century, by Giovanni Battista Guglielmini in Bologna, Johann Friedrich Benzenberg in Hamburg and Ferdinand Reich in Freiberg, using taller towers and carefully released weights. A ball dropped from a height of 158.5 m departed by 27.4 mm from the vertical compared with a calculated value of 28.1 mm.

The most celebrated test of Earth's rotation is the Foucault pendulum first built by physicist Léon Foucault in 1851, which consisted of a lead-filled brass sphere suspended 67 m from the top of the Panthéon in Paris. Because of Earth's rotation under the swinging pendulum, the pendulum's plane of oscillation appears to rotate at a rate depending on latitude. At the latitude of Paris the predicted and observed shift was about 11 degrees clockwise per hour. Foucault pendulums now swing in museums around the world.

Periods

Starry circles arc around the south celestial pole, seen overhead at ESO's La Silla Observatory.

 

True solar day

Earth's rotation period relative to the Sun (solar noon to solar noon) is its true solar day or apparent solar day. It depends on Earth's orbital motion and is thus affected by changes in the eccentricity and inclination of Earth's orbit. Both vary over thousands of years, so the annual variation of the true solar day also varies. Generally, it is longer than the mean solar day during two periods of the year and shorter during another two. The true solar day tends to be longer near perihelion when the Sun apparently moves along the ecliptic through a greater angle than usual, taking about 10 seconds longer to do so. Conversely, it is about 10 seconds shorter near aphelion. It is about 20 seconds longer near a solstice when the projection of the Sun's apparent motion along the ecliptic onto the celestial equator causes the Sun to move through a greater angle than usual. Conversely, near an equinox the projection onto the equator is shorter by about 20 seconds. Currently, the perihelion and solstice effects combine to lengthen the true solar day near 22 December by 30 mean solar seconds, but the solstice effect is partially cancelled by the aphelion effect near 19 June when it is only 13 seconds longer. The effects of the equinoxes shorten it near 26 March and 16 September by 18 seconds and 21 seconds, respectively.

Mean solar day

The average of the true solar day during the course of an entire year is the mean solar day, which contains 86,400 mean solar seconds. Currently, each of these seconds is slightly longer than an SI second because Earth's mean solar day is now slightly longer than it was during the 19th century due to tidal friction. The average length of the mean solar day since the introduction of the leap second in 1972 has been about 0 to 2 ms longer than 86,400 SI seconds. Random fluctuations due to core-mantle coupling have an amplitude of about 5 ms. The mean solar second between 1750 and 1892 was chosen in 1895 by Simon Newcomb as the independent unit of time in his Tables of the Sun. These tables were used to calculate the world's ephemerides between 1900 and 1983, so this second became known as the ephemeris second. In 1967 the SI second was made equal to the ephemeris second.

The apparent solar time is a measure of Earth's rotation and the difference between it and the mean solar time is known as the equation of time.

Stellar and sidereal day

On a prograde planet like Earth, the stellar day is shorter than the solar day. At time 1, the Sun and a certain distant star are both overhead. At time 2, the planet has rotated 360° and the distant star is overhead again but the Sun is not (1→2 = one stellar day). It is not until a little later, at time 3, that the Sun is overhead again (1→3 = one solar day).

 

Earth's rotation period relative to the fixed stars, called its stellar day by the International Earth Rotation and Reference Systems Service (IERS), is 86,164.098 903 691 seconds of mean solar time (UT1) (23^h 56^m 4.098 903 691^s, 0.997 269 663 237 16 mean solar days). Earth's rotation period relative to the precessing mean vernal equinox, named sidereal day, is 86,164.090 530 832 88 seconds of mean solar time (UT1) (23^h 56^m 4.090 530 832 88^s, 0.997 269 566 329 08 mean solar days). Thus, the sidereal day is shorter than the stellar day by about 8.4 ms.

Both the stellar day and the sidereal day are shorter than the mean solar day by about 3 minutes 56 seconds. The mean solar day in SI seconds is available from the IERS for the periods 1623–2005 and 1962–2005.

Recently (1999–2010) the average annual length of the mean solar day in excess of 86,400 SI seconds has varied between 0.25 ms and 1 ms, which must be added to both the stellar and sidereal days given in mean solar time above to obtain their lengths in SI seconds.

Angular speed

Plot of latitude vs tangential speed. The dashed line shows the Kennedy Space Center example. The dot-dash line denotes typical airliner cruise speed.

 

The angular speed of Earth's rotation in inertial space is 7.2921150 ± 0.0000001×10⁻⁵ radians per SI second. Multiplying by (180°/π radians) × (86,400 seconds/day) yields 360.985 6°/day, indicating that Earth rotates more than 360° relative to the fixed stars in one solar day. Earth's movement along its nearly circular orbit while it is rotating once around its axis requires that Earth rotate slightly more than once relative to the fixed stars before the mean Sun can pass overhead again, even though it rotates only once (360°) relative to the mean Sun. Multiplying the value in rad/s by Earth's equatorial radius of 6,378,137 m (WGS84 ellipsoid) (factors of 2π radians needed by both cancel) yields an equatorial speed of 465.10 metres per second (1,674.4 km/h). Some sources state that Earth's equatorial speed is slightly less, or 1,669.8 km/h. This is obtained by dividing Earth's equatorial circumference by 24 hours. However, the use of only one circumference unwittingly implies only one rotation in inertial space, so the corresponding time unit must be a sidereal hour. This is confirmed by multiplying by the number of sidereal days in one mean solar day, 1.002 737 909 350 795, which yields the equatorial speed in mean solar hours given above of 1,674.4 km/h. 

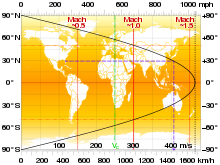
The tangential speed of Earth's rotation at a point on Earth can be approximated by multiplying the speed at the equator by the cosine of the latitude. For example, the Kennedy Space Center is located at latitude 28.59° N, which yields a speed of: cos 28.59° × 1674.4 km/h = 1470.2 km/h. 

Changes

Earth's axial tilt is about 23.4°. It oscillates between 22.1° and 24.5° on a 41,000-year cycle and is currently decreasing.

 

In rotational axis

Earth's rotation axis moves with respect to the fixed stars (inertial space); the components of this motion are precession and nutation. It also moves with respect to Earth's crust; this is called polar motion. 

Precession is a rotation of Earth's rotation axis, caused primarily by external torques from the gravity of the Sun, Moon and other bodies. The polar motion is primarily due to free core nutation and the Chandler wobble.

In rotational velocity

Tidal interactions

Over millions of years, Earth's rotation has been slowed significantly by tidal acceleration through gravitational interactions with the Moon. Thus angular momentum is slowly transferred to the Moon at a rate proportional to ${\displaystyle r^{-6}}$, where ${\displaystyle r}$ is the orbital radius of the Moon. This process has gradually increased the length of the day to its current value, and resulted in the Moon being tidally locked with Earth. 

This gradual rotational deceleration is empirically documented by estimates of day lengths obtained from observations of tidal rhythmites and stromatolites; a compilation of these measurements found that the length of the day has increased steadily from about 21 hours at 600 Myr ago to the current 24-hour value. By counting the microscopic lamina that form at higher tides, tidal frequencies (and thus day lengths) can be estimated, much like counting tree rings, though these estimates can be increasingly unreliable at older ages.

Resonant stabilization

A simulated history of Earth's day length, depicting a resonant-stabilizing event throughout the Precambrian era.

 

The current rate of tidal deceleration is anomalously high, implying Earth's rotational velocity must have decreased more slowly in the past. Empirical data tentatively shows a sharp increase in rotational deceleration about 600 Myr ago. Some models suggest that Earth maintained a constant day length of 21 hours throughout much of the Precambrian. This day length corresponds to the semidiurnal resonant period of the thermally-driven atmospheric tide; at this day length, the decelerative lunar torque could have been canceled by an accelerative torque from the atmospheric tide, resulting in no net torque and a constant rotational period. This stabilizing effect could have been broken by a sudden change in global temperature. Recent computational simulations support this hypothesis and suggest the Marinoan or Sturtian glaciations broke this stable configuration about 600 Myr ago; the simulated results agree quite closely with existing paleorotational data.

Global events

Deviation of day length from SI based day

 

Some recent large-scale events, such as the 2004 Indian Ocean earthquake, have caused the length of a day to shorten by 3 microseconds by reducing Earth's moment of inertia. Post-glacial rebound, ongoing since the last Ice age, is also changing the distribution of Earth's mass, thus affecting the moment of inertia of Earth and, by the conservation of angular momentum, Earth's rotation period.

The length of the day can also be influenced by manmade structures. For example, NASA scientists calculated that the water stored in the Three Gorges Dam has increased the length of Earth's day by 0.06 microseconds due to the shift in mass.

Measurement

The primary monitoring of Earth's rotation is performed by very-long-baseline interferometry coordinated with the Global Positioning System, satellite laser ranging, and other satellite techniques. This provides an absolute reference for the determination of universal time, precession, and nutation.

Ancient observations

There are recorded observations of solar and lunar eclipses by Babylonian and Chinese astronomers beginning in the 8th century BCE, as well as from the medieval Islamic world and elsewhere. These observations can be used to determine changes in Earth's rotation over the last 27 centuries, since the length of the day is a critical parameter in the calculation of the place and time of eclipses. A change in day length of milliseconds per century shows up as a change of hours and thousands of kilometers in eclipse observations. The ancient data are consistent with a shorter day, meaning Earth was turning faster throughout the past.

Cyclic variability

Around every 25-30 years Earth's rotation slows temporarily by a few milliseconds per day, usually lasting around 5 years. 2017 was the fourth consecutive year that Earth's rotation has slowed. The cause of this variability has not yet been determined.

Origin

An artist's rendering of the protoplanetary disk.

 

Earth's original rotation was a vestige of the original angular momentum of the cloud of dust, rocks, and gas that coalesced to form the Solar System. This primordial cloud was composed of hydrogen and helium produced in the Big Bang, as well as heavier elements ejected by supernovas. As this interstellar dust is heterogeneous, any asymmetry during gravitational accretion resulted in the angular momentum of the eventual planet.

However, if the giant-impact hypothesis for the origin of the Moon is correct, this primordial rotation rate would have been reset by the Theia impact 4.5 billion years ago. Regardless of the speed and tilt of Earth's rotation before the impact, it would have experienced a day some five hours long after the impact. Tidal effects would then have slowed this rate to its modern value.

Sidereal time

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Sidereal_time

 

One of the two known surviving sidereal angle clocks in the world. It was made for Sir George Shuckburgh-Evelyn. It is on display in the Royal Observatory, Greenwich, London.

 

This astronomical clock uses dials showing both sidereal and solar time.

 

Sidereal time /saɪˈdɪəriəl/ is a timekeeping system that astronomers use to locate celestial objects. Using sidereal time, it is possible to easily point a telescope to the proper coordinates in the night sky. Briefly, sidereal time is a "time scale that is based on Earth's rate of rotation measured relative to the fixed stars".

Photo of the face of one of the two Sidereal Angle clocks in the Royal Observatory in Greenwich, England.

 

Viewed from the same location, a star seen at one position in the sky will be seen at the same position on another night at the same sidereal time. This is similar to how the time kept by a sundial can be used to find the location of the Sun. Just as the Sun and Moon appear to rise in the east and set in the west due to the rotation of Earth, so do the stars. Both solar time and sidereal time make use of the regularity of Earth's rotation about its polar axis, solar time following the Sun while sidereal time roughly follows the stars.

More exactly, sidereal time is the angle, measured along the celestial equator, from the observer's meridian to the great circle that passes through the March equinox and both celestial poles, and is usually expressed in hours, minutes, and seconds. Common time on a typical clock measures a slightly longer cycle, accounting not only for Earth's axial rotation but also for Earth's orbit around the Sun.

A sidereal day is approximately 23 hours, 56 minutes, 4.0905 SI seconds (24 hours - 4 minutes + 4 seconds = 86164.0905 s = 23.9344696 h). The March equinox itself precesses slowly westward relative to the fixed stars, completing one revolution in about 26,000 years, so the misnamed sidereal day ("sidereal" is derived from the Latin sidus meaning "star") is 0.0084 seconds shorter than the stellar day, Earth's period of rotation relative to the fixed stars. The slightly longer "true" sidereal period is measured as the Earth Rotation Angle (ERA), formerly the stellar angle. An increase of 360° in the ERA is a full rotation of the Earth. 

Because Earth orbits the Sun once a year, the sidereal time at any given place and time will gain about four minutes against local civil time, every 24 hours, until, after a year has passed, one additional sidereal "day" has elapsed compared to the number of solar days that have gone by. 

Comparison to solar time

Sidereal time vs solar time. Above left: a distant star (the small orange star) and the Sun are at culmination, on the local meridian m. Centre: only the distant star is at culmination (a mean sidereal day). Right: a few minutes later the Sun is on the local meridian again. A solar day is complete.

 

Solar time is measured by the apparent diurnal motion of the Sun, and local noon in apparent solar time is the moment when the Sun is exactly due south or north (depending on the observer's latitude and the season). A mean solar day (what we normally measure as a "day") is the average time between local solar noons ("average" since this varies slightly over the year). 

Earth makes one rotation around its axis in a sidereal day; during that time it moves a short distance (about 1°) along its orbit around the Sun. So after a sidereal day has passed, Earth still needs to rotate slightly more before the Sun reaches local noon according to solar time. A mean solar day is, therefore, nearly 4 minutes longer than a sidereal day.

The stars are so far away that Earth's movement along its orbit makes nearly no difference to their apparent direction (see, however, parallax), and so they return to their highest point in a sidereal day.

Another way to see this difference is to notice that, relative to the stars, the Sun appears to move around Earth once per year. Therefore, there is one fewer solar day per year than there are sidereal days. This makes a sidereal day approximately 365.24366.24 times the length of the 24-hour solar day, giving approximately 23 h 56 min 4.1 s (86,164.1 s). 

Precession effects

Earth's rotation is not a simple rotation around an axis that would always remain parallel to itself. Earth's rotational axis itself rotates about a second axis, orthogonal to Earth's orbit, taking about 25,800 years to perform a complete rotation. This phenomenon is called the precession of the equinoxes. Because of this precession, the stars appear to move around Earth in a manner more complicated than a simple constant rotation. 

For this reason, to simplify the description of Earth's orientation in astronomy and geodesy, it was conventional to chart the positions of the stars in the sky according to right ascension and declination, which are based on a frame that follows Earth's precession, and to keep track of Earth's rotation, through sidereal time, relative to this frame as well. In this reference frame, Earth's rotation is close to constant, but the stars appear to rotate slowly with a period of about 25,800 years. It is also in this reference frame that the tropical year, the year related to Earth's seasons, represents one orbit of Earth around the Sun. The precise definition of a sidereal day is the time taken for one rotation of Earth in this precessing reference frame. 

Modern definitions

In the past, time was measured by observing stars with instruments such as photographic zenith tubes and Danjon astrolabes, and the passage of stars across defined lines would be timed with the observatory clock. Then, using the right ascension of the stars from a star catalog, the time when the star should have passed through the meridian of the observatory was computed, and a correction to the time kept by the observatory clock was computed. Sidereal time was defined such that the March equinox would transit the meridian of the observatory at 0 hours local sidereal time.

Beginning in the 1970s the radio astronomy methods Very Long Baseline Interferometry (VLBI) and pulsar timing overtook optical instruments for the most precise astrometry. This led to the determination of UT1 (mean solar time at 0° longitude) using VLBI, a new measure of the rotation of the Earth named Earth Rotation Angle, and new definitions of sidereal time. These changes were put into practice on 1 January 2003.

Earth Rotation Angle

The Earth Rotation Angle (ERA) measures the rotation of the Earth from an origin on the celestial equator, the Celestial Intermediate Origin, that has no instantaneous motion along the equator; it was originally referred to as the non-rotating origin. ERA replaces Greenwich Apparent Sidereal Time (GAST). The origin on the celestial equator for GAST, called the true equinox, does move, due to the movement of the equator and the ecliptic. The lack of motion of the origin of ERA is considered a significant advantage.

ERA, measured in radians, is related to UT1 by the expression

${\displaystyle \theta (t_{U})=2\pi (0.779\,057\,273\,2640+1.002\,737\,811\,911\,354\,48t_{U})}$

where t_U is the Julian UT1 date − 2451545.0. 

The ERA may be converted to other units; for example, the Astronomical Almanac for the Year 2017 tabulated it in degrees, minutes, and seconds.

As an example, the Astronomical Almanac for the Year 2017 gave the ERA at 0 h 1 January 2017 UT1 as 100° 37′ 12.4365″.

Sidereal time

Although ERA is intended to replace sidereal time, there is a need to maintain definitions for sidereal time during the transition, and when working with older data and documents.

Similarly to mean solar time, every location on Earth has its own local sidereal time (LST), depending on the longitude of the point. Since it is not feasible to publish tables for every longitude, astronomical tables make use of Greenwich sidereal time (GST), which is sidereal time on the IERS Reference Meridian, less precisely called the Greenwich, or prime meridian. There are two varieties, mean sidereal time if the mean equator and equinox of date are used, or apparent sidereal time if the apparent equator and equinox of date are used. The former ignores the effect of nutation while the latter includes nutation. When the choice of location is combined with the choice of including nutation or not, the acronyms GMST, LMST, GAST, and LAST result. 

The following relationships hold:

local mean sidereal time = GMST + east longitude

local apparent sidereal time = GAST + east longitude

The new definitions of Greenwich mean and apparent sidereal time (since 2003, see above) are:

${\displaystyle \mathrm {GMST} (t_{U},t)=\theta (t_{U})-E_{\mathrm {PREC} }(t)}$

${\displaystyle \mathrm {GAST} (t_{U},t)=\theta (t_{U})-E_{0}(t)}$

where θ is the Earth Rotation Angle, E_PREC is the accumulated precession, and E₀ is equation of the origins, which represents accumulated precession and nutation. The calculation of precession and nutation was described in Chapter 6 of Urban & Seidelmann. 

As an example, the Astronomical Almanac for the Year 2017 gave the ERA at 0 h 1 January 2017 UT1 as 100° 37′ 12.4365″. The GAST was 6 h 43 m 20.7109 s. For GMST the hour and minute were the same but the second was 21.1060.

Relationship between solar time and sidereal time intervals

If a certain interval I is measured in both mean solar time (UT1) and sidereal time, the numerical value will be greater in sidereal time than in UT1, because sidereal days are shorter than UT1 days. The ratio is:

${\displaystyle {\frac {I_{\mathrm {mean\,sidereal} }}{I_{\mathrm {UT1} }}}=r'=1.002\,737\,379\,093\,507\,95+5.9006\times 10^{-11}t-5.9\times 10^{-15}t^{2}}$

where t represents the number of Julian centuries elapsed since noon 1 January 2000 Terrestrial Time.

Sidereal days compared to solar days on other planets

Of the eight solar planets, all but Venus and Uranus have prograde rotation—that is, they rotate more than once per year in the same direction as they orbit the Sun, so the Sun rises in the east. Venus and Uranus, however, have retrograde rotation. For prograde rotation, the formula relating the lengths of the sidereal and solar days is:

number of sidereal days per orbital period = 1 + number of solar days per orbital period

or, equivalently:

length of solar day = length of sidereal day/1 − length of sidereal day/orbital period.

On the other hand, the formula in the case of retrograde rotation is:

number of sidereal days per orbital period = −1 + number of solar days per orbital period

or, equivalently:

length of solar day = length of sidereal day/1 + length of sidereal day/orbital period.

All the solar planets more distant from the Sun than Earth are similar to Earth in that, since they experience many rotations per revolution around the Sun, there is only a small difference between the length of the sidereal day and that of the solar day – the ratio of the former to the latter never being less than Earth's ratio of 0.997. But the situation is quite different for Mercury and Venus. Mercury's sidereal day is about two-thirds of its orbital period, so by the prograde formula its solar day lasts for two revolutions around the Sun – three times as long as its sidereal day. Venus rotates retrograde with a sidereal day lasting about 243.0 Earth days, or about 1.08 times its orbital period of 224.7 Earth days; hence by the retrograde formula its solar day is about 116.8 Earth days, and it has about 1.9 solar days per orbital period.

By convention, rotation periods of planets are given in sidereal terms unless otherwise specified.

Day

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Day

A day is approximately the period of time during which the Earth completes one rotation around its axis. A solar day is the length of time which elapses between the Sun reaching its highest point in the sky two consecutive times.

In 1960, the second was redefined in terms of the orbital motion of the Earth in the year 1900, and was designated the SI base unit of time. The unit of measurement "day", was redefined as 86,400 SI seconds and symbolized d. In 1967, the second and so the day were redefined by atomic electron transition. A civil day is usually 86,400 seconds, plus or minus a possible leap second in Coordinated Universal Time (UTC), and occasionally plus or minus an hour in those locations that change from or to daylight saving time.

Day can be defined as each of the twenty-four-hour periods, reckoned from one midnight to the next, into which a week, month, or year is divided, and corresponding to a rotation of the earth on its axis. However, its use depends on its context; for example, when people say 'day and night', 'day' will have a different meaning: the interval of light between two successive nights, the time between sunrise and sunset; the time of light between one night and the next. However, in order to be clear when using 'day' in that sense, "daytime" should be used to distinguish it from "day" referring to a 24-hour period; this is since daytime usually means 'the time of the day between sunrise and sunset.^[8] The word day may also refer to a day of the week or to a calendar date, as in answer to the question, "On which day?" The life patterns (circadian rhythms) of humans and many other species are related to Earth's solar day and the day-night cycle.

Daytime image of the bay of Naples, Italy

Introduction

Dagr, the Norse god of the day, rides his horse in this 19th-century painting by Peter Nicolai Arbo.

Apparent and mean solar day

Several definitions of this universal human concept are used according to context, need and convenience. Besides the day of 24 hours (86, 400 seconds), the word day is used for several different spans of time based on the rotation of the Earth around its axis. An important one is the solar day, defined as the time it takes for the Sun to return to its culmination point (its highest point in the sky). Because celestial orbits are not perfectly circular, and thus objects travel at different speeds at various positions in their orbit, a solar day is not the same length of time throughout the orbital year. Because the Earth orbits the Sun elliptically as the Earth spins on an inclined axis, this period can be up to 7.9 seconds more than (or less than) 24 hours. In recent decades, the average length of a solar day on Earth has been about 86, 400.002 seconds (24.000 000 6 hours) and there are currently about 365.242199 solar days in one mean tropical year.

Ancient custom has a new day start at either the rising or setting of the Sun on the local horizon (Italian reckoning, for example, being 24 hours from sunset, oldstyle). The exact moment of, and the interval between, two sunrises or sunsets depends on the geographical position (longitude as well as latitude), and the time of year (as indicated by ancient hemispherical sundials).

A more constant day can be defined by the Sun passing through the local meridian, which happens at local noon (upper culmination) or midnight (lower culmination). The exact moment is dependent on the geographical longitude, and to a lesser extent on the time of the year. The length of such a day is nearly constant (24 hours ± 30 seconds). This is the time as indicated by modern sundials.

A further improvement defines a fictitious mean Sun that moves with constant speed along the celestial equator; the speed is the same as the average speed of the real Sun, but this removes the variation over a year as the Earth moves along its orbit around the Sun (due to both its velocity and its axial tilt).

Stellar day

A day, understood as the span of time it takes for the Earth to make one entire rotation with respect to the celestial background or a distant star (assumed to be fixed), is called a stellar day. This period of rotation is about 4 minutes less than 24 hours (23 hours 56 minutes and 4.1 seconds) and there are about 366.2422 stellar days in one mean tropical year (one stellar day more than the number of solar days). Other planets and moons have stellar and solar days of different lengths from Earth's.

Daytime

A day, in the sense of daytime that is distinguished from night time, is commonly defined as the period during which sunlight directly reaches the ground, assuming that there are no local obstacles. The length of daytime averages slightly more than half of the 24-hour day. Two effects make daytime on average longer than nights. The Sun is not a point, but has an apparent size of about 32 minutes of arc. Additionally, the atmosphere refracts sunlight in such a way that some of it reaches the ground even when the Sun is below the horizon by about 34 minutes of arc. So the first light reaches the ground when the centre of the Sun is still below the horizon by about 50 minutes of arc.^[12] Thus, daytime is on average around 7 minutes longer than 12 hours.

Etymology

The term comes from the Old English dæg, with its cognates such as dagur in Icelandic, Tag in German, and dag in Norwegian, Danish, Swedish and Dutch. All of them from the Indo-European root dyau which explains the similarity with Latin dies though the word is known to come from the Germanic branch. As of October 17, 2015, day is the 205th most common word in US English, and the 210th most common in UK English.

International System of Units (SI)

A day, symbol d, defined as 86, 400 seconds, is not an SI unit, but is accepted for use with SI. The Second is the base unit of time in SI units.

In 1967–68, during the 13th CGPM (Resolution 1), the International Bureau of Weights and Measures (BIPM) redefined a second as

... the duration of 9 192 631 770 periods of the radiation corresponding to the transition between two hyperfine levels of the ground state of the caesium 133 atom.

This makes the SI-based day last exactly 794, 243, 384, 928, 000 of those periods.

Leap seconds

Mainly due to tidal effects, the Earth's rotational period is not constant, resulting in minor variations for both solar days and stellar "days". The Earth's day has increased in length over time due to tides raised by the Moon which slow Earth's rotation. Because of the way the second is defined, the mean length of a day is now about 86, 400.002 seconds, and is increasing by about 1.7 milliseconds per century (an average over the last 2, 700 years). The length of a day circa 620 million years ago has been estimated from rhythmites (alternating layers in sandstone) as having been about 21.9 hours.

In order to keep the civil day aligned with the apparent movement of the Sun, a day according to Coordinated Universal Time (UTC) can include a negative or positive leap second. Therefore, although typically 86, 400 SI seconds in duration, a civil day can be either 86, 401 or 86, 399 SI seconds long on such a day.

Leap seconds are announced in advance by the International Earth Rotation and Reference Systems Service (IERS), which measures the Earth's rotation and determines whether a leap second is necessary.

Civil day

For civil purposes, a common clock time is typically defined for an entire region based on the local mean solar time at a central meridian. Such time zones began to be adopted about the middle of the 19th century when railroads with regularly occurring schedules came into use, with most major countries having adopted them by 1929. As of 2015, throughout the world, 40 such zones are now in use: the central zone, from which all others are defined as offsets, is known as UTC±00, which uses Coordinated Universal Time (UTC).

The most common convention starts the civil day at midnight: this is near the time of the lower culmination of the Sun on the central meridian of the time zone. Such a day may be referred to as a calendar day.

A day is commonly divided into 24 hours of 60 minutes, with each minute composed of 60 seconds.

Decimal and metric time

In the 19th century, an idea circulated to make a decimal fraction (​¹⁄_{10, 000} or ​¹⁄_{100, 000}) of an astronomical day the base unit of time. This was an afterglow of the short-lived movement toward a decimalisation of timekeeping and the calendar, which had been given up already due to its difficulty in transitioning from traditional, more familiar units. The most successful alternative is the centiday, equal to 14.4 minutes (864 seconds), being not only a shorter multiple of an hour (0.24 vs 2.4) but also closer to the SI multiple kilosecond (1, 000 seconds) and equal to the traditional Chinese unit, kè.

Colloquial

The word refers to various similarly defined ideas, such as:

Full day

• 24 hours (exactly)
• The full day covering both the dark and light periods, beginning from the start of the dark period or from a point near the middle of the dark period
• A full dark and light period, sometimes called a nychthemeron in English, from the Greek for night-day;^[18] or more colloquially the term 24 hours. In other languages, 24 hours is also often used. Other languages also have a separate word for a full day.

Daytime

• The period of light when the Sun is above the local horizon (that is, the time period from sunrise to sunset)
• The time period from 06:00–18:00 (6:00 am – 6:00 pm) or 21:00 (9:00 pm) or another fixed clock period overlapping or offset from other time periods such as "morning", "evening", or "night".
• The time period from first-light "dawn" to last-light "twilight".

 

Boundaries

Sun and Moon, Hartmann Schedel's Nuremberg Chronicle, 1493

For most diurnal animals, the day naturally begins at dawn and ends at sunset. Humans, with their cultural norms and scientific knowledge, have employed several different conceptions of the day's boundaries. Common convention among the ancient Romans, ancient Chinese and in modern times is for the civil day to begin at midnight, i.e. 00:00, and last a full 24 hours until 24:00 (i.e. 00:00 of the next day). In ancient Egypt, the day was reckoned from sunrise to sunrise. The Jewish day begins at either sunset or nightfall (when three second-magnitude stars appear).

Medieval Europe also followed this tradition, known as Florentine reckoning: in this system, a reference like "two hours into the day" meant two hours after sunset and thus times during the evening need to be shifted back one calendar day in modern reckoning. Days such as Christmas Eve, Halloween, and the Eve of Saint Agnes are remnants of the older pattern when holidays began during the prior evening. Prior to 1926, Turkey had two time systems: Turkish (counting the hours from sunset) and French (counting the hours from midnight).

Validity of tickets, passes, etc., for a day or a number of days may end at midnight, or closing time, when that is earlier. However, if a service (e.g., public transport) operates from for example, 6:00 to 1:00 the next day (which may be noted as 25:00), the last hour may well count as being part of the previous day. For services depending on the day ("closed on Sundays", "does not run on Fridays", and so on) there is a risk of ambiguity. For example, a day ticket on the Nederlandse Spoorwegen (Dutch Railways) is valid for 28 hours, from 0:00 to 28:00 (that is, 4:00 the next day); the validity of a pass on Transport for London (TfL) services is until the end of the "transport day" – that is to say, until 4:30 am on the day after the "expires" date stamped on the pass.

Midnight sun

In places which experience the midnight sun (polar day), daytime may extend beyond one 24-hour period and could even extend to months.

Extraterrestrial bodies

Besides a stellar day on Earth, determined to be 23 hours, 56 minutes and 4.1 seconds, there are related such days for bodies in the Solar System other than the Earth. For example:

• Mercury: 58 days, 15 hours, 30 minutes
• Venus: 243 days
• Earth's Moon: 27 days, 7 hours, 12 minutes
• Mars: 1 day, 37 minutes
• Ceres: 9 hours, 4 minutes
• Jupiter: 9 hours, 56 minutes
• Saturn: 10 hours, 33 minutes, 38 seconds (+1m52s;-1m19s)
• Uranus: 17 hours, 14 minutes
• Neptune: 16 hours, 6 minutes
• Pluto: 6 days, 9 hours