From Wikipedia, the free encyclopedia
Spontaneous symmetry breaking is a spontaneous process of symmetry breaking, by which a physical system in a symmetric state ends up in an asymmetric state. In particular, it can describe systems where the equations of motion or the Lagrangian obey symmetries, but the lowest-energy vacuum solutions do not exhibit that same symmetry.
When the system goes to one of those vacuum solutions, the symmetry is
broken for perturbations around that vacuum even though the entire
Lagrangian retains that symmetry.
Overview
In explicit symmetry breaking,
if two outcomes are considered, the probability of a pair of outcomes
can be different. By definition, spontaneous symmetry breaking requires
the existence of a symmetric probability distribution—any pair of
outcomes has the same probability. In other words, the underlying laws are invariant under a symmetry transformation.
The system, as a whole, changes under such transformations.
Phases of matter, such as crystals, magnets, and conventional
superconductors, as well as simple phase transitions can be described by
spontaneous symmetry breaking. Notable exceptions include topological
phases of matter like the fractional quantum Hall effect.
Examples
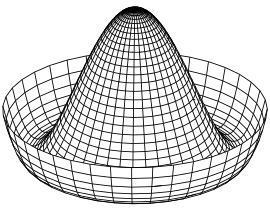
Sombrero potential
Consider
a symmetric upward dome with a trough circling the bottom. If a ball is
put at the very peak of the dome, the system is symmetric with respect
to a rotation around the center axis. But the ball may spontaneously break
this symmetry by rolling down the dome into the trough, a point of
lowest energy. Afterward, the ball has come to a rest at some fixed
point on the perimeter. The dome and the ball retain their individual
symmetry, but the system does not.
Graph of Goldstone's "
sombrero" potential function

.
In the simplest idealized relativistic model, the spontaneously broken symmetry is summarized through an illustrative scalar field theory. The relevant Lagrangian of a scalar field  , which essentially dictates how a system behaves, can be split up into kinetic and potential terms,
, which essentially dictates how a system behaves, can be split up into kinetic and potential terms,
-
 |
|
(1)
|
It is in this potential term  that the symmetry breaking is triggered. An example of a potential, due to Jeffrey Goldstone is illustrated in the graph at the left.
that the symmetry breaking is triggered. An example of a potential, due to Jeffrey Goldstone is illustrated in the graph at the left.
-
 . |
|
(2)
|
This potential has an infinite number of possible minima (vacuum states) given by
-
 . |
|
(3)
|
for any real θ between 0 and 2π. The system also has an unstable vacuum state corresponding to Φ = 0. This state has a U(1) symmetry. However, once the system falls into a specific stable vacuum state (amounting to a choice of θ), this symmetry will appear to be lost, or "spontaneously broken".
In fact, any other choice of θ would have exactly the same energy, implying the existence of a massless Nambu–Goldstone boson,
the mode running around the circle at the minimum of this potential,
and indicating there is some memory of the original symmetry in the
Lagrangian.
Other examples
- For ferromagnetic materials, the underlying laws are invariant under spatial rotations. Here, the order parameter is the magnetization, which measures the magnetic dipole density. Above the Curie temperature,
the order parameter is zero, which is spatially invariant, and there is
no symmetry breaking. Below the Curie temperature, however, the
magnetization acquires a constant nonvanishing value, which points in a
certain direction (in the idealized situation where we have full
equilibrium; otherwise, translational symmetry gets broken as well). The
residual rotational symmetries which leave the orientation of this
vector invariant remain unbroken, unlike the other rotations which do
not and are thus spontaneously broken.
- The laws describing a solid are invariant under the full Euclidean group, but the solid itself spontaneously breaks this group down to a space group. The displacement and the orientation are the order parameters.
- General relativity has a Lorentz symmetry, but in FRW cosmological models,
the mean 4-velocity field defined by averaging over the velocities of
the galaxies (the galaxies act like gas particles at cosmological
scales) acts as an order parameter breaking this symmetry. Similar
comments can be made about the cosmic microwave background.
- For the electroweak
model, as explained earlier, a component of the Higgs field provides
the order parameter breaking the electroweak gauge symmetry to the
electromagnetic gauge symmetry. Like the ferromagnetic example, there is
a phase transition at the electroweak temperature. The same comment
about us not tending to notice broken symmetries suggests why it took so
long for us to discover electroweak unification.
- In superconductors, there is a condensed-matter collective field ψ,
which acts as the order parameter breaking the electromagnetic gauge
symmetry.
- Take a thin cylindrical plastic rod and push both ends together.
Before buckling, the system is symmetric under rotation, and so visibly
cylindrically symmetric. But after buckling, it looks different, and
asymmetric. Nevertheless, features of the cylindrical symmetry are still
there: ignoring friction, it would take no force to freely spin the rod
around, displacing the ground state in time, and amounting to an
oscillation of vanishing frequency, unlike the radial oscillations in
the direction of the buckle. This spinning mode is effectively the
requisite Nambu–Goldstone boson.
- Consider a uniform layer of fluid
over an infinite horizontal plane. This system has all the symmetries
of the Euclidean plane. But now heat the bottom surface uniformly so
that it becomes much hotter than the upper surface. When the temperature
gradient becomes large enough, convection cells will form, breaking the Euclidean symmetry.
- Consider a bead on a circular hoop that is rotated about a vertical diameter. As the rotational velocity is increased gradually from rest, the bead will initially stay at its initial equilibrium point at the bottom of the hoop (intuitively stable, lowest gravitational potential).
At a certain critical rotational velocity, this point will become
unstable and the bead will jump to one of two other newly created
equilibria, equidistant
from the center. Initially, the system is symmetric with respect to the
diameter, yet after passing the critical velocity, the bead ends up in
one of the two new equilibrium points, thus breaking the symmetry.
Spontaneous symmetry breaking in physics
Spontaneous symmetry breaking illustrated: At high energy levels (
left), the ball settles in the center, and the result is symmetric. At lower energy levels (
right), the overall "rules" remain symmetric, but the symmetric "
Sombrero"
enforces an asymmetric outcome, since eventually the ball must rest at
some random spot on the bottom, "spontaneously", and not all others.
Particle physics
In particle physics, the force carrier particles are normally specified by field equations with gauge symmetry;
their equations predict that certain measurements will be the same at
any point in the field. For instance, field equations might predict that
the mass of two quarks is constant. Solving the equations to find the
mass of each quark might give two solutions. In one solution, quark A is
heavier than quark B. In the second solution, quark B is heavier than
quark A by the same amount. The symmetry of the equations is not reflected by the individual solutions, but it is reflected by the range of solutions.
An actual measurement reflects only one solution, representing a
breakdown in the symmetry of the underlying theory. "Hidden" is a better
term than "broken", because the symmetry is always there in these
equations. This phenomenon is called spontaneous symmetry breaking (SSB) because nothing (that we know of) breaks the symmetry in the equations.
Chiral symmetry
Chiral symmetry breaking is an example of spontaneous symmetry breaking affecting the chiral symmetry of the strong interactions in particle physics. It is a property of quantum chromodynamics, the quantum field theory describing these interactions, and is responsible for the bulk of the mass (over 99%) of the nucleons, and thus of all common matter, as it converts very light bound quarks into 100 times heavier constituents of baryons. The approximate Nambu–Goldstone bosons in this spontaneous symmetry breaking process are the pions,
whose mass is an order of magnitude lighter than the mass of the
nucleons. It served as the prototype and significant ingredient of the
Higgs mechanism underlying the electroweak symmetry breaking.
Higgs mechanism
The strong, weak, and electromagnetic forces can all be understood as arising from gauge symmetries. The Higgs mechanism, the spontaneous symmetry breaking of gauge symmetries, is an important component in understanding the superconductivity
of metals and the origin of particle masses in the standard model of
particle physics. One important consequence of the distinction between
true symmetries and gauge symmetries, is that the spontaneous
breaking of a gauge symmetry does not give rise to characteristic
massless Nambu–Goldstone physical modes, but only massive modes, like
the plasma mode in a superconductor, or the Higgs mode observed in
particle physics.
In the standard model of particle physics, spontaneous symmetry breaking of the SU(2) × U(1)
gauge symmetry associated with the electro-weak force generates masses
for several particles, and separates the electromagnetic and weak
forces. The W and Z bosons are the elementary particles that mediate the weak interaction, while the photon mediates the electromagnetic interaction. At energies much greater than 100 GeV, all these particles behave in a similar manner. The Weinberg–Salam theory predicts that, at lower energies, this symmetry is broken so that the photon and the massive W and Z bosons emerge. In addition, fermions develop mass consistently.
Without spontaneous symmetry breaking, the Standard Model of elementary particle interactions requires the existence of a number of particles. However, some particles (the W and Z bosons)
would then be predicted to be massless, when, in reality, they are
observed to have mass. To overcome this, spontaneous symmetry breaking
is augmented by the Higgs mechanism to give these particles mass. It also suggests the presence of a new particle, the Higgs boson, detected in 2012.
Superconductivity
of metals is a condensed-matter analog of the Higgs phenomena, in which
a condensate of Cooper pairs of electrons spontaneously breaks the U(1)
gauge symmetry associated with light and electromagnetism.
Condensed matter physics
Most
phases of matter can be understood through the lens of spontaneous
symmetry breaking. For example, crystals are periodic arrays of atoms
that are not invariant under all translations (only under a small subset
of translations by a lattice vector). Magnets have north and south
poles that are oriented in a specific direction, breaking rotational symmetry.
In addition to these examples, there are a whole host of other
symmetry-breaking phases of matter — including nematic phases of liquid
crystals, charge- and spin-density waves, superfluids, and many others.
There are several known examples of matter that cannot be
described by spontaneous symmetry breaking, including: topologically
ordered phases of matter, such as fractional quantum Hall liquids, and spin-liquids.
These states do not break any symmetry, but are distinct phases of
matter. Unlike the case of spontaneous symmetry breaking, there is not a
general framework for describing such states.
Continuous symmetry
The ferromagnet is the canonical system that spontaneously breaks the continuous symmetry of the spins below the Curie temperature and at h = 0, where h is the external magnetic field. Below the Curie temperature, the energy of the system is invariant under inversion of the magnetization m(x) such that m(x) = −m(−x). The symmetry is spontaneously broken as h → 0 when the Hamiltonian becomes invariant under the inversion transformation, but the expectation value is not invariant.
Spontaneously-symmetry-broken phases of matter are characterized
by an order parameter that describes the quantity which breaks the
symmetry under consideration. For example, in a magnet, the order
parameter is the local magnetization.
Spontaneous breaking of a continuous symmetry is inevitably
accompanied by gapless (meaning that these modes do not cost any energy
to excite) Nambu–Goldstone modes associated with slow, long-wavelength
fluctuations of the order parameter. For example, vibrational modes in a
crystal, known as phonons, are associated with slow density
fluctuations of the crystal's atoms. The associated Goldstone mode for
magnets are oscillating waves of spin known as spin-waves. For
symmetry-breaking states, whose order parameter is not a conserved
quantity, Nambu–Goldstone modes are typically massless and propagate at a
constant velocity.
An important theorem, due to Mermin and Wagner, states that, at
finite temperature, thermally activated fluctuations of Nambu–Goldstone
modes destroy the long-range order, and prevent spontaneous symmetry
breaking in one- and two-dimensional systems. Similarly, quantum
fluctuations of the order parameter prevent most types of continuous
symmetry breaking in one-dimensional systems even at zero temperature.
(An important exception is ferromagnets, whose order parameter,
magnetization, is an exactly conserved quantity and does not have any
quantum fluctuations.)
Other long-range interacting systems, such as cylindrical curved surfaces interacting via the Coulomb potential or Yukawa potential, have been shown to break translational and rotational symmetries.
It was shown, in the presence of a symmetric Hamiltonian, and in the
limit of infinite volume, the system spontaneously adopts a chiral
configuration — i.e., breaks mirror plane symmetry.
Dynamical symmetry breaking
Dynamical
symmetry breaking (DSB) is a special form of spontaneous symmetry
breaking in which the ground state of the system has reduced symmetry
properties compared to its theoretical description (i.e., Lagrangian).
Dynamical breaking of a global symmetry is a spontaneous symmetry
breaking, which happens not at the (classical) tree level (i.e., at the
level of the bare action), but due to quantum corrections (i.e., at the
level of the effective action).
Dynamical breaking of a gauge symmetry is subtler. In the conventional spontaneous gauge symmetry breaking, there exists an unstable Higgs particle in the theory, which drives the vacuum to a symmetry-broken phase. (See, for example, electroweak interaction.)
In dynamical gauge symmetry breaking, however, no unstable Higgs
particle operates in the theory, but the bound states of the system
itself provide the unstable fields that render the phase transition. For
example, Bardeen, Hill, and Lindner published a paper that attempts to
replace the conventional Higgs mechanism in the standard model
by a DSB that is driven by a bound state of top-antitop quarks. (Such
models, in which a composite particle plays the role of the Higgs boson,
are often referred to as "Composite Higgs models".) Dynamical breaking of gauge symmetries is often due to creation of a fermionic condensate — e.g., the quark condensate, which is connected to the dynamical breaking of chiral symmetry in quantum chromodynamics. Conventional superconductivity
is the paradigmatic example from the condensed matter side, where
phonon-mediated attractions lead electrons to become bound in pairs and
then condense, thereby breaking the electromagnetic gauge symmetry.
Generalisation and technical usage
For
spontaneous symmetry breaking to occur, there must be a system in which
there are several equally likely outcomes. The system as a whole is
therefore symmetric
with respect to these outcomes. However, if the system is sampled (i.e.
if the system is actually used or interacted with in any way), a
specific outcome must occur. Though the system as a whole is symmetric,
it is never encountered with this symmetry, but only in one specific
asymmetric state. Hence, the symmetry is said to be spontaneously broken
in that theory. Nevertheless, the fact that each outcome is equally
likely is a reflection of the underlying symmetry, which is thus often
dubbed "hidden symmetry", and has crucial formal consequences.
When a theory is symmetric with respect to a symmetry group,
but requires that one element of the group be distinct, then
spontaneous symmetry breaking has occurred. The theory must not dictate which member is distinct, only that one is.
From this point on, the theory can be treated as if this element
actually is distinct, with the proviso that any results found in this
way must be resymmetrized, by taking the average of each of the elements
of the group being the distinct one.
The crucial concept in physics theories is the order parameter. If there is a field (often a background field) which acquires an expectation value (not necessarily a vacuum expectation value) which is not invariant under the symmetry in question, we say that the system is in the ordered phase,
and the symmetry is spontaneously broken. This is because other
subsystems interact with the order parameter, which specifies a "frame
of reference" to be measured against. In that case, the vacuum state does not obey the initial symmetry (which would keep it invariant, in the linearly realized Wigner mode in which it would be a singlet), and, instead changes under the (hidden) symmetry, now implemented in the (nonlinear) Nambu–Goldstone mode. Normally, in the absence of the Higgs mechanism, massless Goldstone bosons arise.
The symmetry group can be discrete, such as the space group of a crystal, or continuous (e.g., a Lie group),
such as the rotational symmetry of space. However, if the system
contains only a single spatial dimension, then only discrete symmetries
may be broken in a vacuum state of the full quantum theory, although a classical solution may break a continuous symmetry.
Nobel Prize
On October 7, 2008, the
Royal Swedish Academy of Sciences awarded the 2008
Nobel Prize in Physics to three scientists for their work in subatomic physics symmetry breaking.
Yoichiro Nambu, of the
University of Chicago,
won half of the prize for the discovery of the mechanism of spontaneous
broken symmetry in the context of the strong interactions, specifically
chiral symmetry breaking. Physicists
Makoto Kobayashi and
Toshihide Maskawa, of
Kyoto University, shared the other half of the prize for discovering the origin of the
explicit breaking of CP symmetry in the weak interactions.
This origin is ultimately reliant on the Higgs mechanism, but, so far
understood as a "just so" feature of Higgs couplings, not a
spontaneously broken symmetry phenomenon.