| |
| Exact values | |
|---|---|
| metres per second | 299792458 |
| Approximate values (to three significant digits) | |
| kilometres per hour | 1080000000 |
| miles per second | 186000 |
| miles per hour | 671000000 |
| astronomical units per day | 173 |
| parsecs per year | 0.307 |
| Approximate light signal travel times | |
| Distance | Time |
| one foot | 1.0 ns |
| one metre | 3.3 ns |
| from geostationary orbit to Earth | 119 ms |
| the length of Earth's equator | 134 ms |
| from Moon to Earth | 1.3 s |
| from Sun to Earth (1 AU) | 8.3 min |
| one light year | 1.0 year |
| one parsec | 3.26 years |
| from nearest star to Sun (1.3 pc) | 4.2 years |
| from the nearest galaxy (the Canis Major Dwarf Galaxy) to Earth | 25000 years |
| across the Milky Way | 100000 years |
| from the Andromeda Galaxy to Earth | 2.5 million years |
The speed of light in vacuum, commonly denoted c, is a universal physical constant important in many areas of physics. Its exact value is defined as 299792458 metres per second (approximately 300000 km/s, or 186000 mi/s). It is exact because, by international agreement, a metre is defined as the length of the path travelled by light in vacuum during a time interval of 1⁄299792458 second. According to special relativity, c is the upper limit for the speed at which conventional matter, energy or any signal carrying information can travel through space.
Though this speed is most commonly associated with light, it is also the speed at which all massless particles and field perturbations travel in vacuum, including electromagnetic radiation (of which light is a small range in the frequency spectrum) and gravitational waves. Such particles and waves travel at c regardless of the motion of the source or the inertial reference frame of the observer. Particles with nonzero rest mass can approach c, but can never actually reach it, regardless of the frame of reference in which their speed is measured. In the special and general theories of relativity, c interrelates space and time, and also appears in the famous equation of mass–energy equivalence, E = mc2. In some cases objects or waves may appear to travel faster than light (e.g. phase velocities of waves, the appearance of certain high-speed astronomical objects, and particular quantum effects). The expansion of the universe is understood to exceed the speed of light beyond a certain boundary.
The speed at which light propagates through transparent materials, such as glass or air, is less than c; similarly, the speed of electromagnetic waves in wire cables is slower than c. The ratio between c and the speed v at which light travels in a material is called the refractive index n of the material (n = c / v). For example, for visible light, the refractive index of glass is typically around 1.5, meaning that light in glass travels at c / 1.5 ≈ 200000 km/s (124000 mi/s); the refractive index of air for visible light is about 1.0003, so the speed of light in air is about 90 km/s (56 mi/s) slower than c.
For many practical purposes, light and other electromagnetic waves will appear to propagate instantaneously, but for long distances and very sensitive measurements, their finite speed has noticeable effects. In communicating with distant space probes, it can take minutes to hours for a message to get from Earth to the spacecraft, or vice versa. The light seen from stars left them many years ago, allowing the study of the history of the universe by looking at distant objects. The finite speed of light also ultimately limits the data transfer between the CPU and memory chips in computers. The speed of light can be used with time of flight measurements to measure large distances to high precision.
Ole Rømer first demonstrated in 1676 that light travels at a finite speed (non-instantaneously) by studying the apparent motion of Jupiter's moon Io. In 1865, James Clerk Maxwell proposed that light was an electromagnetic wave, and therefore travelled at the speed c appearing in his theory of electromagnetism. In 1905, Albert Einstein postulated that the speed of light c with respect to any inertial frame is a constant and is independent of the motion of the light source. He explored the consequences of that postulate by deriving the theory of relativity and in doing so showed that the parameter c had relevance outside of the context of light and electromagnetism.
After centuries of increasingly precise measurements, in 1975 the speed of light was known to be 299792458 m/s (983571056 ft/s; 186282.397 mi/s) with a measurement uncertainty of 4 parts per billion. In 1983, the metre was redefined in the International System of Units (SI) as the distance travelled by light in vacuum in 1 / 299792458 of a second.
Numerical value, notation, and units
The speed of light in vacuum is usually denoted by a lowercase c, for "constant" or the Latin celeritas (meaning "swiftness, celerity"). In 1856, Wilhelm Eduard Weber and Rudolf Kohlrausch had used c for a different constant that was later shown to equal √2 times the speed of light in vacuum. Historically, the symbol V was used as an alternative symbol for the speed of light, introduced by James Clerk Maxwell in 1865. In 1894, Paul Drude redefined c with its modern meaning. Einstein used V in his original German-language papers on special relativity in 1905, but in 1907 he switched to c, which by then had become the standard symbol for the speed of light.
Sometimes c is used for the speed of waves in any material medium, and c0 for the speed of light in vacuum. This subscripted notation, which is endorsed in official SI literature, has the same form as other related constants: namely, μ0 for the vacuum permeability or magnetic constant, ε0 for the vacuum permittivity or electric constant, and Z0 for the impedance of free space. This article uses c exclusively for the speed of light in vacuum.
Since 1983, the metre has been defined in the International System of Units (SI) as the distance light travels in vacuum in 1⁄299792458 of a second. This definition fixes the speed of light in vacuum at exactly 299792458 m/s. As a dimensional physical constant, the numerical value of c is different for different unit systems. In branches of physics in which c appears often, such as in relativity, it is common to use systems of natural units of measurement or the geometrized unit system where c = 1. Using these units, c does not appear explicitly because multiplication or division by 1 does not affect the result.
Fundamental role in physics
The speed at which light waves propagate in vacuum is independent both of the motion of the wave source and of the inertial frame of reference of the observer. This invariance of the speed of light was postulated by Einstein in 1905, after being motivated by Maxwell's theory of electromagnetism and the lack of evidence for the luminiferous aether; it has since been consistently confirmed by many experiments. It is only possible to verify experimentally that the two-way speed of light (for example, from a source to a mirror and back again) is frame-independent, because it is impossible to measure the one-way speed of light (for example, from a source to a distant detector) without some convention as to how clocks at the source and at the detector should be synchronized. However, by adopting Einstein synchronization for the clocks, the one-way speed of light becomes equal to the two-way speed of light by definition. The special theory of relativity explores the consequences of this invariance of c with the assumption that the laws of physics are the same in all inertial frames of reference. One consequence is that c is the speed at which all massless particles and waves, including light, must travel in vacuum.
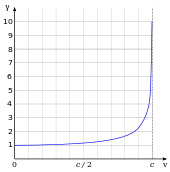
Special relativity has many counterintuitive and experimentally verified implications. These include the equivalence of mass and energy (E = mc2), length contraction (moving objects shorten), and time dilation (moving clocks run more slowly). The factor γ by which lengths contract and times dilate is known as the Lorentz factor and is given by γ = (1 − v2/c2)−1/2, where v is the speed of the object. The difference of γ from 1 is negligible for speeds much slower than c, such as most everyday speeds—in which case special relativity is closely approximated by Galilean relativity—but it increases at relativistic speeds and diverges to infinity as v approaches c. For example, a time dilation factor of γ = 2 occurs at a relative velocity of 86.6% of the speed of light (v = 0.866 c). Similarly, a time dilation factor of γ = 10 occurs at v = 99.5% c.
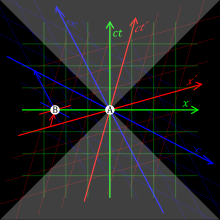
The results of special relativity can be summarized by treating space and time as a unified structure known as spacetime (with c relating the units of space and time), and requiring that physical theories satisfy a special symmetry called Lorentz invariance, whose mathematical formulation contains the parameter c. Lorentz invariance is an almost universal assumption for modern physical theories, such as quantum electrodynamics, quantum chromodynamics, the Standard Model of particle physics, and general relativity. As such, the parameter c is ubiquitous in modern physics, appearing in many contexts that are unrelated to light. For example, general relativity predicts that c is also the speed of gravity and of gravitational waves. In non-inertial frames of reference (gravitationally curved spacetime or accelerated reference frames), the local speed of light is constant and equal to c, but the speed of light along a trajectory of finite length can differ from c, depending on how distances and times are defined.
It is generally assumed that fundamental constants such as c have the same value throughout spacetime, meaning that they do not depend on location and do not vary with time. However, it has been suggested in various theories that the speed of light may have changed over time. No conclusive evidence for such changes has been found, but they remain the subject of ongoing research.
It also is generally assumed that the speed of light is isotropic, meaning that it has the same value regardless of the direction in which it is measured. Observations of the emissions from nuclear energy levels as a function of the orientation of the emitting nuclei in a magnetic field (see Hughes–Drever experiment), and of rotating optical resonators (see Resonator experiments) have put stringent limits on the possible two-way anisotropy.
Upper limit on speeds
According to special relativity, the energy of an object with rest mass m and speed v is given by γmc2, where γ is the Lorentz factor defined above. When v is zero, γ is equal to one, giving rise to the famous E = mc2 formula for mass–energy equivalence. The γ factor approaches infinity as v approaches c, and it would take an infinite amount of energy to accelerate an object with mass to the speed of light. The speed of light is the upper limit for the speeds of objects with positive rest mass, and individual photons cannot travel faster than the speed of light. This is experimentally established in many tests of relativistic energy and momentum.
More generally, it is impossible for signals or energy to travel faster than c. One argument for this follows from the counter-intuitive implication of special relativity known as the relativity of simultaneity. If the spatial distance between two events A and B is greater than the time interval between them multiplied by c then there are frames of reference in which A precedes B, others in which B precedes A, and others in which they are simultaneous. As a result, if something were travelling faster than c relative to an inertial frame of reference, it would be travelling backwards in time relative to another frame, and causality would be violated. In such a frame of reference, an "effect" could be observed before its "cause". Such a violation of causality has never been recorded, and would lead to paradoxes such as the tachyonic antitelephone.
Faster-than-light observations and experiments
There are situations in which it may seem that matter, energy, or information-carrying signal travels at speeds greater than c, but they do not. For example, as is discussed in the propagation of light in a medium section below, many wave velocities can exceed c. For example, the phase velocity of X-rays through most glasses can routinely exceed c, but phase velocity does not determine the velocity at which waves convey information.
If a laser beam is swept quickly across a distant object, the spot of light can move faster than c, although the initial movement of the spot is delayed because of the time it takes light to get to the distant object at the speed c. However, the only physical entities that are moving are the laser and its emitted light, which travels at the speed c from the laser to the various positions of the spot. Similarly, a shadow projected onto a distant object can be made to move faster than c, after a delay in time. In neither case does any matter, energy, or information travel faster than light.
The rate of change in the distance between two objects in a frame of reference with respect to which both are moving (their closing speed) may have a value in excess of c. However, this does not represent the speed of any single object as measured in a single inertial frame.
Certain quantum effects appear to be transmitted instantaneously and therefore faster than c, as in the EPR paradox. An example involves the quantum states of two particles that can be entangled. Until either of the particles is observed, they exist in a superposition of two quantum states. If the particles are separated and one particle's quantum state is observed, the other particle's quantum state is determined instantaneously. However, it is impossible to control which quantum state the first particle will take on when it is observed, so information cannot be transmitted in this manner.
Another quantum effect that predicts the occurrence of faster-than-light speeds is called the Hartman effect: under certain conditions the time needed for a virtual particle to tunnel through a barrier is constant, regardless of the thickness of the barrier. This could result in a virtual particle crossing a large gap faster-than-light. However, no information can be sent using this effect.
So-called superluminal motion is seen in certain astronomical objects, such as the relativistic jets of radio galaxies and quasars. However, these jets are not moving at speeds in excess of the speed of light: the apparent superluminal motion is a projection effect caused by objects moving near the speed of light and approaching Earth at a small angle to the line of sight: since the light which was emitted when the jet was farther away took longer to reach the Earth, the time between two successive observations corresponds to a longer time between the instants at which the light rays were emitted.
In models of the expanding universe, the farther galaxies are from each other, the faster they drift apart. This receding is not due to motion through space, but rather to the expansion of space itself. For example, galaxies far away from Earth appear to be moving away from the Earth with a speed proportional to their distances. Beyond a boundary called the Hubble sphere, the rate at which their distance from Earth increases becomes greater than the speed of light.
Propagation of light
In classical physics, light is described as a type of electromagnetic wave. The classical behaviour of the electromagnetic field is described by Maxwell's equations, which predict that the speed c with which electromagnetic waves (such as light) propagate in vacuum is related to the distributed capacitance and inductance of vacuum, otherwise respectively known as the electric constant ε0 and the magnetic constant μ0, by the equation
In modern quantum physics, the electromagnetic field is described by the theory of quantum electrodynamics (QED). In this theory, light is described by the fundamental excitations (or quanta) of the electromagnetic field, called photons. In QED, photons are massless particles and thus, according to special relativity, they travel at the speed of light in vacuum.
Extensions of QED in which the photon has a mass have been considered. In such a theory, its speed would depend on its frequency, and the invariant speed c of special relativity would then be the upper limit of the speed of light in vacuum. No variation of the speed of light with frequency has been observed in rigorous testing, putting stringent limits on the mass of the photon. The limit obtained depends on the model used: if the massive photon is described by Proca theory, the experimental upper bound for its mass is about 10−57 grams; if photon mass is generated by a Higgs mechanism, the experimental upper limit is less sharp, m ≤ 10−14 eV/c2 [56] (roughly 2 × 10−47 g).
Another reason for the speed of light to vary with its frequency would be the failure of special relativity to apply to arbitrarily small scales, as predicted by some proposed theories of quantum gravity. In 2009, the observation of gamma-ray burst GRB 090510 found no evidence for a dependence of photon speed on energy, supporting tight constraints in specific models of spacetime quantization on how this speed is affected by photon energy for energies approaching the Planck scale.
In a medium
In a medium, light usually does not propagate at a speed equal to c; further, different types of light wave will travel at different speeds. The speed at which the individual crests and troughs of a plane wave (a wave filling the whole space, with only one frequency) propagate is called the phase velocity vp. A physical signal with a finite extent (a pulse of light) travels at a different speed. The largest part of the pulse travels at the group velocity vg, and its earliest part travels at the front velocity vf.
The phase velocity is important in determining how a light wave travels through a material or from one material to another. It is often represented in terms of a refractive index. The refractive index of a material is defined as the ratio of c to the phase velocity vp in the material: larger indices of refraction indicate lower speeds. The refractive index of a material may depend on the light's frequency, intensity, polarization, or direction of propagation; in many cases, though, it can be treated as a material-dependent constant. The refractive index of air is approximately 1.0003. Denser media, such as water, glass, and diamond, have refractive indexes of around 1.3, 1.5 and 2.4, respectively, for visible light. In exotic materials like Bose–Einstein condensates near absolute zero, the effective speed of light may be only a few metres per second. However, this represents absorption and re-radiation delay between atoms, as do all slower-than-c speeds in material substances. As an extreme example of light "slowing" in matter, two independent teams of physicists claimed to bring light to a "complete standstill" by passing it through a Bose–Einstein condensate of the element rubidium. However, the popular description of light being "stopped" in these experiments refers only to light being stored in the excited states of atoms, then re-emitted at an arbitrarily later time, as stimulated by a second laser pulse. During the time it had "stopped", it had ceased to be light. This type of behaviour is generally microscopically true of all transparent media which "slow" the speed of light.
In transparent materials, the refractive index generally is greater than 1, meaning that the phase velocity is less than c. In other materials, it is possible for the refractive index to become smaller than 1 for some frequencies; in some exotic materials it is even possible for the index of refraction to become negative. The requirement that causality is not violated implies that the real and imaginary parts of the dielectric constant of any material, corresponding respectively to the index of refraction and to the attenuation coefficient, are linked by the Kramers–Kronig relations. In practical terms, this means that in a material with refractive index less than 1, the absorption of the wave is so quick that no signal can be sent faster than c.
A pulse with different group and phase velocities (which occurs if the phase velocity is not the same for all the frequencies of the pulse) smears out over time, a process known as dispersion. Certain materials have an exceptionally low (or even zero) group velocity for light waves, a phenomenon called slow light, which has been confirmed in various experiments. The opposite, group velocities exceeding c, has also been shown in experiment. It should even be possible for the group velocity to become infinite or negative, with pulses travelling instantaneously or backwards in time.
None of these options, however, allow information to be transmitted faster than c. It is impossible to transmit information with a light pulse any faster than the speed of the earliest part of the pulse (the front velocity). It can be shown that this is (under certain assumptions) always equal to c.
It is possible for a particle to travel through a medium faster than the phase velocity of light in that medium (but still slower than c). When a charged particle does that in a dielectric material, the electromagnetic equivalent of a shock wave, known as Cherenkov radiation, is emitted.
Practical effects of finiteness
The speed of light is of relevance to communications: the one-way and round-trip delay time are greater than zero. This applies from small to astronomical scales. On the other hand, some techniques depend on the finite speed of light, for example in distance measurements.
Small scales
In supercomputers, the speed of light imposes a limit on how quickly data can be sent between processors. If a processor operates at 1 gigahertz, a signal can travel only a maximum of about 30 centimetres (1 ft) in a single cycle. Processors must therefore be placed close to each other to minimize communication latencies; this can cause difficulty with cooling. If clock frequencies continue to increase, the speed of light will eventually become a limiting factor for the internal design of single chips.
Large distances on Earth
Given that the equatorial circumference of the Earth is about 40075 km and that c is about 300000 km/s, the theoretical shortest time for a piece of information to travel half the globe along the surface is about 67 milliseconds. When light is travelling around the globe in an optical fibre, the actual transit time is longer, in part because the speed of light is slower by about 35% in an optical fibre, depending on its refractive index n. Furthermore, straight lines rarely occur in global communications situations, and delays are created when the signal passes through an electronic switch or signal regenerator.
Spaceflights and astronomy
Similarly, communications between the Earth and spacecraft are not instantaneous. There is a brief delay from the source to the receiver, which becomes more noticeable as distances increase. This delay was significant for communications between ground control and Apollo 8 when it became the first manned spacecraft to orbit the Moon: for every question, the ground control station had to wait at least three seconds for the answer to arrive. The communications delay between Earth and Mars can vary between five and twenty minutes depending upon the relative positions of the two planets. As a consequence of this, if a robot on the surface of Mars were to encounter a problem, its human controllers would not be aware of it until at least five minutes later, and possibly up to twenty minutes later; it would then take a further five to twenty minutes for instructions to travel from Earth to Mars.
Receiving light and other signals from distant astronomical sources can even take much longer. For example, it has taken 13 billion (13×109) years for light to travel to Earth from the faraway galaxies viewed in the Hubble Ultra Deep Field images. Those photographs, taken today, capture images of the galaxies as they appeared 13 billion years ago, when the universe was less than a billion years old. The fact that more distant objects appear to be younger, due to the finite speed of light, allows astronomers to infer the evolution of stars, of galaxies, and of the universe itself.
Astronomical distances are sometimes expressed in light-years, especially in popular science publications and media. A light-year is the distance light travels in one year, around 9461 billion kilometres, 5879 billion miles, or 0.3066 parsecs. In round figures, a light year is nearly 10 trillion kilometres or nearly 6 trillion miles. Proxima Centauri, the closest star to Earth after the Sun, is around 4.2 light-years away.
Distance measurement
Radar systems measure the distance to a target by the time it takes a radio-wave pulse to return to the radar antenna after being reflected by the target: the distance to the target is half the round-trip transit time multiplied by the speed of light. A Global Positioning System (GPS) receiver measures its distance to GPS satellites based on how long it takes for a radio signal to arrive from each satellite, and from these distances calculates the receiver's position. Because light travels about 300000 kilometres (186000 mi) in one second, these measurements of small fractions of a second must be very precise. The Lunar Laser Ranging Experiment, radar astronomy and the Deep Space Network determine distances to the Moon, planets and spacecraft, respectively, by measuring round-trip transit times.
High-frequency trading
The speed of light has become important in high-frequency trading, where traders seek to gain minute advantages by delivering their trades to exchanges fractions of a second ahead of other traders. For example, traders have been switching to microwave communications between trading hubs, because of the advantage which microwaves travelling at near to the speed of light in air have over fibre optic signals, which travel 30–40% slower.
Measurement
There are different ways to determine the value of c. One way is to measure the actual speed at which light waves propagate, which can be done in various astronomical and earth-based setups. However, it is also possible to determine c from other physical laws where it appears, for example, by determining the values of the electromagnetic constants ε0 and μ0 and using their relation to c. Historically, the most accurate results have been obtained by separately determining the frequency and wavelength of a light beam, with their product equalling c.
In 1983 the metre was defined as "the length of the path travelled by light in vacuum during a time interval of 1⁄299792458 of a second", fixing the value of the speed of light at 299792458 m/s by definition, as described below. Consequently, accurate measurements of the speed of light yield an accurate realization of the metre rather than an accurate value of c.
Astronomical measurements
Outer space is a convenient setting for measuring the speed of light because of its large scale and nearly perfect vacuum. Typically, one measures the time needed for light to traverse some reference distance in the solar system, such as the radius of the Earth's orbit. Historically, such measurements could be made fairly accurately, compared to how accurately the length of the reference distance is known in Earth-based units. It is customary to express the results in astronomical units (AU) per day.
Ole Christensen Rømer used an astronomical measurement to make the first quantitative estimate of the speed of light in the year 1676. When measured from Earth, the periods of moons orbiting a distant planet are shorter when the Earth is approaching the planet than when the Earth is receding from it. The distance travelled by light from the planet (or its moon) to Earth is shorter when the Earth is at the point in its orbit that is closest to its planet than when the Earth is at the farthest point in its orbit, the difference in distance being the diameter of the Earth's orbit around the Sun. The observed change in the moon's orbital period is caused by the difference in the time it takes light to traverse the shorter or longer distance. Rømer observed this effect for Jupiter's innermost moon Io and deduced that light takes 22 minutes to cross the diameter of the Earth's orbit.
Another method is to use the aberration of light, discovered and explained by James Bradley in the 18th century. This effect results from the vector addition of the velocity of light arriving from a distant source (such as a star) and the velocity of its observer (see diagram on the right). A moving observer thus sees the light coming from a slightly different direction and consequently sees the source at a position shifted from its original position. Since the direction of the Earth's velocity changes continuously as the Earth orbits the Sun, this effect causes the apparent position of stars to move around. From the angular difference in the position of stars (maximally 20.5 arcseconds) it is possible to express the speed of light in terms of the Earth's velocity around the Sun, which with the known length of a year can be converted to the time needed to travel from the Sun to the Earth. In 1729, Bradley used this method to derive that light travelled 10210 times faster than the Earth in its orbit (the modern figure is 10066 times faster) or, equivalently, that it would take light 8 minutes 12 seconds to travel from the Sun to the Earth.
Astronomical unit
An astronomical unit (AU) is approximately the average distance between the Earth and Sun. It was redefined in 2012 as exactly 149597870700 m. Previously the AU was not based on the International System of Units but in terms of the gravitational force exerted by the Sun in the framework of classical mechanics. The current definition uses the recommended value in metres for the previous definition of the astronomical unit, which was determined by measurement. This redefinition is analogous to that of the metre and likewise has the effect of fixing the speed of light to an exact value in astronomical units per second (via the exact speed of light in metres per second).
Previously, the inverse of c expressed in seconds per astronomical unit was measured by comparing the time for radio signals to reach different spacecraft in the Solar System, with their position calculated from the gravitational effects of the Sun and various planets. By combining many such measurements, a best fit value for the light time per unit distance could be obtained. For example, in 2009, the best estimate, as approved by the International Astronomical Union (IAU), was:
- light time for unit distance: tau = 499.004783836(10) s
- c = 0.00200398880410(4) AU/s = 173.144632674(3) AU/day.
The relative uncertainty in these measurements is 0.02 parts per billion (2×10−11), equivalent to the uncertainty in Earth-based measurements of length by interferometry. Since the metre is defined to be the length travelled by light in a certain time interval, the measurement of the light time in terms of the previous definition of the astronomical unit can also be interpreted as measuring the length of an AU (old definition) in metres.
Time of flight techniques
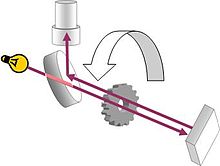
A method of measuring the speed of light is to measure the time needed for light to travel to a mirror at a known distance and back. This is the working principle behind the Fizeau–Foucault apparatus developed by Hippolyte Fizeau and Léon Foucault.
The setup as used by Fizeau consists of a beam of light directed at a mirror 8 kilometres (5 mi) away. On the way from the source to the mirror, the beam passes through a rotating cogwheel. At a certain rate of rotation, the beam passes through one gap on the way out and another on the way back, but at slightly higher or lower rates, the beam strikes a tooth and does not pass through the wheel. Knowing the distance between the wheel and the mirror, the number of teeth on the wheel, and the rate of rotation, the speed of light can be calculated.
The method of Foucault replaces the cogwheel with a rotating mirror. Because the mirror keeps rotating while the light travels to the distant mirror and back, the light is reflected from the rotating mirror at a different angle on its way out than it is on its way back. From this difference in angle, the known speed of rotation and the distance to the distant mirror the speed of light may be calculated.
Nowadays, using oscilloscopes with time resolutions of less than one nanosecond, the speed of light can be directly measured by timing the delay of a light pulse from a laser or an LED reflected from a mirror. This method is less precise (with errors of the order of 1%) than other modern techniques, but it is sometimes used as a laboratory experiment in college physics classes.
Electromagnetic constants
An option for deriving c that does not directly depend on a measurement of the propagation of electromagnetic waves is to use the relation between c and the vacuum permittivity ε0 and vacuum permeability μ0 established by Maxwell's theory: c2 = 1/(ε0μ0). The vacuum permittivity may be determined by measuring the capacitance and dimensions of a capacitor, whereas the value of the vacuum permeability is fixed at exactly 4π×10−7 H⋅m−1 through the definition of the ampere. Rosa and Dorsey used this method in 1907 to find a value of 299710±22 km/s.
Cavity resonance
Another way to measure the speed of light is to independently measure the frequency f and wavelength λ of an electromagnetic wave in vacuum. The value of c can then be found by using the relation c = fλ. One option is to measure the resonance frequency of a cavity resonator. If the dimensions of the resonance cavity are also known, these can be used to determine the wavelength of the wave. In 1946, Louis Essen and A.C. Gordon-Smith established the frequency for a variety of normal modes of microwaves of a microwave cavity of precisely known dimensions. The dimensions were established to an accuracy of about ±0.8 μm using gauges calibrated by interferometry. As the wavelength of the modes was known from the geometry of the cavity and from electromagnetic theory, knowledge of the associated frequencies enabled a calculation of the speed of light.
The Essen–Gordon-Smith result, 299792±9 km/s, was substantially more precise than those found by optical techniques. By 1950, repeated measurements by Essen established a result of 299792.5±3.0 km/s.
A household demonstration of this technique is possible, using a microwave oven and food such as marshmallows or margarine: if the turntable is removed so that the food does not move, it will cook the fastest at the antinodes (the points at which the wave amplitude is the greatest), where it will begin to melt. The distance between two such spots is half the wavelength of the microwaves; by measuring this distance and multiplying the wavelength by the microwave frequency (usually displayed on the back of the oven, typically 2450 MHz), the value of c can be calculated, "often with less than 5% error".
Interferometry
Interferometry is another method to find the wavelength of electromagnetic radiation for determining the speed of light. A coherent beam of light (e.g. from a laser), with a known frequency (f), is split to follow two paths and then recombined. By adjusting the path length while observing the interference pattern and carefully measuring the change in path length, the wavelength of the light (λ) can be determined. The speed of light is then calculated using the equation c = λf.
Before the advent of laser technology, coherent radio sources were used for interferometry measurements of the speed of light. However interferometric determination of wavelength becomes less precise with wavelength and the experiments were thus limited in precision by the long wavelength (~4 mm (0.16 in)) of the radiowaves. The precision can be improved by using light with a shorter wavelength, but then it becomes difficult to directly measure the frequency of the light. One way around this problem is to start with a low frequency signal of which the frequency can be precisely measured, and from this signal progressively synthesize higher frequency signals whose frequency can then be linked to the original signal. A laser can then be locked to the frequency, and its wavelength can be determined using interferometry. This technique was due to a group at the National Bureau of Standards (NBS) (which later became NIST). They used it in 1972 to measure the speed of light in vacuum with a fractional uncertainty of 3.5×10−9.
History
| <1638 | Galileo, covered lanterns | inconclusive | |
| <1667 | Accademia del Cimento, covered lanterns | inconclusive | |
| 1675 | Rømer and Huygens, moons of Jupiter | 220000 | ‒27% error |
| 1729 | James Bradley, aberration of light | 301000 | +0.40% error |
| 1849 | Hippolyte Fizeau, toothed wheel | 315000 | +5.1% error |
| 1862 | Léon Foucault, rotating mirror | 298000±500 | ‒0.60% error |
| 1907 | Rosa and Dorsey, EM constants | 299710±30 | ‒280 ppm error |
| 1926 | Albert A. Michelson, rotating mirror | 299796±4 | +12 ppm error |
| 1950 | Essen and Gordon-Smith, cavity resonator | 299792.5±3.0 | +0.14 ppm error |
| 1958 | K.D. Froome, radio interferometry | 299792.50±0.10 | +0.14 ppm error |
| 1972 | Evenson et al., laser interferometry | 299792.4562±0.0011 | ‒0.006 ppm error |
| 1983 | 17th CGPM, definition of the metre | 299792.458 (exact) | exact, as defined |
Until the early modern period, it was not known whether light travelled instantaneously or at a very fast finite speed. The first extant recorded examination of this subject was in ancient Greece. The ancient Greeks, Muslim scholars, and classical European scientists long debated this until Rømer provided the first calculation of the speed of light. Einstein's Theory of Special Relativity concluded that the speed of light is constant regardless of one's frame of reference. Since then, scientists have provided increasingly accurate measurements.
Early history
Empedocles (c. 490–430 BC) was the first to propose a theory of light and claimed that light has a finite speed. He maintained that light was something in motion, and therefore must take some time to travel. Aristotle argued, to the contrary, that "light is due to the presence of something, but it is not a movement". Euclid and Ptolemy advanced Empedocles' emission theory of vision, where light is emitted from the eye, thus enabling sight. Based on that theory, Heron of Alexandria argued that the speed of light must be infinite because distant objects such as stars appear immediately upon opening the eyes. Early Islamic philosophers initially agreed with the Aristotelian view that light had no speed of travel. In 1021, Alhazen (Ibn al-Haytham) published the Book of Optics, in which he presented a series of arguments dismissing the emission theory of vision in favour of the now accepted intromission theory, in which light moves from an object into the eye. This led Alhazen to propose that light must have a finite speed, and that the speed of light is variable, decreasing in denser bodies. He argued that light is substantial matter, the propagation of which requires time, even if this is hidden from our senses. Also in the 11th century, Abū Rayhān al-Bīrūnī agreed that light has a finite speed, and observed that the speed of light is much faster than the speed of sound.
In the 13th century, Roger Bacon argued that the speed of light in air was not infinite, using philosophical arguments backed by the writing of Alhazen and Aristotle. In the 1270s, Witelo considered the possibility of light travelling at infinite speed in vacuum, but slowing down in denser bodies.
In the early 17th century, Johannes Kepler believed that the speed of light was infinite since empty space presents no obstacle to it. René Descartes argued that if the speed of light were to be finite, the Sun, Earth, and Moon would be noticeably out of alignment during a lunar eclipse. Since such misalignment had not been observed, Descartes concluded the speed of light was infinite. Descartes speculated that if the speed of light were found to be finite, his whole system of philosophy might be demolished. In Descartes' derivation of Snell's law, he assumed that even though the speed of light was instantaneous, the denser the medium, the faster was light's speed. Pierre de Fermat derived Snell's law using the opposing assumption, the denser the medium the slower light travelled. Fermat also argued in support of a finite speed of light.
First measurement attempts
In 1629, Isaac Beeckman proposed an experiment in which a person observes the flash of a cannon reflecting off a mirror about one mile (1.6 km) away. In 1638, Galileo Galilei proposed an experiment, with an apparent claim to having performed it some years earlier, to measure the speed of light by observing the delay between uncovering a lantern and its perception some distance away. He was unable to distinguish whether light travel was instantaneous or not, but concluded that if it were not, it must nevertheless be extraordinarily rapid. In 1667, the Accademia del Cimento of Florence reported that it had performed Galileo's experiment, with the lanterns separated by about one mile, but no delay was observed. The actual delay in this experiment would have been about 11 microseconds.
The first quantitative estimate of the speed of light was made in 1676 by Rømer. From the observation that the periods of Jupiter's innermost moon Io appeared to be shorter when the Earth was approaching Jupiter than when receding from it, he concluded that light travels at a finite speed, and estimated that it takes light 22 minutes to cross the diameter of Earth's orbit. Christiaan Huygens combined this estimate with an estimate for the diameter of the Earth's orbit to obtain an estimate of speed of light of 220000 km/s, 26% lower than the actual value.
In his 1704 book Opticks, Isaac Newton reported Rømer's calculations of the finite speed of light and gave a value of "seven or eight minutes" for the time taken for light to travel from the Sun to the Earth (the modern value is 8 minutes 19 seconds). Newton queried whether Rømer's eclipse shadows were coloured; hearing that they were not, he concluded the different colours travelled at the same speed. In 1729, James Bradley discovered stellar aberration. From this effect he determined that light must travel 10210 times faster than the Earth in its orbit (the modern figure is 10066 times faster) or, equivalently, that it would take light 8 minutes 12 seconds to travel from the Sun to the Earth.
Connections with electromagnetism
In the 19th century Hippolyte Fizeau developed a method to determine the speed of light based on time-of-flight measurements on Earth and reported a value of 315000 km/s. His method was improved upon by Léon Foucault who obtained a value of 298000 km/s in 1862. In the year 1856, Wilhelm Eduard Weber and Rudolf Kohlrausch measured the ratio of the electromagnetic and electrostatic units of charge, 1/√ε0μ0, by discharging a Leyden jar, and found that its numerical value was very close to the speed of light as measured directly by Fizeau. The following year Gustav Kirchhoff calculated that an electric signal in a resistanceless wire travels along the wire at this speed. In the early 1860s, Maxwell showed that, according to the theory of electromagnetism he was working on, electromagnetic waves propagate in empty space at a speed equal to the above Weber/Kohlrausch ratio, and drawing attention to the numerical proximity of this value to the speed of light as measured by Fizeau, he proposed that light is in fact an electromagnetic wave.
"Luminiferous aether"
It was thought at the time that empty space was filled with a background medium called the luminiferous aether in which the electromagnetic field existed. Some physicists thought that this aether acted as a preferred frame of reference for the propagation of light and therefore it should be possible to measure the motion of the Earth with respect to this medium, by measuring the isotropy of the speed of light. Beginning in the 1880s several experiments were performed to try to detect this motion, the most famous of which is the experiment performed by Albert A. Michelson and Edward W. Morley in 1887. The detected motion was always less than the observational error. Modern experiments indicate that the two-way speed of light is isotropic (the same in every direction) to within 6 nanometres per second. Because of this experiment Hendrik Lorentz proposed that the motion of the apparatus through the aether may cause the apparatus to contract along its length in the direction of motion, and he further assumed that the time variable for moving systems must also be changed accordingly ("local time"), which led to the formulation of the Lorentz transformation. Based on Lorentz's aether theory, Henri Poincaré (1900) showed that this local time (to first order in v/c) is indicated by clocks moving in the aether, which are synchronized under the assumption of constant light speed. In 1904, he speculated that the speed of light could be a limiting velocity in dynamics, provided that the assumptions of Lorentz's theory are all confirmed. In 1905, Poincaré brought Lorentz's aether theory into full observational agreement with the principle of relativity.
Special relativity
In 1905 Einstein postulated from the outset that the speed of light in vacuum, measured by a non-accelerating observer, is independent of the motion of the source or observer. Using this and the principle of relativity as a basis he derived the special theory of relativity, in which the speed of light in vacuum c featured as a fundamental constant, also appearing in contexts unrelated to light. This made the concept of the stationary aether (to which Lorentz and Poincaré still adhered) useless and revolutionized the concepts of space and time.
Increased accuracy of c and redefinition of the metre and second
In the second half of the 20th century, much progress was made in increasing the accuracy of measurements of the speed of light, first by cavity resonance techniques and later by laser interferometer techniques. These were aided by new, more precise, definitions of the metre and second. In 1950, Louis Essen determined the speed as 299792.5±3.0 km/s, using cavity resonance. This value was adopted by the 12th General Assembly of the Radio-Scientific Union in 1957. In 1960, the metre was redefined in terms of the wavelength of a particular spectral line of krypton-86, and, in 1967, the second was redefined in terms of the hyperfine transition frequency of the ground state of caesium-133.
In 1972, using the laser interferometer method and the new definitions, a group at the US National Bureau of Standards in Boulder, Colorado determined the speed of light in vacuum to be c = 299792456.2±1.1 m/s. This was 100 times less uncertain than the previously accepted value. The remaining uncertainty was mainly related to the definition of the metre. As similar experiments found comparable results for c, the 15th General Conference on Weights and Measures in 1975 recommended using the value 299792458 m/s for the speed of light.
Defining the speed of light as an explicit constant
In 1983 the 17th meeting of the General Conference on Weights and Measures (CGPM) found that wavelengths from frequency measurements and a given value for the speed of light are more reproducible than the previous standard. They kept the 1967 definition of second, so the caesium hyperfine frequency would now determine both the second and the metre. To do this, they redefined the metre as: "The metre is the length of the path traveled by light in vacuum during a time interval of 1/299792458 of a second." As a result of this definition, the value of the speed of light in vacuum is exactly 299792458 m/s and has become a defined constant in the SI system of units. Improved experimental techniques that, prior to 1983, would have measured the speed of light no longer affect the known value of the speed of light in SI units, but instead allow a more precise realization of the metre by more accurately measuring the wavelength of Krypton-86 and other light sources.
In 2011, the CGPM stated its intention to redefine all seven SI base units using what it calls "the explicit-constant formulation", where each "unit is defined indirectly by specifying explicitly an exact value for a well-recognized fundamental constant", as was done for the speed of light. It proposed a new, but completely equivalent, wording of the metre's definition: "The metre, symbol m, is the unit of length; its magnitude is set by fixing the numerical value of the speed of light in vacuum to be equal to exactly 299792458 when it is expressed in the SI unit m s−1." This was one of the changes that was incorporated in the 2019 redefinition of the SI base units, also termed the New SI.