Poisson distribution

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Poisson_distribution 

 

Poisson Distribution

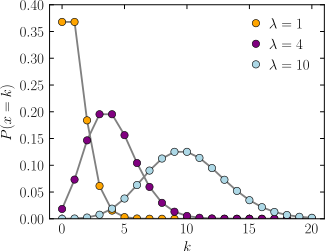
Probability mass function The horizontal axis is the index k, the number of occurrences. λ is the expected rate of occurrences. The vertical axis is the probability of k occurrences given λ. The function is defined only at integer values of k; the connecting lines are only guides for the eye.
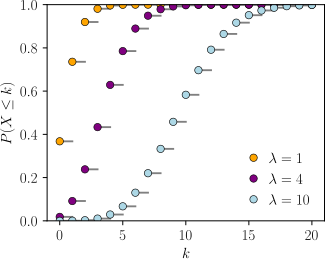
Cumulative distribution function The horizontal axis is the index k, the number of occurrences. The CDF is discontinuous at the integers of k and flat everywhere else because a variable that is Poisson distributed takes on only integer values.
Notation	${\displaystyle \operatorname {Pois} (\lambda )}$
Parameters	${\displaystyle \lambda \in (0,\infty )}$ (rate)
Support	${\displaystyle k\in \mathbb {N} _{0}}$ (Natural numbers starting from 0)
PMF	${\displaystyle {\frac {\lambda ^{k}e^{-\lambda }}{k!}}}$
CDF	${\displaystyle {\frac {\Gamma (\lfloor k+1\rfloor ,\lambda )}{\lfloor k\rfloor !}}}$, or ${\displaystyle e^{-\lambda }\sum _{i=0}^{\lfloor k\rfloor }{\frac {\lambda ^{i}}{i!}}\ }$, or ${\displaystyle Q(\lfloor k+1\rfloor ,\lambda )}$ (for ${\displaystyle k\geq 0}$, where ${\displaystyle \Gamma (x,y)}$ is the upper incomplete gamma function, ${\displaystyle \lfloor k\rfloor }$ is the floor function, and Q is the regularized gamma function)
Mean	${\displaystyle \lambda }$
Median	${\displaystyle \approx \lfloor \lambda +1/3-0.02/\lambda \rfloor }$
Mode	${\displaystyle \lceil \lambda \rceil -1,\lfloor \lambda \rfloor }$
Variance	${\displaystyle \lambda }$
Skewness	${\displaystyle \lambda ^{-1/2}}$
Ex. kurtosis	${\displaystyle \lambda ^{-1}}$
Entropy	${\displaystyle \lambda [1-\log(\lambda )]+e^{-\lambda }\sum _{k=0}^{\infty }{\frac {\lambda ^{k}\log(k!)}{k!}}}$ (for large ${\displaystyle \lambda }$) ${\displaystyle {\begin{aligned}{\frac {1}{2}}\log(2\pi e\lambda )-{\frac {1}{12\lambda }}-{\frac {1}{24\lambda ^{2}}}\\-{\frac {19}{360\lambda ^{3}}}+O\left({\frac {1}{\lambda ^{4}}}\right)\end{aligned}}}$
MGF	${\displaystyle \exp[\lambda (e^{t}-1)]}$
CF	${\displaystyle \exp[\lambda (e^{it}-1)]}$
PGF	${\displaystyle \exp[\lambda (z-1)]}$
Fisher information	${\displaystyle {\frac {1}{\lambda }}}$

In probability theory and statistics, the Poisson distribution is a discrete probability distribution that expresses the probability of a given number of events occurring in a fixed interval of time or space if these events occur with a known constant mean rate and independently of the time since the last event. It is named after French mathematician Siméon Denis Poisson (/ˈpwɑːsɒn/; French pronunciation: ​[pwasɔ̃]). The Poisson distribution can also be used for the number of events in other specified interval types such as distance, area or volume.

For instance, a call center receives an average of 180 calls per hour, 24 hours a day. The calls are independent; receiving one does not change the probability of when the next one will arrive. The number of calls received during any minute has a Poisson probability distribution: the most likely numbers are 2 and 3 but 1 and 4 are also likely and there is a small probability of it being as low as zero and a very small probability it could be 10. Another example is the number of decay events that occur from a radioactive source during a defined observation period.

History

The distribution was first introduced by Siméon Denis Poisson (1781–1840) and published together with his probability theory in his work Recherches sur la probabilité des jugements en matière criminelle et en matière civile (1837). The work theorized about the number of wrongful convictions in a given country by focusing on certain random variables N that count, among other things, the number of discrete occurrences (sometimes called "events" or "arrivals") that take place during a time-interval of given length. The result had already been given in 1711 by Abraham de Moivre in De Mensura Sortis seu; de Probabilitate Eventuum in Ludis a Casu Fortuito Pendentibus. This makes it an example of Stigler's law and it has prompted some authors to argue that the Poisson distribution should bear the name of de Moivre.

In 1860, Simon Newcomb fitted the Poisson distribution to the number of stars found in a unit of space. A further practical application of this distribution was made by Ladislaus Bortkiewicz in 1898 when he was given the task of investigating the number of soldiers in the Prussian army killed accidentally by horse kicks; this experiment introduced the Poisson distribution to the field of reliability engineering.

Definitions

Probability mass function

A discrete random variable X is said to have a Poisson distribution, with parameter ${\displaystyle \lambda >0}$, if it has a probability mass function given by:

${\displaystyle \!f(k;\lambda )=\Pr(X{=}k)={\frac {\lambda ^{k}e^{-\lambda }}{k!}},}$

where

• k is the number of occurrences (${\displaystyle k=0,1,2\dots }$)
• e is Euler's number (${\displaystyle e=2.71828...}$)
• ! is the factorial function.

The positive real number λ is equal to the expected value of X and also to its variance.

${\displaystyle \lambda =\operatorname {E} (X)=\operatorname {Var} (X).}$

The Poisson distribution can be applied to systems with a large number of possible events, each of which is rare. The number of such events that occur during a fixed time interval is, under the right circumstances, a random number with a Poisson distribution.

The equation can be adapted if, instead of the average number of events ${\displaystyle \lambda }$, we are given the average rate ${\displaystyle r}$ at which events occur. Then ${\displaystyle \lambda =rt}$, and

${\displaystyle P(k{\text{ events in interval }}t)={\frac {(rt)^{k}e^{-rt}}{k!}}.}$

Example

Chewing gum on a sidewalk. The number of chewing gums on a single tile is approximately Poisson distributed.

The Poisson distribution may be useful to model events such as:

• the number of meteorites greater than 1 meter diameter that strike Earth in a year;
• the number of patients arriving in an emergency room between 10 and 11 pm; and
• the number of laser photons hitting a detector in a particular time interval.

Assumptions and validity

The Poisson distribution is an appropriate model if the following assumptions are true:

• k is the number of times an event occurs in an interval and k can take values 0, 1, 2, ….
• The occurrence of one event does not affect the probability that a second event will occur. That is, events occur independently.
• The average rate at which events occur is independent of any occurrences. For simplicity, this is usually assumed to be constant, but may in practice vary with time.
• Two events cannot occur at exactly the same instant; instead, at each very small sub-interval, either exactly one event occurs, or no event occurs.

If these conditions are true, then k is a Poisson random variable, and the distribution of k is a Poisson distribution.

The Poisson distribution is also the limit of a binomial distribution, for which the probability of success for each trial equals λ divided by the number of trials, as the number of trials approaches infinity (see Related distributions).

Examples of probability for Poisson distributions

Once in an interval events: The special case of λ = 1 and k = 0

Suppose that astronomers estimate that large meteorites (above a certain size) hit the earth on average once every 100 years (λ = 1 event per 100 years), and that the number of meteorite hits follows a Poisson distribution. What is the probability of k = 0 meteorite hits in the next 100 years?

${\displaystyle P(k={\text{0 meteorites hit in next 100 years}})={\frac {1^{0}e^{-1}}{0!}}={\frac {1}{e}}\approx 0.37}$

Under these assumptions, the probability that no large meteorites hit the earth in the next 100 years is roughly 0.37. The remaining 1 − 0.37 = 0.63 is the probability of 1, 2, 3, or more large meteorite hits in the next 100 years. In an example above, an overflow flood occurred once every 100 years (λ = 1). The probability of no overflow floods in 100 years was roughly 0.37, by the same calculation.

In general, if an event occurs on average once per interval (λ = 1), and the events follow a Poisson distribution, then P(0 events in next interval) = 0.37. In addition, P(exactly one event in next interval) = 0.37, as shown in the table for overflow floods.

Examples that violate the Poisson assumptions

The number of students who arrive at the student union per minute will likely not follow a Poisson distribution, because the rate is not constant (low rate during class time, high rate between class times) and the arrivals of individual students are not independent (students tend to come in groups).

The number of magnitude 5 earthquakes per year in a country may not follow a Poisson distribution if one large earthquake increases the probability of aftershocks of similar magnitude.

Examples in which at least one event is guaranteed are not Poisson distributed; but may be modeled using a zero-truncated Poisson distribution.

Count distributions in which the number of intervals with zero events is higher than predicted by a Poisson model may be modeled using a zero-inflated model.

Properties

Descriptive statistics

• The expected value and variance of a Poisson-distributed random variable are both equal to λ.
• The coefficient of variation is ${\textstyle \lambda ^{-1/2}}$, while the index of dispersion is 1.
• The mean absolute deviation about the mean is
  $${\displaystyle \operatorname {E} [|X-\lambda |]={\frac {2\lambda ^{\lfloor \lambda \rfloor +1}e^{-\lambda }}{\lfloor \lambda \rfloor !}}.}$$

  
• The mode of a Poisson-distributed random variable with non-integer λ is equal to ${\displaystyle \lfloor \lambda \rfloor }$, which is the largest integer less than or equal to λ. This is also written as floor(λ). When λ is a positive integer, the modes are λ and λ − 1.
• All of the cumulants of the Poisson distribution are equal to the expected value λ. The nth factorial moment of the Poisson distribution is λⁿ.
• The expected value of a Poisson process is sometimes decomposed into the product of intensity and exposure (or more generally expressed as the integral of an "intensity function" over time or space, sometimes described as “exposure”).

Median

Bounds for the median (${\displaystyle \nu }$) of the distribution are known and are sharp:

$${\displaystyle \lambda -\ln 2\leq \nu <\lambda +{\frac {1}{3}}.}$$

Higher moments

The higher non-centered moments, m_k of the Poisson distribution, are Touchard polynomials in λ:

$${\displaystyle m_{k}=\sum _{i=0}^{k}\lambda ^{i}{\begin{Bmatrix}k\\i\end{Bmatrix}},}$$

where the {braces} denote Stirling numbers of the second kind. The coefficients of the polynomials have a combinatorial meaning. In fact, when the expected value of the Poisson distribution is 1, then Dobinski's formula says that the nth moment equals the number of partitions of a set of size n.

A simple bound is

$${\displaystyle m_{k}=E[X^{k}]\leq \left({\frac {k}{\log(k/\lambda +1)}}\right)^{k}\leq \lambda ^{k}\exp \left({\frac {k^{2}}{2\lambda }}\right).}$$

Sums of Poisson-distributed random variables

If ${\displaystyle X_{i}\sim \operatorname {Pois} (\lambda _{i})}$ for ${\displaystyle i=1,\dotsc ,n}$ are independent, then ${\textstyle \sum _{i=1}^{n}X_{i}\sim \operatorname {Pois} \left(\sum _{i=1}^{n}\lambda _{i}\right).}$ A converse is Raikov's theorem, which says that if the sum of two independent random variables is Poisson-distributed, then so are each of those two independent random variables.

Other properties

• The Poisson distributions are infinitely divisible probability distributions.
• The directed Kullback–Leibler divergence of ${\displaystyle \operatorname {Pois} (\lambda _{0})}$ from ${\displaystyle \operatorname {Pois} (\lambda )}$ is given by
  $${\displaystyle \operatorname {D} _{\text{KL}}(\lambda \mid \lambda _{0})=\lambda _{0}-\lambda +\lambda \log {\frac {\lambda }{\lambda _{0}}}.}$$

  
• Bounds for the tail probabilities of a Poisson random variable ${\displaystyle X\sim \operatorname {Pois} (\lambda )}$ can be derived using a Chernoff bound argument.
  $${\displaystyle P(X\geq x)\leq {\frac {(e\lambda )^{x}e^{-\lambda }}{x^{x}}},{\text{ for }}x>\lambda ,}$$

  
  $${\displaystyle P(X\leq x)\leq {\frac {(e\lambda )^{x}e^{-\lambda }}{x^{x}}},{\text{ for }}x<\lambda .}$$

  
• The upper tail probability can be tightened (by a factor of at least two) as follows:
  $${\displaystyle P(X\geq x)\leq {\frac {e^{-\operatorname {D} _{\text{KL}}(x\mid \lambda )}}{\max {(2,{\sqrt {4\pi \operatorname {D} _{\text{KL}}(x\mid \lambda )}}})}},{\text{ for }}x>\lambda ,}$$

  
  where ${\displaystyle \operatorname {D} _{\text{KL}}(x\mid \lambda )}$ is the directed Kullback–Leibler divergence, as described above.
• Inequalities that relate the distribution function of a Poisson random variable ${\displaystyle X\sim \operatorname {Pois} (\lambda )}$ to the Standard normal distribution function ${\displaystyle \Phi (x)}$ are as follows:
  $${\displaystyle \Phi \left(\operatorname {sign} (k-\lambda ){\sqrt {2\operatorname {D} _{\text{KL}}(k\mid \lambda )}}\right)<P(X\leq k)<\Phi \left(\operatorname {sign} (k-\lambda +1){\sqrt {2\operatorname {D} _{\text{KL}}(k+1\mid \lambda )}}\right),{\text{ for }}k>0,}$$

  
  where ${\displaystyle \operatorname {D} _{\text{KL}}(k\mid \lambda )}$ is again the directed Kullback–Leibler divergence.

Poisson races

Let ${\displaystyle X\sim \operatorname {Pois} (\lambda )}$ and ${\displaystyle Y\sim \operatorname {Pois} (\mu )}$ be independent random variables, with ${\displaystyle \lambda <\mu }$, then we have that

$${\displaystyle {\frac {e^{-({\sqrt {\mu }}-{\sqrt {\lambda }})^{2}}}{(\lambda +\mu )^{2}}}-{\frac {e^{-(\lambda +\mu )}}{2{\sqrt {\lambda \mu }}}}-{\frac {e^{-(\lambda +\mu )}}{4\lambda \mu }}\leq P(X-Y\geq 0)\leq e^{-({\sqrt {\mu }}-{\sqrt {\lambda }})^{2}}}$$

The upper bound is proved using a standard Chernoff bound.

The lower bound can be proved by noting that ${\displaystyle P(X-Y\geq 0\mid X+Y=i)}$ is the probability that ${\textstyle Z\geq {\frac {i}{2}}}$, where ${\textstyle Z\sim \operatorname {Bin} \left(i,{\frac {\lambda }{\lambda +\mu }}\right)}$, which is bounded below by ${\textstyle {\frac {1}{(i+1)^{2}}}e^{-iD\left(0.5\|{\frac {\lambda }{\lambda +\mu }}\right)}}$, where ${\displaystyle D}$ is relative entropy (See the entry on bounds on tails of binomial distributions for details). Further noting that ${\displaystyle X+Y\sim \operatorname {Pois} (\lambda +\mu )}$, and computing a lower bound on the unconditional probability gives the result. More details can be found in the appendix of Kamath et al..

Related distributions

General

• If ${\displaystyle X_{1}\sim \mathrm {Pois} (\lambda _{1})\,}$ and ${\displaystyle X_{2}\sim \mathrm {Pois} (\lambda _{2})\,}$ are independent, then the difference ${\displaystyle Y=X_{1}-X_{2}}$ follows a Skellam distribution.
• If ${\displaystyle X_{1}\sim \mathrm {Pois} (\lambda _{1})\,}$ and ${\displaystyle X_{2}\sim \mathrm {Pois} (\lambda _{2})\,}$ are independent, then the distribution of ${\displaystyle X_{1}}$ conditional on ${\displaystyle X_{1}+X_{2}}$ is a binomial distribution.
  Specifically, if ${\displaystyle X_{1}+X_{2}=k}$, then ${\displaystyle \!X_{1}|X_{1}+X_{2}=k\sim \mathrm {Binom} (k,\lambda _{1}/(\lambda _{1}+\lambda _{2}))}$.
  More generally, if X₁, X₂, …, X_n are independent Poisson random variables with parameters λ₁, λ₂, …, λ_n then

  given ${\displaystyle \sum _{j=1}^{n}X_{j}=k,}$ it follows that ${\displaystyle X_{i}{\Big |}\sum _{j=1}^{n}X_{j}=k\sim \mathrm {Binom} \left(k,{\frac {\lambda _{i}}{\sum _{j=1}^{n}\lambda _{j}}}\right)}$. In fact, ${\displaystyle \{X_{i}\}\sim \mathrm {Multinom} \left(k,\left\{{\frac {\lambda _{i}}{\sum _{j=1}^{n}\lambda _{j}}}\right\}\right)}$.

• If ${\displaystyle X\sim \mathrm {Pois} (\lambda )\,}$ and the distribution of ${\displaystyle Y}$, conditional on X = k, is a binomial distribution, ${\displaystyle Y\mid (X=k)\sim \mathrm {Binom} (k,p)}$, then the distribution of Y follows a Poisson distribution ${\displaystyle Y\sim \mathrm {Pois} (\lambda \cdot p)\,}$. In fact, if ${\displaystyle \{Y_{i}\}}$, conditional on X = k, follows a multinomial distribution, ${\displaystyle \{Y_{i}\}\mid (X=k)\sim \mathrm {Multinom} \left(k,p_{i}\right)}$, then each ${\displaystyle Y_{i}}$ follows an independent Poisson distribution ${\displaystyle Y_{i}\sim \mathrm {Pois} (\lambda \cdot p_{i}),\rho (Y_{i},Y_{j})=0}$.
• The Poisson distribution can be derived as a limiting case to the binomial distribution as the number of trials goes to infinity and the expected number of successes remains fixed — see law of rare events below. Therefore, it can be used as an approximation of the binomial distribution if n is sufficiently large and p is sufficiently small. There is a rule of thumb stating that the Poisson distribution is a good approximation of the binomial distribution if n is at least 20 and p is smaller than or equal to 0.05, and an excellent approximation if n ≥ 100 and np ≤ 10.
  $${\displaystyle F_{\mathrm {Binomial} }(k;n,p)\approx F_{\mathrm {Poisson} }(k;\lambda =np)}$$

  
• The Poisson distribution is a special case of the discrete compound Poisson distribution (or stuttering Poisson distribution) with only a parameter. The discrete compound Poisson distribution can be deduced from the limiting distribution of univariate multinomial distribution. It is also a special case of a compound Poisson distribution.
• For sufficiently large values of λ, (say λ>1000), the normal distribution with mean λ and variance λ (standard deviation ${\displaystyle {\sqrt {\lambda }}}$) is an excellent approximation to the Poisson distribution. If λ is greater than about 10, then the normal distribution is a good approximation if an appropriate continuity correction is performed, i.e., if P(X ≤ x), where x is a non-negative integer, is replaced by P(X ≤ x + 0.5).
  $${\displaystyle F_{\mathrm {Poisson} }(x;\lambda )\approx F_{\mathrm {normal} }(x;\mu =\lambda ,\sigma ^{2}=\lambda )}$$

  
• Variance-stabilizing transformation: If ${\displaystyle X\sim \mathrm {Pois} (\lambda )\,}$, then
  $${\displaystyle Y=2{\sqrt {X}}\approx {\mathcal {N}}(2{\sqrt {\lambda }};1),}$$

  
  and
  $${\displaystyle Y={\sqrt {X}}\approx {\mathcal {N}}({\sqrt {\lambda }};1/4).}$$

  
  Under this transformation, the convergence to normality (as ${\displaystyle \lambda }$ increases) is far faster than the untransformed variable. Other, slightly more complicated, variance stabilizing transformations are available, one of which is Anscombe transform. See Data transformation (statistics) for more general uses of transformations.
• If for every t > 0 the number of arrivals in the time interval [0, t] follows the Poisson distribution with mean λt, then the sequence of inter-arrival times are independent and identically distributed exponential random variables having mean 1/λ.
• The cumulative distribution functions of the Poisson and chi-squared distributions are related in the following ways:
  $${\displaystyle F_{\text{Poisson}}(k;\lambda )=1-F_{\chi ^{2}}(2\lambda ;2(k+1))\quad \quad {\text{ integer }}k,}$$

  
  and
  $${\displaystyle \Pr(X=k)=F_{\chi ^{2}}(2\lambda ;2(k+1))-F_{\chi ^{2}}(2\lambda ;2k).}$$

  

Poisson approximation

Assume ${\displaystyle X_{1}\sim \operatorname {Pois} (\lambda _{1}),X_{2}\sim \operatorname {Pois} (\lambda _{2}),\dots ,X_{n}\sim \operatorname {Pois} (\lambda _{n})}$ where ${\displaystyle \lambda _{1}+\lambda _{2}+\dots +\lambda _{n}=1}$, then ${\displaystyle (X_{1},X_{2},\dots ,X_{n})}$ is multinomially distributed ${\displaystyle (X_{1},X_{2},\dots ,X_{n})\sim \operatorname {Mult} (N,\lambda _{1},\lambda _{2},\dots ,\lambda _{n})}$ conditioned on ${\displaystyle N=X_{1}+X_{2}+\dots X_{n}}$.

This means, among other things, that for any nonnegative function ${\displaystyle f(x_{1},x_{2},\dots ,x_{n})}$, if ${\displaystyle (Y_{1},Y_{2},\dots ,Y_{n})\sim \operatorname {Mult} (m,\mathbf {p} )}$ is multinomially distributed, then

$${\displaystyle \operatorname {E} [f(Y_{1},Y_{2},\dots ,Y_{n})]\leq e{\sqrt {m}}\operatorname {E} [f(X_{1},X_{2},\dots ,X_{n})]}$$

where ${\displaystyle (X_{1},X_{2},\dots ,X_{n})\sim \operatorname {Pois} (\mathbf {p} )}$.

The factor of ${\displaystyle e{\sqrt {m}}}$ can be replaced by 2 if ${\displaystyle f}$ is further assumed to be monotonically increasing or decreasing.

Bivariate Poisson distribution

This distribution has been extended to the bivariate case. The generating function for this distribution is

$${\displaystyle g(u,v)=\exp[(\theta _{1}-\theta _{12})(u-1)+(\theta _{2}-\theta _{12})(v-1)+\theta _{12}(uv-1)]}$$

with

$${\displaystyle \theta _{1},\theta _{2}>\theta _{12}>0}$$

The marginal distributions are Poisson(θ₁) and Poisson(θ₂) and the correlation coefficient is limited to the range

$${\displaystyle 0\leq \rho \leq \min \left\{{\sqrt {\frac {\theta _{1}}{\theta _{2}}}},{\sqrt {\frac {\theta _{2}}{\theta _{1}}}}\right\}}$$

A simple way to generate a bivariate Poisson distribution ${\displaystyle X_{1},X_{2}}$ is to take three independent Poisson distributions ${\displaystyle Y_{1},Y_{2},Y_{3}}$ with means ${\displaystyle \lambda _{1},\lambda _{2},\lambda _{3}}$ and then set ${\displaystyle X_{1}=Y_{1}+Y_{3},X_{2}=Y_{2}+Y_{3}}$. The probability function of the bivariate Poisson distribution is

$${\displaystyle \Pr(X_{1}=k_{1},X_{2}=k_{2})=\exp \left(-\lambda _{1}-\lambda _{2}-\lambda _{3}\right){\frac {\lambda _{1}^{k_{1}}}{k_{1}!}}{\frac {\lambda _{2}^{k_{2}}}{k_{2}!}}\sum _{k=0}^{\min(k_{1},k_{2})}{\binom {k_{1}}{k}}{\binom {k_{2}}{k}}k!\left({\frac {\lambda _{3}}{\lambda _{1}\lambda _{2}}}\right)^{k}}$$

Free Poisson distribution

The free Poisson distribution with jump size ${\displaystyle \alpha }$ and rate ${\displaystyle \lambda }$ arises in free probability theory as the limit of repeated free convolution

$${\displaystyle \left(\left(1-{\frac {\lambda }{N}}\right)\delta _{0}+{\frac {\lambda }{N}}\delta _{\alpha }\right)^{\boxplus N}}$$

as N → ∞.

In other words, let ${\displaystyle X_{N}}$ be random variables so that ${\displaystyle X_{N}}$ has value ${\displaystyle \alpha }$ with probability ${\textstyle {\frac {\lambda }{N}}}$ and value 0 with the remaining probability. Assume also that the family ${\displaystyle X_{1},X_{2},\ldots }$ are freely independent. Then the limit as ${\displaystyle N\to \infty }$ of the law of ${\displaystyle X_{1}+\cdots +X_{N}}$ is given by the Free Poisson law with parameters ${\displaystyle \lambda ,\alpha }$.

This definition is analogous to one of the ways in which the classical Poisson distribution is obtained from a (classical) Poisson process.

The measure associated to the free Poisson law is given by

$${\displaystyle \mu ={\begin{cases}(1-\lambda )\delta _{0}+\lambda \nu ,&{\text{if }}0\leq \lambda \leq 1\\\nu ,&{\text{if }}\lambda >1,\end{cases}}}$$

where

$${\displaystyle \nu ={\frac {1}{2\pi \alpha t}}{\sqrt {4\lambda \alpha ^{2}-(t-\alpha (1+\lambda ))^{2}}}\,dt}$$

and has support ${\displaystyle [\alpha (1-{\sqrt {\lambda }})^{2},\alpha (1+{\sqrt {\lambda }})^{2}]}$.

This law also arises in random matrix theory as the Marchenko–Pastur law. Its free cumulants are equal to ${\displaystyle \kappa _{n}=\lambda \alpha ^{n}}$.

Some transforms of this law

We give values of some important transforms of the free Poisson law; the computation can be found in e.g. in the book Lectures on the Combinatorics of Free Probability by A. Nica and R. Speicher.

The R-transform of the free Poisson law is given by

$${\displaystyle R(z)={\frac {\lambda \alpha }{1-\alpha z}}.}$$

The Cauchy transform (which is the negative of the Stieltjes transformation) is given by

$${\displaystyle G(z)={\frac {z+\alpha -\lambda \alpha -{\sqrt {(z-\alpha (1+\lambda ))^{2}-4\lambda \alpha ^{2}}}}{2\alpha z}}}$$

The S-transform is given by

$${\displaystyle S(z)={\frac {1}{z+\lambda }}}$$

in the case that ${\displaystyle \alpha =1}$.

Weibull and Stable count

Poisson's probability mass function ${\displaystyle f(k;\lambda )}$ can be expressed in a form similar to the product distribution of a Weibull distribution and a variant form of the stable count distribution. The variable ${\displaystyle (k+1)}$ can be regarded as inverse of Lévy's stability parameter in the stable count distribution:

$${\displaystyle f(k;\lambda )=\displaystyle \int _{0}^{\infty }{\frac {1}{u}}\,W_{k+1}({\frac {\lambda }{u}})\left[\left(k+1\right)u^{k}\,{\mathfrak {N}}_{\frac {1}{k+1}}\left(u^{k+1}\right)\right]\,du,}$$

where ${\displaystyle {\mathfrak {N}}_{\alpha }(\nu )}$ is a standard stable count distribution of shape ${\displaystyle \alpha =1/\left(k+1\right)}$, and ${\displaystyle W_{k+1}(x)}$ is a standard Weibull distribution of shape ${\displaystyle k+1}$.

Statistical inference

See also: Poisson regression

Parameter estimation

Given a sample of n measured values ${\displaystyle k_{i}\in \{0,1,\dots \}}$, for i = 1, …, n, we wish to estimate the value of the parameter λ of the Poisson population from which the sample was drawn. The maximum likelihood estimate is 

${\displaystyle {\widehat {\lambda }}_{\mathrm {MLE} }={\frac {1}{n}}\sum _{i=1}^{n}k_{i}.}$

Since each observation has expectation λ so does the sample mean. Therefore, the maximum likelihood estimate is an unbiased estimator of λ. It is also an efficient estimator since its variance achieves the Cramér–Rao lower bound (CRLB). Hence it is minimum-variance unbiased. Also it can be proven that the sum (and hence the sample mean as it is a one-to-one function of the sum) is a complete and sufficient statistic for λ.

To prove sufficiency we may use the factorization theorem. Consider partitioning the probability mass function of the joint Poisson distribution for the sample into two parts: one that depends solely on the sample ${\displaystyle \mathbf {x} }$ (called ${\displaystyle h(\mathbf {x} )}$) and one that depends on the parameter ${\displaystyle \lambda }$ and the sample ${\displaystyle \mathbf {x} }$ only through the function ${\displaystyle T(\mathbf {x} )}$. Then ${\displaystyle T(\mathbf {x} )}$ is a sufficient statistic for ${\displaystyle \lambda }$.

${\displaystyle P(\mathbf {x} )=\prod _{i=1}^{n}{\frac {\lambda ^{x_{i}}e^{-\lambda }}{x_{i}!}}={\frac {1}{\prod _{i=1}^{n}x_{i}!}}\times \lambda ^{\sum _{i=1}^{n}x_{i}}e^{-n\lambda }}$

The first term, ${\displaystyle h(\mathbf {x} )}$, depends only on ${\displaystyle \mathbf {x} }$. The second term, ${\displaystyle g(T(\mathbf {x} )|\lambda )}$, depends on the sample only through ${\textstyle T(\mathbf {x} )=\sum _{i=1}^{n}x_{i}}$. Thus, ${\displaystyle T(\mathbf {x} )}$ is sufficient.

To find the parameter λ that maximizes the probability function for the Poisson population, we can use the logarithm of the likelihood function:

${\displaystyle {\begin{aligned}\ell (\lambda )&=\ln \prod _{i=1}^{n}f(k_{i}\mid \lambda )\\&=\sum _{i=1}^{n}\ln \!\left({\frac {e^{-\lambda }\lambda ^{k_{i}}}{k_{i}!}}\right)\\&=-n\lambda +\left(\sum _{i=1}^{n}k_{i}\right)\ln(\lambda )-\sum _{i=1}^{n}\ln(k_{i}!).\end{aligned}}}$

We take the derivative of ${\displaystyle \ell }$ with respect to λ and compare it to zero:

${\displaystyle {\frac {\mathrm {d} }{\mathrm {d} \lambda }}\ell (\lambda )=0\iff -n+\left(\sum _{i=1}^{n}k_{i}\right){\frac {1}{\lambda }}=0.\!}$

Solving for λ gives a stationary point.

${\displaystyle \lambda ={\frac {\sum _{i=1}^{n}k_{i}}{n}}}$

So λ is the average of the k_i values. Obtaining the sign of the second derivative of L at the stationary point will determine what kind of extreme value λ is.

${\displaystyle {\frac {\partial ^{2}\ell }{\partial \lambda ^{2}}}=-\lambda ^{-2}\sum _{i=1}^{n}k_{i}}$

Evaluating the second derivative at the stationary point gives:

${\displaystyle {\frac {\partial ^{2}\ell }{\partial \lambda ^{2}}}=-{\frac {n^{2}}{\sum _{i=1}^{n}k_{i}}}}$

which is the negative of n times the reciprocal of the average of the k_i. This expression is negative when the average is positive. If this is satisfied, then the stationary point maximizes the probability function.

For completeness, a family of distributions is said to be complete if and only if ${\displaystyle E(g(T))=0}$ implies that ${\displaystyle P_{\lambda }(g(T)=0)=1}$ for all ${\displaystyle \lambda }$. If the individual ${\displaystyle X_{i}}$ are iid ${\displaystyle \mathrm {Po} (\lambda )}$, then ${\textstyle T(\mathbf {x} )=\sum _{i=1}^{n}X_{i}\sim \mathrm {Po} (n\lambda )}$. Knowing the distribution we want to investigate, it is easy to see that the statistic is complete.

${\displaystyle E(g(T))=\sum _{t=0}^{\infty }g(t){\frac {(n\lambda )^{t}e^{-n\lambda }}{t!}}=0}$

For this equality to hold, ${\displaystyle g(t)}$ must be 0. This follows from the fact that none of the other terms will be 0 for all ${\displaystyle t}$ in the sum and for all possible values of ${\displaystyle \lambda }$. Hence, ${\displaystyle E(g(T))=0}$ for all ${\displaystyle \lambda }$ implies that ${\displaystyle P_{\lambda }(g(T)=0)=1}$, and the statistic has been shown to be complete.

Confidence interval

The confidence interval for the mean of a Poisson distribution can be expressed using the relationship between the cumulative distribution functions of the Poisson and chi-squared distributions. The chi-squared distribution is itself closely related to the gamma distribution, and this leads to an alternative expression. Given an observation k from a Poisson distribution with mean μ, a confidence interval for μ with confidence level 1 – α is

${\displaystyle {\tfrac {1}{2}}\chi ^{2}(\alpha /2;2k)\leq \mu \leq {\tfrac {1}{2}}\chi ^{2}(1-\alpha /2;2k+2),}$

or equivalently,

${\displaystyle F^{-1}(\alpha /2;k,1)\leq \mu \leq F^{-1}(1-\alpha /2;k+1,1),}$

where ${\displaystyle \chi ^{2}(p;n)}$ is the quantile function (corresponding to a lower tail area p) of the chi-squared distribution with n degrees of freedom and ${\displaystyle F^{-1}(p;n,1)}$ is the quantile function of a gamma distribution with shape parameter n and scale parameter 1. This interval is 'exact' in the sense that its coverage probability is never less than the nominal 1 – α.

When quantiles of the gamma distribution are not available, an accurate approximation to this exact interval has been proposed (based on the Wilson–Hilferty transformation):

${\displaystyle k\left(1-{\frac {1}{9k}}-{\frac {z_{\alpha /2}}{3{\sqrt {k}}}}\right)^{3}\leq \mu \leq (k+1)\left(1-{\frac {1}{9(k+1)}}+{\frac {z_{\alpha /2}}{3{\sqrt {k+1}}}}\right)^{3},}$

where ${\displaystyle z_{\alpha /2}}$ denotes the standard normal deviate with upper tail area α / 2.

For application of these formulae in the same context as above (given a sample of n measured values k_i each drawn from a Poisson distribution with mean λ), one would set

${\displaystyle k=\sum _{i=1}^{n}k_{i},}$

calculate an interval for μ = nλ, and then derive the interval for λ.

Bayesian inference

In Bayesian inference, the conjugate prior for the rate parameter λ of the Poisson distribution is the gamma distribution. Let

${\displaystyle \lambda \sim \mathrm {Gamma} (\alpha ,\beta )}$

denote that λ is distributed according to the gamma density g parameterized in terms of a shape parameter α and an inverse scale parameter β:

${\displaystyle g(\lambda \mid \alpha ,\beta )={\frac {\beta ^{\alpha }}{\Gamma (\alpha )}}\;\lambda ^{\alpha -1}\;e^{-\beta \,\lambda }\qquad {\text{ for }}\lambda >0\,\!.}$

Then, given the same sample of n measured values k_i as before, and a prior of Gamma(α, β), the posterior distribution is

${\displaystyle \lambda \sim \mathrm {Gamma} \left(\alpha +\sum _{i=1}^{n}k_{i},\beta +n\right).\!}$

Note that the posterior mean is linear and is given by

${\displaystyle E[\lambda |k_{1},...k_{n}]={\frac {\alpha +\sum _{i=1}^{n}k_{i}}{\beta +n}}.\!}$

It can be show that gamma distribution is the only prior that induces linearity of the conditional mean. Moreover, a converse results exists which states that if the conditional mean is close to a linear function in the ${\displaystyle L_{2}}$ distance than the prior distribution of λ must be close to gamma distribution in Levy distance.

The posterior mean E[λ] approaches the maximum likelihood estimate ${\displaystyle {\widehat {\lambda }}_{\mathrm {MLE} }}$ in the limit as ${\displaystyle \alpha \to 0,\ \beta \to 0}$, which follows immediately from the general expression of the mean of the gamma distribution.

The posterior predictive distribution for a single additional observation is a negative binomial distribution, sometimes called a gamma–Poisson distribution.

Simultaneous estimation of multiple Poisson means

Suppose ${\displaystyle X_{1},X_{2},\dots ,X_{p}}$ is a set of independent random variables from a set of ${\displaystyle p}$ Poisson distributions, each with a parameter ${\displaystyle \lambda _{i}}$, ${\displaystyle i=1,\dots ,p}$, and we would like to estimate these parameters. Then, Clevenson and Zidek show that under the normalized squared error loss ${\textstyle L(\lambda ,{\hat {\lambda }})=\sum _{i=1}^{p}\lambda _{i}^{-1}({\hat {\lambda }}_{i}-\lambda _{i})^{2}}$, when ${\displaystyle p>1}$, then, similar as in Stein's example for the Normal means, the MLE estimator ${\displaystyle {\hat {\lambda }}_{i}=X_{i}}$ is inadmissible. 

In this case, a family of minimax estimators is given for any ${\displaystyle 0<c\leq 2(p-1)}$ and ${\displaystyle b\geq (p-2+p^{-1})}$ as

${\displaystyle {\hat {\lambda }}_{i}=\left(1-{\frac {c}{b+\sum _{i=1}^{p}X_{i}}}\right)X_{i},\qquad i=1,\dots ,p.}$

Occurrence and applications

Applications of the Poisson distribution can be found in many fields including:

• count data in general
• Telecommunication example: telephone calls arriving in a system.
• Astronomy example: photons arriving at a telescope.
• Chemistry example: the molar mass distribution of a living polymerization.
• Biology example: the number of mutations on a strand of DNA per unit length.
• Management example: customers arriving at a counter or call centre.
• Finance and insurance example: number of losses or claims occurring in a given period of time.
• Earthquake seismology example: an asymptotic Poisson model of seismic risk for large earthquakes.
• Radioactivity example: number of decays in a given time interval in a radioactive sample.
• Optics example: the number of photons emitted in a single laser pulse. This is a major vulnerability to most Quantum key distribution protocols known as Photon Number Splitting (PNS).

The Poisson distribution arises in connection with Poisson processes. It applies to various phenomena of discrete properties (that is, those that may happen 0, 1, 2, 3, … times during a given period of time or in a given area) whenever the probability of the phenomenon happening is constant in time or space. Examples of events that may be modelled as a Poisson distribution include:

• The number of soldiers killed by horse-kicks each year in each corps in the Prussian cavalry. This example was used in a book by Ladislaus Bortkiewicz (1868–1931).
• The number of yeast cells used when brewing Guinness beer. This example was used by William Sealy Gosset (1876–1937).
• The number of phone calls arriving at a call centre within a minute. This example was described by A.K. Erlang (1878–1929).
• Internet traffic.
• The number of goals in sports involving two competing teams.
• The number of deaths per year in a given age group.
• The number of jumps in a stock price in a given time interval.
• Under an assumption of homogeneity, the number of times a web server is accessed per minute.
• The number of mutations in a given stretch of DNA after a certain amount of radiation.
• The proportion of cells that will be infected at a given multiplicity of infection.
• The number of bacteria in a certain amount of liquid.
• The arrival of photons on a pixel circuit at a given illumination and over a given time period.
• The targeting of V-1 flying bombs on London during World War II investigated by R. D. Clarke in 1946.

Gallagher showed in 1976 that the counts of prime numbers in short intervals obey a Poisson distribution provided a certain version of the unproved prime r-tuple conjecture of Hardy-Littlewood is true.

Law of rare events

Main article: Poisson limit theorem

 

Comparison of the Poisson distribution (black lines) and the binomial distribution with n = 10 (red circles), n = 20 (blue circles), n = 1000 (green circles). All distributions have a mean of 5. The horizontal axis shows the number of events k. As n gets larger, the Poisson distribution becomes an increasingly better approximation for the binomial distribution with the same mean.

The rate of an event is related to the probability of an event occurring in some small subinterval (of time, space or otherwise). In the case of the Poisson distribution, one assumes that there exists a small enough subinterval for which the probability of an event occurring twice is "negligible". With this assumption one can derive the Poisson distribution from the Binomial one, given only the information of expected number of total events in the whole interval.

Let the total number of events in the whole interval be denoted by ${\displaystyle \lambda }$. Divide the whole interval into ${\displaystyle n}$ subintervals ${\displaystyle I_{1},\dots ,I_{n}}$ of equal size, such that ${\displaystyle n>\lambda }$ (since we are interested in only very small portions of the interval this assumption is meaningful). This means that the expected number of events in each of the n subintervals is equal to ${\displaystyle \lambda /n}$.

Now we assume that the occurrence of an event in the whole interval can be seen as a sequence of n Bernoulli trials, where the ${\displaystyle i}$-th Bernoulli trial corresponds to looking whether an event happens at the subinterval ${\displaystyle I_{i}}$ with probability ${\displaystyle \lambda /n}$. The expected number of total events in ${\displaystyle n}$ such trials would be ${\displaystyle \lambda }$, the expected number of total events in the whole interval. Hence for each subdivision of the interval we have approximated the occurrence of the event as a Bernoulli process of the form ${\displaystyle {\textrm {B}}(n,\lambda /n)}$. As we have noted before we want to consider only very small subintervals. Therefore, we take the limit as ${\displaystyle n}$ goes to infinity.

In this case the binomial distribution converges to what is known as the Poisson distribution by the Poisson limit theorem.

In several of the above examples — such as, the number of mutations in a given sequence of DNA—the events being counted are actually the outcomes of discrete trials, and would more precisely be modelled using the binomial distribution, that is

$${\displaystyle X\sim {\textrm {B}}(n,p).}$$

In such cases n is very large and p is very small (and so the expectation np is of intermediate magnitude). Then the distribution may be approximated by the less cumbersome Poisson distribution

$${\displaystyle X\sim {\textrm {Pois}}(np).}$$

This approximation is sometimes known as the law of rare events, since each of the n individual Bernoulli events rarely occurs.

The name "law of rare events" may be misleading because the total count of success events in a Poisson process need not be rare if the parameter np is not small. For example, the number of telephone calls to a busy switchboard in one hour follows a Poisson distribution with the events appearing frequent to the operator, but they are rare from the point of view of the average member of the population who is very unlikely to make a call to that switchboard in that hour.

The variance of the binomial distribution is 1 − p times that of the Poisson distribution, so almost equal when p is very small.

The word law is sometimes used as a synonym of probability distribution, and convergence in law means convergence in distribution. Accordingly, the Poisson distribution is sometimes called the "law of small numbers" because it is the probability distribution of the number of occurrences of an event that happens rarely but has very many opportunities to happen. The Law of Small Numbers is a book by Ladislaus Bortkiewicz about the Poisson distribution, published in 1898.

Poisson point process

Main article: Poisson point process

The Poisson distribution arises as the number of points of a Poisson point process located in some finite region. More specifically, if D is some region space, for example Euclidean space R^d, for which |D|, the area, volume or, more generally, the Lebesgue measure of the region is finite, and if N(D) denotes the number of points in D, then

${\displaystyle P(N(D)=k)={\frac {(\lambda |D|)^{k}e^{-\lambda |D|}}{k!}}.}$

Poisson regression and negative binomial regression

Poisson regression and negative binomial regression are useful for analyses where the dependent (response) variable is the count (0, 1, 2, …) of the number of events or occurrences in an interval.

Other applications in science

In a Poisson process, the number of observed occurrences fluctuates about its mean λ with a standard deviation ${\displaystyle \sigma _{k}={\sqrt {\lambda }}}$. These fluctuations are denoted as Poisson noise or (particularly in electronics) as shot noise.

The correlation of the mean and standard deviation in counting independent discrete occurrences is useful scientifically. By monitoring how the fluctuations vary with the mean signal, one can estimate the contribution of a single occurrence, even if that contribution is too small to be detected directly. For example, the charge e on an electron can be estimated by correlating the magnitude of an electric current with its shot noise. If N electrons pass a point in a given time t on the average, the mean current is ${\displaystyle I=eN/t}$; since the current fluctuations should be of the order ${\displaystyle \sigma _{I}=e{\sqrt {N}}/t}$ (i.e., the standard deviation of the Poisson process), the charge ${\displaystyle e}$ can be estimated from the ratio ${\displaystyle t\sigma _{I}^{2}/I}$.

An everyday example is the graininess that appears as photographs are enlarged; the graininess is due to Poisson fluctuations in the number of reduced silver grains, not to the individual grains themselves. By correlating the graininess with the degree of enlargement, one can estimate the contribution of an individual grain (which is otherwise too small to be seen unaided). Many other molecular applications of Poisson noise have been developed, e.g., estimating the number density of receptor molecules in a cell membrane.

${\displaystyle \Pr(N_{t}=k)=f(k;\lambda t)={\frac {(\lambda t)^{k}e^{-\lambda t}}{k!}}.}$

In causal set theory the discrete elements of spacetime follow a Poisson distribution in the volume.

Computational methods

The Poisson distribution poses two different tasks for dedicated software libraries: Evaluating the distribution ${\displaystyle P(k;\lambda )}$, and drawing random numbers according to that distribution.

Evaluating the Poisson distribution

Computing ${\displaystyle P(k;\lambda )}$ for given ${\displaystyle k}$ and ${\displaystyle \lambda }$ is a trivial task that can be accomplished by using the standard definition of ${\displaystyle P(k;\lambda )}$ in terms of exponential, power, and factorial functions. However, the conventional definition of the Poisson distribution contains two terms that can easily overflow on computers: λ^k and k!. The fraction of λ^k to k! can also produce a rounding error that is very large compared to e^−λ, and therefore give an erroneous result. For numerical stability the Poisson probability mass function should therefore be evaluated as

${\displaystyle \!f(k;\lambda )=\exp \left[k\ln \lambda -\lambda -\ln \Gamma (k+1)\right],}$

which is mathematically equivalent but numerically stable. The natural logarithm of the Gamma function can be obtained using the lgamma function in the C standard library (C99 version) or R, the gammaln function in MATLAB or SciPy, or the log_gamma function in Fortran 2008 and later.

Some computing languages provide built-in functions to evaluate the Poisson distribution, namely

• R: function dpois(x, lambda);
• Excel: function POISSON( x, mean, cumulative), with a flag to specify the cumulative distribution;
• Mathematica: univariate Poisson distribution as PoissonDistribution[${\displaystyle \lambda }$], bivariate Poisson distribution as MultivariatePoissonDistribution[${\displaystyle \theta _{12}}$,{ ${\displaystyle \theta _{1}-\theta _{12}}$, ${\displaystyle \theta _{2}-\theta _{12}}$}].

Random drawing from the Poisson distribution

The less trivial task is to draw random integers from the Poisson distribution with given ${\displaystyle \lambda }$.

Solutions are provided by:

• R: function rpois(n, lambda);
• GNU Scientific Library (GSL): function gsl_ran_poisson

Generating Poisson-distributed random variables

A simple algorithm to generate random Poisson-distributed numbers (pseudo-random number sampling) has been given by Knuth:

algorithm poisson random number (Knuth):
    init:
        Let L ← e−λ, k ← 0 and p ← 1.
    do:
        k ← k + 1.
        Generate uniform random number u in [0,1] and let p ← p × u.
    while p > L.
    return k − 1.

The complexity is linear in the returned value k, which is λ on average. There are many other algorithms to improve this. Some are given in Ahrens & Dieter.

For large values of λ, the value of L = e^−λ may be so small that it is hard to represent. This can be solved by a change to the algorithm which uses an additional parameter STEP such that e^−STEP does not underflow:

algorithm poisson random number (Junhao, based on Knuth):
    init:
        Let λLeft ← λ, k ← 0 and p ← 1.
    do:
        k ← k + 1.
        Generate uniform random number u in (0,1) and let p ← p × u.
        while p < 1 and λLeft > 0:
            if λLeft > STEP:
                p ← p × eSTEP
                λLeft ← λLeft − STEP
            else:
                p ← p × eλLeft
                λLeft ← 0
    while p > 1.
    return k − 1.

The choice of STEP depends on the threshold of overflow. For double precision floating point format the threshold is near e⁷⁰⁰, so 500 should be a safe STEP.

Other solutions for large values of λ include rejection sampling and using Gaussian approximation.

Inverse transform sampling is simple and efficient for small values of λ, and requires only one uniform random number u per sample. Cumulative probabilities are examined in turn until one exceeds u.

algorithm Poisson generator based upon the inversion by sequential search:
    init:
        Let x ← 0, p ← e−λ, s ← p.
        Generate uniform random number u in [0,1].
    while u > s do:
        x ← x + 1.
        p ← p × λ / x.
        s ← s + p.
    return x.

Vegetable oil

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Vegetable_oil

 

Plant oils
Olive oil
Types
Vegetable oil (list) Macerated oil (list) Essential oil (list)
Uses
Drying oil Oil paint Cooking oil Fuel Biodiesel
Components
Saturated fat Monounsaturated fat Polyunsaturated fat Trans fat

Vegetable oils, or vegetable fats, are oils extracted from seeds or from other parts of fruits. Like animal fats, vegetable fats are mixtures of triglycerides. Soybean oil, grape seed oil, and cocoa butter are examples of seed oils, or fats from seeds. Olive oil, palm oil, and rice bran oil are examples of fats from other parts of fruits. In common usage, vegetable oil may refer exclusively to vegetable fats which are liquid at room temperature. Vegetable oils are usually edible.

Uses

In antiquity

Oils extracted from plants have been used since ancient times and in many cultures. Archaeological evidence shows that olives were turned into olive oil by 6000 BCE and 4500 BCE in present-day Israel and Palestine.

In addition to use as food, fats and oils (both vegetable and mineral) have long been used as fuel, typically in lamps which were a principal source of illumination in ancient times. Oils may have been used for lubrication, but there is no evidence for this. Vegetable oils were probably more valuable as food and lamp-oil; Babylonian mineral oil was known to be used as fuel, but there are no references to lubrication. Pliny the Elder reported that animal-derived fats such as lard were used to lubricate the axles of carts.

Culinary

See also: Cooking oil

Many vegetable oils are consumed directly, or indirectly as ingredients in food – a role that they share with some animal fats, including butter, ghee, lard, and schmaltz. The oils serve a number of purposes in this role:

• Shortening – as in giving pastries a crumbly texture.
• Enriching – adding calories and satisfaction in consumption
• Texture – altering how ingredients combine, especially fats and starches
• Flavoring – examples include olive, sesame, or almond oil
• Flavor base – oils can also "carry" flavors of other ingredients, such as peppers, since many flavors are due to chemicals that are soluble in oil.

Oils can be heated to temperatures significantly higher than the boiling point of water, 100 °C (212 °F), and used to fry foods. Oils for this purpose must have a high flash point. Such oils include both the major cooking oils – soybean, rapeseed, canola, sunflower, safflower, peanut, cottonseed, etc. – and tropical oils, such as coconut, palm, and rice bran. The latter are particularly valued in Asian cultures for high-temperature cooking, because of their unusually high flash points.

Hydrogenated oils

Unsaturated vegetable oils can be transformed through partial or complete "hydrogenation" into oils of higher melting point, some of which, such as vegetable shortening, will remain solid at room temperature.

The hydrogenation process involves "sparging" the oil at high temperature and pressure with hydrogen in the presence of a catalyst, typically a powdered nickel compound, such as Raney nickel. Chemically, hydrogenation is the reduction of a carbon-carbon double bond to a single bond, by addition of hydrogen atoms. Since the surface of the metal catalyst is covered with hydrogen atoms, when the double bonds of the unsaturated oil come into contact with the catalyst, it reacts with the hydrogen atoms, forming new bonds with the two carbon atoms; each carbon atom becomes single-bonded to an individual hydrogen atom, and the double bond between carbons can no longer exist. In organic chemistry, unsaturation is considered as a pair of hydrogen atoms missing from the (hypothetical) fully-saturated carbon chain. The level to which an organic molecule is deficient in hydrogen, is called the degree of unsaturation (DoU); as the degree of unsaturation decreases, the oil progresses toward being fully hydrogenated (when DoU = 0). A fully hydrogenated oil, also called a saturated fat, has had all of its double bonds converted into single bonds. If a polyunsaturated oil is left incompletely-hydrogenated (not all of the double bonds are reduced to single bonds), then it is a "partially hydrogenated oil" (PHO). PHOs are the primary dietary source of artificial trans fat in processed foods. An oil may be hydrogenated to increase resistance to rancidity (oxidation) or to change its physical characteristics. As the degree of saturation is raised by full or partial hydrogenation, the oil's viscosity and melting point increase.

The use of hydrogenated oils in foods has never been completely satisfactory. Because the center arm of the triglyceride is shielded somewhat by the end fatty acids, most of the hydrogenation occurs on the end fatty acids, thus making the resulting fat more brittle. A margarine made from naturally more saturated oils will be more plastic (more "spreadable") than a margarine made from hydrogenated soy oil. While full hydrogenation produces largely saturated fatty acids, partial hydrogenation results in the transformation of unsaturated cis fatty acids to unsaturated trans fatty acids in the oil mixture due to the heat used in hydrogenation. Partially hydrogenated oils and their trans fats have been linked to an increased risk of mortality from coronary heart disease, among other increased health risks.

In the US, the Standard of Identity for a product labeled as "vegetable oil margarine" specifies only canola, safflower, sunflower, corn, soybean, or peanut oil may be used. Products not labeled "vegetable oil margarine" do not have that restriction.

Industrial

Vegetable oils are used as an ingredient or component in many manufactured products.

Many vegetable oils are used to make soaps, skin products, candles, perfumes and other personal care and cosmetic products. Some oils are particularly suitable as drying oils, and are used in making paints and other wood treatment products. They are used in alkyd resin production. Dammar oil (a mixture of linseed oil and dammar resin), for example, is used almost exclusively in treating the hulls of wooden boats. Vegetable oils are increasingly being used in the electrical industry as insulators as vegetable oils are not toxic to the environment, biodegradable if spilled and have high flash and fire points. However, vegetable oils are less stable chemically, so they are generally used in systems where they are not exposed to oxygen, and they are more expensive than crude oil distillate. Synthetic tetraesters, which are similar to vegetable oils but with four fatty acid chains compared to the normal three found in a natural ester, are manufactured by Fischer esterification. Tetraesters generally have high stability to oxidation and have found use as engine lubricants. Vegetable oil is being used to produce biodegradable hydraulic fluid and lubricant.

One limiting factor in industrial uses of vegetable oils is that all such oils are susceptible to becoming rancid. Oils that are more stable, such as ben oil or mineral oil, are thus preferred for industrial uses. Castor oil has numerous industrial uses, owing to the presence of hydroxyl group on the fatty acid. Castor oil is a precursor to Nylon 11.Castor oil may also be reacted with epichlorohydrin to make a glycidyl ether which is used as a diluent and flexibilizer with epoxy resins.

Pet food additive

Vegetable oil is used in the production of some pet foods. AAFCO defines vegetable oil in this context as the product of vegetable origin obtained by extracting the oil from seeds or fruits which are processed for edible purposes.

Fuel

Main article: Vegetable oil fuel

Vegetable oils are also used to make biodiesel, which can be used like conventional diesel. Some vegetable oil blends are used in unmodified vehicles but straight vegetable oil, also known as pure plant oil, needs specially prepared vehicles which have a method of heating the oil to reduce its viscosity. The use of vegetable oils as alternative energy is growing and the availability of biodiesel around the world is increasing.

The NNFCC estimates that the total net greenhouse gas savings when using vegetable oils in place of fossil fuel-based alternatives for fuel production, range from 18 to 100%.

Production

The production process of vegetable oil involves the removal of oil from plant components, typically seeds. This can be done via mechanical extraction using an oil mill or chemical extraction using a solvent. The extracted oil can then be purified and, if required, refined or chemically altered.

Mechanical extraction

Oils can be removed via mechanical extraction, termed "crushing" or "pressing." This method is typically used to produce the more traditional oils (e.g., olive, coconut etc.), and it is preferred by most "health-food" customers in the United States and in Europe. There are several different types of mechanical extraction. Expeller-pressing extraction is common, though the screw press, ram press, and ghani (powered mortar and pestle) are also used. Oilseed presses are commonly used in developing countries, among people for whom other extraction methods would be prohibitively expensive; the ghani is primarily used in India. The amount of oil extracted using these methods varies widely, as shown in the following table for extracting mowrah butter in India:

Method	Percentage extracted
Ghani	20–30%
Expellers	34–37%
Solvent	40–43%

Solvent extraction

The processing of vegetable oil in commercial applications is commonly done by chemical extraction, using solvent extracts, which produces higher yields and is quicker and less expensive. The most common solvent is petroleum-derived hexane. This technique is used for most of the "newer" industrial oils such as soybean and corn oils. After extraction, the solvent is evaporated out by heating the mixture to about 300 °F (149 °C).

Supercritical carbon dioxide can be used as a non-toxic alternative to other solvents.

Hydrogenation

Oils may be partially hydrogenated to produce various ingredient oils. Lightly hydrogenated oils have very similar physical characteristics to regular soy oil, but are more resistant to becoming rancid. Margarine oils need to be mostly solid at 32 °C (90 °F) so that the margarine does not melt in warm rooms, yet it needs to be completely liquid at 37 °C (98 °F), so that it doesn't leave a "lardy" taste in the mouth.

Hardening vegetable oil is done by raising a blend of vegetable oil and a catalyst in near-vacuum to very high temperatures, and introducing hydrogen. This causes the carbon atoms of the oil to break double-bonds with other carbons, each carbon forming a new single-bond with a hydrogen atom. Adding these hydrogen atoms to the oil makes it more solid, raises the smoke point, and makes the oil more stable.

Hydrogenated vegetable oils differ in two major ways from other oils which are equally saturated. During hydrogenation, it is easier for hydrogen to come into contact with the fatty acids on the end of the triglyceride, and less easy for them to come into contact with the center fatty acid. This makes the resulting fat more brittle than a tropical oil; soy margarines are less "spreadable". The other difference is that trans fatty acids (often called trans fat) are formed in the hydrogenation reactor, and may amount to as much as 40 percent by weight of a partially hydrogenated oil. Hydrogenated oils, especially partially hydrogenated oils with their higher amounts of trans fatty acids, are increasingly thought to be unhealthy.

Deodorization

In the processing of edible oils, the oil is heated under vacuum to near the smoke point or to about 450 °F (232 °C), and water is introduced at the bottom of the oil. The water immediately is converted to steam, which bubbles through the oil, carrying with it any chemicals which are water-soluble. The steam sparging removes impurities that can impart unwanted flavors and odors to the oil. Deodorization is key to the manufacture of vegetable oils. Nearly all soybean, corn, and canola oils found on supermarket shelves go through a deodorization stage that removes trace amounts of odors and flavors, and lightens the color of the oil. However, the process commonly results in higher levels of trans fatty acids and distillation of the oil's natural compounds.

Occupational exposure

People can breathe in vegetable oil mist in the workplace. The U.S. Occupational Safety and Health Administration (OSHA) has set the legal limit (permissible exposure limit) for vegetable oil mist exposure in the workplace as 15 mg/m³ total exposure and 5 mg/m³ respiratory exposure over an 8-hour workday. The U.S. National Institute for Occupational Safety and Health (NIOSH) has set a recommended exposure limit (REL) of 10 mg/m³ total exposure and 5 mg/m³ respiratory exposure over an 8-hour workday.

Yield

Typical productivity of some oil crops, measured in tons (t) of oil produced per hectare (ha) of land per year (yr). Oil palm is by far the highest yielding crop, capable of producing about 4 tons of palm oil per hectare per year.

Crop	Yield (t/ha/yr)
Palm oil	4.0
Coconut oil	1.4
Canola oil	1.4
Soybean oil	0.6
Sunflower oil	0.6

Particular oils

For a more comprehensive list, see List of vegetable oils.

The following triglyceride vegetable oils account for almost all worldwide production, by volume. All are used as both cooking oils and as SVO or to make biodiesel. According to the USDA, the total world consumption of major vegetable oils in 2007/08 was:

Oil source	World consumption (million metric tons)	Notes
Palm	41.31	The most widely produced tropical oil, also used to make biofuel
Soybean	41.28	One of the most widely consumed cooking oils
Rapeseed	18.24	One of the most widely used cooking oils, also used as fuel. Canola is a variety (cultivar) of rapeseed.
Sunflower seed	9.91	A common cooking oil, also used to make biodiesel
Peanut	4.82	Mild-flavored cooking oil
Cottonseed	4.99	A major food oil, often used in industrial food processing
Palm kernel	4.85	From the seed of the African palm tree
Coconut	3.48	Used in cooking, cosmetics and soaps
Olive	2.84	Used in cooking, cosmetics, soaps and as a fuel for traditional oil lamps

Note that these figures include industrial and animal feed use. The majority of European rapeseed oil production is used to produce biodiesel, or used directly as fuel in diesel cars which may require modification to heat the oil to reduce its higher viscosity.

Other significant oils include:

• Corn oil, one of the most common cooking oils, is used for cooking oil, salad dressing, margarine, mayonnaise, prepared goods like spaghetti sauce and baking mixes, and to fry prepared foods like potato chips and French fries.
• Grape seed oil, used in cooking and cosmetics
• Hazelnut oil and other nut oils
• Linseed oil, from flax seeds
• Rice bran oil, from rice grains
• Safflower oil, a flavorless and colorless cooking oil
• Sesame oil, used as a cooking oil, and as a massage oil, particularly in India
• Açaí palm oil, used in culinary and cosmetics
• Jambú oil, is extracted from the flowers, leaves and stem from jambu (Acmella oleracea), contains spilanthol
• Graviola oil, derived from Annona muricata
• Tucumã oil, from Astrocaryum aculeatum is used to manufacture soap.
• Brazil nut oil, culinary and cosmetics use
• Carapa oil, pharmaceutical use and anti-mosquito candle
• Buriti oil, from Mauritia flexuosa, used in cosmetics (skin and hair care)
• Passion fruit oil, derived from Passiflora edulis, has varied applications in cosmetics manufacturing and for uses as a human or animal food.
• Pracaxi oil, obtained from Pentaclethra macroloba, cosmetics use
• Solarium oil, derived from chloroplasts, various applications in cooking

History

Such oils have been part of human culture for millennia. Oils such as poppy seed, rapeseed, linseed, almond oil, sesame seed, safflower, and cottonseed were variously used since at least the Bronze Age in the Middle East, Africa and Central Asia. Vegetable oils have been used for lighting fuel, cooking, medicine and lubrication. The Chinese started to use vegetable oil for stir-frying instead of animal fats during the Song dynasty (960–1279) Palm oil has long been recognized in West and Central African countries, and European merchants trading with West Africa occasionally purchased palm oil for use as a cooking oil in Europe and it became highly sought-after commodity by British traders for use as an industrial lubricant for machinery during Britain's Industrial Revolution. Palm oil formed the basis of soap products, such as Lever Brothers' (now Unilever) "Sunlight", and B. J. Johnson Company's (now Colgate-Palmolive) "Palmolive", and by around 1870, palm oil constituted the primary export of some West African countries.

In 1780 Carl Wilhelm Scheele demonstrated that fats were derived from glycerol. Thirty years later Michel Eugène Chevreul deduced that these fats were esters of fatty acids and glycerol. Wilhelm Normann, a German chemist introduced the hydrogenation of liquid fats in 1901, creating what later became known as trans fats, leading to the development of the global production of margarine and vegetable shortening.

In the USA cottonseed oil was developed, and marketed by Procter & Gamble as a creamed shortening – Crisco – as early as 1911. Ginning mills were happy to have someone haul away the cotton seeds. The extracted oil was refined and partially hydrogenated to give a solid at room temperature and thus mimic natural lard, and canned under nitrogen gas. Compared to the rendered lard Procter & Gamble was already selling to consumers, Crisco was cheaper, easier to stir into a recipe, and could be stored at room temperature for two years without turning rancid.

Soybean oil has been used in China since before historical records. It arrived in the US in the 1930s. Soybeans are protein-rich, and the medium viscosity oil rendered from them was high in polyunsaturates. Henry Ford established a soybean research laboratory, developed soybean plastics and a soy-based synthetic wool, and built a car "almost entirely" out of soybeans. Roger Drackett had a successful new product with Windex, but he invested heavily in soybean research, seeing it as a smart investment. By the 1950s and 1960s, soybean oil had become the most popular vegetable oil in the US; today it is second only to palm oil. In 2018–2019, world production was at 57.4 MT with the leading producers including China (16.6 MT), US (10.9 MT), Argentina (8.4 MT), Brazil (8.2 MT), and EU (3.2 MT).

The early 20th century also saw the start of the use of vegetable oil as a fuel in diesel engines and in heating oil burners. Rudolf Diesel designed his engine to run on vegetable oil. The idea, he hoped, would make his engines more attractive to farmers having a source of fuel readily available. Diesel's first engine ran on its own power for the first time in Augsburg, Germany, on 10 August 1893 on nothing but peanut oil. In remembrance of this event, 10 August has been declared "International Biodiesel Day". The first patent on Biodiesel was granted in 1937. Periodic petroleum shortages spurred research into vegetable oil as a diesel substitute during the 1930s and 1940s, and again in the 1970s and early 1980s when straight vegetable oil enjoyed its highest level of scientific interest. The 1970s also saw the formation of the first commercial enterprise to allow consumers to run straight vegetable oil in their vehicles. However, biodiesel, produced from oils or fats using transesterification is more widely used. It is Led by Brazil, many countries built biodiesel plants during the 1990s, and it is now widely available for use in motor vehicles, and is the most common biofuel in Europe today. In France, biodiesel is incorporated at a rate of 8% in the fuel used by all French diesel vehicles.

In the mid-1970s, Canadian researchers developed a low-erucic-acid rapeseed cultivar. Because the word "rape" was not considered optimal for marketing, they coined the name "canola" (from "Canada Oil low acid"). The U.S. Food and Drug Administration approved use of the canola name in January 1985, and U.S. farmers started planting large areas that spring. Canola oil is lower in saturated fats, and higher in monounsaturates. Canola is very thin (unlike corn oil) and flavorless (unlike olive oil), so it largely succeeds by displacing soy oil, just as soy oil largely succeeded by displacing cottonseed oil.

Used oil

Main article: Yellow grease

A large quantity of used vegetable oil is produced and recycled, mainly from industrial deep fryers in potato processing plants, snack food factories and fast food restaurants.

Recycled oil has numerous uses, including use as a direct fuel, as well as in the production of biodiesel, livestock feed, pet food, soap, detergent, cosmetics, and industrial chemicals.

Since 2002, an increasing number of European Union countries have prohibited the inclusion of recycled vegetable oil from catering in animal feed. Used cooking oils from food manufacturing, however, as well as fresh or unused cooking oil, continue to be used in their animal feed.

Shelf life

Due to their susceptibility to oxidation from the exposure to oxygen, heat and light, resulting in the formation of oxidation products, such as peroxides and hydroperoxides, plant oils rich in polyunsaturated fatty acids have a limited shelf-life.

Product labeling

In Canada, palm oil is one of five vegetable oils, along with palm kernel oil, coconut oil, peanut oil, and cocoa butter, which must be specifically named in the list of ingredients for a food product. Also, oils in Canadian food products which have been modified or hydrogenated must contain the word "modified" or "hydrogenated" when listed as an ingredient. A mix of oils other than the aforementioned exceptions may simply be listed as "vegetable oil" in Canada; however, if the food product is a cooking oil, salad oil or table oil, the type of oil must be specified and listing "vegetable oil" as an ingredient is not acceptable.

From December 2014, all food products produced in the European Union were legally required to indicate the specific vegetable oil used in their manufacture, following the introduction of the Food Information to Consumers Regulation.