The
shape of the Universe is the
local and
global geometry of the
universe, in terms of both
curvature and
topology (though, strictly speaking, the concept goes beyond both). When physicists describe the Universe as being flat or nearly flat, they're talking geometry: how space and time are warped according to
general relativity. When they talk about whether it is open or closed, they're referring to its topology.
[1] Although the shape of the Universe is still a matter of debate in
physical cosmology, the recent
Wilkinson Microwave Anisotropy Probe (WMAP) measurements allow the statement that "We now know that the universe is flat with only a 0.4% margin of error", according to
NASA scientists.
[2] [3] Theorists have been trying to construct a formal mathematical model of the shape of the Universe. In formal terms, this is a
3-manifold model corresponding to the spatial section (in
comoving coordinates) of the 4-dimensional
space-time of the Universe. The model most theorists currently use is the so-called
Friedmann–Lemaître–Robertson–Walker (FLRW) model. According to cosmologists, on this model the observational data best fit with the conclusion that the shape of the Universe is infinite and flat,
[4] but the data are also consistent with other possible shapes, such as the so-called
Poincaré dodecahedral space[5][6] and the
Picard horn.
[7]
Two aspects of shape
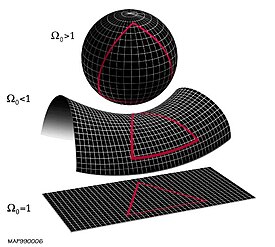
The local geometry of the Universe is determined by whether the
density parameter Ω is greater than, less than, or equal to 1.
From top to bottom: a
spherical universe with
Ω > 1, a
hyperbolic universe with
Ω < 1, and a
flat universe with
Ω = 1. Note that these depictions of two-dimensional surfaces are merely easily visualizable analogs to the 3-dimensional structure of (local) space.
Describing the shape of the Universe requires a consideration of two aspects:
- its local geometry, which mostly concerns the curvature of the Universe, particularly the observable universe, and
- its global geometry, which concerns the topology of the Universe as a whole.
If the observable universe encompasses the entire universe, we may be able to determine the global structure of the entire universe by observation. However, if the observable universe is smaller than the entire universe, our observations will be limited to only a part of the whole, and we may not be able to determine its global geometry through measurement. It is possible to construct different mathematical models of the global geometry of the entire universe all of which are consistent with current observational data. For example, the observable universe may be many orders of magnitude smaller than the entire universe. The Universe may be small in some dimensions and not in others (analogous to the way a cuboid is longer in the dimension of length than it is in the dimensions of width and depth). To test whether a given mathematical model describes the Universe accurately, scientists look for the model's novel implications—what are some phenomena in the Universe that we have not yet observed, but that must exist if the model is correct—and they devise experiments to test whether those phenomena occur or not. For example, if the Universe is a small closed loop, one would expect to see multiple images of an object in the sky, although not necessarily images of the same age.
Cosmologists normally work with a given
space-like slice of spacetime called the
comoving coordinates, the existence of a preferred set of which is possible and widely accepted in present-day physical cosmology. The section of spacetime that can be observed is the backward
light cone (all points within the
cosmic light horizon, given time to reach a given observer), while the related term
Hubble volume can be used to describe either the past light cone or comoving space up to the surface of last scattering. To speak of "the shape of the universe (at a point in time)" is
ontologically naive from the point of view of
special relativity alone: due to the
relativity of simultaneity we cannot speak of different points in space as being "at the same point in time" nor, therefore, of "the shape of the universe at a point in time".
Local geometry (spatial curvature)
The
local geometry is the curvature describing any arbitrary point in the observable universe (averaged on a sufficiently large scale). Many astronomical observations, such as those from
supernovae and the
Cosmic Microwave Background (CMB) radiation, show the observable universe to be very close to homogeneous and isotropic and infer it to be accelerating.
FLRW model of the universe
In
General Relativity, this is modelled by the
Friedmann–Lemaître–Robertson–Walker (FLRW) model. This model, which can be represented by the
Friedmann equations, provides a curvature (often referred to as
geometry) of the Universe based on the mathematics of
fluid dynamics, i.e. it models the matter within the Universe as a perfect fluid. Although stars and structures of mass can be introduced into an "almost FLRW" model, a strictly FLRW model is used to approximate the local geometry of the observable universe.
Another way of saying this is that if all forms of
dark energy are ignored, then the curvature of the Universe can be determined by measuring the average density of matter within it, assuming that all matter is evenly distributed (rather than the distortions caused by 'dense' objects such as galaxies).
This assumption is justified by the observations that, while the Universe is "weakly"
inhomogeneous and
anisotropic (see the
large-scale structure of the cosmos), it is on average homogeneous and
isotropic.
The homogeneous and isotropic universe allows for a spatial geometry with a
constant curvature. One aspect of local geometry to emerge from General Relativity and the FLRW model is that the
density parameter, Omega (
Ω), is related to the curvature of space. Omega is the average density of the Universe divided by the critical energy density, i.e. that required for the Universe to be flat (zero curvature).
The curvature of space is a mathematical description of whether or not the
Pythagorean theorem is valid for spatial coordinates. In the latter case, it provides an alternative formula for expressing local relationships between distances:
- If the curvature is zero, then Ω = 1, and the Pythagorean theorem is correct;
- If Ω < 1, there is positive curvature; and
- if Ω < 1 there is negative curvature.
In the last two cases, the Pythagorean theorem is invalid (but discrepancies are only detectable in triangles whose sides' lengths are of
cosmological scale).
If you measure the circumferences of circles of steadily larger diameters and divide the former by the latter, all three geometries give a value very close to π for small enough diameters but the ratio departs from π for larger diameters unless
Ω = 1:
- For Ω < 1 (the sphere, see diagram) the ratio falls below π: indeed, a great circle on a sphere has circumference only twice its diameter.
- For Ω < 1 the ratio rises above π.
Astronomical measurements of both matter-energy density of the Universe and spacetime intervals using supernova events constrain the spatial curvature to be very close to zero, although they do not constrain its sign. This means that although the local geometries of spacetime are generated by the
theory of relativity based on
spacetime intervals, we can approximate
3-space by the familiar
Euclidean geometry.
Possible local geometries
There are three categories for the possible spatial geometries of
constant curvature, depending on the sign of the curvature. If the curvature is exactly zero, then the local geometry is flat; if it is positive, then the local geometry is spherical, and if it is negative then the local geometry is hyperbolic.
The geometry of the Universe is usually represented in the system of
comoving coordinates, according to which the expansion of the Universe can be ignored. Comoving coordinates form a single
frame of reference according to which the Universe has a static geometry of three spatial dimensions.
Under the assumption that the Universe is homogeneous and
isotropic, the curvature of the observable universe, or the local geometry, is described by one of the three "primitive" geometries (in mathematics these are called the
model geometries):
Even if the Universe is not exactly spatially flat, the spatial curvature is close enough to zero to place the
radius at approximately the horizon of the observable universe or beyond.
Global structure: geometry and topology
Global structure covers the
geometry and the
topology of the whole universe—both the observable universe and beyond. While the local geometry does not determine the global geometry completely, it does limit the possibilities, particularly a geometry of a constant curvature. For this discussion, the Universe is taken to be a
geodesic manifold, free of
topological defects; relaxing either of these complicates the analysis considerably.
A global geometry is a local geometry plus a topology. It follows that a topology alone does not give a global geometry: for instance, Euclidean 3-space and
hyperbolic 3-space have the same topology but different global geometries.
Investigations within the study of global structure of include
- Whether the Universe is infinite or finite in extent
- The scale or size of the entire universe (if it is finite)
- Whether the geometry is flat, positively curved, or negatively curved
- Whether the topology is simply connected like a sphere or multiply connected like a torus
Infinite or finite
One of the presently unanswered questions about the Universe is whether it is infinite or finite in extent.
Mathematically, the question of whether the Universe is infinite or finite is referred to as
boundedness. An infinite universe (unbounded metric space) means that there are points
arbitrarily far apart: for any distance
d, there are points that are of a distance at least
d apart. A finite universe is a bounded metric space, where there is some distance
d such that all points are within distance
d of each other. The smallest such
d is called the
diameter of the Universe, in which case the Universe has a well-defined "volume" or "scale."
Closed manifolds
Many finite mathematical spaces, e.g. a
disc, have an edge or boundary. Spaces that have an edge are difficult to treat, both conceptually and mathematically. Namely, it is very difficult to state what would happen at the edge of such a universe. For this reason, spaces that have an edge are typically excluded from consideration. However, there exist many finite spaces, such as the 3-sphere and 3-torus, which have no edges. Mathematically, these spaces are referred to as being
compact without boundary. The term compact basically means that it is finite in extent ("bounded") and is a
closed set. The term "without boundary" means that the space has no edges. Moreover, so that calculus can be applied, the Universe is typically assumed to be a
differentiable manifold. A mathematical object that possess all these properties, compact without boundary and differentiable, is termed a
closed manifold. The 3-sphere and 3-torus are both closed manifolds.
Scale
For spherical and hyperbolic spatial geometries, the curvature gives a scale (either by using the radius of curvature or its
inverse), a fact noted by
Carl Friedrich Gauss in an 1824 letter to
Franz Taurinus.
[8]
For a flat spatial geometry, the scale of any properties of the topology is arbitrary and may or may not be directly detectable.
The probability of detection of the topology by direct observation depends on the spatial curvature: a small curvature of the local geometry, with a corresponding radius of curvature greater than the observable horizon, makes the topology difficult or impossible to detect if the curvature is hyperbolic. A spherical geometry with a small curvature (large radius of curvature) does not make detection difficult.
Analysis of data from
WMAP implies that on the scale to the surface of last scattering, the density parameter of the Universe is within about 0.5% of the value representing
spatial flatness.
[9]
Curvature
The curvature of the Universe places constraints on the topology. If the spatial geometry is
spherical, i.e. possess positive curvature, the topology is compact. For a flat (zero curvature) or a hyperbolic (negative curvature) spatial geometry, the topology can be either compact or infinite.
[10] Many textbooks erroneously state that a flat universe implies an infinite universe; however, the correct statement is that a flat universe that is also
simply connected implies an infinite universe.
[10] For example, Euclidean space is flat, simply connected and infinite, but the
torus is flat, multiply connected, finite and compact.
In general,
local to global theorems in
Riemannian geometry relate the local geometry to the global geometry. If the local geometry has constant curvature, the global geometry is very constrained, as described in
Thurston geometries.
The latest research shows that even the most powerful future experiments (like SKA, Planck..) will not be able to distinguish between flat, open and closed universe if the true value of cosmological curvature parameter is smaller than 10
−4. If the true value of the cosmological curvature parameter is larger than 10
−3 we will be able to distinguish between these three models even now.
[11]
Results of the
Planck mission released in 2015 show the cosmological curvature parameter, Ω
K, to be 0.000±0.005, coincident with a flat Universe.
[12]
Universe with zero curvature
In a universe with zero curvature, the local geometry is
flat. The most obvious global structure is that of
Euclidean space, which is infinite in extent. Flat universes that are finite in extent include the
torus and
Klein bottle. Moreover, in three dimensions, there are 10 finite closed flat 3-manifolds, of which 6 are orientable and 4 are non-orientable. The most familiar is the aforementioned
3-Torus universe.
In the absence of dark energy, a flat universe expands forever but at a continually decelerating rate, with expansion asymptotically approaching zero. With dark energy, the expansion rate of the Universe initially slows down, due to the effect of gravity, but eventually increases. The
ultimate fate of the universe is the same as that of an open universe.
A flat universe can have
zero total energy.
Universe with positive curvature
A positively curved universe is described by
spherical geometry, and can be thought of as a three-dimensional
hypersphere, or some other
spherical 3-manifold (such as the
Poincaré dodecahedral space), all of which are quotients of the 3-sphere.
Poincaré dodecahedral space, a positively curved space, colloquially described as "soccerball-shaped", as it is the quotient of the 3-sphere by the
binary icosahedral group, which is very close to
icosahedral symmetry, the symmetry of a soccer ball. This was proposed by
Jean-Pierre Luminet and colleagues in 2003
[5][13] and an optimal orientation on the sky for the model was estimated in 2008.
[6]
Universe with negative curvature
A hyperbolic universe, one of a negative spatial curvature, is described by
hyperbolic geometry, and can be thought of locally as a three-dimensional analog of an infinitely extended saddle shape. There are a great variety of
hyperbolic 3-manifolds, and their classification is not completely understood. For hyperbolic local geometry, many of the possible three-dimensional spaces are informally called
horn topologies, so called because of the shape of the
pseudosphere, a canonical model of hyperbolic geometry. An example is the
Picard horn, a negatively curved space, colloquially described as "funnel-shaped".
[7]
Curvature: Open or closed
When cosmologists speak of the Universe as being "open" or "closed", they most commonly are referring to whether the curvature is negative or positive. These meanings of open and closed are different from the mathematical meaning of open and closed used for sets in metric spaces and for the mathematical meaning of open and closed manifolds, which gives rise to ambiguity and confusion. In mathematics, there are definitions for a
closed manifold (i.e. compact without boundary) and
open manifold (i.e. one that is not compact and without boundary,
[14]). A "closed universe" is necessarily a closed manifold. An "open universe" can be either a closed or open manifold. For example, the
Friedmann–Lemaître–Robertson–Walker (FLRW) model the Universe is considered to be without boundaries, in which case "compact universe" could describe a universe that is a closed manifold.
Milne model ("spherical" expanding)

Universe in an expanding sphere. The galaxies farthest away are moving fastest and hence experience length contraction and so become smaller to an
observer in the centre.
If one applies
Minkowski space-based
Special Relativity to expansion of the Universe, without resorting to the concept of a
curved spacetime, then one obtains the Milne model. Any spatial section of the Universe of a constant age (the
proper time elapsed from the Big Bang) will have a negative curvature; this is merely a
pseudo-Euclidean geometric fact analogous to one that
concentric spheres in the
flat Euclidean space are nevertheless curved. Spacial geometry of this model is an unbounded
hyperbolic space. The entire universe is contained within a
light cone, namely the future cone of the Big Bang. For any given moment
t > 0 of
coordinate time (assuming the Big Bang has
t = 0), the entire universe is bounded by a
sphere of radius exactly
c t. The apparent paradox of an infinite universe contained within a sphere is explained with
length contraction: the galaxies farther away, which are travelling away from the observer the fastest, will appear thinner.
This model is essentially a
degenerate FLRW for
Ω = 0. It is incompatible with observations that definitely rule out such a large negative spatial curvature. However, as a background in which gravitational fields (or gravitons) can operate, due to diffeomorphism invariance, the space on the macroscopic scale, is equivalent to any other (open) solution of Einstein's field equations.


