Friedmann–Lemaître–Robertson–Walker metric

From Wikipedia, the free encyclopedia

The Friedmann–Lemaître–Robertson–Walker (FLRW) metric is an exact solution of Einstein's field equations of general relativity; it describes a homogeneous, isotropic, expanding or contracting universe that is path connected, but not necessarily simply connected.^[1][2][3] The general form of the metric follows from the geometric properties of homogeneity and isotropy; Einstein's field equations are only needed to derive the scale factor of the universe as a function of time. Depending on geographical or historical preferences, the set of the four scientists — Alexander Friedmann, Georges Lemaître, Howard P. Robertson and Arthur Geoffrey Walker are customarily grouped as Friedmann or Friedmann–Robertson–Walker (FRW) or Robertson–Walker (RW) or Friedmann–Lemaître (FL). This model is sometimes called the Standard Model of modern cosmology,^[4] although such a description is also associated with the further developed Lambda-CDM model. The FLRW model was developed independently by the named authors in the 1920s and 1930s.

General metric

The FLRW metric starts with the assumption of homogeneity and isotropy of space. It also assumes that the spatial component of the metric can be time-dependent. The generic metric which meets these conditions is

${\displaystyle -c^{2}\mathrm {d} \tau ^{2}=-c^{2}\mathrm {d} t^{2}+{a(t)}^{2}\mathrm {d} \mathbf {\Sigma } ^{2}}$

where ${\displaystyle \mathbf {\Sigma } }$ ranges over a 3-dimensional space of uniform curvature, that is, elliptical space, Euclidean space, or hyperbolic space. It is normally written as a function of three spatial coordinates, but there are several conventions for doing so, detailed below. ${\displaystyle \mathrm {d} \mathbf {\Sigma } }$ does not depend on t — all of the time dependence is in the function a(t), known as the "scale factor".

Reduced-circumference polar coordinates

In reduced-circumference polar coordinates the spatial metric has the form

${\displaystyle \mathrm {d} \mathbf {\Sigma } ^{2}={\frac {\mathrm {d} r^{2}}{1-kr^{2}}}+r^{2}\mathrm {d} \mathbf {\Omega } ^{2},\quad {\text{where }}\mathrm {d} \mathbf {\Omega } ^{2}=\mathrm {d} \theta ^{2}+\sin ^{2}\theta \,\mathrm {d} \phi ^{2}.}$

k is a constant representing the curvature of the space. There are two common unit conventions:

• k may be taken to have units of length⁻², in which case r has units of length and a(t) is unitless. k is then the Gaussian curvature of the space at the time when a(t) = 1. r is sometimes called the reduced circumference because it is equal to the measured circumference of a circle (at that value of r), centered at the origin, divided by 2π (like the r of Schwarzschild coordinates). Where appropriate, a(t) is often chosen to equal 1 in the present cosmological era, so that ${\displaystyle \mathrm {d} \mathbf {\Sigma } }$ measures comoving distance.
• Alternatively, k may be taken to belong to the set {−1,0,+1} (for negative, zero, and positive curvature respectively). Then r is unitless and a(t) has units of length. When k = ±1, a(t) is the radius of curvature of the space, and may also be written R(t).

A disadvantage of reduced circumference coordinates is that they cover only half of the 3-sphere in the case of positive curvature—circumferences beyond that point begin to decrease, leading to degeneracy. (This is not a problem if space is elliptical, i.e. a 3-sphere with opposite points identified.)

Hyperspherical coordinates

In hyperspherical or curvature-normalized coordinates the coordinate r is proportional to radial distance; this gives

${\displaystyle \mathrm {d} \mathbf {\Sigma } ^{2}=\mathrm {d} r^{2}+S_{k}(r)^{2}\,\mathrm {d} \mathbf {\Omega } ^{2}}$

where ${\displaystyle \mathrm {d} \mathbf {\Omega } }$ is as before and

${\displaystyle S_{k}(r)={\begin{cases}{\sqrt {k}}^{\,-1}\sin(r{\sqrt {k}}),&k>0\\r,&k=0\\{\sqrt {|k|}}^{\,-1}\sinh(r{\sqrt {|k|}}),&k<0 .="" annotation="" cases="" end="">$

As before, there are two common unit conventions:

• k may be taken to have units of length⁻², in which case r has units of length and a(t ) is unitless. k is then the Gaussian curvature of the space at the time when a(t ) = 1. Where appropriate, a(t ) is often chosen to equal 1 in the present cosmological era, so that ${\displaystyle \mathrm {d} \mathbf {\Sigma } }$ measures comoving distance.
• Alternatively, as before, k may be taken to belong to the set {−1,0,+1} (for negative, zero, and positive curvature respectively). Then r is unitless and a(t ) has units of length. When k = ±1, a(t ) is the radius of curvature of the space, and may also be written R(t ). Note that, when k = +1, r is essentially a third angle along with θ and φ. The letter χ may be used instead of r.

Though it is usually defined piecewise as above, S is an analytic function of both k and r. It can also be written as a power series

${\displaystyle S_{k}(r)=\sum _{n=0}^{\infty }{\frac {(-1)^{n}k^{n}r^{2n+1}}{(2n+1)!}}=r-{\frac {kr^{3}}{6}}+{\frac {k^{2}r^{5}}{120}}-\cdots }$

or as

${\displaystyle S_{k}(r)=r\;\mathrm {sinc} \,(r{\sqrt {k}})}$

where sinc is the unnormalized sinc function and ${\displaystyle {\sqrt {k}}}$ is one of the imaginary, zero or real square roots of k. These definitions are valid for all k.

Cartesian coordinates

When k = 0 one may write simply

${\displaystyle \mathrm {d} \mathbf {\Sigma } ^{2}=\mathrm {d} x^{2}+\mathrm {d} y^{2}+\mathrm {d} z^{2}.}$

This can be extended to k ≠ 0 by defining

${\displaystyle x=r\cos \theta \,}$,

${\displaystyle y=r\sin \theta \cos \phi \,}$, and

${\displaystyle z=r\sin \theta \sin \phi \,}$,

where r is one of the radial coordinates defined above, but this is rare.

Curvature

Cartesian coordinates

In flat ${\displaystyle (k=0)}$ FLRW space using Cartesian coordinates, the surviving components of the Ricci tensor are^[5]

${\displaystyle R_{tt}=-3{\frac {\ddot {a}}{a}},\quad R_{xx}=R_{yy}=R_{zz}=c^{-2}(a{\ddot {a}}+2{\dot {a}}^{2})}$

and the Ricci scalar is

${\displaystyle R=6c^{-2}\left({\frac {{\ddot {a}}(t)}{a(t)}}+{\frac {{\dot {a}}^{2}(t)}{a^{2}(t)}}\right).}$

Spherical coordinates

In more general FLRW space using spherical coordinates (called "reduced-circumference polar coordinates" above), the surviving components of the Ricci tensor are^[6]

${\displaystyle R_{tt}=-3{\frac {\ddot {a}}{a}},}$

${\displaystyle R_{rr}={\frac {c^{-2}(a(t){\ddot {a}}(t)+2{\dot {a}}^{2}(t))+2k}{1-kr^{2}}}}$

${\displaystyle R_{\theta \theta }=r^{2}(c^{-2}(a(t){\ddot {a}}(t)+2{\dot {a}}^{2}(t))+2k)}$

${\displaystyle R_{\phi \phi }=r^{2}(c^{-2}(a(t){\ddot {a}}(t)+2{\dot {a}}^{2}(t))+2k)\sin ^{2}(\theta )}$

and the Ricci scalar is

${\displaystyle R=6\left({\frac {{\ddot {a}}(t)}{c^{2}a(t)}}+{\frac {{\dot {a}}^{2}(t)}{c^{2}a^{2}(t)}}+{\frac {k}{a^{2}(t)}}\right).}$

Solutions

Einstein's field equations are not used in deriving the general form for the metric: it follows from the geometric properties of homogeneity and isotropy. However, determining the time evolution of ${\displaystyle a(t)}$ does require Einstein's field equations together with a way of calculating the density, ${\displaystyle \rho (t),}$ such as a cosmological equation of state.
This metric has an analytic solution to Einstein's field equations ${\displaystyle G_{\mu \nu }+\Lambda g_{\mu \nu }={\frac {8\pi G}{c^{4}}}T_{\mu \nu }}$ giving the Friedmann equations when the energy-momentum tensor is similarly assumed to be isotropic and homogeneous. The resulting equations are:^[7]

${\displaystyle \left({\frac {\dot {a}}{a}}\right)^{2}+{\frac {kc^{2}}{a^{2}}}-{\frac {\Lambda c^{2}}{3}}={\frac {8\pi G}{3}}\rho }$

${\displaystyle 2{\frac {\ddot {a}}{a}}+\left({\frac {\dot {a}}{a}}\right)^{2}+{\frac {kc^{2}}{a^{2}}}-\Lambda c^{2}=-{\frac {8\pi G}{c^{2}}}p.}$

These equations are the basis of the standard big bang cosmological model including the current ΛCDM model. Because the FLRW model assumes homogeneity, some popular accounts mistakenly assert that the big bang model cannot account for the observed lumpiness of the universe. In a strictly FLRW model, there are no clusters of galaxies, stars or people, since these are objects much denser than a typical part of the universe. Nonetheless, the FLRW model is used as a first approximation for the evolution of the real, lumpy universe because it is simple to calculate, and models which calculate the lumpiness in the universe are added onto the FLRW models as extensions. Most cosmologists agree that the observable universe is well approximated by an almost FLRW model, i.e., a model which follows the FLRW metric apart from primordial density fluctuations. As of 2003, the theoretical implications of the various extensions to the FLRW model appear to be well understood, and the goal is to make these consistent with observations from COBE and WMAP.

If the spacetime is multiply connected, then each event will be represented by more than one tuple of coordinates.^{[citation needed]}

Interpretation

The pair of equations given above is equivalent to the following pair of equations

${\displaystyle {\dot {\rho }}=-3{\frac {\dot {a}}{a}}\left(\rho +{\frac {p}{c^{2}}}\right)}$

${\displaystyle {\frac {\ddot {a}}{a}}=-{\frac {4\pi G}{3}}\left(\rho +{\frac {3p}{c^{2}}}\right)+{\frac {\Lambda c^{2}}{3}}}$

with ${\displaystyle k}$, the spatial curvature index, serving as a constant of integration for the first equation.

The first equation can be derived also from thermodynamical considerations and is equivalent to the first law of thermodynamics, assuming the expansion of the universe is an adiabatic process (which is implicitly assumed in the derivation of the Friedmann–Lemaître–Robertson–Walker metric).

The second equation states that both the energy density and the pressure cause the expansion rate of the universe ${\displaystyle {\dot {a}}}$ to decrease, i.e., both cause a deceleration in the expansion of the universe. This is a consequence of gravitation, with pressure playing a similar role to that of energy (or mass) density, according to the principles of general relativity. The cosmological constant, on the other hand, causes an acceleration in the expansion of the universe.

Cosmological constant

The cosmological constant term can be omitted if we make the following replacements

${\displaystyle \rho \rightarrow \rho +{\frac {\Lambda c^{2}}{8\pi G}}}$

${\displaystyle p\rightarrow p-{\frac {\Lambda c^{4}}{8\pi G}}.}$

Therefore, the cosmological constant can be interpreted as arising from a form of energy which has negative pressure, equal in magnitude to its (positive) energy density:

${\displaystyle p=-\rho c^{2}.\,}$

Such form of energy—a generalization of the notion of a cosmological constant—is known as dark energy.

In fact, in order to get a term which causes an acceleration of the universe expansion, it is enough to have a scalar field which satisfies

${\displaystyle p<- annotation="" c="" frac="" rho="">$

Such a field is sometimes called quintessence.

Newtonian interpretation

This is due to McCrea and Milne ^[8] although sometimes incorrectly ascribed to Friedmann. The Friedmann equations are equivalent to this pair of equations:

${\displaystyle -a^{3}{\dot {\rho }}=3a^{2}{\dot {a}}\rho +{\frac {3a^{2}p{\dot {a}}}{c^{2}}}\,}$

${\displaystyle {\frac {{\dot {a}}^{2}}{2}}-{\frac {G{\frac {4\pi a^{3}}{3}}\rho }{a}}=-{\frac {kc^{2}}{2}}\,.}$

The first equation says that the decrease in the mass contained in a fixed cube (whose side is momentarily a) is the amount which leaves through the sides due to the expansion of the universe plus the mass equivalent of the work done by pressure against the material being expelled. This is the conservation of mass-energy (first law of thermodynamics) contained within a part of the universe.

The second equation says that the kinetic energy (seen from the origin) of a particle of unit mass moving with the expansion plus its (negative) gravitational potential energy (relative to the mass contained in the sphere of matter closer to the origin) is equal to a constant related to the curvature of the universe. In other words, the energy (relative to the origin) of a co-moving particle in free-fall is conserved. General relativity merely adds a connection between the spatial curvature of the universe and the energy of such a particle: positive total energy implies negative curvature and negative total energy implies positive curvature.

The cosmological constant term is assumed to be treated as dark energy and thus merged into the density and pressure terms.

During the Planck epoch, one cannot neglect quantum effects. So they may cause a deviation from the Friedmann equations.

Name and history

The Soviet mathematician Alexander Friedmann first derived the main results of the FLRW model in 1922 and 1924. Although the prestigious physics journal Zeitschrift für Physik published his work, it remained relatively unnoticed by his contemporaries. Friedmann was in direct communication with Albert Einstein, who, on behalf of Zeitschrift für Physik, acted as the scientific referee of Friedmann's work. Eventually Einstein acknowledged the correctness of Friedmann's calculations, but failed to appreciate the physical significance of Friedmann's predictions.

Friedmann died in 1925. In 1927, Georges Lemaître, a Belgian priest, astronomer and periodic professor of physics at the Catholic University of Leuven, arrived independently at results similar to those of Friedmann and published them in the Annales de la Société Scientifique de Bruxelles (Annals of the Scientific Society of Brussels).^[9] In the face of the observational evidence for the expansion of the universe obtained by Edwin Hubble in the late 1920s, Lemaître's results were noticed in particular by Arthur Eddington, and in 1930–31 Lemaître's paper was translated into English and published in the Monthly Notices of the Royal Astronomical Society.

Howard P. Robertson from the US and Arthur Geoffrey Walker from the UK explored the problem further during the 1930s. In 1935 Robertson and Walker rigorously proved that the FLRW metric is the only one on a spacetime that is spatially homogeneous and isotropic (as noted above, this is a geometric result and is not tied specifically to the equations of general relativity, which were always assumed by Friedmann and Lemaître).

Because the dynamics of the FLRW model were derived by Friedmann and Lemaître, the latter two names are often omitted by scientists outside the US. Conversely, US physicists often refer to it as simply "Robertson–Walker". The full four-name title is the most democratic and it is frequently used.^{[citation needed]} Often the "Robertson–Walker" metric, so-called since they proved its generic properties, is distinguished from the dynamical "Friedmann-Lemaître" models, specific solutions for a(t) which assume that the only contributions to stress-energy are cold matter ("dust"), radiation, and a cosmological constant.

Einstein's radius of the universe

Einstein's radius of the universe is the radius of curvature of space of Einstein's universe, a long-abandoned static model that was supposed to represent our universe in idealized form. Putting

${\displaystyle {\dot {a}}={\ddot {a}}=0}$

in the Friedmann equation, the radius of curvature of space of this universe (Einstein's radius) is^{[citation needed]}

${\displaystyle R_{E}=c/{\sqrt {4\pi G\rho }}}$,

where ${\displaystyle c}$ is the speed of light, ${\displaystyle G}$ is the Newtonian gravitational constant, and ${\displaystyle \rho }$ is the density of space of this universe. The numerical value of Einstein's radius is of the order of 10¹⁰ light years.

Evidence

By combining the observation data from some experiments such as WMAP and Planck with theoretical results of Ehlers–Geren–Sachs theorem and its generalization,^[10] astrophysicists now agree that the universe is almost homogeneous and isotropic (when averaged over a very large scale) and thus nearly a FLRW spacetime.

Gravity

From Wikipedia, the free encyclopedia

Play media

Hammer and feather drop: astronaut David Scott (from mission Apollo 15) on the Moon enacting the legend of Galileo's gravity experiment. (1.38 MB, ogg/Theora format).

Gravity, or gravitation, is a natural phenomenon by which all things with mass are brought toward (or gravitate toward) one another, including objects ranging from electrons and atoms, to planets, stars, and galaxies. Since energy and mass are equivalent, all forms of energy (including photons and light) cause gravitation and are under the influence of it.^[1] On Earth, gravity gives weight to physical objects, and the Moon's gravity causes the ocean tides. The gravitational attraction of the original gaseous matter present in the Universe caused it to begin coalescing, forming stars – and for the stars to group together into galaxies – so gravity is responsible for many of the large scale structures in the Universe. Gravity has an infinite range, although its effects become increasingly weaker on farther objects.

Gravity is most accurately described by the general theory of relativity (proposed by Albert Einstein in 1915) which describes gravity not as a force, but as a consequence of the curvature of spacetime caused by the uneven distribution of mass. The most extreme example of this curvature of spacetime is a black hole, from which nothing—not even light—can escape once past the black hole's event horizon.^[2] However, for most applications, gravity is well approximated by Newton's law of universal gravitation, which describes gravity as a force which causes any two bodies to be attracted to each other, with the force proportional to the product of their masses and inversely proportional to the square of the distance between them.

Gravity is the weakest of the four fundamental forces of physics, approximately 10³⁸ times weaker than the strong force, 10³⁶ times weaker than the electromagnetic force and 10²⁹ times weaker than the weak force. As a consequence, it has no significant influence at the level of subatomic particles.^[3] In contrast, it is the dominant force at the macroscopic scale, and is the cause of the formation, shape and trajectory (orbit) of astronomical bodies. For example, gravity causes the Earth and the other planets to orbit the Sun, it also causes the Moon to orbit the Earth, and causes the formation of tides, the formation and evolution of the Solar System, stars and galaxies.

The earliest instance of gravity in the Universe, possibly in the form of quantum gravity, supergravity or a gravitational singularity, along with ordinary space and time, developed during the Planck epoch (up to 10⁻⁴³ seconds after the birth of the Universe), possibly from a primeval state, such as a false vacuum, quantum vacuum or virtual particle, in a currently unknown manner.^[4] Attempts to develop a theory of gravity consistent with quantum mechanics, a quantum gravity theory, which would allow gravity to be united in a common mathematical framework (a theory of everything) with the other three forces of physics, are a current area of research.

History of gravitational theory

Scientific revolution

Modern work on gravitational theory began with the work of Galileo Galilei in the late 16th and early 17th centuries. In his famous (though possibly apocryphal^[5]) experiment dropping balls from the Tower of Pisa, and later with careful measurements of balls rolling down inclines, Galileo showed that gravitational acceleration is the same for all objects. This was a major departure from Aristotle's belief that heavier objects have a higher gravitational acceleration.^[6] Galileo postulated air resistance as the reason that objects with less mass fall more slowly in an atmosphere. Galileo's work set the stage for the formulation of Newton's theory of gravity.^[7]

Newton's theory of gravitation

Sir Isaac Newton, an English physicist who lived from 1642 to 1727

In 1687, English mathematician Sir Isaac Newton published Principia, which hypothesizes the inverse-square law of universal gravitation. In his own words, "I deduced that the forces which keep the planets in their orbs must [be] reciprocally as the squares of their distances from the centers about which they revolve: and thereby compared the force requisite to keep the Moon in her Orb with the force of gravity at the surface of the Earth; and found them answer pretty nearly."^[8] The equation is the following:

${\displaystyle F=G{\frac {m_{1}m_{2}}{r^{2}}}\ }$

Where F is the force, m₁ and m₂ are the masses of the objects interacting, r is the distance between the centers of the masses and G is the gravitational constant.

Newton's theory enjoyed its greatest success when it was used to predict the existence of Neptune based on motions of Uranus that could not be accounted for by the actions of the other planets. Calculations by both John Couch Adams and Urbain Le Verrier predicted the general position of the planet, and Le Verrier's calculations are what led Johann Gottfried Galle to the discovery of Neptune.

A discrepancy in Mercury's orbit pointed out flaws in Newton's theory. By the end of the 19th century, it was known that its orbit showed slight perturbations that could not be accounted for entirely under Newton's theory, but all searches for another perturbing body (such as a planet orbiting the Sun even closer than Mercury) had been fruitless. The issue was resolved in 1915 by Albert Einstein's new theory of general relativity, which accounted for the small discrepancy in Mercury's orbit.

Although Newton's theory has been superseded by Einstein's general relativity, most modern non-relativistic gravitational calculations are still made using Newton's theory because it is simpler to work with and it gives sufficiently accurate results for most applications involving sufficiently small masses, speeds and energies.

Equivalence principle

The equivalence principle, explored by a succession of researchers including Galileo, Loránd Eötvös, and Einstein, expresses the idea that all objects fall in the same way, and that the effects of gravity are indistinguishable from certain aspects of acceleration and deceleration. The simplest way to test the weak equivalence principle is to drop two objects of different masses or compositions in a vacuum and see whether they hit the ground at the same time. Such experiments demonstrate that all objects fall at the same rate when other forces (such as air resistance and electromagnetic effects) are negligible. More sophisticated tests use a torsion balance of a type invented by Eötvös. Satellite experiments, for example STEP, are planned for more accurate experiments in space.^[9]

Formulations of the equivalence principle include:

• The weak equivalence principle: The trajectory of a point mass in a gravitational field depends only on its initial position and velocity, and is independent of its composition.^[10]
• The Einsteinian equivalence principle: The outcome of any local non-gravitational experiment in a freely falling laboratory is independent of the velocity of the laboratory and its location in spacetime.^[11]
• The strong equivalence principle requiring both of the above.

General relativity

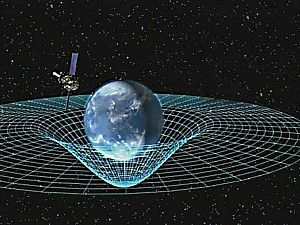
Two-dimensional analogy of spacetime distortion generated by the mass of an object. Matter changes the geometry of spacetime, this (curved) geometry being interpreted as gravity. White lines do not represent the curvature of space but instead represent the coordinate system imposed on the curved spacetime, which would be rectilinear in a flat spacetime.

In general relativity, the effects of gravitation are ascribed to spacetime curvature instead of a force. The starting point for general relativity is the equivalence principle, which equates free fall with inertial motion and describes free-falling inertial objects as being accelerated relative to non-inertial observers on the ground.^[12][13] In Newtonian physics, however, no such acceleration can occur unless at least one of the objects is being operated on by a force.

Einstein proposed that spacetime is curved by matter, and that free-falling objects are moving along locally straight paths in curved spacetime. These straight paths are called geodesics. Like Newton's first law of motion, Einstein's theory states that if a force is applied on an object, it would deviate from a geodesic. For instance, we are no longer following geodesics while standing because the mechanical resistance of the Earth exerts an upward force on us, and we are non-inertial on the ground as a result. This explains why moving along the geodesics in spacetime is considered inertial.

Einstein discovered the field equations of general relativity, which relate the presence of matter and the curvature of spacetime and are named after him. The Einstein field equations are a set of 10 simultaneous, non-linear, differential equations. The solutions of the field equations are the components of the metric tensor of spacetime. A metric tensor describes a geometry of spacetime. The geodesic paths for a spacetime are calculated from the metric tensor.

Solutions

Notable solutions of the Einstein field equations include:

• The Schwarzschild solution, which describes spacetime surrounding a spherically symmetric non-rotating uncharged massive object. For compact enough objects, this solution generated a black hole with a central singularity. For radial distances from the center which are much greater than the Schwarzschild radius, the accelerations predicted by the Schwarzschild solution are practically identical to those predicted by Newton's theory of gravity.
• The Reissner-Nordström solution, in which the central object has an electrical charge. For charges with a geometrized length which are less than the geometrized length of the mass of the object, this solution produces black holes with double event horizons.
• The Kerr solution for rotating massive objects. This solution also produces black holes with multiple event horizons.
• The Kerr-Newman solution for charged, rotating massive objects. This solution also produces black holes with multiple event horizons.
• The cosmological Friedmann-Lemaître-Robertson-Walker solution, which predicts the expansion of the Universe.

Tests

The tests of general relativity included the following:^[14]

• General relativity accounts for the anomalous perihelion precession of Mercury.^[15]
• The prediction that time runs slower at lower potentials (gravitational time dilation) has been confirmed by the Pound–Rebka experiment (1959), the Hafele–Keating experiment, and the GPS.
• The prediction of the deflection of light was first confirmed by Arthur Stanley Eddington from his observations during the Solar eclipse of 29 May 1919.^[16][17] Eddington measured starlight deflections twice those predicted by Newtonian corpuscular theory, in accordance with the predictions of general relativity. However, his interpretation of the results was later disputed.^[18] More recent tests using radio interferometric measurements of quasars passing behind the Sun have more accurately and consistently confirmed the deflection of light to the degree predicted by general relativity.^[19] See also gravitational lens.
• The time delay of light passing close to a massive object was first identified by Irwin I. Shapiro in 1964 in interplanetary spacecraft signals.
• Gravitational radiation has been indirectly confirmed through studies of binary pulsars. On 11 February 2016, the LIGO and Virgo collaborations announced the first observation of a gravitational wave.
• Alexander Friedmann in 1922 found that Einstein equations have non-stationary solutions (even in the presence of the cosmological constant). In 1927 Georges Lemaître showed that static solutions of the Einstein equations, which are possible in the presence of the cosmological constant, are unstable, and therefore the static Universe envisioned by Einstein could not exist. Later, in 1931, Einstein himself agreed with the results of Friedmann and Lemaître. Thus general relativity predicted that the Universe had to be non-static—it had to either expand or contract. The expansion of the Universe discovered by Edwin Hubble in 1929 confirmed this prediction.^[20]
• The theory's prediction of frame dragging was consistent with the recent Gravity Probe B results.^[21]
• General relativity predicts that light should lose its energy when traveling away from massive bodies through gravitational redshift. This was verified on earth and in the solar system around 1960.

Gravity and quantum mechanics

In the decades after the discovery of general relativity, it was realized that general relativity is incompatible with quantum mechanics.^[22] It is possible to describe gravity in the framework of quantum field theory like the other fundamental forces, such that the attractive force of gravity arises due to exchange of virtual gravitons, in the same way as the electromagnetic force arises from exchange of virtual photons.^[23][24] This reproduces general relativity in the classical limit. However, this approach fails at short distances of the order of the Planck length,^[22] where a more complete theory of quantum gravity (or a new approach to quantum mechanics) is required.

Specifics

Earth's gravity

An initially-stationary object which is allowed to fall freely under gravity drops a distance which is proportional to the square of the elapsed time. This image spans half a second and was captured at 20 flashes per second.

Every planetary body (including the Earth) is surrounded by its own gravitational field, which can be conceptualized with Newtonian physics as exerting an attractive force on all objects. Assuming a spherically symmetrical planet, the strength of this field at any given point above the surface is proportional to the planetary body's mass and inversely proportional to the square of the distance from the center of the body.

If an object with comparable mass to that of the Earth were to fall towards it, then the corresponding acceleration of the Earth would be observable.

The strength of the gravitational field is numerically equal to the acceleration of objects under its influence.^[25] The rate of acceleration of falling objects near the Earth's surface varies very slightly depending on latitude, surface features such as mountains and ridges, and perhaps unusually high or low sub-surface densities.^[26] For purposes of weights and measures, a standard gravity value is defined by the International Bureau of Weights and Measures, under the International System of Units (SI).

That value, denoted g, is g = 9.80665 m/s² (32.1740 ft/s²).^[27][28]

The standard value of 9.80665 m/s² is the one originally adopted by the International Committee on Weights and Measures in 1901 for 45° latitude, even though it has been shown to be too high by about five parts in ten thousand.^[29] This value has persisted in meteorology and in some standard atmospheres as the value for 45° latitude even though it applies more precisely to latitude of 45°32'33".^[30]

Assuming the standardized value for g and ignoring air resistance, this means that an object falling freely near the Earth's surface increases its velocity by 9.80665 m/s (32.1740 ft/s or 22 mph) for each second of its descent. Thus, an object starting from rest will attain a velocity of 9.80665 m/s (32.1740 ft/s) after one second, approximately 19.62 m/s (64.4 ft/s) after two seconds, and so on, adding 9.80665 m/s (32.1740 ft/s) to each resulting velocity. Also, again ignoring air resistance, any and all objects, when dropped from the same height, will hit the ground at the same time.

According to Newton's 3rd Law, the Earth itself experiences a force equal in magnitude and opposite in direction to that which it exerts on a falling object. This means that the Earth also accelerates towards the object until they collide. Because the mass of the Earth is huge, however, the acceleration imparted to the Earth by this opposite force is negligible in comparison to the object's. If the object doesn't bounce after it has collided with the Earth, each of them then exerts a repulsive contact force on the other which effectively balances the attractive force of gravity and prevents further acceleration.

The apparent force of gravity on Earth is the resultant (vector sum) of two forces:^[31] (a) The gravitational attraction in accordance with Newton's universal law of gravitation, and (b) the centrifugal force, which results from the choice of an earthbound, rotating frame of reference. The force of gravity is the weakest at the equator because of the centrifugal force caused by the Earth's rotation and because points on the equator are furthest from the center of the Earth. The force of gravity varies with latitude and increases from about 9.780 m/s² at the Equator to about 9.832 m/s² at the poles.

Equations for a falling body near the surface of the Earth

Under an assumption of constant gravitational attraction, Newton's law of universal gravitation simplifies to F = mg, where m is the mass of the body and g is a constant vector with an average magnitude of 9.81 m/s² on Earth. This resulting force is the object's weight. The acceleration due to gravity is equal to this g. An initially stationary object which is allowed to fall freely under gravity drops a distance which is proportional to the square of the elapsed time. The image on the right, spanning half a second, was captured with a stroboscopic flash at 20 flashes per second. During the first ​¹⁄₂₀ of a second the ball drops one unit of distance (here, a unit is about 12 mm); by ​²⁄₂₀ it has dropped at total of 4 units; by ​³⁄₂₀, 9 units and so on.

Under the same constant gravity assumptions, the potential energy, E_p, of a body at height h is given by E_p = mgh (or E_p = Wh, with W meaning weight). This expression is valid only over small distances h from the surface of the Earth. Similarly, the expression ${\displaystyle h={\tfrac {v^{2}}{2g}}}$ for the maximum height reached by a vertically projected body with initial velocity v is useful for small heights and small initial velocities only.

Gravity and astronomy

Gravity acts on stars that form the Milky Way.^[32]

The application of Newton's law of gravity has enabled the acquisition of much of the detailed information we have about the planets in the Solar System, the mass of the Sun, and details of quasars; even the existence of dark matter is inferred using Newton's law of gravity. Although we have not traveled to all the planets nor to the Sun, we know their masses. These masses are obtained by applying the laws of gravity to the measured characteristics of the orbit. In space an object maintains its orbit because of the force of gravity acting upon it. Planets orbit stars, stars orbit galactic centers, galaxies orbit a center of mass in clusters, and clusters orbit in superclusters. The force of gravity exerted on one object by another is directly proportional to the product of those objects' masses and inversely proportional to the square of the distance between them.

The earliest gravity (possibly in the form of quantum gravity, supergravity or a gravitational singularity), along with ordinary space and time, developed during the Planck epoch (up to 10⁻⁴³ seconds after the birth of the Universe), possibly from a primeval state (such as a false vacuum, quantum vacuum or virtual particle), in a currently unknown manner.^[4]

Gravitational radiation

According to general relativity, gravitational radiation is generated in situations where the curvature of spacetime is oscillating, such as is the case with co-orbiting objects. The gravitational radiation emitted by the Solar System is far too small to measure. However, gravitational radiation has been indirectly observed as an energy loss over time in binary pulsar systems such as PSR B1913+16. It is believed that neutron star mergers and black hole formation may create detectable amounts of gravitational radiation. Gravitational radiation observatories such as the Laser Interferometer Gravitational Wave Observatory (LIGO) have been created to study the problem. In February 2016, the Advanced LIGO team announced that they had detected gravitational waves from a black hole collision. On 14 September 2015, LIGO registered gravitational waves for the first time, as a result of the collision of two black holes 1.3 billion light-years from Earth.^[33][34] This observation confirms the theoretical predictions of Einstein and others that such waves exist. The event confirms that binary black holes exist. It also opens the way for practical observation and understanding of the nature of gravity and events in the Universe including the Big Bang and what happened after it.^[35][36]

Speed of gravity

In December 2012, a research team in China announced that it had produced measurements of the phase lag of Earth tides during full and new moons which seem to prove that the speed of gravity is equal to the speed of light.^[37] This means that if the Sun suddenly disappeared, the Earth would keep orbiting it normally for 8 minutes, which is the time light takes to travel that distance. The team's findings were released in the Chinese Science Bulletin in February 2013.^[38]

In October 2017, the LIGO and Virgo detectors received gravitational wave signals within 2 seconds of gamma ray satellites and optical telescopes seeing signals from the same direction. This confirmed that the speed of gravitational waves was the same as the speed of light.^[39]

Anomalies and discrepancies

There are some observations that are not adequately accounted for, which may point to the need for better theories of gravity or perhaps be explained in other ways.

Rotation curve of a typical spiral galaxy: predicted (A) and observed (B). The discrepancy between the curves is attributed to dark matter.

• Extra-fast stars: Stars in galaxies follow a distribution of velocities where stars on the outskirts are moving faster than they should according to the observed distributions of normal matter. Galaxies within galaxy clusters show a similar pattern. Dark matter, which would interact through gravitation but not electromagnetically, would account for the discrepancy. Various modifications to Newtonian dynamics have also been proposed.
• Flyby anomaly: Various spacecraft have experienced greater acceleration than expected during gravity assist maneuvers.
• Accelerating expansion: The metric expansion of space seems to be speeding up. Dark energy has been proposed to explain this. A recent alternative explanation is that the geometry of space is not homogeneous (due to clusters of galaxies) and that when the data are reinterpreted to take this into account, the expansion is not speeding up after all,^[40] however this conclusion is disputed.^[41]
• Anomalous increase of the astronomical unit: Recent measurements indicate that planetary orbits are widening faster than if this were solely through the Sun losing mass by radiating energy.
• Extra energetic photons: Photons travelling through galaxy clusters should gain energy and then lose it again on the way out. The accelerating expansion of the Universe should stop the photons returning all the energy, but even taking this into account photons from the cosmic microwave background radiation gain twice as much energy as expected. This may indicate that gravity falls off faster than inverse-squared at certain distance scales.^[42]
• Extra massive hydrogen clouds: The spectral lines of the Lyman-alpha forest suggest that hydrogen clouds are more clumped together at certain scales than expected and, like dark flow, may indicate that gravity falls off slower than inverse-squared at certain distance scales.^[42]

Alternative theories

Historical alternative theories

• Aristotelian theory of gravity
• Le Sage's theory of gravitation (1784) also called LeSage gravity, proposed by Georges-Louis Le Sage, based on a fluid-based explanation where a light gas fills the entire Universe.
• Ritz's theory of gravitation, Ann. Chem. Phys. 13, 145, (1908) pp. 267–71, Weber-Gauss electrodynamics applied to gravitation. Classical advancement of perihelia.
• Nordström's theory of gravitation (1912, 1913), an early competitor of general relativity.
• Kaluza Klein theory (1921)
• Whitehead's theory of gravitation (1922), another early competitor of general relativity.

Modern alternative theories

• Brans–Dicke theory of gravity (1961)^[43]
• Induced gravity (1967), a proposal by Andrei Sakharov according to which general relativity might arise from quantum field theories of matter
• ƒ(R) gravity (1970)
• Horndeski theory (1974)^[44]
• Supergravity (1976)
• String theory
• In the modified Newtonian dynamics (MOND) (1981), Mordehai Milgrom proposes a modification of Newton's second law of motion for small accelerations^[45]
• The self-creation cosmology theory of gravity (1982) by G.A. Barber in which the Brans-Dicke theory is modified to allow mass creation
• Loop quantum gravity (1988) by Carlo Rovelli, Lee Smolin, and Abhay Ashtekar
• Nonsymmetric gravitational theory (NGT) (1994) by John Moffat
• Conformal gravity^[46]
• Tensor–vector–scalar gravity (TeVeS) (2004), a relativistic modification of MOND by Jacob Bekenstein
• Gravity as an entropic force, gravity arising as an emergent phenomenon from the thermodynamic concept of entropy.
• In the superfluid vacuum theory the gravity and curved space-time arise as a collective excitation mode of non-relativistic background superfluid.
• Chameleon theory (2004) by Justin Khoury and Amanda Weltman.
• Pressuron theory (2013) by Olivier Minazzoli and Aurélien Hees.