Cell growth

From Wikipedia, the free encyclopedia

The term cell growth is used in the contexts of biological cell development and cell division (reproduction). When used in the context of cell development, the term refers to increase in cytoplasmic and organelle volume (G1 phase), as well as increase in genetic material (G2 phase) following the replication during S phase. This is not to be confused with growth in the context of cell division, referred to as proliferation, where a cell, known as the "mother cell", grows and divides to produce two "daughter cells" (M phase).

Cell populations

Cell populations go through a particular type of exponential growth called doubling. Thus, each generation of cells should be twice as numerous as the previous generation. However, the number of generations only gives a maximum figure as not all cells survive in each generation.

Cell size

Cell size is highly variable among organisms, with some algae such as Caulerpa taxifolia being a single cell several meters in length. Plant cells are much larger than animal cells, and protists such as Paramecium can be 330 μm long, while a typical human cell might be 10 μm. How these cells "decide" how big they should be before dividing is an open question. Chemical gradients are known to be partly responsible, and it is hypothesized that mechanical stress detection by cytoskeletal structures is involved. Work on the topic generally requires an organism whose cell cycle is well-characterized.

Yeast cell size regulation

The relationship between cell size and cell division has been extensively studied in yeast. For some cells, there is a mechanism by which cell division is not initiated until a cell has reached a certain size. If the nutrient supply is restricted (after time t = 2 in the diagram, below), and the rate of increase in cell size is slowed, the time period between cell divisions is increased. Yeast cell-size mutants were isolated that begin cell division before reaching a normal/regular size (wee mutants).

Figure 1:Cell cycle and growth

 

Wee1 protein is a tyrosine kinase that normally phosphorylates the Cdc2 cell cycle regulatory protein (the homolog of CDK1 in humans), a cyclin-dependent kinase, on a tyrosine residue. Cdc2 drives entry into mitosis by phosphorylating a wide range of targets. This covalent modification of the molecular structure of Cdc2 inhibits the enzymatic activity of Cdc2 and prevents cell division. Wee1 acts to keep Cdc2 inactive during early G2 when cells are still small. When cells have reached sufficient size during G2, the phosphatase Cdc25 removes the inhibitory phosphorylation, and thus activates Cdc2 to allow mitotic entry. A balance of Wee1 and Cdc25 activity with changes in cell size is coordinated by the mitotic entry control system. It has been shown in Wee1 mutants, cells with weakened Wee1 activity, that Cdc2 becomes active when the cell is smaller. Thus, mitosis occurs before the yeast reach their normal size. This suggests that cell division may be regulated in part by dilution of Wee1 protein in cells as they grow larger.

Linking Cdr2 to Wee1

The protein kinase Cdr2 (which negatively regulates Wee1) and the Cdr2-related kinase Cdr1 (which directly phosphorylates and inhibits Wee1 in vitro) are localized to a band of cortical nodes in the middle of interphase cells. After entry into mitosis, cytokinesis factors such as myosin II are recruited to similar nodes; these nodes eventually condense to form the cytokinetic ring. A previously un-characterized protein, Blt1, was found to co-localize with Cdr2 in the medial interphase nodes. Blt1 knockout cells had increased length at division, which is consistent with a delay in mitotic entry. This finding connects a physical location, a band of cortical nodes, with factors that have been shown to directly regulate mitotic entry, namely Cdr1, Cdr2, and Blt1. 

Further experimentation with GFP-tagged proteins and mutant proteins indicates that the medial cortical nodes are formed by the ordered, Cdr2-dependent assembly of multiple interacting proteins during interphase. Cdr2 is at the top of this hierarchy and works upstream of Cdr1 and Blt1. Mitosis is promoted by the negative regulation of Wee1 by Cdr2. It has also been shown that Cdr2 recruits Wee1 to the medial cortical node. The mechanism of this recruitment has yet to be discovered. A Cdr2 kinase mutant, which is able to localize properly despite a loss of function in phosphorylation, disrupts the recruitment of Wee1 to the medial cortex and delays entry into mitosis. Thus, Wee1 localizes with its inhibitory network, which demonstrates that mitosis is controlled through Cdr2-dependent negative regulation of Wee1 at the medial cortical nodes.

Cell polarity factors

Cell polarity factors positioned at the cell tips provide spatial cues to limit Cdr2 distribution to the cell middle. In fission yeast Schizosaccharomyces pombe (S. Pombe), cells divide at a defined, reproducible size during mitosis because of the regulated activity of Cdk1. The cell polarity protein kinase Pom1, a member of the dual-specificity tyrosine-phosphorylation regulated kinase (DYRK) family of kinases, localizes to cell ends. In Pom1 knockout cells, Cdr2 was no longer restricted to the cell middle, but was seen diffusely through half of the cell. From this data it becomes apparent that Pom1 provides inhibitory signals that confine Cdr2 to the middle of the cell. It has been further shown that Pom1-dependent signals lead to the phosphorylation of Cdr2. Pom1 knockout cells were also shown to divide at a smaller size than wild-type, which indicates a premature entry into mitosis.

Pom1 forms polar gradients that peak at cell ends, which shows a direct link between size control factors and a specific physical location in the cell. As a cell grows in size, a gradient in Pom1 grows. When cells are small, Pom1 is spread diffusely throughout the cell body. As the cell increases in size, Pom1 concentration decreases in the middle and becomes concentrated at cell ends. Small cells in early G2 which contain sufficient levels of Pom1 in the entirety of the cell have inactive Cdr2 and cannot enter mitosis. It is not until the cells grow into late G2, when Pom1 is confined to the cell ends that Cdr2 in the medial cortical nodes is activated and able to start the inhibition of Wee1. This finding shows how cell size plays a direct role in regulating the start of mitosis. In this model, Pom1 acts as a molecular link between cell growth and mitotic entry through a Cdr2-Cdr1-Wee1-Cdk1 pathway. The Pom1 polar gradient successfully relays information about cell size and geometry to the Cdk1 regulatory system. Through this gradient, the cell ensures it has reached a defined, sufficient size to enter mitosis.

Cell cycle regulation in mammals

Many different types of eukaryotic cells undergo size-dependent transitions during the cell cycle. These transitions are controlled by the cyclin-dependent kinase Cdk1. Though the proteins that control Cdk1 are well understood, their connection to mechanisms monitoring cell size remains elusive. A postulated model for mammalian size control situates mass as the driving force of the cell cycle. A cell is unable to grow to an abnormally large size because at a certain cell size or cell mass, the S phase is initiated. The S phase starts the sequence of events leading to mitosis and cytokinesis. A cell is unable to get too small because the later cell cycle events, such as S, G2, and M, are delayed until mass increases sufficiently to begin S phase.

Many of the signal molecules that convey information to cells during the control of cellular differentiation or growth are called growth factors. The protein mTOR is a serine/threonine kinase that regulates translation and cell division. Nutrient availability influences mTOR so that when cells are not able to grow to normal size they will not undergo cell division. The details of the molecular mechanisms of mammalian cell size control are currently being investigated. The size of post-mitotic neurons depends on the size of the cell body, axon and dendrites. In vertebrates, neuron size is often a reflection of the number of synaptic contacts onto the neuron or from a neuron onto other cells. For example, the size of motoneurons usually reflects the size of the motor unit that is controlled by the motoneuron. Invertebrates often have giant neurons and axons that provide special functions such as rapid action potential propagation. Mammals also use this trick for increasing the speed of signals in the nervous system, but they can also use myelin to accomplish this, so most human neurons are relatively small cells.

Other experimental systems for the study of cell size regulation

One common means to produce very large cells is by cell fusion to form syncytia. For example, very long (several inches) skeletal muscle cells are formed by fusion of thousands of myocytes. Genetic studies of the fruit fly Drosophila have revealed several genes that are required for the formation of multinucleated muscle cells by fusion of myoblasts. Some of the key proteins are important for cell adhesion between myocytes and some are involved in adhesion-dependent cell-to-cell signal transduction that allows for a cascade of cell fusion events. 

Oocytes can be unusually large cells in species for which embryonic development takes place away from the mother's body. Their large size can be achieved either by pumping in cytosolic components from adjacent cells through cytoplasmic bridges (Drosophila) or by internalization of nutrient storage granules (yolk granules) by endocytosis (frogs). 

Increases in the size of plant cells are complicated by the fact that almost all plant cells are inside of a solid cell wall. Under the influence of certain plant hormones the cell wall can be remodeled, allowing for increases in cell size that are important for the growth of some plant tissues.

Most unicellular organisms are microscopic in size, but there are some giant bacteria and protozoa that are visible to the naked eye. See: Table of cell sizes —Dense populations of a giant sulfur bacterium in Namibian shelf sediments — Large protists of the genus Chaos, closely related to the genus Amoeba.

 

In the rod-shaped bacteria E. coli, Caulobacter crescentus and B. subtilis cell size is controlled by a simple mechanisms in which cell division occurs after a constant volume has been added since the previous division. By always growing by the same amount, cells born smaller or larger than average naturally converge to an average size equivalent to the amount added during each generation.

Cell division

Cell reproduction is asexual. For most of the constituents of the cell, growth is a steady, continuous process, interrupted only briefly at M phase when the nucleus and then the cell divide in two.

The process of cell division, called cell cycle, has four major parts called phases. The first part, called G₁ phase is marked by synthesis of various enzymes that are required for DNA replication. The second part of the cell cycle is the S phase, where DNA replication produces two identical sets of chromosomes. The third part is the G₂ phase in which a significant protein synthesis occurs, mainly involving the production of microtubules that are required during the process of division, called mitosis. The fourth phase, M phase, consists of nuclear division (karyokinesis) and cytoplasmic division (cytokinesis), accompanied by the formation of a new cell membrane. This is the physical division of "mother" and "daughter" cells. The M phase has been broken down into several distinct phases, sequentially known as prophase, prometaphase, metaphase, anaphase and telophase leading to cytokinesis. 

Cell division is more complex in eukaryotes than in other organisms. Prokaryotic cells such as bacterial cells reproduce by binary fission, a process that includes DNA replication, chromosome segregation, and cytokinesis. Eukaryotic cell division either involves mitosis or a more complex process called meiosis. Mitosis and meiosis are sometimes called the two "nuclear division" processes. Binary fission is similar to eukaryote cell reproduction that involves mitosis. Both lead to the production of two daughter cells with the same number of chromosomes as the parental cell. Meiosis is used for a special cell reproduction process of diploid organisms. It produces four special daughter cells (gametes) which have half the normal cellular amount of DNA. A male and a female gamete can then combine to produce a zygote, a cell which again has the normal amount of chromosomes. 

The rest of this article is a comparison of the main features of the three types of cell reproduction that either involve binary fission, mitosis, or meiosis. The diagram below depicts the similarities and differences of these three types of cell reproduction. 

Cell growth

Comparison of the three types of cell division

The DNA content of a cell is duplicated at the start of the cell reproduction process. Prior to DNA replication, the DNA content of a cell can be represented as the amount Z (the cell has Z chromosomes). After the DNA replication process, the amount of DNA in the cell is 2Z (multiplication: 2 x Z = 2Z). During Binary fission and mitosis the duplicated DNA content of the reproducing parental cell is separated into two equal halves that are destined to end up in the two daughter cells. The final part of the cell reproduction process is cell division, when daughter cells physically split apart from a parental cell. During meiosis, there are two cell division steps that together produce the four daughter cells. 

After the completion of binary fission or cell reproduction involving mitosis, each daughter cell has the same amount of DNA (Z) as what the parental cell had before it replicated its DNA. These two types of cell reproduction produced two daughter cells that have the same number of chromosomes as the parental cell. Chromosomes duplicate prior to cell division when forming new skin cells for reproduction. After meiotic cell reproduction the four daughter cells have half the number of chromosomes that the parental cell originally had. This is the haploid amount of DNA, often symbolized as N. Meiosis is used by diploid organisms to produce haploid gametes. In a diploid organism such as the human organism, most cells of the body have the diploid amount of DNA, 2N. Using this notation for counting chromosomes we say that human somatic cells have 46 chromosomes (2N = 46) while human sperm and eggs have 23 chromosomes (N = 23). Humans have 23 distinct types of chromosomes, the 22 autosomes and the special category of sex chromosomes. There are two distinct sex chromosomes, the X chromosome and the Y chromosome. A diploid human cell has 23 chromosomes from that person's father and 23 from the mother. That is, your body has two copies of human chromosome number 2, one from each of your parents.

Chromosomes

Immediately after DNA replication a human cell will have 46 "double chromosomes". In each double chromosome there are two copies of that chromosome's DNA molecule. During mitosis the double chromosomes are split to produce 92 "single chromosomes", half of which go into each daughter cell. During meiosis, there are two chromosome separation steps which assure that each of the four daughter cells gets one copy of each of the 23 types of chromosome.

Sexual reproduction

Though cell reproduction that uses mitosis can reproduce eukaryotic cells, eukaryotes bother with the more complicated process of meiosis because sexual reproduction such as meiosis confers a selective advantage. Notice that when meiosis starts, the two copies of sister chromatids number 2 are adjacent to each other. During this time, there can be genetic recombination events. Parts of the chromosome 2 DNA gained from one parent (red) will swap over to the chromosome 2 DNA molecule that received from the other parent (green). Notice that in mitosis the two copies of chromosome number 2 do not interact. It is these new combinations of parts of chromosomes that provide the major advantage for sexually reproducing organisms by allowing for new combinations of genes and more efficient evolution. However, in organisms with more than one set of chromosomes at the main life cycle stage, sex may also provide an advantage because, under random mating, it produces homozygotes and heterozygotes according to the Hardy-Weinberg ratio.

Disorders

A series of growth disorders can occur at the cellular level and these consequently underpin much of the subsequent course in cancer, in which a group of cells display uncontrolled growth and division beyond the normal limits, invasion (intrusion on and destruction of adjacent tissues), and sometimes metastasis (spread to other locations in the body via lymph or blood).

Measurement methods

The cell growth can be detected by a variety of methods. The cell size growth can be visualized by microscopy, using suitable stains. But the increase of cells number is usually more significant. It can be measured by manual counting of cells under microscopy observation, using the dye exclusion method (i.e. trypan blue) to count only viable cells. Less fastidious, scalable, methods include the use of cytometers, while flow cytometry allows combining cell counts ('events') with other specific parameters: fluorescent probes for membranes, cytoplasm or nuclei allow distinguishing dead/viable cells, cell types, cell differentiation, expression of a biomarker such as Ki67. 

Beside the increasing number of cells, one can be assessed regarding the metabolic activity growth, that is, the CFDA and calcein-AM measure (fluorimetrically) not only the membrane functionality (dye retention), but also the functionality of cytoplasmic enzymes (esterases). The MTT assays (colorimetric) and the resazurin assay (fluorimetric) dose the mitochondrial redox potential. 

All these assays may correlate well, or not, depending on cell growth conditions and desired aspects (activity, proliferation). The task is even more complicated with populations of different cells, furthermore when combining cell growth interferences or toxicity.

Exponential growth (updated)

From Wikipedia, the free encyclopedia

 

The graph illustrates how exponential growth (green) surpasses both linear (red) and cubic (blue) growth.

  Exponential growth

  Cubic growth

  Linear growth

Exponential growth is exhibited when the rate of change—the change per instant or unit of time—of the value of a mathematical function is proportional to the function's current value, resulting in its value at any time being an exponential function of time, i.e., a function in which the time value is the exponent. Exponential decay occurs in the same way when the growth rate is negative. In the case of a discrete domain of definition with equal intervals, it is also called geometric growth or geometric decay, the function values forming a geometric progression. In either exponential growth or exponential decay, the ratio of the rate of change of the quantity to its current size remains constant over time. 

The formula for exponential growth of a variable x at the growth rate r, as time t goes on in discrete intervals (that is, at integer times 0, 1, 2, 3, ...), is

${\displaystyle x_{t}=x_{0}(1+r)^{t}}$

where x₀ is the value of x at time 0. This formula is transparent when the exponents are converted to multiplication. For instance, with a starting value of 50 and a growth rate of r = 5% = 0.05 per interval, the passage of one interval would give 50 × 1.05¹ = 50 × 1.05; two intervals would give 50 × 1.05² = 50 × 1.05 × 1.05; and three intervals would give 50 × 1.05³ = 50 × 1.05 × 1.05 × 1.05. In this way, each increase in the exponent by a full interval can be seen to increase the previous total by another five percent. (The order of multiplication does not change the result based on the associative property of multiplication.) 

Since the time variable, which is the input to this function, occurs as the exponent, this is an exponential function. This contrasts with growth based on a power function, where the time variable is the base value raised to a fixed exponent, such as cubic growth (or in general terms denoted as polynomial growth).

Examples

Bacteria exhibit exponential growth under optimal conditions.

• Biology
  • The number of microorganisms in a culture will increase exponentially until an essential nutrient is exhausted. Typically the first organism splits into two daughter organisms, who then each split to form four, who split to form eight, and so on. Because exponential growth indicates constant growth rate, it is frequently assumed that exponentially growing cells are at a steady-state. However, cells can grow exponentially at a constant rate while remodeling their metabolism and gene expression.
  • A virus (for example SARS, or smallpox) typically will spread exponentially at first, if no artificial immunization is available. Each infected person can infect multiple new people.
  • Human population, if the number of births and deaths per person per year were to remain at current levels (but also see logistic growth). For example, according to the United States Census Bureau, over the last 100 years (1910 to 2010), the population of the United States of America is exponentially increasing at an average rate of one and a half percent a year (1.5%). This means that the doubling time of the American population (depending on the yearly growth in population) is approximately 50 years.
• Physics
  • Avalanche breakdown within a dielectric material. A free electron becomes sufficiently accelerated by an externally applied electrical field that it frees up additional electrons as it collides with atoms or molecules of the dielectric media. These secondary electrons also are accelerated, creating larger numbers of free electrons. The resulting exponential growth of electrons and ions may rapidly lead to complete dielectric breakdown of the material.
  • Nuclear chain reaction (the concept behind nuclear reactors and nuclear weapons). Each uranium nucleus that undergoes fission produces multiple neutrons, each of which can be absorbed by adjacent uranium atoms, causing them to fission in turn. If the probability of neutron absorption exceeds the probability of neutron escape (a function of the shape and mass of the uranium), k > 0 and so the production rate of neutrons and induced uranium fissions increases exponentially, in an uncontrolled reaction. "Due to the exponential rate of increase, at any point in the chain reaction 99% of the energy will have been released in the last 4.6 generations. It is a reasonable approximation to think of the first 53 generations as a latency period leading up to the actual explosion, which only takes 3–4 generations."
  • Positive feedback within the linear range of electrical or electroacoustic amplification can result in the exponential growth of the amplified signal, although resonance effects may favor some component frequencies of the signal over others.
• Economics
  • Economic growth is expressed in percentage terms, implying exponential growth.
• Finance
  • Compound interest at a constant interest rate provides exponential growth of the capital. See also rule of 72.
  • Pyramid schemes or Ponzi schemes also show this type of growth resulting in high profits for a few initial investors and losses among great numbers of investors.
• Computer technology
  • Processing power of computers. (Under exponential growth, there are no singularities. The singularity here is a metaphor, meant to convey an unimaginable future. The link of this hypothetical concept with exponential growth is most vocally made by futurist Ray Kurzweil.)
  • In computational complexity theory, computer algorithms of exponential complexity require an exponentially increasing amount of resources (e.g. time, computer memory) for only a constant increase in problem size. So for an algorithm of time complexity 2^x, if a problem of size x = 10 requires 10 seconds to complete, and a problem of size x = 11 requires 20 seconds, then a problem of size x = 12 will require 40 seconds. This kind of algorithm typically becomes unusable at very small problem sizes, often between 30 and 100 items (most computer algorithms need to be able to solve much larger problems, up to tens of thousands or even millions of items in reasonable times, something that would be physically impossible with an exponential algorithm). Also, the effects of Moore's Law do not help the situation much because doubling processor speed merely allows you to increase the problem size by a constant. E.g. if a slow processor can solve problems of size x in time t, then a processor twice as fast could only solve problems of size x + constant in the same time t. So exponentially complex algorithms are most often impractical, and the search for more efficient algorithms is one of the central goals of computer science today.

Basic formula

A quantity x depends exponentially on time t if

${\displaystyle x(t)=a\cdot b^{t/\tau }}$

where the constant a is the initial value of x,

${\displaystyle x(0)=a\,,}$

the constant b is a positive growth factor, and τ is the time constant—the time required for x to increase by one factor of b:

${\displaystyle x(t+\tau )=a\cdot b^{\frac {t+\tau }{\tau }}=a\cdot b^{\frac {t}{\tau }}\cdot b^{\frac {\tau }{\tau }}=x(t)\cdot b\,.}$

If τ > 0 and b > 1, then x has exponential growth. If τ < 0 and b > 1, or τ > 0 and 0 < b < 1, then x has exponential decay. 

Example: If a species of bacteria doubles every ten minutes, starting out with only one bacterium, how many bacteria would be present after one hour? The question implies a = 1, b = 2 and τ = 10 min.

${\displaystyle x(t)=a\cdot b^{t/\tau }=1\cdot 2^{(60{\text{ min}})/(10{\text{ min}})}}$

${\displaystyle x(1{\text{ hr}})=1\cdot 2^{6}=64.}$

After one hour, or six ten-minute intervals, there would be sixty-four bacteria. 

Many pairs (b, τ) of a dimensionless non-negative number b and an amount of time τ (a physical quantity which can be expressed as the product of a number of units and a unit of time) represent the same growth rate, with τ proportional to log b. For any fixed b not equal to 1 (e.g. e or 2), the growth rate is given by the non-zero time τ. For any non-zero time τ the growth rate is given by the dimensionless positive number b. 

Thus the law of exponential growth can be written in different but mathematically equivalent forms, by using a different base. The most common forms are the following:

${\displaystyle x(t)=x_{0}\cdot e^{kt}=x_{0}\cdot e^{t/\tau }=x_{0}\cdot 2^{t/T}=x_{0}\cdot \left(1+{\frac {r}{100}}\right)^{t/p},}$

where x₀ expresses the initial quantity x(0). 

Parameters (negative in the case of exponential decay):

• The growth constant k is the frequency (number of times per unit time) of growing by a factor e; in finance it is also called the logarithmic return, continuously compounded return, or force of interest.
• The e-folding time τ is the time it takes to grow by a factor e.
• The doubling time T is the time it takes to double.
• The percent increase r (a dimensionless number) in a period p.

The quantities k, τ, and T, and for a given p also r, have a one-to-one connection given by the following equation (which can be derived by taking the natural logarithm of the above):

${\displaystyle k={\frac {1}{\tau }}={\frac {\ln 2}{T}}={\frac {\ln \left(1+{\frac {r}{100}}\right)}{p}}}$

where k = 0 corresponds to r = 0 and to τ and T being infinite.

If p is the unit of time the quotient t/p is simply the number of units of time. Using the notation t for the (dimensionless) number of units of time rather than the time itself, t/p can be replaced by t, but for uniformity this has been avoided here. In this case the division by p in the last formula is not a numerical division either, but converts a dimensionless number to the correct quantity including unit.

A popular approximated method for calculating the doubling time from the growth rate is the rule of 70, i.e. ${\displaystyle T\simeq 70/r}$. 

Graphs comparing doubling times and half lives of exponential growths (bold lines) and decay (faint lines), and their 70/t and 72/t approximations. In the SVG version, hover over a graph to highlight it and its complement.

Reformulation as log-linear growth

If a variable x exhibits exponential growth according to ${\displaystyle x(t)=x_{0}(1+r)^{t}}$, then the log (to any base) of x grows linearly over time, as can be seen by taking logarithms of both sides of the exponential growth equation:

${\displaystyle \log x(t)=\log x_{0}+t\cdot \log(1+r).}$

This allows an exponentially growing variable to be modeled with a log-linear model. For example, if one wishes to empirically estimate the growth rate from intertemporal data on x, one can linearly regress log x on t.

Differential equation

The exponential function ${\displaystyle x(t)=x(0)e^{kt}}$ satisfies the linear differential equation:

${\displaystyle \!\,{\frac {dx}{dt}}=kx}$

saying that the change per instant of time of x at time t is proportional to the value of x(t), and x(t) has the initial value

${\displaystyle x(0).}$

The differential equation is solved by direct integration:

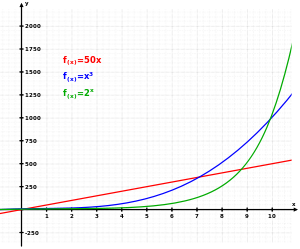
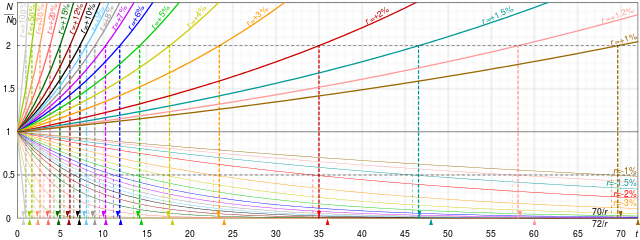
${\displaystyle {\begin{aligned}{\frac {dx}{dt}}&=kx\\[5pt]{\frac {dx}{x}}&=k\,dt\\[5pt]\int _{x(0)}^{x(t)}{\frac {dx}{x}}&=k\int _{0}^{t}\,dt\\[5pt]\ln {\frac {x(t)}{x(0)}}&=kt.\end{aligned}}}$

so that

${\displaystyle x(t)=x(0)e^{kt}}$

In the above differential equation, if k < 0, then the quantity experiences exponential decay. 

For a nonlinear variation of this growth model see logistic function.

Difference equation

The difference equation

${\displaystyle x_{t}=a\cdot x_{t-1}}$

has solution

${\displaystyle x_{t}=x_{0}\cdot a^{t},}$

showing that x experiences exponential growth.

Other growth rates

In the long run, exponential growth of any kind will overtake linear growth of any kind (the basis of the Malthusian catastrophe) as well as any polynomial growth, i.e., for all α:

${\displaystyle \lim _{t\rightarrow \infty }{t^{\alpha } \over ae^{t}}=0.}$

There is a whole hierarchy of conceivable growth rates that are slower than exponential and faster than linear (in the long run). See Degree of a polynomial#The degree computed from the function values. 

Growth rates may also be faster than exponential. In the most extreme case, when growth increases without bound in finite time, it is called hyperbolic growth. In between exponential and hyperbolic growth lie more classes of growth behavior, like the hyperoperations beginning at tetration, and ${\displaystyle A(n,n)}$, the diagonal of the Ackermann function.

Limitations of models

Exponential growth models of physical phenomena only apply within limited regions, as unbounded growth is not physically realistic. Although growth may initially be exponential, the modelled phenomena will eventually enter a region in which previously ignored negative feedback factors become significant (leading to a logistic growth model) or other underlying assumptions of the exponential growth model, such as continuity or instantaneous feedback, break down.

Exponential stories

Rice on a chessboard

According to an old legend, vizier Sissa Ben Dahir presented an Indian King Sharim with a beautiful, hand-made chessboard. The king asked what he would like in return for his gift and the courtier surprised the king by asking for one grain of rice on the first square, two grains on the second, four grains on the third etc. The king readily agreed and asked for the rice to be brought. All went well at first, but the requirement for 2ⁿ⁻¹ grains on the nth square demanded over a million grains on the 21st square, more than a million million (a.k.a. trillion) on the 41st and there simply was not enough rice in the whole world for the final squares. (From Swirski, 2006)

The second half of the chessboard is the time when an exponentially growing influence is having a significant economic impact on an organization's overall business strategy.

Water lily

French children are told a story in which they imagine having a pond with water lily leaves floating on the surface. The lily population doubles in size every day and, if left unchecked, it will smother the pond in 30 days killing all the other living things in the water. Day after day, the plant's growth is small and so it is decided that it shall be cut down when the water lilies cover half of the pond. The children are then asked on what day will half of the pond be covered in water lilies. The solution is simple when one considers that the water lilies must double to completely cover the pond on the 30th day. Therefore, the water lilies will cover half of the pond on the 29th day. There is only one day to save the pond. (From Meadows et al. 1972)

Thomas Robert Malthus (updated)

From Wikipedia, the free encyclopedia

Thomas Robert Malthus
Portrait by John Linnell
Born	13/14 February 1766 Westcott, Surrey, England
Died	23 December 1834 (aged 68) Bath, Somerset, England
Nationality	British
Field	Demography, macroeconomics
School or tradition	Classical economics
Alma mater	Jesus College, Cambridge
Influences	David Ricardo, Jean Charles Léonard de Sismondi
Contributions	Malthusian growth model

Thomas Robert Malthus FRS (/ˈmælθəs/; 13 February 1766 – 23 December 1834) was an English cleric and scholar, influential in the fields of political economy and demography. Malthus himself used only his middle name, Robert.

In his 1798 book An Essay on the Principle of Population, Malthus observed that an increase in a nation's food production improved the well-being of the populace, but the improvement was temporary because it led to population growth, which in turn restored the original per capita production level. In other words, mankind had a propensity to utilize abundance for population growth rather than for maintaining a high standard of living, a view that has become known as the "Malthusian trap" or the "Malthusian spectre". Populations had a tendency to grow until the lower class suffered hardship and want and greater susceptibility to famine and disease, a view that is sometimes referred to as a Malthusian catastrophe. Malthus wrote in opposition to the popular view in 18th-century Europe that saw society as improving and in principle as perfectible. He saw population growth as being inevitable whenever conditions improved, thereby precluding real progress towards a utopian society: "The power of population is indefinitely greater than the power in the earth to produce subsistence for man". As an Anglican cleric, Malthus saw this situation as divinely imposed to teach virtuous behavior. Malthus wrote:

That the increase of population is necessarily limited by the means of subsistence,
That population does invariably increase when the means of subsistence increase, and,
That the superior power of population is repressed by moral restraint, vice and misery.

Malthus criticized the Poor Laws for leading to inflation rather than improving the well-being of the poor. He supported taxes on grain imports (the Corn Laws), because food security was more important than maximizing wealth. His views became influential, and controversial, across economic, political, social and scientific thought. Pioneers of evolutionary biology read him, notably Charles Darwin and Alfred Russel Wallace. He remains a much-debated writer.

Early life and education

The sixth child of Henrietta Catherine (Graham) and Daniel Malthus, Robert Malthus grew up in The Rookery, a country house in Westcott, near Dorking in Surrey. Thomas was bullied from an early age because of his syndactyly, or webbed feet. This sparked his controversial ideas about eugenics. Petersen describes Daniel Malthus as "a gentleman of good family and independent means... [and] a friend of David Hume and Jean-Jacques Rousseau". The young Malthus received his education at home in Bramcote, Nottinghamshire, and then at the Warrington Academy from 1782. Warrington was a dissenting academy, which closed in 1783; Malthus continued for a period to be tutored by Gilbert Wakefield who had taught him there.

Malthus entered Jesus College, Cambridge in 1784. There he took prizes in English declamation, Latin and Greek, and graduated with honors, Ninth Wrangler in mathematics. His tutor was William Frend. He took the MA degree in 1791, and was elected a Fellow of Jesus College two years later. In 1789, he took orders in the Church of England, and became a curate at Oakwood Chapel (also Okewood) in the parish of Wotton, Surrey.

Population growth

Essay on the principle of population, 1826

 

Malthus came to prominence for his 1798 essay on population growth. In it, he argued that population multiplies geometrically and food arithmetically; therefore, whenever the food supply increases, population will rapidly grow to eliminate the abundance. Between 1798 and 1826 he published six editions of An Essay on the Principle of Population, updating each edition to incorporate new material, to address criticism, and to convey changes in his own perspectives on the subject. He wrote the original text in reaction to the optimism of his father and his father's associates (notably Rousseau) regarding the future improvement of society. Malthus also constructed his case as a specific response to writings of William Godwin (1756–1836) and of the Marquis de Condorcet (1743–1794). 

The Essay gave rise to the Malthusian controversy during the next decades. The content saw an emphasis on the birth rate and marriage rates. The neo-Malthusian controversy, or related debates of many years later, has seen a similar central role assigned to the numbers of children born.

In 1799 Malthus made a European tour with William Otter, a close college friend, travelling part of the way with Edward Daniel Clarke and John Marten Cripps, visiting Germany, Scandinavia and Russia. Malthus used the trip to gather population data. Otter later wrote a Memoir of Malthus for the second (1836) edition of his Principles of Political Economy. During the Peace of Amiens of 1802 he traveled to France and Switzerland, in a party that included his relation and future wife Harriet. In 1803 he became rector of Walesby, Lincolnshire.

Academic

In 1805 Malthus became Professor of History and Political Economy at the East India Company College in Hertfordshire. His students affectionately referred to him as "Pop", "Population", or "web-toe" Malthus. 

At the end of 1816 the proposed appointment of Graves Champney Haughton to the College was made a pretext by Randle Jackson and Joseph Hume to launch an attempt to close it down. Malthus wrote a pamphlet defending the College, which was reprieved by the East India Company in 1817. In 1818 Malthus became a Fellow of the Royal Society.

Malthus–Ricardo debate on political economy

During the 1820s there took place a setpiece intellectual discussion within the proponents of political economy, often called the "Malthus–Ricardo debate", after the leading figures of Malthus and David Ricardo, a theorist of free trade, both of whom had written books with the title Principles of Political Economy. Under examination were the nature and methods of political economy itself, while it was simultaneously under attack from others. The roots of the debate were in the previous decade. In The Nature of Rent (1815), Malthus had dealt with economic rent, a major concept in classical economics. Ricardo defined a theory of rent in his Principles of Political Economy and Taxation (1817): he regarded rent as value in excess of real production—something caused by ownership rather than by free trade. Rent therefore represented a kind of negative money that landlords could pull out of the production of the land, by means of its scarcity. Contrary to this concept, Malthus proposed rent to be a kind of economic surplus.

The debate developed over the economic concept of a general glut, and the possibility of failure of Say's Law. Malthus laid importance on economic development and the persistence of disequilibrium. The context was the post-war depression; Malthus had a supporter in William Blake, in denying that capital accumulation (saving) was always good in such circumstances, and John Stuart Mill attacked Blake on the fringes of the debate.

Ricardo corresponded with Malthus from 1817 and his Principles. He was drawn into considering political economy in a less restricted sense, which might be adapted to legislation and its multiple objectives, by the thought of Malthus. In his own work Principles of Political Economy (1820), and elsewhere, Malthus addressed the tension, amounting to conflict, he saw between a narrow view of political economy, and the broader moral and political plane. Leslie Stephen wrote:

If Malthus and Ricardo differed, it was a difference of men who accepted the same first principles. They both professed to interpret Adam Smith as the true prophet, and represented different shades of opinion rather than diverging sects.

After Ricardo's death in 1823, Malthus became isolated among the younger British political economists, who tended to think he had lost the debate.It is now considered that the different purposes seen by Malthus and Ricardo for political economy affected their technical discussion, and contributed to the lack of compatible definitions. For example, Jean-Baptiste Say used a definition of production based on goods and services and so queried the restriction of Malthus to "goods" alone.

In terms of public policy, Malthus was a supporter of the protectionist Corn Laws from the end of the Napoleonic Wars. He emerged as the only economist of note to support duties on imported grain. He changed his mind after 1814. By encouraging domestic production, Malthus argued, the Corn Laws would guarantee British self-sufficiency in food.

Later life

Malthus was a founding member of the Political Economy Club in 1821; there John Cazenove tended to be his ally, against Ricardo and Mill. He was elected in the beginning of 1824 as one of the ten royal associates of the Royal Society of Literature. He was also one of the first fellows of the Statistical Society, founded in March 1834. In 1827 he gave evidence to a committee of the House of Commons on emigration.

In 1827, he published Definitions in Political Economy, preceded by an inquiry into the rules which ought to guide political economists in the definition and use of their terms; with remarks on the deviation from these rules in their writings. The first chapter put forth "Rules for the Definition and Application of Terms in Political Economy". In chapter 10, the penultimate chapter, he presented 60 numbered paragraphs putting forth terms and their definitions that he proposed, following those rules, should be used in discussing political economy. This collection of terms and definitions is remarkable for two reasons: first, Malthus was the first economist to explicitly organize, define, and publish his terms as a coherent glossary of defined terms; and second, his definitions were, for the most part, well-formed definitional statements. Between these chapters, he criticized several contemporary economists—Jean-Baptiste Say, David Ricardo, James Mill, John Ramsay McCulloch, and Samuel Bailey—for sloppiness in choosing, attaching meaning to, and using their technical terms.

McCulloch was the editor of The Scotsman of Edinburgh; he replied cuttingly in a review printed on the front page of his newspaper in March, 1827. He implied that Malthus wanted to dictate terms and theories to other economists. McCulloch clearly felt his ox gored, and his review of Definitions is largely a bitter defense of his own Principles of Political Economy, and his counter-attack "does little credit to his reputation", being largely "personal derogation" of Malthus. The purpose of Malthus's Definitions was terminological clarity, and Malthus discussed appropriate terms, their definitions, and their use by himself and his contemporaries. This motivation of Malthus's work was disregarded by McCulloch, who responded that there was nothing to be gained "by carping at definitions, and quibbling about the meaning to be attached to" words. Given that statement, it is not surprising that McCulloch's review failed to address the rules of chapter 1 and did not discuss the definitions of chapter 10; he also barely mentioned Malthus's critiques of other writers.

In spite of this, in the wake of McCulloch's scathing review, the reputation of Malthus as economist dropped away, for the rest of his life. On the other hand, Malthus did have supporters: Thomas Chalmers, some of the Oriel Noetics, Richard Jones and William Whewell from Cambridge.

Malthus died suddenly of heart disease on 23 December 1834, at his father-in-law's house. He was buried in Bath Abbey. His portrait, and descriptions by contemporaries, present him as tall and good-looking, but with a cleft lip and palate. The cleft palate affected his speech: such birth defects had occurred before among his relatives.

Family

On 13 March 1804, Malthus married Harriet, daughter of John Eckersall of Claverton House, near Bath. They had a son and two daughters. His firstborn, son Henry, became vicar of Effingham, Surrey, in 1835, and of Donnington, Sussex, in 1837; he married Sofia Otter (1807–1889), daughter of Bishop William Otter, and died in August 1882, aged 76. His middle child, Emily, died in 1885, outliving her parents and siblings. The youngest, Lucille, died unmarried and childless in 1825, months before her 18th birthday.

An Essay on the Principle of Population

Malthus argued in his Essay (1798) that population growth generally expanded in times and in regions of plenty until the size of the population relative to the primary resources caused distress:

Yet in all societies, even those that are most vicious, the tendency to a virtuous attachment [i.e., marriage] is so strong that there is a constant effort towards an increase of population. This constant effort as constantly tends to subject the lower classes of the society to distress and to prevent any great permanent amelioration of their condition.

— Malthus, T. R. 1798. An Essay on the Principle of Population. Chapter II, p. 18 in Oxford World's Classics reprint.

Malthus argued that two types of checks hold population within resource limits: positive checks, which raise the death rate; and preventive ones, which lower the birth rate. The positive checks include hunger, disease and war; the preventive checks: birth control, postponement of marriage and celibacy.

The rapid increase in the global population of the past century exemplifies Malthus's predicted population patterns; it also appears to describe socio-demographic dynamics of complex pre-industrial societies. These findings are the basis for neo-malthusian modern mathematical models of long-term historical dynamics.

Malthus wrote that in a period of resource abundance, a population could double in 25 years. However, the margin of abundance could not be sustained as population grew, leading to checks on population growth:

If the subsistence for man that the earth affords was to be increased every twenty-five years by a quantity equal to what the whole world at present produces, this would allow the power of production in the earth to be absolutely unlimited, and its ratio of increase much greater than we can conceive that any possible exertions of mankind could make it ... yet still the power of population being a power of a superior order, the increase of the human species can only be kept commensurate to the increase of the means of subsistence by the constant operation of the strong law of necessity acting as a check upon the greater power.

— Malthus T. R. 1798. An Essay on the Principle of Population. Chapter 2, p. 8

In later editions of his essay, Malthus clarified his view that if society relied on human misery to limit population growth, then sources of misery (e.g., hunger, disease, and war) would inevitably afflict society, as would volatile economic cycles. On the other hand, "preventive checks" to population that limited birthrates, such as later marriages, could ensure a higher standard of living for all, while also increasing economic stability. Regarding possibilities for freeing man from these limits, Malthus argued against a variety of imaginable solutions, such as the notion that agricultural improvements could expand without limit.

Of the relationship between population and economics, Malthus wrote that when the population of laborers grows faster than the production of food, real wages fall because the growing population causes the cost of living (i.e., the cost of food) to go up. Difficulties of raising a family eventually reduce the rate of population growth, until the falling population again leads to higher real wages. 

In the second and subsequent editions Malthus put more emphasis on moral restraint as the best means of easing the poverty of the lower classes."

Editions and versions

• 1798: An Essay on the Principle of Population, as it affects the future improvement of society with remarks on the speculations of Mr. Godwin, M. Condorcet, and other writers.. Anonymously published.
• 1803: Second and much enlarged edition: An Essay on the Principle of Population; or, a view of its past and present effects on human happiness; with an enquiry into our prospects respecting the future removal or mitigation of the evils which it occasions. Authorship acknowledged.
• 1806, 1807, 1816 and 1826: editions 3–6, with relatively minor changes from the second edition.
• 1823: Malthus contributed the article on Population to the supplement of the Encyclopædia Britannica.
• 1830: Malthus had a long extract from the 1823 article reprinted as A summary view of the Principle of Population.

Other works

1800: The present high price of provisions

In this work, his first published pamphlet, Malthus argues against the notion prevailing in his locale that the greed of intermediaries caused the high price of provisions. Instead, Malthus says that the high price stems from the Poor Laws, which "increase the parish allowances in proportion to the price of corn." Thus, given a limited supply, the Poor Laws force up the price of daily necessities. But he concludes by saying that in time of scarcity such Poor Laws, by raising the price of corn more evenly, actually produce a beneficial effect.

1814: Observations on the effects of the Corn Laws

Although government in Britain had regulated the prices of grain, the Corn Laws originated in 1815. At the end of the Napoleonic Wars that year, Parliament passed legislation banning the importation of foreign corn into Britain until domestic corn cost 80 shillings per quarter. The high price caused the cost of food to increase and caused distress among the working classes in the towns. It led to serious rioting in London and to the Peterloo Massacre in Manchester in 1819.

In this pamphlet, printed during the parliamentary discussion, Malthus tentatively supported the free-traders. He argued that given the increasing cost of growing British corn, advantages accrued from supplementing it from cheaper foreign sources.

1820: Principles of political economy

In 1820 Malthus published Principles of Political Economy. 1836: Second edition, posthumously published. Malthus intended this work to rival Ricardo's Principles (1817). It, and his 1827 Definitions in political economy, defended Sismondi's views on "general glut" rather than Say's Law, which in effect states "there can be no general glut".

Other publications

• 1807. A letter to Samuel Whitbread, Esq. M.P. on his proposed Bill for the Amendment of the Poor Laws. Johnson and Hatchard, London.
• 1808. Spence on Commerce. Edinburgh Review 11, January, 429–448.
• 1808. Newneham and others on the state of Ireland. Edinburgh Review 12, July, 336–355.
• 1809. Newneham on the state of Ireland, Edinburgh Review 14 April, 151–170.
• 1811. Depreciation of paper currency. Edinburgh Review 17, February, 340–372.
• 1812. Pamphlets on the bullion question. Edinburgh Review 18, August, 448–470.
• 1813. A letter to the Rt. Hon. Lord Grenville. Johnson, London.
• 1817. Statement respecting the East-India College. Murray, London.
• 1821. Godwin on Malthus. Edinburgh Review 35, July, 362–377.
• 1823. The Measure of Value, stated and illustrated
• 1823. Tooke – On high and low prices. Quarterly Review, 29 (57), April, 214–239.
• 1824. Political economy. Quarterly Review 30 (60), January, 297–334.
• 1829. On the measure of the conditions necessary to the supply of commodities. Transactions of the Royal Society of Literature of the United Kingdom. 1, 171–180. John Murray, London.
• 1829. On the meaning which is most usually and most correctly attached to the term Value of a Commodity. Transactions of the Royal Society of Literature of the United Kingdom. 2, 74–81. John Murray.

Reception and influence

Malthus developed the theory of demand-supply mismatches that he called gluts. Discounted at the time, this theory foreshadowed later works of an admirer, John Maynard Keynes.

The vast bulk of continuing commentary on Malthus, however, extends and expands on the "Malthusian controversy" of the early 19th century.

In popular culture

• Ebenezer Scrooge from A Christmas Carol by Charles Dickens, represents the perceived ideas of Malthus, famously illustrated by his explanation as to why he refuses to donate to the poor and destitute: "If they would rather die they had better do it, and decrease the surplus population". In general, Dickens had some Malthusian concerns (evident in Oliver Twist, Hard Times and other novels), and he concentrated his attacks on Utilitarianism and many of its proponents, like Bentham, whom he thought of, along with Malthus, as unjust and inhumane people.
• In Aldous Huxley's novel, Brave New World, people generally regard fertility as a nuisance, as in vitro breeding has enabled the society to maintain its population at precisely the level the controllers want. The women, therefore, carry contraceptives with them at all times in a "Malthusian belt".
• Malthus and his ideas feature prominently in Adolfo Bioy Casares's novel The Invention of Morel
• In Robert A. Heinlein's novel The Moon Is a Harsh Mistress, Professor Bernardo de la Paz asks Manuel "Mannie" Garcia O'Kelly-Davis if he has read Malthus. After Mannie tells him he doesn't think so the Professor tells him to read Malthus but not until after their diplomatic work is over since "too many facts hamper a diplomat, especially an honest one." The Professor calls Malthus "a depressing man" and warns Mannie "it is never safe to laugh at Dr. Malthus; he always has the last laugh."
• In George R. R. Martin's science fiction fix-up novel Tuf Voyaging, a planet struggling with overpopulation is named "S'uthlam", an anagram for Malthus.
• In the television show Wiseguy, Kevin Spacey played Mel Proffitt, a self-professed "Malthusian" who quotes Thomas Malthus and keeps a bust of his likeness on display.
• In the show Sliders, episode "Luck of the Draw", the gang slides to an Earth where Malthus’ theories are taken seriously and population is controlled through a lottery.
• At the end of Urinetown, a Broadway musical about a dystopia where, in response to a devastating drought, people too poor to pay for restroom usage are killed as a means of population control, Officer Lockstock cries "Hail, Malthus!" and is echoed by the cast before the last chords of the finale play.
• In the video game Victoria: An Empire Under the Sun the player can research the technology "Malthusian Thought" as a benefit to their country.
• The video game Hydrophobia tells about some eco-terrorists who name themselves "Malthusians" because their ideology is based on Malthus' theories.
• In Marvel's film Avengers: Infinity War, the main villain called Thanos appears to be motivated by Malthusian views about population growth.

Epitaph

The epitaph of Rev. Thomas Robert Malthus, just inside the entrance to Bath Abbey.

The epitaph of Malthus in Bath Abbey reads [with commas inserted for clarity]:

Sacred to the memory of the Rev THOMAS ROBERT MALTHUS, long known to the lettered world by his admirable writings on the social branches of political economy, particularly by his essay on population.

One of the best men and truest philosophers of any age or country, raised by native dignity of mind above the misrepresentation of the ignorant and the neglect of the great, he lived a serene and happy life devoted to the pursuit and communication of truth, supported by a calm but firm conviction of the usefulness of his labours, content with the approbation of the wise and good.

His writings will be a lasting monument of the extent and correctness of his understanding.

The spotless integrity of his principles, the equity and candor of his nature, his sweetness of temper, urbanity of manners and tenderness of heart, his benevolence and his piety are still dearer recollections of his family and friends.

Born February 14, 1766 - Died 29 December 1834.