Steam-methane reforming is a mature production process in which
high-temperature steam (700 °C–1,000 °C) is used to produce hydrogen
from natural gas. Methane reacts with steam under 3–25 bar pressure in
the presence of a catalyst to produce hydrogen, carbon monoxide, and a
relatively small amount of carbon dioxide. For steam reforming to
proceed, heat must be supplied to the process. In a separate reactor
vessel, the carbon monoxide and steam are reacted using a catalyst to
produce carbon dioxide and more hydrogen. In a final process step called
"pressure-swing adsorption," carbon dioxide and other impurities are
removed from the gas stream, leaving essentially pure hydrogen. Steam
reforming can also be used to produce hydrogen from other fuels, such as
coal and oil products.
There are no natural hydrogen deposits, but hydrogen is required for essential chemical processes. Therefore, the production of hydrogen plays a key role in any industrialized society. The hydrogen generation market is expected to be valued at $115.25 billion USD in 2017. Millions of tons of hydrogen were consumed on-site in oil refining, and in the production of ammonia (Haber process) and methanol (reduction of carbon monoxide). Hydrogen is also produced as a by-product of the chlor-alkali process.
As of 1999, the majority of hydrogen (∼95%) is produced from fossil fuels by steam reforming or partial oxidation of methane and coal gasification with only a small quantity by other routes such as biomass gasification or electrolysis of water. Around 8GW of electrolysis capacity is installed worldwide, accounting for around 4% of global hydrogen production. Developing affordable methods for producing hydrogen with less damage to the environment is a goal of the hydrogen economy. Electrolysis of water using electricity produced from fossil fuels emits significant amounts of CO2.
There are no natural hydrogen deposits, but hydrogen is required for essential chemical processes. Therefore, the production of hydrogen plays a key role in any industrialized society. The hydrogen generation market is expected to be valued at $115.25 billion USD in 2017. Millions of tons of hydrogen were consumed on-site in oil refining, and in the production of ammonia (Haber process) and methanol (reduction of carbon monoxide). Hydrogen is also produced as a by-product of the chlor-alkali process.
As of 1999, the majority of hydrogen (∼95%) is produced from fossil fuels by steam reforming or partial oxidation of methane and coal gasification with only a small quantity by other routes such as biomass gasification or electrolysis of water. Around 8GW of electrolysis capacity is installed worldwide, accounting for around 4% of global hydrogen production. Developing affordable methods for producing hydrogen with less damage to the environment is a goal of the hydrogen economy. Electrolysis of water using electricity produced from fossil fuels emits significant amounts of CO2.
Steam reforming
There are four main sources for the commercial production of
hydrogen: natural gas, oil, coal, and electrolysis; which account for
48%, 30%, 18% and 4% of the world’s hydrogen production respectively.
Fossil fuels are the dominant source of industrial hydrogen. Carbon dioxide can be separated from natural gas with a 70-85% efficiency for hydrogen production and from other hydrocarbons to varying degrees of efficiency. Specifically, bulk hydrogen is usually produced by the steam reforming of methane or natural gas.
The production of hydrogen from natural gas is the cheapest source of
hydrogen currently. This process consists of heating the gas to between
700-1100 °C in the presence of steam and a nickel catalyst. The
resulting endothermic reaction breaks up the methane molecules and forms carbon monoxide CO and hydrogen H2. The carbon monoxide gas can then be passed with steam over iron oxide or other oxides and undergo a water gas shift reaction to obtain further quantities of H2. The downside to this process is that its major byproducts are CO, CO2 and other greenhouse gases.
Depending on the quality of the feedstock (natural gas, rich gases,
naphtha, etc.), one ton of hydrogen produced will also produce 9 to 12
tons of CO2.
For this process high temperature (700–1100 °C) steam (H2O) reacts with methane (CH4) in an endothermic reaction to yield syngas.
Gasification
- CH4 + H2O → CO + 3 H2
In a second stage, additional hydrogen is generated through the lower-temperature, exothermic, water gas shift reaction, performed at about 360 °C:
- CO + H2O → CO2 + H2
Essentially, the oxygen (O) atom is stripped from the additional water (steam) to oxidize CO to CO2.
This oxidation also provides energy to maintain the reaction.
Additional heat required to drive the process is generally supplied by
burning some portion of the methane.
CO2 sequestration
Steam reforming generates carbon dioxide (CO2). Since the production is concentrated in one facility, it is possible to separate the CO2 and dispose of it without atmospheric release, for example by injecting it in an oil or gas reservoir, although this is not currently done in most cases. A carbon dioxide injection project has been started by the Norwegian company Statoil in the North Sea, at the Sleipner field.
Integrated steam reforming / co-generation - It is possible to combine steam reforming and co-generation of steam and power into a single plant. This can deliver benefits for an oil refinery because it is more efficient than separate hydrogen, steam and power plants. Air Products recently built an integrated steam reforming / co-generation plant in Port Arthur, Texas.
Other production methods from fossil fuels
Partial oxidation
Hydrogen
production from natural gas or other hydrocarbons is achieved by
partial oxidation. A fuel-air or fuel-oxygen mixture is partially
combusted resulting in a hydrogen rich syngas. Hydrogen and carbon monoxide are obtained via the water-gas shift reaction. Carbon dioxide can be co-fed to lower the hydrogen to carbon monoxide ratio.
The partial oxidation reaction occurs when a substoichiometric fuel-air mixture or fuel-oxygen is partially combusted in a reformer or partial oxidation reactor. A distinction is made between thermal partial oxidation (TPOX) and catalytic partial oxidation (CPOX). The chemical reaction takes the general form:
- CnHm + n/2 O2 → n CO + m/2 H2
Idealized examples for heating oil and coal, assuming compositions C12H24 and C24H12 respectively, are as follows:
- C12H24 + 6 O2 → 12 CO + 12 H2
- C24H12 + 12 O2 → 24 CO + 6 H2
Plasma reforming
The Kværner-process or Kvaerner carbon black & hydrogen process (CB&H) is a plasma reforming method, developed in the 1980s by a Norwegian company of the same name, for the production of hydrogen and carbon black from liquid hydrocarbons (CnHm). Of the available energy of the feed, approximately 48% is contained in the hydrogen, 40% is contained in activated carbon and 10% in superheated steam. CO2 is not produced in the process.
A variation of this process is presented in 2009 using plasma arc waste disposal technology for the production of hydrogen, heat and carbon from methane and natural gas in a plasma converter.
Coal
For the production of hydrogen from coal, coal
gasification is used. The process of coal gasification uses steam and a
carefully controlled concentration of gases to break molecular bonds in
coal and form a gaseous mix of hydrogen and carbon monoxide.
This source of hydrogen is advantageous since its main product is
coal-derived gas which can be used for fuel. The gas obtained from coal
gasification can later be used to produce electricity more efficiently
and allow a better capture of greenhouse gases than the traditional
burning of coal.
Another method for conversion is low temperature and high temperature coal carbonization.
Petroleum coke
Similarly to coal, petroleum coke can also be converted in hydrogen rich syngas, via coal gasification. The syngas in this case consists mainly of hydrogen, carbon monoxide and H2S, depending on the sulfur content of the coke feed. Gasification
is an attractive option for producing hydrogen from almost any carbon
source, while providing attractive hydrogen utilization alternatives
through process integration.
From water
Many technologies have been explored but, as of 2007, "Thermal,
thermochemical, biochemical and photochemical processes have so far not
found industrial applications." High temperature electrolysis of alkaline solutions has been used for the industrial scale production of hydrogen and there are now a number of small scale polymer electrolyte membrane (PEM) electrolysis units available commercially.
Gas Extraction
Electrolysis consists of using electricity to split water into hydrogen and oxygen. Electrolysis of water is 70-80% efficient (a 20-30% conversion loss) while steam reforming of natural gas has a thermal efficiency between 70-85%. The (electrical) efficiency of electrolysis is expected to reach 82-86% before 2030, while also maintaining durability as progress in this area continues at a pace. Water electrolysis can operate between 50-80 °C, while steam methane reforming requires temperatures between 700-1100 °C.
The difference between the two methods is the primary energy used;
either electricity (for electrolysis) or natural gas (for steam methane
reforming). Due to their use of water, a readily available resource,
electrolysis and similar water-splitting methods have attracted the
interest of the scientific community. With the objective of reducing the
cost of hydrogen production, renewable sources of energy have been
targeted to allow electrolysis.
There are three main types of cells, solid oxide electrolysis cells (SOECs), polymer electrolyte membrane cells (PEM) and alkaline electrolysis cells (AECs).
SOECs operate at high temperatures, typically around 800 °C. At these
high temperatures a significant amount of the energy required can be
provided as thermal energy (heat), and as such is termed High temperature electrolysis.
The heat energy can be provided from a number of different sources,
including waste industrial heat, nuclear power stations or concentrated
solar thermal plants. This has the potential to reduce the overall cost
of the hydrogen produced by reducing the amount of electrical energy
required for electrolysis. PEM electrolysis cells typically operate below 100 °C and are becoming increasingly available commercially.
These cells have the advantage of being comparatively simple and can be
designed to accept widely varying voltage inputs which makes them ideal
for use with renewable sources of energy such as solar PV.
AECs optimally operate at high concentrations electrolyte (KOH or
potassium carbonate) and at high temperatures, often near 200 °C.
Industrial output and efficiency
Efficiency of modern hydrogen generators is measured by energy consumed per standard volume of hydrogen (MJ/m3), assuming standard temperature and pressure of the H2.
The lower the energy used by a generator, the higher would be its
efficiency; a 100%-efficient electrolyser would consume 39.4
kilowatt-hours per kilogram (142 MJ/kg) of hydrogen, 12,749 joules per litre (12.75 MJ/m3).
Practical electrolysis (using a rotating electrolyser at 15 bar
pressure) may consume 50 kilowatt-hours per kilogram (180 MJ/kg), and a
further 15 kilowatt-hours (54 MJ) if the hydrogen is compressed for use
in hydrogen cars.
Electrolyser vendors provide efficiencies based on enthalpy.
To assess the claimed efficiency of an electrolyser it is important to
establish how it was defined by the vendor (i.e. what enthalpy value,
what current density, etc.).
There are two main technologies available on the market, alkaline and proton exchange membrane
(PEM) electrolysers.
Traditionally, alkaline electrolysers are cheaper in terms of investment
(they generally use nickel catalysts), but less efficient; PEM
electrolysers, conversely, are more expensive (they generally use
expensive platinum-group metal catalysts) but are more efficient and can
operate at higher current densities, and can therefore be possibly
cheaper if the hydrogen production is large enough.
Conventional alkaline electrolysis has an efficiency of about 70%, however thyssenkrupp have recently developed an advanced alkaline water electrolyser with an efficiency of 82%.
Accounting for the use of the higher heat value (because inefficiency
via heat can be redirected back into the system to create the steam
required by the catalyst), average working efficiencies for PEM electrolysis are around 80%, or 82% using the most modern alkaline electrolysers. PEM efficiency is expected to increase to approximately 86% before 2030. Theoretical efficiency for PEM electrolysers are predicted up to 94%.
H2 production cost ($-gge untaxed) at varying natural gas prices
Considering the industrial production of hydrogen, and using current
best processes for water electrolysis (PEM or alkaline electrolysis)
which have an effective electrical efficiency of 70-82%, producing 1 kg of hydrogen (which has a specific energy
of 143 MJ/kg or about 40 kWh/kg) requires 50–55 kWh of electricity. At
an electricity cost of $0.06/kWh, as set out in the Department of Energy
hydrogen production
targets for 2015, the hydrogen cost is $3/kg. With the range of natural gas prices from 2016 as shown in the graph (Hydrogen Production Tech Team Roadmap, November 2017)
putting the cost of SMR hydrogen at between $1.20 and $1.50, the cost
price of hydrogen via electrolysis is still over double 2015 DOE
hydrogen target prices. The US DOE target price for hydrogen in 2020 is
$2.30/kg, requiring an electricity cost of $0.037/kWh, which is
achievable given recent PPA tenders
for wind and solar in many regions. This puts the $4/gge H2 dispensed
objective well within reach, and close to a slightly elevated natural
gas production cost for SMR.
In many cases, the advantage of electrolysis over SMR hydrogen is
that the hydrogen can be produced on-site, meaning that the costly
process of delivery via truck or pipeline is avoided.
In other parts of the world, steam methane reforming is between
$1–3/kg on average. This makes production of hydrogen via electrolysis
cost competitive in many regions already, as outlined by Nel Hydrogen and others, including an article by the IEA examining the conditions which could lead to a competitive advantage for electrolysis.
Chemically assisted electrolysis (Carbon/hydrocarbon assisted water electrolysis; CAWE)
In
addition to reducing the voltage required for electrolysis via the
increasing of the temperature of the electrolysis cell it is also
possible to electrochemically consume the oxygen produced in an
electrolyser by introducing a fuel (such as carbon/coal, methanol, ethanol, formic acid, glycerol,
etc.) into the oxygen side of the reactor. This reduces the required
electrical energy and has the potential to reduce the cost of hydrogen
to less than 40~60% with the remaining energy provided in this manner.
In addition, carbon/hydrocarbon assisted electrolysis has the potential
to offer a less energy intensive, cleaner method of using chemical
energy in various sources of carbon, such as low-rank and high sulfur
coals, biomass, alcohols and methane (Natural Gas), where pure CO2 produced can be easily sequestered without the need for separation.
Radiolysis
Nuclear radiation can break water bonds(citation needed). In the Mponeng gold mine, South Africa, researchers found in a naturally high radiation zone a community dominated by a new phylotype of Desulfotomaculum, feeding on primarily radiolytically produced H2. Spent nuclear fuel is also being looked at as a potential source of hydrogen.
Thermolysis
Water spontaneously dissociates at around 2500 °C, but this thermolysis
occurs at temperatures too high for usual process piping and equipment.
Catalysts are required to reduce the dissociation temperature.
Thermochemical cycle
Thermochemical cycles combine solely heat sources (thermo) with chemical reactions to split water into its hydrogen and oxygen components. The term cycle
is used because aside from water, hydrogen and oxygen, the chemical
compounds used in these processes are continuously recycled. If
electricity is partially used as an input, the resulting thermochemical
cycle is defined as a hybrid one.
The sulfur-iodine cycle
(S-I cycle) is a thermochemical cycle processes which generates
hydrogen from water with an efficiency of approximately 50%. The sulfur
and iodine used in the process are recovered and reused, and not
consumed by the process. The cycle can be performed with any source of
very high temperatures, approximately 950 °C, such as by Concentrating solar power systems (CSP) and is regarded as being well suited to the production of hydrogen by high-temperature nuclear reactors, and as such, is being studied in the High Temperature Test Reactor in Japan. There are other hybrid cycles that use both high temperatures and some electricity, such as the Copper–chlorine cycle, it is classified as a hybrid thermochemical cycle because it uses an electrochemical reaction in one of the reaction steps, it operates at 530 °C and has an efficiency of 43 percent.
Ferrosilicon method
Ferrosilicon is used by the military to quickly produce hydrogen for balloons. The chemical reaction uses sodium hydroxide, ferrosilicon,
and water. The generator is small enough to fit a truck and requires
only a small amount of electric power, the materials are stable and not
combustible, and they do not generate hydrogen until mixed. The method has been in use since World War I. A heavy steel pressure vessel
is filled with sodium hydroxide and ferrosilicon, closed, and a
controlled amount of water is added; the dissolving of the hydroxide
heats the mixture to about 93 °C and starts the reaction; sodium silicate, hydrogen and steam are produced.
Photobiological water splitting

An algae bioreactor for hydrogen production.
Biological hydrogen can be produced in an algae bioreactor. In the late 1990s it was discovered that if the algae are deprived of sulfur it will switch from the production of oxygen, i.e. normal photosynthesis,
to the production of hydrogen. It seems that the production is now
economically feasible by surpassing the 7–10 percent energy efficiency
(the conversion of sunlight into hydrogen) barrier. with a hydrogen production rate of 10-12 ml per liter culture per hour.
Photocatalytic water splitting
The conversion of solar energy to hydrogen by means of water
splitting process is one of the most interesting ways to achieve clean
and renewable energy systems. However, if this process is assisted by
photocatalysts suspended directly in water instead of using photovoltaic
and an electrolytic system the reaction is in just one step, it can be
made more efficient.
Biohydrogen routes
Biomass and waste streams can in principle be converted into biohydrogen with biomass gasification, steam reforming, or biological conversion like biocatalysed electrolysis or fermentative hydrogen production.
Among hydrogen production methods such as steam methane
reforming, thermal cracking, coal and biomass gasification and
pyrolysis, electrolysis, and photolysis, biological ones are more
eco-friendly and less energy intensive. In addition, a wide variety of
waste and low-value materials such as agricultural biomass as renewable
sources can be utilized to produce hydrogen via biochemical pathways.
Nevertheless, at present hydrogen is produced mainly from fossil fuels,
in particular, natural gas which are non-renewable sources. Hydrogen is
not only the cleanest fuel but also widely used in a number of
industries, especially fertilizer, petrochemical and food ones. This
makes it logical to investigate alternative sources for hydrogen
production. The main biochemical technologies to produce hydrogen are
dark and photo fermentation processes. In dark fermentation,
carbohydrates are converted to hydrogen by fermentative microorganisms
including strict anaerobe and facultative anaerobe bacteria. A
theoretical maximum of 4 mol H2/mol glucose can be produced
and, besides hydrogen, sugars are converted to volatile fatty acids
(VFAs) and alcohols as by-products during this process. Photo
fermentative bacteria are able to generate hydrogen from VFAs. Hence,
metabolites formed in dark fermentation can be used as feedstock in
photo fermentation to enhance the overall yield of hydrogen.
Fermentative hydrogen production
Fermentative hydrogen production is the fermentative conversion of organic substrate to biohydrogen manifested by a diverse group of bacteria using multi enzyme systems involving three steps similar to anaerobic conversion. Dark fermentation reactions do not require light energy, so they are capable of constantly producing hydrogen from organic compounds throughout the day and night. Photofermentation differs from dark fermentation because it only proceeds in the presence of light. For example, photo-fermentation with Rhodobacter sphaeroides SH2C can be employed to convert small molecular fatty acids into hydrogen.
Fermentative hydrogen production can be done using direct
biophotolysis by green algae, indirect biophotolysis by cyanobacteria,
photo-fermentation by anaerobic photosynthetic bacteria and dark
fermentation by anaerobic fermentative bacteria. For example, studies on
hydrogen production using H. salinarium, an anaerobic photosynthetic bacteria, coupled to a hydrogenase donor like E. coli, are reported in literature.
Enterobacter aerogenes is an outstanding hydrogen
producer. It is an anaerobic facultative and mesophilic bacterium that
is able to consume different sugars and in contrast to cultivation of
strict anaerobes, no special operation is required to remove all oxygen
from the fermenter. E. aerogenes has a short doubling time and
high hydrogen productivity and evolution rate. Furthermore, hydrogen
production by this bacterium is not inhibited at high hydrogen partial
pressures; however, its yield is lower compared to strict anaerobes like
Clostridia. A theoretical maximum of 4 mol H2/mol glucose can be produced by strict anaerobic bacteria. Facultative anaerobic bacteria such as E. aerogenes have a theoretical maximum yield of 2 mol H2/mol glucose.
Biohydrogen can be produced in bioreactors that utilize
feedstocks, the most common feedstock being waste streams. The process
involves bacteria feeding on hydrocarbons and exhaling hydrogen and CO2. The CO2
can be sequestered successfully by several methods, leaving hydrogen
gas. In 2006-2007, NanoLogix first demonstrated a prototype hydrogen
bioreactor using waste as a feedstock at Welch's grape juice factory in
Pennsylvania (U.S.).
Enzymatic hydrogen generation
Due to the Thauer limit (four H2/glucose)
for dark fermentation, a non-natural enzymatic pathway was designed
that can generate 12 moles of hydrogen per mole of glucose units of
polysaccharides and water in 2007. The stoichiometric reaction is:
- C6H10O5 + 7 H2O → 12 H2 + 6 CO2
The key technology is cell-free synthetic enzymatic pathway biotransformation (SyPaB).
A biochemist can understand it as "glucose oxidation by using water as
oxidant". A chemist can describe it as "water splitting by energy in
carbohydrate". A thermodynamics scientist can describe it as the first
entropy-driving chemical reaction that can produce hydrogen by absorbing
waste heat. In 2009, cellulosic materials were first used to generate high-yield hydrogen.
Furthermore, the use of carbohydrate as a high-density hydrogen carrier
was proposed so to solve the largest obstacle to the hydrogen economy
and propose the concept of sugar fuel cell vehicles.
Biocatalysed electrolysis
A microbial electrolysis cell
Besides dark fermentation, electrohydrogenesis (electrolysis using microbes) is another possibility. Using microbial fuel cells, wastewater or plants can be used to generate power. Biocatalysed electrolysis should not be confused with biological hydrogen production,
as the latter only uses algae and with the latter, the algae itself
generates the hydrogen instantly, where with biocatalysed electrolysis,
this happens after running through the microbial fuel cell and a variety
of aquatic plants can be used. These include reed sweetgrass, cordgrass, rice, tomatoes, lupines and algae.
Xylose
In 2014 a low-temperature 50 °C (122 °F), atmospheric-pressure enzyme-driven
process to convert xylose into hydrogen with nearly 100% of the
theoretical yield was announced. The process employs 13 enzymes,
including a novel polyphosphatexylulokinase (XK).
Carbon-neutral hydrogen
Currently there are two practical ways of producing hydrogen in a renewable industrial process. One is to use power to gas, in which electric power is used to produce hydrogen from electrolysis, and the other is to use landfill gas
to produce hydrogen in a steam reformer. Hydrogen fuel, when produced
by renewable sources of energy like wind or solar power, is a renewable fuel.
Use of hydrogen
Hydrogen is mainly used for the conversion of heavy petroleum fractions into lighter ones via the process of hydrocracking and other processes (dehydrocyclization and the aromatization process). It is also required for cleaning fossil fuels via hydrodesulfurization.
Hydrogen is mainly used for the production of ammonia via Haber process. In this case, the hydrogen is produced in situ. Ammonia is the major component of most fertilizers.
Earlier it was common to vent the surplus hydrogen off, nowadays the process systems are balanced with hydrogen pinch to collect hydrogen for further use.
Hydrogen may be used in fuel cells for local electricity generation, making it possible for hydrogen to be used as a transportation fuel for an electric vehicle.
Hydrogen is also produced as a by-product of industrial chlorine production by electrolysis.
Although requiring expensive technologies, hydrogen can be cooled,
compressed and purified for use in other processes on site or sold to a
customer via pipeline, cylinders or trucks. The discovery and
development of less expensive methods of production of bulk hydrogen is
relevant to the establishment of a hydrogen economy.



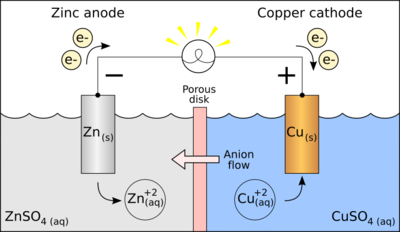
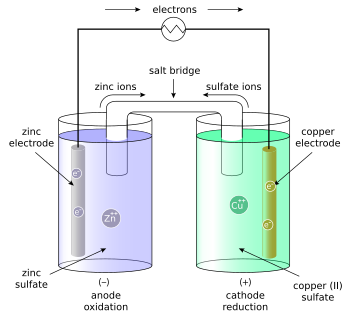





![{\displaystyle E_{\text{half-cell}}=E^{o}-{\frac {0.05918\ {\text{V}}}{\nu _{e}}}\log _{10}\left[{\text{M}}^{n+}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6a037534b006cae64ae53d028a0cc0212beab99d)








![E_{eq,K^+} = \frac{RT}{zF} \ln \frac{[K^+]_{o}}{[K^+]_{i}} ,](https://wikimedia.org/api/rest_v1/media/math/render/svg/b7eb1afcc5d7a5032ff24be5c403b43b1307b01e)