Membrane potential

From Wikipedia, the free encyclopedia

Differences in the concentrations of ions on opposite sides of a cellular membrane lead to a voltage called the membrane potential. Typical values of membrane potential are in the range –40 mV to –70 mV. Many ions have a concentration gradient across the membrane, including potassium (K⁺), which is at a high concentration inside and a low concentration outside the membrane. Sodium (Na⁺) and chloride (Cl⁻) ions are at high concentrations in the extracellular region, and low concentrations in the intracellular regions. These concentration gradients provide the potential energy to drive the formation of the membrane potential. This voltage is established when the membrane has permeability to one or more ions. In the simplest case, illustrated here, if the membrane is selectively permeable to potassium, these positively charged ions can diffuse down the concentration gradient to the outside of the cell, leaving behind uncompensated negative charges. This separation of charges is what causes the membrane potential. Note that the system as a whole is electro-neutral. The uncompensated positive charges outside the cell, and the uncompensated negative charges inside the cell, physically line up on the membrane surface and attract each other across the lipid bilayer. Thus, the membrane potential is physically located only in the immediate vicinity of the membrane. It is the separation of these charges across the membrane that is the basis of the membrane voltage. Note also that this diagram is only an approximation of the ionic contributions to the membrane potential. Other ions including sodium, chloride, calcium, and others play a more minor role, even though they have strong concentration gradients, because they have more limited permeability than potassium. Key: Blue pentagons – sodium ions; Purple squares – potassium ions; Yellow circles – chloride ions; Orange rectangles – membrane-impermeable anions (these arise from a variety of sources including proteins). The large purple structure with an arrow represents a transmembrane potassium channel and the direction of net potassium movement.

 

Membrane potential (also transmembrane potential or membrane voltage) is the difference in electric potential between the interior and the exterior of a biological cell. With respect to the exterior of the cell, typical values of membrane potential, normally given in millivolts, range from –40 mV to –80 mV. 

All animal cells are surrounded by a membrane composed of a lipid bilayer with proteins embedded in it. The membrane serves as both an insulator and a diffusion barrier to the movement of ions. Transmembrane proteins, also known as ion transporter or ion pump proteins, actively push ions across the membrane and establish concentration gradients across the membrane, and ion channels allow ions to move across the membrane down those concentration gradients. Ion pumps and ion channels are electrically equivalent to a set of batteries and resistors inserted in the membrane, and therefore create a voltage between the two sides of the membrane. 

Almost all plasma membranes have an electrical potential across them, with the inside usually negative with respect to the outside. The membrane potential has two basic functions. First, it allows a cell to function as a battery, providing power to operate a variety of "molecular devices" embedded in the membrane. Second, in electrically excitable cells such as neurons and muscle cells, it is used for transmitting signals between different parts of a cell. Signals are generated by opening or closing of ion channels at one point in the membrane, producing a local change in the membrane potential. This change in the electric field can be quickly affected by either adjacent or more distant ion channels in the membrane. Those ion channels can then open or close as a result of the potential change, reproducing the signal. 

In non-excitable cells, and in excitable cells in their baseline states, the membrane potential is held at a relatively stable value, called the resting potential. For neurons, typical values of the resting potential range from –70 to –80 millivolts; that is, the interior of a cell has a negative baseline voltage of a bit less than one-tenth of a volt. The opening and closing of ion channels can induce a departure from the resting potential. This is called a depolarization if the interior voltage becomes less negative (say from –70 mV to –60 mV), or a hyperpolarization if the interior voltage becomes more negative (say from –70 mV to –80 mV). In excitable cells, a sufficiently large depolarization can evoke an action potential, in which the membrane potential changes rapidly and significantly for a short time (on the order of 1 to 100 milliseconds), often reversing its polarity. Action potentials are generated by the activation of certain voltage-gated ion channels. 

In neurons, the factors that influence the membrane potential are diverse. They include numerous types of ion channels, some of which are chemically gated and some of which are voltage-gated. Because voltage-gated ion channels are controlled by the membrane potential, while the membrane potential itself is influenced by these same ion channels, feedback loops that allow for complex temporal dynamics arise, including oscillations and regenerative events such as action potentials.

Physical basis

The membrane potential in a cell derives ultimately from two factors: electrical force and diffusion. Electrical force arises from the mutual attraction between particles with opposite electrical charges (positive and negative) and the mutual repulsion between particles with the same type of charge (both positive or both negative). Diffusion arises from the statistical tendency of particles to redistribute from regions where they are highly concentrated to regions where the concentration is low.

Voltage

Electric field (arrows) and contours of constant voltage created by a pair of oppositely charged objects. The electric field is at right angles to the voltage contours, and the field is strongest where the spacing between contours is the smallest.

 

Voltage, which is synonymous with difference in electrical potential, is the ability to drive an electric current across a resistance. Indeed, the simplest definition of a voltage is given by Ohm's law: V=IR, where V is voltage, I is current and R is resistance. If a voltage source such as a battery is placed in an electrical circuit, the higher the voltage of the source the greater the amount of current that it will drive across the available resistance. The functional significance of voltage lies only in potential differences between two points in a circuit. The idea of a voltage at a single point is meaningless. It is conventional in electronics to assign a voltage of zero to some arbitrarily chosen element of the circuit, and then assign voltages for other elements measured relative to that zero point. There is no significance in which element is chosen as the zero point—the function of a circuit depends only on the differences not on voltages per se. However, in most cases and by convention, the zero level is most often assigned to the portion of a circuit that is in contact with ground.

 

The same principle applies to voltage in cell biology. In electrically active tissue, the potential difference between any two points can be measured by inserting an electrode at each point, for example one inside and one outside the cell, and connecting both electrodes to the leads of what is in essence a specialized voltmeter. By convention, the zero potential value is assigned to the outside of the cell and the sign of the potential difference between the outside and the inside is determined by the potential of the inside relative to the outside zero. 

In mathematical terms, the definition of voltage begins with the concept of an electric field E, a vector field assigning a magnitude and direction to each point in space. In many situations, the electric field is a conservative field, which means that it can be expressed as the gradient of a scalar function V, that is, E = –∇V. This scalar field V is referred to as the voltage distribution. Note that the definition allows for an arbitrary constant of integration—this is why absolute values of voltage are not meaningful. In general, electric fields can be treated as conservative only if magnetic fields do not significantly influence them, but this condition usually applies well to biological tissue.

Because the electric field is the gradient of the voltage distribution, rapid changes in voltage within a small region imply a strong electric field; on the converse, if the voltage remains approximately the same over a large region, the electric fields in that region must be weak. A strong electric field, equivalent to a strong voltage gradient, implies that a strong force is exerted on any charged particles that lie within the region.

Ions and the forces driving their motion

Ions (pink circles) will flow across a membrane from the higher concentration to the lower concentration (down a concentration gradient), causing a current. However, this creates a voltage across the membrane that opposes the ions' motion. When this voltage reaches the equilibrium value, the two balance and the flow of ions stops.

 

Electrical signals within biological organisms are, in general, driven by ions. The most important cations for the action potential are sodium (Na⁺) and potassium (K⁺). Both of these are monovalent cations that carry a single positive charge. Action potentials can also involve calcium (Ca²⁺), which is a divalent cation that carries a double positive charge. The chloride anion (Cl⁻) plays a major role in the action potentials of some algae, but plays a negligible role in the action potentials of most animals.

Ions cross the cell membrane under two influences: diffusion and electric fields. A simple example wherein two solutions—A and B—are separated by a porous barrier illustrates that diffusion will ensure that they will eventually mix into equal solutions. This mixing occurs because of the difference in their concentrations. The region with high concentration will diffuse out toward the region with low concentration. To extend the example, let solution A have 30 sodium ions and 30 chloride ions. Also, let solution B have only 20 sodium ions and 20 chloride ions. Assuming the barrier allows both types of ions to travel through it, then a steady state will be reached whereby both solutions have 25 sodium ions and 25 chloride ions. If, however, the porous barrier is selective to which ions are let through, then diffusion alone will not determine the resulting solution. Returning to the previous example, let's now construct a barrier that is permeable only to sodium ions. Now, only sodium is allowed to diffuse cross the barrier from its higher concentration in solution A to the lower concentration in solution B. This will result in a greater accumulation of sodium ions than chloride ions in solution B and a lesser number of sodium ions than chloride ions in solution A.

This means that there is a net positive charge in solution B from the higher concentration of positively charged sodium ions than negatively charged chloride ions. Likewise, there is a net negative charge in solution A from the greater concentration of negative chloride ions than positive sodium ions. Since opposite charges attract and like charges repel, the ions are now also influenced by electrical fields as well as forces of diffusion. Therefore, positive sodium ions will be less likely to travel to the now-more-positive B solution and remain in the now-more-negative A solution. The point at which the forces of the electric fields completely counteract the force due to diffusion is called the equilibrium potential. At this point, the net flow of the specific ion (in this case sodium) is zero.

Plasma membranes

The cell membrane, also called the plasma membrane or plasmalemma, is a semipermeable lipid bilayer common to all living cells. It contains a variety of biological molecules, primarily proteins and lipids, which are involved in a vast array of cellular processes.

 

Every animal cell is enclosed in a plasma membrane, which has the structure of a lipid bilayer with many types of large molecules embedded in it. Because it is made of lipid molecules, the plasma membrane intrinsically has a high electrical resistivity, in other words a low intrinsic permeability to ions. However, some of the molecules embedded in the membrane are capable either of actively transporting ions from one side of the membrane to the other or of providing channels through which they can move.

In electrical terminology, the plasma membrane functions as a combined resistor and capacitor. Resistance arises from the fact that the membrane impedes the movement of charges across it. Capacitance arises from the fact that the lipid bilayer is so thin that an accumulation of charged particles on one side gives rise to an electrical force that pulls oppositely charged particles toward the other side. The capacitance of the membrane is relatively unaffected by the molecules that are embedded in it, so it has a more or less invariant value estimated at about 2 µF/cm² (the total capacitance of a patch of membrane is proportional to its area). The conductance of a pure lipid bilayer is so low, on the other hand, that in biological situations it is always dominated by the conductance of alternative pathways provided by embedded molecules. Thus, the capacitance of the membrane is more or less fixed, but the resistance is highly variable. 

The thickness of a plasma membrane is estimated to be about 7-8 nanometers. Because the membrane is so thin, it does not take a very large transmembrane voltage to create a strong electric field within it. Typical membrane potentials in animal cells are on the order of 100 millivolts (that is, one tenth of a volt), but calculations show that this generates an electric field close to the maximum that the membrane can sustain—it has been calculated that a voltage difference much larger than 200 millivolts could cause dielectric breakdown, that is, arcing across the membrane.

Facilitated diffusion and transport

Facilitated diffusion in cell membranes, showing ion channels and carrier proteins

 

The resistance of a pure lipid bilayer to the passage of ions across it is very high, but structures embedded in the membrane can greatly enhance ion movement, either actively or passively, via mechanisms called facilitated transport and facilitated diffusion. The two types of structure that play the largest roles are ion channels and ion pumps, both usually formed from assemblages of protein molecules. Ion channels provide passageways through which ions can move. In most cases, an ion channel is permeable only to specific types of ions (for example, sodium and potassium but not chloride or calcium), and sometimes the permeability varies depending on the direction of ion movement. Ion pumps, also known as ion transporters or carrier proteins, actively transport specific types of ions from one side of the membrane to the other, sometimes using energy derived from metabolic processes to do so.

Ion pumps

The sodium-potassium pump uses energy derived from ATP to exchange sodium for potassium ions across the membrane.

Ion pumps are integral membrane proteins that carry out active transport, i.e., use cellular energy (ATP) to "pump" the ions against their concentration gradient. Such ion pumps take in ions from one side of the membrane (decreasing its concentration there) and release them on the other side (increasing its concentration there). 

The ion pump most relevant to the action potential is the sodium–potassium pump, which transports three sodium ions out of the cell and two potassium ions in. As a consequence, the concentration of potassium ions K⁺ inside the neuron is roughly 20-fold larger than the outside concentration, whereas the sodium concentration outside is roughly ninefold larger than inside. In a similar manner, other ions have different concentrations inside and outside the neuron, such as calcium, chloride and magnesium.

If the numbers of each type of ion were equal, the sodium–potassium pump would be electrically neutral, but, because of the three-for-two exchange, it gives a net movement of one positive charge from intracellular to extracellular for each cycle, thereby contributing to a positive voltage difference. The pump has three effects: (1) it makes the sodium concentration high in the extracellular space and low in the intracellular space; (2) it makes the potassium concentration high in the intracellular space and low in the extracellular space; (3) it gives the intracellular space a negative voltage with respect to the extracellular space. 

The sodium-potassium pump is relatively slow in operation. If a cell were initialized with equal concentrations of sodium and potassium everywhere, it would take hours for the pump to establish equilibrium. The pump operates constantly, but becomes progressively less efficient as the concentrations of sodium and potassium available for pumping are reduced. 

Ion pumps influence the action potential only by establishing the relative ratio of intracellular and extracellular ion concentrations. The action potential involves mainly the opening and closing of ion channels not ion pumps. If the ion pumps are turned off by removing their energy source, or by adding an inhibitor such as ouabain, the axon can still fire hundreds of thousands of action potentials before their amplitudes begin to decay significantly. In particular, ion pumps play no significant role in the repolarization of the membrane after an action potential.

Another functionally important ion pump is the sodium-calcium exchanger. This pump operates in a conceptually similar way to the sodium-potassium pump, except that in each cycle it exchanges three Na⁺ from the extracellular space for one Ca⁺⁺ from the intracellular space. Because the net flow of charge is inward, this pump runs "downhill", in effect, and therefore does not require any energy source except the membrane voltage. Its most important effect is to pump calcium outward—it also allows an inward flow of sodium, thereby counteracting the sodium-potassium pump, but, because overall sodium and potassium concentrations are much higher than calcium concentrations, this effect is relatively unimportant. The net result of the sodium-calcium exchanger is that in the resting state, intracellular calcium concentrations become very low.

Ion channels

Despite the small differences in their radii, ions rarely go through the "wrong" channel. For example, sodium or calcium ions rarely pass through a potassium channel.

 

Ion channels are integral membrane proteins with a pore through which ions can travel between extracellular space and cell interior. Most channels are specific (selective) for one ion; for example, most potassium channels are characterized by 1000:1 selectivity ratio for potassium over sodium, though potassium and sodium ions have the same charge and differ only slightly in their radius. The channel pore is typically so small that ions must pass through it in single-file order. Channel pores can be either open or closed for ion passage, although a number of channels demonstrate various sub-conductance levels. When a channel is open, ions permeate through the channel pore down the transmembrane concentration gradient for that particular ion. Rate of ionic flow through the channel, i.e. single-channel current amplitude, is determined by the maximum channel conductance and electrochemical driving force for that ion, which is the difference between the instantaneous value of the membrane potential and the value of the reversal potential.

Depiction of the open potassium channel, with the potassium ion shown in purple in the middle, and hydrogen atoms omitted. When the channel is closed, the passage is blocked.

 

A channel may have several different states (corresponding to different conformations of the protein), but each such state is either open or closed. In general, closed states correspond either to a contraction of the pore—making it impassable to the ion—or to a separate part of the protein, stoppering the pore. For example, the voltage-dependent sodium channel undergoes inactivation, in which a portion of the protein swings into the pore, sealing it. This inactivation shuts off the sodium current and plays a critical role in the action potential. 

Ion channels can be classified by how they respond to their environment. For example, the ion channels involved in the action potential are voltage-sensitive channels; they open and close in response to the voltage across the membrane. Ligand-gated channels form another important class; these ion channels open and close in response to the binding of a ligand molecule, such as a neurotransmitter. Other ion channels open and close with mechanical forces. Still other ion channels—such as those of sensory neurons—open and close in response to other stimuli, such as light, temperature or pressure.

Leakage channels

Leakage channels are the simplest type of ion channel, in that their permeability is more or less constant. The types of leakage channels that have the greatest significance in neurons are potassium and chloride channels. It should be noted that even these are not perfectly constant in their properties: First, most of them are voltage-dependent in the sense that they conduct better in one direction than the other (in other words, they are rectifiers); second, some of them are capable of being shut off by chemical ligands even though they do not require ligands in order to operate.

Ligand-gated channels

Ligand-gated calcium channel in closed and open states

 

Ligand-gated ion channels are channels whose permeability is greatly increased when some type of chemical ligand binds to the protein structure. Animal cells contain hundreds, if not thousands, of types of these. A large subset function as neurotransmitter receptors—they occur at postsynaptic sites, and the chemical ligand that gates them is released by the presynaptic axon terminal. One example of this type is the AMPA receptor, a receptor for the neurotransmitter glutamate that when activated allows passage of sodium and potassium ions. Another example is the GABA_A receptor, a receptor for the neurotransmitter GABA that when activated allows passage of chloride ions. 

Neurotransmitter receptors are activated by ligands that appear in the extracellular area, but there are other types of ligand-gated channels that are controlled by interactions on the intracellular side.

Voltage-dependent channels

Voltage-gated ion channels, also known as voltage dependent ion channels, are channels whose permeability is influenced by the membrane potential. They form another very large group, with each member having a particular ion selectivity and a particular voltage dependence. Many are also time-dependent—in other words, they do not respond immediately to a voltage change but only after a delay. 

One of the most important members of this group is a type of voltage-gated sodium channel that underlies action potentials—these are sometimes called Hodgkin-Huxley sodium channels because they were initially characterized by Alan Lloyd Hodgkin and Andrew Huxley in their Nobel Prize-winning studies of the physiology of the action potential. The channel is closed at the resting voltage level, but opens abruptly when the voltage exceeds a certain threshold, allowing a large influx of sodium ions that produces a very rapid change in the membrane potential. Recovery from an action potential is partly dependent on a type of voltage-gated potassium channel that is closed at the resting voltage level but opens as a consequence of the large voltage change produced during the action potential.

Reversal potential

The reversal potential (or equilibrium potential) of an ion is the value of transmembrane voltage at which diffusive and electrical forces counterbalance, so that there is no net ion flow across the membrane. This means that the transmembrane voltage exactly opposes the force of diffusion of the ion, such that the net current of the ion across the membrane is zero and unchanging. The reversal potential is important because it gives the voltage that acts on channels permeable to that ion—in other words, it gives the voltage that the ion concentration gradient generates when it acts as a battery. 

The equilibrium potential of a particular ion is usually designated by the notation E_ion.The equilibrium potential for any ion can be calculated using the Nernst equation. For example, reversal potential for potassium ions will be as follows:

${\displaystyle E_{eq,K^{+}}={\frac {RT}{zF}}\ln {\frac {[K^{+}]_{o}}{[K^{+}]_{i}}},}$

where

• E_eq,K⁺ is the equilibrium potential for potassium, measured in volts
• R is the universal gas constant, equal to 8.314 joules·K⁻¹·mol⁻¹
• T is the absolute temperature, measured in kelvins (= K = degrees Celsius + 273.15)
• z is the number of elementary charges of the ion in question involved in the reaction
• F is the Faraday constant, equal to 96,485 coulombs·mol⁻¹ or J·V⁻¹·mol⁻¹
• [K⁺]_o is the extracellular concentration of potassium, measured in mol·m⁻³ or mmol·l⁻¹
• [K⁺]_i is the intracellular concentration of potassium

Even if two different ions have the same charge (i.e., K⁺ and Na⁺), they can still have very different equilibrium potentials, provided their outside and/or inside concentrations differ. Take, for example, the equilibrium potentials of potassium and sodium in neurons. The potassium equilibrium potential E_K is −84 mV with 5 mM potassium outside and 140 mM inside. On the other hand, the sodium equilibrium potential, E_Na, is approximately +66 mV with approximately 12 mM sodium inside and 140 mM outside.

Changes to membrane potential during development

A neuron’s resting membrane potential actually changes during the development of an organism. In order for a neuron to eventually adopt its full adult function, its potential must be tightly regulated during development. As an organism progresses through development the resting membrane potential becomes more negative. Glial cells are also differentiating and proliferating as development progresses in the brain. The addition of these glial cells increases the organism’s ability to regulate extracellular potassium. The drop in extracellular potassium can lead to a decrease in membrane potential of 35 mV.

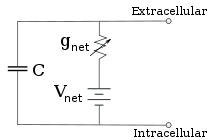
Equivalent circuit

Equivalent circuit for a patch of membrane, consisting of a fixed capacitance in parallel with four pathways each containing a battery in series with a variable conductance

 

Electrophysiologists model the effects of ionic concentration differences, ion channels, and membrane capacitance in terms of an equivalent circuit, which is intended to represent the electrical properties of a small patch of membrane. The equivalent circuit consists of a capacitor in parallel with four pathways each consisting of a battery in series with a variable conductance. The capacitance is determined by the properties of the lipid bilayer, and is taken to be fixed. Each of the four parallel pathways comes from one of the principal ions, sodium, potassium, chloride, and calcium. The voltage of each ionic pathway is determined by the concentrations of the ion on each side of the membrane; see the Reversal potential section above. The conductance of each ionic pathway at any point in time is determined by the states of all the ion channels that are potentially permeable to that ion, including leakage channels, ligand-gated channels, and voltage-gated ion channels.

Reduced circuit obtained by combining the ion-specific pathways using the Goldman equation

 

For fixed ion concentrations and fixed values of ion channel conductance, the equivalent circuit can be further reduced, using the Goldman equation as described below, to a circuit containing a capacitance in parallel with a battery and conductance. In electrical terms, this is a type of RC circuit (resistance-capacitance circuit), and its electrical properties are very simple. Starting from any initial state, the current flowing across either the conductance or the capacitance decays with an exponential time course, with a time constant of τ = RC, where C is the capacitance of the membrane patch, and R = 1/g_net is the net resistance. For realistic situations, the time constant usually lies in the 1—100 millisecond range. In most cases, changes in the conductance of ion channels occur on a faster time scale, so an RC circuit is not a good approximation; however, the differential equation used to model a membrane patch is commonly a modified version of the RC circuit equation.

Resting potential

When the membrane potential of a cell goes for a long period of time without changing significantly, it is referred to as a resting potential or resting voltage. This term is used for the membrane potential of non-excitable cells, but also for the membrane potential of excitable cells in the absence of excitation. In excitable cells, the other possible states are graded membrane potentials (of variable amplitude), and action potentials, which are large, all-or-nothing rises in membrane potential that usually follow a fixed time course. Excitable cells include neurons, muscle cells, and some secretory cells in glands. Even in other types of cells, however, the membrane voltage can undergo changes in response to environmental or intracellular stimuli. For example, depolarization of the plasma membrane appears to be an important step in programmed cell death.

The interactions that generate the resting potential are modeled by the Goldman equation. This is similar in form to the Nernst equation shown above, in that it is based on the charges of the ions in question, as well as the difference between their inside and outside concentrations. However, it also takes into consideration the relative permeability of the plasma membrane to each ion in question.

${\displaystyle E_{m}={\frac {RT}{F}}\ln {\left({\frac {P_{\mathrm {K} }[\mathrm {K} ^{+}]_{\mathrm {out} }+P_{\mathrm {Na} }[\mathrm {Na} ^{+}]_{\mathrm {out} }+P_{\mathrm {Cl} }[\mathrm {Cl} ^{-}]_{\mathrm {in} }}{P_{\mathrm {K} }[\mathrm {K} ^{+}]_{\mathrm {in} }+P_{\mathrm {Na} }[\mathrm {Na} ^{+}]_{\mathrm {in} }+P_{\mathrm {Cl} }[\mathrm {Cl} ^{-}]_{\mathrm {out} }}}\right)}}$

The three ions that appear in this equation are potassium (K⁺), sodium (Na⁺), and chloride (Cl⁻). Calcium is omitted, but can be added to deal with situations in which it plays a significant role. Being an anion, the chloride terms are treated differently from the cation terms; the intracellular concentration is in the numerator, and the extracellular concentration in the denominator, which is reversed from the cation terms. P_i stands for the relative permeability of the ion type i.

In essence, the Goldman formula expresses the membrane potential as a weighted average of the reversal potentials for the individual ion types, weighted by permeability. (Although the membrane potential changes about 100 mV during an action potential, the concentrations of ions inside and outside the cell do not change significantly. They remain close to their respective concentrations when then membrane is at resting potential.) In most animal cells, the permeability to potassium is much higher in the resting state than the permeability to sodium. As a consequence, the resting potential is usually close to the potassium reversal potential. The permeability to chloride can be high enough to be significant, but, unlike the other ions, chloride is not actively pumped, and therefore equilibrates at a reversal potential very close to the resting potential determined by the other ions.

Values of resting membrane potential in most animal cells usually vary between the potassium reversal potential (usually around -80 mV) and around -40 mV. The resting potential in excitable cells (capable of producing action potentials) is usually near -60 mV—more depolarized voltages would lead to spontaneous generation of action potentials. Immature or undifferentiated cells show highly variable values of resting voltage, usually significantly more positive than in differentiated cells. In such cells, the resting potential value correlates with the degree of differentiation: undifferentiated cells in some cases may not show any transmembrane voltage difference at all. 

Maintenance of the resting potential can be metabolically costly for a cell because of its requirement for active pumping of ions to counteract losses due to leakage channels. The cost is highest when the cell function requires an especially depolarized value of membrane voltage. For example, the resting potential in daylight-adapted blowfly (Calliphora vicina) photoreceptors can be as high as -30 mV. This elevated membrane potential allows the cells to respond very rapidly to visual inputs; the cost is that maintenance of the resting potential may consume more than 20% of overall cellular ATP.

On the other hand, the high resting potential in undifferentiated cells can be a metabolic advantage. This apparent paradox is resolved by examination of the origin of that resting potential. Little-differentiated cells are characterized by extremely high input resistance, which implies that few leakage channels are present at this stage of cell life. As an apparent result, potassium permeability becomes similar to that for sodium ions, which places resting potential in-between the reversal potentials for sodium and potassium as discussed above. The reduced leakage currents also mean there is little need for active pumping in order to compensate, therefore low metabolic cost.

Graded potentials

As explained above, the potential at any point in a cell's membrane is determined by the ion concentration differences between the intracellular and extracellular areas, and by the permeability of the membrane to each type of ion. The ion concentrations do not normally change very quickly (with the exception of Ca²⁺, where the baseline intracellular concentration is so low that even a small influx may increase it by orders of magnitude), but the permeabilities of the ions can change in a fraction of a millisecond, as a result of activation of ligand-gated ion channels. The change in membrane potential can be either large or small, depending on how many ion channels are activated and what type they are, and can be either long or short, depending on the lengths of time that the channels remain open. Changes of this type are referred to as graded potentials, in contrast to action potentials, which have a fixed amplitude and time course. 

As can be derived from the Goldman equation shown above, the effect of increasing the permeability of a membrane to a particular type of ion shifts the membrane potential toward the reversal potential for that ion. Thus, opening Na⁺ channels shifts the membrane potential toward the Na⁺ reversal potential, which is usually around +100 mV. Likewise, opening K⁺ channels shifts the membrane potential toward about –90 mV, and opening Cl⁻ channels shifts it toward about –70 mV (resting potential of most membranes). Thus, Na⁺ channels shift the membrane potential in a positive direction, K⁺ channels shift it in a negative direction (except when the membrane is hyperpolarized to a value more negative than the K⁺ reversal potential), and Cl⁻ channels tend to shift it towards the resting potential. 

Graph displaying an EPSP, an IPSP, and the summation of an EPSP and an IPSP

 

Graded membrane potentials are particularly important in neurons, where they are produced by synapses—a temporary change in membrane potential produced by activation of a synapse by a single graded or action potential is called a postsynaptic potential. Neurotransmitters that act to open Na⁺ channels typically cause the membrane potential to become more positive, while neurotransmitters that activate K⁺ channels typically cause it to become more negative; those that inhibit these channels tend to have the opposite effect. 

Whether a postsynaptic potential is considered excitatory or inhibitory depends on the reversal potential for the ions of that current, and the threshold for the cell to fire an action potential (around –50mV). A postsynaptic current with a reversal potential above threshold, such as a typical Na⁺ current, is considered excitatory. A current with a reversal potential below threshold, such as a typical K⁺ current, is considered inhibitory. A current with a reversal potential above the resting potential, but below threshold, will not by itself elicit action potentials, but will produce subthreshold membrane potential oscillations. Thus, neurotransmitters that act to open Na⁺ channels produce excitatory postsynaptic potentials, or EPSPs, whereas neurotransmitters that act to open K⁺ or Cl⁻ channels typically produce inhibitory postsynaptic potentials, or IPSPs. When multiple types of channels are open within the same time period, their postsynaptic potentials summate (are added together).

Other values

From the viewpoint of biophysics, the resting membrane potential is merely the membrane potential that results from the membrane permeabilities that predominate when the cell is resting. The above equation of weighted averages always applies, but the following approach may be more easily visualized. At any given moment, there are two factors for an ion that determine how much influence that ion will have over the membrane potential of a cell:

1. That ion's driving force
2. That ion's permeability

If the driving force is high, then the ion is being "pushed" across the membrane. If the permeability is high, it will be easier for the ion to diffuse across the membrane.

• Driving force is the net electrical force available to move that ion across the membrane. It is calculated as the difference between the voltage that the ion "wants" to be at (its equilibrium potential) and the actual membrane potential (E_m). So, in formal terms, the driving force for an ion = E_m - E_ion
• For example, at our earlier calculated resting potential of −73 mV, the driving force on potassium is 7 mV : (−73 mV) − (−80 mV) = 7 mV. The driving force on sodium would be (−73 mV) − (60 mV) = −133 mV.
• Permeability is a measure of how easily an ion can cross the membrane. It is normally measured as the (electrical) conductance and the unit, siemens, corresponds to 1 C·s⁻¹·V⁻¹, that is one coulomb per second per volt of potential.

So, in a resting membrane, while the driving force for potassium is low, its permeability is very high. Sodium has a huge driving force but almost no resting permeability. In this case, potassium carries about 20 times more current than sodium, and thus has 20 times more influence over E_m than does sodium. 

However, consider another case—the peak of the action potential. Here, permeability to Na is high and K permeability is relatively low. Thus, the membrane moves to near E_Na and far from E_K. 

The more ions are permeant the more complicated it becomes to predict the membrane potential. However, this can be done using the Goldman-Hodgkin-Katz equation or the weighted means equation. By plugging in the concentration gradients and the permeabilities of the ions at any instant in time, one can determine the membrane potential at that moment. What the GHK equations means is that, at any time, the value of the membrane potential will be a weighted average of the equilibrium potentials of all permeant ions. The "weighting" is the ions relative permeability across the membrane.

Effects and implications

While cells expend energy to transport ions and establish a transmembrane potential, they use this potential in turn to transport other ions and metabolites such as sugar. The transmembrane potential of the mitochondria drives the production of ATP, which is the common currency of biological energy. 

Cells may draw on the energy they store in the resting potential to drive action potentials or other forms of excitation. These changes in the membrane potential enable communication with other cells (as with action potentials) or initiate changes inside the cell, which happens in an egg when it is fertilized by a sperm. 

In neuronal cells, an action potential begins with a rush of sodium ions into the cell through sodium channels, resulting in depolarization, while recovery involves an outward rush of potassium through potassium channels. Both of these fluxes occur by passive diffusion.