Scanning SQUID microscopy

From Wikipedia, the free encyclopedia

 

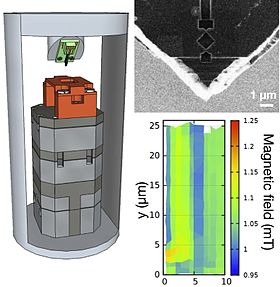
Left: Schematic of a scanning SQUID microscope in a helium-4 refrigerator. Green holder for the SQUID probe is attached to a quartz tuning fork. Bottom part is a piezoelectric sample stage. Right: electron micrograph of a SQUID probe and a test image of Nb/Au strips recorded with it.

 

Scanning SQUID microscopy is a technique where a superconducting quantum interference device (SQUID) is used to image surface magnetic field strength with micrometre scale resolution. A tiny SQUID is mounted onto a tip which is then rastered near the surface of the sample to be measured. As the SQUID is the most sensitive detector of magnetic fields available and can be constructed at submicrometre widths via lithography, the scanning SQUID microscope allows magnetic fields to be measured with unparalleled resolution and sensitivity. The first scanning SQUID microscope was built in 1992 by Black et al. Since then the technique has been used to confirm unconventional superconductity in several high-temperature superconductors including YBCO and BSCCO compounds.

Operating principles

Diagram of a DC SQUID. The current ${\displaystyle I}$ enters and splits into the two paths, each with currents ${\displaystyle I_{a}}$ and ${\displaystyle I_{b}}$. The thin barriers on each path are Josephson junctions, which together separate the two superconducting regions. ${\displaystyle \Phi }$ represents the magnetic flux entering the inside of the DC SQUID loop.

 

The scanning SQUID microscope is based upon the thin-film DC SQUID. A DC SQUID consists of superconducting electrodes in a ring pattern connected by two weak-link Josephson junctions (see figure). Above the critical current of the Josephson junctions, the idealized difference in voltage between the electrodes is given by

${\displaystyle {\begin{aligned}V&={\frac {R}{2}}{\sqrt {I^{2}-I_{0}^{2}}},\\&={\frac {R}{2}}\left(I^{2}-\left(2I_{c}\cos \left(\pi {\frac {\Phi }{\Phi _{0}}}\right)\right)^{2}\right)^{\frac {1}{2}},\end{aligned}}}$

where R is the resistance between the electrodes, I is the current, I₀ is the maximum supercurrent, I_c is the critical current of the Josephson junctions, Φ is the total magnetic flux through the ring, and Φ₀ is the magnetic flux quantum. 

Hence, a DC SQUID can be used as a flux-to-voltage transducer. However, as noted by the figure, the voltage across the electrodes oscillates sinusoidally with respect to the amount of magnetic flux passing through the device. As a result, alone a SQUID can only be used to measure the change in magnetic field from some known value, unless the magnetic field or device size is very small such that Φ < Φ₀. To use the DC SQUID to measure standard magnetic fields, one must either count the number of oscillations in the voltage as the field is changed, which is very difficult in practice, or use a separate DC bias magnetic field parallel to the device to maintain a constant voltage and consequently constant magnetic flux through the loop. The strength of the field being measured will then be equal to the strength of the bias magnetic field passing through the SQUID.

Although it is possible to read the DC voltage between the two terminals of the SQUID directly, because noise tends to be a problem in DC measurements, an alternating current technique is used. In addition to the DC bias magnetic field, an AC magnetic field of constant amplitude, with field strength generating Φ << Φ₀, is also emitted in the bias coil. This AC field produces an AC voltage with amplitude proportional to the DC component in the SQUID. The advantage of this technique is that the frequency of the voltage signal can be chosen to be far away from that of any potential noise sources. By using a lock-in amplifier the device can read only the frequency corresponding to the magnetic field, ignoring many other sources of noise.

Instrumentation

As the SQUID material must be superconducting, measurements must be performed at low temperatures. Typically, experiments are carried out below liquid helium temperature (4.2 K) in a helium-3 refrigerator or dilution refrigerator. However, advances in high-temperature superconductor thin-film growth have allowed relatively inexpensive liquid nitrogen cooling to instead be used. It is even possible to measure room-temperature samples by only cooling a high T_c squid and maintaining thermal separation with the sample. In either case, due to the extreme sensitivity of the SQUID probe to stray magnetic fields, in general some form of magnetic shielding is used. Most common is a shield made of mu-metal, possibly in combination with a superconducting "can" (all superconductors repel magnetic fields via the Meissner effect). 

The actual SQUID probe is generally made via thin-film deposition with the SQUID area outlined via lithography. A wide variety of superconducting materials can be used, but the two most common are Niobium, due to its relatively good resistance to damage from thermal cycling, and YBCO, for its high T_c > 77 K and relative ease of deposition compared to other high T_c superconductors. In either case, a superconductor with critical temperature higher than that of the operating temperature should be chosen. The SQUID itself can be used as the pickup coil for measuring the magnetic field, in which case the resolution of the device is proportional to the size of the SQUID. However, currents in or near the SQUID generate magnetic fields which are then registered in the coil and can be a source of noise. To reduce this effect it is also possible to make the size of the SQUID itself very small, but attach the device to a larger external superconducting loop located far from the SQUID. The flux through the loop will then be detected and measured, inducing a voltage in the SQUID.

The resolution and sensitivity of the device are both proportional to the size of the SQUID. A smaller device will have greater resolution but less sensitivity. The change in voltage induced is proportional to the inductance of the device, and limitations in the control of the bias magnetic field as well as electronics issues prevent a perfectly constant voltage from being maintained at all times. However, in practice, the sensitivity in most scanning SQUID microscopes is sufficient for almost any SQUID size for many applications, and therefore the tendency is to make the SQUID as small as possible to enhance resolution. Via e-beam lithography techniques it is possible to fabricate devices with total area of 1–10 μm², although devices in the tens to hundreds of square micrometres are more common.

The SQUID itself is mounted onto a cantilever and operated either in direct contact with or just above the sample surface. The position of the SQUID is usually controlled by some form of electric stepping motor. Depending on the particular application, different levels of precision may be required in the height of the apparatus. Operating at lower-tip sample distances increases the sensitivity and resolution of the device, but requires more advanced mechanisms in controlling the height of the probe. In addition such devices require extensive vibration dampening if precise height control is to be maintained.

Operation

Operation of a scanning SQUID microscope consists of simply cooling down the probe and sample, and rastering the tip across the area where measurements are desired. As the change in voltage corresponding to the measured magnetic field is quite rapid, the strength of the bias magnetic field is typically controlled by feedback electronics. This field strength is then recorded by a computer system that also keeps track of the position of the probe. An optical camera can also be used to track the position of the SQUID with respect to the sample.

Applications

Quantum vortices in YBCO imaged by the scanning SQUID microscopy

 

The scanning SQUID microscope was originally developed for an experiment to test the pairing symmetry of the high-temperature cuprate superconductor YBCO. Standard superconductors are isotropic with respect to their superconducting properties, that is, for any direction of electron momentum k in the superconductor, the magnitude of the order parameter and consequently the superconducting energy gap will be the same. However, in the high-temperature cuprate superconductors, the order parameter instead follows the equation Δ(k) = Δ₀(cos(k_xa)-cos(k_ya)), meaning that when crossing over any of the [110] directions in momentum space one will observe a sign change in the order parameter. The form of this function is equal to that of the l = 2 spherical harmonic function, giving it the name d-wave superconductivity. As the superconducting electrons are described by a single coherent wavefunction, proportional to exp(-iφ), where φ is known as the phase of the wavefunction, this property can be also interpreted as a phase shift of π under a 90 degree rotation.

This property was exploited by Tsuei et al. by manufacturing a series of YBCO ring Josephson junctions which crossed Bragg planes of a single YBCO crystal (figure). In a Josephson junction ring the superconducting electrons form a coherent wave function, just as in a superconductor. As the wavefunction must have only one value at each point, the overall phase factor obtained after traversing the entire Josephson circuit must be an integer multiple of 2π, as otherwise, one would obtain a different value of the probability density depending on the number of times one traversed the ring. 

In YBCO, upon crossing the [110] planes in momentum (and real) space, the wavefunction will undergo a phase shift of π. Hence if one forms a Josephson ring device where this plane is crossed (2n+1), number of times, a phase difference of (2n+1)π will be observed between the two junctions. For 2n, or even number of crossings, as in B, C, and D, a phase difference of (2n)π will be observed. Compared to the case of standard s-wave junctions, where no phase shift is observed, no anomalous effects were expected in the B, C, and D cases, as the single valued property is conserved, but for device A, the system must do something to for the φ=2nπ condition to be maintained. In the same property behind the scanning SQUID microscope, the phase of the wavefunction is also altered by the amount of magnetic flux passing through the junction, following the relationship Δφ=π(Φ₀). As was predicted by Sigrist and Rice, the phase condition can then be maintained in the junction by a spontaneous flux in the junction of value Φ₀/2.

Tsuei et al. used a scanning SQUID microscope to measure the local magnetic field at each of the devices in the figure, and observed a field in ring A approximately equal in magnitude Φ₀/2A, where A was the area of the ring. The device observed zero field at B, C, and D. The results provided one of the earliest and most direct experimental confirmations of d-wave pairing in YBCO.

Quantum vortex

From Wikipedia, the free encyclopedia

 

Vortices in a 200-nm-thick YBCO film imaged by scanning SQUID microscopy

 

In physics, a quantum vortex represents a quantized flux circulation of some physical quantity. In most cases quantum vortices are a type of topological defect exhibited in superfluids and superconductors. The existence of quantum vortices was first predicted by Lars Onsager in 1949 in connection with superfluid helium. Onsager reasoned that quantisation of vorticity is a direct consequence of the existence of a superfluid order parameter as a spatially continuous wavefunction. Onsager also pointed out that quantum vortices describe the circulation of superfluid and conjectured that their excitations are responsible for superfluid phase transitions. These ideas of Onsager were further developed by Richard Feynman in 1955 and in 1957 were applied to describe the magnetic phase diagram of type-II superconductors by Alexei Alexeyevich Abrikosov. In 1935 Fritz London published a very closely related work on magnetic flux quantization in superconductors. London's fluxoid can also be viewed as a quantum vortex.

Quantum vortices are observed experimentally in type-II superconductors (the Abrikosov vortex), liquid helium, and atomic gases, as well as in photon fields (optical vortex) and exciton-polariton superfluids. 

In a superfluid, a quantum vortex "carries" quantized orbital angular momentum, thus allowing the superfluid to rotate; in a superconductor, the vortex carries quantized magnetic flux. 

The term "quantum vortex" is also used in the study of few body problems. Under the De Broglie–Bohm theory, it is possible to derive a "velocity field" from the wave function. In this context, quantum vortices are zeros on the wave function, around which this velocity field has a solenoidal shape, similar to that of irrotational vortex on potential flows of traditional fluid dynamics

Vortex-quantisation in a superfluid

In a superfluid, a quantum vortex is a hole with the superfluid circulating around the vortex axis; the inside of the vortex may contain excited particles, air, vacuum, etc. The thickness of the vortex depends on a variety of factors; in liquid helium, the thickness is of the order of a few Angstroms. 

A superfluid has the special property of having phase, given by the wavefunction, and the velocity of the superfluid is proportional to the gradient of the phase (in the parabolic mass approximation). The circulation around any closed loop in the superfluid is zero if the region enclosed is simply connected. The superfluid is deemed irrotational; however, if the enclosed region actually contains a smaller region with an absence of superfluid, for example a rod through the superfluid or a vortex, then the circulation is:

${\displaystyle \oint _{C}\mathbf {v} \cdot \,d\mathbf {l} ={\frac {\hbar }{m}}\oint _{C}\nabla \phi _{v}\cdot \,d\mathbf {l} ={\frac {\hbar }{m}}\Delta ^{tot}\phi _{v},}$

where ${\displaystyle \hbar }$ is Planck's constant divided by ${\displaystyle 2\pi }$, m is the mass of the superfluid particle, and ${\displaystyle \Delta ^{tot}\phi _{v}}$ is the total phase difference around the vortex. Because the wave-function must return to its same value after an integer number of turns around the vortex (similar to what is described in the Bohr model), then ${\displaystyle \Delta ^{tot}\phi _{v}=2\pi n}$, where n is an integer. Thus, the circulation is quantized:

${\displaystyle \oint _{C}\mathbf {v} \cdot \,d\mathbf {l} \equiv {\frac {2\pi \hbar }{m}}n}$.

London's flux quantization in a superconductor

A principal property of superconductors is that they expel magnetic fields; this is called the Meissner effect. If the magnetic field becomes sufficiently strong it will, in some cases, “quench” the superconductive state by inducing a phase transition. In other cases, however, it will be energetically favorable for the superconductor to form a lattice of quantum vortices, which carry quantized magnetic flux through the superconductor. A superconductor that is capable of supporting vortex lattices is called a type-II superconductor, vortex-quantization in superconductors is general.

Over some enclosed area S, the magnetic flux is

${\displaystyle \Phi =\iint _{S}\mathbf {B} \cdot \mathbf {\hat {n}} \,d^{2}x=\oint _{\partial S}\mathbf {A} \cdot d\mathbf {l} ,}$ where ${\displaystyle \mathbf {A} }$ is the vector potential of the magnetic induction ${\displaystyle \mathbf {B} .}$

Substituting a result of London's equation: ${\displaystyle \mathbf {j} _{s}=-{\frac {n_{s}e_{s}^{2}}{m}}\mathbf {A} +{\frac {n_{s}e_{s}\hbar }{m}}\mathbf {\nabla } \phi }$, we find (with ${\displaystyle \mathbf {B} =\mathrm {curl} \,\,\mathbf {A} }$):

${\displaystyle \Phi =-{\frac {m}{n_{s}e^{2}}}\oint _{\partial S}\mathbf {j} _{s}\cdot d\mathbf {l} +{\frac {\hbar }{e_{s}}}\oint _{\partial S}\mathbf {\nabla } \phi \cdot d\mathbf {l} }$,

where n_s, m, and e_s are, respectively, number density, mass, and charge of the Cooper pairs. 

If the region, S, is large enough so that ${\displaystyle \mathbf {j} _{s}=0}$ along ${\displaystyle \partial S}$, then

${\displaystyle \Phi ={\frac {\hbar }{e_{s}}}\oint _{\partial S}\mathbf {\nabla } \phi \cdot d\mathbf {l} ={\frac {\hbar }{e_{s}}}\Delta ^{tot}\phi ={\frac {2\pi \hbar }{e_{s}}}n.}$

The flow of current can cause vortices in a superconductor to move, causing the electric field due to the phenomenon of electromagnetic induction. This leads to energy dissipation and causes the material to display a small amount of electrical resistance while in the superconducting state.

Constrained vortices in ferromagnets and antiferromagnets

The vortex states in ferromagnetic or antiferromagnetic material are also important, mainly for information technology They are exceptional, since in contrast to superfluids or superconducting material one has a more subtle mathematics: instead of the usual equation of the type ${\displaystyle \operatorname {curl} \ {\vec {v}}(x,y,z,t)\propto {\vec {\Omega }}(\mathrm {r} ,t)\cdot \delta (x,y),}$ where ${\displaystyle {\vec {\Omega }}(\mathrm {r} ,t)}$ is the vorticity at the spatial and temporal coordinates, and where ${\displaystyle \delta (x,y)}$ is the Dirac function, one has:

${\displaystyle \operatorname {curl} \,{\vec {v}}(x,y,z,t)\propto {\vec {m}}_{\mathrm {eff} }(\mathrm {r} ,t)\cdot \delta (x,y)\ \ (eqn.*),}$

where now at any point and at any time there is the constraint ${\displaystyle m_{x}^{2}(\mathrm {r} ,t)+m_{y}^{2}(\mathrm {r} ,t)+m_{z}^{2}(\mathrm {r} ,t)\equiv M_{0}^{2}}$. Here ${\displaystyle M_{0}}$ is constant, the constant magnitude of the non-constant magnetization vector ${\displaystyle {\vec {m}}(x,y,z,t)}$. As a consequence the vector ${\displaystyle {\vec {m}}}$ in eqn. (*) has been modified to a more complex entity ${\displaystyle {\vec {m}}_{\mathrm {eff} }}$. This leads, among other points, to the following fact: 

In ferromagnetic or antiferromagnetic material a vortex can be moved to generate bits for information storage and recognition, corresponding, e.g., to changes of the quantum number n. But although the magnetization has the usual azimuthal direction, and although one has vorticity quantization as in superfluids, as long as the circular integration lines surround the central axis at far enough perpendicular distance, this apparent vortex magnetization will change with the distance from an azimuthal direction to an upward or downward one, as soon as the vortex center is approached.

Thus, for each directional element ${\displaystyle \mathrm {d} \varphi \,\mathrm {d} \vartheta }$ there are now not two, but four bits to be stored by a change of vorticity: The first two bits concern the sense of rotation, clockwise or counterclockwise; the remaining bits three and four concern the polarization of the central singular line, which may be polarized up- or downwards. The change of rotation and/or polarization involves subtle topology.

Statistical mechanics of vortex lines

As first discussed by Onsager and Feynman, if the temperature in a superfluid or a superconductor is raised, the vortex loops undergo a second-order phase transition. This happens when the configurational entropy overcomes the Boltzmann factor which suppresses the thermal or heat generation of vortex lines. The lines form a condensate. Since the center of the lines, the vortex cores, are normal liquid or normal conductors, respectively, the condensation transforms the superfluid or superconductor into the normal state. The ensembles of vortex lines and their phase transitions can be described efficiently by a gauge theory.

Statistical mechanics of point vortices

In 1949 Onsager analysed a toy model consisting of a neutral system of point vortices confined to a finite area. He was able to show that, due to the properties of two-dimensional point vortices the bounded area (and consequently, bounded phase space), allows the system to exhibit negative temperatures. Onsager provided the first prediction that some isolated systems can exhibit negative Boltzmann temperature. Onsager's prediction was confirmed experimentally for a system of quantum vortices in a Bose-Einstein condensate in 2019.

Pair-interactions of quantum vortices

In a nonlinear quantum fluid, the dynamics and configurations of the vortex cores can be studied in terms of effective vortex-vortex pair interactions. The effective intervortex potential is predicted to affect quantum phase transitions and giving rise to different few-vortex molecules and many-body vortex patterns. Preliminary experiments in the specific system of exciton-polaritons fluids showed an effective attractive-repulsive intervortex dynamics between two cowinding vortices, whose attractive component can be modulated by the nonlinearity amount in the fluid.

Spontaneous vortices

Quantum vortices can form via the Kibble-Zurek mechanism. As a condensate forms by quench cooling, separate protocondensates form with independent phases. As these phase domains merge quantum vortices can be trapped in the emerging condensate order parameter. Spontaneous quantum vortices were observed in atomic Bose-Einstein condensates in 2008.

Superfluidity

From Wikipedia, the free encyclopedia

 

Helium II will "creep" along surfaces in order to find its own level—after a short while, the levels in the two containers will equalize. The Rollin film also covers the interior of the larger container; if it were not sealed, the helium II would creep out and escape.

 

The liquid helium is in the superfluid phase. A thin invisible film creeps up the inside wall of the cup and down on the outside. A drop forms. It will fall off into the liquid helium below. This will repeat until the cup is empty—provided the liquid remains superfluid.

 

Superfluidity is the characteristic property of a fluid with zero viscosity which therefore flows without loss of kinetic energy. When stirred, a superfluid forms cellular vortices that continue to rotate indefinitely. Superfluidity occurs in two isotopes of helium (helium-3 and helium-4) when they are liquefied by cooling to cryogenic temperatures. It is also a property of various other exotic states of matter theorized to exist in astrophysics, high-energy physics, and theories of quantum gravity. Superfluidity is often coincidental with Bose–Einstein condensation, but neither phenomenon is directly related to the other; not all Bose-Einstein condensates can be regarded as superfluids, and not all superfluids are Bose–Einstein condensates. The semiphenomenological theory of superfluidity was developed by Lev Landau.

Superfluidity of liquid helium

Superfluidity was originally discovered in liquid helium, by Pyotr Kapitsa and John F. Allen. It has since been described through phenomenology and microscopic theories. In liquid helium-4, the superfluidity occurs at far higher temperatures than it does in helium-3. Each atom of helium-4 is a boson particle, by virtue of its integer spin. A helium-3 atom is a fermion particle; it can form bosons only by pairing with itself at much lower temperatures. The discovery of superfluidity in helium-3 was the basis for the award of the 1996 Nobel Prize in Physics. This process is similar to the electron pairing in superconductivity.

Ultracold atomic gases

Superfluidity in an ultracold fermionic gas was experimentally proven by Wolfgang Ketterle and his team who observed quantum vortices in ⁶Li at a temperature of 50 nK at MIT in April 2005. Such vortices had previously been observed in an ultracold bosonic gas using ⁸⁷Rb in 2000, and more recently in two-dimensional gases. As early as 1999 Lene Hau created such a condensate using sodium atoms for the purpose of slowing light, and later stopping it completely. Her team subsequently used this system of compressed light to generate the superfluid analogue of shock waves and tornadoes:

These dramatic excitations result in the formation of solitons that in turn decay into quantized vortices—created far out of equilibrium, in pairs of opposite circulation—revealing directly the process of superfluid breakdown in Bose-Einstein condensates. With a double light-roadblock setup, we can generate controlled collisions between shock waves resulting in completely unexpected, nonlinear excitations. We have observed hybrid structures consisting of vortex rings embedded in dark solitonic shells. The vortex rings act as 'phantom propellers' leading to very rich excitation dynamics.

— Lene Hau, SIAM Conference on Nonlinear Waves and Coherent Structures

Superfluid in astrophysics

The idea that superfluidity exists inside neutron stars was first proposed by Arkady Migdal. By analogy with electrons inside superconductors forming Cooper pairs because of electron-lattice interaction, it is expected that nucleons in a neutron star at sufficiently high density and low temperature can also form Cooper pairs because of the long-range attractive nuclear force and lead to superfluidity and superconductivity.

In high-energy physics and quantum gravity

Superfluid vacuum theory (SVT) is an approach in theoretical physics and quantum mechanics where the physical vacuum is viewed as superfluid. 

The ultimate goal of the approach is to develop scientific models that unify quantum mechanics (describing three of the four known fundamental interactions) with gravity. This makes SVT a candidate for the theory of quantum gravity and an extension of the Standard Model. 

It is hoped that development of such theory would unify into a single consistent model of all fundamental interactions, and to describe all known interactions and elementary particles as different manifestations of the same entity, superfluid vacuum. 

On the macro-scale a larger similar phenomenon has been suggested as happening in the murmurations of starlings. The rapidity of change in flight patterns mimics the phase change leading to superfluidity in some liquid states.

Degenerate matter

From Wikipedia, the free encyclopedia

Degenerate matter is a highly dense state of fermionic matter in which particles must occupy high states of kinetic energy to satisfy the Pauli exclusion principle. The description applies to matter composed of electrons, protons, neutrons or other fermions. The term is mainly used in astrophysics to refer to dense stellar objects where gravitational pressure is so extreme that quantum mechanical effects are significant. This type of matter is naturally found in stars in their final evolutionary states, like white dwarfs and neutron stars, where thermal pressure alone is not enough to avoid gravitational collapse. 

Degenerate matter is usually modelled as an ideal Fermi gas, an ensemble of non-interacting fermions. In a quantum mechanical description, particles limited to a finite volume may take only a discrete set of energies, called quantum states. The Pauli exclusion principle prevents identical fermions from occupying the same quantum state. At lowest total energy (when the thermal energy of the particles is negligible), all the lowest energy quantum states are filled. This state is referred to as full degeneracy. This degeneracy pressure remains non-zero even at absolute zero temperature. Adding particles or reducing the volume forces the particles into higher-energy quantum states. In this situation, a compression force is required, and is made manifest as a resisting pressure. The key feature is that this degeneracy pressure does not depend on the temperature but only on the density of the fermions. Degeneracy pressure keeps dense stars in equilibrium, independent of the thermal structure of the star. 

A degenerate mass whose fermions have velocities close to the speed of light (particle energy larger than its rest mass energy) is called relativistic degenerate matter.

The concept of degenerate stars, stellar objects composed of degenerate matter, was originally developed in a joint effort between Arthur Eddington, Ralph Fowler and Arthur Milne. Eddington had suggested that the atoms in Sirius B were almost completely ionised and closely packed. Fowler described white dwarfs as composed of a gas of particles that became degenerate at low temperature. Milne proposed that degenerate matter is found in most of the nuclei of stars, not only in compact stars.

Concept

If a plasma is cooled and under increasing pressure, it will eventually not be possible to compress the plasma any further. This constraint is due to the Pauli exclusion principle, which states that two fermions cannot share the same quantum state. When in this highly compressed state, since there is no extra space for any particles, a particle's location is extremely defined. Since the locations of the particles of a highly compressed plasma have very low uncertainty, their momentum is extremely uncertain. The Heisenberg uncertainty principle states

${\displaystyle \Delta p\Delta x\geq {\frac {\hbar }{2}}}$,

where Δp is the uncertainty in the particle's momentum and Δx is the uncertainty in position (and ħ is the reduced Planck constant). Therefore, even though the plasma is cold, such particles must on average be moving very fast. Large kinetic energies lead to the conclusion that, in order to compress an object into a very small space, tremendous force is required to control its particles' momentum.

Unlike a classical ideal gas, whose pressure is proportional to its temperature

${\displaystyle P=k_{\rm {B}}{\frac {NT}{V}}}$,

where P is pressure, k_B is Boltzmann's constant, N is the number of particles—typically atoms or molecules—, T is temperature, and V is the volume, the pressure exerted by degenerate matter depends only weakly on its temperature. In particular, the pressure remains nonzero even at absolute zero temperature. At relatively low densities, the pressure of a fully degenerate gas can be derived by treating the system as an ideal Fermi gas, in this way

${\displaystyle P={\frac {(3\pi ^{2})^{2/3}\hbar ^{2}}{5m}}\left({\frac {N}{V}}\right)^{5/3}}$,

where m is the mass of the individual particles making up the gas. At very high densities, where most of the particles are forced into quantum states with relativistic energies, the pressure is given by

${\displaystyle P=K\left({\frac {N}{V}}\right)^{4/3}}$,

where K is another proportionality constant depending on the properties of the particles making up the gas.

All matter experiences both normal thermal pressure and degeneracy pressure, but in commonly encountered gases, thermal pressure dominates so much that degeneracy pressure can be ignored. Likewise, degenerate matter still has normal thermal pressure, the degeneracy pressure dominates to the point that temperature has a negligible effect on the total pressure.

While degeneracy pressure usually dominates at extremely high densities, it is the ratio of the two which determines degeneracy. Given a sufficiently drastic increase in temperature (such as during a red giant star's helium flash), matter can become non-degenerate without reducing its density.

Degeneracy pressure contributes to the pressure of conventional solids, but these are not usually considered to be degenerate matter because a significant contribution to their pressure is provided by electrical repulsion of atomic nuclei and the screening of nuclei from each other by electrons. The free electron model of metals derives their physical properties by considering the conduction electrons alone as a degenerate gas, while the majority of the electrons are regarded as occupying bound quantum states. This solid state contrasts with degenerate matter that forms the body of a white dwarf, where most of the electrons would be treated as occupying free particle momentum states. 

Exotic examples of degenerate matter include neutron degenerate matter, strange matter, metallic hydrogen and white dwarf matter.

Degenerate gases

Degenerate gases are gases composed of fermions such as electrons, protons, and neutrons rather than molecules of ordinary matter. The electron gas in ordinary metals and in the interior of white dwarfs are two examples. Following the Pauli exclusion principle, there can be only one fermion occupying each quantum state. In a degenerate gas, all quantum states are filled up to the Fermi energy. Most stars are supported against their own gravitation by normal thermal gas pressure, while in white dwarf stars the supporting force comes from the degeneracy pressure of the electron gas in their interior. In neutron stars, the degenerate particles are neutrons.

A fermion gas in which all quantum states below a given energy level are filled is called a fully degenerate fermion gas. The difference between this energy level and the lowest energy level is known as the Fermi energy.

Electron degeneracy

In an ordinary fermion gas in which thermal effects dominate, most of the available electron energy levels are unfilled and the electrons are free to move to these states. As particle density is increased, electrons progressively fill the lower energy states and additional electrons are forced to occupy states of higher energy even at low temperatures. Degenerate gases strongly resist further compression because the electrons cannot move to already filled lower energy levels due to the Pauli exclusion principle. Since electrons cannot give up energy by moving to lower energy states, no thermal energy can be extracted. The momentum of the fermions in the fermion gas nevertheless generates pressure, termed "degeneracy pressure". 

Under high densities the matter becomes a degenerate gas when the electrons are all stripped from their parent atoms. In the core of a star, once hydrogen burning in nuclear fusion reactions stops, it becomes a collection of positively charged ions, largely helium and carbon nuclei, floating in a sea of electrons, which have been stripped from the nuclei. Degenerate gas is an almost perfect conductor of heat and does not obey the ordinary gas laws. White dwarfs are luminous not because they are generating any energy but rather because they have trapped a large amount of heat which is gradually radiated away. Normal gas exerts higher pressure when it is heated and expands, but the pressure in a degenerate gas does not depend on the temperature. When gas becomes super-compressed, particles position right up against each other to produce degenerate gas that behaves more like a solid. In degenerate gases the kinetic energies of electrons are quite high and the rate of collision between electrons and other particles is quite low, therefore degenerate electrons can travel great distances at velocities that approach the speed of light. Instead of temperature, the pressure in a degenerate gas depends only on the speed of the degenerate particles; however, adding heat does not increase the speed of most of the electrons, because they are stuck in fully occupied quantum states. Pressure is increased only by the mass of the particles, which increases the gravitational force pulling the particles closer together. Therefore, the phenomenon is the opposite of that normally found in matter where if the mass of the matter is increased, the object becomes bigger. In degenerate gas, when the mass is increased, the pressure is increased, and the particles become spaced closer together, so the object becomes smaller. Degenerate gas can be compressed to very high densities, typical values being in the range of 10,000 kilograms per cubic centimeter. 

There is an upper limit to the mass of an electron-degenerate object, the Chandrasekhar limit, beyond which electron degeneracy pressure cannot support the object against collapse. The limit is approximately 1.44 solar masses for objects with typical compositions expected for white dwarf stars (carbon and oxygen with 2 baryons per electron). This mass cutoff is appropriate only for a star supported by ideal electron degeneracy pressure under Newtonian gravity; in general relativity and with realistic Coulomb corrections, the corresponding mass limit is around 1.38 solar masses.^[8] The limit may also change with the chemical composition of the object, as it affects the ratio of mass to number of electrons present. The object's rotation, which counteracts the gravitational force, also changes the limit for any particular object. Celestial objects below this limit are white dwarf stars, formed by the gradual shrinking of the cores of stars that run out of fuel. During this shrinking, an electron-degenerate gas forms in the core, providing sufficient degeneracy pressure as it is compressed to resist further collapse. Above this mass limit, a neutron star (partially supported by neutron degeneracy pressure) or a black hole may be formed instead.

Neutron degeneracy

Neutron degeneracy is analogous to electron degeneracy and is demonstrated in neutron stars, which are partially supported by the pressure from a degenerate neutron gas. The collapse may happen when the core of a white dwarf is above the vicinity of 1.4 solar masses, which is the Chandrasekhar limit, and the collapse is not halted by the pressure of degenerate electrons. As the star collapses, the Fermi energy of the electrons increases to the point where it is energetically favorable for them to combine with protons to produce neutrons (via inverse beta decay, also termed electron capture and "neutronization"). The result is an extremely compact star composed of nuclear matter, which is predominantly a degenerate neutron gas, sometimes called neutronium, with a small admixture of degenerate proton and electron gases (and at higher densities, muons). 

Neutrons in a degenerate neutron gas are spaced much more closely than electrons in an electron-degenerate gas because the more massive neutron has a much shorter wavelength at a given energy. Typical separations are comparable with the size of the neutron and the range of the strong nuclear force, and it is actually the repulsive nature of the latter at small separations that primarily supports neutron stars more massive than 0.7 solar masses (which includes all measured neutron stars). In the case of neutron stars and white dwarfs, this phenomenon is compounded by the fact that the pressures within neutron stars are much higher than those in white dwarfs. The pressure increase is caused by the fact that the compactness of a neutron star causes gravitational forces to be much higher than in a less compact body with similar mass. The result is a star with a diameter on the order of a thousandth that of a white dwarf.

There is an upper limit to the mass of a neutron-degenerate object, the Tolman–Oppenheimer–Volkoff limit, which is analogous to the Chandrasekhar limit for electron-degenerate objects. The limit for objects supported by ideal neutron degeneracy pressure is only 0.75 solar masses. For more realistic models including baryon interaction, the precise limit is unknown, as it depends on the equations of state of nuclear matter, for which a highly accurate model is not yet available. Above this limit, a neutron star may collapse into a black hole or into other, denser forms of degenerate matter (such as quark matter) if these forms exist and have suitable properties (mainly related to degree of compressibility, or "stiffness", described by the equations of state).

Proton degeneracy

Sufficiently dense matter containing protons experiences proton degeneracy pressure, in a manner similar to the electron degeneracy pressure in electron-degenerate matter: protons confined to a sufficiently small volume have a large uncertainty in their momentum due to the Heisenberg uncertainty principle. However, because protons are much more massive than electrons, the same momentum represents a much smaller velocity for protons than for electrons. As a result, in matter with approximately equal numbers of protons and electrons, proton degeneracy pressure is much smaller than electron degeneracy pressure, and proton degeneracy is usually modelled as a correction to the equations of state of electron-degenerate matter.

Quark degeneracy

At densities greater than those supported by neutron degeneracy, quark matter is expected to occur.^{[citation needed]} Several variations of this hypothesis have been proposed that represent quark-degenerate states. Strange matter is a degenerate gas of quarks that is often assumed to contain strange quarks in addition to the usual up and down quarks. Color superconductor materials are degenerate gases of quarks in which quarks pair up in a manner similar to Cooper pairing in electrical superconductors. The equations of state for the various proposed forms of quark-degenerate matter vary widely, and are usually also poorly defined, due to the difficulty of modeling strong force interactions.

Quark-degenerate matter may occur in the cores of neutron stars, depending on the equations of state of neutron-degenerate matter. It may also occur in hypothetical quark stars, formed by the collapse of objects above the Tolman–Oppenheimer–Volkoff mass limit for neutron-degenerate objects. Whether quark-degenerate matter forms at all in these situations depends on the equations of state of both neutron-degenerate matter and quark-degenerate matter, both of which are poorly known. Quark stars are considered to be an intermediate category between neutron stars and black holes.

Singularity

At densities greater than those supported by any degeneracy, gravity overwhelms all other forces. The stellar body collapses to form a black hole, though this is not well modeled by quantum mechanics. At the same time, the material must be converted from fermions, which are subject to degeneracy pressure, to bosons, which are not. A current hypothesis suggest gluons as the most likely boson thought possible. 

In the frame of reference that is co-moving with the collapsing matter, general relativity models without quantum mechanics have all the matter ending up in an infinitely dense singularity at the center of the event horizon. (If one uses the UFT Einstein–Maxwell–Dirac system or its generalizations, then the singularity is avoided and one ends up with a quark star, possibly surrounded by an event horizon.) It is a general result of quantum mechanics that no fermion can be confined in a space smaller than its own wavelength, making such a singularity impossible, unless only bosons are present, but there is no widely accepted theory that combines general relativity and quantum mechanics sufficiently to tell us what the structure inside a black hole might be. If bosons can be conclusively ruled out, one possible theory is that constituent particles decompose into strings, forming a structure called a fuzzball.