Scanning SQUID microscopy

From Wikipedia, the free encyclopedia

 

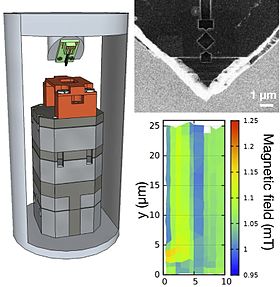
Left: Schematic of a scanning SQUID microscope in a helium-4 refrigerator. Green holder for the SQUID probe is attached to a quartz tuning fork. Bottom part is a piezoelectric sample stage. Right: electron micrograph of a SQUID probe and a test image of Nb/Au strips recorded with it.

 

Scanning SQUID microscopy is a technique where a superconducting quantum interference device (SQUID) is used to image surface magnetic field strength with micrometre scale resolution. A tiny SQUID is mounted onto a tip which is then rastered near the surface of the sample to be measured. As the SQUID is the most sensitive detector of magnetic fields available and can be constructed at submicrometre widths via lithography, the scanning SQUID microscope allows magnetic fields to be measured with unparalleled resolution and sensitivity. The first scanning SQUID microscope was built in 1992 by Black et al. Since then the technique has been used to confirm unconventional superconductity in several high-temperature superconductors including YBCO and BSCCO compounds.

Operating principles

Diagram of a DC SQUID. The current ${\displaystyle I}$ enters and splits into the two paths, each with currents ${\displaystyle I_{a}}$ and ${\displaystyle I_{b}}$. The thin barriers on each path are Josephson junctions, which together separate the two superconducting regions. ${\displaystyle \Phi }$ represents the magnetic flux entering the inside of the DC SQUID loop.

 

The scanning SQUID microscope is based upon the thin-film DC SQUID. A DC SQUID consists of superconducting electrodes in a ring pattern connected by two weak-link Josephson junctions (see figure). Above the critical current of the Josephson junctions, the idealized difference in voltage between the electrodes is given by

${\displaystyle {\begin{aligned}V&={\frac {R}{2}}{\sqrt {I^{2}-I_{0}^{2}}},\\&={\frac {R}{2}}\left(I^{2}-\left(2I_{c}\cos \left(\pi {\frac {\Phi }{\Phi _{0}}}\right)\right)^{2}\right)^{\frac {1}{2}},\end{aligned}}}$

where R is the resistance between the electrodes, I is the current, I₀ is the maximum supercurrent, I_c is the critical current of the Josephson junctions, Φ is the total magnetic flux through the ring, and Φ₀ is the magnetic flux quantum. 

Hence, a DC SQUID can be used as a flux-to-voltage transducer. However, as noted by the figure, the voltage across the electrodes oscillates sinusoidally with respect to the amount of magnetic flux passing through the device. As a result, alone a SQUID can only be used to measure the change in magnetic field from some known value, unless the magnetic field or device size is very small such that Φ < Φ₀. To use the DC SQUID to measure standard magnetic fields, one must either count the number of oscillations in the voltage as the field is changed, which is very difficult in practice, or use a separate DC bias magnetic field parallel to the device to maintain a constant voltage and consequently constant magnetic flux through the loop. The strength of the field being measured will then be equal to the strength of the bias magnetic field passing through the SQUID.

Although it is possible to read the DC voltage between the two terminals of the SQUID directly, because noise tends to be a problem in DC measurements, an alternating current technique is used. In addition to the DC bias magnetic field, an AC magnetic field of constant amplitude, with field strength generating Φ << Φ₀, is also emitted in the bias coil. This AC field produces an AC voltage with amplitude proportional to the DC component in the SQUID. The advantage of this technique is that the frequency of the voltage signal can be chosen to be far away from that of any potential noise sources. By using a lock-in amplifier the device can read only the frequency corresponding to the magnetic field, ignoring many other sources of noise.

Instrumentation

As the SQUID material must be superconducting, measurements must be performed at low temperatures. Typically, experiments are carried out below liquid helium temperature (4.2 K) in a helium-3 refrigerator or dilution refrigerator. However, advances in high-temperature superconductor thin-film growth have allowed relatively inexpensive liquid nitrogen cooling to instead be used. It is even possible to measure room-temperature samples by only cooling a high T_c squid and maintaining thermal separation with the sample. In either case, due to the extreme sensitivity of the SQUID probe to stray magnetic fields, in general some form of magnetic shielding is used. Most common is a shield made of mu-metal, possibly in combination with a superconducting "can" (all superconductors repel magnetic fields via the Meissner effect). 

The actual SQUID probe is generally made via thin-film deposition with the SQUID area outlined via lithography. A wide variety of superconducting materials can be used, but the two most common are Niobium, due to its relatively good resistance to damage from thermal cycling, and YBCO, for its high T_c > 77 K and relative ease of deposition compared to other high T_c superconductors. In either case, a superconductor with critical temperature higher than that of the operating temperature should be chosen. The SQUID itself can be used as the pickup coil for measuring the magnetic field, in which case the resolution of the device is proportional to the size of the SQUID. However, currents in or near the SQUID generate magnetic fields which are then registered in the coil and can be a source of noise. To reduce this effect it is also possible to make the size of the SQUID itself very small, but attach the device to a larger external superconducting loop located far from the SQUID. The flux through the loop will then be detected and measured, inducing a voltage in the SQUID.

The resolution and sensitivity of the device are both proportional to the size of the SQUID. A smaller device will have greater resolution but less sensitivity. The change in voltage induced is proportional to the inductance of the device, and limitations in the control of the bias magnetic field as well as electronics issues prevent a perfectly constant voltage from being maintained at all times. However, in practice, the sensitivity in most scanning SQUID microscopes is sufficient for almost any SQUID size for many applications, and therefore the tendency is to make the SQUID as small as possible to enhance resolution. Via e-beam lithography techniques it is possible to fabricate devices with total area of 1–10 μm², although devices in the tens to hundreds of square micrometres are more common.

The SQUID itself is mounted onto a cantilever and operated either in direct contact with or just above the sample surface. The position of the SQUID is usually controlled by some form of electric stepping motor. Depending on the particular application, different levels of precision may be required in the height of the apparatus. Operating at lower-tip sample distances increases the sensitivity and resolution of the device, but requires more advanced mechanisms in controlling the height of the probe. In addition such devices require extensive vibration dampening if precise height control is to be maintained.

Operation

Operation of a scanning SQUID microscope consists of simply cooling down the probe and sample, and rastering the tip across the area where measurements are desired. As the change in voltage corresponding to the measured magnetic field is quite rapid, the strength of the bias magnetic field is typically controlled by feedback electronics. This field strength is then recorded by a computer system that also keeps track of the position of the probe. An optical camera can also be used to track the position of the SQUID with respect to the sample.

Applications

Quantum vortices in YBCO imaged by the scanning SQUID microscopy

 

The scanning SQUID microscope was originally developed for an experiment to test the pairing symmetry of the high-temperature cuprate superconductor YBCO. Standard superconductors are isotropic with respect to their superconducting properties, that is, for any direction of electron momentum k in the superconductor, the magnitude of the order parameter and consequently the superconducting energy gap will be the same. However, in the high-temperature cuprate superconductors, the order parameter instead follows the equation Δ(k) = Δ₀(cos(k_xa)-cos(k_ya)), meaning that when crossing over any of the [110] directions in momentum space one will observe a sign change in the order parameter. The form of this function is equal to that of the l = 2 spherical harmonic function, giving it the name d-wave superconductivity. As the superconducting electrons are described by a single coherent wavefunction, proportional to exp(-iφ), where φ is known as the phase of the wavefunction, this property can be also interpreted as a phase shift of π under a 90 degree rotation.

This property was exploited by Tsuei et al. by manufacturing a series of YBCO ring Josephson junctions which crossed Bragg planes of a single YBCO crystal (figure). In a Josephson junction ring the superconducting electrons form a coherent wave function, just as in a superconductor. As the wavefunction must have only one value at each point, the overall phase factor obtained after traversing the entire Josephson circuit must be an integer multiple of 2π, as otherwise, one would obtain a different value of the probability density depending on the number of times one traversed the ring. 

In YBCO, upon crossing the [110] planes in momentum (and real) space, the wavefunction will undergo a phase shift of π. Hence if one forms a Josephson ring device where this plane is crossed (2n+1), number of times, a phase difference of (2n+1)π will be observed between the two junctions. For 2n, or even number of crossings, as in B, C, and D, a phase difference of (2n)π will be observed. Compared to the case of standard s-wave junctions, where no phase shift is observed, no anomalous effects were expected in the B, C, and D cases, as the single valued property is conserved, but for device A, the system must do something to for the φ=2nπ condition to be maintained. In the same property behind the scanning SQUID microscope, the phase of the wavefunction is also altered by the amount of magnetic flux passing through the junction, following the relationship Δφ=π(Φ₀). As was predicted by Sigrist and Rice, the phase condition can then be maintained in the junction by a spontaneous flux in the junction of value Φ₀/2.

Tsuei et al. used a scanning SQUID microscope to measure the local magnetic field at each of the devices in the figure, and observed a field in ring A approximately equal in magnitude Φ₀/2A, where A was the area of the ring. The device observed zero field at B, C, and D. The results provided one of the earliest and most direct experimental confirmations of d-wave pairing in YBCO.