Reproductive success

From Wikipedia, the free encyclopedia

 

A sperm fertilizing an egg in sexual reproduction is one stage of reproductive success

 

Reproductive success is defined as an individual's production of offspring per breeding event or lifetime. This is not limited by the number of offspring produced by one individual, but also the reproductive success of these offspring themselves. Reproductive success is different from fitness in that individual success is not necessarily a determinant for adaptive strength of a genotype since the effects of chance and the environment have no influence on those specific genes. Reproductive success turns into a part of fitness when the offspring are actually recruited into the breeding population. If offspring quantity is not correlated with quality this holds up, but if not then reproductive success must be adjusted by traits that predict juvenile survival in order to be measured effectively. Quality and quantity is about finding the right balance between reproduction and maintenance and the disposable soma theory of aging tells us that a longer lifespan will come at the cost of reproduction and thus longevity is not always correlated with high fecundity. Parental investment is a key factor in reproductive success since taking better care to offspring is what often will give them a fitness advantage later in life. This includes mate choice and sexual selection as an important factor in reproductive success, which is another reason why reproductive success is different from fitness as individual choices and outcomes are more important than genetic differences. As reproductive success is measured over generations, Longitudinal studies are the preferred study type as they follow a population or an individual over a longer period of time in order to monitor the progression of the individual(s). These long term studies are preferable since they negate the effects of the variation in a single year or breeding season.

Nutritional contribution

Nutrition is one of the factors that influences reproductive success. For example, different amounts of consumption and more specifically carbohydrate to protein ratios. In some cases, the amounts or ratios of intake are more influential during certain stages of the lifespan. For example, in the Mexican fruit fly, male protein intake is critical only at eclosion. Intake at this time provides longer lasting reproductive ability. After this developmental stage, protein intake will have no effect and is not necessary for reproductive success. In addition, Ceratitis capitata males were experimented on to see how protein influence during the larval stage affects mating success. Males were fed either a high protein diet, which consisted of 6.5g/100mL, or a no protein diet during the larval stage. Males that were fed protein had more copulations than those that weren't fed protein, which ultimately correlates with a higher mating success. Protein-deprived black blow fly males have been seen to exhibit lower numbers of oriented mounts and inseminate fewer females than more lively fed males. In still other instances, prey deprivation or an inadequate diet has been shown to lead to a partial or complete halt in male mating activity. Copulation time lasted longer for sugar-fed males than protein-fed flies, showing that carbohydrates were more necessary for a longer copulation duration.

In mammals, amounts of protein, carbohydrates, and fats are seen to influence reproductive success. This was evaluated among 28 female black bears evaluated by measuring the number of cubs born. Using different foods during the fall including corn, herbaceous, red oak, beech, and cherry, nutritional facts of protein, carbohydrate, and fat were noted, as each varied in percent compositions. Seventy-percent of the bears who had high fat and high carbohydrate diets produced cubs. Conversely, all 10 females who had low carbohydrate diets did not reproduce cubs, deeming carbohydrates a critical factor for reproductive success where fat was not a hindrance.

Adequate nutrition at pre-mating time periods showed to have the most effect on various reproductive processes in mammals. Increased nutrition, in general, during this time was most beneficial for oocyte and embryo development. As a result, offspring number and viability was also improved. Thus, proper nutrition timing during the pre-mating time is key for development and long-term benefit of the offspring. Two different diets were fed to Florida scrub-jays and breeding performance was noted to have different effects. One diet consisted of high protein and high fat, and the other consisting of just high fat. The significant result was that the birds with the high protein and high fat diet laid heavier eggs than the birds with the rich-in-fat diet. There was a difference in the amount of water inside the eggs, which accounted for the different weights. It is hypothesized that the added water resulting from the adequate protein-rich and fat-rich diet may contribute to development and survival of the chick, therefore aiding reproductive success.

Dietary intake also improves egg production, which can also be considered to help create viable offspring. Post-mating changes are seen in organisms in response to necessary conditions for development. This is depicted in the two-spotted cricket where feeding was tested for in females. It was found that mated females exhibited more overall consumption than unmated. Observations of female crickets showed that after laying their eggs, their protein intake increased towards the end of the second day. The female crickets therefore require a larger consumption of protein to nourish the development of subsequent eggs and even mating. More specifically, using geometrical framework analysis, mated females fed off of a more protein rich diet after mating. Unmated and mated female crickets were found to prefer a 2:1 and 3.5:1 protein to carbohydrate, respectively. In the Japanese quail, the influence of diet quality on egg production was studied. The diet quality differed in the percent composition of protein, with the high-protein diet having 20%, and the low-protein diet having 12%. It was found that both the number of eggs produced and the size of the eggs were greater in the high-protein diet than the low. What was found unaffected, however, was the maternal antibody transmission. Thus, immune response was not affected since there was still a source of protein, although low. This means that the bird is able to compensate for the lack of protein in the diet by protein reserves, for example.

Higher concentrations of protein in diet have also positively correlated with gamete production across various animals. The formation of oothecae in brown-banded cockroaches based on protein intake was tested. A protein intake of 5% deemed too low as it delayed mating and an extreme of 65% protein directly killed the cockroach. Oothecae production for the female as was more optimal at a 25% protein diet.

Although there is a trend of protein and carbohydrates being essential for various reproductive functions including copulation success, egg development, and egg production, the ratio and amounts of each are not fixed. These values vary across a span of animals, from insects to mammals. For example, many insects may need a diet consisting of both protein and carbohydrates with a slightly higher protein ratio for reproductive success. On the other hand, a mammal like a black bear would need a higher amount of carbohydrates and fats, but not necessarily protein. Different types of animals have different necessities based on their make-up. One cannot generalize as the results may vary across different types of animals, and even more across different species.

Cooperative breeding

Evolutionarily, humans are socially well adapted to their environment and coexist with one another in a way that benefits the entire species. Cooperative breeding, the ability for humans to invest in and help raise others' offspring, is an example of some of their unique characteristics that sets them apart from other non-human primates even though some practice this system at a low frequency. One of the reasons why humans require significantly more non-parental investment in comparison to other species is because they are still dependent on adults to take care of them throughout most of their juvenile period. Cooperative breeding can be expressed through economic support that requires humans to financially invest in someone else's offspring or through social support, which may require active energy investment and time. This parenting system eventually aids people in increasing their survival rate and reproductive success as a whole. Hamilton's rule and kin selection are used to explain why this altruistic behavior has been naturally selected and what non-parents gain by investing in offspring that is not their own. Hamilton's rule states that rb > c where r= relatedness, b= benefit to recipient, c= cost of the helper. This formula describes the relationship that has to occur among the three variables for kin selection take place. If the relative genetic relatedness of the helper with the offspring is closer and their benefit is greater than the cost of the helper, then kin selection will be most likely be favored. Even though kin selection does not benefit individuals who invest in relatives' offspring, it still highly increases the reproduction success of a population by ensuring genes are being passed down to the next generation.

Humans

Some research has suggested that historically, women have had a far higher reproductive success rate than men. Dr. Baumeister has suggested that the modern human has twice as many female ancestors as male ancestors. 

Males and females should be considered separately in reproduction success for their different limitations in producing the maximum amount of offspring. Females have limitations such as gestation time (typically 9 months), then followed by lactation which suppresses ovulation and her chances of becoming pregnant again quickly. In addition, a females ultimate reproductive success is limited due to ability to distribute her time and energy towards reproducing. Peter T. Ellison states, "The metabolic task of converting energy from the environment into viable offspring falls to the female, and the rate at which she can produce offspring is limited by the rate at which she can direct metabolic energy to the task" The reasoning for the transfer of energy from one category to another takes away from each individual category overall. For example, if a female has not reached menarche yet, she will only need to be focusing her energy into growth and maintenance because she cannot yet place energy towards reproducing. However, once a female is ready to begin putting forth energy into reproduction she will then have less energy to put towards overall growth and maintenance.

Females have a constraint on the amount of energy they will need to put forth into reproduction. Since females go through gestation they have a set obligation for energy output into reproduction. Males, however, do no have this constraint and therefore could potentially put forth more offspring as their commitment of energy into reproduction is less than a females. All things considered, men and women are constrained for different reasons and the number of offspring they can produce. Males contrastingly are not constrained by the time and energy of gestation or lactation. Females are reliant on the genetic quality of their mate as well. This refers to sperm quality of the male and the compatibility of the sperms antigens with the females immune system. If the Humans in general, consider phenotypic traits that present their health and body symmetry. The pattern of constraints on female reproduction is consistent with human life-history and across all populations. 

A difficulty in studying human reproductive success is its high variability. Every person, male or female, is different, especially when it comes to reproductive success and also fertility. Reproductive success is determined not only by behavior (choices), but also physiological variables that cannot be controlled.

The Blurnton-Jones 'backload model' "tested a hypothesis that the length of the birth intervals of !Kung hunter-gatherers allowed women to balance optimally the energetic demands of child bearing and foraging in a society where women had to carry small children and foraged substantial distances". Behind this hypothesis is the fact that spacing birth intervals allowed for a better chance of child survival and that ultimately promoted evolutionary fitness. This hypothesis goes along with the evolutionary trend of having three areas to divide up one's individual energy: growth, maintenance, and reproduction. This hypothesis is good for gaining an understanding of "individual-level variation in fertility in small-scale, high fertility, societies( sometimes referred to by demographers as 'natural-fertility' populations". Reproduction success is hard to study as there are many different variables, and a lot of the concept is subject to each condition and environment.   

Natural selection and evolution

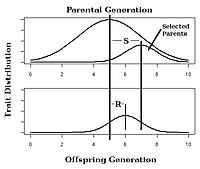
To supplement a complete understanding of reproductive success or biological fitness it is necessary to understand the theory of natural selection. Darwin's theory of natural selection explains how the change of genetic variation over time within a species allows some individuals to be better suited to their environmental pressures, finding suitable mates, and/or finding food sources than others. Over time those same individuals pass on their genetic makeup onto their offspring and therefore the frequency of this advantageous trait or gene increases within that population.

The same may be true for the opposite as well. If an individual is born with a genetic makeup that makes them less suited for their environment, they may have less of a chance of surviving and passing on their genes and therefore may see these disadvantageous traits decrease in frequency. This is one example of how reproductive success as well as biological fitness is a main component of the theory of Natural Selection and Evolution.

Evolutionary trade-offs

Throughout evolutionary history, often an advantageous trait or gene will continue to increase in frequency within a population only due to a loss or decrease in functionality of another trait. This is known as an evolutionary trade-off. From Oxford Academic, "The resulting 'evolutionary tradeoffs' reflect necessary compromises among the functions of multiple traits". Due to a variety of limitations like energy availability, resource allocation during biological development or growth, or limitations of the genetic makeup itself means that there is a balance between traits. The increase in effectiveness in one trait may lead to a decrease in effectiveness of other traits as result. 

This is important to understand because if certain individuals within a population have a certain trait that raises their reproductive fitness, this trait may have developed at the expense of others. Changes in genetic makeup through natural selection is not necessarily changes that are either just beneficial or deleterious but are changes that may be both. For example, an evolutionary change over time that results in higher reproductive success at younger ages might ultimately result in a decrease in life expectancy for those with that particular trait.

Fitness (biology)

From Wikipedia, the free encyclopedia

 

Fitness (often denoted ${\displaystyle w}$ or ω in population genetics models) is the quantitative representation of natural and sexual selection within evolutionary biology. It can be defined either with respect to a genotype or to a phenotype in a given environment. In either case, it describes individual reproductive success and is equal to the average contribution to the gene pool of the next generation that is made by individuals of the specified genotype or phenotype. The fitness of a genotype is manifested through its phenotype, which is also affected by the developmental environment. The fitness of a given phenotype can also be different in different selective environments.

With asexual reproduction, it is sufficient to assign fitnesses to genotypes. With sexual reproduction, genotypes are scrambled every generation. In this case, fitness values can be assigned to alleles by averaging over possible genetic backgrounds. Natural selection tends to make alleles with higher fitness more common over time, resulting in Darwinian evolution.

The term "Darwinian fitness" can be used to make clear the distinction with physical fitness. Fitness does not include a measure of survival or life-span; Herbert Spencer's well-known phrase "survival of the fittest" should be interpreted as: "Survival of the form (phenotypic or genotypic) that will leave the most copies of itself in successive generations."

Inclusive fitness differs from individual fitness by including the ability of an allele in one individual to promote the survival and/or reproduction of other individuals that share that allele, in preference to individuals with a different allele. One mechanism of inclusive fitness is kin selection.

Fitness is a propensity

Fitness is often defined as a propensity or probability, rather than the actual number of offspring. For example, according to Maynard Smith, "Fitness is a property, not of an individual, but of a class of individuals — for example homozygous for allele A at a particular locus. Thus the phrase ’expected number of offspring’ means the average number, not the number produced by some one individual. If the first human infant with a gene for levitation were struck by lightning in its pram, this would not prove the new genotype to have low fitness, but only that the particular child was unlucky." 

Alternatively, "the fitness of the individual - having an array x of phenotypes — is the probability, s(x), that the individual will be included among the group selected as parents of the next generation."

Models of fitness: asexuals

To avoid the complications of sex and recombination, we initially restrict our attention to an asexual population without genetic recombination. Then fitnesses can be assigned directly to genotypes rather than having to worry about individual alleles. There are two commonly used measures of fitness; absolute fitness and relative fitness.

Absolute fitness

The absolute fitness (${\displaystyle W}$) of a genotype is defined as the proportional change in the abundance of that genotype over one generation attributable to selection. For example, if ${\displaystyle n(t)}$ is the abundance of a genotype in generation ${\displaystyle t}$ in an infinitely large population (so that there is no genetic drift), and neglecting the change in genotype abundances due to mutations, then

${\displaystyle n(t+1)=Wn(t)}$.

An absolute fitness larger than 1 indicates growth in that genotype's abundance; an absolute fitness smaller than 1 indicates decline.

Relative fitness

Whereas absolute fitness determines changes in genotype abundance, relative fitness (${\displaystyle w}$) determines changes in genotype frequency. If ${\displaystyle N(t)}$ is the total population size in generation ${\displaystyle t}$, and the relevant genotype's frequency is ${\displaystyle p(t)=n(t)/N(t)}$, then

${\displaystyle p(t+1)={\frac {w}{\overline {w}}}p(t)}$,

where ${\displaystyle {\overline {w}}}$ is the mean relative fitness in the population (again setting aside changes in frequency due to drift and mutation). Relative fitnesses only indicate the change in prevalence of different genotypes relative to each other, and so only their values relative to each other are important; relative fitnesses can be any nonnegative number, including 0. It is often convenient to choose one genotype as a reference and set its relative fitness to 1. Relative fitness is used in the standard Wright-Fisher and Moran models of population genetics.

Absolute fitnesses can be used to calculate relative fitness, since ${\displaystyle p(t+1)=n(t+1)/N(t+1)=(W/{\overline {W}})p(t)}$ (we have used the fact that ${\displaystyle N(t+1)={\overline {W}}N(t)}$, where ${\displaystyle {\overline {W}}}$ is the mean absolute fitness in the population). This implies that ${\displaystyle w/{\overline {w}}=W/{\overline {W}}}$, or in other words, relative fitness is proportional to ${\displaystyle W/{\overline {W}}}$. It is not possible to calculate absolute fitnesses from relative fitnesses alone, since relative fitnesses contain no information about changes in overall population abundance ${\displaystyle N(t)}$.

Assigning relative fitness values to genotypes is mathematically appropriate when two conditions are met: first, the population is at demographic equilibrium, and second, individuals vary in their birth rate, contest ability, or death rate, but not a combination of these traits.

Change in genotype frequencies due to selection

Increase in frequency over time of genotype ${\displaystyle A}$, which has a 1% greater relative fitness than the other genotype present, ${\displaystyle B}$.

 

The change in genotype frequencies due to selection follows immediately from the definition of relative fitness,

${\displaystyle \Delta p=p(t+1)-p(t)={\frac {w-{\overline {w}}}{\overline {w}}}p(t)}$.

Thus, a genotype's frequency will decline or increase depending on whether its fitness is lower or greater than the mean fitness, respectively. 

In the particular case that there are only two genotypes of interest (e.g. representing the invasion of a new mutant allele), the change in genotype frequencies is often written in a different form. Suppose that two genotypes ${\displaystyle A}$ and ${\displaystyle B}$ have fitnesses ${\displaystyle w_{A}}$ and ${\displaystyle w_{B}}$, and frequencies ${\displaystyle p}$ and ${\displaystyle 1-p}$, respectively. Then ${\displaystyle {\overline {w}}=w_{A}p+w_{B}(1-p)}$, and so

${\displaystyle \Delta p={\frac {w-{\overline {w}}}{\overline {w}}}p={\frac {w_{A}-w_{B}}{\overline {w}}}p(1-p)}$.

Thus, the change in genotype ${\displaystyle A}$'s frequency depends crucially on the difference between its fitness and the fitness of genotype ${\displaystyle B}$. Supposing that ${\displaystyle A}$ is more fit than ${\displaystyle B}$, and defining the selection coefficient ${\displaystyle s}$ by ${\displaystyle w_{A}=(1+s)w_{B}}$, we obtain

${\displaystyle \Delta p={\frac {w-{\overline {w}}}{\overline {w}}}p={\frac {s}{1+sp}}p(1-p)\approx sp(1-p)}$,

where the last approximation holds for ${\displaystyle s\ll 1}$. In other words, the fitter genotype's frequency grows approximately logistically.

History

Herbert Spencer.

 

The British sociologist Herbert Spencer coined the phrase "survival of the fittest" in his 1864 work Principles of Biology to characterise what Charles Darwin had called natural selection.

The British biologist J.B.S. Haldane was the first to quantify fitness, in terms of the modern evolutionary synthesis of Darwinism and Mendelian genetics starting with his 1924 paper A Mathematical Theory of Natural and Artificial Selection. The next further advance was the introduction of the concept of inclusive fitness by the British biologist W.D. Hamilton in 1964 in his paper on The Genetical Evolution of Social Behaviour.

Genetic load

Genetic load measures the average fitness of a population of individuals, relative either to a theoretical genotype of optimal fitness, or relative to the most fit genotype actually present in the population. Consider n genotypes ${\displaystyle \mathbf {A} _{1}\dots \mathbf {A} _{n}}$, which have the fitnesses ${\displaystyle w_{1}\dots w_{n}}$ and the genotype frequencies ${\displaystyle p_{1}\dots p_{n}}$ respectively. Ignoring frequency-dependent selection, then genetic load (${\displaystyle L}$) may be calculated as:

${\displaystyle L={{w_{\max }-{\bar {w}}} \over w_{\max }}}$

Genetic load may increase when deleterious mutations, migration, inbreeding, or outcrossing lower mean fitness. Genetic load may also increase when beneficial mutations increase the maximum fitness against which other mutations are compared; this is known as the substitutional load or cost of selection.

Heritability

From Wikipedia, the free encyclopedia

 

Studies of heritability ask questions such as how much genetic factors play a role in differences in height between people. This is not the same as asking how much genetic factors influence height in any one person.

 

Heritability is a statistic used in the fields of breeding and genetics that estimates the degree of variation in a phenotypic trait in a population that is due to genetic variation between individuals in that population. In other words, the concept of heritability can alternately be expressed in the form of the following question: "What is the proportion of the variation in a given trait within a population that is not explained by the environment or random chance?"

Other causes of measured variation in a trait are characterized as environmental factors, including measurement error. In human studies of heritability these are often apportioned into factors from "shared environment" and "non-shared environment" based on whether they tend to result in persons brought up in the same household being more or less similar to persons who were not.

Heritability is estimated by comparing individual phenotypic variation among related individuals in a population. Heritability is an important concept in quantitative genetics, particularly in selective breeding and behavior genetics (for instance, twin studies). It is the source of much confusion due to the fact that its technical definition is different from its commonly-understood folk definition. Therefore, its use conveys the incorrect impression that behavioral traits are "inherited" or specifically passed down through the genes. Behavioral geneticists also conduct heritability analyses based on the assumption that genes and environments contribute in a separate, additive manner to behavioral traits.

Overview

Heritability measures the fraction of phenotype variability that can be attributed to genetic variation. This is not the same as saying that this fraction of an individual phenotype is caused by genetics. For example, it is incorrect to say that since the heritability of personality traits is about .6, that means that 60% of your personality is inherited from your parents and 40% comes from the environment. In addition, heritability can change without any genetic change occurring, such as when the environment starts contributing to more variation. As a case in point, consider that both genes and environment have the potential to influence intelligence. Heritability could increase if genetic variation increases, causing individuals to show more phenotypic variation, like showing different levels of intelligence. On the other hand, heritability might also increase if the environmental variation decreases, causing individuals to show less phenotypic variation, like showing more similar levels of intelligence. Heritability increases when genetics are contributing more variation or because non-genetic factors are contributing less variation; what matters is the relative contribution. Heritability is specific to a particular population in a particular environment. High heritability of a trait, consequently, does not necessarily mean that the trait is not very susceptible to environmental influences. Heritability can also change as a result of changes in the environment, migration, inbreeding, or the way in which heritability itself is measured in the population under study. The heritability of a trait should not be interpreted as a measure of the extent to which said trait is genetically determined in an individual.

The extent of dependence of phenotype on environment can also be a function of the genes involved. Matters of heritability are complicated because genes may canalize a phenotype, making its expression almost inevitable in all occurring environments. Individuals with the same genotype can also exhibit different phenotypes through a mechanism called phenotypic plasticity, which makes heritability difficult to measure in some cases. Recent insights in molecular biology have identified changes in transcriptional activity of individual genes associated with environmental changes. However, there are a large number of genes whose transcription is not affected by the environment.

Estimates of heritability use statistical analyses to help to identify the causes of differences between individuals. Since heritability is concerned with variance, it is necessarily an account of the differences between individuals in a population. Heritability can be univariate – examining a single trait – or multivariate – examining the genetic and environmental associations between multiple traits at once. This allows a test of the genetic overlap between different phenotypes: for instance hair color and eye color. Environment and genetics may also interact, and heritability analyses can test for and examine these interactions (GxE models).

A prerequisite for heritability analyses is that there is some population variation to account for. This last point highlights the fact that heritability cannot take into account the effect of factors which are invariant in the population. Factors may be invariant if they are absent and do not exist in the population, such as no one having access to a particular antibiotic, or because they are omni-present, like if everyone is drinking coffee. In practice, all human behavioral traits vary and almost all traits show some heritability.

Definition

Any particular phenotype can be modeled as the sum of genetic and environmental effects:

Phenotype (P) = Genotype (G) + Environment (E).

Likewise the phenotypic variance in the trait – Var (P) – is the sum of effects as follows:

Var(P) = Var(G) + Var(E) + 2 Cov(G,E).

In a planned experiment Cov(G,E) can be controlled and held at 0. In this case, heritability is defined as:

${\displaystyle H^{2}={\frac {\mathrm {Var} (G)}{\mathrm {Var} (P)}}}$ .

H² is the broad-sense heritability. This reflects all the genetic contributions to a population's phenotypic variance including additive, dominant, and epistatic (multi-genic interactions), as well as maternal and paternal effects, where individuals are directly affected by their parents' phenotype, such as with milk production in mammals.

A particularly important component of the genetic variance is the additive variance, Var(A), which is 

the variance due to the average effects (additive effects) of the alleles. Since each parent passes a single allele per locus to each offspring, parent-offspring resemblance depends upon the average effect of single alleles. Additive variance represents, therefore, the genetic component of variance responsible for parent-offspring resemblance. The additive genetic portion of the phenotypic variance is known as Narrow-sense heritability and is defined as

${\displaystyle h^{2}={\frac {\mathrm {Var} (A)}{\mathrm {Var} (P)}}}$

An upper case H² is used to denote broad sense, and lower case h² for narrow sense.

For traits which are not continuous but dichotomous such as an additional toe or certain diseases, the contribution of the various alleles can be considered to be a sum, which past a threshold, manifests itself as the trait, giving the liability threshold model in which heritability can be estimated and selection modeled.

Additive variance is important for selection. If a selective pressure such as improving livestock is exerted, the response of the trait is directly related to narrow-sense heritability. The mean of the trait will increase in the next generation as a function of how much the mean of the selected parents differs from the mean of the population from which the selected parents were chosen. The observed response to selection leads to an estimate of the narrow-sense heritability (called realized heritability). This is the principle underlying artificial selection or breeding.

Example

Figure 1. Relationship of phenotypic values to additive and dominance effects using a completely dominant locus.

 

The simplest genetic model involves a single locus with two alleles (b and B) affecting one quantitative phenotype.

The number of B alleles can vary from 0, 1, or 2. For any genotype, B_iB_j, the expected phenotype can then be written as the sum of the overall mean, a linear effect, and a dominance deviation:

${\displaystyle P_{ij}=\mu +\alpha _{i}+\alpha _{j}+d_{ij}}$ = Population mean + 

Additive Effect (${\displaystyle a_{ij}=\alpha _{i}+\alpha _{j}}$) + 

Dominance Deviation (${\displaystyle d_{ij}}$).

The additive genetic variance at this locus is the weighted average of the squares of the additive effects:

${\displaystyle \mathrm {Var} (A)=f(bb)a_{bb}^{2}+f(Bb)a_{Bb}^{2}+f(BB)a_{BB}^{2},}$

where ${\displaystyle f(bb)a_{bb}+f(Bb)a_{Bb}+f(BB)a_{BB}=0.}$

There is a similar relationship for variance of dominance deviations:

${\displaystyle \mathrm {Var} (D)=f(bb)d_{bb}^{2}+f(Bb)d_{Bb}^{2}+f(BB)d_{BB}^{2},}$

where ${\displaystyle f(bb)d_{bb}+f(Bb)d_{Bb}+f(BB)d_{BB}=0.}$

The linear regression of phenotype on genotype is shown in Figure 1.

Assumptions

Estimates of the total heritability of human traits assume the absence of epistasis, which has been called the "assumption of additivity". Although some researchers have cited such estimates in support of the existence of "missing heritability" unaccounted for by known genetic loci, the assumption of additivity may render these estimates invalid. There is also some empirical evidence that the additivity assumption is frequently violated in behavior genetic studies of adolescent intelligence and academic achievement.

Estimating heritability

Since only P can be observed or measured directly, heritability must be estimated from the similarities observed in subjects varying in their level of genetic or environmental similarity. The statistical analyses required to estimate the genetic and environmental components of variance depend on the sample characteristics. Briefly, better estimates are obtained using data from individuals with widely varying levels of genetic relationship - such as twins, siblings, parents and offspring, rather than from more distantly related (and therefore less similar) subjects. The standard error for heritability estimates is improved with large sample sizes.

In non-human populations it is often possible to collect information in a controlled way. For example, among farm animals it is easy to arrange for a bull to produce offspring from a large number of cows and to control environments. Such experimental control is generally not possible when gathering human data, relying on naturally occurring relationships and environments.

In classical quantitative genetics, there were two schools of thought regarding estimation of heritability.

One school of thought was developed by Sewall Wright at The University of Chicago, and further popularized by C. C. Li (University of Chicago) and J. L. Lush (Iowa State University). It is based on the analysis of correlations and, by extension, regression. Path Analysis was developed by Sewall Wright as a way of estimating heritability.

The second was originally developed by R. A. Fisher and expanded at The University of Edinburgh, Iowa State University, and North Carolina State University, as well as other schools. It is based on the analysis of variance of breeding studies, using the intraclass correlation of relatives. Various methods of estimating components of variance (and, hence, heritability) from ANOVA are used in these analyses.

Today, heritability can be estimated from general pedigrees using linear mixed models and from genomic relatedness estimated from genetic markers.

Studies of human heritability often utilize adoption study designs, often with identical twins who have been separated early in life and raised in different environments. Such individuals have identical genotypes and can be used to separate the effects of genotype and environment. A limit of this design is the common prenatal environment and the relatively low numbers of twins reared apart. A second and more common design is the twin study in which the similarity of identical and fraternal twins is used to estimate heritability. These studies can be limited by the fact that identical twins are not completely genetically identical, potentially resulting in an underestimation of heritability.

In observational studies, or because of evocative effects (where a genome evokes environments by its effect on them), G and E may covary: gene environment correlation. Depending on the methods used to estimate heritability, correlations between genetic factors and shared or non-shared environments may or may not be confounded with heritability.

Regression/correlation methods of estimation

The first school of estimation uses regression and correlation to estimate heritability.

Comparison of close relatives

In the comparison of relatives, we find that in general,

${\displaystyle h^{2}={\frac {b}{r}}={\frac {t}{r}}}$

where r can be thought of as the coefficient of relatedness, b is the coefficient of regression and t is the coefficient of correlation.

Parent-offspring regression

Figure 2. Sir Francis Galton's (1889) data showing the relationship between offspring height (928 individuals) as a function of mean parent height (205 sets of parents).

 

Heritability may be estimated by comparing parent and offspring traits (as in Fig. 2). The slope of the line (0.57) approximates the heritability of the trait when offspring values are regressed against the average trait in the parents. If only one parent's value is used then heritability is twice the slope. (Note that this is the source of the term "regression," since the offspring values always tend to regress to the mean value for the population, i.e., the slope is always less than one). This regression effect also underlies the DeFries–Fulker method for analyzing twins selected for one member being affected.

Sibling comparison

A basic approach to heritability can be taken using full-Sib designs: comparing similarity between siblings who share both a biological mother and a father. When there is only additive gene action, this sibling phenotypic correlation is an index of familiarity – the sum of half the additive genetic variance plus full effect of the common environment. It thus places an upper-limit on additive heritability of twice the full-Sib phenotypic correlation. Half-Sib designs compare phenotypic traits of siblings that share one parent with other sibling groups.

Twin studies

Figure 3. Twin concordances for seven psychological traits (sample size shown inside bars), with DZ being fraternal and MZ being identical twins.

 

Heritability for traits in humans is most frequently estimated by comparing resemblances between twins. "The advantage of twin studies, is that the total variance can be split up into genetic, shared or common environmental, and unique environmental components, enabling an accurate estimation of heritability". Fraternal or dizygotic (DZ) twins on average share half their genes (assuming there is no assortative mating for the trait), and so identical or monozygotic (MZ) twins on average are twice as genetically similar as DZ twins. A crude estimate of heritability, then, is approximately twice the difference in correlation between MZ and DZ twins, i.e. Falconer's formula H²=2(r(MZ)-r(DZ)). 

The effect of shared environment, c², contributes to similarity between siblings due to the commonality of the environment they are raised in. Shared environment is approximated by the DZ correlation minus half heritability, which is the degree to which DZ twins share the same genes, c²=DZ-1/2h². Unique environmental variance, e², reflects the degree to which identical twins raised together are dissimilar, e²=1-r(MZ).

Analysis of variance methods of estimation

The second set of methods of estimation of heritability involves ANOVA and estimation of variance components.

Basic model

We use the basic discussion of Kempthorne. Considering only the most basic of genetic models, we can look at the quantitative contribution of a single locus with genotype G_i as

${\displaystyle y_{i}=\mu +g_{i}+e}$

where ${\displaystyle g_{i}}$ is the effect of genotype G_i and ${\displaystyle e}$ is the environmental effect.

Consider an experiment with a group of sires and their progeny from random dams. Since the progeny get half of their genes from the father and half from their (random) mother, the progeny equation is

${\displaystyle z_{i}=\mu +{\frac {1}{2}}g_{i}+e}$

Intraclass correlations

Consider the experiment above. We have two groups of progeny we can compare. The first is comparing the various progeny for an individual sire (called within sire group). The variance will include terms for genetic variance (since they did not all get the same genotype) and environmental variance. This is thought of as an error term.

The second group of progeny are comparisons of means of half sibs with each other (called among sire group). In addition to the error term as in the within sire groups, we have an addition term due to the differences among different means of half sibs. The intraclass correlation is

${\displaystyle \mathrm {corr} (z,z')=\mathrm {corr} (\mu +{\frac {1}{2}}g+e,\mu +{\frac {1}{2}}g+e')={\frac {1}{4}}V_{g}}$ ,

since environmental effects are independent of each other.

The ANOVA

In an experiment with ${\displaystyle n}$ sires and ${\displaystyle r}$ progeny per sire, we can calculate the following ANOVA, using ${\displaystyle V_{g}}$ as the genetic variance and ${\displaystyle V_{e}}$ as the environmental variance: 

Table 1: ANOVA for Sire experiment

Source	d.f.	Mean Square	Expected Mean Square
Among sire groups	${\displaystyle n-1}$	${\displaystyle S}$	${\displaystyle {\frac {3}{4}}V_{g}+V_{e}+r({{\frac {1}{4}}V_{g}})}$
Within sire groups	${\displaystyle n(r-1)}$	${\displaystyle W}$	${\displaystyle {\frac {3}{4}}V_{g}+V_{e}}$

The ${\displaystyle {\frac {1}{4}}V_{g}}$ term is the intraclass correlation among half sibs. We can easily calculate ${\displaystyle H^{2}={\frac {V_{g}}{V_{g}+V_{e}}}={\frac {4(S-W)}{S+(r-1)W}}}$. The Expected Mean Square is calculated from the relationship of the individuals (progeny within a sire are all half-sibs, for example), and an understanding of intraclass correlations. 

The use of ANOVA to calculate heritability often fails to account for the presence of gene-environment interactions, because ANOVA has a much lower statistical power for testing for interaction effects than for direct effects.

Model with additive and dominance terms

For a model with additive and dominance terms, but not others, the equation for a single locus is

${\displaystyle y_{ij}=\mu +\alpha _{i}+\alpha _{j}+d_{ij}+e,}$

where is the additive effect of the i^th allele, ${\displaystyle \alpha _{j}}$ is the additive effect of the j^th allele, ${\displaystyle d_{ij}}$ is the dominance deviation for the ij^th genotype, and ${\displaystyle e}$ is the environment. 

Experiments can be run with a similar setup to the one given in Table 1. Using different relationship groups, we can evaluate different intraclass correlations. Using ${\displaystyle V_{a}}$ as the additive genetic variance and ${\displaystyle V_{d}}$ as the dominance deviation variance, intraclass correlations become linear functions of these parameters. In general,

Intraclass correlation${\displaystyle =rV_{a}+\theta V_{d},}$

where ${\displaystyle r}$ and ${\displaystyle \theta }$ are found as

${\displaystyle r=}$P[ alleles drawn at random from the relationship pair are identical by descent], and

${\displaystyle \theta =}$P[ genotypes drawn at random from the relationship pair are identical by descent].

Some common relationships and their coefficients are given in Table 2.

Table 2: Coefficients for calculating variance components

Relationship	${\displaystyle r}$	${\displaystyle \theta }$
Identical Twins	${\displaystyle 1}$	${\displaystyle 1}$
Parent-Offspring	${\displaystyle {\frac {1}{2}}}$	${\displaystyle 0}$
Half Siblings	${\displaystyle {\frac {1}{4}}}$	${\displaystyle 0}$
Full Siblings	${\displaystyle {\frac {1}{2}}}$	${\displaystyle {\frac {1}{4}}}$
First Cousins	${\displaystyle {\frac {1}{8}}}$	${\displaystyle 0}$
Double First Cousins	${\displaystyle {\frac {1}{4}}}$	${\displaystyle {\frac {1}{16}}}$

Linear mixed models

A wide variety approaches using linear mixed models have been reported in literature. Via these methods, phenotypic variance is partitioned into genetic, environmental and experimental design variances to estimate heritability. Environmental variance can be explicitly modeled by studying individuals across a broad range of environments, although inference of genetic variance from phenotypic and environmental variance may lead to underestimation of heritability due to the challenge of capturing the full range of environmental influence affecting a trait. Other methods for calculating heritability use data from genome-wide association studies to estimate the influence on a trait by genetic factors, which is reflected by the rate and influence of putatively associated genetic loci (usually single-nucleotide polymorphisms) on the trait. This can lead to underestimation of heritability, however. This discrepancy is referred to as "missing heritability" and reflects the challenge of accurately modeling both genetic and environmental variance in heritability models.

When a large, complex pedigree or another aforementioned type of data is available, heritability and other quantitative genetic parameters can be estimated by restricted maximum likelihood (REML) or Bayesian methods. The raw data will usually have three or more data points for each individual: a code for the sire, a code for the dam and one or several trait values. Different trait values may be for different traits or for different time points of measurement. 

The currently popular methodology relies on high degrees of certainty over the identities of the sire and dam; it is not common to treat the sire identity probabilistically. This is not usually a problem, since the methodology is rarely applied to wild populations (although it has been used for several wild ungulate and bird populations), and sires are invariably known with a very high degree of certainty in breeding programmes. There are also algorithms that account for uncertain paternity.

The pedigrees can be viewed using programs such as Pedigree Viewer , and analyzed with programs such as ASReml, VCE , WOMBAT  or the BLUPF90 family of programs.

Pedigree models are helpful for untangling confounds such as reverse causality, maternal effects such as the prenatal environment, and confounding of genetic dominance, shared environment, and maternal gene effects.

Genomic heritability

When genome-wide genotype data and phenotypes from large population samples are available, one can estimate the relationships between individuals based on their genotypes and use a linear mixed model to estimate the variance explained by the genetic markers. This gives a genomic heritability estimate based on the variance captured by common genetic variants. There are multiple methods that make different adjustments for allele frequency and linkage disequilibrium.

Response to selection

Figure 4. Strength of selection (S) and response to selection (R) in an artificial selection experiment, h²=R/S.

In selective breeding of plants and animals, the expected response to selection of a trait with known narrow-sense heritability ${\displaystyle (h^{2})}$ can be estimated using the breeder's equation:

${\displaystyle R=h^{2}S}$

In this equation, the Response to Selection (R) is defined as the realized average difference between the parent generation and the next generation, and the Selection Differential (S) is defined as the average difference between the parent generation and the selected parents.

For example, imagine that a plant breeder is involved in a selective breeding project with the aim of increasing the number of kernels per ear of corn. For the sake of argument, let us assume that the average ear of corn in the parent generation has 100 kernels. Let us also assume that the selected parents produce corn with an average of 120 kernels per ear. If h² equals 0.5, then the next generation will produce corn with an average of 0.5(120-100) = 10 additional kernels per ear. Therefore, the total number of kernels per ear of corn will equal, on average, 110. 

Observing the response to selection in an artificial selection experiment will allow calculation of realized heritability as in Fig. 5. 

Note that heritability in the above equation is equal to the ratio ${\displaystyle \mathrm {Var} (A)/\mathrm {Var} (P)}$ only if the genotype and the environmental noise follow Gaussian distributions.

Controversies

Heritability estimates' prominent critics, such as Steven Rose, Jay Joseph, and Richard Bentall, focus largely on heritability estimates in behavioral sciences and social sciences. Bentall has claimed that such heritability scores are typically calculated counterintuitively to derive numerically high scores, that heritability is misinterpreted as genetic determination, and that this alleged bias distracts from other factors that researches have found more causally important, such as childhood abuse causing later psychosis. Heritability estimates are also inherently limited because they do not convey any information regarding whether genes or environment play a larger role in the development of the trait under study. For this reason, David Moore and David Shenk describe the term "heritability" in the context of behavior genetics as "...one of the most misleading in the history of science" and argue that it has no value except in very rare cases. When studying complex human traits, it is impossible to use heritability analysis to determine the relative contributions of genes and environment, as such traits result from multiple causes interacting.

The controversy over heritability estimates is largely via their basis in twin studies. The scarce success of molecular-genetic studies to corroborate such population-genetic studies' conclusions is the missing heritability problem. Eric Turkheimer has argued that newer molecular methods have vindicated the conventional interpretation of twin studies, although it remains mostly unclear how to explain the relations between genes and behaviors. According to Turkheimer, both genes and environment are heritable, genetic contribution varies by environment, and a focus on heritability distracts from other important factors. Overall, however, heritability is a concept widely applicable.