Heritability

From Wikipedia, the free encyclopedia

 

Studies of heritability ask questions such as how much genetic factors play a role in differences in height between people. This is not the same as asking how much genetic factors influence height in any one person.

 

Heritability is a statistic used in the fields of breeding and genetics that estimates the degree of variation in a phenotypic trait in a population that is due to genetic variation between individuals in that population. In other words, the concept of heritability can alternately be expressed in the form of the following question: "What is the proportion of the variation in a given trait within a population that is not explained by the environment or random chance?"

Other causes of measured variation in a trait are characterized as environmental factors, including measurement error. In human studies of heritability these are often apportioned into factors from "shared environment" and "non-shared environment" based on whether they tend to result in persons brought up in the same household being more or less similar to persons who were not.

Heritability is estimated by comparing individual phenotypic variation among related individuals in a population. Heritability is an important concept in quantitative genetics, particularly in selective breeding and behavior genetics (for instance, twin studies). It is the source of much confusion due to the fact that its technical definition is different from its commonly-understood folk definition. Therefore, its use conveys the incorrect impression that behavioral traits are "inherited" or specifically passed down through the genes. Behavioral geneticists also conduct heritability analyses based on the assumption that genes and environments contribute in a separate, additive manner to behavioral traits.

Overview

Heritability measures the fraction of phenotype variability that can be attributed to genetic variation. This is not the same as saying that this fraction of an individual phenotype is caused by genetics. For example, it is incorrect to say that since the heritability of personality traits is about .6, that means that 60% of your personality is inherited from your parents and 40% comes from the environment. In addition, heritability can change without any genetic change occurring, such as when the environment starts contributing to more variation. As a case in point, consider that both genes and environment have the potential to influence intelligence. Heritability could increase if genetic variation increases, causing individuals to show more phenotypic variation, like showing different levels of intelligence. On the other hand, heritability might also increase if the environmental variation decreases, causing individuals to show less phenotypic variation, like showing more similar levels of intelligence. Heritability increases when genetics are contributing more variation or because non-genetic factors are contributing less variation; what matters is the relative contribution. Heritability is specific to a particular population in a particular environment. High heritability of a trait, consequently, does not necessarily mean that the trait is not very susceptible to environmental influences. Heritability can also change as a result of changes in the environment, migration, inbreeding, or the way in which heritability itself is measured in the population under study. The heritability of a trait should not be interpreted as a measure of the extent to which said trait is genetically determined in an individual.

The extent of dependence of phenotype on environment can also be a function of the genes involved. Matters of heritability are complicated because genes may canalize a phenotype, making its expression almost inevitable in all occurring environments. Individuals with the same genotype can also exhibit different phenotypes through a mechanism called phenotypic plasticity, which makes heritability difficult to measure in some cases. Recent insights in molecular biology have identified changes in transcriptional activity of individual genes associated with environmental changes. However, there are a large number of genes whose transcription is not affected by the environment.

Estimates of heritability use statistical analyses to help to identify the causes of differences between individuals. Since heritability is concerned with variance, it is necessarily an account of the differences between individuals in a population. Heritability can be univariate – examining a single trait – or multivariate – examining the genetic and environmental associations between multiple traits at once. This allows a test of the genetic overlap between different phenotypes: for instance hair color and eye color. Environment and genetics may also interact, and heritability analyses can test for and examine these interactions (GxE models).

A prerequisite for heritability analyses is that there is some population variation to account for. This last point highlights the fact that heritability cannot take into account the effect of factors which are invariant in the population. Factors may be invariant if they are absent and do not exist in the population, such as no one having access to a particular antibiotic, or because they are omni-present, like if everyone is drinking coffee. In practice, all human behavioral traits vary and almost all traits show some heritability.

Definition

Any particular phenotype can be modeled as the sum of genetic and environmental effects:

Phenotype (P) = Genotype (G) + Environment (E).

Likewise the phenotypic variance in the trait – Var (P) – is the sum of effects as follows:

Var(P) = Var(G) + Var(E) + 2 Cov(G,E).

In a planned experiment Cov(G,E) can be controlled and held at 0. In this case, heritability is defined as:

${\displaystyle H^{2}={\frac {\mathrm {Var} (G)}{\mathrm {Var} (P)}}}$ .

H² is the broad-sense heritability. This reflects all the genetic contributions to a population's phenotypic variance including additive, dominant, and epistatic (multi-genic interactions), as well as maternal and paternal effects, where individuals are directly affected by their parents' phenotype, such as with milk production in mammals.

A particularly important component of the genetic variance is the additive variance, Var(A), which is 

the variance due to the average effects (additive effects) of the alleles. Since each parent passes a single allele per locus to each offspring, parent-offspring resemblance depends upon the average effect of single alleles. Additive variance represents, therefore, the genetic component of variance responsible for parent-offspring resemblance. The additive genetic portion of the phenotypic variance is known as Narrow-sense heritability and is defined as

${\displaystyle h^{2}={\frac {\mathrm {Var} (A)}{\mathrm {Var} (P)}}}$

An upper case H² is used to denote broad sense, and lower case h² for narrow sense.

For traits which are not continuous but dichotomous such as an additional toe or certain diseases, the contribution of the various alleles can be considered to be a sum, which past a threshold, manifests itself as the trait, giving the liability threshold model in which heritability can be estimated and selection modeled.

Additive variance is important for selection. If a selective pressure such as improving livestock is exerted, the response of the trait is directly related to narrow-sense heritability. The mean of the trait will increase in the next generation as a function of how much the mean of the selected parents differs from the mean of the population from which the selected parents were chosen. The observed response to selection leads to an estimate of the narrow-sense heritability (called realized heritability). This is the principle underlying artificial selection or breeding.

Example

Figure 1. Relationship of phenotypic values to additive and dominance effects using a completely dominant locus.

 

The simplest genetic model involves a single locus with two alleles (b and B) affecting one quantitative phenotype.

The number of B alleles can vary from 0, 1, or 2. For any genotype, B_iB_j, the expected phenotype can then be written as the sum of the overall mean, a linear effect, and a dominance deviation:

${\displaystyle P_{ij}=\mu +\alpha _{i}+\alpha _{j}+d_{ij}}$ = Population mean + 

Additive Effect (${\displaystyle a_{ij}=\alpha _{i}+\alpha _{j}}$) + 

Dominance Deviation (${\displaystyle d_{ij}}$).

The additive genetic variance at this locus is the weighted average of the squares of the additive effects:

${\displaystyle \mathrm {Var} (A)=f(bb)a_{bb}^{2}+f(Bb)a_{Bb}^{2}+f(BB)a_{BB}^{2},}$

where ${\displaystyle f(bb)a_{bb}+f(Bb)a_{Bb}+f(BB)a_{BB}=0.}$

There is a similar relationship for variance of dominance deviations:

${\displaystyle \mathrm {Var} (D)=f(bb)d_{bb}^{2}+f(Bb)d_{Bb}^{2}+f(BB)d_{BB}^{2},}$

where ${\displaystyle f(bb)d_{bb}+f(Bb)d_{Bb}+f(BB)d_{BB}=0.}$

The linear regression of phenotype on genotype is shown in Figure 1.

Assumptions

Estimates of the total heritability of human traits assume the absence of epistasis, which has been called the "assumption of additivity". Although some researchers have cited such estimates in support of the existence of "missing heritability" unaccounted for by known genetic loci, the assumption of additivity may render these estimates invalid. There is also some empirical evidence that the additivity assumption is frequently violated in behavior genetic studies of adolescent intelligence and academic achievement.

Estimating heritability

Since only P can be observed or measured directly, heritability must be estimated from the similarities observed in subjects varying in their level of genetic or environmental similarity. The statistical analyses required to estimate the genetic and environmental components of variance depend on the sample characteristics. Briefly, better estimates are obtained using data from individuals with widely varying levels of genetic relationship - such as twins, siblings, parents and offspring, rather than from more distantly related (and therefore less similar) subjects. The standard error for heritability estimates is improved with large sample sizes.

In non-human populations it is often possible to collect information in a controlled way. For example, among farm animals it is easy to arrange for a bull to produce offspring from a large number of cows and to control environments. Such experimental control is generally not possible when gathering human data, relying on naturally occurring relationships and environments.

In classical quantitative genetics, there were two schools of thought regarding estimation of heritability.

One school of thought was developed by Sewall Wright at The University of Chicago, and further popularized by C. C. Li (University of Chicago) and J. L. Lush (Iowa State University). It is based on the analysis of correlations and, by extension, regression. Path Analysis was developed by Sewall Wright as a way of estimating heritability.

The second was originally developed by R. A. Fisher and expanded at The University of Edinburgh, Iowa State University, and North Carolina State University, as well as other schools. It is based on the analysis of variance of breeding studies, using the intraclass correlation of relatives. Various methods of estimating components of variance (and, hence, heritability) from ANOVA are used in these analyses.

Today, heritability can be estimated from general pedigrees using linear mixed models and from genomic relatedness estimated from genetic markers.

Studies of human heritability often utilize adoption study designs, often with identical twins who have been separated early in life and raised in different environments. Such individuals have identical genotypes and can be used to separate the effects of genotype and environment. A limit of this design is the common prenatal environment and the relatively low numbers of twins reared apart. A second and more common design is the twin study in which the similarity of identical and fraternal twins is used to estimate heritability. These studies can be limited by the fact that identical twins are not completely genetically identical, potentially resulting in an underestimation of heritability.

In observational studies, or because of evocative effects (where a genome evokes environments by its effect on them), G and E may covary: gene environment correlation. Depending on the methods used to estimate heritability, correlations between genetic factors and shared or non-shared environments may or may not be confounded with heritability.

Regression/correlation methods of estimation

The first school of estimation uses regression and correlation to estimate heritability.

Comparison of close relatives

In the comparison of relatives, we find that in general,

${\displaystyle h^{2}={\frac {b}{r}}={\frac {t}{r}}}$

where r can be thought of as the coefficient of relatedness, b is the coefficient of regression and t is the coefficient of correlation.

Parent-offspring regression

Figure 2. Sir Francis Galton's (1889) data showing the relationship between offspring height (928 individuals) as a function of mean parent height (205 sets of parents).

 

Heritability may be estimated by comparing parent and offspring traits (as in Fig. 2). The slope of the line (0.57) approximates the heritability of the trait when offspring values are regressed against the average trait in the parents. If only one parent's value is used then heritability is twice the slope. (Note that this is the source of the term "regression," since the offspring values always tend to regress to the mean value for the population, i.e., the slope is always less than one). This regression effect also underlies the DeFries–Fulker method for analyzing twins selected for one member being affected.

Sibling comparison

A basic approach to heritability can be taken using full-Sib designs: comparing similarity between siblings who share both a biological mother and a father. When there is only additive gene action, this sibling phenotypic correlation is an index of familiarity – the sum of half the additive genetic variance plus full effect of the common environment. It thus places an upper-limit on additive heritability of twice the full-Sib phenotypic correlation. Half-Sib designs compare phenotypic traits of siblings that share one parent with other sibling groups.

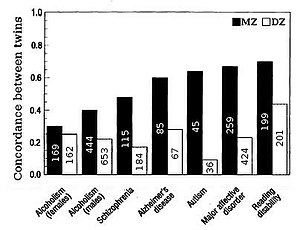
Twin studies

Figure 3. Twin concordances for seven psychological traits (sample size shown inside bars), with DZ being fraternal and MZ being identical twins.

 

Heritability for traits in humans is most frequently estimated by comparing resemblances between twins. "The advantage of twin studies, is that the total variance can be split up into genetic, shared or common environmental, and unique environmental components, enabling an accurate estimation of heritability". Fraternal or dizygotic (DZ) twins on average share half their genes (assuming there is no assortative mating for the trait), and so identical or monozygotic (MZ) twins on average are twice as genetically similar as DZ twins. A crude estimate of heritability, then, is approximately twice the difference in correlation between MZ and DZ twins, i.e. Falconer's formula H²=2(r(MZ)-r(DZ)). 

The effect of shared environment, c², contributes to similarity between siblings due to the commonality of the environment they are raised in. Shared environment is approximated by the DZ correlation minus half heritability, which is the degree to which DZ twins share the same genes, c²=DZ-1/2h². Unique environmental variance, e², reflects the degree to which identical twins raised together are dissimilar, e²=1-r(MZ).

Analysis of variance methods of estimation

The second set of methods of estimation of heritability involves ANOVA and estimation of variance components.

Basic model

We use the basic discussion of Kempthorne. Considering only the most basic of genetic models, we can look at the quantitative contribution of a single locus with genotype G_i as

${\displaystyle y_{i}=\mu +g_{i}+e}$

where ${\displaystyle g_{i}}$ is the effect of genotype G_i and ${\displaystyle e}$ is the environmental effect.

Consider an experiment with a group of sires and their progeny from random dams. Since the progeny get half of their genes from the father and half from their (random) mother, the progeny equation is

${\displaystyle z_{i}=\mu +{\frac {1}{2}}g_{i}+e}$

Intraclass correlations

Consider the experiment above. We have two groups of progeny we can compare. The first is comparing the various progeny for an individual sire (called within sire group). The variance will include terms for genetic variance (since they did not all get the same genotype) and environmental variance. This is thought of as an error term.

The second group of progeny are comparisons of means of half sibs with each other (called among sire group). In addition to the error term as in the within sire groups, we have an addition term due to the differences among different means of half sibs. The intraclass correlation is

${\displaystyle \mathrm {corr} (z,z')=\mathrm {corr} (\mu +{\frac {1}{2}}g+e,\mu +{\frac {1}{2}}g+e')={\frac {1}{4}}V_{g}}$ ,

since environmental effects are independent of each other.

The ANOVA

In an experiment with ${\displaystyle n}$ sires and ${\displaystyle r}$ progeny per sire, we can calculate the following ANOVA, using ${\displaystyle V_{g}}$ as the genetic variance and ${\displaystyle V_{e}}$ as the environmental variance: 

Table 1: ANOVA for Sire experiment

Source	d.f.	Mean Square	Expected Mean Square
Among sire groups	${\displaystyle n-1}$	${\displaystyle S}$	${\displaystyle {\frac {3}{4}}V_{g}+V_{e}+r({{\frac {1}{4}}V_{g}})}$
Within sire groups	${\displaystyle n(r-1)}$	${\displaystyle W}$	${\displaystyle {\frac {3}{4}}V_{g}+V_{e}}$

The ${\displaystyle {\frac {1}{4}}V_{g}}$ term is the intraclass correlation among half sibs. We can easily calculate ${\displaystyle H^{2}={\frac {V_{g}}{V_{g}+V_{e}}}={\frac {4(S-W)}{S+(r-1)W}}}$. The Expected Mean Square is calculated from the relationship of the individuals (progeny within a sire are all half-sibs, for example), and an understanding of intraclass correlations. 

The use of ANOVA to calculate heritability often fails to account for the presence of gene-environment interactions, because ANOVA has a much lower statistical power for testing for interaction effects than for direct effects.

Model with additive and dominance terms

For a model with additive and dominance terms, but not others, the equation for a single locus is

${\displaystyle y_{ij}=\mu +\alpha _{i}+\alpha _{j}+d_{ij}+e,}$

where is the additive effect of the i^th allele, ${\displaystyle \alpha _{j}}$ is the additive effect of the j^th allele, ${\displaystyle d_{ij}}$ is the dominance deviation for the ij^th genotype, and ${\displaystyle e}$ is the environment. 

Experiments can be run with a similar setup to the one given in Table 1. Using different relationship groups, we can evaluate different intraclass correlations. Using ${\displaystyle V_{a}}$ as the additive genetic variance and ${\displaystyle V_{d}}$ as the dominance deviation variance, intraclass correlations become linear functions of these parameters. In general,

Intraclass correlation${\displaystyle =rV_{a}+\theta V_{d},}$

where ${\displaystyle r}$ and ${\displaystyle \theta }$ are found as

${\displaystyle r=}$P[ alleles drawn at random from the relationship pair are identical by descent], and

${\displaystyle \theta =}$P[ genotypes drawn at random from the relationship pair are identical by descent].

Some common relationships and their coefficients are given in Table 2.

Table 2: Coefficients for calculating variance components

Relationship	${\displaystyle r}$	${\displaystyle \theta }$
Identical Twins	${\displaystyle 1}$	${\displaystyle 1}$
Parent-Offspring	${\displaystyle {\frac {1}{2}}}$	${\displaystyle 0}$
Half Siblings	${\displaystyle {\frac {1}{4}}}$	${\displaystyle 0}$
Full Siblings	${\displaystyle {\frac {1}{2}}}$	${\displaystyle {\frac {1}{4}}}$
First Cousins	${\displaystyle {\frac {1}{8}}}$	${\displaystyle 0}$
Double First Cousins	${\displaystyle {\frac {1}{4}}}$	${\displaystyle {\frac {1}{16}}}$

Linear mixed models

A wide variety approaches using linear mixed models have been reported in literature. Via these methods, phenotypic variance is partitioned into genetic, environmental and experimental design variances to estimate heritability. Environmental variance can be explicitly modeled by studying individuals across a broad range of environments, although inference of genetic variance from phenotypic and environmental variance may lead to underestimation of heritability due to the challenge of capturing the full range of environmental influence affecting a trait. Other methods for calculating heritability use data from genome-wide association studies to estimate the influence on a trait by genetic factors, which is reflected by the rate and influence of putatively associated genetic loci (usually single-nucleotide polymorphisms) on the trait. This can lead to underestimation of heritability, however. This discrepancy is referred to as "missing heritability" and reflects the challenge of accurately modeling both genetic and environmental variance in heritability models.

When a large, complex pedigree or another aforementioned type of data is available, heritability and other quantitative genetic parameters can be estimated by restricted maximum likelihood (REML) or Bayesian methods. The raw data will usually have three or more data points for each individual: a code for the sire, a code for the dam and one or several trait values. Different trait values may be for different traits or for different time points of measurement. 

The currently popular methodology relies on high degrees of certainty over the identities of the sire and dam; it is not common to treat the sire identity probabilistically. This is not usually a problem, since the methodology is rarely applied to wild populations (although it has been used for several wild ungulate and bird populations), and sires are invariably known with a very high degree of certainty in breeding programmes. There are also algorithms that account for uncertain paternity.

The pedigrees can be viewed using programs such as Pedigree Viewer , and analyzed with programs such as ASReml, VCE , WOMBAT  or the BLUPF90 family of programs.

Pedigree models are helpful for untangling confounds such as reverse causality, maternal effects such as the prenatal environment, and confounding of genetic dominance, shared environment, and maternal gene effects.

Genomic heritability

When genome-wide genotype data and phenotypes from large population samples are available, one can estimate the relationships between individuals based on their genotypes and use a linear mixed model to estimate the variance explained by the genetic markers. This gives a genomic heritability estimate based on the variance captured by common genetic variants. There are multiple methods that make different adjustments for allele frequency and linkage disequilibrium.

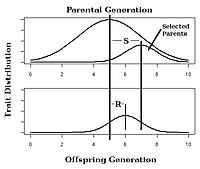
Response to selection

Figure 4. Strength of selection (S) and response to selection (R) in an artificial selection experiment, h²=R/S.

In selective breeding of plants and animals, the expected response to selection of a trait with known narrow-sense heritability ${\displaystyle (h^{2})}$ can be estimated using the breeder's equation:

${\displaystyle R=h^{2}S}$

In this equation, the Response to Selection (R) is defined as the realized average difference between the parent generation and the next generation, and the Selection Differential (S) is defined as the average difference between the parent generation and the selected parents.

For example, imagine that a plant breeder is involved in a selective breeding project with the aim of increasing the number of kernels per ear of corn. For the sake of argument, let us assume that the average ear of corn in the parent generation has 100 kernels. Let us also assume that the selected parents produce corn with an average of 120 kernels per ear. If h² equals 0.5, then the next generation will produce corn with an average of 0.5(120-100) = 10 additional kernels per ear. Therefore, the total number of kernels per ear of corn will equal, on average, 110. 

Observing the response to selection in an artificial selection experiment will allow calculation of realized heritability as in Fig. 5. 

Note that heritability in the above equation is equal to the ratio ${\displaystyle \mathrm {Var} (A)/\mathrm {Var} (P)}$ only if the genotype and the environmental noise follow Gaussian distributions.

Controversies

Heritability estimates' prominent critics, such as Steven Rose, Jay Joseph, and Richard Bentall, focus largely on heritability estimates in behavioral sciences and social sciences. Bentall has claimed that such heritability scores are typically calculated counterintuitively to derive numerically high scores, that heritability is misinterpreted as genetic determination, and that this alleged bias distracts from other factors that researches have found more causally important, such as childhood abuse causing later psychosis. Heritability estimates are also inherently limited because they do not convey any information regarding whether genes or environment play a larger role in the development of the trait under study. For this reason, David Moore and David Shenk describe the term "heritability" in the context of behavior genetics as "...one of the most misleading in the history of science" and argue that it has no value except in very rare cases. When studying complex human traits, it is impossible to use heritability analysis to determine the relative contributions of genes and environment, as such traits result from multiple causes interacting.

The controversy over heritability estimates is largely via their basis in twin studies. The scarce success of molecular-genetic studies to corroborate such population-genetic studies' conclusions is the missing heritability problem. Eric Turkheimer has argued that newer molecular methods have vindicated the conventional interpretation of twin studies, although it remains mostly unclear how to explain the relations between genes and behaviors. According to Turkheimer, both genes and environment are heritable, genetic contribution varies by environment, and a focus on heritability distracts from other important factors. Overall, however, heritability is a concept widely applicable.