From Wikipedia, the free encyclopedia
The polar jet stream can travel at speeds greater than 100 miles per
hour (160 km/h). Here, the fastest winds are coloured red; slower winds
are blue.
Clouds along a jet stream over Canada.
Jet streams are fast flowing, narrow, meandering
air currents found in the
atmosphere of some
planets, including
Earth.
[1] On Earth, the main jet streams are located near the altitude of the
tropopause and are westerly winds (flowing west to east). Their paths typically have a
meandering
shape. Jet streams may start, stop, split into two or more parts,
combine into one stream, or flow in various directions including
opposite to the direction of the remainder of the jet. The strongest jet
streams are the
polar jets, at 9–12 km (30,000–39,000 ft) above sea level, and the higher altitude and somewhat weaker
subtropical jets at 10–16 km (33,000–52,000 ft). The
Northern Hemisphere and the
Southern Hemisphere each have a polar jet and a subtropical jet. The northern hemisphere polar jet flows over the middle to northern latitudes of
North America,
Europe, and
Asia and their intervening
oceans, while the southern hemisphere polar jet mostly circles
Antarctica all year round.
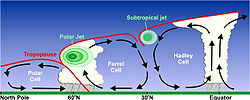
Jet streams are the product of two factors: the atmospheric heating by
solar radiation that produces the large scale
Polar, Ferrel, and Hadley circulation cells, and the action of the
Coriolis force acting on those moving masses. The Coriolis force is caused by the planet's
rotation on its axis. On other planets,
internal heat
rather than solar heating drives their jet streams. The Polar jet
stream forms near the interface of the Polar and Ferrel circulation
cells; while the subtropical jet forms near the boundary of the Ferrel
and Hadley circulation cells.
[2]
Other jet streams also exist. During the Northern Hemisphere summer,
easterly jets can form in tropical regions, typically where dry air
encounters more humid air at high altitudes. Low-level jets also are
typical of various regions such as the central United States.
Meteorologists use the location of some of the jet streams as an aid in
weather forecasting.
The main commercial relevance of the jet streams is in air travel, as
flight time can be dramatically affected by either flying with the flow
or against, which results in significant fuel and time cost savings for
airlines. Often, the airlines work to fly 'with' the jet stream for this
reason. Dynamic
North Atlantic Tracks are one example of how airlines and
air traffic control work together to accommodate the jet steam and winds aloft that results in the maximum benefit for airlines and other users.
Clear-air turbulence,
a potential hazard to aircraft passenger safety, is often found in a
jet stream's vicinity, but it does not create a substantial alteration
on flight times.
Discovery
After the
1883 eruption of the Krakatoa volcano,
weather watchers tracked and mapped the effects on the sky over several
years. They labelled the phenomenon the "equatorial smoke stream".
[3][4] In the 1920s, a Japanese meteorologist,
Wasaburo Oishi, detected the jet stream from a site near
Mount Fuji.
[5][6] He tracked
pilot balloons, also known as pibals (balloons used to determine upper level winds),
[7] as they rose into the atmosphere. Oishi's work largely went unnoticed outside Japan because it was published in
Esperanto. American pilot
Wiley Post,
the first man to fly around the world solo in 1933, is often given some
credit for discovery of jet streams. Post invented a pressurized suit
that let him fly above 6,200 metres (20,300 ft). In the year before his
death, Post made several attempts at a high-altitude transcontinental
flight, and noticed that at times his ground speed greatly exceeded his
air speed.
[8] German meteorologist
Heinrich Seilkopf is credited with coining a special term,
Strahlströmung (literally "
jet current"), for the phenomenon in 1939.
[9][10] (Modern German usage is
"Strahlstrom".
[citation needed]) Many sources credit real understanding of the nature of jet streams to regular and repeated flight-path traversals during
World War II. Flyers consistently noticed westerly tailwinds in excess of 100 mph (160 km/h) in flights, for example, from the US to the UK.
[11] Similarly in 1944 a team of American meteorologists in Guam, including
Reid Bryson, had enough observations to forecast very high west winds that would slow bombers going to Japan.
[12]
Description
General configuration of the polar and subtropical jet streams
Cross section of the subtropical and polar jet streams by latitude
Polar jet streams are typically located near the 250
hPa (about 1/4 atmosphere) pressure level, or 7 to 12 kilometres (4.3 to 7.5 mi) above
sea level,
while the weaker subtropical jet streams are much higher, between 10
and 16 kilometres (6.2 and 9.9 mi). Jet streams wander laterally
dramatically, and have large changes in their altitude. The jet streams
form near breaks in the tropopause, at the transitions between the
Polar, Ferrel and Hadley circulation cells,
and whose circulation, with the Coriolis force acting on those masses,
drives the jet streams. The Polar jets, at lower altitude, and often
intruding into mid-latitudes, strongly affects weather and aviation.
[13][14]
The polar jet stream is most commonly found between latitudes 30° and
60° (closer to 60°), while the subtropical jet streams are located close
to latitude 30°. The northern Polar jet stream is said to "follow the
sun" as it slowly migrates northward as that hemisphere warms, and
southward again as it cools.
[15][16]
The width of a jet stream is typically a few hundred kilometres or
miles and its vertical thickness often less than five kilometres (3 mi).
[17]
Meanders (Rossby Waves) of the Northern Hemisphere's polar jet stream
developing (a), (b); then finally detaching a "drop" of cold air (c).
Orange: warmer masses of air; pink: jet stream.
Jet streams are typically continuous over long distances, but discontinuities are common.
[18]
The path of the jet typically has a meandering shape, and these
meanders themselves propagate eastward, at lower speeds than that of the
actual wind within the flow. Each large meander, or wave, within the
jet stream is known as a
Rossby wave (planetary wave). Rossby waves are caused by changes in the
Coriolis effect with latitude.
[citation needed] Shortwave troughs, are smaller scale waves superimposed on the Rossby waves, with a scale of 1,000 to 4,000 kilometres (620–2,490 mi) long,
[19] that move along through the flow pattern around large scale, or longwave, "ridges" and "troughs" within Rossby waves.
[20]
Jet streams can split into two when it encounters an upper-level low,
that diverts a portion of the jet stream under its base, while the
remainder of the jet moves by to its north.
The wind speeds are greatest where temperature differences (
gradient) between air masses are greatest, and often exceed 92 km/h (50 kn; 57 mph),
[18] to over 398 km/h (215 kn; 247 mph) have been measured.
[21]
The jet stream moves from West to East bringing changes of weather.
[22] Meteorologists now understand that the path of jet streams affects
cyclonic
storm systems at lower levels in the atmosphere, and so knowledge of
their course has become an important part of weather forecasting. For
example, in 2007 and 2012, Britain experienced severe flooding as a
result of the polar jet staying south for the summer.
[23][24][25]
The polar and subtropical jets merge at some locations and times, while at other times they are well separated.
Cause
Highly idealised depiction of the global circulation. The upper-level jets tend to flow latitudinally along the cell boundaries.
In general, winds are strongest immediately under the
tropopause (except locally, during
tornadoes,
tropical cyclones
or other anomalous situations). If two air masses of different
temperatures or densities meet, the resulting pressure difference caused
by the density difference (which ultimately causes wind) is highest
within the transition zone. The wind does not flow directly from the hot
to the cold area, but is deflected by the
Coriolis effect and flows along the boundary of the two air masses.
[26]
All these facts are consequences of the
thermal wind
relation. The balance of forces acting on an atmospheric air parcel in
the vertical direction is primarily between the gravitational force
acting on the mass of the parcel and the buoyancy force, or the
difference in pressure between the top and bottom surfaces of the
parcel. Any imbalance between these forces results in the acceleration
of the parcel in the imbalance direction: upward if the buoyant force
exceeds the weight, and downward if the weight exceeds the buoyancy
force. The balance in the vertical direction is referred to as
hydrostatic.
Beyond the tropics, the dominant forces act in the horizontal
direction, and the primary struggle is between the Coriolis force and
the pressure gradient force. Balance between these two forces is
referred to as
geostrophic.
Given both hydrostatic and geostrophic balance, one can derive the
thermal wind relation: the vertical gradient of the horizontal wind is
proportional to the horizontal temperature gradient. If two air masses,
one cold and dense to the North and the other hot and less dense to the
South, are separated by a vertical boundary and that boundary should be
removed, the difference in densities will result in the cold air mass
slipping under the hotter and less dense air mass. The Coriolis effect
will then cause poleward-moving mass to deviate to the East, while
equatorward-moving mass will deviate toward the west. The general trend
in the atmosphere is for temperatures to decrease in the poleward
direction. As a result, winds develop an eastward component and that
component grows with altitude. Therefore, the strong eastward moving jet
streams are in part a simple consequence of the fact that the Equator
is warmer than the North and South poles.
[26]
Polar jet stream
The
thermal wind relation does not explain why the winds are organized into
tight jets, rather than distributed more broadly over the hemisphere.
One factor that contributes to the creation of a concentrated polar jet
is the undercutting of sub-tropical air masses by the more dense polar
air masses at the polar front. This causes surface low pressure and
higher pressure at altitude. At high altitudes, lack of friction allows
air to respond freely to the steep pressure gradient with low pressure
at high altitude over the pole. This results in the formation of
planetary wind circulations that experience a strong Coriolis deflection
and thus can be considered 'quasi-geostrophic'. The polar front jet
stream is closely linked to the
frontogenesis
process in midlatitudes, as the acceleration/deceleration of the air
flow induces areas of low/high pressure respectively, which link to the
formation of cyclones and anticyclones along the polar front in a
relatively narrow region.
[18]
Subtropical jet
A
second factor which contributes to a concentrated jet, that is more
applicable to the subtropical jet, which forms at the poleward limit of
the tropical
Hadley cell
and to first order this circulation is symmetric with respect to
longitude. Tropical air rises to the tropopause, and moves poleward
before sinking; this is the Hadley cell circulation. As it does so it
tends to conserve angular momentum, since friction with the ground is
significant. Air masses that begin moving northward are deflected
eastward by the
Coriolis force (true for either hemisphere), which for poleward moving air implies an increased eastward component of the winds
[27] (note that leftward deflection in the southern hemisphere).
Other planets
Jupiter's
atmosphere has multiple jet streams, caused by the convection cells
that form the familiar banded color structure; on Jupiter, these
convection cells are driven by internal heating.
[21]
The factors that control the number of jet streams in a planetary
atmosphere is an active area of research in dynamical meteorology. In
models, as one increases the planetary radius, holding all other
parameters fixed, the number of jet streams decreases.
Some effects
Hurricane protection
Note the large band of moisture that developed East of Hawaii Island that came from the hurricane.
The subtropical jet stream rounding the base of the mid-oceanic upper
trough is thought to be one of the reasons most of the Hawaiian Islands
have been resistant to the long
list of Hawaii hurricanes that have approached. For example, when
Hurricane Flossie (2007) approached and dissipated just before reaching landfall, the U.S.
National Oceanic and Atmospheric Administration (NOAA) cited vertical
wind shear as evidenced in the photo.
[28]
Uses
On Earth, the
northern polar jet stream is the most important one for aviation and
weather forecasting, as it is much stronger and at a much lower altitude
than the subtropical jet streams and also covers many countries in the
Northern Hemisphere, while the southern polar jet stream mostly circles
Antarctica and sometimes the southern tip of
South America. The term
jet stream in these contexts thus usually implies the northern polar jet stream.
Aviation
The location of the jet stream is extremely important for aviation.
Commercial use of the jet stream began on 18 November 1952, when
Pan Am
flew from Tokyo to Honolulu at an altitude of 7,600 metres (24,900 ft).
It cut the trip time by over one-third, from 18 to 11.5 hours.
[29] Not only does it cut time off the flight, it also nets fuel savings for the airline industry.
[30] Within North America, the time needed to fly east across the
continent can be decreased by about 30
minutes if an
airplane can fly with the jet stream, or increased by more than that amount if it must fly west against it.
Associated with jet streams is a phenomenon known as
clear-air turbulence (CAT), caused by vertical and horizontal
wind shear caused by jet streams.
[31] The CAT is strongest on the cold
air side of the jet,
[32] next to and just under the axis of the jet.
[33]
Clear-air turbulence can cause aircraft to plunge and so present a
passenger safety hazard that has caused fatal accidents, such as the
death of one passenger on
United Airlines Flight 826 (1997).
[34][35]
Future power generation
Scientists are investigating ways to harness the wind energy within
the jet stream. According to one estimate, of the potential wind energy
in the jet stream, only 1 percent would be needed to meet the world's
current energy needs. The required technology would reportedly take
10–20 years to develop.
[36] There are two major scientific articles about jet stream power. Archer & Caldeira
[37]
claim that the jet streams can generate the total power of 1700 TW, and
that the climatic impact will be negligible. Miller, Gans, &
Kleidon
[38] claim that the jet streams can generate the total power of only 7.5 TW, and that the climatic impact will be catastrophic.
Unpowered aerial attack
Near the end of
World War II the Japanese
fire balloon was designed as a cheap weapon intended to make use of the jet stream over the
Pacific Ocean to reach the west coast of
Canada and the
United States. They were relatively ineffective as weapons, but they were used in one of the few
attacks on North America during World War II, causing six deaths and a small amount of damage.
[39]
Changes due to climate cycles
Effects of ENSO
Impact of El Niño and La Niña on North America
El Niño-Southern Oscillation
(ENSO) influences the average location of upper-level jet streams, and
leads to cyclical variations in precipitation and temperature across
North America, as well as affecting
tropical cyclone development across the eastern Pacific and Atlantic basins. Combined with the
Pacific Decadal Oscillation, ENSO can also impact cold season rainfall in Europe.
[40]
Changes in ENSO also change the location of the jet stream over South
America, which partially affects precipitation distribution over the
continent.
[41]
El Niño
During
El Niño events, increased precipitation is expected in California due to a more southerly, zonal, storm track.
[42]
During the Niño portion of ENSO, increased precipitation falls along
the Gulf coast and Southeast due to a stronger than normal, and more
southerly, polar jet stream.
[43]
Snowfall is greater than average across the southern Rockies and Sierra
Nevada mountain range, and is well below normal across the Upper
Midwest and Great Lakes states.
[44]
The northern tier of the lower 48 exhibits above normal temperatures
during the fall and winter, while the Gulf coast experiences below
normal temperatures during the winter season.
[45][46] The subtropical jet stream across the deep
tropics of the
Northern Hemisphere is enhanced due to increased convection in the equatorial Pacific, which decreases
tropical cyclogenesis within the Atlantic tropics below what is normal, and increases tropical cyclone activity across the eastern Pacific.
[47]
In the Southern Hemisphere, the subtropical jet stream is displaced
equatorward, or north, of its normal position, which diverts frontal
systems and thunderstorm complexes from reaching central portions of the
continent.
[41]
La Niña
Across North America during
La Niña, increased precipitation is diverted into the
Pacific Northwest due to a more northerly storm track and jet stream.
[48]
The storm track shifts far enough northward to bring wetter than normal
conditions (in the form of increased snowfall) to the Midwestern
states, as well as hot and dry summers.
[49][50] Snowfall is above normal across the Pacific Northwest and western Great Lakes.
[44]
Across the North Atlantic, the jet stream is stronger than normal,
which directs stronger systems with increased precipitation towards
Europe.
[51]
Dust Bowl
Evidence suggests the jet stream was at least partly responsible for the widespread drought conditions during the 1930s
Dust Bowl in the Midwest United States. Normally, the jet stream flows east over the
Gulf of Mexico and turns northward pulling up moisture and dumping
rain onto the
Great Plains. During the Dust Bowl, the jet stream weakened and changed course
traveling farther south than normal. This starved the Great Plains and
other areas of the Midwest of rainfall, causing extraordinary drought
conditions.
[52]
Longer-term climatic changes
Climate scientists have hypothesized that the jet stream will gradually weaken as a result of
global warming. Trends such as
Arctic sea ice decline, reduced snow cover,
evapotranspiration
patterns, and other weather anomalies are expected to make the Arctic
heat up faster than other parts of the globe. This in turn reduces the
temperature gradient that drives jet stream winds, causing the jet
stream to become weaker and more variable in its course.
[53][54][55][56][57][58][59]
Since 2007, and particularly in 2012 and early 2013, the jet stream
has been at an abnormally low latitude across the UK, lying closer to
the
English Channel, around 50°N rather than its more usual north of Scotland latitude of around 60°N.
[not in citation given]
However, between 1979 and 2001, it has been found that the average
position of the jet stream has been moving northward at a rate of 2.01
kilometres (1.25 mi) per year across the
Northern Hemisphere.
Across North America, this type of change could lead to drier
conditions across the southern tier of the United States and more
frequent and more intense
tropical cyclones in the tropics. A similar slow poleward drift was found when studying the
Southern Hemisphere jet stream over the same time frame.
[60]
Other upper-level jets
Polar night jet
The polar-night jet stream forms only during the winter months when the nights are much longer, hence
polar nights,
in their respective hemispheres at around 60° latitude. The polar night
jet moves at a greater height of about 80,000 feet (24,000 m) than it
does during the summer.
[61]
During these dark months the air high over the poles becomes much
colder than the air over the equator. This difference in temperature
gives rise to extreme air pressure differences in the stratosphere,
which, when combined with the Coriolis effect, create the polar night
jets, that race eastward at an altitude of about 30 miles (48 km).
[62] The
polar vortex
is circled by the polar night jet. The warmer air can only move along
the edge of the polar vortex, but not enter it. Within the vortex, the
cold polar air becomes increasingly cold with neither warmer air from
lower latitudes nor energy from the Sun during the
polar night.
[63]
Low level jets
There are wind maxima at lower levels of the atmosphere that are also referred to as jets.
Barrier jet
A
barrier jet in the low levels forms just upstream of mountain chains,
with the mountains forcing the jet to be oriented parallel to the
mountains. The mountain barrier increases the strength of the low level
wind by 45 percent.
[64] In the North American
Great Plains a southerly low-level jet helps fuel overnight thunderstorm activity during the warm season, normally in the form of
mesoscale convective systems which form during the overnight hours.
[65] A similar phenomenon develops across Australia, which pulls moisture poleward from the
Coral Sea towards cut-off lows which form mainly across southwestern portions of the
continent.
[66]
Valley exit jet
A
valley exit jet
is a strong, down-valley, elevated air current that emerges above the
intersection of the valley and its adjacent plain. These winds
frequently reach a maximum of 20 m/s (45 mph or 72 km/h) at a height of
40–200 m above the ground. Surface winds below the jet may sway
vegetation, but are significantly weaker.
They are likely to be found in valley regions that exhibit diurnal
mountain wind systems, such as those of the dry mountain ranges of the
US. Deep valleys that terminate abruptly at a plain are more impacted by
these factors than are those that gradually become shallower as
downvalley distance increases.
[67]
Africa
The mid-level
African easterly jet
occurs during the Northern Hemisphere summer between 10°N and 20°N
above West Africa, and the nocturnal poleward low-level jet occurs in
the
Great Plains of east and South Africa.
[68] The low-level easterly African jet stream is considered to play a crucial role in the southwest
monsoon of Africa,
[69] and helps form the
tropical waves which move across the tropical Atlantic and eastern Pacific oceans during the warm season.
[70] The formation of the
thermal low over northern Africa leads to a low-level westerly jet stream from June into October.
[71]
 is one which satisfies both of the following properties:
is one which satisfies both of the following properties: is a linear map (as defined above) and nonlinear otherwise. The equation is called homogeneous if
is a linear map (as defined above) and nonlinear otherwise. The equation is called homogeneous if  .
. is very general in that
is very general in that  can be any sensible mathematical object (number, vector, function, etc.), and the function
can be any sensible mathematical object (number, vector, function, etc.), and the function  can literally be any mapping, including integration or differentiation with associated constraints (such as boundary values). If
can literally be any mapping, including integration or differentiation with associated constraints (such as boundary values). If  contains differentiation with respect to
contains differentiation with respect to  , the result will be a differential equation.
, the result will be a differential equation. as a general solution (and also u = 0 as a particular solution, corresponding to the limit of the general solution when C tends to infinity). The equation is nonlinear because it may be written as
as a general solution (and also u = 0 as a particular solution, corresponding to the limit of the general solution when C tends to infinity). The equation is nonlinear because it may be written as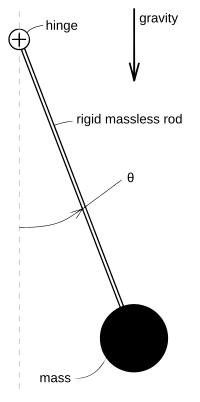
 is the angle the pendulum forms with its rest position, as shown in the
figure at right. One approach to "solving" this equation is to use
is the angle the pendulum forms with its rest position, as shown in the
figure at right. One approach to "solving" this equation is to use  as an integrating factor, which would eventually yield
as an integrating factor, which would eventually yield ).
). , called the small angle approximation, is
, called the small angle approximation, is for
for  . This is a simple harmonic oscillator corresponding to oscillations of the pendulum near the bottom of its path. Another linearization would be at
. This is a simple harmonic oscillator corresponding to oscillations of the pendulum near the bottom of its path. Another linearization would be at  , corresponding to the pendulum being straight up:
, corresponding to the pendulum being straight up: for
for  . The solution to this problem involves hyperbolic sinusoids, and note that unlike the small angle approximation, this approximation is unstable, meaning that
. The solution to this problem involves hyperbolic sinusoids, and note that unlike the small angle approximation, this approximation is unstable, meaning that  will usually grow without limit, though bounded solutions are possible.
This corresponds to the difficulty of balancing a pendulum upright, it
is literally an unstable state.
will usually grow without limit, though bounded solutions are possible.
This corresponds to the difficulty of balancing a pendulum upright, it
is literally an unstable state. , around which
, around which  :
: