Square root of 2

From Wikipedia, the free encyclopedia

Binary	1.01101010000010011110…
Decimal	1.4142135623730950488…
Hexadecimal	1.6A09E667F3BCC908B2F…
Continued fraction	${\displaystyle 1+{\cfrac {1}{2+{\cfrac {1}{2+{\cfrac {1}{2+{\cfrac {1}{2+\ddots }}}}}}}}}$

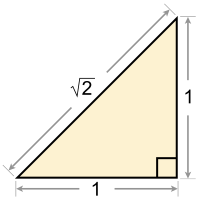
The square root of 2 is equal to the length of the hypotenuse of a right triangle with legs of length 1

The square root of 2, or the (1/2)th power of 2, written in mathematics as √2 or 2^​1⁄₂, is the positive algebraic number that, when multiplied by itself, gives the number 2. Technically, it is called the principal square root of 2, to distinguish it from the negative number with the same property.

Geometrically the square root of 2 is the length of a diagonal across a square with sides of one unit of length; this follows from the Pythagorean theorem. It was probably the first number known to be irrational.

The rational approximation of the square root of two, 665,857/470,832, derived from the fourth step in the Babylonian algorithm starting with a₀ = 1, is too large by approx. 1.6×10⁻¹²: its square is 2.0000000000045…

The rational approximation 99/70 (≈ 1.4142857) is frequently used. Despite having a denominator of only 70, it differs from the correct value by less than 1/10,000 (approx. +0.72×10⁻⁴). Since it is a convergent of the continued fraction representation of the square root of two, any better rational approximation has a denominator not less than 169, since 239/169 (≈ 1.4142012) is the next convergent with an error of approx. −0.12×10⁻⁴.

The numerical value for the square root of two, truncated to 65 decimal places, is:

1.41421356237309504880168872420969807856967187537694807317667973799... (sequence A002193 in the OEIS).

History

Babylonian clay tablet YBC 7289 with annotations. Besides showing the square root of 2 in sexagesimal (1 24 51 10), the tablet also gives an example where one side of the square is 30 and the diagonal then is 42 25 35. The sexagesimal digit 30 can also stand for 0 30 = 1/2, in which case 0 42 25 35 is approximately 0.7071065.

The Babylonian clay tablet YBC 7289 (c. 1800–1600 BC) gives an approximation of √2 in four sexagesimal figures, 1 24 51 10, which is accurate to about six decimal digits,^[1] and is the closest possible three-place sexagesimal representation of √2:

${\displaystyle 1+{\frac {24}{60}}+{\frac {51}{60^{2}}}+{\frac {10}{60^{3}}}={\frac {30547}{21600}}=1.41421{\overline {296}}.}$

Another early close approximation is given in ancient Indian mathematical texts, the Sulbasutras (c. 800–200 BC) as follows: Increase the length [of the side] by its third and this third by its own fourth less the thirty-fourth part of that fourth.^[2] That is,

${\displaystyle 1+{\frac {1}{3}}+{\frac {1}{3\times 4}}-{\frac {1}{3\times 4\times 34}}={\frac {577}{408}}=1.41421{\overline {56862745098039}}.}$

This approximation is the seventh in a sequence of increasingly accurate approximations based on the sequence of Pell numbers, which can be derived from the continued fraction expansion of √2. Despite having a smaller denominator, it is only slightly less accurate than the Babylonian approximation.

Pythagoreans discovered that the diagonal of a square is incommensurable with its side, or in modern language, that the square root of two is irrational. Little is known with certainty about the time or circumstances of this discovery, but the name of Hippasus of Metapontum is often mentioned. For a while, the Pythagoreans treated as an official secret the discovery that the square root of two is irrational, and, according to legend, Hippasus was murdered for divulging it.^[3][4][5] The square root of two is occasionally called "Pythagoras' number" or "Pythagoras' constant", for example by Conway & Guy (1996).^[6]

Computation algorithms

There are a number of algorithms for approximating √2, which in expressions as a ratio of integers or as a decimal can only be approximated. The most common algorithm for this, one used as a basis in many computers and calculators, is the Babylonian method^[7] of computing square roots, which is one of many methods of computing square roots. It goes as follows:
First, pick a guess, a₀ > 0; the value of the guess affects only how many iterations are required to reach an approximation of a certain accuracy. Then, using that guess, iterate through the following recursive computation:

${\displaystyle a_{n+1}={\frac {a_{n}+{\frac {2}{a_{n}}}}{2}}={\frac {a_{n}}{2}}+{\frac {1}{a_{n}}}.}$

The more iterations through the algorithm (that is, the more computations performed and the greater "n"), the better approximation of the square root of 2 is achieved. Each iteration approximately doubles the number of correct digits. Starting with a₀ = 1 the next approximations are

• 3/2 = 1.5
• 17/12 = 1.416...
• 577/408 = 1.414215...
• 665857/470832 = 1.4142135623746...

The value of √2 was calculated to 137,438,953,444 decimal places by Yasumasa Kanada's team in 1997. In February 2006 the record for the calculation of √2 was eclipsed with the use of a home computer. Shigeru Kondo calculated 1 trillion decimal places in 2010.^[8] For a development of this record, see the table below. Among mathematical constants with computationally challenging decimal expansions, only π has been calculated more precisely.^[9] Such computations aim to check empirically whether such numbers are normal.

Record progression

This is a table of recent records in calculating digits of √2 ( 1 trillion = 10¹² = 1,000,000,000,000 ).

Reference:^[10]

Date	Name	Number of digits
June 28, 2016	Ron Watkins	10 trillion
April 3, 2016	Ron Watkins	5 trillion
February 9, 2012	Alexander Yee	2 trillion
March 22, 2010	Shigeru Kondo	1 trillion= 1012

Proofs of irrationality

A short proof of the irrationality of √2 can be obtained from the rational root theorem, that is, if p(x) is a monic polynomial with integer coefficients, then any rational root of p(x) is necessarily an integer. Applying this to the polynomial p(x) = x² − 2, it follows that √2 is either an integer or irrational. Because √2 is not an integer (2 is not a perfect square), √2 must therefore be irrational. This proof can be generalized to show that any root of any natural number which is not the square of a natural number is irrational.

See quadratic irrational or infinite descent for a proof that the square root of any non-square natural number is irrational.

Proof by infinite descent

One proof of the number's irrationality is the following proof by infinite descent. It is also a proof by contradiction, also known as an indirect proof, in that the proposition is proved by assuming that the opposite of the proposition is true and showing that this assumption is false, thereby implying that the proposition must be true.

1. Assume that √2 is a rational number, meaning that there exists a pair of integers whose ratio is √2.
2. If the two integers have a common factor, it can be eliminated using the Euclidean algorithm.
3. Then √2 can be written as an irreducible fraction a/b such that a and b are coprime integers (having no common factor).
4. It follows that a²/b² = 2 and a² = 2b².   ( (a/b)ⁿ = aⁿ/bⁿ  )
5. Therefore, a² is even because it is equal to 2b². (2b² is necessarily even because it is 2 times another whole number and multiples of 2 are even.)
6. It follows that a must be even (as squares of odd integers are never even).
7. Because a is even, there exists an integer k that fulfills: a = 2k.
8. Substituting 2k from step 7 for a in the second equation of step 4: 2b² = (2k)² is equivalent to 2b² = 4k², which is equivalent to b² = 2k².
9. Because 2k² is divisible by two and therefore even, and because 2k² = b², it follows that b² is also even which means that b is even.
10. By steps 5 and 8 a and b are both even, which contradicts that a/b is irreducible as stated in step 3.

Q.E.D.

Because there is a contradiction, the assumption (1) that √2 is a rational number must be false. This means that √2 is not a rational number; i.e., √2 is irrational.

This proof was hinted at by Aristotle, in his Analytica Priora, §I.23.^[11] It appeared first as a full proof in Euclid's Elements, as proposition 117 of Book X. However, since the early 19th century historians have agreed that this proof is an interpolation and not attributable to Euclid.^[12]

Proof by unique factorization

An alternative proof uses the same approach with the fundamental theorem of arithmetic which says every integer greater than 1 has a unique factorization into powers of primes.

1. Assume that √2 is a rational number. Then there are integers a and b such that a is coprime to b and √2 = a/b. In other words, √2 can be written as an irreducible fraction.
2. The value of b cannot be 1 as there is no integer a the square of which is 2.
3. There must be a prime p which divides b and which does not divide a, otherwise the fraction would not be irreducible.
4. The square of a can be factored as the product of the primes into which a is factored but with each power doubled.
5. Therefore, by unique factorization the prime p which divides b, and also its square, cannot divide the square of a.
6. Therefore, the square of an irreducible fraction cannot be reduced to an integer.
7. Therefore, √2 cannot be a rational number.

This proof can be generalized to show that if an integer is not an exact kth power of another integer then its kth root is irrational. For a proof of the same result which does not rely on the fundamental theorem of arithmetic.

Proof by infinite descent, not involving factoring

The following reductio ad absurdum argument showing the irrationality of √2 is less well-known. It uses the additional information 2 > √2 > 1 so that 1 > √2 − 1 > 0.^[13]

1. Assume that √2 is a rational number. This would mean that there exist positive integers m and n with n ≠ 0 such that m/n = √2. Then m = n√2 and m√2 = 2n.
2. We may assume that n is the smallest integer so that n√2 is an integer. That is, that the fraction m/n is in lowest terms.
3. Because 1 > √2 − 1 > 0, it follows from (1) that n > n(√2 − 1) = m − n > 0. So n > m − n > 0.
4. Also from (1), we have √2 = m/n = m(√2 − 1)/n(√2 − 1) = 2n − m/m − n.
5. Thus the fraction m/n for √2, which according to (2) is already in lowest terms, is represented by (4) in yet lower terms (which follows from the result (3)). This is a contradiction, so the assumption that √2 is rational must be false.

This argument may be tightened as follows.

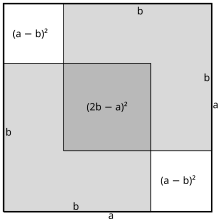
Let b be the least positive integer for which √2 is a rational a/b. Then b has the property that twice its square is a square, that is, 2b² = a². For a contradiction, we show that a − b is a smaller positive integer with the same property. Multiply the inequalities 1 > √2 − 1 > 0 by b to show b > a − b > 0. Now twice the square of a − b is 2a² − 4ab + 2b². Rewrite the first and last terms using b's property to yield a² − 4ab + 4b², which is just the expansion of (2b − a)², the promised square. Thus, √2 can also be written as (a − b)/(2 b − a). This procedure can be iterated and understood geometrically, as shown below.

Geometric proof

Figure 1. Stanley Tennenbaum's geometric proof of the irrationality of √2.

The immediately preceding argument has a simple geometric formulation attributed by John Horton Conway to Stanley Tennenbaum when the latter was a student in the early 1950s^[14] and whose most recent appearance is in an article by Noson Yanofsky in the May–June 2016 issue of American Scientist.^[15] Given two squares with integer sides respectively a and b, one of which has twice the area of the other, place two copies of the smaller square in the larger as shown in Figure 1. The square overlap region in the middle ((2b − a)²) must equal the sum of the two uncovered squares (2(a − b)²). But these squares on the diagonal have positive integer sides that are smaller than the original squares. Repeating this process we can find arbitrarily small squares one twice the area of the other, yet both having positive integer sides, which is impossible since positive integers cannot be less than 1.

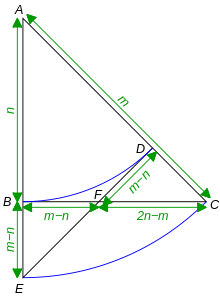
Figure 2. Tom Apostol's geometric proof of the irrationality of sqrt(2).

Another geometric reductio ad absurdum argument showing that √2 is irrational appeared in 2000 in the American Mathematical Monthly.^[16] It is also an example of proof by infinite descent. It makes use of classic compass and straightedge construction, proving the theorem by a method similar to that employed by ancient Greek geometers. It is essentially the algebraic proof of the previous section viewed geometrically in yet another way.

Let △ABC be a right isosceles triangle with hypotenuse length m and legs n as shown in Figure 2. By the Pythagorean theorem, m/n = √2. Suppose m and n are integers. Let m:n be a ratio given in its lowest terms.

Draw the arcs BD and CE with centre A. Join DE. It follows that AB = AD, AC = AE and the ∠BAC and ∠DAE coincide. Therefore, the triangles ABC and ADE are congruent by SAS.

Because ∠EBF is a right angle and ∠BEF is half a right angle, △BEF is also a right isosceles triangle. Hence BE = m − n implies BF = m − n. By symmetry, DF = m − n, and △FDC is also a right isosceles triangle. It also follows that FC = n − (m − n) = 2n − m.

Hence we have an even smaller right isosceles triangle, with hypotenuse length 2n − m and legs m − n. These values are integers even smaller than m and n and in the same ratio, contradicting the hypothesis that m:n is in lowest terms. Therefore, m and n cannot be both integers, hence √2 is irrational.

Pythagorean theorem proof

The square root of 2 is the diagonal of a square with side lengths 1.

This is another proof by contradiction, supposing that √2 is rational.

1. That means that we can make a right isosceles triangle where the side lengths are natural numbers and the legs and the hypotenuse do not share any common factors (except 1).
2. Since the legs are equal, so are their squares. So in order for the Pythagorean theorem to work for this special right triangle, the square of the hypotenuse has to be an even number (and if we cut it in half once then we have the area of the square of the leg).
3. Recall that the square of an even number is even and the square of an odd number is odd. So if the square of the hypotenuse is even the hypotenuse is even as well.
4. Remember that a square is a quadrilateral with 2 pairs of parallel sides which are equal in length and has 4 right angles. So both sides of the square of the hypotenuse are even.
5. So the square of the hypotenuse of this right triangle can be cut in half twice and still have integer area. Since we only want to cut it in half once, then we'll get an even number.
6. So the square of the leg is even. Now according to (2) the leg must be even.
7. This contradicts our assumption at (1) that the leg and hypotenuse have no common factors (except 1). Because if they're both even they share a common factor of 2. So the assumption that √2 was rational has to be false. Or in other words √2 is an irrational number. Q. E. D.

Analytic proof

• Lemma: let α ∈ ℝ⁺ and p₁, p₂,… q₁, q₂,… ∈ ℕ such that |αq_n − p_n| ≠ 0 for all n ∈ ℕ and

${\displaystyle \lim _{n\rightarrow \infty }p_{n}=\lim _{n\rightarrow \infty }q_{n}=\infty }$

${\displaystyle \lim _{n\rightarrow \infty }\left|\alpha q_{n}-p_{n}\right|=0.}$

Then α is irrational.

Proof: suppose α = a/b with a,b ∈ ℕ⁺.

For sufficiently big n

${\displaystyle 0<\left|\alpha q_{n}-p_{n}\right|<{\frac {1}{b}}}$

then

${\displaystyle 0<\left|{\frac {aq_{n}}{b}}-p_{n}\right|<{\frac {1}{b}}}$

${\displaystyle 0<\left|aq_{n}-bp_{n}\right|<1 annotation="">$

but aq_n − bp_n is an integer, absurd, then α is irrational.

• √2 is irrational.

Proof: let p₁ = q₁ = 1 and

${\displaystyle p_{n+1}=p_{n}^{2}+2q_{n}^{2}}$

${\displaystyle q_{n+1}=2p_{n}q_{n}}$

for all n ∈ ℕ.

By induction,

${\displaystyle 0<\left|{\sqrt {2}}q_{n}-p_{n}\right|<{\frac {1}{2^{2^{n-1}}}}}$

for all n ∈ ℕ. For n = 1,

${\displaystyle 0<\left|{\sqrt {2}}q_{1}-p_{1}\right|<{\frac {1}{2}}}$

and if this is true for n then it is true for n + 1. In fact

${\displaystyle 0<\left|{\sqrt {2}}q_{n}-p_{n}\right|^{2}<{\frac {1}{2^{2^{n}}}}}$

${\displaystyle 0<\left|{\sqrt {2}}(2p_{n}q_{n})-\left(p_{n}^{2}+2q_{n}^{2}\right)\right|<{\frac {1}{2^{2^{n}}}}}$

${\displaystyle 0<\left|{\sqrt {2}}q_{n+1}-p_{n+1}\right|<{\frac {1}{2^{2^{n}}}}.}$

By application of the lemma, √2 is irrational.

Constructive proof

In a constructive approach, one distinguishes between on the one hand not being rational, and on the other hand being irrational (i.e., being quantifiably apart from every rational), the latter being a stronger property. Given positive integers a and b, because the valuation (i.e., highest power of 2 dividing a number) of 2b² is odd, while the valuation of a² is even, they must be distinct integers; thus |2b² − a²| ≥ 1. Then^[17]

${\displaystyle \left|{\sqrt {2}}-{\frac {a}{b}}\right|={\frac {|2b^{2}-a^{2}|}{b^{2}\left({\sqrt {2}}+{\frac {a}{b}}\right)}}\geq {\frac {1}{b^{2}\left({\sqrt {2}}+{\frac {a}{b}}\right)}}\geq {\frac {1}{3b^{2}}},}$

the latter inequality being true because we assume a/b ≤ 3 − √2 (otherwise the quantitative apartness can be trivially established). This gives a lower bound of 1/3b² for the difference |√2 − a/b|, yielding a direct proof of irrationality not relying on the law of excluded middle; see Errett Bishop (1985, p. 18). This proof constructively exhibits a discrepancy between √2 and any rational.

Properties of the square root of two

Angle size and sector area are the same when the conic radius is √2. This diagram illustrates the circular and hyperbolic functions based on sector areas u.

One-half of √2, also the reciprocal of √2, approximately 0.707106781186548, is a common quantity in geometry and trigonometry because the unit vector that makes a 45° angle with the axes in a plane has the coordinates

${\displaystyle \left({\frac {\sqrt {2}}{2}},{\frac {\sqrt {2}}{2}}\right).}$

This number satisfies

${\displaystyle {\tfrac {1}{2}}{\sqrt {2}}={\sqrt {\tfrac {1}{2}}}={\frac {1}{\sqrt {2}}}=\cos 45^{\circ }=\sin 45^{\circ }.}$

One interesting property of √2 is as follows:

${\displaystyle \!\ {1 \over {{\sqrt {2}}-1}}={\sqrt {2}}+1}$

since

${\displaystyle \left({\sqrt {2}}+1\right)\left({\sqrt {2}}-1\right)=2-1=1.}$

This is related to the property of silver ratios.

√2 can also be expressed in terms of the copies of the imaginary unit i using only the square root and arithmetic operations:

${\displaystyle {\frac {{\sqrt {i}}+i{\sqrt {i}}}{i}}{\text{ and }}{\frac {{\sqrt {-i}}-i{\sqrt {-i}}}{-i}}}$

if the square root symbol is interpreted suitably for the complex numbers i and −i.

√2 is also the only real number other than 1 whose infinite tetrate (i.e., infinite exponential tower) is equal to its square. In other words: if for c > 1 we define x₁ = c and x_n+1 = c^x_n for n > 1, we will call the limit of x_n as n → ∞ (if this limit exists) f(c). Then √2 is the only number c > 1 for which f(c) = c². Or symbolically:

${\displaystyle {\sqrt {2}}^{({\sqrt {2}}^{({\sqrt {2}}^{(\ \cdot ^{\cdot ^{\cdot })))}}}}=2.}$

√2 appears in Viète's formula for π:

${\displaystyle 2^{m}{\sqrt {2-{\sqrt {2+{\sqrt {2+\cdots +{\sqrt {2}}}}}}}}\to \pi {\text{ as }}m\to \infty }$

for m square roots and only one minus sign.^[18]

Similar in appearance but with a finite number of terms, √2 appears in various trigonometric constants:^[19]

${\displaystyle \sin(\pi /32)={\tfrac {1}{2}}{\sqrt {2-{\sqrt {2+{\sqrt {2+{\sqrt {2}}}}}}}};}$

${\displaystyle \sin(\pi /16)={\tfrac {1}{2}}{\sqrt {2-{\sqrt {2+{\sqrt {2}}}}}};}$

${\displaystyle \sin(3\pi /32)={\tfrac {1}{2}}{\sqrt {2-{\sqrt {2+{\sqrt {2-{\sqrt {2}}}}}}}};}$

${\displaystyle \sin(\pi /8)={\tfrac {1}{2}}{\sqrt {2-{\sqrt {2}}}};}$

${\displaystyle \sin(5\pi /32)={\tfrac {1}{2}}{\sqrt {2-{\sqrt {2-{\sqrt {2-{\sqrt {2}}}}}}}};}$

${\displaystyle \sin(3\pi /16)={\tfrac {1}{2}}{\sqrt {2-{\sqrt {2-{\sqrt {2}}}}}};}$

${\displaystyle \sin(7\pi /32)={\tfrac {1}{2}}{\sqrt {2-{\sqrt {2-{\sqrt {2+{\sqrt {2}}}}}}}};}$

${\displaystyle \sin(\pi /4)={\tfrac {1}{2}}{\sqrt {2}};}$

${\displaystyle \sin(9\pi /32)={\tfrac {1}{2}}{\sqrt {2+{\sqrt {2-{\sqrt {2+{\sqrt {2}}}}}}}};}$

${\displaystyle \sin(5\pi /16)={\tfrac {1}{2}}{\sqrt {2+{\sqrt {2-{\sqrt {2}}}}}};}$

${\displaystyle \sin(11\pi /32)={\tfrac {1}{2}}{\sqrt {2+{\sqrt {2-{\sqrt {2-{\sqrt {2}}}}}}}};}$

${\displaystyle \sin(3\pi /8)={\tfrac {1}{2}}{\sqrt {2+{\sqrt {2}}}};}$

${\displaystyle \sin(13\pi /32)={\tfrac {1}{2}}{\sqrt {2+{\sqrt {2+{\sqrt {2-{\sqrt {2}}}}}}}};}$

${\displaystyle \sin(7\pi /16)={\tfrac {1}{2}}{\sqrt {2+{\sqrt {2+{\sqrt {2}}}}}};}$

${\displaystyle \sin(15\pi /32)={\tfrac {1}{2}}{\sqrt {2+{\sqrt {2+{\sqrt {2+{\sqrt {2}}}}}}}}.}$

It is not known whether √2 is a normal number, a stronger property than irrationality, but statistical analyses of its binary expansion are consistent with the hypothesis that it is normal to base two.^[20]

Series and product representations

The identity cos π/4 = sin π/4 = 1/√2, along with the infinite product representations for the sine and cosine, leads to products such as

${\displaystyle {\frac {1}{\sqrt {2}}}=\prod _{k=0}^{\infty }\left(1-{\frac {1}{(4k+2)^{2}}}\right)=\left(1-{\frac {1}{4}}\right)\left(1-{\frac {1}{36}}\right)\left(1-{\frac {1}{100}}\right)\cdots }$

and

${\displaystyle {\sqrt {2}}=\prod _{k=0}^{\infty }{\frac {(4k+2)^{2}}{(4k+1)(4k+3)}}=\left({\frac {2\cdot 2}{1\cdot 3}}\right)\left({\frac {6\cdot 6}{5\cdot 7}}\right)\left({\frac {10\cdot 10}{9\cdot 11}}\right)\left({\frac {14\cdot 14}{13\cdot 15}}\right)\cdots }$

or equivalently,

${\displaystyle {\sqrt {2}}=\prod _{k=0}^{\infty }\left(1+{\frac {1}{4k+1}}\right)\left(1-{\frac {1}{4k+3}}\right)=\left(1+{\frac {1}{1}}\right)\left(1-{\frac {1}{3}}\right)\left(1+{\frac {1}{5}}\right)\left(1-{\frac {1}{7}}\right)\cdots .}$

The number can also be expressed by taking the Taylor series of a trigonometric function. For example, the series for cos π/4 gives

${\displaystyle {\frac {1}{\sqrt {2}}}=\sum _{k=0}^{\infty }{\frac {(-1)^{k}\left({\frac {\pi }{4}}\right)^{2k}}{(2k)!}}.}$

The Taylor series of √1 + x with x = 1 and using the double factorial n!! gives

${\displaystyle {\sqrt {2}}=\sum _{k=0}^{\infty }(-1)^{k+1}{\frac {(2k-3)!!}{(2k)!!}}=1+{\frac {1}{2}}-{\frac {1}{2\cdot 4}}+{\frac {1\cdot 3}{2\cdot 4\cdot 6}}-{\frac {1\cdot 3\cdot 5}{2\cdot 4\cdot 6\cdot 8}}+\cdots .}$

The convergence of this series can be accelerated with an Euler transform, producing

${\displaystyle {\sqrt {2}}=\sum _{k=0}^{\infty }{\frac {(2k+1)!}{2^{3k+1}(k!)^{2}}}={\frac {1}{2}}+{\frac {3}{8}}+{\frac {15}{64}}+{\frac {35}{256}}+{\frac {315}{4096}}+{\frac {693}{16384}}+\cdots .}$

It is not known whether √2 can be represented with a BBP-type formula. BBP-type formulas are known for π√2 and √2ln(1+√2), however.^[21]

The number can be represented by an infinite series of Egyptian fractions, with denominators defined by 2ⁿth terms of a Fibonacci-like recurrence relation a(n)=34a(n-1)-a(n-2), a(0)=0, a(1)=6.^[22]

${\displaystyle {\sqrt {2}}={\frac {3}{2}}-{\frac {1}{2}}\sum _{n=0}^{\infty }{\frac {1}{a(2^{n})}}={\frac {3}{2}}-{\frac {1}{2}}\left({\frac {1}{6}}+{\frac {1}{204}}+{\frac {1}{235416}}+\dots \right)}$

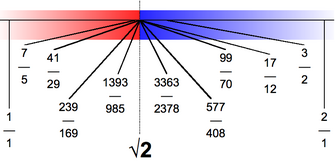
Continued fraction representation

The square root of 2 and approximations by convergents of continued fractions

The square root of two has the following continued fraction representation:

${\displaystyle \!\ {\sqrt {2}}=1+{\cfrac {1}{2+{\cfrac {1}{2+{\cfrac {1}{2+{\cfrac {1}{2+\ddots }}}}}}}}.}$

The convergents formed by truncating this representation form a sequence of fractions that approximate the square root of two to increasing accuracy, and that are described by the Pell numbers (known as side and diameter numbers to the ancient Greeks because of their use in approximating the ratio between the sides and diagonal of a square). The first convergents are: 1/1, 3/2, 7/5, 17/12, 41/29, 99/70, 239/169, 577/408. The convergent p/q differs from √2 by almost exactly 1/2q²√2^{[citation needed]} and then the next convergent is p + 2q/p + q.

Nested square representations

The following nested square expressions converge to ${\displaystyle {\sqrt {2}}}$:

${\displaystyle \!\ {\sqrt {2}}={\frac {3}{2}}-2\left({\frac {1}{4}}-\left({\frac {1}{4}}-\left({\frac {1}{4}}-\left({\frac {1}{4}}-\dots \right)^{2}\right)^{2}\right)^{2}\right)^{2}={\frac {3}{2}}-4\left({\frac {1}{8}}+\left({\frac {1}{8}}+\left({\frac {1}{8}}+\left({\frac {1}{8}}+\dots \right)^{2}\right)^{2}\right)^{2}\right)^{2}.}$

Derived constants

The reciprocal of the square root of two (the square root of 1/2) is a widely used constant.
${\displaystyle {\frac {1}{\sqrt {2}}}={\frac {\sqrt {2}}{2}}=\sin 45^{\circ }=\cos 45^{\circ }=0.70710\,67811\,86547\,52440\,08443\,62104\,84903\,928...}$ (sequence A010503 in the OEIS)

Paper size

The (approximate) aspect ratio of paper sizes under ISO 216 (A4, A0, etc.) is 1:√2. This ratio of lengths of the shorter over the longer side guarantees that cutting a sheet in half along a line parallel to its shorter side results in the smaller sheets having the same (approximate) ratio as the original sheet.

Proof:
Let ${\displaystyle S=}$ shorter length and ${\displaystyle L=}$ longer length of the sides of a sheet of paper, with

${\displaystyle R={\frac {L}{S}}={\sqrt {2}}}$ as required by ISO 216.

Let ${\displaystyle R'={\frac {L'}{S'}}}$ be the analogue ratio of the halved sheet, then

${\displaystyle R'={\frac {S}{L/2}}={\frac {2S}{L}}={\frac {2}{(L/S)}}={\frac {2}{\sqrt {2}}}={\sqrt {2}}=R}$.