| |
| General | |
|---|---|
| Symbol | 3H |
| Names | tritium, H-3, hydrogen-3, T, 3T |
| Protons | 1 |
| Neutrons | 2 |
| Nuclide data | |
| Natural abundance | 10−18 in hydrogen |
| Half-life | 12.32 years |
| Decay products | 3He |
| Isotope mass | 3.0160492 u |
| Spin | 1⁄2 |
| Excess energy | 14,949.794± 0.001 keV |
| Binding energy | 8,481.821± 0.004 keV |
| Decay modes | |
| Decay mode | Decay energy (MeV) |
| Beta emission | 0.018590 |
Tritium (/ˈtrɪtiəm/ or /ˈtrɪʃiəm/) or hydrogen-3 (symbol T or 3H) is a rare and radioactive isotope of hydrogen. The nucleus of tritium (sometimes called a triton) contains one proton and two neutrons, whereas the nucleus of the common isotope hydrogen-1 (protium) contains just one proton, and that of hydrogen-2 (deuterium) contains one proton and one neutron.
Naturally occurring tritium is extremely rare on Earth. The atmosphere has only trace amounts, formed by the interaction of its gases with cosmic rays. It can be artificially produced by irradiating lithium metal or lithium-bearing ceramic pebbles in a nuclear reactor, and is a low abundance byproduct in normal operations of nuclear reactors.
Tritium is used as the energy source in radioluminescent lights for watches, numerous instruments and tools, and even novelty items such as self-illuminating key chains. It is used in a medical and scientific setting as a radioactive tracer. Tritium is also used as a nuclear fusion fuel, along with more abundant deuterium, in tokamak reactors and in hydrogen bombs.
The name of this isotope is derived from Greek τρίτος (trítos), meaning "third".
History
Tritium was first detected in 1934 by Ernest Rutherford, Mark Oliphant, and Paul Harteck after bombarding deuterium with deuterons (a proton and neutron, comprising a deuterium nucleus). Deuterium is another isotope of hydrogen. However, their experiment could not isolate tritium, which was later accomplished by Luis Alvarez and Robert Cornog, who also realized tritium's radioactivity. Willard F. Libby recognized that tritium could be used for radiometric dating of water and wine.
Decay
While tritium has several different experimentally determined values of its half-life, the National Institute of Standards and Technology lists 4,500 ± 8 days (12.32 ± 0.02 years). It decays into helium-3 by beta decay as in this nuclear equation:
and it releases 18.6 keV of energy in the process. The electron's kinetic energy varies, with an average of 5.7 keV, while the remaining energy is carried off by the nearly undetectable electron antineutrino. Beta particles from tritium can penetrate only about 6.0 mm of air, and they are incapable of passing through the dead outermost layer of human skin. The unusually low energy released in the tritium beta decay makes the decay (along with that of rhenium-187) appropriate for absolute neutrino mass measurements in the laboratory (the most recent experiment being KATRIN).
The low energy of tritium's radiation makes it difficult to detect tritium-labeled compounds except by using liquid scintillation counting.
Production
Lithium
Tritium is most often produced in nuclear reactors by neutron activation of lithium-6. The release and diffusion of tritium and helium produced by the fission of lithium can take place within ceramics referred to as breeder ceramics. The production of tritium from lithium-6 in such breeder ceramics is possible with neutrons of any energy, and is an exothermic reaction yielding 4.8 MeV. In comparison, the fusion of deuterium with tritium releases about 17.6 MeV of energy. For applications in proposed fusion energy reactors, such as ITER, pebbles consisting of lithium bearing ceramics including Li2TiO3 and Li4SiO4, are being developed for tritium breeding within a helium cooled pebble bed, also known as a breeder blanket.
High-energy neutrons can also produce tritium from lithium-7 in an endothermic (net heat consuming) reaction, consuming 2.466 MeV. This was discovered when the 1954 Castle Bravo nuclear test produced an unexpectedly high yield.
Boron
High-energy neutrons irradiating boron-10 will also occasionally produce tritium:
A more common result of boron-10 neutron capture is 7
Li
and a single alpha particle.
Deuterium
Tritium is also produced in heavy water-moderated reactors whenever a deuterium nucleus captures a neutron. This reaction has a quite small absorption cross section, making heavy water a good neutron moderator, and relatively little tritium is produced. Even so, cleaning tritium from the moderator may be desirable after several years to reduce the risk of its escaping to the environment. Ontario Power Generation's "Tritium Removal Facility" processes up to 2,500 tonnes (2,500 long tons; 2,800 short tons) of heavy water a year, and it separates out about 2.5 kg (5.5 lb) of tritium, making it available for other uses.
Deuterium's absorption cross section for thermal neutrons is about 0.52 millibarns, whereas that of oxygen-16 (16
8O
) is about 0.19 millibarns and that of oxygen-17 (17
8O
) is about 240 millibarns.
Fission
Tritium is an uncommon product of the nuclear fission of uranium-235, plutonium-239, and uranium-233, with a production of about one atom per 10,000 fissions. The release or recovery of tritium needs to be considered in the operation of nuclear reactors, especially in the reprocessing of nuclear fuels and in the storage of spent nuclear fuel. The production of tritium is not a goal, but rather a side-effect. It is discharged to the atmosphere in small quantities by some nuclear power plants.
Fukushima Daiichi
In June 2016 the Tritiated Water Task Force released a report on the status of tritium in tritiated water at Fukushima Daiichi nuclear plant, as part of considering options for final disposal of the stored contaminated cooling water. This identified that the March 2016 holding of tritium on-site was 760 TBq (equivalent to 2.1 g of tritium or 14 mL of pure tritiated water) in a total of 860,000 m3 of stored water. This report also identified the reducing concentration of tritium in the water extracted from the buildings etc. for storage, seeing a factor of ten decrease over the five years considered (2011–2016), 3.3 MBq/L to 0.3 MBq/L (after correction for the 5% annual decay of tritium).
According to a report by an expert panel considering the best approach to dealing with this issue, "Tritium could be separated theoretically, but there is no practical separation technology on an industrial scale. Accordingly, a controlled environmental release is said to be the best way to treat low-tritium-concentration water."
Helium-3
Tritium's decay product helium-3 has a very large cross section (5330 barns) for reacting with thermal neutrons, expelling a proton, hence it is rapidly converted back to tritium in nuclear reactors.
Cosmic rays
Tritium occurs naturally due to cosmic rays interacting with atmospheric gases. In the most important reaction for natural production, a fast neutron (which must have energy greater than 4.0 MeV) interacts with atmospheric nitrogen:
Worldwide, the production of tritium from natural sources is 148 petabecquerels per year. The global equilibrium inventory of tritium created by natural sources remains approximately constant at 2,590 petabecquerels. This is due to a fixed production rate and losses proportional to the inventory.
Production history
According to a 1996 report from Institute for Energy and Environmental Research on the US Department of Energy, only 225 kg (496 lb) of tritium had been produced in the United States from 1955 to 1996. Since it continually decays into helium-3, the total amount remaining was about 75 kg (165 lb) at the time of the report.
Tritium for American nuclear weapons was produced in special heavy water reactors at the Savannah River Site until their closures in 1988. With the Strategic Arms Reduction Treaty (START) after the end of the Cold War, the existing supplies were sufficient for the new, smaller number of nuclear weapons for some time.
The production of tritium was resumed with irradiation of rods containing lithium (replacing the usual control rods containing boron, cadmium, or hafnium), at the reactors of the commercial Watts Bar Nuclear Generating Station from 2003 to 2005 followed by extraction of tritium from the rods at the new Tritium Extraction Facility at the Savannah River Site beginning in November 2006. Tritium leakage from the rods during reactor operations limits the number that can be used in any reactor without exceeding the maximum allowed tritium levels in the coolant.
Properties
Tritium has an atomic mass of 3.0160492 u. Diatomic tritium (
T
2 or 3
H
2) is a gas at standard temperature and pressure. Combined with oxygen, it forms a liquid called tritiated water (
T
2
O
).
Tritium's specific activity is 9,650 curies per gram (3.57×1014 Bq/g).
Tritium figures prominently in studies of nuclear fusion because of its favorable reaction cross section and the large amount of energy (17.6 MeV) produced through its reaction with deuterium:
All atomic nuclei contain protons as their only electrically charged particles. They therefore repel one another because like charges repel. However, if the atoms have a high enough temperature and pressure (for example, in the core of the Sun), then their random motions can overcome such electrical repulsion (called the Coulomb force), and they can come close enough for the strong nuclear force to take effect, fusing them into heavier atoms.
The tritium nucleus, containing one proton and two neutrons, has the same charge as the nucleus of ordinary hydrogen, and it experiences the same electrostatic repulsive force when brought close to another atomic nucleus. However, the neutrons in the tritium nucleus increase the attractive strong nuclear force when brought close enough to another atomic nucleus. As a result, tritium can more easily fuse with other light atoms, compared with the ability of ordinary hydrogen to do so.
The same is true, albeit to a lesser extent, of deuterium. This is why brown dwarfs (so-called 'failed' stars) cannot utilize ordinary hydrogen, but they do fuse the small minority of deuterium nuclei.
Like the other isotopes of hydrogen, tritium is difficult to confine. Rubber, plastic, and some kinds of steel are all somewhat permeable. This has raised concerns that if tritium were used in large quantities, in particular for fusion reactors, it may contribute to radioactive contamination, although its short half-life should prevent significant long-term accumulation in the atmosphere.
The high levels of atmospheric nuclear weapons testing that took place prior to the enactment of the Partial Test Ban Treaty proved to be unexpectedly useful to oceanographers. The high levels of tritium oxide introduced into upper layers of the oceans have been used in the years since then to measure the rate of mixing of the upper layers of the oceans with their lower levels.
Health risks
Tritium is an isotope of hydrogen, which allows it to readily bind to hydroxyl radicals, forming tritiated water (HTO), and to carbon atoms. Since tritium is a low energy beta emitter, it is not dangerous externally (its beta particles are unable to penetrate the skin), but it can be a radiation hazard when inhaled, ingested via food or water, or absorbed through the skin. HTO has a short biological half-life in the human body of 7 to 14 days, which both reduces the total effects of single-incident ingestion and precludes long-term bioaccumulation of HTO from the environment. The biological half life of tritiated water in the human body, which is a measure of body water turn-over, varies with the season. Studies on the biological half life of occupational radiation workers for free water tritium in a coastal region of Karnataka, India, show that the biological half life in the winter season is twice that of the summer season.
Environmental contamination
Tritium has leaked from 48 of 65 nuclear sites in the US. In one case, leaking water contained 7.5 microcuries (280 kBq) of tritium per liter, which is 375 times the EPA limit for drinking water.
The US Nuclear Regulatory Commission states that in normal operation in 2003, 56 pressurized water reactors released 40,600 curies (1.50 PBq) of tritium (maximum: 2,080 Ci; minimum: 0.1 Ci; average: 725 Ci) and 24 boiling water reactors released 665 curies (24.6 TBq) (maximum: 174 Ci; minimum: 0 Ci; average: 27.7 Ci), in liquid effluents.
According to the U.S. Environmental Protection Agency, self-illuminating exit signs improperly disposed in municipal landfills have been recently found to contaminate waterways.
Regulatory limits
The legal limits for tritium in drinking water vary widely from country to country. Some figures are given below:
Tritium drinking water limits by country Country Tritium limit
(Bq/l)Australia 76,103 Japan 60,000 Finland 100 World Health Organization 10,000 Switzerland 10,000 Russia 7,700 Canada (Ontario) 7,000 United States 740
The American limit is calculated to yield a dose of 4.0 millirems (or 40 microsieverts in SI units) per year. This is about 1.3% of the natural background radiation (roughly 3,000 μSv).
Use
Self-powered lighting
The beta particles emitted by the radioactive decay of small amounts of tritium cause chemicals called phosphors to glow.
This radioluminescence is used in self-powered lighting devices called betalights, which are used for night illumination of firearm sights, watches, exit signs, map lights, navigational compasses (such as current-use M-1950 U.S. military compasses), knives and a variety of other devices. As of 2000, commercial demand for tritium is 400 grams per year and the cost is approximately US$30,000 per gram.
Nuclear weapons
Tritium is an important component in nuclear weapons. It is used to enhance the efficiency and yield of fission bombs and the fission stages of hydrogen bombs in a process known as "boosting" as well as in external neutron initiators for such weapons.
Neutron initiator
These are devices incorporated in nuclear weapons which produce a pulse of neutrons when the bomb is detonated to initiate the fission reaction in the fissionable core (pit) of the bomb, after it is compressed to a critical mass by explosives. Actuated by an ultrafast switch like a krytron, a small particle accelerator drives ions of tritium and deuterium to energies above the 15 keV or so needed for deuterium-tritium fusion and directs them into a metal target where the tritium and deuterium are adsorbed as hydrides. High-energy fusion neutrons from the resulting fusion radiate in all directions. Some of these strike plutonium or uranium nuclei in the primary's pit, initiating nuclear chain reaction. The quantity of neutrons produced is large in absolute numbers, allowing the pit to quickly achieve neutron levels that would otherwise need many more generations of chain reaction, though still small compared to the total number of nuclei in the pit.
Boosting
Before detonation, a few grams of tritium-deuterium gas are injected into the hollow "pit" of fissile plutonium or uranium. The early stages of the fission chain reaction supply enough heat and compression to start deuterium-tritium fusion, then both fission and fusion proceed in parallel, the fission assisting the fusion by continuing heating and compression, and the fusion assisting the fission with highly energetic (14.1 MeV) neutrons. As the fission fuel depletes and also explodes outward, it falls below the density needed to stay critical by itself, but the fusion neutrons make the fission process progress faster and continue longer than it would without boosting. Increased yield comes overwhelmingly from the increase in fission. The energy released by the fusion itself is much smaller because the amount of fusion fuel is so much smaller. The effects of boosting include:
- increased yield (for the same amount of fission fuel, compared to detonation without boosting)
- the possibility of variable yield by varying the amount of fusion fuel
- allowing the bomb to require a smaller amount of the very expensive fissile material – and also eliminating the risk of predetonation by nearby nuclear explosions
- not so stringent requirements on the implosion setup, allowing for a smaller and lighter amount of high-explosives to be used
The tritium in a warhead is continually undergoing radioactive decay, hence becoming unavailable for fusion. Furthermore, its decay product, helium-3, absorbs neutrons if exposed to the ones emitted by nuclear fission. This potentially offsets or reverses the intended effect of the tritium, which was to generate many free neutrons, if too much helium-3 has accumulated from the decay of tritium. Therefore, it is necessary to replenish tritium in boosted bombs periodically. The estimated quantity needed is 4 grams per warhead. To maintain constant levels of tritium, about 0.20 grams per warhead per year must be supplied to the bomb.
One mole of deuterium-tritium gas would contain about 3.0 grams of tritium and 2.0 grams of deuterium. In comparison, the 20 moles of plutonium in a nuclear bomb consists of about 4.5 kilograms of plutonium-239.
Tritium in hydrogen bomb secondaries
Since tritium undergoes radioactive decay, and is also difficult to confine physically, the much larger secondary charge of heavy hydrogen isotopes needed in a true hydrogen bomb uses solid lithium deuteride as its source of deuterium and tritium, producing the tritium in situ during secondary ignition.
During the detonation of the primary fission bomb stage in a thermonuclear weapon (Teller-Ullam staging), the sparkplug, a cylinder of 235U/239Pu at the center of the fusion stage(s), begins to fission in a chain reaction, from excess neutrons channeled from the primary. The neutrons released from the fission of the sparkplug split lithium-6 into tritium and helium-4, while lithium-7 is split into helium-4, tritium, and one neutron. As these reactions occur, the fusion stage is compressed by photons from the primary and fission of the 238U or 238U/235U jacket surrounding the fusion stage. Therefore, the fusion stage breeds its own tritium as the device detonates. In the extreme heat and pressure of the explosion, some of the tritium is then forced into fusion with deuterium, and that reaction releases even more neutrons.
Since this fusion process requires an extremely high temperature
for ignition, and it produces fewer and less energetic neutrons (only
fission, deuterium-tritium fusion, and 7
3Li
splitting are net neutron producers), lithium deuteride is not used in boosted bombs, but rather for multi-stage hydrogen bombs.
Controlled nuclear fusion
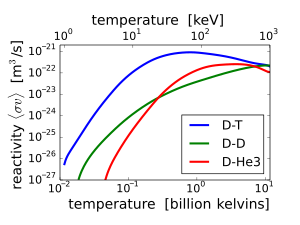
Tritium is an important fuel for controlled nuclear fusion in both magnetic confinement and inertial confinement fusion reactor designs. The experimental fusion reactor ITER and the National Ignition Facility (NIF) will use deuterium-tritium fuel. The deuterium-tritium reaction is favorable since it has the largest fusion cross section (about 5.0 barns) and it reaches this maximum cross section at the lowest energy (about 65 keV center-of-mass) of any potential fusion fuel.
The Tritium Systems Test Assembly (TSTA) was a facility at the Los Alamos National Laboratory dedicated to the development and demonstration of technologies required for fusion-relevant deuterium-tritium processing.
Analytical chemistry
Tritium is sometimes used as a radiolabel. It has the advantage that almost all organic chemicals contain hydrogen, making it easy to find a place to put tritium on the molecule under investigation. It has the disadvantage of producing a comparatively weak signal.
Electrical power source
Tritium can be used in a betavoltaic device to create an atomic battery to generate electricity.
Use as an oceanic transient tracer
Aside from chlorofluorocarbons, tritium can act as a transient tracer and has the ability to "outline" the biological, chemical, and physical paths throughout the world oceans because of its evolving distribution. Tritium has thus been used as a tool to examine ocean circulation and ventilation and, for such purposes, is usually measured in Tritium Units where 1 TU is defined as the ratio of 1 tritium atom to 1018 hydrogen atoms, approximately equal to 0.118 Bq/liter. As noted earlier, nuclear weapons testing, primarily in the high-latitude regions of the Northern Hemisphere, throughout the late 1950s and early 1960s introduced large amounts of tritium into the atmosphere, especially the stratosphere. Before these nuclear tests, there were only about 3 to 4 kilograms of tritium on the Earth's surface; but these amounts rose by 2 or 3 orders of magnitude during the post-test period. Some sources reported natural background levels were exceeded by approximately 1,000 TU in 1963 and 1964 and the isotope is used in the northern hemisphere to estimate the age of groundwater and construct hydrogeologic simulation models. Recent scientific sources have estimated atmospheric levels at the height of weapons testing to approach 1,000 TU and pre-fallout levels of rainwater to be between 5 and 10 TU. In 1963 Valentia Island Ireland recorded 2,000 TU in precipitation.
North Atlantic Ocean
While in the stratosphere (post-test period), the tritium interacted with and oxidized to water molecules and was present in much of the rapidly produced rainfall, making tritium a prognostic tool for studying the evolution and structure of the hydrologic cycle as well as the ventilation and formation of water masses in the North Atlantic Ocean.
Bomb-tritium data were used from the Transient Tracers in the Ocean (TTO) program in order to quantify the replenishment and overturning rates for deep water located in the North Atlantic.
Bomb-tritium also enters the deep ocean around the Antarctic. Most of the bomb tritiated water (HTO) throughout the atmosphere can enter the ocean through the following processes:
- (a) precipitation
- (b) vapor exchange
- (c) river runoff
These processes make HTO a great tracer for time-scales up to a few decades.
Using the data from these processes for 1981, the 1 TU isosurface lies between 500 and 1,000 meters deep in the subtropical regions and then extends to 1,500–2,000 meters south of the Gulf Stream due to recirculation and ventilation in the upper portion of the Atlantic Ocean. To the north, the isosurface deepens and reaches the floor of the abyssal plain which is directly related to the ventilation of the ocean floor over 10–20 year time-scales.
Also evident in the Atlantic Ocean is the tritium profile near Bermuda between the late 1960s and late 1980s. There is a downward propagation of the tritium maximum from the surface (1960s) to 400 meters (1980s), which corresponds to a deepening rate of approximately 18 meters per year. There are also tritium increases at 1,500 meters depth in the late 1970s and 2,500 meters in the middle of the 1980s, both of which correspond to cooling events in the deep water and associated deep water ventilation.
From a study in 1991, the tritium profile was used as a tool for studying the mixing and spreading of newly formed North Atlantic Deep Water (NADW), corresponding to tritium increases to 4 TU. This NADW tends to spill over sills that divide the Norwegian Sea from the North Atlantic Ocean and then flows to the west and equatorward in deep boundary currents. This process was explained via the large-scale tritium distribution in the deep North Atlantic between 1981 and 1983. The sub-polar gyre tends to be freshened (ventilated) by the NADW and is directly related to the high tritium values (> 1.5 TU). Also evident was the decrease in tritium in the deep western boundary current by a factor of 10 from the Labrador Sea to the Tropics, which is indicative of loss to ocean interior due to turbulent mixing and recirculation.
Pacific and Indian oceans
In a 1998 study, tritium concentrations in surface seawater and atmospheric water vapor (10 meters above the surface) were sampled at the following locations: the Sulu Sea, the Fremantle Bay, the Bay of Bengal, the Penang Bay, and the Strait of Malacca. Results indicated that the tritium concentration in surface seawater was highest at the Fremantle Bay (approximately 0.40 Bq/liter), which could be accredited to the mixing of runoff of freshwater from nearby lands due to large amounts found in coastal waters. Typically, lower concentrations were found between 35 and 45 degrees south latitude and near the equator. Results also indicated that (in general) tritium has decreased over the years (up to 1997) due to the physical decay of bomb tritium in the Indian Ocean. As for water vapor, the tritium concentration was approximately one order of magnitude greater than surface seawater concentrations (ranging from 0.46 to 1.15 Bq/liter). Therefore, the water vapor tritium is not affected by the surface seawater concentration; thus, the high tritium concentrations in the vapor were concluded to be a direct consequence of the downward movement of natural tritium from the stratosphere to the troposphere (therefore, the ocean air showed a dependence on latitudinal change).
In the North Pacific Ocean, the tritium (introduced as bomb tritium in the Northern Hemisphere) spread in three dimensions. There were subsurface maxima in the middle and low latitude regions, which is indicative of lateral mixing (advection) and diffusion processes along lines of constant potential density (isopycnals) in the upper ocean. Some of these maxima even correlate well with salinity extrema. In order to obtain the structure for ocean circulation, the tritium concentrations were mapped on 3 surfaces of constant potential density (23.90, 26.02, and 26.81). Results indicated that the tritium was well-mixed (at 6 to 7 TU) on the 26.81 isopycnal in the subarctic cyclonic gyre and there appeared to be a slow exchange of tritium (relative to shallower isopycnals) between this gyre and the anticyclonic gyre to the south; also, the tritium on the 23.90 and 26.02 surfaces appeared to be exchanged at a slower rate between the central gyre of the North Pacific and the equatorial regions.
The depth penetration of bomb tritium can be separated into 3 distinct layers:
- Layer 1
- Layer 1 is the shallowest layer and includes the deepest, ventilated layer in winter; it has received tritium via radioactive fallout and lost some due to advection and/or vertical diffusion and contains approximately 28% of the total amount of tritium.
- Layer 2
- Layer 2 is below the first layer but above the 26.81 isopycnal and is no longer part of the mixed layer. Its 2 sources are diffusion downward from the mixed layer and lateral expansions outcropping strata (poleward); it contains about 58% of the total tritium.
- Layer 3
- Layer 3 is representative of waters that are deeper than the outcrop isopycnal and can only receive tritium via vertical diffusion; it contains the remaining 14% of the total tritium.
Mississippi River System
The impacts of the nuclear fallout were felt in the United States throughout the Mississippi River System. Tritium concentrations can be used to understand the residence times of continental hydrologic systems (as opposed to the usual oceanic hydrologic systems) which include surface waters such as lakes, streams, and rivers. Studying these systems can also provide societies and municipals with information for agricultural purposes and overall river water quality.
In a 2004 study, several rivers were taken into account during the examination of tritium concentrations (starting in the 1960s) throughout the Mississippi River Basin: Ohio River (largest input to the Mississippi River flow), Missouri River, and Arkansas River. The largest tritium concentrations were found in 1963 at all the sampled locations throughout these rivers and correlate well with the peak concentrations in precipitation due to the nuclear bomb tests in 1962. The overall highest concentrations occurred in the Missouri River (1963) and were greater than 1,200 TU while the lowest concentrations were found in the Arkansas River (never greater than 850 TU and less than 10 TU in the mid-1980s).
Several processes can be identified using the tritium data from the rivers: direct runoff and outflow of water from groundwater reservoirs. Using these processes, it becomes possible to model the response of the river basins to the transient tritium tracer. Two of the most common models are the following:
- Piston-flow approach
- tritium signal appears immediately; and
- Well-mixed reservoir approach
- outflow concentration depends upon the residence time of the basin water.
Unfortunately, both models fail to reproduce the tritium in river waters; thus, a two-member mixing model was developed that consists of 2 components: a prompt-flow component (recent precipitation – "piston") and a component where waters reside in the basin for longer than 1 year ("well-mixed reservoir"). Therefore, the basin tritium concentration becomes a function of the residence times within the basin, sinks (radioactive decay) or sources of tritium, and the input function.
For the Ohio River, the tritium data indicated that about 40% of the flow was composed of precipitation with residence times of less than 1 year (in the Ohio basin) and older waters consisted of residence times of about 10 years. Thus, the short residence times (less than 1 year) corresponded to the "prompt-flow" component of the two-member mixing model. As for the Missouri River, results indicated that residence times were approximately 4 years with the prompt-flow component being around 10% (these results are due to the series of dams in the area of the Missouri River).
As for the mass flux of tritium through the main stem of the Mississippi River into the Gulf of Mexico, data indicated that approximately 780 grams of tritium has flowed out of the River and into the Gulf between 1961 and 1997, an average of 7.7 PBq/yr. And current fluxes through the Mississippi River are about 1 to 2 grams per year as opposed to the pre-bomb period fluxes of roughly 0.4 grams per year.