Coverage of Extreme Events in the IPCC AR5

Posted by Roger Pielke, Jr. at 10/03/2013 03:40:00 PM

 I had been scheduled to testify before the House Science Committee next week in a hearing on extreme events, but the gong show in Washington has put that off.

In the process of updating Senate testimony given back in July (here in PDF) I did compile some key statements from the IPCC AR5 WGI Chapter 2 on extremes.

Here are a few:

• “Overall, the most robust global changes in climate extremes are seen in measures of daily temperature, including to some extent, heat waves. Precipitation extremes also appear to be increasing, but there is large spatial variability"
• "There is limited evidence of changes in extremes associated with other climate variables since the mid-20th century”
• “Current datasets indicate no significant observed trends in global tropical cyclone frequency over the past century … No robust trends in annual numbers of tropical storms, hurricanes and major hurricanes counts have been identified over the past 100 years in the North Atlantic basin”
• “In summary, there continues to be a lack of evidence and thus low confidence regarding the sign of trend in the magnitude and/or frequency of floods on a global scale”
• “In summary, there is low confidence in observed trends in small-scale severe weather phenomena such as hail and thunderstorms because of historical data inhomogeneities and inadequacies in monitoring systems”
• “In summary, the current assessment concludes that there is not enough evidence at present to suggest more than low confidence in a global-scale observed trend in drought or dryness (lack of rainfall) since the middle of the 20th century due to lack of direct observations, geographical inconsistencies in the trends, and dependencies of inferred trends on the index choice. Based on updated studies, AR4 conclusions regarding global increasing trends in drought since the 1970s were probably overstated. However, it is likely that the frequency and intensity of drought has increased in the Mediterranean and West Africa and decreased in central North America and north-west Australia since 1950” 
• “In summary, confidence in large scale changes in the intensity of extreme extratropical cyclones since 1900 is low”

There is really not much more to be said here -- the data says what it says, and what it says is so unavoidably obvious that the IPCC has recognized it in its consensus. 

Of course, I have no doubts that claims will still be made associating floods, drought, hurricanes and tornadoes with human-caused climate change -- Zombie science -- but I am declaring victory in this debate. Climate campaigners would do their movement a favor by getting themselves on the right side of the evidence.

1918 flu pandemic

From Wikipedia, the free encyclopedia

 

Soldiers from Fort Riley, Kansas, ill with Spanish influenza at a hospital ward at Camp Funston.

The 1918 flu pandemic (January 1918 – December 1920) was an unusually deadly influenza pandemic, the first of the two pandemics Involving H1N1 influenza virus.^[1] It infected 500 million people around the world,^[2] including remote Pacific islands and the Arctic, and resulted in the deaths of 50 to 100 million (three to five percent of the world's population^[3]), making it one of the deadliest natural disasters in human history.^[4][5][6] Disease had already greatly limited life expectancy in the early 20th century. A considerable spike occurred at the time of the pandemic, specifically the year 1918. Life expectancy in the United States alone dropped by about 12 years.^{[7][8][9][10]}

Most influenza outbreaks disproportionately kill juvenile, elderly, or already weakened patients; in contrast, the 1918 pandemic predominantly killed previously healthy young adults.

There are several possible explanations for the high mortality rate of the 1918 influenza pandemic. Some research suggests that the specific variant of the virus had an unusually aggressive nature. One group of researchers recovered the original virus from the bodies of frozen victims, and found that transfection in animals caused a rapid progressive respiratory failure and death through a cytokine storm (overreaction of the body's immune system). It was then postulated that the strong immune reactions of young adults ravaged the body, whereas the weaker immune systems of children and middle-aged adults resulted in fewer deaths among those groups.^[11]

More recent investigations, mainly based on original medical reports from the period of the pandemic,^[12][13] found that the viral infection itself was not more aggressive than any previous influenza, but that the special circumstances (malnourishment, overcrowded medical camps and hospitals, poor hygiene) promoted bacterial superinfection that killed most of the victims typically after a somewhat prolonged death bed.^[14][15]

Historical and epidemiological data are inadequate to identify the pandemic's geographic origin.^[2] It was implicated in the outbreak of encephalitis lethargica in the 1920s.^[16]

To maintain morale, wartime censors minimized early reports of illness and mortality in Germany, the United Kingdom, France, and the United States.^[17][18] However, papers were free to report the epidemic's effects in neutral Spain (such as the grave illness of King Alfonso XIII).^[19] This reporting dichotomy created a false impression of Spain as especially hard hit,^[20] thereby giving rise to the pandemic's nickname, Spanish Flu.^[21] In Spain, a different nickname was adopted, the Naples Soldier (Soldado de Nápoles), which came from a musical operetta (zarzuela) titled La canción del olvido (The Song of Forgetting), which premiered in Madrid during the first epidemic wave. Federico Romero, one of the librettists, quipped that the play's most popular musical number, Naples Soldier, was as catchy as the flu.^[22]

History

Hypotheses about source

The site of the very first confirmed outbreak was at Camp Funston, Fort Riley, Kansas, then a military training facility preparing American troops for involvement in World War I. The first victim diagnosed with the new strain of flu on Monday, March 11, 1918, was mess cook Private Albert Gitchell.^[23][24] Historian Alfred W. Crosby recorded that the flu originated in Kansas,^[25] and popular writer John Barry echoed Crosby in describing Haskell County, Kansas, as the point of origin.^[26]

In contrast, investigative work in 1999 by a British team led by virologist John Oxford^[27] of St Bartholomew's Hospital and the Royal London Hospital identified the major troop staging and hospital camp in Étaples, France, as being the center of the 1918 flu pandemic. These researchers postulated that a significant precursor virus, harbored in birds, mutated to pigs that were kept near the front.^[28]

Earlier hypotheses of the epidemic's origin have varied. Some hypothesized the flu originated in East Asia.^[29][30] Dr. C. Hannoun, leading expert of the 1918 flu for the Institut Pasteur, asserted the former virus was likely to have come from China, mutating in the United States near Boston and spreading to Brest, France, Europe's battlefields, Europe, and the world using Allied soldiers and sailors as main spreaders.^[31] He considered several other hypotheses of origin, such as Spain, Kansas, and Brest, as being possible, but not likely.

Political scientist Andrew Price-Smith published data from the Austrian archives suggesting the influenza had earlier origins, beginning in Austria in the spring of 1917.^[32]

In 2014, historian Mark Humphries of Canada's Memorial University of Newfoundland stated that newly unearthed records confirmed that one of the side stories of the war, the mobilization of 96,000 Chinese laborers to work behind the British and French lines on World War I's western front, might have been the source of the pandemic. In the report, Humphries found archival evidence that a respiratory illness that struck northern China in November 1917 was identified a year later by Chinese health officials as identical to the Spanish flu.^[33][34] However, a report published in 2016 in the Journal of the Chinese Medical Association found no evidence that the 1918 virus was imported to Europe from Chinese and Southeast Asian soldiers and workers. In fact, it found evidence that the virus had been circulating in the European armies for months and potentially years before the 1918 pandemic.^[35]

Spread

When an infected person sneezes or coughs, more than half a million virus particles can be spread to those close by.^[36] The close quarters and massive troop movements of World War I hastened the pandemic, and probably both increased transmission and augmented mutation; the war may also have increased the lethality of the virus. Some speculate the soldiers' immune systems were weakened by malnourishment, as well as the stresses of combat and chemical attacks, increasing their susceptibility.^[37]

A large factor in the worldwide occurrence of this flu was increased travel. Modern transportation systems made it easier for soldiers, sailors, and civilian travelers to spread the disease.^[38]

In the United States, the disease was first observed in Haskell County, Kansas, in January 1918, prompting local doctor Loring Miner to warn the U.S. Public Health Service's academic journal. On 4 March 1918, company cook Albert Gitchell reported sick at Fort Riley, Kansas. By noon on 11 March 1918, over 100 soldiers were in the hospital.^[39] Within days, 522 men at the camp had reported sick.^[40] By 11 March 1918, the virus had reached Queens, New York.^[41] Failure to take preventative measures in March/April was later criticised.^[5]

In August 1918, a more virulent strain appeared simultaneously in Brest, France; in Freetown, Sierra Leone; and in the U.S. in Boston, Massachusetts. The Spanish flu also spread through Ireland, carried there by returning Irish soldiers. The Allies of World War I came to call it the Spanish flu, primarily because the pandemic received greater press attention after it moved from France to Spain in November 1918. Spain was not involved in the war and had not imposed wartime censorship.^[42]

Mortality

Around the globe

The difference between the influenza mortality age-distributions of the 1918 epidemic and normal epidemics – deaths per 100,000 persons in each age group, United States, for the interpandemic years 1911–1917 (dashed line) and the pandemic year 1918 (solid line)^[43]

Three pandemic waves: weekly combined influenza and pneumonia mortality, United Kingdom, 1918–1919^[44]

The global mortality rate from the 1918/1919 pandemic is not known, but an estimated 10% to 20% of those who were infected died. With about a third of the world population infected, this case-fatality ratio means 3% to 6% of the entire global population died.^[2] Influenza may have killed as many as 25 million people in its first 25 weeks. Older estimates say it killed 40–50 million people,^[4] while current estimates say 50–100 million people worldwide were killed.^[45]

This pandemic has been described as "the greatest medical holocaust in history" and may have killed more people than the Black Death.^[46] It is said that this flu killed more people in 24 weeks than AIDS killed in 24 years, and more in a year than the Black Death killed in a century.^[11]

The disease killed in every corner of the globe. As many as 17 million died in India, about 5% of the population.^[47] The death toll in India's British-ruled districts alone was 13.88 million.^[48]

In Japan, of the 23 million people who were affected, 390,000 died.^[49] In the Dutch East Indies (now Indonesia), 1.5 million were assumed to have died among 30 million inhabitants.^[50] In Tahiti 13% of the population died during only a month. Similarly, in Samoa 22% of the population of 38,000 died within two months.^[51]

In the U.S., about 28% of the population became infected, and 500,000 to 675,000 died.^[52] Native American tribes were particularly hard hit. In the Four Corners area alone, 3,293 deaths were registered among Native Americans.^[53] Entire village communities perished in Alaska.^[54] In Canada 50,000 died.^[55] In Brazil 300,000 died, including president Rodrigues Alves.^[56] In Britain, as many as 250,000 died; in France, more than 400,000.^[57] In West Africa an influenza epidemic killed at least 100,000 people in Ghana.^[58] Tafari Makonnen (the future Haile Selassie, Emperor of Ethiopia) was one of the first Ethiopians who contracted influenza but survived,^[59][60] although many of his family's subjects did not; estimates for the fatalities in the capital city, Addis Ababa, range from 5,000 to 10,000, or higher.^[61] In British Somaliland one official estimated that 7% of the native population died.^[62]

This huge death toll was caused by an extremely high infection rate of up to 50% and the extreme severity of the symptoms, suspected to be caused by cytokine storms.^[4] Symptoms in 1918 were so unusual that initially influenza was misdiagnosed as dengue, cholera, or typhoid. One observer wrote, "One of the most striking of the complications was hemorrhage from mucous membranes, especially from the nose, stomach, and intestine. Bleeding from the ears and petechial hemorrhages in the skin also occurred".^[45] The majority of deaths were from bacterial pneumonia,^[63][64] a common secondary infection associated with influenza, but the virus also killed people directly, by causing massive hemorrhages and edema in the lung.^[64]

The unusually severe disease killed up to 20% of those infected, as opposed to the usual flu epidemic mortality rate of 0.1%.^[2][45]

Patterns of fatality

An unusual feature of this pandemic was that it mostly killed young adults. In 1918–1919, 99% of pandemic influenza deaths in the US occurred in people under 65, and nearly half in young adults 20 to 40 years old. In 1920 the mortality rate among people under 65 had decreased six-fold to half the mortality rate of people over 65, but still 92% of deaths occurred in people under 65.^[65] This is noteworthy, since influenza is normally most deadly to weak individuals, such as infants (under age two), the very old (over age 70), and the immunocompromised. In 1918, older adults may have had partial protection caused by exposure to the 1889–1890 flu pandemic, known as the Russian flu.^[66] According to historian John M. Barry, the most vulnerable of all – "those most likely, of the most likely", to die – were pregnant women. He reported that in thirteen studies of hospitalized women in the pandemic, the death rate ranged from 23% to 71%.^[67] Of the pregnant women who survived childbirth, over one-quarter (26%) lost the child.^[68]

Another oddity was that the outbreak was widespread in the summer and autumn (in the Northern Hemisphere); influenza is usually worse in winter.^[69]

Modern analysis has shown the virus to be particularly deadly because it triggers a cytokine storm, which ravages the stronger immune system of young adults.^[26]

In fast-progressing cases, mortality was primarily from pneumonia, by virus-induced pulmonary consolidation. Slower-progressing cases featured secondary bacterial pneumonias, and there may have been neural involvement that led to mental disorders in some cases. Some deaths resulted from malnourishment.

A study – conducted by He et al. – used a mechanistic modelling approach to study the three waves of the 1918 influenza pandemic. They tried to study the factors that underlie variability in temporal patterns, and the patterns of mortality and morbidity. Their analysis suggests that temporal variations in transmission rate provide the best explanation and the variation in transmission required to generate these three waves is within biologically plausible values.^[70]

Another study by He et al. used a simple epidemic model, to incorporate three factors including: school opening and closing, temperature changes over the course of the outbreak, and human behavioral changes in response to the outbreak to infer the cause of the three waves of the 1918 influenza pandemic. Their modelling results showed that all three factors are important but human behavioral responses showed the largest effects.^[71]

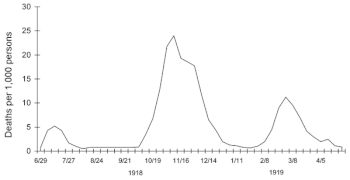
Deadly second wave

American Expeditionary Force victims of the flu pandemic at U.S. Army Camp Hospital no. 45 in Aix-les-Bains, France, in 1918

The second wave of the 1918 pandemic was much deadlier than the first. The first wave had resembled typical flu epidemics; those most at risk were the sick and elderly, while younger, healthier people recovered easily. But in August, when the second wave began in France, Sierra Leone and the United States,^[72] the virus had mutated to a much deadlier form.

This increased severity has been attributed to the circumstances of the First World War.^[73] In civilian life, natural selection favours a mild strain. Those who get very ill stay home, and those mildly ill continue with their lives, preferentially spreading the mild strain. In the trenches, natural selection was reversed. Soldiers with a mild strain stayed where they were, while the severely ill were sent on crowded trains to crowded field hospitals, spreading the deadlier virus. The second wave began and the flu quickly spread around the world again. Consequently, during modern pandemics health officials pay attention when the virus reaches places with social upheaval (looking for deadlier strains of the virus).^[74]

The fact that most of those who recovered from first-wave infections were now immune showed that it must have been the same strain of flu. This was most dramatically illustrated in Copenhagen, which escaped with a combined mortality rate of just 0.29% (0.02% in the first wave and 0.27% in the second wave) because of exposure to the less-lethal first wave.^[75] On the rest of the population it was far more deadly now; the most vulnerable people were those like the soldiers in the trenches – young previously healthy adults.^[76]

Devastated communities

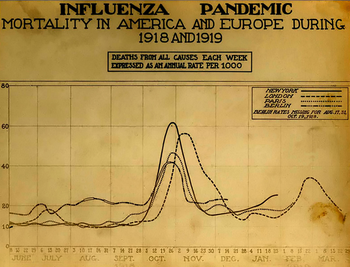
A chart of deaths in major cities, showing a peak in the autumn of 1918.

Even in areas where mortality was low, so many were incapacitated that much of everyday life was hampered. Some communities closed all stores or required customers to leave orders outside. There were reports that the health-care workers could not tend the sick nor the gravediggers bury the dead because they too were ill. Mass graves were dug by steam shovel and bodies buried without coffins in many places.^[77]

Several Pacific island territories were particularly hard-hit. The pandemic reached them from New Zealand, which was too slow to implement measures to prevent ships carrying the flu from leaving its ports. From New Zealand, the flu reached Tonga (killing 8% of the population), Nauru (16%) and Fiji (5%, 9,000 people).^[78]

Worst affected was German Samoa, today the independent state of Samoa, which had been occupied by New Zealand in 1914. A crippling 90% of the population was infected; 30% of adult men, 22% of adult women and 10% of children died. By contrast, the flu was kept away from American Samoa when Governor John Martin Poyer imposed a blockade.^[78] In New Zealand itself, 8,573 deaths were attributed to the 1918 pandemic influenza, resulting in a total population fatality rate of 0.74%.^[79] In Ireland, the Spanish Flu accounted for 10% of the total deaths in 1918 which can be seen as quite detrimental considering World War 1 was still occurring.

Less-affected areas

In Japan, 257,363 deaths were attributed to influenza by July 1919, giving an estimated 0.425% mortality rate, much lower than nearly all other Asian countries for which data are available. The Japanese government severely restricted maritime travel to and from the home islands when the pandemic struck.

In the Pacific, American Samoa^[80] and the French colony of New Caledonia^[81] also succeeded in preventing even a single death from influenza through effective quarantines. In Australia, nearly 12,000 perished.^[82]

By the end of the pandemic, the isolated island of Marajó, in Brazil's Amazon River Delta had not reported an outbreak.^[83]

Aspirin poisoning

In a 2009 paper published in the journal Clinical Infectious Diseases, Karen Starko proposed that aspirin poisoning had contributed substantially to the fatalities. She based this on the reported symptoms in those dying from the flu, as reported in the post mortem reports still available, and also the timing of the big "death spike" in October 1918 which happened right after the Surgeon General of the United States Army, and the Journal of the American Medical Association both recommended very large doses of 8.0–31.2 g of aspirin per day.^[84] Starko also suggests that the wave of aspirin poisonings was due to a "perfect storm" of events: Bayer's patent on aspirin expired, so that many companies rushed in to make a profit and greatly increased the supply; this coincided with the flu pandemic; and the symptoms of aspirin poisoning were not known at the time.^[84]

As an explanation for the universally high mortality rate, this hypothesis was questioned in a letter to the journal published in April 2010 by Andrew Noymer and Daisy Carreon of the University of California, Irvine, and Niall Johnson of the Australian Commission on Safety and Quality in Health Care. They questioned this universal applicability given the high mortality rate in countries such as India, where there was little or no access to aspirin at the time.^[85] They concluded that "the salicylate [aspirin] poisoning hypothesis [was] difficult to sustain as the primary explanation for the unusual virulence of the 1918–1919 influenza pandemic".^[85]

But they overlooked that inexpensive aspirin had become available in India and other places after October 1918, when the Bayer patent expired. In responding, Starko pointed to anecdotal evidence of aspirin over-prescription in India and argued that even if aspirin over-prescription had not contributed to the high Indian mortality rate, it could still have been a major factor for other high rates in areas where other exacerbating factors present in India played less of a role.^[86]

End of the pandemic

After the lethal second wave struck in late 1918, new cases dropped abruptly – almost to nothing after the peak in the second wave.^[11] In Philadelphia, for example, 4,597 people died in the week ending 16 October, but by 11 November, influenza had almost disappeared from the city. One explanation for the rapid decline of the lethality of the disease is that doctors simply got better at preventing and treating the pneumonia that developed after the victims had contracted the virus, although John Barry stated in his book that researchers have found no evidence to support this.^[26]

Another theory holds that the 1918 virus mutated extremely rapidly to a less lethal strain. This is a common occurrence with influenza viruses: there is a tendency for pathogenic viruses to become less lethal with time, as the hosts of more dangerous strains tend to die out^[26] (see also "Deadly Second Wave", above).

Legacy

American Red Cross nurses tend to flu patients in temporary wards set up inside Oakland Municipal Auditorium, 1918.

Academic Andrew Price-Smith has made the argument that the virus helped tip the balance of power in the later days of the war towards the Allied cause. He provides data that the viral waves hit the Central Powers before they hit the Allied powers, and that both morbidity and mortality in Germany and Austria were considerably higher than in Britain and France.^[32]

In the United States, Britain and other countries, despite the relatively high morbidity and mortality rates that resulted from the epidemic in 1918–1919, the Spanish flu began to fade from public awareness over the decades until the arrival of news about bird flu and other pandemics in the 1990s and 2000s.^[87] This has led some historians to label the Spanish flu a "forgotten pandemic".^[25]

Various theories of why the Spanish flu was "forgotten" include the rapid pace of the pandemic, which killed most of its victims in the United States, for example, within a period of less than nine months, resulting in limited media coverage. The general population was familiar with patterns of pandemic disease in the late 19th and early 20th centuries: typhoid, yellow fever, diphtheria, and cholera all occurred near the same time. These outbreaks probably lessened the significance of the influenza pandemic for the public.^[88] In some areas, the flu was not reported on, the only mention being that of advertisements for medicines claiming to cure it.^[89]

In addition, the outbreak coincided with the deaths and media focus on the First World War.^[90] Another explanation involves the age group affected by the disease. The majority of fatalities, from both the war and the epidemic, were among young adults. The deaths caused by the flu may have been overlooked due to the large numbers of deaths of young men in the war or as a result of injuries. When people read the obituaries, they saw the war or postwar deaths and the deaths from the influenza side by side. Particularly in Europe, where the war's toll was extremely high, the flu may not have had a great, separate, psychological impact, or may have seemed a mere extension of the war's tragedies.^[65]

The duration of the pandemic and the war could have also played a role. The disease would usually only affect a certain area for a month before leaving, while the war, which most had initially expected to end quickly, had lasted for four years by the time the pandemic struck. This left little time for the disease to have a significant impact on the economy.

Regarding global economic effects, many businesses in the entertainment and service industries suffered losses in revenue, while the health care industry reported profit gains.^[91]

Historian Nancy Bristow has argued that the pandemic, when combined with the increasing number of women attending college, contributed to the success of women in the field of nursing. This was due in part to the failure of medical doctors, who were predominantly men, to contain and prevent the illness. Nursing staff, who were predominantly women, felt more inclined to celebrate the success of their patient care and less inclined to identify the spread of the disease with their own work.^[92]

In Spain, sources from the period explicitly linked the Spanish flu to the cultural figure of Don Juan. The nickname for the flu, the "Naples Soldier", was adopted from Federico Romero and Guillermo Fernández Shaw's operetta, The Song of Forgetting (La canción del olvido), the protagonist of which is a stock Don Juan type. Davis has argued the Spanish flu–Don Juan connection served a cognitive function, allowing Spaniards to make sense of their epidemic experience by interpreting it through a familiar template, namely the Don Juan story.^[93]

Spanish flu research

An electron micrograph showing recreated 1918 influenza virions.

Centers for Disease Control and Prevention as Dr. Terrence Tumpey examines a reconstructed version of the 1918 flu.

The origin of the Spanish flu pandemic, and the relationship between the near-simultaneous outbreaks in humans and swine, have been controversial. One hypothesis is that the virus strain originated at Fort Riley, Kansas, in viruses in poultry and swine which the fort bred for food; the soldiers were then sent from Fort Riley around the world, where they spread the disease.^[94] Similarities between a reconstruction of the virus and avian viruses, combined with the human pandemic preceding the first reports of influenza in swine, led researchers to conclude the influenza virus jumped directly from birds to humans, and swine caught the disease from humans.^[95][96]

Others have disagreed,^[97] and more recent research has suggested the strain may have originated in a nonhuman, mammalian species.^[98] An estimated date for its appearance in mammalian hosts has been put at the period 1882–1913.^[99] This ancestor virus diverged about 1913–1915 into two clades (or biological groups), which gave rise to the classical swine and human H1N1 influenza lineages. The last common ancestor of human strains dates to between February 1917 and April 1918. Because pigs are more readily infected with avian influenza viruses than are humans, they were suggested as the original recipients of the virus, passing the virus to humans sometime between 1913 and 1918.

An effort to recreate the 1918 flu strain (a subtype of avian strain H1N1) was a collaboration among the Armed Forces Institute of Pathology, the USDA ARS Southeast Poultry Research Laboratory and Mount Sinai School of Medicine in New York City. The effort resulted in the announcement (on 5 October 2005) that the group had successfully determined the virus's genetic sequence, using historic tissue samples recovered by pathologist Johan Hultin from a female flu victim buried in the Alaskan permafrost and samples preserved from American soldiers.^[100]

On 18 January 2007, Kobasa et al. (2007) reported that monkeys (Macaca fascicularis) infected with the recreated flu strain exhibited classic symptoms of the 1918 pandemic, and died from a cytokine storm^[101]—an overreaction of the immune system. This may explain why the 1918 flu had its surprising effect on younger, healthier people, as a person with a stronger immune system would potentially have a stronger overreaction.^[102]

On 16 September 2008, the body of British politician and diplomat Sir Mark Sykes was exhumed to study the RNA of the flu virus in efforts to understand the genetic structure of modern H5N1 bird flu. Sykes had been buried in 1919 in a lead coffin which scientists hoped had helped preserve the virus.^[103] However, the coffin was found to be split because of the weight of soil over it, and the cadaver was badly decomposed. Nonetheless, samples of lung and brain tissue were taken through the split, with the coffin remaining in situ in the grave during this process.^[104]

In December 2008, research by Yoshihiro Kawaoka of the University of Wisconsin linked the presence of three specific genes (termed PA, PB1, and PB2) and a nucleoprotein derived from 1918 flu samples to the ability of the flu virus to invade the lungs and cause pneumonia. The combination triggered similar symptoms in animal testing.^[105]

In June 2010, a team at the Mount Sinai School of Medicine reported the 2009 flu pandemic vaccine provided some cross-protection against the 1918 flu pandemic strain.^[106]

One of the few things known for certain about the influenza in 1918 and for some years after was that it was, out of the laboratory, exclusively a disease of human beings.^[107]

In 2013, the AIR Worldwide Research and Modeling Group "characterized the historic 1918 pandemic and estimated the effects of a similar pandemic occurring today using the AIR Pandemic Flu Model". In the model, "a modern day "Spanish flu" event would result in additional life insurance losses of between USD 15.3–27.8 billion in the United States alone" with 188,000–337,000 deaths in the United States.^[108]

In popular culture

The 1995 film Outbreak,^[109] the 2011 film Contagion and the 2013 film World War Z make reference to the pandemic.^[110]

The television show Resurrection uses the pandemic, in the episode "Afflictions" that aired on November 2, 2014, as the explanation for why many of the Returned were getting sick and disappearing.

In season four of British drama Upstairs, Downstairs, Hazel Bellamy dies of Spanish flu in 1918, after her husband James Bellamy survives injuries in the "Great War" (World War I). Her funeral takes place on 11 November, the day the war ends.

In season two of British drama Downton Abbey, Lavinia Swire dies of the Spanish flu in April 1919, after her fiancé Matthew Crawley recovers from injuries and temporary paralysis from the Great War.

Twentieth-century fiction includes at least three novels with the flu pandemic as a major theme: Katherine Anne Porter's Pale Horse, Pale Rider, Thomas Mullen's The Last Town on Earth, and Thomas Wolfe's Look Homeward, Angel.

In the one-act play 1918 by Horton Foote (part of his Orphans' Home Cycle (1979)), the presence and threat of the flu (and the tragedy it ultimately causes) is a major element of the plot. The play was made into a film of the same title, released in 1985, which was subsequently edited for broadcast by PBS as the last part of the miniseries "The Story of A Marriage".

Maxwell–Boltzmann distribution

From Wikipedia, the free encyclopedia

Maxwell–Boltzmann

Probability density function
Cumulative distribution function
Parameters	${\displaystyle a>0}$
Support	${\displaystyle x\in (0;\infty )}$
PDF	${\displaystyle {\sqrt {\frac {2}{\pi }}}{\frac {x^{2}e^{-x^{2}/\left(2a^{2}\right)}}{a^{3}}}}$
CDF	${\displaystyle \operatorname {erf} \left({\frac {x}{{\sqrt {2}}a}}\right)-{\sqrt {\frac {2}{\pi }}}{\frac {xe^{-x^{2}/\left(2a^{2}\right)}}{a}}}$ where erf is the error function
Mean	${\displaystyle \mu =2a{\sqrt {\frac {2}{\pi }}}}$
Mode	${\displaystyle {\sqrt {2}}a}$
Variance	${\displaystyle \sigma ^{2}={\frac {a^{2}(3\pi -8)}{\pi }}}$
Skewness	${\displaystyle \gamma _{1}={\frac {2{\sqrt {2}}(16-5\pi )}{(3\pi -8)^{3/2}}}}$
Ex. kurtosis	${\displaystyle \gamma _{2}=4{\frac {\left(-96+40\pi -3\pi ^{2}\right)}{(3\pi -8)^{2}}}}$
Entropy	${\displaystyle \ln \left(a{\sqrt {2\pi }}\right)+\gamma -{\frac {1}{2}}}$

In statistics the Maxwell–Boltzmann distribution is a particular probability distribution named after James Clerk Maxwell and Ludwig Boltzmann. It was first defined and used in physics (in particular in statistical mechanics) for describing particle speeds in idealized gases where the particles move freely inside a stationary container without interacting with one another, except for very brief collisions in which they exchange energy and momentum with each other or with their thermal environment. Particle in this context refers to gaseous particles (atoms or molecules), and the system of particles is assumed to have reached thermodynamic equilibrium.^[1] While the distribution was first derived by Maxwell in 1860 on heuristic grounds,^[2] Boltzmann later carried out significant investigations into the physical origins of this distribution.

A particle speed probability distribution indicates which speeds are more likely: a particle will have a speed selected randomly from the distribution, and is more likely to be within one range of speeds than another. The distribution depends on the temperature of the system and the mass of the particle.^[3] The Maxwell–Boltzmann distribution applies to the classical ideal gas, which is an idealization of real gases. In real gases, there are various effects (e.g., van der Waals interactions, vortical flow, relativistic speed limits, and quantum exchange interactions) that can make their speed distribution different from the Maxwell–Boltzmann form. However, rarefied gases at ordinary temperatures behave very nearly like an ideal gas and the Maxwell speed distribution is an excellent approximation for such gases. Thus, it forms the basis of the Kinetic theory of gases, which provides a simplified explanation of many fundamental gaseous properties, including pressure and diffusion.^[4]

Distribution function

The speed probability density functions of the speeds of a few noble gases at a temperature of 298.15 K (25 °C). The y-axis is in s/m so that the area under any section of the curve (which represents the probability of the speed being in that range) is dimensionless.

The Maxwell–Boltzmann distribution is the function^[5]

${\displaystyle f(v)={\sqrt {\left({\frac {m}{2\pi kT}}\right)^{3}}}\,4\pi v^{2}e^{-{\frac {mv^{2}}{2kT}}},}$

where ${\displaystyle m}$ is the particle mass and ${\displaystyle kT}$ is the product of Boltzmann's constant and thermodynamic temperature. An interesting point to be noted is that the Maxwell-Boltzmann distribution will not vary with the value of m/T i.e the ratio of mass of the molecule to its absolute temperature; mathematically (Derivative of f(v)/derivative of (m/T))=0. This probability density function gives the probability, per unit speed, of finding the particle with a speed near ${\displaystyle v}$. This equation is simply the Maxwell distribution (given in the infobox) with distribution parameter ${\displaystyle a={\sqrt {kT/m}}}$. In probability theory the Maxwell–Boltzmann distribution is a chi distribution with three degrees of freedom and scale parameter ${\displaystyle a={\sqrt {kT/m}}}$.

The simplest ordinary differential equation satisfied by the distribution is:

${\displaystyle kTvf'(v)+f(v)(mv^{2}-2kT)=0,}$

${\displaystyle f(1)={\sqrt {\frac {2}{\pi }}}e^{-{\frac {m}{2kT}}}\left({\frac {m}{kT}}\right)^{3/2}}$

or in unitless presentation:

${\displaystyle a^{2}xf'(x)+\left(x^{2}-2a^{2}\right)f(x)=0,}$

${\displaystyle f(1)={\frac {{\sqrt {\frac {2}{\pi }}}e^{-{\frac {1}{2a^{2}}}}}{a^{3}}}.}$

Note that a distribution (function) is not the same as the probability. The distribution (function) stands for an average number, as in all three kinds of statistics (Maxwell–Boltzmann, Bose–Einstein, Fermi–Dirac). With the Darwin–Fowler method of mean values the Maxwell–Boltzmann distribution is obtained as an exact result.

Typical speeds

The mean speed, most probable speed (mode), and root-mean-square can be obtained from properties of the Maxwell distribution.

• The most probable speed, v_p, is the speed most likely to be possessed by any molecule (of the same mass m) in the system and corresponds to the maximum value or mode of f(v). To find it, we calculate the derivative df/dv, set it to zero and solve for v:

  ${\displaystyle {\frac {df(v)}{dv}}=0}$

  which yields:
  

  ${\displaystyle v_{p}={\sqrt {\frac {2kT}{m}}}={\sqrt {\frac {2RT}{M}}}}$

  where R is the gas constant and M = N_A m is the molar mass of the substance.
  For diatomic nitrogen (N₂, the primary component of air) at room temperature (300 K), this gives ${\displaystyle v_{p}=422}$ m/s
• The mean speed is the expected value of the speed distribution

  ${\displaystyle \langle v\rangle =\int _{0}^{\infty }v\,f(v)\,dv={\sqrt {\frac {8kT}{\pi m}}}={\sqrt {\frac {8RT}{\pi M}}}={\frac {2}{\sqrt {\pi }}}v_{p}}$

• The root mean square speed is the second-order moment of speed:

  ${\displaystyle {\sqrt {\langle v^{2}\rangle }}=\left(\int _{0}^{\infty }v^{2}\,f(v)\,dv\right)^{1/2}={\sqrt {\frac {3kT}{m}}}={\sqrt {\frac {3RT}{M}}}={\sqrt {\frac {3}{2}}}v_{p}}$

The typical speeds are related as follows:

${\displaystyle 0.886\langle v\rangle =v_{p}<\langle v\rangle <{\sqrt {\langle v^{2}\rangle }}=1.085\langle v\rangle .}$

Derivation and related distributions

The original derivation in 1860 by James Clerk Maxwell was an argument based on molecular collisions of the Kinetic theory of gases as well as certain symmetries in the speed distribution function; Maxwell also gave an early argument that these molecular collisions entail a tendency towards equilibrium.^[2][6] After Maxwell, Ludwig Boltzmann in 1872^[7] also derived the distribution on mechanical grounds and argued that gases should over time tend toward this distribution, due to collisions (see H-theorem). He later (1877)^[8] derived the distribution again under the framework of statistical thermodynamics. The derivations in this section are along the lines of Boltzmann's 1877 derivation, starting with result known as Maxwell–Boltzmann statistics (from statistical thermodynamics). Maxwell–Boltzmann statistics gives the average number of particles found in a given single-particle microstate, under certain assumptions:^[1][9]

${\displaystyle {\frac {N_{i}}{N}}={\frac {\exp(-E_{i}/kT)}{\sum _{j}\exp(-E_{j}/kT)}}}$

(1)

where:

• i and j are indices (or labels) of the single-particle micro states,
• N_i is the average number of particles in the single-particle microstate i,
• N is the total number of particles in the system,
• E_i is the energy of microstate i,
• T is the equilibrium temperature of the system,
• k is the Boltzmann constant.

The assumptions of this equation are that the particles do not interact, and that they are classical; this means that each particle's state can be considered independently from the other particles' states. Additionally, the particles are assumed to be in thermal equilibrium. The denominator in Equation (1) is simply a normalizing factor so that the N_i/N add up to 1 — in other words it is a kind of partition function (for the single-particle system, not the usual partition function of the entire system).

Because velocity and speed are related to energy, Equation (1) can be used to derive relationships between temperature and the speeds of gas particles. All that is needed is to discover the density of microstates in energy, which is determined by dividing up momentum space into equal sized regions.

Distribution for the momentum vector

The potential energy is taken to be zero, so that all energy is in the form of kinetic energy. The relationship between kinetic energy and momentum for massive non-relativistic particles is

${\displaystyle E={\frac {p^{2}}{2m}}}$

(2)

where p² is the square of the momentum vector p = [p_x, p_y, p_z]. We may therefore rewrite Equation (1) as:

${\displaystyle {\frac {N_{i}}{N}}={\frac {1}{Z}}\exp \left[-{\frac {p_{i,x}^{2}+p_{i,y}^{2}+p_{i,z}^{2}}{2mkT}}\right]}$

(3)

where Z is the partition function, corresponding to the denominator in Equation (1). Here m is the molecular mass of the gas, T is the thermodynamic temperature and k is the Boltzmann constant. This distribution of N_i/N is proportional to the probability density function f_p for finding a molecule with these values of momentum components, so:

${\displaystyle f_{\mathbf {p} }(p_{x},p_{y},p_{z})={\frac {c}{Z}}\exp \left[-{\frac {p_{x}^{2}+p_{y}^{2}+p_{z}^{2}}{2mkT}}\right]}$

(4)

The normalizing constant c, can be determined by recognizing that the probability of a molecule having some momentum must be 1. Therefore the integral of equation (4) over all p_x, p_y, and p_z must be 1.

It can be shown that:

${\displaystyle c={\frac {Z}{(2\pi mkT)^{3/2}}}}$

(5)

Substituting Equation (5) into Equation (4) gives:

${\displaystyle f_{\mathbf {p} }(p_{x},p_{y},p_{z})=\left(2\pi mkT\right)^{-3/2}\exp \left[-{\frac {p_{x}^{2}+p_{y}^{2}+p_{z}^{2}}{2mkT}}\right]}$   (6)

The distribution is seen to be the product of three independent normally distributed variables ${\displaystyle p_{x}}$, ${\displaystyle p_{y}}$, and ${\displaystyle p_{z}}$, with variance ${\displaystyle mkT}$. Additionally, it can be seen that the magnitude of momentum will be distributed as a Maxwell–Boltzmann distribution, with ${\displaystyle a={\sqrt {mkT}}}$. The Maxwell–Boltzmann distribution for the momentum (or equally for the velocities) can be obtained more fundamentally using the H-theorem at equilibrium within the Kinetic theory of gases framework.

Distribution for the energy

The energy distribution is found imposing

${\displaystyle f_{E}(E)dE=f_{p}({\textbf {p}})d^{3}{\textbf {p}},}$

(7)

where ${\displaystyle d^{3}{\textbf {p}}}$ is the infinitesimal phase-space volume of momenta corresponding to the energy interval ${\displaystyle dE}$. Making use of the spherical symmetry of the energy-momentum dispersion relation ${\displaystyle E=|{\textbf {p}}|^{2}/2m}$, this can be expressed in terms of ${\displaystyle dE}$ as

${\displaystyle d^{3}{\textbf {p}}=4\pi |{\textbf {p}}|^{2}d|{\textbf {p}}|=4\pi m{\sqrt {2mE}}dE.}$

(8)

Using then (8) in (7), and expressing everything in terms of the energy ${\displaystyle E}$, we get

${\displaystyle f_{E}(E)dE={\frac {1}{(2\pi mkT)^{3/2}}}e^{-E/kT}4\pi m{\sqrt {2mE}}dE=2{\sqrt {\frac {E}{\pi }}}\left({\frac {1}{kT}}\right)^{3/2}\exp \left({\frac {-E}{kT}}\right)dE}$

and finally

${\displaystyle f_{E}(E)=2{\sqrt {\frac {E}{\pi }}}\left({\frac {1}{kT}}\right)^{3/2}\exp \left({\frac {-E}{kT}}\right)}$   (9)

Since the energy is proportional to the sum of the squares of the three normally distributed momentum components, this distribution is a gamma distribution; in particular, it is a chi-squared distribution with three degrees of freedom.

By the equipartition theorem, this energy is evenly distributed among all three degrees of freedom, so that the energy per degree of freedom is distributed as a chi-squared distribution with one degree of freedom:^[10]

${\displaystyle f_{\epsilon }(\epsilon )\,d\epsilon ={\sqrt {\frac {1}{\pi \epsilon kT}}}~\exp \left[{\frac {-\epsilon }{kT}}\right]\,d\epsilon }$

where ${\displaystyle \epsilon }$ is the energy per degree of freedom. At equilibrium, this distribution will hold true for any number of degrees of freedom. For example, if the particles are rigid mass dipoles of fixed dipole moment, they will have three translational degrees of freedom and two additional rotational degrees of freedom. The energy in each degree of freedom will be described according to the above chi-squared distribution with one degree of freedom, and the total energy will be distributed according to a chi-squared distribution with five degrees of freedom. This has implications in the theory of the specific heat of a gas.

The Maxwell–Boltzmann distribution can also be obtained by considering the gas to be a type of quantum gas for which the approximation ε >> k T may be made.

Distribution for the velocity vector

Recognizing that the velocity probability density f_v is proportional to the momentum probability density function by

${\displaystyle f_{\mathbf {v} }d^{3}v=f_{\mathbf {p} }\left({\frac {dp}{dv}}\right)^{3}d^{3}v}$

and using p = mv we get

${\displaystyle f_{\mathbf {v} }(v_{x},v_{y},v_{z})=\left({\frac {m}{2\pi kT}}\right)^{3/2}\exp \left[-{\frac {m(v_{x}^{2}+v_{y}^{2}+v_{z}^{2})}{2kT}}\right]}$

which is the Maxwell–Boltzmann velocity distribution. The probability of finding a particle with velocity in the infinitesimal element [dv_x, dv_y, dv_z] about velocity v = [v_x, v_y, v_z] is

${\displaystyle f_{\mathbf {v} }\left(v_{x},v_{y},v_{z}\right)\,dv_{x}\,dv_{y}\,dv_{z}.}$

Like the momentum, this distribution is seen to be the product of three independent normally distributed variables ${\displaystyle v_{x}}$, ${\displaystyle v_{y}}$, and ${\displaystyle v_{z}}$, but with variance ${\displaystyle {\frac {kT}{m}}}$. It can also be seen that the Maxwell–Boltzmann velocity distribution for the vector velocity [v_x, v_y, v_z] is the product of the distributions for each of the three directions:

${\displaystyle f_{v}\left(v_{x},v_{y},v_{z}\right)=f_{v}(v_{x})f_{v}(v_{y})f_{v}(v_{z})}$

where the distribution for a single direction is

${\displaystyle f_{v}(v_{i})={\sqrt {\frac {m}{2\pi kT}}}\exp \left[{\frac {-mv_{i}^{2}}{2kT}}\right].}$

Each component of the velocity vector has a normal distribution with mean ${\displaystyle \mu _{v_{x}}=\mu _{v_{y}}=\mu _{v_{z}}=0}$ and standard deviation ${\displaystyle \sigma _{v_{x}}=\sigma _{v_{y}}=\sigma _{v_{z}}={\sqrt {\frac {kT}{m}}}}$, so the vector has a 3-dimensional normal distribution, a particular kind of multivariate normal distribution, with mean ${\displaystyle \mu _{\mathbf {v} }={\mathbf {0} }}$ and standard deviation ${\displaystyle \sigma _{\mathbf {v} }={\sqrt {\frac {3kT}{m}}}}$.

The Maxwell–Boltzmann distribution for the speed follows immediately from the distribution of the velocity vector, above. Note that the speed is

${\displaystyle v={\sqrt {v_{x}^{2}+v_{y}^{2}+v_{z}^{2}}}}$

and the volume element in spherical coordinates

${\displaystyle dv_{x}\,dv_{y}\,dv_{z}=v^{2}\sin \theta \,dv\,d\theta \,d\phi }$

where ${\displaystyle \phi }$ and ${\displaystyle \theta }$ are the "course" (azimuth of the velocity vector) and "path angle" (elevation angle of the velocity vector). Integration of the normal probability density function of the velocity, above, over the course (from 0 to ${\displaystyle 2\pi }$) and path angle (from 0 to ${\displaystyle \pi }$), with substitution of the speed for the sum of the squares of the vector components, yields the speed distribution.