Electromagnetic absorption by water

From Wikipedia, the free encyclopedia

 

Absorption spectrum (attenuation coefficient vs. wavelength) of liquid water (red),^[1][2][3] atmospheric water vapor (green)^{[4][5][6][4][7]} and ice (blue line)^[8][9][10] between 667 nm and 200 μm.^[11] The plot for vapor is a transformation of data Synthetic spectrum for gas mixture 'Pure H₂O' (296K, 1 atm) retrieved from Hitran on the Web Information System.^[6]

Liquid water absorption spectrum across a wide wavelength range.

The absorption of electromagnetic radiation by water depends on the state of the water.

The absorption in the gas phase occurs in three regions of the spectrum. Rotational transitions are responsible for absorption in the microwave and far-infrared, vibrational transitions in the mid-infrared and near-infrared. Vibrational bands have rotational fine structure. Electronic transitions occur in the vacuum ultraviolet regions.

Liquid water has no rotational spectrum but does absorb in the microwave region.

Overview

The water molecule, in the gaseous state, has three types of transition that can give rise to absorption of electromagnetic radiation

• Rotational transitions, in which the molecule gains a quantum of rotational energy. Atmospheric water vapour at ambient temperature and pressure gives rise to absorption in the far-infrared region of the spectrum, from about 200 cm⁻¹ (50 μm) to longer wavelengths towards the microwave region.
• Vibrational transitions in which a molecule gains a quantum of vibrational energy. The fundamental transitions give rise to absorption in the mid-infrared in the regions around 1650 cm⁻¹ (μ band, 6 μm) and 3500 cm⁻¹ (so-called X band, 2.9 μm)
• Electronic transitions in which a molecule is promoted to an excited electronic state. The lowest energy transition of this type is in the vacuum ultraviolet region.

In reality, vibrations of molecules in the gaseous state are accompanied by rotational transitions, giving rise to a vibration-rotation spectrum. Furthermore, vibrational overtones and combination bands occur in the near-infrared region. The HITRAN spectroscopy database lists more than 37,000 spectral lines for gaseous H₂¹⁶O, ranging from the microwave region to the visible spectrum.^[5][12]

In liquid water the rotational transitions are effectively quenched, but absorption bands are affected by hydrogen bonding. In crystalline ice the vibrational spectrum is also affected by hydrogen bonding and there are lattice vibrations causing absorption in the far-infrared. Electronic transitions of gaseous molecules will show both vibrational and rotational fine structure.

Units

Infrared absorption band positions may be given either in wavelength (usually in micrometers, μm) or wavenumber (usually in reciprocal centimeters, cm⁻¹) scale.

Rotational spectrum

Rotating water molecule

The water molecule is an asymmetric top, that is, it has three independent moments of inertia. Consequently, the rotational spectrum has no obvious structure. A large number of transitions can be observed; lines due to atmospheric water vapor can easily be observed from about 50 μm (200 cm⁻¹) to longer wavelengths. Measurements of microwave spectra have provided a very precise value for the O−H bond length, 95.84 ± 0.05 pm and H−O−H bond angle, 104.5 ± 0.3°.^[13]

Part of the pure rotation (microwave) spectrum of water vapour between 1000 GHz (33 cm⁻¹, 300 μm) and 3000 GHz (100 cm⁻¹, 100 μm)

Vibrational spectrum

The three fundamental vibrations of the water molecule

ν₁,O-H symmetric stretching
3657 cm⁻¹ (2.734 μm)

ν₂, H-O-H bending
1595 cm⁻¹ (6.269 μm)

ν₃, O-H asymmetric stretching
3756 cm⁻¹ (2.662 μm)

The water molecule has three fundamental molecular vibrations. The O-H stretching vibrations give rise to absorption bands with band origins at 3657 cm⁻¹ (ν₁, 2.734 μm) and 3756 cm⁻¹ (ν₃, 2.662 μm) in the gas phase. The asymmetric stretching vibration, of B₂ symmetry in the point group C_2v is a normal vibration. The H-O-H bending mode origin is at 1595 cm⁻¹ (ν₂, 6.269 μm). Both symmetric stretching and bending vibrations have A₁ symmetry, but the frequency difference between them is so large that mixing is effectively zero. In the gas phase all three bands show extensive rotational fine structure.^[14] ν₃ has a series of overtones at wavenumbers somewhat less than n ν₃, n=2,3,4,5... Combination bands, such as ν₂ + ν₃ are also easily observed in the near infrared region.^[15][16] The presence of water vapor in the atmosphere is important for atmospheric chemistry especially as the infrared and near infrared spectra are easy to observe. Standard (atmospheric optical) codes are assigned to absorption bands as follows. 0.718 μm (visible): α, 0.810 μm: μ, 0.935 μm: ρστ, 1.13 μm: φ, 1.38 μm: ψ, 1.88 μm: Ω, 2.68 μm: X. The gaps between the bands define the infrared window in the Earth's atmosphere.^[17]

The infrared spectrum of liquid water is dominated by the intense absorption due to the fundamental O-H stretching vibrations. Because of the high intensity, very short path lengths, usually less than 50 μm, are needed to record the spectra of aqueous solutions. There is no rotational fine structure, but the absorption band are broader than might be expected, because of hydrogen bonding.^[18] Peak maxima for liquid water are observed at 3450 cm⁻¹ (2.898 μm), 3615 cm⁻¹ (2.766 μm) and 1640 cm ⁻¹ (6.097 μm).^[14] Direct measurement of the infrared spectra of aqueous solutions requires that the cuvette windows be made of substances such as calcium fluoride which are water-insoluble. This difficulty can be overcome by using an attenuated total reflectance (ATR) device.

In the near-infrared range liquid water has absorption bands around 1950 nm (5128 cm⁻¹), 1450 nm (6896 cm⁻¹), 1200 nm (8333 cm⁻¹) and 970 nm, (10300 cm⁻¹).^[19][20][15] The regions between these bands can be used in near-infrared spectroscopy to measure the spectra of aqueous solutions, with the advantage that glass is transparent in this region, so glass cuvettes can be used. The absorption intensity is weaker than for the fundamental vibrations, but this is not important as longer path-length cuvettes are used. The absorption band at 698 nm (14300 cm⁻¹) is a 3rd overtone (n=4). It tails off onto the visible region and is responsible for the intrinsic blue color of water. This can be observed with a standard UV/vis spectrophotometer, using a 10 cm path-length. The colour can be seen by eye by looking through a column of water about 10m in length; the water must be passed through an ultrafilter to eliminate color due to Rayleigh scattering which also can make water appear blue.^[16][21][22] In both liquid water and ice cluster vibrations occur, which involve the stretching (TS) or bending (TB) of intermolecular hydrogen bonds (O–H . . . O). Bands at wavelengths λ = 50-55 μm (44 μm in ice) have been attributed to TS, intermolecular stretch, and 200 μm (166 μm in ice), to TB, intermolecular bend^[11]

The spectrum of ice is similar to that of liquid water, with peak maxima at 3400 cm⁻¹ (2.941 μm), 3220 cm⁻¹ (3.105 μm) and 1620 cm⁻¹ (6.17 μm)^[14]

Visible region

Predicted wavelengths of overtones and combination bands of liquid water in the visible region^[16]

ν1, ν3	ν2	wavelength /nm
4	0	742
4	1	662
5	0	605
5	1	550
6	0	514
6	1	474
7	0	449
7	1	418
8	0	401
8	1	376

Absorption coefficients for 200 nm and 900 nm are almost equal at 6.9 m⁻¹ (attenuation length of 14.5 cm). Very weak light absorption, in the visible region, by liquid water has been measured using an integrating cavity absorption meter (ICAM).^[16] The absorption was attributed to a sequence of overtone and combination bands whose intensity decreases at each step, giving rise to an absolute minimum at 418 nm, at which wavelength the attenuation coefficient is about 0.0044 m⁻¹, which is an attenuation length of about 227 meters. These values correspond to pure absorption without scattering effects. The attenuation of, e.g., a laser beam would be slightly stronger.

Visible light absorption spectrum of pure water (absorption coefficient vs. wavelength).^[16][21][22]

Electronic spectrum

The electronic transitions of the water molecule lie in the vacuum ultraviolet region. For water vapor the bands have been assigned as follows.^[11]

• 65 nm band - many different electronic transitions, photo-ionization, photodissociation
• discrete features between 115 and 180 nm
  • set of narrow bands between 115 and 125 nm
    Rydberg series: 1b₁ (n₂) → many different Rydberg states and 3a₁ (n₁) → 3sa₁ Rydberg state
  • 128 nm band
    Rydberg series: 3a₁ (n₁) → 3sa₁ Rydberg state and 1b₁ (n₂) → 3sa₁ Rydberg state
  • 166.5 nm band
    1b₁ (n₂) → 4a₁ (σ₁*-like orbital)

At least some of these transitions result in photodissociation of water into H+OH. Among them the best known is that at 166.5 nm.

Microwaves and radio waves

Dielectric permittivity and dielectric loss of water between 0°C and 100°C, the arrows showing the effect of increasing temperature.^[23]

The pure rotation spectrum of water vapor extends into the microwave region.

Liquid water has a broad absorption spectrum in the microwave region, which has been explained in terms of changes in the hydrogen bond network giving rise to a broad, featureless, microwave spectrum.^[24] The absorption (equivalent to dielectric loss) is used in microwave ovens to heat food that contains water molecules. A frequency of 2.45 GHz, wavelength 122 mm, is commonly used.

Radiocommunication at GHz frequencies is very difficult in fresh waters and even more so in salt waters.^[11]

Atmospheric effects

Synthetic stick absorption spectrum of a simple gas mixture corresponding to the Earth's atmosphere composition based on HITRAN data^[5] created using Hitran on the Web system.^[6] Green color - water vapor, WN – wavenumber (caution: lower wavelengths on the right, higher on the left). Water vapor concentration for this gas mixture is 0.4%

Water vapor is a greenhouse gas in the Earth's atmosphere, responsible for 70% of the known absorption of incoming sunlight, particularly in the infrared region, and about 60% of the atmospheric absorption of thermal radiation by the Earth known as the greenhouse effect.^[25] It is also an important factor in multispectral imaging and hyperspectral imaging used in remote sensing^[12] because water vapor absorbs radiation differently in different spectral bands. Its effects are also an important consideration in infrared astronomy and radio astronomy in the microwave or millimeter wave bands. The South Pole Telescope was constructed in Antarctica in part because the elevation and low temperatures there mean there is very little water vapor in the atmosphere.^[26]

Similarly, carbon dioxide absorption bands occur around 1400, 1600 and 2000 nm,^[27] but its presence in the Earth's atmosphere accounts for just 26% of the greenhouse effect.^[25] Carbon dioxide gas absorbs energy in some small segments of the thermal infrared spectrum that water vapor misses. This extra absorption within the atmosphere causes the air to warm just a bit more and the warmer the atmosphere the greater its capacity to hold more water vapor. This extra water vapor absorption further enhances the Earth’s greenhouse effect.^[28]

In the atmospheric window between approximately 8000 and 14000 nm, in the far-infrared spectrum, carbon dioxide and water absorption is weak.^[29] This window allows most of the thermal radiation in this band to be radiated out to space directly from the Earth's surface. This band is also used for remote sensing of the Earth from space, for example with thermal Infrared imaging.

As well as absorbing radiation, water vapour occasionally emits radiation in all directions, according to the Black Body Emission curve for its current temperature overlaid on the water absorption spectrum. Much of this energy will be recaptured by other water molecules, but at higher altitudes, radiation sent towards space is less likely to be recaptured, as there is less water available to recapture radiation of water-specific absorbing wavelengths. By the top of the troposphere, about 12 km above sea level, most water vapor condenses to liquid water or ice as it releases its heat of vapourisation. Once changed state, liquid water and ice fall away to lower altitudes. This will be balanced by incoming water vapour rising via convection currents.

Liquid water and ice emit radiation at a higher rate than water vapour (see graph above). Water at the top of the troposphere, particularly in liquid and solid states, cools as it emits net photons to space. Neighboring gas molecules other than water (e.g. Nitrogen) are cooled by passing their heat kinetically to the water. This is why temperatures at the top of the troposphere (known as the tropopause) are about -50 degrees Celsius

Black body

From Wikipedia, the free encyclopedia

As the temperature of a black body decreases, its intensity also decreases and its peak moves to longer wavelengths. Shown for comparison is the classical Rayleigh–Jeans law and its ultraviolet catastrophe.

A black body is an idealized physical body that absorbs all incident electromagnetic radiation, regardless of frequency or angle of incidence. A white body is one with a "rough surface [that] reflects all incident rays completely and uniformly in all directions."^[1]

A black body in thermal equilibrium (that is, at a constant temperature) emits electromagnetic radiation called black-body radiation. The radiation is emitted according to Planck's law, meaning that it has a spectrum that is determined by the temperature alone (see figure at right), not by the body's shape or composition.

A black body in thermal equilibrium has two notable properties:^[2]

1. It is an ideal emitter: at every frequency, it emits as much energy as – or more energy than – any other body at the same temperature.
2. It is a diffuse emitter: the energy is radiated isotropically, independent of direction.

An approximate realization of a black surface is a hole in the wall of a large enclosure. Any light entering the hole is reflected indefinitely or absorbed inside and is unlikely to re-emerge, making the hole a nearly perfect absorber. The radiation confined in such an enclosure may or may not be in thermal equilibrium, depending upon the nature of the walls and the other contents of the enclosure.^[3][4]

Real materials emit energy at a fraction—called the emissivity—of black-body energy levels. By definition, a black body in thermal equilibrium has an emissivity of ε = 1.0. A source with lower emissivity independent of frequency often is referred to as a gray body.^[5][6] Construction of black bodies with emissivity as close to one as possible remains a topic of current interest.^[7]

In astronomy, the radiation from stars and planets is sometimes characterized in terms of an effective temperature, the temperature of a black body that would emit the same total flux of electromagnetic energy.

Definition

The idea of a black body originally was introduced by Gustav Kirchhoff in 1860 as follows:

...the supposition that bodies can be imagined which, for infinitely small thicknesses, completely absorb all incident rays, and neither reflect nor transmit any. I shall call such bodies perfectly black, or, more briefly, black bodies.^[8]

A more modern definition drops the reference to "infinitely small thicknesses":^[9]

An ideal body is now defined, called a blackbody. A blackbody allows all incident radiation to pass into it (no reflected energy) and internally absorbs all the incident radiation (no energy transmitted through the body). This is true for radiation of all wavelengths and for all angles of incidence. Hence the blackbody is a perfect absorber for all incident radiation.^[10]

Idealizations

This section describes some concepts developed in connection with black bodies.

An approximate realization of a black body as a tiny hole in an insulated enclosure

Cavity with a hole

A widely used model of a black surface is a small hole in a cavity with walls that are opaque to radiation.^[10] Radiation incident on the hole will pass into the cavity, and is very unlikely to be re-emitted if the cavity is large. The hole is not quite a perfect black surface — in particular, if the wavelength of the incident radiation is longer than the diameter of the hole, part will be reflected. Similarly, even in perfect thermal equilibrium, the radiation inside a finite-sized cavity will not have an ideal Planck spectrum for wavelengths comparable to or larger than the size of the cavity.^[11]

Suppose the cavity is held at a fixed temperature T and the radiation trapped inside the enclosure is at thermal equilibrium with the enclosure. The hole in the enclosure will allow some radiation to escape. If the hole is small, radiation passing in and out of the hole has negligible effect upon the equilibrium of the radiation inside the cavity. This escaping radiation will approximate black-body radiation that exhibits a distribution in energy characteristic of the temperature T and does not depend upon the properties of the cavity or the hole, at least for wavelengths smaller than the size of the hole.^[11] See the figure in the Introduction for the spectrum as a function of the frequency of the radiation, which is related to the energy of the radiation by the equation E=hf, with E = energy, h = Planck's constant, f = frequency.

At any given time the radiation in the cavity may not be in thermal equilibrium, but the second law of thermodynamics states that if left undisturbed it will eventually reach equilibrium,^[12] although the time it takes to do so may be very long.^[13] Typically, equilibrium is reached by continual absorption and emission of radiation by material in the cavity or its walls.^{[3][4][14][15]} Radiation entering the cavity will be "thermalized"; by this mechanism: the energy will be redistributed until the ensemble of photons achieves a Planck distribution. The time taken for thermalization is much faster with condensed matter present than with rarefied matter such as a dilute gas. At temperatures below billions of Kelvin, direct photon–photon interactions^[16] are usually negligible compared to interactions with matter.^[17] Photons are an example of an interacting boson gas,^[18] and as described by the H-theorem,^[19] under very general conditions any interacting boson gas will approach thermal equilibrium.

Transmission, absorption, and reflection

A body's behavior with regard to thermal radiation is characterized by its transmission τ, absorption α, and reflection ρ.

The boundary of a body forms an interface with its surroundings, and this interface may be rough or smooth. A nonreflecting interface separating regions with different refractive indices must be rough, because the laws of reflection and refraction governed by the Fresnel equations for a smooth interface require a reflected ray when the refractive indices of the material and its surroundings differ.^[20] A few idealized types of behavior are given particular names:

An opaque body is one that transmits none of the radiation that reaches it, although some may be reflected.^[21][22] That is, τ=0 and α+ρ=1

A transparent body is one that transmits all the radiation that reaches it. That is, τ=1 and α=ρ=0.
A gray body is one where α, ρ and τ are uniform for all wavelengths. This term also is used to mean a body for which α is temperature and wavelength independent.

A white body is one for which all incident radiation is reflected uniformly in all directions: τ=0, α=0, and ρ=1.

For a black body, τ=0, α=1, and ρ=0. Planck offers a theoretical model for perfectly black bodies, which he noted do not exist in nature: besides their opaque interior, they have interfaces that are perfectly transmitting and non-reflective.^[23]

Kirchhoff's perfect black bodies

Kirchhoff in 1860 introduced the theoretical concept of a perfect black body with a completely absorbing surface layer of infinitely small thickness, but Planck noted some severe restrictions upon this idea. Planck noted three requirements upon a black body: the body must (i) allow radiation to enter but not reflect; (ii) possess a minimum thickness adequate to absorb the incident radiation and prevent its re-emission; (iii) satisfy severe limitations upon scattering to prevent radiation from entering and bouncing back out. As a consequence, Kirchhoff's perfect black bodies that absorb all the radiation that falls on them cannot be realized in an infinitely thin surface layer, and impose conditions upon scattering of the light within the black body that are difficult to satisfy.^[24][25]

Realizations

A realization of a black body is a real world, physical embodiment. Here are a few.

Cavity with a hole

In 1898, Otto Lummer and Ferdinand Kurlbaum published an account of their cavity radiation source.^[26] Their design has been used largely unchanged for radiation measurements to the present day. It was a hole in the wall of a platinum box, divided by diaphragms, with its interior blackened with iron oxide. It was an important ingredient for the progressively improved measurements that led to the discovery of Planck's law.^[27][28] A version described in 1901 had its interior blackened with a mixture of chromium, nickel, and cobalt oxides.^[29] See also Hohlraum.

Near-black materials

There is interest in blackbody-like materials for camouflage and radar-absorbent materials for radar invisibility.^[30][31] They also have application as solar energy collectors, and infrared thermal detectors. As a perfect emitter of radiation, a hot material with black body behavior would create an efficient infrared heater, particularly in space or in a vacuum where convective heating is unavailable.^[32] They are also useful in telescopes and cameras as anti-reflection surfaces to reduce stray light, and to gather information about objects in high-contrast areas (for example, observation of planets in orbit around their stars), where blackbody-like materials absorb light that comes from the wrong sources.

It has long been known that a lamp-black coating will make a body nearly black. An improvement on lamp-black is found in manufactured carbon nanotubes. Nano-porous materials can achieve refractive indices nearly that of vacuum, in one case obtaining average reflectance of 0.045%.^[7][33] In 2009, a team of Japanese scientists created a material called nanoblack which is close to an ideal black body, based on vertically aligned single-walled carbon nanotubes. This absorbs between 98% and 99% of the incoming light in the spectral range from the ultra-violet to the far-infrared regions.^[32]

Other examples of nearly perfect black materials are super black, prepared by chemically etching a nickel–phosphorus alloy,^[34] and vantablack made of carbon nanotubes; both absorb 99.9% of light or more.

Stars and planets

An idealized view of the cross-section of a star. The photosphere contains photons of light nearly in thermal equilibrium, and some escape into space as near-black-body radiation.

A star or planet often is modeled as a black body, and electromagnetic radiation emitted from these bodies as black-body radiation. The figure shows a highly schematic cross-section to illustrate the idea. The photosphere of the star, where the emitted light is generated, is idealized as a layer within which the photons of light interact with the material in the photosphere and achieve a common temperature T that is maintained over a long period of time. Some photons escape and are emitted into space, but the energy they carry away is replaced by energy from within the star, so that the temperature of the photosphere is nearly steady. Changes in the core lead to changes in the supply of energy to the photosphere, but such changes are slow on the time scale of interest here. Assuming these circumstances can be realized, the outer layer of the star is somewhat analogous to the example of an enclosure with a small hole in it, with the hole replaced by the limited transmission into space at the outside of the photosphere. With all these assumptions in place, the star emits black-body radiation at the temperature of the photosphere.^[35]

Effective temperature of a black body compared with the B-V and U-B color index of main sequence and super giant stars in what is called a color-color diagram.^[36]

Using this model the effective temperature of stars is estimated, defined as the temperature of a black body that yields the same surface flux of energy as the star. If a star were a black body, the same effective temperature would result from any region of the spectrum. For example, comparisons in the B (blue) or V (visible) range lead to the so-called B-V color index, which increases the redder the star,^[37] with the Sun having an index of +0.648 ± 0.006.^[38] Combining the U (ultraviolet) and the B indices leads to the U-B index, which becomes more negative the hotter the star and the more the UV radiation. Assuming the Sun is a type G2 V star, its U-B index is +0.12.^[39] The two indices for two types of stars are compared in the figure with the effective surface temperature of the stars assuming they are black bodies. It can be seen that there is only a rough correlation. For example, for a given B-V index from the blue-visible region of the spectrum., the curves for both types of star lie below the corresponding black-body U-B index that includes the ultraviolet spectrum, showing that both types of star emit less ultraviolet light than a black body with the same B-V index. It is perhaps surprising that they fit a black body curve as well as they do, considering that stars have greatly different temperatures at different depths.^[40] For example, the Sun has an effective temperature of 5780 K,^[41] which can be compared to the temperature of the photosphere of the Sun (the region generating the light), which ranges from about 5000 K at its outer boundary with the chromosphere to about 9500 K at its inner boundary with the convection zone approximately 500 km (310 mi) deep.^[42]

Black holes

A black hole is a region of spacetime from which nothing escapes. Around a black hole there is a mathematically defined surface called an event horizon that marks the point of no return. It is called "black" because it absorbs all the light that hits the horizon, reflecting nothing, making it almost an ideal black body^[43] (radiation with a wavelength equal to or larger than the radius of the hole may not be absorbed, so black holes are not perfect black bodies).^[44] Physicists believe that to an outside observer, black holes have a non-zero temperature and emit radiation with a nearly perfect black-body spectrum, ultimately evaporating.^[45] The mechanism for this emission is related to vacuum fluctuations in which a virtual pair of particles is separated by the gravity of the hole, one member being sucked into the hole, and the other being emitted.^[46] The energy distribution of emission is described by Planck's law with a temperature T:

${\displaystyle T={\frac {\hbar c^{3}}{8\pi Gk_{B}M}}\ ,}$

where c is the speed of light, ℏ is the reduced Planck constant, k_B is Boltzmann's constant, G is the gravitational constant and M is the mass of the black hole.^[47] These predictions have not yet been tested either observationally or experimentally.^[48]

Cosmic microwave background radiation

See also: Big Bang and Cosmic microwave background radiation

The big bang theory is based upon the cosmological principle, which states that on large scales the Universe is homogeneous and isotropic. According to theory, the Universe approximately a second after its formation was a near-ideal black body in thermal equilibrium at a temperature above 10¹⁰ K. The temperature decreased as the Universe expanded and the matter and radiation in it cooled. The cosmic microwave background radiation observed today is "the most perfect black body ever measured in nature".^[49] It has a nearly ideal Planck spectrum at a temperature of about 2.7 K. It departs from the perfect isotropy of true black-body radiation by an observed anisotropy that varies with angle on the sky only to about one part in 100,000.

Radiative cooling

See also: Radiative cooling and Radiosity (heat transfer)

The integration of Planck's law over all frequencies provides the total energy per unit of time per unit of surface area radiated by a black body maintained at a temperature T, and is known as the Stefan–Boltzmann law:

${\displaystyle P/A=\sigma T^{4}\ ,}$

where σ is the Stefan–Boltzmann constant, σ ≈ 5.67 × 10⁻⁸ W/(m²K⁴).^[50] To remain in thermal equilibrium at constant temperature T, the black body must absorb or internally generate this amount of power P over the given area A.
The cooling of a body due to thermal radiation is often approximated using the Stefan–Boltzmann law supplemented with a "gray body" emissivity ε ≤ 1 (P/A = εσT⁴). The rate of decrease of the temperature of the emitting body can be estimated from the power radiated and the body's heat capacity.^[51] This approach is a simplification that ignores details of the mechanisms behind heat redistribution (which may include changing composition, phase transitions or restructuring of the body) that occur within the body while it cools, and assumes that at each moment in time the body is characterized by a single temperature. It also ignores other possible complications, such as changes in the emissivity with temperature,^[52][53] and the role of other accompanying forms of energy emission, for example, emission of particles like neutrinos.^[54]

If a hot emitting body is assumed to follow the Stefan–Boltzmann law and its power emission P and temperature T are known, this law can be used to estimate the dimensions of the emitting object, because the total emitted power is proportional to the area of the emitting surface. In this way it was found that X-ray bursts observed by astronomers originated in neutron stars with a radius of about 10 km, rather than black holes as originally conjectured.^[55] It should be noted that an accurate estimate of size requires some knowledge of the emissivity, particularly its spectral and angular dependence.^[56]

Infrared

From Wikipedia, the free encyclopedia

A false color image of two people taken in long-wavelength infrared (body-temperature thermal) light.

This infrared space telescope image has (false color) blue, green and red corresponding to 3.4, 4.6, and 12 µm wavelengths, respectively.

Infrared radiation, or simply infrared or IR, is electromagnetic radiation (EMR) with longer wavelengths than those of visible light, and is therefore invisible, although it is sometimes loosely called infrared light. It extends from the nominal red edge of the visible spectrum at 700 nanometers (frequency 430 THz), to 1000000 nm (300 GHz)^[1] (although people can see infrared up to at least 1050 nm in experiments^[2][3][4][5]). Most of the thermal radiation emitted by objects near room temperature is infrared. Like all EMR, IR carries radiant energy, and behaves both like a wave and like its quantum particle, the photon.

Infrared was discovered in 1800 by astronomer Sir William Herschel, who discovered a type of invisible radiation in the spectrum lower in energy than red light, by means of its effect on a thermometer.^[6] Slightly more than half of the total energy from the Sun was eventually found to arrive on Earth in the form of infrared. The balance between absorbed and emitted infrared radiation has a critical effect on Earth's climate.

Infrared radiation is emitted or absorbed by molecules when they change their rotational-vibrational movements. It excites vibrational modes in a molecule through a change in the dipole moment, making it a useful frequency range for study of these energy states for molecules of the proper symmetry. Infrared spectroscopy examines absorption and transmission of photons in the infrared range.^[7]

Infrared radiation is used in industrial, scientific, and medical applications. Night-vision devices using active near-infrared illumination allow people or animals to be observed without the observer being detected. Infrared astronomy uses sensor-equipped telescopes to penetrate dusty regions of space such as molecular clouds, detect objects such as planets, and to view highly red-shifted objects from the early days of the universe.^[8] Infrared thermal-imaging cameras are used to detect heat loss in insulated systems, to observe changing blood flow in the skin, and to detect overheating of electrical apparatus.

Thermal-infrared imaging is used extensively for military and civilian purposes. Military applications include target acquisition, surveillance, night vision, homing, and tracking. Humans at normal body temperature radiate chiefly at wavelengths around 10 μm (micrometers). Non-military uses include thermal efficiency analysis, environmental monitoring, industrial facility inspections, remote temperature sensing, short-ranged wireless communication, spectroscopy, and weather forecasting.

Definition and relationship to the electromagnetic spectrum

Infrared radiation extends from the nominal red edge of the visible spectrum at 700 nanometers (nm) to 1 mm. This range of wavelengths corresponds to a frequency range of approximately 430 THz down to 300 GHz. Below infrared is the microwave portion of the electromagnetic spectrum.

 

Infrared in relation to electromagnetic spectrum

Light comparison[9]
Name	Wavelength	Frequency (Hz)	Photon Energy (eV)
Gamma ray	less than 0.01 nm	more than 30 EHz	124 keV – 300+ GeV
X-ray	0.01 nm – 10 nm	30 EHz – 30 PHz	124 eV  – 124 keV
Ultraviolet	10 nm – 400 nm	30 PHz – 790 THz	3.3 eV – 124 eV
Visible	400 nm–700 nm	790 THz – 430 THz	1.7 eV – 3.3 eV
Infrared	700 nm – 1 mm	430 THz – 300 GHz	1.24 meV – 1.7 eV
Microwave	1 mm – 1 meter	300 GHz – 300 MHz	1.24 µeV – 1.24 meV
Radio	1 meter – 100,000 km	300 MHz – 3 Hz	12.4 feV – 1.24 µeV

Natural infrared

Sunlight, at an effective temperature of 5,780 kelvins, is composed of near thermal-spectrum radiation that is slightly more than half infrared. At zenith, sunlight provides an irradiance of just over 1 kilowatt per square meter at sea level. Of this energy, 527 watts is infrared radiation, 445 watts is visible light, and 32 watts is ultraviolet radiation.^[10] Nearly all the infrared radiation in sunlight is near infrared, shorter than 4 micrometers.

On the surface of Earth, at far lower temperatures than the surface of the Sun, almost all thermal radiation consists of infrared in mid-infrared region, much longer than in sunlight. Of these natural thermal radiation processes only lightning and natural fires are hot enough to produce much visible energy, and fires produce far more infrared than visible-light energy.

Regions within the infrared

In general, objects emit infrared radiation across a spectrum of wavelengths, but sometimes only a limited region of the spectrum is of interest because sensors usually collect radiation only within a specific bandwidth. Thermal infrared radiation also has a maximum emission wavelength, which is inversely proportional to the absolute temperature of object, in accordance with Wien's displacement law.
Therefore, the infrared band is often subdivided into smaller sections.

Commonly used sub-division scheme

Division Name	Abbreviation	Wavelength	Frequency	Photon Energy	Temperature†	Characteristics
Near-infrared	NIR, IR-A DIN	0.75–1.4 µm	214–400 THz	886–1653 meV	3,864–2,070 K (3,591–1,797 °C)	Defined by the water absorption, and commonly used in fiber optic telecommunication because of low attenuation losses in the SiO2 glass (silica) medium. Image intensifiers are sensitive to this area of the spectrum. Examples include night vision devices such as night vision goggles.
Short-wavelength infrared	SWIR, IR-B DIN	1.4–3 µm	100–214 THz	413–886 meV	2,070–966 K (1,797–693 °C)	Water absorption increases significantly at 1450 nm. The 1530 to 1560 nm range is the dominant spectral region for long-distance telecommunications.
Mid-wavelength infrared	MWIR, IR-C DIN; MidIR.[12] Also called intermediate infrared (IIR)	3–8 µm	37–100 THz	155–413 meV	966–362 K (693–89 °C)	In guided missile technology the 3–5 µm portion of this band is the atmospheric window in which the homing heads of passive IR 'heat seeking' missiles are designed to work, homing on to the Infrared signature of the target aircraft, typically the jet engine exhaust plume. This region is also known as thermal infrared.
Long-wavelength infrared	LWIR, IR-C DIN	8–15 µm	20–37 THz	83–155 meV	362–193 K (89 – −80 °C)	The "thermal imaging" region, in which sensors can obtain a completely passive image of objects only slightly higher in temperature than room temperature - for example, the human body - based on thermal emissions only and requiring no illumination such as the sun, moon, or infrared illuminator. This region is also called the "thermal infrared".
Far-infrared	FIR	15–1000 µm	0.3–20 THz	1.2–83 meV	193–3 K (−80.15 – −270.15 °C)	(see also far-infrared laser and far infrared)

† Temperatures of black bodies for which spectral peaks fall at the given wavelengths, according to Wien's displacement law^[13]

A comparison of a thermal image (top) and an ordinary photograph (bottom) shows that a trash bag is transparent but glass (the man's spectacles) is opaque in long-wavelength infrared.

NIR and SWIR is sometimes called "reflected infrared", whereas MWIR and LWIR is sometimes referred to as "thermal infrared". Due to the nature of the blackbody radiation curves, typical "hot" objects, such as exhaust pipes, often appear brighter in the MW compared to the same object viewed in the LW.

CIE division scheme

The International Commission on Illumination (CIE) recommended the division of infrared radiation into the following three bands:^[14]

Abbreviation	Wavelength	Frequency
IR-A	700 nm – 1400 nm (0.7 µm – 1.4 µm)	215 THz – 430 THz
IR-B	1400 nm – 3000 nm (1.4 µm – 3 µm)	100 THz – 215 THz
IR-C	3000 nm – 1 mm (3 µm – 1000 µm)	300 GHz – 100 THz

ISO 20473 scheme

ISO 20473 specifies the following scheme:^[15]

Designation	Abbreviation	Wavelength
Near-Infrared	NIR	0.78–3 µm
Mid-Infrared	MIR	3–50 µm
Far-Infrared	FIR	50–1000 µm

Astronomy division scheme

Astronomers typically divide the infrared spectrum as follows:^[16]

Designation	Abbreviation	Wavelength
Near-Infrared	NIR	(0.7–1) to 2.5 µm
Mid-Infrared	MIR	2.5 to (25–40) µm
Far-Infrared	FIR	(25–40) to (200–350) µm.

These divisions are not precise and can vary depending on the publication. The three regions are used for observation of different temperature ranges, and hence different environments in space.

The most common photometric system used in astronomy allocates capital letters to different spectral regions according to filters used; I, J, H, and K cover the near-infrared wavelengths; L, M, N, and Q refer to the mid-infrared region. These letters are commonly understood in reference to atmospheric windows and appear, for instance, in the titles of many papers.

Sensor response division scheme

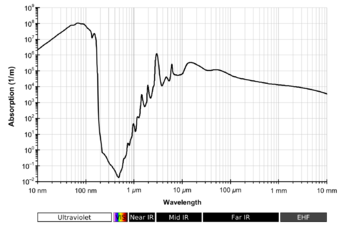
Plot of atmospheric transmittance in part of the infrared region.

A third scheme divides up the band based on the response of various detectors:^[17]

• Near-infrared: from 0.7 to 1.0 µm (from the approximate end of the response of the human eye to that of silicon).
• Short-wave infrared: 1.0 to 3 µm (from the cut-off of silicon to that of the MWIR atmospheric window). InGaAs covers to about 1.8 µm; the less sensitive lead salts cover this region.
• Mid-wave infrared: 3 to 5 µm (defined by the atmospheric window and covered by Indium antimonide [InSb] and HgCdTe and partially by lead selenide [PbSe]).
• Long-wave infrared: 8 to 12, or 7 to 14 µm (this is the atmospheric window covered by HgCdTe and microbolometers).
• Very-long wave infrared (VLWIR) (12 to about 30 µm, covered by doped silicon).

Near-infrared is the region closest in wavelength to the radiation detectable by the human eye. mid- and far-infrared are progressively further from the visible spectrum. Other definitions follow different physical mechanisms (emission peaks, vs. bands, water absorption) and the newest follow technical reasons (the common silicon detectors are sensitive to about 1,050 nm, while InGaAs's sensitivity starts around 950 nm and ends between 1,700 and 2,600 nm, depending on the specific configuration). No international standards for these specifications are currently available.

The onset of infrared is defined (according to different standards) at various values typically between 700 nm and 800 nm, but the boundary between visible and infrared light is not precisely defined. The human eye is markedly less sensitive to light above 700 nm wavelength, so longer wavelengths make insignificant contributions to scenes illuminated by common light sources. However, particularly intense near-IR light (e.g., from IR lasers, IR LED sources, or from bright daylight with the visible light removed by colored gels) can be detected up to approximately 780 nm, and will be perceived as red light. Intense light sources providing wavelengths as long as 1050 nm can be seen as a dull red glow, causing some difficulty in near-IR illumination of scenes in the dark (usually this practical problem is solved by indirect illumination). Leaves are particularly bright in the near IR, and if all visible light leaks from around an IR-filter are blocked, and the eye is given a moment to adjust to the extremely dim image coming through a visually opaque IR-passing photographic filter, it is possible to see the Wood effect that consists of IR-glowing foliage.^[18]

Telecommunication bands in the infrared

In optical communications, the part of the infrared spectrum that is used is divided into seven bands based on availability of light sources transmitting/absorbing materials (fibers) and detectors:^[19]

Band	Descriptor	Wavelength range
O band	Original	1260–1360 nm
E band	Extended	1360–1460 nm
S band	Short wavelength	1460–1530 nm
C band	Conventional	1530–1565 nm
L band	Long wavelength	1565–1625 nm
U band	Ultralong wavelength	1625–1675 nm

The C-band is the dominant band for long-distance telecommunication networks. The S and L bands are based on less well established technology, and are not as widely deployed.

Heat

Materials with higher emissivity appear to be hotter. In this thermal image, the ceramic cylinder appears to be hotter than its cubic container (made of silicon carbide), while in fact they have the same temperature.

Infrared radiation is popularly known as "heat radiation"^{[citation needed]}, but light and electromagnetic waves of any frequency will heat surfaces that absorb them. Infrared light from the Sun accounts for 49%^[20] of the heating of Earth, with the rest being caused by visible light that is absorbed then re-radiated at longer wavelengths. Visible light or ultraviolet-emitting lasers can char paper and incandescently hot objects emit visible radiation. Objects at room temperature will emit radiation concentrated mostly in the 8 to 25 µm band, but this is not distinct from the emission of visible light by incandescent objects and ultraviolet by even hotter objects (see black body and Wien's displacement law).^[21]

Heat is energy in transit that flows due to temperature difference. Unlike heat transmitted by thermal conduction or thermal convection, thermal radiation can propagate through a vacuum. Thermal radiation is characterized by a particular spectrum of many wavelengths that is associated with emission from an object, due to the vibration of its molecules at a given temperature. Thermal radiation can be emitted from objects at any wavelength, and at very high temperatures such radiations are associated with spectra far above the infrared, extending into visible, ultraviolet, and even X-ray regions (e.g. the solar corona). Thus, the popular association of infrared radiation with thermal radiation is only a coincidence based on typical (comparatively low) temperatures often found near the surface of planet Earth.

The concept of emissivity is important in understanding the infrared emissions of objects. This is a property of a surface that describes how its thermal emissions deviate from the ideal of a black body. To further explain, two objects at the same physical temperature will not show the same infrared image if they have differing emissivity. For example, for any pre-set emissivity value, objects with higher emissivity will appear hotter, and those with a lower emissivity will appear cooler. For that reason, incorrect selection of emissivity will give inaccurate results when using infrared cameras and pyrometers.

Applications

Night vision

Active-infrared night vision : the camera illuminates the scene at infrared wavelengths invisible to the human eye. Despite a dark back-lit scene, active-infrared night vision delivers identifying details, as seen on the display monitor.

Infrared is used in night vision equipment when there is insufficient visible light to see.^[22] Night vision devices operate through a process involving the conversion of ambient light photons into electrons that are then amplified by a chemical and electrical process and then converted back into visible light.^[22] Infrared light sources can be used to augment the available ambient light for conversion by night vision devices, increasing in-the-dark visibility without actually using a visible light source.^[22]

The use of infrared light and night vision devices should not be confused with thermal imaging, which creates images based on differences in surface temperature by detecting infrared radiation (heat) that emanates from objects and their surrounding environment.^[23]

Thermography

Thermography helped to determine the temperature profile of the Space Shuttle thermal protection system during re-entry.

Infrared radiation can be used to remotely determine the temperature of objects (if the emissivity is known). This is termed thermography, or in the case of very hot objects in the NIR or visible it is termed pyrometry. Thermography (thermal imaging) is mainly used in military and industrial applications but the technology is reaching the public market in the form of infrared cameras on cars due to the massively reduced production costs.

Thermographic cameras detect radiation in the infrared range of the electromagnetic spectrum (roughly 900–14,000 nanometers or 0.9–14 μm) and produce images of that radiation. Since infrared radiation is emitted by all objects based on their temperatures, according to the black body radiation law, thermography makes it possible to "see" one's environment with or without visible illumination. The amount of radiation emitted by an object increases with temperature, therefore thermography allows one to see variations in temperature (hence the name).

Hyperspectral imaging

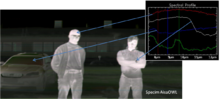
Hyperspectral thermal infrared emission measurement, an outdoor scan in winter conditions, ambient temperature −15 °C, image produced with a Specim LWIR hyperspectral imager. Relative radiance spectra from various targets in the image are shown with arrows. The infrared spectra of the different objects such as the watch clasp have clearly distinctive characteristics. The contrast level indicates the temperature of the object.^[24]

Infrared light from the LED of a remote control as recorded by a digital camera.

A hyperspectral image is a "picture" containing continuous spectrum through a wide spectral range at each pixel. Hyperspectral imaging is gaining importance in the field of applied spectroscopy particularly with NIR, SWIR, MWIR, and LWIR spectral regions. Typical applications include biological, mineralogical, defence, and industrial measurements.

Thermal infrared hyperspectral imaging can be similarly performed using a Thermographic camera, with the fundamental difference that each pixel contains a full LWIR spectrum. Consequently, chemical identification of the object can be performed without a need for an external light source such as the sun or the moon. Such cameras are typically applied for geological measurements, outdoor surveillance and UAV applications.^[25]

Other imaging

In infrared photography, infrared filters are used to capture the near-infrared spectrum. Digital cameras often use infrared blockers. Cheaper digital cameras and camera phones have less effective filters and can "see" intense near-infrared, appearing as a bright purple-white color. This is especially pronounced when taking pictures of subjects near IR-bright areas (such as near a lamp), where the resulting infrared interference can wash out the image. There is also a technique called 'T-ray' imaging, which is imaging using far-infrared or terahertz radiation. Lack of bright sources can make terahertz photography more challenging than most other infrared imaging techniques. Recently T-ray imaging has been of considerable interest due to a number of new developments such as terahertz time-domain spectroscopy.

Reflected light photograph in various infrared spectra to illustrate the appearance as the wavelength of light changes.

Tracking

Infrared tracking, also known as infrared homing, refers to a passive missile guidance system, which uses the emission from a target of electromagnetic radiation in the infrared part of the spectrum to track it. Missiles that use infrared seeking are often referred to as "heat-seekers", since infrared (IR) is just below the visible spectrum of light in frequency and is radiated strongly by hot bodies. Many objects such as people, vehicle engines, and aircraft generate and retain heat, and as such, are especially visible in the infrared wavelengths of light compared to objects in the background.^[26]

Heating

Infrared radiation can be used as a deliberate heating source. For example, it is used in infrared saunas to heat the occupants. It may also be used in other heating applications, such as to remove ice from the wings of aircraft (de-icing).^[27] Infrared can be used in cooking and heating food as it predominantly heats the opaque, absorbent objects, rather than the air around them.

Infrared heating is also becoming more popular in industrial manufacturing processes, e.g. curing of coatings, forming of plastics, annealing, plastic welding, and print drying. In these applications, infrared heaters replace convection ovens and contact heating.

Efficiency is achieved by matching the wavelength of the infrared heater to the absorption characteristics of the material.

Communications

IR data transmission is also employed in short-range communication among computer peripherals and personal digital assistants. These devices usually conform to standards published by IrDA, the Infrared Data Association. Remote controls and IrDA devices use infrared light-emitting diodes (LEDs) to emit infrared radiation that is focused by a plastic lens into a narrow beam. The beam is modulated, i.e. switched on and off, to prevent interference from other sources of infrared (like sunlight or artificial lighting). The receiver uses a silicon photodiode to convert the infrared radiation to an electric current. It responds only to the rapidly pulsing signal created by the transmitter, and filters out slowly changing infrared radiation from ambient light. Infrared communications are useful for indoor use in areas of high population density. IR does not penetrate walls and so does not interfere with other devices in adjoining rooms. Infrared is the most common way for remote controls to command appliances. Infrared remote control protocols like RC-5, SIRC, are used to communicate with infrared.

Free space optical communication using infrared lasers can be a relatively inexpensive way to install a communications link in an urban area operating at up to 4 gigabit/s, compared to the cost of burying fiber optic cable, except for the radiation damage. "Since the eye cannot detect IR, blinking or closing the eyes to help prevent or reduce damage may not happen."^[28]

Infrared lasers are used to provide the light for optical fiber communications systems. Infrared light with a wavelength around 1,330 nm (least dispersion) or 1,550 nm (best transmission) are the best choices for standard silica fibers.

IR data transmission of encoded audio versions of printed signs is being researched as an aid for visually impaired people through the RIAS (Remote Infrared Audible Signage) project. Transmitting IR data from one device to another is sometimes referred to as beaming.

Spectroscopy

Infrared vibrational spectroscopy (see also near-infrared spectroscopy) is a technique that can be used to identify molecules by analysis of their constituent bonds. Each chemical bond in a molecule vibrates at a frequency characteristic of that bond. A group of atoms in a molecule (e.g., CH₂) may have multiple modes of oscillation caused by the stretching and bending motions of the group as a whole. If an oscillation leads to a change in dipole in the molecule then it will absorb a photon that has the same frequency. The vibrational frequencies of most molecules correspond to the frequencies of infrared light. Typically, the technique is used to study organic compounds using light radiation from 4000–400 cm⁻¹, the mid-infrared. A spectrum of all the frequencies of absorption in a sample is recorded. This can be used to gain information about the sample composition in terms of chemical groups present and also its purity (for example, a wet sample will show a broad O-H absorption around 3200 cm⁻¹).

Thin film metrology

In the semiconductor industry, infrared light can be used to characterize materials such as thin films and periodic trench structures. By measuring the reflectance of light from the surface of a semiconductor wafer, the index of refraction (n) and the extinction Coefficient (k) can be determined via the Forouhi-Bloomer dispersion equations. The reflectance from the infrared light can also be used to determine the critical dimension, depth, and sidewall angle of high aspect ratio trench structures.

Meteorology

IR Satellite picture taken 1315 Z on 15th October 2006. A frontal system can be seen in the Gulf of Mexico with embedded Cumulonimbus cloud. Shallower Cumulus and Stratocumulus can be seen off the Eastern Seaboard.

Weather satellites equipped with scanning radiometers produce thermal or infrared images, which can then enable a trained analyst to determine cloud heights and types, to calculate land and surface water temperatures, and to locate ocean surface features. The scanning is typically in the range 10.3–12.5 µm (IR4 and IR5 channels).

High, cold ice clouds such as Cirrus or Cumulonimbus show up bright white, lower warmer clouds such as Stratus or Stratocumulus show up as grey with intermediate clouds shaded accordingly. Hot land surfaces will show up as dark-grey or black. One disadvantage of infrared imagery is that low cloud such as stratus or fog can be a similar temperature to the surrounding land or sea surface and does not show up. However, using the difference in brightness of the IR4 channel (10.3–11.5 µm) and the near-infrared channel (1.58–1.64 µm), low cloud can be distinguished, producing a fog satellite picture. The main advantage of infrared is that images can be produced at night, allowing a continuous sequence of weather to be studied.

These infrared pictures can depict ocean eddies or vortices and map currents such as the Gulf Stream, which are valuable to the shipping industry. Fishermen and farmers are interested in knowing land and water temperatures to protect their crops against frost or increase their catch from the sea. Even El Niño phenomena can be spotted. Using color-digitized techniques, the gray-shaded thermal images can be converted to color for easier identification of desired information.

The main water vapour channel at 6.40 to 7.08 µm can be imaged by some weather satellites and shows the amount of moisture in the atmosphere.

Climatology

In the field of climatology, atmospheric infrared radiation is monitored to detect trends in the energy exchange between the earth and the atmosphere. These trends provide information on long-term changes in Earth's climate. It is one of the primary parameters studied in research into global warming, together with solar radiation.

Schematic of the greenhouse effect

A pyrgeometer is utilized in this field of research to perform continuous outdoor measurements. This is a broadband infrared radiometer with sensitivity for infrared radiation between approximately 4.5 µm and 50 µm.

Astronomy

Beta Pictoris with its planet Beta Pictoris b, the light-blue dot off-center, as seen in infrared. It combines two images, the inner disc is at 3.6 µm.

Astronomers observe objects in the infrared portion of the electromagnetic spectrum using optical components, including mirrors, lenses and solid state digital detectors. For this reason it is classified as part of optical astronomy. To form an image, the components of an infrared telescope need to be carefully shielded from heat sources, and the detectors are chilled using liquid helium.

The sensitivity of Earth-based infrared telescopes is significantly limited by water vapor in the atmosphere, which absorbs a portion of the infrared radiation arriving from space outside of selected atmospheric windows. This limitation can be partially alleviated by placing the telescope observatory at a high altitude, or by carrying the telescope aloft with a balloon or an aircraft. Space telescopes do not suffer from this handicap, and so outer space is considered the ideal location for infrared astronomy.

The infrared portion of the spectrum has several useful benefits for astronomers. Cold, dark molecular clouds of gas and dust in our galaxy will glow with radiated heat as they are irradiated by imbedded stars. Infrared can also be used to detect protostars before they begin to emit visible light. Stars emit a smaller portion of their energy in the infrared spectrum, so nearby cool objects such as planets can be more readily detected. (In the visible light spectrum, the glare from the star will drown out the reflected light from a planet.)

Infrared light is also useful for observing the cores of active galaxies, which are often cloaked in gas and dust. Distant galaxies with a high redshift will have the peak portion of their spectrum shifted toward longer wavelengths, so they are more readily observed in the infrared.^[8]

Infrared cleaning

Infrared cleaning is a technique used by some motion picture film scanners, film scanners and flatbed scanners to reduce or remove the effect of dust and scratches upon the finished scan. It works by collecting an additional infrared channel from the scan at the same position and resolution as the three visible color channels (red, green, and blue). The infrared channel, in combination with the other channels, is used to detect the location of scratches and dust. Once located, those defects can be corrected by scaling or replaced by inpainting.^[29]

Art conservation and analysis

The Arnolfini Portrait by Jan van Eyck, National Gallery, London

Infrared reflectography (fr; it; es), as called by art conservators,^[30] can be applied to paintings to reveal underlying layers in a completely non-destructive manner, in particular the underdrawing or outline drawn by the artist as a guide. This often reveals the artist's use of carbon black, which shows up well in reflectograms, as long as it has not also been used in the ground underlying the whole painting. Art conservators are looking to see whether the visible layers of paint differ from the underdrawing or layers in between – such alterations are called pentimenti when made by the original artist. This is very useful information in deciding whether a painting is the prime version by the original artist or a copy, and whether it has been altered by over-enthusiastic restoration work. In general, the more pentimenti the more likely a painting is to be the prime version. It also gives useful insights into working practices.^[31]

Among many other changes in the Arnolfini Portrait of 1434 (left), the man's face was originally higher by about the height of his eye; the woman's was higher, and her eyes looked more to the front. Each of his feet was underdrawn in one position, painted in another, and then overpainted in a third. These alterations are seen in infrared reflectograms.^[32]

Recent progress in the design of infrared sensitive cameras made it possible to discover and depict not only underpaintings and pentimenti but entire paintings which were later overpainted by the artist.^[33] Notable examples are Picasso's "Woman ironing" and "Blue room", where in both cases, a portrait of a man has been made visible under the painting as it is known today.

Similar uses of infrared are made by conservators and scientists on various types of objects, especially very old written documents such as the Dead Sea Scrolls, the Roman works in the Villa of the Papyri, and the Silk Road texts found in the Dunhuang Caves.^[34] Carbon black used in ink can show up extremely well.

Biological systems

Thermographic image of a snake eating a mouse

The pit viper has a pair of infrared sensory pits on its head. There is uncertainty regarding the exact thermal sensitivity of this biological infrared detection system.^[35][36]

Other organisms that have thermoreceptive organs are pythons (family Pythonidae), some boas (family Boidae), the Common Vampire Bat (Desmodus rotundus), a variety of jewel beetles (Melanophila acuminata),^[37] darkly pigmented butterflies (Pachliopta aristolochiae and Troides rhadamantus plateni), and possibly blood-sucking bugs (Triatoma infestans).^[38]

Although near-infrared vision (780–1000 nm) has long been deemed impossible due to noise in visual pigments,^[39] sensation of near-infrared light was reported in the common carp and in three cichlid species.^{[39][40][41][42][43]} Fish use NIR to capture prey^[39] and for phototactic swimming orientation.^[43] NIR sensation in fish may be relevant under poor lighting conditions during twilight^[39] and in turbid surface waters.^[43]

Photobiomodulation

Near-infrared light, or photobiomodulation, is used for treatment of chemotherapy-induced oral ulceration as well as wound healing. There is some work relating to anti-herpes virus treatment.^[44] Research projects include work on central nervous system healing effects via cytochrome c oxidase upregulation and other possible mechanisms.^[45]

Health hazard

Strong infrared radiation in certain industry high-heat settings may be hazardous to the eyes, resulting in damage or blindness to the user. Since the radiation is invisible, special IR-proof goggles must be worn in such places.^[46]

History of infrared science

The discovery of infrared radiation is ascribed to William Herschel, the astronomer, in the early 19th century. Herschel published his results in 1800 before the Royal Society of London. Herschel used a prism to refract light from the sun and detected the infrared, beyond the red part of the spectrum, through an increase in the temperature recorded on a thermometer. He was surprised at the result and called them "Calorific Rays". The term 'Infrared' did not appear until late in the 19th century.^[47][48]
Other important dates include:^[17]

Infrared radiation was discovered in 1800 by William Herschel.

• 1737: Émilie du Châtelet predicted what is today known as infrared radiation in Dissertation sur la nature et la propagation du feu.
• 1835: Macedonio Melloni made the first thermopile IR detector.
• 1840: John Herschel produces the first thermal image thermogram.
• 1860: Gustav Kirchhoff formulated the blackbody theorem ${\displaystyle E=J(T,n)}$.
• 1873: Willoughby Smith discovered the photoconductivity of selenium.
• 1879: Stefan-Boltzmann law formulated empirically that the power radiated by a blackbody is proportional to T⁴.
• 1880s & 1890s: Lord Rayleigh and Wilhelm Wien solved part of the blackbody equation, but both solutions diverged in parts of the electromagnetic spectrum. This problem was called the "Ultraviolet catastrophe and Infrared Catastrophe".
• 1901: Max Planck published the blackbody equation and theorem. He solved the problem by quantizing the allowable energy transitions.
• 1905: Albert Einstein developed the theory of the photoelectric effect.
• 1917: Theodore Case developed the thallous sulfide detector; British scientist built the first infra-red search and track (IRST) device able to detect aircraft at a range of one mile (1.6 km).
• 1935: Lead salts – early missile guidance in World War II.
• 1938: Teau Ta – predicted that the pyroelectric effect could be used to detect infrared radiation.
• 1945: The Zielgerät 1229 "Vampir" infrared weapon system was introduced as the first portable infrared device for military applications.
• 1952: H. Welker grew synthetic InSb crystals.
• 1950s: Paul Kruse (at Honeywell) and Texas Instruments recorded infrared images.
• 1950s and 1960s: Nomenclature and radiometric units defined by Fred Nicodemenus, G.J. Zissis and R. Clark; Robert Clark Jones defined D*.
• 1958: W.D. Lawson (Royal Radar Establishment in Malvern) discovered IR detection properties of HgCdTe.
• 1958: Falcon and Sidewinder missiles were developed using infrared technology.
• 1961: J. Cooper demonstrated pyroelectric detection.
• 1964: W.G. Evans discovered infrared thermoreceptors in a pyrophile beetle.^[37]
• 1965: First IR Handbook; first commercial imagers (Barnes, Agema {now part of FLIR Systems Inc.}; Richard Hudson's landmark text; F4 TRAM FLIR by Hughes; phenomenology pioneered by Fred Simmons and A.T. Stair; U.S. Army's night vision lab formed (now Night Vision and Electronic Sensors Directorate (NVESD), and Rachets develops detection, recognition and identification modeling there.
• 1970: Willard Boyle and George E. Smith proposed CCD at Bell Labs for picture phone.
• 1972: Common module program started by NVESD.
• 1978: Infrared imaging astronomy came of age, observatories planned, IRTF on Mauna Kea opened; 32 by 32 and 64 by 64 arrays produced using InSb, HgCdTe and other materials.
• 2013: On February 14 researchers developed a neural implant that gives rats the ability to sense infrared light which for the first time provides living creatures with new abilities, instead of simply replacing or augmenting existing abilities.^[49]