Minkowski space

From Wikipedia, the free encyclopedia

Hermann Minkowski (1864–1909) found that the theory of special relativity, introduced by his former student Albert Einstein, could be best understood as a four-dimensional space, since known as the Minkowski spacetime.

In mathematical physics, Minkowski space (or Minkowski spacetime) is a combining of three-dimensional Euclidean space and time into a four-dimensional manifold where the spacetime interval between any two events is independent of the inertial frame of reference in which they are recorded. Although initially developed by mathematician Hermann Minkowski for Maxwell's equations of electromagnetism, the mathematical structure of Minkowski spacetime was shown to be an immediate consequence of the postulates of special relativity.^[1]

Minkowski space is closely associated with Einstein's theory of special relativity, and is the most common mathematical structure on which special relativity is formulated. While the individual components in Euclidean space and time may differ due to length contraction and time dilation, in Minkowski spacetime, all frames of reference will agree on the total distance in spacetime between events.^{[nb 1]} Because it treats time differently than it treats the 3 spatial dimensions, Minkowski space differs from four-dimensional Euclidean space.

In 3-dimensional Euclidean space (e.g. simply space in Galilean relativity), the isometry group (the maps preserving the regular Euclidean distance) is the Euclidean group. It is generated by rotations, reflections and translations. When time is amended as a fourth dimension, the further transformations of translations in time and Galilean boosts are added, and the group of all these transformations is called the Galilean group. All Galilean transformations preserve the 3-dimensional Euclidean distance. This distance is purely spatial. Time differences are separately preserved as well. This changes in the spacetime of special relativity, where space and time are interwoven.

Spacetime is equipped with an indefinite non-degenerate bilinear form, variously called the Minkowski metric,^[2] the Minkowski norm squared or Minkowski inner product depending on the context^{[nb 2]} The Minkowski inner product is defined as to yield the spacetime interval between two events when given their coordinate difference vector as argument.^[3] Equipped with this inner product, the mathematical model of spacetime is called Minkowski space. The analogue of the Galilean group for Minkowski space, preserving the spacetime interval (as opposed to the spatial Euclidean distance) is the Poincaré group.

In summary, Galilean spacetime and Minkowski spacetime are, when viewed as manifolds, actually the same. They differ in what further structures are defined on them. The former has the Euclidean distance function and time (separately) together with inertial frames whose coordinates are related by Galilean transformations, while the latter has the Minkowski metric together with inertial frames whose coordinates are related by Poincaré transformations.

History

Four-dimensional Euclidean spacetime

In 1905–06 Henri Poincaré showed^[4] that by taking time to be an imaginary fourth spacetime coordinate ict, where c is the speed of light and i is the imaginary unit, a Lorentz transformation can formally be regarded as a rotation of coordinates in a four-dimensional space with three real coordinates representing space, and one imaginary coordinate representing time, as the fourth dimension. In physical spacetime special relativity stipulates that the quantity

${\displaystyle -t^{2}+x^{2}+y^{2}+z^{2}}$

is invariant under coordinate changes from one inertial frame to another, i. e. under Lorentz transformations. Here the speed of light c is, following Poincaré, set to unity. In the space suggested by him (Poincaré mentions this only in passing) where physical spacetime is coordinatized by (t, x, y, z) ↦ (x, y, z, it), call it coordinate space, Lorentz transformations appear as ordinary rotations preserving the quadratic form

${\displaystyle x^{2}+y^{2}+z^{2}+t^{2}}$

on coordinate space. The naming and ordering of coordinates, with the same labels for space coordinates, but with the imaginary time coordinate as the fourth coordinate, is conventional. The above expression, while making the former expression more familiar,^{[nb 3]} may potentially be confusing because it is not the same t that appears in the latter (time coordinate) as in the former (time itself in some inertial system as measured by clocks stationary in that system).

Rotations in planes spanned by two space unit vectors appear in coordinate space as well as in physical spacetime appear as Euclidean rotations and are interpreted in the ordinary sense. The "rotation" in a plane spanned by a space unit vector and a time unit vector, while formally still a rotation in coordinate space, is a Lorentz boost in physical spacetime with real inertial coordinates. The analogy with Euclidean rotations is thus only partial.

This idea was elaborated by Hermann Minkowski,^[5] who used it to restate the Maxwell equations in four dimensions, showing directly their invariance under the Lorentz transformation. He further reformulated in four dimensions the then-recent theory of special relativity of Einstein. From this he concluded that time and space should be treated equally, and so arose his concept of events taking place in a unified four-dimensional spacetime continuum.

Minkowski space

In a further development in his 1908 "Space and Time" lecture,^[6] he gave an alternative formulation of this idea that used a real time coordinate instead of an imaginary one, representing the four variables (x, y, z, t) of space and time in coordinate form in a four dimensional real vector space. Points in this space correspond to events in spacetime. In this space, there is a defined light-cone associated with each point, and events not on the light-cone are classified by their relation to the apex as spacelike or timelike. It is principally this view of spacetime that is current nowadays, although the older view involving imaginary time has also influenced special relativity.

In the English translation of Minkowski's paper, the Minkowski metric as defined below is referred to as the line element. The Minkowski inner product of below appears unnamed when referring to orthogonality (which he calls normality) of certain vectors, and the Minkowski norm squared is referred to (somewhat cryptically, perhaps this is translation dependent) as "sum".

Minkowski's principal tool is the Minkowski diagram, and he uses it to define concepts and demonstrate properties of Lorentz transformations (e.g. proper time and length contraction) and to provide geometrical interpretation to the generalization of Newtonian mechanics to relativistic mechanics. For these special topics, see the referenced articles, as the presentation below will be principally confined to the mathematical structure (Minkowski metric and from it derived quantities and the Poincaré group as symmetry group of spacetime) following from the invariance of the spacetime interval on the spacetime manifold as consequences of the postulates of special relativity, not to specific application or derivation of the invariance of the spacetime interval. This structure provides the background setting of all present relativistic theories, barring general relativity for which flat Minkowski spacetime still provides a springboard as curved spacetime is locally Lorentzian.

Minkowski, aware of the fundamental restatement of the theory which he had made, said

The views of space and time which I wish to lay before you have sprung from the soil of experimental physics, and therein lies their strength. They are radical. Henceforth space by itself, and time by itself, are doomed to fade away into mere shadows, and only a kind of union of the two will preserve an independent reality.

— Hermann Minkowski, 1908, 1909^[6]

Though Minkowski took an important step for physics, Einstein saw its limitation:

At a time when Minkowski was giving the geometrical interpretation of special relativity by extending the Euclidean three-space to a quasi-Euclidean four-space that included time, Einstein was already aware that this is not valid, because it excludes the phenomenon of gravitation. He was still far from the study of curvilinear coordinates and Riemannian geometry, and the heavy mathematical apparatus entailed.^[7]

Mathematical structure

A pictorial representation of the tangent space at a point, x, on a sphere. This vector space can be thought of as a subspace of ℝ³ itself. Then vectors in it would be called geometrical tangent vectors. By the same principle, the tangent space at a point in flat spacetime can be thought of as a subspace of spacetime which happens to be all of spacetime.

It is assumed below that spacetime is endowed with a coordinate system corresponding to an inertial frame. This provides an origin, which is necessary in order to be able to refer to spacetime as being modeled as a vector space. This is not really physically motivated in that a canonical origin ("central" event in spacetime) should exist. One can get away with less structure, that of an affine space, but this would needlessly complicate the discussion and would not reflect how flat spacetime is normally treated mathematically in modern introductory literature.

For an overview, Minkowski space is a 4-dimensional real vector space equipped with a nondegenerate, symmetric bilinear form on the tangent space at each point in spacetime, here simply called the Minkowski inner product, with metric signature either (+ − − −) or (− + + +). The tangent space at each event is a vector space of the same dimension as spacetime, 4.

Tangent vectors

In practice, one need not be concerned with the tangent spaces. The vector space nature of Minkowski space allows for the canonical identification of vectors in tangent spaces at points (events) with vectors (points, events) in Minkowski space itself. See e.g. Lee (2003, Proposition 3.8.) These identifications are routinely done in mathematics. They can be expressed formally in Cartesian coordinates as^[8]

${\displaystyle (x^{0},x^{1},x^{2},x^{3})\leftrightarrow x^{0}\mathbf {e} _{0}|_{p}+x^{1}\mathbf {e} _{1}|_{p}+x^{2}\mathbf {e} _{2}|_{p}+x^{3}\mathbf {e} _{3}|_{p}\leftrightarrow x^{0}\mathbf {e} _{0}|_{q}+x^{1}\mathbf {e} _{1}|_{q}+x^{2}\mathbf {e} _{2}|_{q}+x^{3}\mathbf {e} _{3}|_{q},}$

with basis vectors in the tangent spaces defined by

${\displaystyle \mathbf {e} _{\mu }|_{p}=\left.{\frac {\partial }{\partial x^{\mu }}}\right|_{p}{\text{ or }}\mathbf {e} _{0}|_{p}=\left({\begin{matrix}1\\0\\0\\0\end{matrix}}\right){\text{, etc}}.}$

Here p and q are any two events and the last identification is referred to as parallel transport. The first identification is the canonical identification of vectors in the tangent space at any point with vectors in the space itself. The appearance of basis vectors in tangent spaces as first order differential operators is due to this identification. It is motivated by the observation that a geometrical tangent vector can be associated in a one-to-one manner with a directional derivative operator on the set of smooth functions. This is promoted to a definition of tangent vectors in manifolds not necessarily being embedded in ℝⁿ. This definition of tangent vectors is not the only possible one as ordinary n-tuples can be used as well.

Definitions of tangent vectors as ordinary vectors

For some purposes it is desirable to identify tangent vectors at a point p with displacement vectors at p, which is, of course, admissible by essentially the same canonical identification.^[9] The identifications of vectors referred to above in the mathematical setting can correspondingly be found in a more physical and explicitly geometrical setting in Misner, Thorne & Wheeler (1970). They offer various degree of sophistication (and rigor) depending on which part of the material one chooses to read.

Metric signature

The metric signature refers to which sign the Minkowski inner product yields when given space (spacelike to be specific, defined further down) and time basis vectors (timelike) as arguments. Further discussion about this theoretically inconsequential, but practically necessary choice for purposes of internal consistency and convenience is deferred to the hide box below.

The choice of metric signature

Terminology

Mathematically associated to the bilinear form is a tensor of type (0,2) at each point in spacetime, called the Minkowski metric.^{[nb 4]} The Minkowski metric, the bilinear form, and the Minkowski inner product are actually all the very same object; it is a bilinear function that accepts two (contravariant) vectors and returns a real number. In coordinates, this is the 4×4 matrix representing the bilinear form.

For comparison, in general relativity, a Lorentzian manifold L is likewise equipped with a metric tensor g, which is a nondegenerate symmetric bilinear form on the tangent space T_pL at each point p of L. In coordinates, it may be represented by a 4×4 matrix depending on spacetime position. Minkowski space is thus a comparatively simple special case of a Lorentzian manifold. Its metric tensor is in coordinates the same symmetric matrix at every point of M, and its arguments can, per above, be taken as vectors in spacetime itself.

Introducing more terminology (but not more structure), Minkowski space is thus a pseudo-Euclidean space with total dimension n = 4 and signature (3, 1) or (1, 3). Elements of Minkowski space are called events. Minkowski space is often denoted R^3,1 or R^1,3 to emphasize the chosen signature, or just M. It is perhaps the simplest example of a pseudo-Riemannian manifold.

An interesting example of non-inertial coordinates for (part of) Minkowski spacetime are the Born coordinates. Another useful set of coordinates are the lightcone coordinates.

Pseudo-Euclidean metrics

The Minkowski metric^{[nb 5]} η is the metric tensor of Minkowski space. It is a pseudo-Euclidean metric, or more generally a constant pseudo-Riemannian metric in Cartesian coordinates. As such it is a nondegenerate symmetric bilinear form, a type (0,2) tensor. It accepts two arguments u_p, v_p, vectors in T_pM, p ∈ M, the tangent space at p in M. Due to the above-mentioned canonical identification of T_pM with M itself, it accepts arguments u, v with both u and v in M.

As a notational convention, vectors v in M, called 4-vectors, are denoted in sans-serif italics, and not, as is common in the Euclidean setting, with boldface v. The latter is generally reserved for the 3-vector part (to be introduced below) of a 4-vector.

The definition

${\displaystyle u\cdot v=\eta (u,v)}$

yields an inner product-like structure on M, previously and also henceforth, called the Minkowski inner product, similar to the Euclidean inner product, but it describes a different geometry. It is also called the relativistic dot product. If the two arguments are the same,

${\displaystyle u\cdot u=\eta (u,u)\equiv ||u||^{2}\equiv u^{2},}$

the resulting quantity will be called the Minkowski norm squared. The Minkowski inner product satisfies the following properties.

• ${\displaystyle \eta (au+v,w)=a\eta (u,w)+\eta (v,w),\quad \forall u,v\in M,\forall a\in \mathbb {R} \qquad {\text{(linearity in first slot)}}}$
• ${\displaystyle \eta (u,v)=\eta (v,u)\qquad {\text{(symmetry)}}}$
• ${\displaystyle \eta (u,v)=0\quad \forall v\in M\Rightarrow u=0\qquad {\text{(non-degeneracy)}}}$

The first two conditions imply bilinearity. The defining difference between a pseudo-inner product and an inner product proper is that the former is not required to be positive definite, that is, η(u, u) < 0 is allowed.

The most important feature of the inner product and norm squared is that these are quantities unaffected by Lorentz transformations. In fact, it can be taken as the defining property of a Lorentz transformation that it preserves the inner product (i.e. the value of the corresponding bilinear form on two vectors). This approach is taken more generally for all classical groups definable this way in classical group. There, the matrix Φ is identical in the case O(3, 1) (the Lorentz group) to the matrix η to be displayed below.

Two vectors v and w are said to be orthogonal if η(v, w) = 0. For a geometric interpretation of orthogonality in the special case when η(v, v) ≤ 0 and η(w, w) ≥ 0 (or vice versa), see hyperbolic orthogonality.

A vector e is called a unit vector if η(e, e) = ±1. A basis for M consisting of mutually orthogonal unit vectors is called an orthonormal basis.^{[citation needed]}

For a given inertial frame, an orthonormal basis in space, combined by the unit time vector, forms an orthonormal basis in Minkowski space. The number of positive and negative unit vectors in any such basis is a fixed pair of numbers, equal to the signature of the bilinear form associated with the inner product. This is Sylvester's law of inertia.

More terminology (but not more structure): The Minkowski metric is a pseudo-Riemannian metric, more specifically, a Lorentzian metric, even more specifically, the Lorentz metric, reserved for 4-dimensional flat spacetime with the remaining ambiguity only being the signature convention.

Minkowski metric

From the second postulate of special relativity, together with homogeneity of spacetime and isotropy of space, it follows that the spacetime interval between two arbitrary events called 1 and 2 is:

${\displaystyle \pm \left[c^{2}(t_{1}-t_{2})^{2}-(x_{1}-x_{2})^{2}-(y_{1}-y_{2})^{2}-(z_{1}-z_{2})^{2}\right].}$

The interval is independent of the inertial frame chosen, as is shown here. The factor ±1 determines the choice of the metric signature as an arbitrary sign convention.^[10] The numerical values of η, viewed as a matrix representing the Minkowski inner product, follow from the theory of bilinear forms.

Just as the signature of the metric is differently defined in the literature, this quantity is not consistently named. The interval (as defined here) is sometimes referred to as the interval squared.^[11] Even the square root of the present interval occurs.^[12] When signature and interval are fixed, ambiguity still remains as which coordinate is the time coordinate. It may be the fourth, or it may be the zeroth. This is not an exhaustive list of notational inconsistencies. It is a fact of life that one has to check out the definitions first thing when one consults the relativity literature.

The invariance of the interval under coordinate transformations between inertial frames follows from the invariance of

${\displaystyle \pm \left[c^{2}t^{2}-x^{2}-y^{2}-z^{2}\right]}$

(with either sign ± preserved), provided the transformations are linear. This quadratic form can be used to define a bilinear form

${\displaystyle u\cdot v=\pm \left[c^{2}t_{1}t_{2}-x_{1}x_{2}-y_{1}y_{2}-z_{1}z_{2}\right].}$

via the polarization identity. This bilinear form can in turn be written as

${\displaystyle u\cdot v=u^{\mathrm {T} }[\eta ]v,}$

where [η] is a 4×4 matrix associated with η. Possibly confusingly, denote [η] with just η as is common practice. The matrix is read off from the explicit bilinear form as

${\displaystyle \eta =\pm {\begin{pmatrix}-1&0&0&0\\0&1&0&0\\0&0&1&0\\0&0&0&1\end{pmatrix}},}$

and the bilinear form

${\displaystyle u\cdot v=\eta (u,v),}$

with which this section started by assuming its existence, is now identified.

For definiteness and shorter presentation, the signature (− + + +) is adopted below. This choice (or the other possible choice) has no (known) physical implications. The symmetry group preserving the bilinear form with one choice of signature is isomorphic (under the map given here) with the symmetry group preserving the other choice of signature. This means that both choices are in accord with the two postulates of relativity. Switching between the two conventions is straightforward. If the metric tensor η has been used in a derivation, go back to the earliest point where it was used, substitute η for –η, and retrace forward to the desired formula with the desired metric signature.

Standard basis

A standard basis for Minkowski space is a set of four mutually orthogonal vectors { e₀, e₁, e₂, e₃ } such that

${\displaystyle -\eta (e_{0},e_{0})=\eta (e_{1},e_{1})=\eta (e_{2},e_{2})=\eta (e_{3},e_{3})=1.}$

These conditions can be written compactly in the form

${\displaystyle \eta (e_{\mu },e_{\nu })=\eta _{\mu \nu }.}$

Relative to a standard basis, the components of a vector v are written (v⁰, v¹, v², v³) where the Einstein notation is used to write v = v^μe_μ. The component v⁰ is called the timelike component of v while the other three components are called the spatial components. The spatial components of a 4-vector v may be identified with a 3-vector v = (v₁, v₂, v₃).

In terms of components, the Minkowski inner product between two vectors v and w is given by

${\displaystyle \eta (v,w)=\eta _{\mu \nu }v^{\mu }w^{\nu }=v^{0}w_{0}+v^{1}w_{1}+v^{2}w_{2}+v^{3}w_{3}=v^{\mu }w_{\mu }=v_{\mu }w^{\mu },}$

and

${\displaystyle \eta (v,v)=\eta _{\mu \nu }v^{\mu }v^{\nu }=v^{0}v_{0}+v^{1}v_{1}+v^{2}v_{2}+v^{3}v_{3}=v^{\mu }v_{\mu }.}$

Here lowering of an index with the metric was used.

Raising and lowering of indices

Linear functionals (1-forms) α, β and their sum σ

and vectors u, v, w, in 3d Euclidean space. The

number of (1-form) hyperplanes intersected by a

vector equals the inner product.^[13]

Technically, a non-degenerate bilinear form provides a map between a vector space and its dual, in this context, the map is between the tangent spaces of M and the cotangent spaces of M. At a point in M, the tangent and cotangent spaces are dual vector spaces (so the dimension of the cotangent space at an event is also 4). Just as an authentic inner product on a vector space with one argument fixed, by Riesz representation theorem, may be expressed as the action of a linear functional on the vector space, the same holds for the Minkowski inner product of Minkowski space.^[14]

Thus if v^μ are the components of a vector in a tangent space, then η_μνv^μ = v_ν are the components of a vector in the cotangent space (a linear functional). Due to the identification of vectors in tangent spaces with vectors in M itself, this is mostly ignored, and vectors with lower indices are referred to as covariant vectors. In this latter interpretation, the covariant vectors are (almost always implicitly) identified with vectors (linear functionals) in the dual of Minkowski space. The ones with upper indices are contravariant vectors. In the same fashion, the inverse of the map from tangent to cotangent spaces, explicitly given by the inverse of η in matrix representation, can be used to define raising of an index. The components of this inverse are denoted η^μν. It happens that η^μν = η_μν. These maps between a vector space and its dual can be denoted η^♭ (eta-flat) and η^♯ (eta-sharp) by the musical analogy.^[15]

Contravariant and covariant vectors are geometrically very different objects. The first can and should be thought of as arrows. A linear functional can be characterized by two objects: its kernel, which is a hyperplane passing through the origin, and its norm. Geometrically thus covariant vectors should viewed as a set of hyperplanes, with spacing depending on the norm (bigger = smaller spacing), with one of them (the kernel) passing through the origin. The mathematical term for a covariant vector is 1-covector or 1-form (though the latter is usually reserved for covector fields).

Misner, Thorne & Wheeler (1970) uses a vivid analogy with wave fronts of a de Broglie wave (scaled by a factor of Planck's reduced constant) quantum mechanically associated to a momentum four-vector to illustrate how one could imagine a covariant version of a contravariant vector. The inner product of two contravariant vectors could equally well be thought of as the action of the covariant version of one of them on the contravariant version of the other. The inner product is then how many time the arrow pierces the planes. The mathematical reference, Lee (2003), offers the same geometrical view of these objects (but mentions no piercing).

The electromagnetic field tensor is a differential 2-form, which geometrical description can as well be found in MTW.

One may, of course, ignore geometrical views all together (as is the style in e.g. Weinberg (2002) and Landau & Lifshitz 2002) and proceed algebraically in a purely formal fashion. The time-proven robustness of the formalism itself, sometimes referred to as index gymnastics, ensures that moving vectors around and changing from contravariant to covariant vectors and vice versa (as well as higher order tensors) is mathematically sound. Incorrect expressions tend to reveal themselves quickly.

The formalism of the Minkowski metric

The present purpose is to show semi-rigorously how formally one may apply the Minkowski metric to two vectors and obtain a real number, i.e. to display the role of the differentials, and how they disappear in a calculation. The setting is that of smooth manifold theory, and concepts such as convector fields and exterior derivatives are introduced.

A formal approach to the Minkowski metric

Lorentz transformations and symmetry

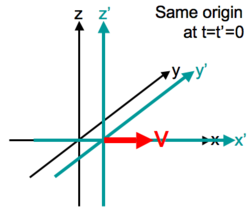
Standard configuration of coordinate systems for Lorentz transformations.

The Poincaré group is the group of all transformations preserving the interval. The interval is quite easily seen to be preserved by the translation group in 4 dimensions. The other transformations are those that preserve the interval and leave the origin fixed. Given the bilinear form associated with the Minkowski metric, the appropriate group follows directly from the theory (in particular the definition) of classical groups. In the linked article, one should identify η (in its a matrix representation) with the matrix Φ.

The appropriate group is O(3,1), in this context called the Lorentz group. Its elements are called (homogeneous) Lorentz transformations. For other methods of derivation, with a more physical twist, see derivations of the Lorentz transformations.

Among the simplest Lorentz transformations is a Lorentz boost. For reference, a boost in the x-direction is given by

${\displaystyle {\begin{bmatrix}U'_{0}\\U'_{1}\\U'_{2}\\U'_{3}\end{bmatrix}}={\begin{bmatrix}\gamma &-\beta \gamma &0&0\\-\beta \gamma &\gamma &0&0\\0&0&1&0\\0&0&0&1\\\end{bmatrix}}{\begin{bmatrix}U_{0}\\U_{1}\\U_{2}\\U_{3}\end{bmatrix}},}$

where

${\displaystyle \gamma ={1 \over {\sqrt {1-{v^{2} \over c^{2}}}}}}$

is the Lorentz factor, and

${\displaystyle \beta ={v \over c}\,.}$

Other Lorentz transformations are pure rotations, and hence elements of the SO(3) subgroup of O(3,1). A general homogeneous Lorentz transformation is a product of a pure boost and a pure rotation. An inhomogeneous Lorentz transformation is a homogeneous transformation followed by a translation in space and time. Special transformations are those that invert the space coordinates (P) and time coordinate (T) respectively, or both (PT).

All four-vectors in Minkowski space transform, by definition, according to the same formula under Lorentz transformations. Minkowski diagrams illustrate Lorentz transformations.

Causal structure

Subdivision of Minkowski spacetime with respect to an event in four disjoint sets. The light cone, the absolute future, the absolute past, and elsewhere. The terminology is from Sard (1970).

The momentarily co-moving inertial frames along the trajectory ("world line") of a rapidly accelerating observer (center). The vertical direction indicates time, while the horizontal indicates distance, the dashed line is the spacetime of the observer. The small dots are specific events in spacetime. Note how the momentarily co-moving inertial frame changes when the observer accelerates.

Where v is velocity, and x, y, and z are Cartesian coordinates in 3-dimensional space, and c is the constant representing the universal speed limit, and t is time, the four-dimensional vector v = (ct, x, y, z) = (ct, r) is classified according to the sign of c²t² − r². A vector is timelike if c²t² > r², spacelike if c²t² < r², and null or lightlike if c²t² = r². This can be expressed in terms of the sign of η(v,v) as well, but depends on the signature. The classification of any vector will be the same in all frames of reference that are related by a Lorentz transformation (but not by a general Poincaré transformation because the origin may then be displaced) because of the invariance of the interval.

The set of all null vectors at an event^{[nb 6]} of Minkowski space constitutes the light cone of that event. Given a timelike vector v, there is a worldline of constant velocity associated with it, represented by a straight line in a Minkowski diagram.

Once a direction of time is chosen,^{[nb 7]} timelike and null vectors can be further decomposed into various classes. For timelike vectors one has

1. future-directed timelike vectors whose first component is positive, (tip of vector located in absolute future in figure) and
2. past-directed timelike vectors whose first component is negative (absolute past).

Null vectors fall into three classes:

1. the zero vector, whose components in any basis are (0, 0, 0, 0) (origin),
2. future-directed null vectors whose first component is positive (upper light cone), and
3. past-directed null vectors whose first component is negative (lower light cone).

Spacelike vectors are in elsewhere. The terminology stems from the fact that spacelike separated events are connected by vectors requiring faster-than-light travel, and so cannot possibly influence each other. Together with spacelike and lightlike vectors there are 7 classes in all.

An orthonormal basis for Minkowski space necessarily consists of one timelike and three spacelike unit vectors. If one wishes to work with non-orthonormal bases it is possible to have other combinations of vectors. For example, one can easily construct a (non-orthonormal) basis consisting entirely of null vectors, called a null basis.

Vector fields are called timelike, spacelike or null if the associated vectors are timelike, spacelike or null at each point where the field is defined.

Chronological and causality relations

Let x, y ∈ M. We say that

1. x chronologically precedes y if y − x is future-directed timelike. This relation has the transitive property and so can be written x < y.
2. x causally precedes y if y − x is future-directed null or future-directed timelike. It gives a partial ordering of space-time and so can be written x ≤ y.

Suppose x ∈ M is timelike. Then the simultaneous hyperplane for x is ${\displaystyle \{y:\eta (x,y)=0\}.}$ Since this hyperplane varies as x varies, there is a relativity of simultaneity in Minkowski space.

Reversed triangle inequality

If v and w are both future-directed timelike four-vectors, then in the (+ − − −) sign convention for norm,

${\displaystyle \left\|v+w\right\|\geq \left\|v\right\|+\left\|w\right\|.}$

Generalizations

A Lorentzian manifold is a generalization of Minkowski space in two ways. The total number of spacetime dimensions is not restricted to be 4 (2 or more) and a Lorentzian manifold need not be flat, i.e. it allows for curvature.

Generalized Minkowski space

Minkowski space refers to a mathematical formulation in four dimensions. However, the mathematics can easily be extended or simplified to create an analogous generalized Minkowski space in any number of dimensions. If n ≥ 2, n-dimensional Minkowski space is a vector space of real dimension n on which there is a constant Minkowski metric of signature (n − 1, 1) or (1, n − 1). These generalizations are used in theories where spacetime is assumed to have more or less than 4 dimensions. String theory and M-theory are two examples where n > 4. In string theory, there appears conformal field theories with 1 + 1 spacetime dimensions.

de Sitter space can be formulated as a submanifold of generalized Minkowski space as can the model spaces of hyperbolic geometry (see below).

Curvature

As a flat spacetime, the three spatial components of Minkowski spacetime always obey the Pythagorean Theorem. Minkowski space is a suitable basis for special relativity, a good description of physical systems over finite distances in systems without significant gravitation. However, in order to take gravity into account, physicists use the theory of general relativity, which is formulated in the mathematics of a non-Euclidean geometry. When this geometry is used as a model of physical space, it is known as curved space.

Even in curved space, Minkowski space is still a good description in an infinitesimal region surrounding any point (barring gravitational singularities).^{[nb 8]} More abstractly, we say that in the presence of gravity spacetime is described by a curved 4-dimensional manifold for which the tangent space to any point is a 4-dimensional Minkowski space. Thus, the structure of Minkowski space is still essential in the description of general relativity.

Geometry

The meaning of the term geometry in the context of Minkowski space depends heavily on what is meant by the term. Minkowski space is not endowed with a Euclidean geometry, and not with any of the generalized Riemannian geometries with intrinsic curvature, those exposed by the model spaces in hyperbolic geometry (negative curvature) and the geometry modeled by the sphere (positive curvature). The reason is the indefiniteness of the Minkowski metric. Minkowski space is, in particular, not a metric space and not a Riemannian manifold with a Riemannian metric. However, Minkowski space contains submanifolds endowed with a Riemannian metric yielding hyperbolic geometry.

Model spaces of hyperbolic geometry of low dimension, say 2 or 3, cannot be isometrically embedded in Euclidean space with one more dimension, i.e. ℝ³ or ℝ⁴ respectively, with the Euclidean metric g, disallowing easy visualization.^{[nb 9][17]} By comparison, model spaces with positive curvature are just spheres in Euclidean space of one higher dimension.^[18] It turns out however that these hyperbolic spaces can be isometrically embedded in spaces of one more dimension when the embedding space is endowed with the Minkowski metric η.

Define H¹⁽ⁿ⁾
_R ⊂ Mⁿ⁺¹ to be the upper sheet (ct > 0) of the hyperboloid

${\displaystyle \mathbf {H} _{R}^{1(n)}=\left\{\left(ct,x^{1},\ldots ,x^{n}\right)\in \mathbf {M} ^{n}:c^{2}t^{2}-\left(x^{1}\right)^{2}\cdots \left(x^{n}\right)^{2}=R^{2},ct>0\right\}}$

in generalized Minkowski space Mⁿ⁺¹ of spacetime dimension n + 1. This is one of the surfaces of transitivity of the generalized Lorentz group. The induced metric on this submanifold,

${\displaystyle h_{R}^{1(n)}=\iota ^{*}\eta ,}$

the pullback of the Minkowski metric η under inclusion, is a Riemannian metric. With this metric H¹⁽ⁿ⁾
_R is a Riemannian manifold. It is one of the model spaces of Riemannian geometry, the hyperboloid model of hyperbolic space. It is a space of constant negative curvature −1/R².^[19] The 1 in the upper index refers to an enumeration of the different model spaces of hyperbolic geometry, and the n for its dimension. A 2(2) corresponds to the Poincaré disk model, while 3(n) corresponds to the Poincaré half-space model of dimension n.

Preliminaries

In the definition above ι:H¹⁽ⁿ⁾
_R → Mⁿ⁺¹ is the inclusion map and the superscript star denotes the pullback. The present purpose is to describe this and similar operations as a preparation for the actual demonstration that H¹⁽ⁿ⁾
_R actually is a hyperbolic space.

Behavior of tensors under inclusion, pullback of covariant tensors under general maps and pushforward of vectors under general maps

Hyperbolic stereographic projection

Red circular arc is geodesic in Poincaré disk model; it projects to the brown geodesic on the green hyperboloid.

In order to exhibit the metric it is necessary to pull it back via a suitable parametrization. A parametrization of a submanifold S of M is a map U ⊂ ℝ^m → M whose range is an open subset of S. If S has the same dimension as M, a parametrization is just the inverse of a coordinate map φ:M → U ⊂ ℝ^m. The parametrization to be used is the inverse of hyperbolic stereographic projection. This is illustrated in the figure to the left for n = 2. It is instructive to compare to stereographic projection for spheres.

Stereographic projection σ:Hⁿ
_R → ℝⁿ and its inverse σ⁻¹:ℝⁿ → Hⁿ
_R are given by

${\displaystyle {\begin{aligned}\sigma (\tau ,\mathbf {x} )&=\mathbf {u} ={\frac {R\mathbf {x} }{R+\tau }},\\\sigma ^{-1}(\mathbf {u} )=(\tau ,\mathbf {x} )&=\left(R{\frac {R^{2}+|u|^{2}}{R^{2}-|u|^{2}}},{\frac {2R^{2}\mathbf {u} }{R^{2}-|u|^{2}}}\right),\end{aligned}}}$

where, for simplicity, τ ≡ ct. The (τ, x) are coordinates on Mⁿ⁺¹ and the u are coordinates on ℝⁿ.

Pulling back the metric

One has

${\displaystyle h_{R}^{1(n)}=\eta |_{\mathbf {H} _{R}^{1(n)}}=\left(dx^{1}\right)^{2}+\cdots +\left(dx^{n}\right)^{2}-d\tau ^{2}}$

and the map

${\displaystyle \sigma ^{-1}:\mathbb {R} ^{n}\rightarrow \mathbf {H} _{R}^{1(n)};\sigma ^{-1}(\mathbf {u} )=(\tau (\mathbf {u} ),\mathbf {x} (\mathbf {u} ))=\left(R{\frac {R^{2}+|u|^{2}}{R^{2}-|u|^{2}}},{\frac {2R^{2}\mathbf {u} }{R^{2}-|u|^{2}}}\right).}$

The pulled back metric can be obtained by straightforward methods of calculus;

${\displaystyle \left.\left(\sigma ^{-1}\right)^{*}\eta \right|_{\mathbf {H} _{R}^{1(n)}}=\left(dx^{1}(\mathbf {u} )\right)^{2}+\cdots +\left(dx^{n}(\mathbf {u} )\right)^{2}-\left(d\tau (\mathbf {u} )\right)^{2}.}$

One computes according to the standard rules for computing differentials (though one is really computing the rigorously defined exterior derivatives),

${\displaystyle {\begin{aligned}dx^{1}(\mathbf {u} )&=d{\frac {2R^{2}u^{1}}{R^{2}-|u|^{2}}}={\frac {\partial }{\partial u^{1}}}{\frac {2R^{2}u^{1}}{R^{2}-|u|^{2}}}du^{1}+\cdots +{\frac {\partial }{\partial u^{n}}}{\frac {2R^{2}u^{1}}{R^{2}-|u|^{2}}}du^{n}+{\frac {\partial }{\partial \tau }}{\frac {2R^{2}u^{1}}{R^{2}-|u|^{2}}}d\tau ,\\&\cdots \\dx^{n}(\mathbf {u} )&=d{\frac {2R^{2}u^{n}}{R^{2}-|u|^{2}}}=\cdots ,\\d\tau (\mathbf {u} )&=d\left(R{\frac {R^{2}+|u|^{2}}{R^{2}-|u|^{2}}}\right)=\cdots ,\end{aligned}}}$

and substitutes the results into the right hand side. This yields

${\displaystyle \left(\sigma ^{-1}\right)^{*}h_{R}^{1(n)}={\frac {4R^{2}\left[\left(du^{1}\right)^{2}+\cdots +\left(du^{n}\right)^{2}\right]}{\left(R^{2}-|u|^{2}\right)^{2}}}\equiv h_{R}^{2(n)}.}$