Black hole (updated)

From Wikipedia, the free encyclopedia

 

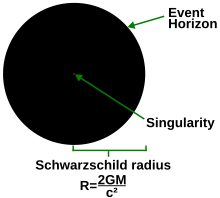
A black hole is a region of spacetime exhibiting such strong gravitational effects that nothing—not even particles and electromagnetic radiation such as light—can escape from inside it. The theory of general relativity predicts that a sufficiently compact mass can deform spacetime to form a black hole. The boundary of the region from which no escape is possible is called the event horizon. Although the event horizon has an enormous effect on the fate and circumstances of an object crossing it, no locally detectable features appear to be observed. In many ways a black hole acts like an ideal black body, as it reflects no light. Moreover, quantum field theory in curved spacetime predicts that event horizons emit Hawking radiation, with the same spectrum as a black body of a temperature inversely proportional to its mass. This temperature is on the order of billionths of a kelvin for black holes of stellar mass, making it essentially impossible to observe.

 

Objects whose gravitational fields are too strong for light to escape were first considered in the 18th century by John Michell and Pierre-Simon Laplace. The first modern solution of general relativity that would characterize a black hole was found by Karl Schwarzschild in 1916, although its interpretation as a region of space from which nothing can escape was first published by David Finkelstein in 1958. Black holes were long considered a mathematical curiosity; it was during the 1960s that theoretical work showed they were a generic prediction of general relativity. The discovery of neutron stars in the late 1960s sparked interest in gravitationally collapsed compact objects as a possible astrophysical reality.

Black holes of stellar mass are expected to form when very massive stars collapse at the end of their life cycle. After a black hole has formed, it can continue to grow by absorbing mass from its surroundings. By absorbing other stars and merging with other black holes, supermassive black holes of millions of solar masses (M_☉) may form. There is general consensus that supermassive black holes exist in the centers of most galaxies.

Despite its invisible interior, the presence of a black hole can be inferred through its interaction with other matter and with electromagnetic radiation such as visible light. Matter that falls onto a black hole can form an external accretion disk heated by friction, forming some of the brightest objects in the universe. If there are other stars orbiting a black hole, their orbits can be used to determine the black hole's mass and location. Such observations can be used to exclude possible alternatives such as neutron stars. In this way, astronomers have identified numerous stellar black hole candidates in binary systems, and established that the radio source known as Sagittarius A*, at the core of the Milky Way galaxy, contains a supermassive black hole of about 4.3 million solar masses.

On 11 February 2016, the LIGO collaboration announced the first direct detection of gravitational waves, which also represented the first observation of a black hole merger. As of December 2018, eleven gravitational wave events have been observed that originated from ten merging black holes (along with one binary neutron star merger).

Simulation of gravitational lensing by a black hole, which distorts the image of a galaxy in the background

 

Gas cloud being ripped apart by black hole at the centre of the Milky Way (observations from 2006, 2010 and 2013 are shown in blue, green and red, respectively).

History

Simulated view of a black hole in front of the Large Magellanic Cloud. Note the gravitational lensing effect, which produces two enlarged but highly distorted views of the Cloud. Across the top, the Milky Way disk appears distorted into an arc.

 

The idea of a body so massive that even light could not escape was briefly proposed by astronomical pioneer and English clergyman John Michell in a letter published in November 1784. Michell's simplistic calculations assumed that such a body might have the same density as the Sun, and concluded that such a body would form when a star's diameter exceeds the Sun's by a factor of 500, and the surface escape velocity exceeds the usual speed of light. Michell correctly noted that such supermassive but non-radiating bodies might be detectable through their gravitational effects on nearby visible bodies. Scholars of the time were initially excited by the proposal that giant but invisible stars might be hiding in plain view, but enthusiasm dampened when the wavelike nature of light became apparent in the early nineteenth century. If light were a wave rather than a "corpuscle", it became unclear what, if any, influence gravity would have on escaping light waves. Modern relativity discredits Michell's notion of a light ray shooting directly from the surface of a supermassive star, being slowed down by the star's gravity, stopping, and then free-falling back to the star's surface.

General relativity

In 1915, Albert Einstein developed his theory of general relativity, having earlier shown that gravity does influence light's motion. Only a few months later, Karl Schwarzschild found a solution to the Einstein field equations, which describes the gravitational field of a point mass and a spherical mass. A few months after Schwarzschild, Johannes Droste, a student of Hendrik Lorentz, independently gave the same solution for the point mass and wrote more extensively about its properties. This solution had a peculiar behavior at what is now called the Schwarzschild radius, where it became singular, meaning that some of the terms in the Einstein equations became infinite. The nature of this surface was not quite understood at the time. In 1924, Arthur Eddington showed that the singularity disappeared after a change of coordinates, although it took until 1933 for Georges Lemaître to realize that this meant the singularity at the Schwarzschild radius was a non-physical coordinate singularity. Arthur Eddington did however comment on the possibility of a star with mass compressed to the Schwarzschild radius in a 1926 book, noting that Einstein's theory allows us to rule out overly large densities for visible stars like Betelgeuse because "a star of 250 million km radius could not possibly have so high a density as the sun. Firstly, the force of gravitation would be so great that light would be unable to escape from it, the rays falling back to the star like a stone to the earth. Secondly, the red shift of the spectral lines would be so great that the spectrum would be shifted out of existence. Thirdly, the mass would produce so much curvature of the space-time metric that space would close up around the star, leaving us outside (i.e., nowhere)."

In 1931, Subrahmanyan Chandrasekhar calculated, using special relativity, that a non-rotating body of electron-degenerate matter above a certain limiting mass (now called the Chandrasekhar limit at 1.4 M_☉) has no stable solutions. His arguments were opposed by many of his contemporaries like Eddington and Lev Landau, who argued that some yet unknown mechanism would stop the collapse. They were partly correct: a white dwarf slightly more massive than the Chandrasekhar limit will collapse into a neutron star, which is itself stable. But in 1939, Robert Oppenheimer and others predicted that neutron stars above another limit (the Tolman–Oppenheimer–Volkoff limit) would collapse further for the reasons presented by Chandrasekhar, and concluded that no law of physics was likely to intervene and stop at least some stars from collapsing to black holes. Their original calculations, based on the Pauli exclusion principle, gave it as 0.7 M_☉; subsequent consideration of strong force-mediated neutron-neutron repulsion raised the estimate to approximately 1.5 M_☉ to 3.0 M_☉. Observations of the neutron star merger GW170817, which is thought to have generated a black hole shortly afterward, have refined the TOV limit estimate to ~2.17 M_☉.

Oppenheimer and his co-authors interpreted the singularity at the boundary of the Schwarzschild radius as indicating that this was the boundary of a bubble in which time stopped. This is a valid point of view for external observers, but not for infalling observers. Because of this property, the collapsed stars were called "frozen stars", because an outside observer would see the surface of the star frozen in time at the instant where its collapse takes it to the Schwarzschild radius.

Golden age

In 1958, David Finkelstein identified the Schwarzschild surface as an event horizon, "a perfect unidirectional membrane: causal influences can cross it in only one direction". This did not strictly contradict Oppenheimer's results, but extended them to include the point of view of infalling observers. Finkelstein's solution extended the Schwarzschild solution for the future of observers falling into a black hole. A complete extension had already been found by Martin Kruskal, who was urged to publish it.

These results came at the beginning of the golden age of general relativity, which was marked by general relativity and black holes becoming mainstream subjects of research. This process was helped by the discovery of pulsars in 1967, which, by 1969, were shown to be rapidly rotating neutron stars. Until that time, neutron stars, like black holes, were regarded as just theoretical curiosities; but the discovery of pulsars showed their physical relevance and spurred a further interest in all types of compact objects that might be formed by gravitational collapse.

In this period more general black hole solutions were found. In 1963, Roy Kerr found the exact solution for a rotating black hole. Two years later, Ezra Newman found the axisymmetric solution for a black hole that is both rotating and electrically charged. Through the work of Werner Israel, Brandon Carter, and David Robinson the no-hair theorem emerged, stating that a stationary black hole solution is completely described by the three parameters of the Kerr–Newman metric: mass, angular momentum, and electric charge.

At first, it was suspected that the strange features of the black hole solutions were pathological artifacts from the symmetry conditions imposed, and that the singularities would not appear in generic situations. This view was held in particular by Vladimir Belinsky, Isaak Khalatnikov, and Evgeny Lifshitz, who tried to prove that no singularities appear in generic solutions. However, in the late 1960s Roger Penrose and Stephen Hawking used global techniques to prove that singularities appear generically.

Work by James Bardeen, Jacob Bekenstein, Carter, and Hawking in the early 1970s led to the formulation of black hole thermodynamics. These laws describe the behaviour of a black hole in close analogy to the laws of thermodynamics by relating mass to energy, area to entropy, and surface gravity to temperature. The analogy was completed when Hawking, in 1974, showed that quantum field theory predicts that black holes should radiate like a black body with a temperature proportional to the surface gravity of the black hole.

Etymology

John Michell used the term "dark star", and in the early 20th century, physicists used the term "gravitationally collapsed object". Science writer Marcia Bartusiak traces the term "black hole" to physicist Robert H. Dicke, who in the early 1960s reportedly compared the phenomenon to the Black Hole of Calcutta, notorious as a prison where people entered but never left alive.

The term "black hole" was used in print by Life magazine and Science News magazine in 1963, and by science journalist Ann Ewing in her article "'Black Holes' in Space", dated 18 January 1964, which was a report on a meeting of the American Association for the Advancement of Science held in Cleveland, Ohio.

In December 1967, a student reportedly suggested the phrase "black hole" at a lecture by John Wheeler; Wheeler adopted the term for its brevity and "advertising value", and it quickly caught on, leading some to credit Wheeler with coining the phrase.

Properties and structure

A simple illustration of a non-spinning black hole

 

The no-hair conjecture postulates that, once it achieves a stable condition after formation, a black hole has only three independent physical properties: mass, charge, and angular momentum; the black hole is otherwise featureless. If the conjecture is true, any two black holes that share the same values for these properties, or parameters, are indistinguishable from one another. The degree to which the conjecture is true for real black holes under the laws of modern physics, is currently an unsolved problem.

These properties are special because they are visible from outside a black hole. For example, a charged black hole repels other like charges just like any other charged object. Similarly, the total mass inside a sphere containing a black hole can be found by using the gravitational analog of Gauss's law, the ADM mass, far away from the black hole. Likewise, the angular momentum can be measured from far away using frame dragging by the gravitomagnetic field.

When an object falls into a black hole, any information about the shape of the object or distribution of charge on it is evenly distributed along the horizon of the black hole, and is lost to outside observers. The behavior of the horizon in this situation is a dissipative system that is closely analogous to that of a conductive stretchy membrane with friction and electrical resistance—the membrane paradigm. This is different from other field theories such as electromagnetism, which do not have any friction or resistivity at the microscopic level, because they are time-reversible. Because a black hole eventually achieves a stable state with only three parameters, there is no way to avoid losing information about the initial conditions: the gravitational and electric fields of a black hole give very little information about what went in. The information that is lost includes every quantity that cannot be measured far away from the black hole horizon, including approximately conserved quantum numbers such as the total baryon number and lepton number. This behavior is so puzzling that it has been called the black hole information loss paradox.

Gravitational time dilation around a black hole

Physical properties

The simplest static black holes have mass but neither electric charge nor angular momentum. These black holes are often referred to as Schwarzschild black holes after Karl Schwarzschild who discovered this solution in 1916. According to Birkhoff's theorem, it is the only vacuum solution that is spherically symmetric. This means that there is no observable difference between the gravitational field of such a black hole and that of any other spherical object of the same mass. The popular notion of a black hole "sucking in everything" in its surroundings is therefore only correct near a black hole's horizon; far away, the external gravitational field is identical to that of any other body of the same mass.

Solutions describing more general black holes also exist. Non-rotating charged black holes are described by the Reissner–Nordström metric, while the Kerr metric describes a non-charged rotating black hole. The most general stationary black hole solution known is the Kerr–Newman metric, which describes a black hole with both charge and angular momentum.

While the mass of a black hole can take any positive value, the charge and angular momentum are constrained by the mass. In Planck units, the total electric charge Q and the total angular momentum J are expected to satisfy

${\displaystyle Q^{2}+\left({\tfrac {J}{M}}\right)^{2}\leq M^{2}\,}$

for a black hole of mass M. Black holes with the minimum possible mass satisfying this inequality are called extremal. Solutions of Einstein's equations that violate this inequality exist, but they do not possess an event horizon. These solutions have so-called naked singularities that can be observed from the outside, and hence are deemed unphysical. The cosmic censorship hypothesis rules out the formation of such singularities, when they are created through the gravitational collapse of realistic matter. This is supported by numerical simulations.

Due to the relatively large strength of the electromagnetic force, black holes forming from the collapse of stars are expected to retain the nearly neutral charge of the star. Rotation, however, is expected to be a universal feature of compact astrophysical objects. The black-hole candidate binary X-ray source GRS 1915+105 appears to have an angular momentum near the maximum allowed value. That uncharged limit is

${\displaystyle J\leq {\frac {GM^{2}}{c}},}$

allowing definition of a dimensionless spin parameter such that

${\displaystyle 0\leq {\frac {cJ}{GM^{2}}}\leq 1.}$

Black hole classifications

Class	Approx. mass	Approx. size
Supermassive black hole	105–1010 MSun	0.001–400 AU
Intermediate-mass black hole	103 MSun	103 km ≈ REarth
Stellar black hole	10 MSun	30 km
Micro black hole	up to MMoon	up to 0.1 mm

Black holes are commonly classified according to their mass, independent of angular momentum, J. The size of a black hole, as determined by the radius of the event horizon, or Schwarzschild radius, is roughly proportional to the mass, M, through

${\displaystyle r_{\mathrm {s} }={\frac {2GM}{c^{2}}}\approx 2.95\,{\frac {M}{M_{\mathrm {Sun} }}}~\mathrm {km,} }$

where r_s is the Schwarzschild radius and M_Sun is the mass of the Sun. For a black hole with nonzero spin and/or electric charge, the radius is smaller, until an extremal black hole could have an event horizon close to

${\displaystyle r_{\mathrm {+} }={\frac {GM}{c^{2}}}.}$

Event horizon

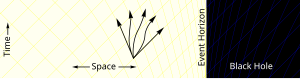
Far away from the black hole, a particle can move in any direction, as illustrated by the set of arrows. It is only restricted by the speed of light.

 

Closer to the black hole, spacetime starts to deform. There are more paths going towards the black hole than paths moving away.

 

Inside of the event horizon, all paths bring the particle closer to the center of the black hole. It is no longer possible for the particle to escape.

 

The defining feature of a black hole is the appearance of an event horizon—a boundary in spacetime through which matter and light can only pass inward towards the mass of the black hole. Nothing, not even light, can escape from inside the event horizon. The event horizon is referred to as such because if an event occurs within the boundary, information from that event cannot reach an outside observer, making it impossible to determine if such an event occurred.

As predicted by general relativity, the presence of a mass deforms spacetime in such a way that the paths taken by particles bend towards the mass. At the event horizon of a black hole, this deformation becomes so strong that there are no paths that lead away from the black hole.

To a distant observer, clocks near a black hole would appear to tick more slowly than those further away from the black hole. Due to this effect, known as gravitational time dilation, an object falling into a black hole appears to slow as it approaches the event horizon, taking an infinite time to reach it. At the same time, all processes on this object slow down, from the view point of a fixed outside observer, causing any light emitted by the object to appear redder and dimmer, an effect known as gravitational redshift. Eventually, the falling object fades away until it can no longer be seen. Typically this process happens very rapidly with an object disappearing from view within less than a second.

On the other hand, indestructible observers falling into a black hole do not notice any of these effects as they cross the event horizon. According to their own clocks, which appear to them to tick normally, they cross the event horizon after a finite time without noting any singular behavior; in classical general relativity, it is impossible to determine the location of the event horizon from local observations, due to Einstein's equivalence principle.

The shape of the event horizon of a black hole is always approximately spherical. For non-rotating (static) black holes the geometry of the event horizon is precisely spherical, while for rotating black holes the event horizon is oblate.

Singularity

At the center of a black hole, as described by general relativity, lies a gravitational singularity, a region where the spacetime curvature becomes infinite. For a non-rotating black hole, this region takes the shape of a single point and for a rotating black hole, it is smeared out to form a ring singularity that lies in the plane of rotation. In both cases, the singular region has zero volume. It can also be shown that the singular region contains all the mass of the black hole solution. The singular region can thus be thought of as having infinite density.

Observers falling into a Schwarzschild black hole (i.e., non-rotating and not charged) cannot avoid being carried into the singularity, once they cross the event horizon. They can prolong the experience by accelerating away to slow their descent, but only up to a limit. When they reach the singularity, they are crushed to infinite density and their mass is added to the total of the black hole. Before that happens, they will have been torn apart by the growing tidal forces in a process sometimes referred to as spaghettification or the "noodle effect".

In the case of a charged (Reissner–Nordström) or rotating (Kerr) black hole, it is possible to avoid the singularity. Extending these solutions as far as possible reveals the hypothetical possibility of exiting the black hole into a different spacetime with the black hole acting as a wormhole. The possibility of traveling to another universe is, however, only theoretical since any perturbation would destroy this possibility. It also appears to be possible to follow closed timelike curves (returning to one's own past) around the Kerr singularity, which lead to problems with causality like the grandfather paradox. It is expected that none of these peculiar effects would survive in a proper quantum treatment of rotating and charged black holes.

The appearance of singularities in general relativity is commonly perceived as signaling the breakdown of the theory. This breakdown, however, is expected; it occurs in a situation where quantum effects should describe these actions, due to the extremely high density and therefore particle interactions. To date, it has not been possible to combine quantum and gravitational effects into a single theory, although there exist attempts to formulate such a theory of quantum gravity. It is generally expected that such a theory will not feature any singularities.

Photon sphere

The photon sphere is a spherical boundary of zero thickness in which photons that move on tangents to that sphere would be trapped in a circular orbit about the black hole. For non-rotating black holes, the photon sphere has a radius 1.5 times the Schwarzschild radius. Their orbits would be dynamically unstable, hence any small perturbation, such as a particle of infalling matter, would cause an instability that would grow over time, either setting the photon on an outward trajectory causing it to escape the black hole, or on an inward spiral where it would eventually cross the event horizon.

While light can still escape from the photon sphere, any light that crosses the photon sphere on an inbound trajectory will be captured by the black hole. Hence any light that reaches an outside observer from the photon sphere must have been emitted by objects between the photon sphere and the event horizon.

Ergosphere

The ergosphere is a pumpkin-shaped region outside of the event horizon, where objects cannot remain stationary.

 

Rotating black holes are surrounded by a region of spacetime in which it is impossible to stand still, called the ergosphere. This is the result of a process known as frame-dragging; general relativity predicts that any rotating mass will tend to slightly "drag" along the spacetime immediately surrounding it. Any object near the rotating mass will tend to start moving in the direction of rotation. For a rotating black hole, this effect is so strong near the event horizon that an object would have to move faster than the speed of light in the opposite direction to just stand still.

The ergosphere of a black hole is a volume whose inner boundary is the black hole's oblate spheroid event horizon and a pumpkin-shaped outer boundary, which coincides with the event horizon at the poles but noticeably wider around the equator. The outer boundary is sometimes called the ergosurface.

Objects and radiation can escape normally from the ergosphere. Through the Penrose process, objects can emerge from the ergosphere with more energy than they entered. This energy is taken from the rotational energy of the black hole causing the latter to slow.

Innermost stable circular orbit (ISCO)

In Newtonian gravity, test particles can stably orbit at arbitrary distances from a central object. In general relativity, however, there exists an innermost stable circular orbit (often called the ISCO), inside of which, any infinitesimal perturbations to a circular orbit will lead to inspiral into the black hole. The location of the ISCO depends on the spin of the black hole, in the case of a Schwarzschild black hole (spin zero) is:

${\displaystyle r_{isco}=3\,r_{s}={\frac {6\,GM}{c^{2}}},}$

and decreases with increasing black hole spin for particles orbiting in the same direction as the spin.

Formation and evolution

Given the bizarre character of black holes, it was long questioned whether such objects could actually exist in nature or whether they were merely pathological solutions to Einstein's equations. Einstein himself wrongly thought that black holes would not form, because he held that the angular momentum of collapsing particles would stabilize their motion at some radius. This led the general relativity community to dismiss all results to the contrary for many years. However, a minority of relativists continued to contend that black holes were physical objects, and by the end of the 1960s, they had persuaded the majority of researchers in the field that there is no obstacle to the formation of an event horizon.

Two Black Holes Colliding

 

Penrose proved that once an event horizon forms, general relativity without quantum mechanics requires that a singularity will form within. Shortly afterwards, Hawking showed that many cosmological solutions that describe the Big Bang have singularities without scalar fields or other exotic matter. The Kerr solution, the no-hair theorem, and the laws of black hole thermodynamics showed that the physical properties of black holes were simple and comprehensible, making them respectable subjects for research. Conventional black holes are formed by gravitational collapse of heavy objects such as stars, but they can also in theory be formed by other processes.

Gravitational collapse

Gravitational collapse occurs when an object's internal pressure is insufficient to resist the object's own gravity. For stars this usually occurs either because a star has too little "fuel" left to maintain its temperature through stellar nucleosynthesis, or because a star that would have been stable receives extra matter in a way that does not raise its core temperature. In either case the star's temperature is no longer high enough to prevent it from collapsing under its own weight. The collapse may be stopped by the degeneracy pressure of the star's constituents, allowing the condensation of matter into an exotic denser state. The result is one of the various types of compact star. Which type forms depends on the mass of the remnant of the original star left after the outer layers have been blown away. Such explosions and pulsations lead to planetary nebula. This mass can be substantially less than the original star. Remnants exceeding 5 M_☉ are produced by stars that were over 20 M_☉ before the collapse.

If the mass of the remnant exceeds about 3–4 M_☉ (the Tolman–Oppenheimer–Volkoff limit), either because the original star was very heavy or because the remnant collected additional mass through accretion of matter, even the degeneracy pressure of neutrons is insufficient to stop the collapse. No known mechanism (except possibly quark degeneracy pressure, see quark star) is powerful enough to stop the implosion and the object will inevitably collapse to form a black hole.

Artist's impression of supermassive black hole seed.

 

The gravitational collapse of heavy stars is assumed to be responsible for the formation of stellar mass black holes. Star formation in the early universe may have resulted in very massive stars, which upon their collapse would have produced black holes of up to 10³ M_☉. These black holes could be the seeds of the supermassive black holes found in the centers of most galaxies. It has further been suggested that supermassive black holes with typical masses of ~10⁵ M_☉ could have formed from the direct collapse of gas clouds in the young universe. Some candidates for such objects have been found in observations of the young universe.

While most of the energy released during gravitational collapse is emitted very quickly, an outside observer does not actually see the end of this process. Even though the collapse takes a finite amount of time from the reference frame of infalling matter, a distant observer would see the infalling material slow and halt just above the event horizon, due to gravitational time dilation. Light from the collapsing material takes longer and longer to reach the observer, with the light emitted just before the event horizon forms delayed an infinite amount of time. Thus the external observer never sees the formation of the event horizon; instead, the collapsing material seems to become dimmer and increasingly red-shifted, eventually fading away.

Primordial black holes and the Big Bang

Gravitational collapse requires great density. In the current epoch of the universe these high densities are only found in stars, but in the early universe shortly after the Big Bang densities were much greater, possibly allowing for the creation of black holes. High density alone is not enough to allow black hole formation since a uniform mass distribution will not allow the mass to bunch up. In order for primordial black holes to have formed in such a dense medium, there must have been initial density perturbations that could then grow under their own gravity. Different models for the early universe vary widely in their predictions of the scale of these fluctuations. Various models predict the creation of primordial black holes ranging in size from a Planck mass to hundreds of thousands of solar masses.

Despite the early universe being extremely dense—far denser than is usually required to form a black hole—it did not re-collapse into a black hole during the Big Bang. Models for gravitational collapse of objects of relatively constant size, such as stars, do not necessarily apply in the same way to rapidly expanding space such as the Big Bang.

High-energy collisions

A simulated event in the CMS detector, a collision in which a micro black hole may be created.

 

Gravitational collapse is not the only process that could create black holes. In principle, black holes could be formed in high-energy collisions that achieve sufficient density. As of 2002, no such events have been detected, either directly or indirectly as a deficiency of the mass balance in particle accelerator experiments. This suggests that there must be a lower limit for the mass of black holes. Theoretically, this boundary is expected to lie around the Planck mass (m_P=√ħ c/G ≈ 1.2×10¹⁹ GeV/c² ≈ 2.2×10⁻⁸ kg), where quantum effects are expected to invalidate the predictions of general relativity. This would put the creation of black holes firmly out of reach of any high-energy process occurring on or near the Earth. However, certain developments in quantum gravity suggest that the Planck mass could be much lower: some braneworld scenarios for example put the boundary as low as 1 TeV/c². This would make it conceivable for micro black holes to be created in the high-energy collisions that occur when cosmic rays hit the Earth's atmosphere, or possibly in the Large Hadron Collider at CERN. These theories are very speculative, and the creation of black holes in these processes is deemed unlikely by many specialists. Even if micro black holes could be formed, it is expected that they would evaporate in about 10⁻²⁵ seconds, posing no threat to the Earth.

Growth

Once a black hole has formed, it can continue to grow by absorbing additional matter. Any black hole will continually absorb gas and interstellar dust from its surroundings. This is the primary process through which supermassive black holes seem to have grown. A similar process has been suggested for the formation of intermediate-mass black holes found in globular clusters. Black holes can also merge with other objects such as stars or even other black holes. This is thought to have been important, especially in the early growth of supermassive black holes, which could have formed from the aggregation of many smaller objects. The process has also been proposed as the origin of some intermediate-mass black holes.

Evaporation

In 1974, Hawking predicted that black holes are not entirely black but emit small amounts of thermal radiation at a temperature ℏ c³/(8 π G M k_B); this effect has become known as Hawking radiation. By applying quantum field theory to a static black hole background, he determined that a black hole should emit particles that display a perfect black body spectrum. Since Hawking's publication, many others have verified the result through various approaches. If Hawking's theory of black hole radiation is correct, then black holes are expected to shrink and evaporate over time as they lose mass by the emission of photons and other particles. The temperature of this thermal spectrum (Hawking temperature) is proportional to the surface gravity of the black hole, which, for a Schwarzschild black hole, is inversely proportional to the mass. Hence, large black holes emit less radiation than small black holes.

A stellar black hole of 1 M_☉ has a Hawking temperature of 62 nanokelvins. This is far less than the 2.7 K temperature of the cosmic microwave background radiation. Stellar-mass or larger black holes receive more mass from the cosmic microwave background than they emit through Hawking radiation and thus will grow instead of shrink. To have a Hawking temperature larger than 2.7 K (and be able to evaporate), a black hole would need a mass less than the Moon. Such a black hole would have a diameter of less than a tenth of a millimeter.

If a black hole is very small, the radiation effects are expected to become very strong. Even a black hole that is heavy compared to a human would evaporate in an instant. A black hole with the mass of a car would have a diameter of about 10⁻²⁴ m and take a nanosecond to evaporate, during which time it would briefly have a luminosity of more than 200 times that of the Sun. Lower-mass black holes are expected to evaporate even faster; for example, a black hole of mass 1 TeV/c² would take less than 10⁻⁸⁸ seconds to evaporate completely. For such a small black hole, quantum gravitation effects are expected to play an important role and could hypothetically make such a small black hole stable, although current developments in quantum gravity do not indicate so.

The Hawking radiation for an astrophysical black hole is predicted to be very weak and would thus be exceedingly difficult to detect from Earth. A possible exception, however, is the burst of gamma rays emitted in the last stage of the evaporation of primordial black holes. Searches for such flashes have proven unsuccessful and provide stringent limits on the possibility of existence of low mass primordial black holes. NASA's Fermi Gamma-ray Space Telescope launched in 2008 will continue the search for these flashes.

If black holes evaporate via Hawking radiation, a solar mass black hole will evaporate (beginning once the temperature of the cosmic microwave background drops below that of the black hole) over 10⁶⁴ years. A supermassive black hole with a mass of 10¹¹ (100 billion) M_☉ will evaporate in around 2×10¹⁰⁰ years. Some monster black holes in the universe are predicted to continue to grow up to perhaps 10¹⁴ M_☉ during the collapse of superclusters of galaxies. Even these would evaporate over a timescale of up to 10¹⁰⁶ years.

Observational evidence

Predicted appearance of non-rotating black hole with toroidal ring of ionised matter, such as has been proposed as a model for Sagittarius A*. The asymmetry is due to the Doppler effect resulting from the enormous orbital speed needed for centrifugal balance of the very strong gravitational attraction of the hole.

 

By their very nature, black holes do not directly emit any electromagnetic radiation other than the hypothetical Hawking radiation, so astrophysicists searching for black holes must generally rely on indirect observations. For example, a black hole's existence can sometimes be inferred by observing its gravitational interactions with its surroundings.

The Event Horizon Telescope (EHT), however, run by MIT's Haystack Observatory, is an attempt to directly observe the immediate environment of the event horizon of Sagittarius A*, the black hole at the center of the Milky Way, and to produce a silhouetted image of it. The first such image may appear as early as 2018. In 2015, the EHT managed to detect magnetic fields just outside the event horizon of Sagittarius A*, and even discern some of their properties. The existence of magnetic fields had been predicted by theoretical studies of black holes.

Detection of gravitational waves from merging black holes

On 14 September 2015 the LIGO gravitational wave observatory made the first-ever successful direct observation of gravitational waves. The signal was consistent with theoretical predictions for the gravitational waves produced by the merger of two black holes: one with about 36 solar masses, and the other around 29 solar masses. This observation provides the most concrete evidence for the existence of black holes to date. For instance, the gravitational wave signal suggests that the separation of the two objects prior to the merger was just 350 km (or roughly 4 times the Schwarzschild radius corresponding to the inferred masses). The objects must therefore have been extremely compact, leaving black holes as the most plausible interpretation.

More importantly, the signal observed by LIGO also included the start of the post-merger ringdown, the signal produced as the newly formed compact object settles down to a stationary state. Arguably, the ringdown is the most direct way of observing a black hole. From the LIGO signal it is possible to extract the frequency and damping time of the dominant mode of the ringdown. From these it is possible to infer the mass and angular momentum of the final object, which match independent predictions from numerical simulations of the merger. The frequency and decay time of the dominant mode are determined by the geometry of the photon sphere. Hence, observation of this mode confirms the presence of a photon sphere, however it cannot exclude possible exotic alternatives to black holes that are compact enough to have a photon sphere.

The observation also provides the first observational evidence for the existence of stellar-mass black hole binaries. Furthermore, it is the first observational evidence of stellar-mass black holes weighing 25 solar masses or more.

On 15 June 2016, a second detection of a gravitational wave event from colliding black holes was announced, and other gravitational wave events have since been observed.

Proper motions of stars orbiting Sagittarius A*

The proper motions of stars near the center of our own Milky Way provide strong observational evidence that these stars are orbiting a supermassive black hole. Since 1995, astronomers have tracked the motions of 90 stars orbiting an invisible object coincident with the radio source Sagittarius A*. By fitting their motions to Keplerian orbits, the astronomers were able to infer, in 1998, that a 2.6 million M_☉ object must be contained in a volume with a radius of 0.02 light-years to cause the motions of those stars. Since then, one of the stars—called S2—has completed a full orbit. From the orbital data, astronomers were able to refine the calculations of the mass to 4.3 million M_☉ and a radius of less than 0.002 light years for the object causing the orbital motion of those stars. The upper limit on the object's size is still too large to test whether it is smaller than its Schwarzschild radius; nevertheless, these observations strongly suggest that the central object is a supermassive black hole as there are no other plausible scenarios for confining so much invisible mass into such a small volume. Additionally, there is some observational evidence that this object might possess an event horizon, a feature unique to black holes.

Accretion of matter

Black hole with corona, X-ray source (artist's concept).

 

Due to conservation of angular momentum, gas falling into the gravitational well created by a massive object will typically form a disc-like structure around the object. Artists' impressions such as the accompanying representation of a black hole with corona commonly depict the black hole as if it were a flat-space body hiding the part of the disc just behind it, but in reality gravitational lensing would greatly distort the image of the accretion disk.

Predicted view from outside the horizon of a Schwarzschild black hole lit by a thin accretion disc

 

Within such a disc, friction would cause angular momentum to be transported outward, allowing matter to fall further inward, thus releasing potential energy and increasing the temperature of the gas.

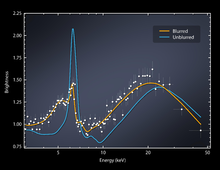
Blurring of X-rays near black hole (NuSTAR; 12 August 2014).

 

When the accreting object is a neutron star or a black hole, the gas in the inner accretion disc orbits at very high speeds because of its proximity to the compact object. The resulting friction is so significant that it heats the inner disc to temperatures at which it emits vast amounts of electromagnetic radiation (mainly X-rays). These bright X-ray sources may be detected by telescopes. This process of accretion is one of the most efficient energy-producing processes known; up to 40% of the rest mass of the accreted material can be emitted as radiation. (In nuclear fusion only about 0.7% of the rest mass will be emitted as energy.) In many cases, accretion discs are accompanied by relativistic jets that are emitted along the poles, which carry away much of the energy. The mechanism for the creation of these jets is currently not well understood, in part due to insufficient data.

As such, many of the universe's more energetic phenomena have been attributed to the accretion of matter on black holes. In particular, active galactic nuclei and quasars are believed to be the accretion discs of supermassive black holes. Similarly, X-ray binaries are generally accepted to be binary star systems in which one of the two stars is a compact object accreting matter from its companion. It has also been suggested that some ultraluminous X-ray sources may be the accretion disks of intermediate-mass black holes.

In November 2011 the first direct observation of a quasar accretion disk around a supermassive black hole was reported.

X-ray binaries

A Chandra X-Ray Observatory image of Cygnus X-1, which was the first strong black hole candidate discovered

 

X-ray binaries are binary star systems that emit a majority of their radiation in the X-ray part of the spectrum. These X-ray emissions are generally thought to result when one of the stars (compact object) accretes matter from another (regular) star. The presence of an ordinary star in such a system provides an opportunity for studying the central object and to determine if it might be a black hole.

If such a system emits signals that can be directly traced back to the compact object, it cannot be a black hole. The absence of such a signal does, however, not exclude the possibility that the compact object is a neutron star. By studying the companion star it is often possible to obtain the orbital parameters of the system and to obtain an estimate for the mass of the compact object. If this is much larger than the Tolman–Oppenheimer–Volkoff limit (that is, the maximum mass a neutron star can have before it collapses) then the object cannot be a neutron star and is generally expected to be a black hole.

The first strong candidate for a black hole, Cygnus X-1, was discovered in this way by Charles Thomas Bolton, Louise Webster and Paul Murdin in 1972. Some doubt, however, remained due to the uncertainties that result from the companion star being much heavier than the candidate black hole. Currently, better candidates for black holes are found in a class of X-ray binaries called soft X-ray transients. In this class of system, the companion star is of relatively low mass allowing for more accurate estimates of the black hole mass. Moreover, these systems are actively emit X-rays for only several months once every 10–50 years. During the period of low X-ray emission (called quiescence), the accretion disc is extremely faint allowing detailed observation of the companion star during this period. One of the best such candidates is V404 Cygni.

Quiescence and advection-dominated accretion flow

The faintness of the accretion disc of an X-ray binary during quiescence is suspected to be caused by the flow of mass entering a mode called an advection-dominated accretion flow (ADAF). In this mode, almost all the energy generated by friction in the disc is swept along with the flow instead of radiated away. If this model is correct, then it forms strong qualitative evidence for the presence of an event horizon, since if the object at the center of the disc had a solid surface, it would emit large amounts of radiation as the highly energetic gas hits the surface, an effect that is observed for neutron stars in a similar state.

Quasi-periodic oscillations

The X-ray emissions from accretion disks sometimes flicker at certain frequencies. These signals are called quasi-periodic oscillations and are thought to be caused by material moving along the inner edge of the accretion disk (the innermost stable circular orbit). As such their frequency is linked to the mass of the compact object. They can thus be used as an alternative way to determine the mass of candidate black holes.

Galactic nuclei

Magnetic waves, called Alfvén S-waves, flow from the base of black hole jets.

 

Astronomers use the term "active galaxy" to describe galaxies with unusual characteristics, such as unusual spectral line emission and very strong radio emission. Theoretical and observational studies have shown that the activity in these active galactic nuclei (AGN) may be explained by the presence of supermassive black holes, which can be millions of times more massive than stellar ones. The models of these AGN consist of a central black hole that may be millions or billions of times more massive than the Sun; a disk of gas and dust called an accretion disk; and two jets perpendicular to the accretion disk.

Detection of unusually bright X-Ray flare from Sagittarius A*, a black hole in the center of the Milky Way galaxy on 5 January 2015.

 

Although supermassive black holes are expected to be found in most AGN, only some galaxies' nuclei have been more carefully studied in attempts to both identify and measure the actual masses of the central supermassive black hole candidates. Some of the most notable galaxies with supermassive black hole candidates include the Andromeda Galaxy, M32, M87, NGC 3115, NGC 3377, NGC 4258, NGC 4889, NGC 1277, OJ 287, APM 08279+5255 and the Sombrero Galaxy.

It is now widely accepted that the center of nearly every galaxy, not just active ones, contains a supermassive black hole. The close observational correlation between the mass of this hole and the velocity dispersion of the host galaxy's bulge, known as the M-sigma relation, strongly suggests a connection between the formation of the black hole and the galaxy itself.

Simulation of gas cloud after close approach to the black hole at the center of the Milky Way.

Microlensing (proposed)

Another way that the black hole nature of an object may be tested in the future is through observation of effects caused by a strong gravitational field in their vicinity. One such effect is gravitational lensing: The deformation of spacetime around a massive object causes light rays to be deflected much as light passing through an optic lens. Observations have been made of weak gravitational lensing, in which light rays are deflected by only a few arcseconds. However, it has never been directly observed for a black hole. One possibility for observing gravitational lensing by a black hole would be to observe stars in orbit around the black hole. There are several candidates for such an observation in orbit around Sagittarius A*.

Alternatives

The evidence for stellar black holes strongly relies on the existence of an upper limit for the mass of a neutron star. The size of this limit heavily depends on the assumptions made about the properties of dense matter. New exotic phases of matter could push up this bound. A phase of free quarks at high density might allow the existence of dense quark stars, and some supersymmetric models predict the existence of Q stars. Some extensions of the standard model posit the existence of preons as fundamental building blocks of quarks and leptons, which could hypothetically form preon stars. These hypothetical models could potentially explain a number of observations of stellar black hole candidates. However, it can be shown from arguments in general relativity that any such object will have a maximum mass.

Since the average density of a black hole inside its Schwarzschild radius is inversely proportional to the square of its mass, supermassive black holes are much less dense than stellar black holes (the average density of a 10⁸ M_☉ black hole is comparable to that of water). Consequently, the physics of matter forming a supermassive black hole is much better understood and the possible alternative explanations for supermassive black hole observations are much more mundane. For example, a supermassive black hole could be modeled by a large cluster of very dark objects. However, such alternatives are typically not stable enough to explain the supermassive black hole candidates.

The evidence for the existence of stellar and supermassive black holes implies that in order for black holes to not form, general relativity must fail as a theory of gravity, perhaps due to the onset of quantum mechanical corrections. A much anticipated feature of a theory of quantum gravity is that it will not feature singularities or event horizons and thus black holes would not be real artifacts. For example, in the fuzzball model based on string theory, the individual states of a black hole solution do not generally have an event horizon or singularity, but for a classical/semi-classical observer the statistical average of such states appears just as an ordinary black hole as deduced from general relativity.

A few theoretical objects have been conjectured to match observations of astronomical black hole candidates identically or near-identically, but which function via a different mechanism. These include the gravastar, the black star (semiclassical gravity), and the dark-energy star.

Open questions

Entropy and thermodynamics

S = 1/4 c³k/Għ A

The formula for the Bekenstein–Hawking entropy (S) of a black hole, which depends on the area of the black hole (A). The constants are the speed of light (c), the Boltzmann constant (k), Newton's constant (G), and the reduced Planck constant (ħ). In Planck units, this reduces to S = A/4.

In 1971, Hawking showed under general conditions that the total area of the event horizons of any collection of classical black holes can never decrease, even if they collide and merge. This result, now known as the second law of black hole mechanics, is remarkably similar to the second law of thermodynamics, which states that the total entropy of a system can never decrease. As with classical objects at absolute zero temperature, it was assumed that black holes had zero entropy. If this were the case, the second law of thermodynamics would be violated by entropy-laden matter entering a black hole, resulting in a decrease of the total entropy of the universe. Therefore, Bekenstein proposed that a black hole should have an entropy, and that it should be proportional to its horizon area.

The link with the laws of thermodynamics was further strengthened by Hawking's discovery that quantum field theory predicts that a black hole radiates blackbody radiation at a constant temperature. This seemingly causes a violation of the second law of black hole mechanics, since the radiation will carry away energy from the black hole causing it to shrink. The radiation, however also carries away entropy, and it can be proven under general assumptions that the sum of the entropy of the matter surrounding a black hole and one quarter of the area of the horizon as measured in Planck units is in fact always increasing. This allows the formulation of the first law of black hole mechanics as an analogue of the first law of thermodynamics, with the mass acting as energy, the surface gravity as temperature and the area as entropy.

One puzzling feature is that the entropy of a black hole scales with its area rather than with its volume, since entropy is normally an extensive quantity that scales linearly with the volume of the system. This odd property led Gerard 't Hooft and Leonard Susskind to propose the holographic principle, which suggests that anything that happens in a volume of spacetime can be described by data on the boundary of that volume.

Although general relativity can be used to perform a semi-classical calculation of black hole entropy, this situation is theoretically unsatisfying. In statistical mechanics, entropy is understood as counting the number of microscopic configurations of a system that have the same macroscopic qualities (such as mass, charge, pressure, etc.). Without a satisfactory theory of quantum gravity, one cannot perform such a computation for black holes. Some progress has been made in various approaches to quantum gravity. In 1995, Andrew Strominger and Cumrun Vafa showed that counting the microstates of a specific supersymmetric black hole in string theory reproduced the Bekenstein–Hawking entropy. Since then, similar results have been reported for different black holes both in string theory and in other approaches to quantum gravity like loop quantum gravity.

Information loss paradox

Because a black hole has only a few internal parameters, most of the information about the matter that went into forming the black hole is lost. Regardless of the type of matter which goes into a black hole, it appears that only information concerning the total mass, charge, and angular momentum are conserved. As long as black holes were thought to persist forever this information loss is not that problematic, as the information can be thought of as existing inside the black hole, inaccessible from the outside, but represented on the event horizon in accordance with the holograpic principle. However, black holes slowly evaporate by emitting Hawking radiation. This radiation does not appear to carry any additional information about the matter that formed the black hole, meaning that this information appears to be gone forever.

The question whether information is truly lost in black holes (the black hole information paradox) has divided the theoretical physics community (see Thorne–Hawking–Preskill bet). In quantum mechanics, loss of information corresponds to the violation of vital property called unitarity, which has to do with the conservation of probability. It has been argued that loss of unitarity would also imply violation of conservation of energy. Over recent years evidence has been building that indeed information and unitarity are preserved in a full quantum gravitational treatment of the problem.

The firewall paradox

According to quantum field theory in curved spacetime, a single emission of Hawking radiation involves two mutually entangled particles. The outgoing particle escapes and is emitted as a quantum of Hawking radiation; the infalling particle is swallowed by the black hole. Assume a black hole formed a finite time in the past and will fully evaporate away in some finite time in the future. Then, it will only emit a finite amount of information encoded within its Hawking radiation. Assume that at time ${\displaystyle t}$, more than half of the information had already been emitted. According to widely accepted research by physicists like Don Page and Leonard Susskind, an outgoing particle emitted at time ${\displaystyle t}$ must be entangled with all the Hawking radiation the black hole has previously emitted. This creates a paradox: a principle called "monogamy of entanglement" requires that, like any quantum system, the outgoing particle cannot be fully entangled with two independent systems at the same time; yet here the outgoing particle appears to be entangled with both the infalling particle and, independently, with past Hawking radiation.

In order to resolve the paradox, physicists may eventually be forced to give up one of three time-tested theories: Einstein's equivalence principle, unitarity, or existing quantum field theory. One possible solution, which violates the equivalence principle, is that a "firewall" destroys incoming particles at the event horizon. A 2016 analysis of LIGO data shows tentative signs of echoes caused by a fuzzy event horizon; such echoes may be possible in firewall or fuzzball theories but should not occur in classical general relativity. Over the next two years, additional LIGO data should establish whether the echoes were just random noise, or whether they are instead evidence of a violation of classical general relativity.