Cyclotron

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Cyclotron 

Lawrence's 60-inch cyclotron, with magnet poles 60 inches (5 feet, 1.5 meters) in diameter, at the University of California Lawrence Radiation Laboratory, Berkeley, in August, 1939, the most powerful accelerator in the world at the time. Glenn T. Seaborg and Edwin M. McMillan (right) used it to discover plutonium, neptunium, and many other transuranic elements and isotopes, for which they received the 1951 Nobel Prize in chemistry. The cyclotron's huge magnet is at left, with the flat accelerating chamber between its poles in the center. The beamline which analyzed the particles is at right.

A cyclotron is a type of particle accelerator invented by Ernest O. Lawrence in 1929–1930 at the University of California, Berkeley, and patented in 1932. A cyclotron accelerates charged particles outwards from the center of a flat cylindrical vacuum chamber along a spiral path. The particles are held to a spiral trajectory by a static magnetic field and accelerated by a rapidly varying electric field. Lawrence was awarded the 1939 Nobel Prize in Physics for this invention.

The cyclotron was the first "cyclical" accelerator. In existing electrostatic accelerators of the time, such as the Cockcroft–Walton accelerator and Van de Graaff generator, particles would cross an accelerating electric field only once. Thus, the energy gained by the particles was limited by the maximum electrical potential that could be achieved across the accelerating region. This was in turn limited by electrostatic breakdown to a few million volts. In a cyclotron, by contrast, the particles encounter the accelerating region many times by following a spiral path, so the output energy can be many times the energy gained in a single accelerating step.

Cyclotrons were the most powerful particle accelerator technology until the 1950s, when they were superseded by the synchrotron. Despite no longer being the highest-energy accelerator, they are still widely used to produce particle beams for basic research and nuclear medicine. Close to 1500 cyclotrons are used in nuclear medicine worldwide for the production of medical radionuclides. In addition, cyclotrons can be used for particle therapy, where particle beams are directly applied to patients.

History

Lawrence's 60-inch cyclotron, circa 1939, showing the beam of accelerated ions (likely protons or deuterons) exiting the machine and ionizing the surrounding air causing a blue glow.

 

The magnet yoke for the 37″ cyclotron on display at the Lawrence Hall of Science, Berkeley California.

In late 1928 and early 1929 Hungarian physicist Leo Szilárd filed patent applications in Germany (later abandoned) for the linear accelerator, cyclotron, and betatron. In these applications, Szilárd became the first person to discuss the resonance condition (what is now called the cyclotron frequency) for a circular accelerating apparatus. Several months later, in the early summer of 1929, Ernest Lawrence independently conceived the cyclotron concept after reading a paper by Rolf Widerøe describing a drift tube accelerator. He published a paper in Science in 1930, and patented the device in 1932.

To construct the first such device, Lawrence used large electromagnets recycled from obsolete arc converters provided by the Federal Telegraph Company. He was assisted by a graduate student, M. Stanley Livingston Their first working cyclotron became operational in January 1931. This machine had a radius of 4.5 inches (11 cm), and accelerated protons to an energy up to 80 keV.

At the Radiation Laboratory of the University of California, Berkeley, Lawrence and his collaborators went on to construct a series of cyclotrons which were the most powerful accelerators in the world at the time; a 27 in (69 cm) 4.8 MeV machine (1932), a 37 in (94 cm) 8 MeV machine (1937), and a 60 in (152 cm) 16 MeV machine (1939). Lawrence received the 1939 Nobel Prize in Physics for the invention and development of the cyclotron and for results obtained with it.

The first European cyclotron was constructed in the Soviet Union in the physics department of the Radium Institute in Leningrad, headed by Vitaly Khlopin [ru]. This Leningrad instrument was first proposed in 1932 by George Gamow and Lev Mysovskii [ru] and was installed and became operative by 1937.

Two cyclotrons were built in Nazi Germany. The first was constructed in 1937, in Otto Hahn's laboratory at the Kaiser Wilhelm Institute in Berlin, and was also used by Rudolf Fleischmann. It was the first cyclotron with a Greinacher multiplier to increase the voltage to 2.8 MV and 3 mA current. A second cyclotron was built in Heidelberg under the supervision of Walther Bothe and Wolfgang Gentner, with support from the Heereswaffenamt, and became operative in 1943.

By the late 1930s it had become clear that there was a practical limit on the beam energy that could be achieved with the traditional cyclotron design, due to the effects of special relativity. As particles reach relativistic speeds, their effective mass increases, which causes the resonant frequency for a given magnetic field to change. To address this issue and reach higher beam energies using cyclotrons, two primary approaches were taken, synchrocyclotrons (which hold the magnetic field constant, but increase the accelerating frequency) and isochronous cyclotrons (which hold the accelerating frequency constant, but alter the magnetic field).

Lawrence's team built one of the first synchrocyclotrons in 1946. This 184 in (4.7 m) machine eventually achieved a maximum beam energy of 350 MeV for protons. However, synchrocyclotrons suffer from low beam intensities (< 1 µA), and must be operated in a "pulsed" mode, further decreasing the available total beam. As such, they were quickly overtaken in popularity by isochronous cyclotrons.

The first isochronous cyclotron (other than classified prototypes) was built by F. Heyn and K.T. Khoe in Delft, the Netherlands, in 1956. Early isochronous cyclotrons were limited to energies of ~50 MeV per nucleon, but as manufacturing and design techniques gradually improved, the construction of "spiral-sector" cyclotrons allowed the acceleration and control of more powerful beams. Later developments included the use of more powerful superconducting magnets and the separation of the magnets into discrete sectors, as opposed to a single large magnet.

Principle of operation

Diagram of a cyclotron. The magnet's pole pieces are shown smaller than in reality; they must actually be at least as wide as the accelerating electrodes ("dees") to create a uniform field.

Cyclotron principle

Illustration of a linear accelerator, showing the increasing separation between gaps.

 

Diagram of cyclotron operation from Lawrence's 1934 patent. The "D" shaped electrodes (left) are enclosed in a flat vacuum chamber, which is installed in a narrow gap between the two poles of a large magnet.(right)

 

Vacuum chamber of Lawrence 69 cm (27 in) 1932 cyclotron with cover removed, showing the dees. The 13,000 V RF accelerating potential at about 27 MHz is applied to the dees by the two feedlines visible at top right. The beam emerges from the dees and strikes the target in the chamber at bottom.

In a particle accelerator, charged particles are accelerated by applying an electric field across a gap. The force on the particle is given by the Lorentz force law:

${\displaystyle {\vec {F}}=q{\vec {E}}+q{\vec {v}}\times {\vec {B}}}$

where q is the charge on the particle, E is the electric field, v is the particle velocity, and B is the magnetic field. Consequently, it is not possible to accelerate particles using a static magnetic field, as the magnetic force always acts perpendicularly to the direction of motion.

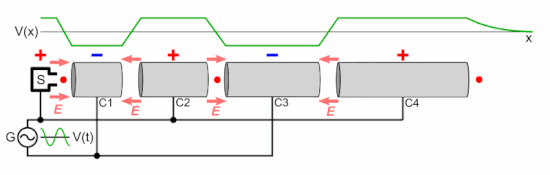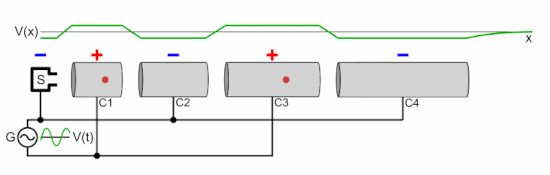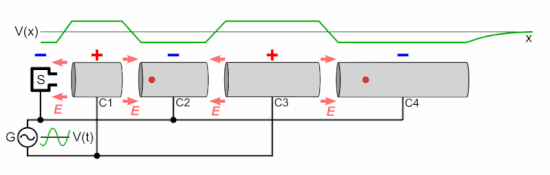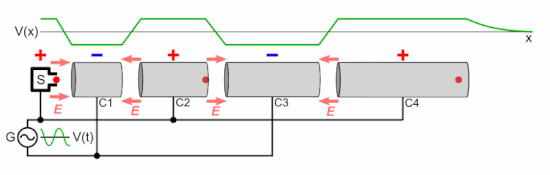
In practice, the magnitude of a static field which can be applied across a gap is limited by the need to avoid electrostatic breakdown. As such, modern particle accelerators use alternating (radio frequency) electric fields for acceleration. Since an alternating field across a gap only provides an acceleration in the forward direction for a portion of its cycle, particles in RF accelerators travel in bunches, rather than a continuous stream. In a linear particle accelerator, in order for a bunch to "see" a forward voltage every time it crosses a gap, the gaps must be placed further and further apart, in order to compensate for the increasing speed of the particle.

A cyclotron, by contrast, uses a magnetic field to bend the particle trajectories into a spiral, thus allowing the same gap to be used many times to accelerate a single bunch. As the bunch spirals outward, the increasing distance between transits of the gap is exactly balanced by the increase in speed, so a bunch will reach the gap at the same point in the RF cycle every time.

The frequency at which a particle will orbit in a perpendicular magnetic field is known as the cyclotron frequency, and depends, in the non-relativistic case, solely on the charge and mass of the particle, and the strength of the magnetic field:

${\displaystyle f={\frac {qB}{2\pi m}}}$

where f is the (linear) frequency, q is the charge of the particle, B is the magnitude of the magnetic field that is perpendicular to the plane in which the particle is travelling, and m is the particle mass. The property that the frequency is independent of particle velocity is what allows a single, fixed gap to be used to accelerate a particle travelling in a spiral.

Particle energy

Each time a particle crosses the accelerating gap in a cyclotron, it is given an accelerating force by the electric field across the gap, and the total particle energy gain can be calculated by multiplying the increase per crossing by the number of times the particle crosses the gap.

However, given the typically high number of revolutions, it is usually simpler to estimate the energy by combining the equation for frequency in circular motion:

${\displaystyle f={\frac {v}{2\pi R}}}$

with the cyclotron frequency equation to yield:

${\displaystyle v={\frac {qBR}{m}}}$

The kinetic energy for particles with velocity v is therefore given by:

${\displaystyle E={\frac {1}{2}}mv^{2}={\frac {q^{2}B^{2}R^{2}}{2m}}}$

where R is the radius at which the energy is to be determined. The limit on the beam energy which can be produced by a given cyclotron thus depends on the maximum radius which can be reached by the magnetic field and the accelerating structures, and on the maximum strength of the magnetic field which can be achieved.

K-factor

In the nonrelativistic approximation, the maximum kinetic energy per atomic mass for a given cyclotron is given by:

${\displaystyle {\frac {T}{A}}={\frac {(eBr_{\max })^{2}}{2m_{a}}}\left({\frac {Q}{A}}\right)^{2}=K\left({\frac {Q}{A}}\right)^{2}}$

where ${\displaystyle e}$ is the elementary charge, ${\displaystyle B}$ is the strength of the magnet, ${\displaystyle r_{\max }}$ is the maximum radius of the beam, ${\displaystyle m_{a}}$ is an atomic mass unit, ${\displaystyle Q}$ is the charge of the beam particles, and ${\displaystyle A}$ is the atomic mass of the beam particles. The value of K

${\displaystyle K={\frac {(eBr_{\max })^{2}}{2m_{a}}}}$

is known as the "K-factor", and is used to characterize the maximum beam energy of a cyclotron. It represents the theoretical maximum energy of protons (with Q and A equal to 1) accelerated in a given machine.

Relativistic considerations

In the non-relativistic approximation, the cyclotron frequency does not depend upon the particle's speed or the radius of the particle's orbit. As the beam spirals outward, the rotation frequency stays constant, and the beam continues to accelerate as it travels a greater distance in the same time period.

In contrast to this approximation, as particles approach the speed of light, the cyclotron frequency decreases due to the change in relativistic mass. This change is proportional to the particle's Lorentz factor.

The relativistic mass can be written as:

${\displaystyle m={\frac {m_{0}}{\sqrt {1-\left({\frac {v}{c}}\right)^{2}}}}={\frac {m_{0}}{\sqrt {1-\beta ^{2}}}}=\gamma {m_{0}},}$

where:

• ${\displaystyle m_{0}}$ is the particle rest mass,
• ${\displaystyle \beta ={\frac {v}{c}}}$ is the relative velocity, and
• ${\displaystyle \gamma ={\frac {1}{\sqrt {1-\beta ^{2}}}}={\frac {1}{\sqrt {1-\left({\frac {v}{c}}\right)^{2}}}}}$ is the Lorentz factor.

Substituting this into the equations for cyclotron frequency and angular frequency gives:

${\displaystyle {\begin{aligned}f&={\frac {qB}{2\pi \gamma m_{0}}}\\[6pt]\omega &={\frac {qB}{\gamma m_{0}}}\end{aligned}}}$

The gyroradius for a particle moving in a static magnetic field is then given by:

${\displaystyle r={\frac {\gamma \beta m_{0}c}{qB}}}$

Approaches to relativistic cyclotrons

Synchrocyclotron

Main article: Synchrocyclotron

Since ${\displaystyle \gamma }$ increases as the particle reaches relativistic velocities, acceleration of relativistic particles therefore requires modification of the cyclotron to ensure the particle crosses the gap at the same point in the RF cycle. If the frequency of the accelerating electric field is varied while the magnetic field is held constant, this leads to the synchrocyclotron. 

${\displaystyle f(r)={\frac {qB}{2\pi \gamma (r)m_{0}}}}$

Here the frequency is a function of particle radius, and is adjusted to balance the relativistic change of particle velocity (incorporated into ${\displaystyle \gamma }$) with radius.

Isochronous cyclotron

If instead the magnetic field is varied with radius while the frequency of the accelerating field is held constant, this leads to the isochronous cyclotron.

${\displaystyle f={\frac {qB(r)}{2\pi \gamma (r)m_{0}}}}$

Here the magnetic field B is a function of radius, chosen to maintain a constant frequency f as ${\displaystyle \gamma }$ increases.

Isochronous cyclotrons are capable of producing much greater beam current than synchrocyclotrons, but require precisely shaped variations in the magnetic field strength to provide a focusing effect and keep the particles captured in their spiral trajectory. For this reason, an isochronous cyclotron is also called an "AVF (azimuthal varying field) cyclotron". This solution for focusing the particle beam was proposed by L. H. Thomas in 1938. Almost all modern cyclotrons use azimuthally-varying fields.

Fixed-field alternating gradient accelerator

Main article: Fixed-field alternating gradient accelerator

An approach which combines static magnetic fields (as in the synchrocyclotron) and alternating gradient focusing (as in a synchrotron) is the fixed-field alternating gradient accelerator (FFA). In an isochronous cyclotron, the magnetic field is shaped by using precisely machined steel magnet poles. This variation provides a focusing effect as the particles cross the edges of the poles. In an FFA, separate magnets with alternating directions are used to focus the beam using the principle of strong focusing. The field of the focusing and bending magnets in an FFA is not varied over time, so the beam chamber must still be wide enough to accommodate a changing beam radius within the field of the focusing magnets as the beam accelerates.

Classifications

A French cyclotron, produced in Zurich, Switzerland in 1937. The vacuum chamber containing the dees (at left) has been removed from the magnet (red, at right)

Cyclotron types

There are a number of basic types of cyclotron:

Classical cyclotron

The earliest and simplest cyclotron. Classical cyclotrons have uniform magnetic fields and a constant accelerating frequency. They are limited to nonrelativistic particle velocities (the output energy small compared to the particle's rest energy), and have no active focusing to keep the beam aligned in the plane of acceleration.

Synchrocyclotron

The synchrocyclotron extended the energy of the cyclotron into the relativistic regime by decreasing the frequency of the accelerating field as the orbit of the particles increased to keep it synchronized with the particle revolution frequency. Because this requires pulsed operation, the integrated total beam current was low compared to the classical cyclotron. In terms of beam energy, these were the most powerful accelerators during the 1950s, before the development of the synchrotron.

Isochronous cyclotron (isocyclotron)

These cyclotrons extend output energy into the relativistic regime by altering the magnetic field to compensate for the change in cyclotron frequency as the particles reached relativistic speed. They use shaped magnet pole pieces to create a nonuniform magnetic field stronger in peripheral regions. Most modern cyclotrons are of this type. The pole pieces can also be shaped to cause the beam to keep the particles focused in the acceleration plane as the orbit. This is known as "sector focusing" or "azimuthally-varying field focusing", and uses the principle of alternating-gradient focusing.

Separated sector cyclotron

Separated sector cyclotrons are machines in which the magnet is in separate sections, separated by gaps without field.

Superconducting cyclotron

"Superconducting" in the cyclotron context refers to the type of magnet used to bend the particle orbits into a spiral. Superconducting magnets can produce substantially higher fields in the same area than normal conducting magnets, allowing for more compact, powerful machines. The first superconducting cyclotron was the K500 at the Michigan State University, which came online in 1981.

Beam types

The particles for cyclotron beams are produced in ion sources of various types.

Proton beams

The simplest type of cyclotron beam, proton beams are typically created by ionizing hydrogen gas.

H⁻ beams

Accelerating negative hydrogen ions simplifies extracting the beam from the machine. At the radius corresponding to the desired beam energy, a metal foil is used to strip the electrons from the H⁻ ions, transforming them into positively charged H⁺ ions. The change in polarity causes the beam to be deflected in the opposite direction by the magnetic field, allowing the beam to be transported out of the machine.

Heavy ion beams

Beams of particles heavier than hydrogen are referred to as heavy ion beams, and can range from deuterium nuclei (one proton and one neutron) up to uranium nuclei. The increase in energy required to accelerate heavier particles is balanced by stripping more electrons from the atom to increase the electric charge of the particles, thus increasing acceleration efficiency.

Target types

To make use of the cyclotron beam, it must be directed to a target.

Internal targets

The simplest way to strike a target with a cyclotron beam is to insert it directly into the path of the beam in the cyclotron. Internal targets have the disadvantage that they must be compact enough to fit within the cyclotron beam chamber, making them impractical for many medical and research uses.

External targets

While extracting a beam from a cyclotron to impinge on an external target is more complicated than using an internal target, it allows for greater control of the placement and focus of the beam, and much more flexibility in the types of targets to which the beam can be directed.

Usage

A modern cyclotron used for radiation therapy. The magnet is painted yellow.

Basic research

For several decades, cyclotrons were the best source of high-energy beams for nuclear physics experiments. With the advent of strong focusing synchrotrons, cyclotrons were supplanted as the accelerators capable of producing the highest energies. However, due to their compactness, and therefore lower expense compared to high energy synchrotrons, cyclotrons are still used to create beams for research where the primary consideration is not achieving the maximum possible energy. Cyclotron based nuclear physics experiments are used to measure basic properties of isotopes (particularly short lived radioactive isotopes) including half life, mass, interaction cross sections, and decay schemes.

Medical uses

Radioisotope production

Cyclotron beams can be used to bombard other atoms to produce short-lived isotopes with a variety of medical uses, including medical imaging and radiotherapy. Positron and gamma emitting isotopes, such as fluorine-18, carbon-11, and technetium-99m are used for PET and SPECT imaging. While cyclotron produced radioisotopes are widely used for diagnostic purposes, therapeutic uses are still largely in development. Proposed isotopes include astatine-211, palladium-103, rhenium-186, and bromine-77, among others.

Beam therapy

Beams from cyclotrons can be used in particle therapy to treat cancer. Ion beams from cyclotrons can be used, as in proton therapy, to penetrate the body and kill tumors by radiation damage, while minimizing damage to healthy tissue along their path. As of 2020, there were approximately 80 facilities worldwide for radiotherapy using beams of protons and heavy ions, consisting of a mixture of cyclotrons and synchrotrons. Cyclotrons are primarily used for proton beams, while synchrotrons are used to produce heavier ions.

Advantages and limitations

M. Stanley Livingston and Ernest O. Lawrence (right) in front of Lawrence's 69 cm (27 in) cyclotron at the Lawrence Radiation Laboratory. The curving metal frame is the magnet's core, the large cylindrical boxes contain the coils of wire that generate the magnetic field. The vacuum chamber containing the "dee" electrodes is in the center between the magnet's poles.

The most obvious advantage of a cyclotron over a linear accelerator is that because the same accelerating gap is used many times, it is both more space efficient and more cost efficient; particles can be brought to higher energies in less space, and with less equipment. The compactness of the cyclotron reduces other costs as well, such as foundations, radiation shielding, and the enclosing building. Cyclotrons have a single electrical driver, which saves both equipment and power costs. Furthermore, cyclotrons are able to produce a continuous beam of particles at the target, so the average power passed from a particle beam into a target is relatively high compared to the pulsed beam of a synchrotron.

However, as discussed above, a constant frequency acceleration method is only possible when the accelerated particles are approximately obeying Newton's laws of motion. If the particles become fast enough that relativistic effects become important, the beam becomes out of phase with the oscillating electric field, and cannot receive any additional acceleration. The classical cyclotron (constant field and frequency) is therefore only capable of accelerating particles up to a few percent of the speed of light. Synchro-, isochronous, and other types of cyclotrons can overcome this limitation, with the tradeoff of increased complexity and cost.

An additional limitation of cyclotrons is due to space charge effects – the mutual repulsion of the particles in the beam. As the amount of particles (beam current) in a cyclotron beam is increased, the effects of electrostatic repulsion grow stronger until they disrupt the orbits of neighboring particles. This puts a functional limit on the beam intensity, or the number of particles which can be accelerated at one time, as distinct from their energy.

Notable examples

Name	Country	Date	Energy	Beam	Diameter	In use?	Comments
Lawrence 4.5-inch Cyclotron	United States	1931	80 keV	Protons	4.5 inches (0.11 m)	No	First working cyclotron
Lawrence 184-inch Cyclotron	United States	1946	380 MeV	Alpha particles, deuterium, protons	184 inches (4.7 m)	No	First synchrocyclotron
TU Delft Isochronous Cyclotron	Netherlands	1958	12 MeV	Protons	0.36 m	No	First isochronous cyclotron
PSI Ring Cyclotron	Switzerland	1974	592 MeV	Protons	15 m	Yes	Highest beam intensity of any cyclotron
TRIUMF 520 MeV	Canada	1976	520 MeV	H−	56 feet (17 m)	Yes	Largest normal conductivity cyclotron
Michigan State University K500	United States	1982	500 MeV/u	Heavy Ion	52 inches (1.3 m)	No	First superconducting cyclotron
RIKEN Superconducting Ring Cyclotron	Japan	2006	400 MeV/u	Heavy Ion	18.4 m	Yes	K-value of 2600 is highest ever achieved

Related technologies

The spiraling of electrons in a cylindrical vacuum chamber within a transverse magnetic field is also employed in the magnetron, a device for producing high frequency radio waves (microwaves). In the magnetron, electrons are bent into a circular path by a magnetic field, and their motion is used to excite resonant cavities, producing electromagnetic radiation.

A betatron uses the change in the magnetic field to accelerate electrons in a circular path. While static magnetic fields cannot provide acceleration, as the force always acts perpendicularly to the direction of particle motion, changing fields can be used to induce an electromotive force in the same manner as in a transformer. The betatron was developed in 1940, although the idea had been proposed substantially earlier.

A synchrotron is another type of particle accelerator that uses magnets to bend particles into a circular trajectory. Unlike in a cyclotron, the particle path in a synchrotron has a fixed radius. Particles in a synchrotron pass accelerating stations at increasing frequency as they get faster. To compensate for this frequency increase, both the frequency of the applied accelerating electric field and the magnetic field must be increased in tandem, leading to the "synchro" portion of the name.

In fiction

The United States Department of War famously asked for dailies of the Superman comic strip to be pulled in April 1945 for having Superman bombarded with the radiation from a cyclotron. In 1950, however, in Atom Man vs. Superman, Lex Luthor uses a cyclotron to start an earthquake.

In the 1984 film Ghostbusters, a miniature cyclotron forms part of the proton pack used for catching ghosts.