Synchronicity

From Wikipedia, the free encyclopedia

Carl Gustav Jung

Synchronicity (German: Synchronizität) is a concept, first introduced by analytical psychologist Carl Jung, which holds that events are "meaningful coincidences" if they occur with no causal relationship yet seem to be meaningfully related.^[1] During his career, Jung furnished several different definitions of it.^[2] Jung defined synchronicity as an "acausal connecting (togetherness) principle," "meaningful coincidence", and "acausal parallelism." He introduced the concept as early as the 1920s but gave a full statement of it only in 1951 in an Eranos lecture.^[3]

In 1952 Jung published a paper "Synchronizität als ein Prinzip akausaler Zusammenhänge" (Synchronicity – An Acausal Connecting Principle)^[4] in a volume which also contained a related study by the physicist and Nobel laureate Wolfgang Pauli,^[5] who was sometimes critical of Jung's ideas.^[6] Jung's belief was that, just as events may be connected by causality, they may also be connected by meaning. Events connected by meaning need not have an explanation in terms of causality, which does not generally contradict the Axiom of Causality.

Jung used the concept in arguing for the existence of the paranormal.^[7] A believer in the paranormal, Arthur Koestler wrote extensively on synchronicity in his 1972 book The Roots of Coincidence.^[8] The idea of synchronicity as extending beyond mere coincidence (as well as the paranormal generally) is widely rejected in the academic and scientific community.

Description

Diagram illustrating Carl Jung's concept of synchronicity

Jung coined the word "synchronicity" to describe "temporally coincident occurrences of acausal events." In his book Synchronicity: An Acausal Connecting Principle, Jung wrote:^[9]

How are we to recognize acausal combinations of events, since it is obviously impossible to examine all chance happenings for their causality? The answer to this is that acausal events may be expected most readily where, on closer reflection, a causal connection appears to be inconceivable.

In the introduction to his book, Jung on Synchronicity and the Paranormal, Roderick Main wrote:^[10]

The culmination of Jung's lifelong engagement with the paranormal is his theory of synchronicity, the view that the structure of reality includes a principle of acausal connection which manifests itself most conspicuously in the form of meaningful coincidences. Difficult, flawed, prone to misrepresentation, this theory none the less remains one of the most suggestive attempts yet made to bring the paranormal within the bounds of intelligibility. It has been found relevant by psychotherapists, parapsychologists, researchers of spiritual experience and a growing number of non-specialists. Indeed, Jung's writings in this area form an excellent general introduction to the whole field of the paranormal.

In his book Synchronicity: An Acausal Connecting Principle, Jung wrote:^[9]

...it is impossible, with our present resources, to explain ESP, or the fact of meaningful coincidence, as a phenomenon of energy. This makes an end of the causal explanation as well, for "effect" cannot be understood as anything except a phenomenon of energy. Therefore it cannot be a question of cause and effect, but of a falling together in time, a kind of simultaneity. Because of this quality of simultaneity, I have picked on the term "synchronicity" to designate a hypothetical factor equal in rank to causality as a principle of explanation.

Synchronicity was a principle which, Jung felt, gave conclusive evidence for his concepts of archetypes and the collective unconscious.^[11] It described a governing dynamic which underlies the whole of human experience and history — social, emotional, psychological, and spiritual. The emergence of the synchronistic paradigm was a significant move away from Cartesian dualism towards an underlying philosophy of double-aspect theory. Some argue this shift was essential to bringing theoretical coherence to Jung's earlier work.^[12][13]

Even at Jung's presentation of his work on synchronicity in 1951 at an Eranos lecture, his ideas on synchronicity were evolving. On Feb. 25, 1953, in a letter to Carl Seelig, the Swiss author and journalist who wrote a biography of Albert Einstein, Jung wrote, "Professor Einstein was my guest on several occasions at dinner. . . These were very early days when Einstein was developing his first theory of relativity [and] It was he who first started me on thinking about a possible relativity of time as well as space, and their psychic conditionality. More than 30 years later the stimulus led to my relation with the physicist professor W. Pauli and to my thesis of psychic synchronicity."^[4]

Following discussions with both Albert Einstein and Wolfgang Pauli, Jung believed there were parallels between synchronicity and aspects of relativity theory and quantum mechanics.^[14]

Jung believed life was not a series of random events but rather an expression of a deeper order, which he and Pauli referred to as Unus mundus. This deeper order led to the insights that a person was both embedded in a universal wholeness and that the realisation of this was more than just an intellectual exercise, but also had elements of a spiritual awakening.^[15] From the religious perspective, synchronicity shares similar characteristics of an "intervention of grace". Jung also believed that in a person's life, synchronicity served a role similar to that of dreams, with the purpose of shifting a person's egocentric conscious thinking to greater wholeness.

Examples

Cetonia aurata

In his book Synchronicity Jung tells the following story as an example of a synchronistic event:

My example concerns a young woman patient who, in spite of efforts made on both sides, proved to be psychologically inaccessible. The difficulty lay in the fact that she always knew better about everything. Her excellent education had provided her with a weapon ideally suited to this purpose, namely a highly polished Cartesian rationalism with an impeccably "geometrical" idea of reality. After several fruitless attempts to sweeten her rationalism with a somewhat more human understanding, I had to confine myself to the hope that something unexpected and irrational would turn up, something that would burst the intellectual retort into which she had sealed herself. Well, I was sitting opposite her one day, with my back to the window, listening to her flow of rhetoric. She had an impressive dream the night before, in which someone had given her a golden scarab — a costly piece of jewellery. While she was still telling me this dream, I heard something behind me gently tapping on the window. I turned round and saw that it was a fairly large flying insect that was knocking against the window-pane from outside in the obvious effort to get into the dark room. This seemed to me very strange. I opened the window immediately and caught the insect in the air as it flew in. It was a scarabaeid beetle, or common rose-chafer (Cetonia aurata), whose gold-green colour most nearly resembles that of a golden scarab. I handed the beetle to my patient with the words, "Here is your scarab." This experience punctured the desired hole in her rationalism and broke the ice of her intellectual resistance. The treatment could now be continued with satisfactory results.^[16]

The French writer Émile Deschamps claims in his memoirs that, in 1805, he was treated to some plum pudding by a stranger named Monsieur de Fontgibu. Ten years later, the writer encountered plum pudding on the menu of a Paris restaurant and wanted to order some, but the waiter told him that the last dish had already been served to another customer, who turned out to be de Fontgibu. Many years later, in 1832, Deschamps was at a dinner and once again ordered plum pudding. He recalled the earlier incident and told his friends that only de Fontgibu was missing to make the setting complete – and in the same instant, the now-senile de Fontgibu entered the room.^[17]

Jung wrote, after describing some examples, "When coincidences pile up in this way, one cannot help being impressed by them – for the greater the number of terms in such a series, or the more unusual its character, the more improbable it becomes."^[18]

Wolfgang Pauli

In his book Thirty Years That Shook Physics – The Story of Quantum Theory (1966), George Gamow writes about Wolfgang Pauli, who was apparently considered a person particularly associated with synchronicity events. Gamow whimsically refers to the "Pauli effect", a mysterious phenomenon which is not understood on a purely materialistic basis, and probably never will be. The following anecdote is told:

It is well known that theoretical physicists cannot handle experimental equipment; it breaks whenever they touch it. Pauli was such a good theoretical physicist that something usually broke in the lab whenever he merely stepped across the threshold. A mysterious event that did not seem at first to be connected with Pauli's presence once occurred in Professor J. Franck's laboratory in Göttingen. Early one afternoon, without apparent cause, a complicated apparatus for the study of atomic phenomena collapsed. Franck wrote humorously about this to Pauli at his Zürich address and, after some delay, received an answer in an envelope with a Danish stamp. Pauli wrote that he had gone to visit Bohr and at the time of the mishap in Franck's laboratory his train was stopped for a few minutes at the Göttingen railroad station. You may believe this anecdote or not, but there are many other observations concerning the reality of the Pauli Effect! ^[19]

Relationship with causality

Causality, when defined expansively (as for instance in the "mystic psychology" book The Kybalion, or in the platonic Kant-style Axiom of Causality), states that "nothing can happen without being caused." Such an understanding of causality may be incompatible with synchronicity. Other definitions of causality (for example, the neo-Humean definition) are concerned only with the relation of cause to effect. As such, they are compatible with synchronicity. There are also opinions which hold that, where there is no external observable cause, the cause can be internal.^[20]

It is also pointed out that, since Jung took into consideration only the narrow definition of causality – only the efficient cause – his notion of "acausality" is also narrow and so is not applicable to final and formal causes as understood in Aristotelian or Thomist systems.^[21] The final causality is inherent^[22] in synchronicity (because it leads to individuation) or synchronicity can be a kind of replacement for final causality; however, such finalism or teleology is considered to be outside the domain of modern science.

Explanations

Religion

Many people believe that the Universe or God causes synchronicities. Among the general public, divine intervention is the most widely accepted explanation for meaningful coincidences.^[7] Faith in something Greater provides them with a cause.

Mathematics

Jung and his followers (e.g., Marie-Louise von Franz) share in common the belief that numbers are the archetypes of order, and the major participants in synchronicity creation.^[23]This hypothesis has implications that are relevant to some of the “chaotic” phenomena in nonlinear dynamics. Dynamical systems theory has provided a new context from which to speculate about synchronicity because it gives predictions about the transitions between emergent states of order and nonlocality.^[24] This view, however, is not part of mainstream mathematical thought.

Quantum Physics

According to a certain view, synchronicity serves as a way of making sense of or describing some aspects of quantum mechanics. It argues that quantum experiments demonstrate that, at least in the microworld of subatomic particles, there is an instantaneous connection between particles no matter how far away they are from one another. Known as quantum non-locality or entanglement, the proponents of this view argue that this points to a unified field that precedes physical reality.^[25] Continuity (non-locality) along one dimension is then correlated with discontinuity (locality) along the other dimension^{[What does this mean?]} of this field. As with archetypal reasoning, the proponents argue that two events can correspond to each other (e.g. particle with particle, or person with person) in a meaningful way.

Synchronicity can also be seen in David Bohm's theory of implicate order. According to Bohm's^[26] theory, there are three major realms of existence: the explicate (unfolded) order, the implicate (enfolded) order, and a source or ground beyond both. The flowing movement of the whole can thus be understood as a process of continuous enfolding and unfolding of order or structure. From moment to moment there is a rhythmic pulse between implicate and explicate realities. Therefore, synchronicity would literally take place as the bridge between implicate and explicate orders, whose complementary nature define the undivided totality.

Probability theory

Mainstream mathematics argues that statistics and probability theory (exemplified in, e.g., Littlewood's law or the law of truly large numbers) suffice to explain any purported synchronistic events as mere coincidences.^[27][28] The law of large numbers, for instance, states that in large enough populations, any strange event is arbitrarily likely to happen by mere chance. However, some proponents of synchronicity question whether it is even sensible in principle to try to evaluate synchronicity statistically. Jung himself and von Franz argued that statistics work precisely by ignoring what is unique about the individual case, whereas synchronicity tries to investigate that uniqueness.

Among some psychologists, Jung's works, such as The Interpretation of Nature and the Psyche, were received as problematic. Fritz Levi, in his 1952 review in Neue Schweizer Rundschau (New Swiss Observations), critiqued Jung's theory of synchronicity as vague in determinability of synchronistic events, saying that Jung never specifically explained his rejection of "magic causality" to which such an acausal principle as synchronicity would be related. He also questioned the theory's usefulness.^[29]

Psychology

In psychology and cognitive science, confirmation bias is a tendency to search for or interpret new information in a way that confirms one's preconceptions, and avoids information and interpretations that contradict prior beliefs. It is a type of cognitive bias and represents an error of inductive inference, or is a form of selection bias toward confirmation of the hypothesis under study, or disconfirmation of an alternative hypothesis. Confirmation bias is of interest in the teaching of critical thinking, as the skill is misused if rigorous critical scrutiny is applied only to evidence that challenges a preconceived idea, but not to evidence that supports it.^[30]

Likewise, in psychology and sociology, the term apophenia is used for the mistaken detection of a pattern or meaning in random or meaningless data.^[31] Skeptics, such as Robert Todd Carroll of the Skeptic's Dictionary, argue that the perception of synchronicity is better explained as apophenia. Primates use pattern detection in their form of intelligence,^[32] and this can lead to erroneous identification of non-existent patterns. A famous example of this is the fact that human face recognition is so robust, and based on such a basic archetype (essentially two dots and a line contained in a circle), that human beings are very prone to identify faces in random data all through their environment, like the "man in the moon", or faces in wood grain, an example of the visual form of apophenia known as pareidolia.^[33]

It has also been argued that Jungian psychology's theory of synchronicity is equivalent to intellectual intuition.^[34]

Physics of magnetic resonance imaging

Modern 3 tesla clinical MRI scanner.

From Wikipedia

Original page:  https://en.m.wikipedia.org/wiki/Physics_of_magnetic_resonance_imaging

The physics of magnetic resonance imaging (MRI) involves the interaction of biological tissue with electromagnetic fields. MRI is a medical imaging technique used in radiology to investigate the anatomy and physiology of the body. The human body is largely composed of water molecules, each containing two hydrogen nuclei, or protons. When inside the magnetic field (B₀) of the scanner, the magnetic moments of these protons align with the direction of the field.

A radio frequency pulse is then applied, causing the protons to alter their magnetization alignment relative to the field. In response to the force bringing them back to their equilibrium orientation, the protons undergo a rotating motion (precession), much like a spin wheel under the effect of gravity. These changes in magnetization alignment cause a changing magnetic flux, which yields a changing voltage in receiver coils to give the signal. The frequency at which a proton or group of protons in a voxel resonates depends on the strength of the local magnetic field around the proton or group of protons. By applying additional magnetic fields (gradients) that vary linearly over space, specific slices to be imaged can be selected, and an image is obtained by taking the 2-D Fourier transform of the spatial frequencies of the signal (a.k.a., k-space). Due to the magnetic Lorentz force from B₀ on the current flowing in the gradient coils, the gradient coils will try to move. The knocking sounds heard during an MRI scan are the result of the gradient coils trying to move against the constraint of the concrete or epoxy in which they are secured. These sounds can be very unnerving to the patient, particularly given the tight space in which the patient lays. This behaviour of MRI scanners can be described in terms of a fully coupled acousto-magneto-mechanical system.^[1] Solutions to such systems can provide useful insight for design engineers.

Diseased tissue, such as tumors, can be detected because the protons in different tissues return to their equilibrium state at different rates (i.e., they have different relaxation times). By changing the parameters on the scanner this effect is used to create contrast between different types of body tissue.

Contrast agents may be injected intravenously to enhance the appearance of blood vessels, tumors or inflammation. Contrast agents may also be directly injected into a joint in the case of arthrograms, MRI images of joints. Unlike CT, MRI uses no ionizing radiation and is generally a very safe procedure. Patients with some metal implants, cochlear implants, and cardiac pacemakers are prevented from having an MRI scan due to effects of the strong magnetic field and powerful radio frequency pulses unless the device they carry is labeled MR-Conditional.^[2]

MRI is used to image every part of the body, and is particularly useful for neurological conditions, for disorders of the muscles and joints, for evaluating tumors, and for showing abnormalities in the heart and blood vessels.

Nuclear magnetism

Subatomic particles have the quantum mechanical property of spin.^[3] Certain nuclei such as ¹H (protons), ²H, ³He, ²³Na or ³¹P, have a non–zero spin and therefore a magnetic moment. In the case of the so-called spin-​¹⁄₂ nuclei, such as ¹H, there are two spin states, sometimes referred to as up and down. Nuclei such as ¹²C have no unpaired neutrons or protons, and no net spin; however, the isotope ¹³C does.

When these spins are placed in a strong external magnetic field they precess around an axis along the direction of the field. Protons align in two energy eigenstates (the Zeeman effect): one low-energy and one high-energy, which are separated by a very small splitting energy.

Resonance and relaxation

In the static magnetic fields commonly used in MRI, the energy difference between the nuclear spin states corresponds to a radio-frequency photon. Resonant absorption of energy by the protons due to an external oscillating magnetic field will occur at the Larmor frequency for the particular nucleus.
The spin of the proton has two states. The net longitudinal magnetization in thermodynamical equilibrium is due to a tiny excess of protons in the lower energy state. This gives a net polarization that is parallel to the external field. Application of a radio frequency (RF) pulse can tip this net polarization vector sideways (with, i.e., a so-called 90° pulse), or even reverse it (with a so-called 180° pulse).

The recovery of longitudinal magnetization is called longitudinal or T₁ relaxation and occurs exponentially with a time constant T₁. The loss of phase coherence in the transverse plane is called transverse or T₂ relaxation. T₁ is thus associated with the enthalpy of the spin system, or the number of nuclei with parallel versus anti-parallel spin. T₂ on the other hand is associated with the entropy of the system, or the number of nuclei in phase.

When the radio frequency pulse is turned off, the transverse vector component produces an oscillating magnetic field which induces a small current in the receiver coil. This signal is called the free induction decay (FID). In an idealized nuclear magnetic resonance experiment, the FID decays approximately exponentially with a time constant T₂. However, in practical MRI there are small differences in the static magnetic field at different spatial locations ("inhomogeneities") that cause the Larmor frequency to vary across the body. This creates destructive interference, which shortens the FID. The time constant for the observed decay of the FID is called the T^*
₂ relaxation time, and is always shorter than T₂. At the same time, the longitudinal magnetization starts to recover exponentially with a time constant T₁ which is much larger than T₂ (see below).

In MRI, the static magnetic field is caused to vary across the body (by using a field gradient), so that different spatial locations become associated with different precession frequencies. Usually these field gradients are pulsed, and it is the almost infinite variety of RF and gradient pulse sequences that gives MRI its versatility. Application of field gradient destroys the FID signal, but this can be recovered and measured by a refocusing gradient (to create a so-called "gradient echo"), or by a radio frequency pulse (to create a so-called "spin-echo"). The whole process can be repeated when some T₁-relaxation has occurred and the thermal equilibrium of the spins has been more or less restored. The repetition time (TR) is the time between two successive excitations of the same slice.^[4]

Typically, in soft tissues T₁ is around one second while T₂ and T^*
₂ are a few tens of milliseconds. However, these values can vary widely between different tissues, as well as between different external magnetic fields. This behavior is one factor giving MRI its tremendous soft tissue contrast.
MRI contrast agents, such as those containing Gadolinium(III) work by altering (shortening) the relaxation parameters, especially T₁.

Imaging

Imaging schemes

A number of schemes have been devised for combining field gradients and radio frequency excitation to create an image:

• 2D or 3D reconstruction from projections, such as in computed tomography.
• Building the image point-by-point or line-by-line.
• Gradients in the RF field rather than the static field.

Although each of these schemes is occasionally used in specialist applications, the majority of MR Images today are created either by the two-dimensional Fourier transform (2DFT) technique with slice selection, or by the three-dimensional Fourier transform (3DFT) technique. Another name for 2DFT is spin-warp. What follows here is a description of the 2DFT technique with slice selection.

The 3DFT technique is rather similar except that there is no slice selection and phase-encoding is performed in two separate directions.

Echo-planar imaging

Another scheme which is sometimes used, especially in brain scanning or where images are needed very rapidly, is called echo-planar imaging (EPI):^[5] In this case, each RF excitation is followed by a train of gradient echoes with different spatial encoding. Multiplexed-EPI is even faster, e.g., for whole brain fMRI or diffusion MRI.^[6]

Image contrast and contrast enhancement

Image contrast is created by differences in the strength of the NMR signal recovered from different locations within the sample. This depends upon the relative density of excited nuclei (usually water protons), on differences in relaxation times (T₁, T₂, and T^*
₂) of those nuclei after the pulse sequence, and often on other parameters discussed under specialized MR scans. Contrast in most MR images is actually a mixture of all these effects, but careful design of the imaging pulse sequence allows one contrast mechanism to be emphasized while the others are minimized. The ability to choose different contrast mechanisms gives MRI tremendous flexibility. In the brain, T₁-weighting causes the nerve connections of white matter to appear white, and the congregations of neurons of gray matter to appear gray, while cerebrospinal fluid (CSF) appears dark. The contrast of white matter, gray matter and cerebrospinal fluid is reversed using T₂ or T^*
₂ imaging, whereas proton-density-weighted imaging provides little contrast in healthy subjects. Additionally, functional parameters such as cerebral blood flow (CBF), cerebral blood volume (CBV) or blood oxygenation can affect T₁, T₂, and T^*
₂ and so can be encoded with suitable pulse sequences.

In some situations it is not possible to generate enough image contrast to adequately show the anatomy or pathology of interest by adjusting the imaging parameters alone, in which case a contrast agent may be administered. This can be as simple as water, taken orally, for imaging the stomach and small bowel. However, most contrast agents used in MRI are selected for their specific magnetic properties. Most commonly, a paramagnetic contrast agent (usually a gadolinium compound^[7][8]) is given. Gadolinium-enhanced tissues and fluids appear extremely bright on T₁-weighted images. This provides high sensitivity for detection of vascular tissues (e.g., tumors) and permits assessment of brain perfusion (e.g., in stroke). There have been concerns raised recently regarding the toxicity of gadolinium-based contrast agents and their impact on persons with impaired kidney function. (See Safety/Contrast agents below.)

More recently, superparamagnetic contrast agents, e.g., iron oxide nanoparticles,^[9][10] have become available. These agents appear very dark on T^*
₂-weighted images and may be used for liver imaging, as normal liver tissue retains the agent, but abnormal areas (e.g., scars, tumors) do not. They can also be taken orally, to improve visualization of the gastrointestinal tract, and to prevent water in the gastrointestinal tract from obscuring other organs (e.g., the pancreas). Diamagnetic agents such as barium sulfate have also been studied for potential use in the gastrointestinal tract, but are less frequently used.

k-space

In 1983, Ljunggren^[11] and Twieg^[12] independently introduced the k-space formalism, a technique that proved invaluable in unifying different MR imaging techniques. They showed that the demodulated MR signal S(t) generated by freely precessing nuclear spins in the presence of a linear magnetic field gradient G equals the Fourier transform of the effective spin density. Mathematically:

${\displaystyle S(t)={\tilde {\rho }}_{\mathrm {eff} }\left({\vec {k}}(t)\right)\equiv \int _{-\infty }^{\infty }\mathrm {d} {\vec {x}}\ \rho ({\vec {x}})\cdot e^{2\pi \imath \ {\vec {k}}(t)\cdot {\vec {x}}}}$

where:

${\displaystyle {\vec {k}}(t)\equiv \int _{0}^{t}{\vec {G}}(\tau )\ \mathrm {d} \tau }$

In other words, as time progresses the signal traces out a trajectory in k-space with the velocity vector of the trajectory proportional to the vector of the applied magnetic field gradient. By the term effective spin density we mean the true spin density ${\displaystyle \rho ({\vec {x}})}$ corrected for the effects of T₁ preparation, T₂ decay, dephasing due to field inhomogeneity, flow, diffusion, etc. and any other phenomena that affect that amount of transverse magnetization available to induce signal in the RF probe or its phase with respect to the receiving coil' s electromagnetic field.

From the basic k-space formula, it follows immediately that we reconstruct an image ${\displaystyle I({\vec {x}})}$ simply by taking the inverse Fourier transform of the sampled data, viz.

${\displaystyle I\left({\vec {x}}\right)=\int _{-\infty }^{\infty }\mathrm {d} {\vec {k}}\ S\left({\vec {k}}(t)\right)\cdot e^{-2\pi \imath \ {\vec {k}}(t)\cdot {\vec {x}}}}$

Using the k-space formalism, a number of seemingly complex ideas became simple. For example, it becomes very easy to understand the role of phase encoding (the so-called spin-warp method). In a standard spin echo or gradient echo scan, where the readout (or view) gradient is constant (e.g., G), a single line of k-space is scanned per RF excitation. When the phase encoding gradient is zero, the line scanned is the k_x axis. When a non-zero phase-encoding pulse is added in between the RF excitation and the commencement of the readout gradient, this line moves up or down in k-space, i.e., we scan the line k_y = constant.

The k-space formalism also makes it very easy to compare different scanning techniques. In single-shot EPI, all of k-space is scanned in a single shot, following either a sinusoidal or zig-zag trajectory. Since alternating lines of k-space are scanned in opposite directions, this must be taken into account in the reconstruction. Multi-shot EPI and fast spin echo techniques acquire only part of k-space per excitation. In each shot, a different interleaved segment is acquired, and the shots are repeated until k-space is sufficiently well-covered. Since the data at the center of k-space represent lower spatial frequencies than the data at the edges of k-space, the T_E value for the center of k-space determines the image's T₂ contrast.

The importance of the center of k-space in determining image contrast can be exploited in more advanced imaging techniques. One such technique is spiral acquisition—a rotating magnetic field gradient is applied, causing the trajectory in k-space to spiral out from the center to the edge. Due to T₂ and T^*
₂ decay the signal is greatest at the start of the acquisition, hence acquiring the center of k-space first improves contrast to noise ratio (CNR) when compared to conventional zig-zag acquisitions, especially in the presence of rapid movement.

Since ${\displaystyle {\vec {x}}}$ and ${\displaystyle {\vec {k}}}$ are conjugate variables (with respect to the Fourier transform) we can use the Nyquist theorem to show that the step in k-space determines the field of view of the image (maximum frequency that is correctly sampled) and the maximum value of k sampled determines the resolution; i.e.,

${\displaystyle FOV\propto {\frac {1}{\Delta k}}\qquad \mathrm {Resolution} \propto |k_{\max }|\ .}$

(These relationships apply to each axis independently.)

Example of a pulse sequence

Simplified timing diagram for two-dimensional-Fourier-transform (2DFT) Spin Echo (SE) pulse sequence

In the timing diagram, the horizontal axis represents time. The vertical axis represents: (top row) amplitude of radio frequency pulses; (middle rows) amplitudes of the three orthogonal magnetic field gradient pulses; and (bottom row) receiver analog-to-digital converter (ADC). Radio frequencies are transmitted at the Larmor frequency of the nuclide to be imaged. For example, for ¹H in a magnetic field of 1 T, a frequency of 42.5781 MHz would be employed. The three field gradients are labeled G_X (typically corresponding to a patient's left-to-right direction and colored red in diagram), G_Y (typically corresponding to a patient's front-to-back direction and colored green in diagram), and G_Z (typically corresponding to a patient's head-to-toe direction and colored blue in diagram). Where negative-going gradient pulses are shown, they represent reversal of the gradient direction, i.e., right-to-left, back-to-front or toe-to-head. For human scanning, gradient strengths of 1–100 mT/m are employed: Higher gradient strengths permit better resolution and faster imaging. The pulse sequence shown here would produce a transverse (axial) image.

The first part of the pulse sequence, SS, achieves "slice selection". A shaped pulse (shown here with a sinc modulation) causes a 90° nutation of longitudinal nuclear magnetization within a slab, or slice, creating transverse magnetization. The second part of the pulse sequence, PE, imparts a phase shift upon the slice-selected nuclear magnetization, varying with its location in the Y direction. The third part of the pulse sequence, another slice selection (of the same slice) uses another shaped pulse to cause a 180° rotation of transverse nuclear magnetization within the slice. This transverse magnetisation refocuses to form a spin echo at a time T_E. During the spin echo, a frequency-encoding (FE) or readout gradient is applied, making the resonant frequency of the nuclear magnetization vary with its location in the X direction. The signal is sampled n_FE times by the ADC during this period, as represented by the vertical lines. Typically n_FE of between 128 and 512 samples are taken.

The longitudinal magnetisation is then allowed to recover somewhat and after a time T_R the whole sequence is repeated n_PE times, but with the phase-encoding gradient incremented (indicated by the horizontal hatching in the green gradient block). Typically n_PE of between 128 and 512 repetitions are made.

The negative-going lobes in G_X and G_Z are imposed to ensure that, at time T_E (the spin echo maximum), phase only encodes spatial location in the Y direction.

Typically T_E is between 5 ms and 100 ms, while T_R is between 100 ms and 2000 ms.

After the two-dimensional matrix (typical dimension between 128 × 128 and 512 × 512) has been acquired, producing the so-called k-space data, a two-dimensional inverse Fourier transform is performed to provide the familiar MR image. Either the magnitude or phase of the Fourier transform can be taken, the former being far more common.

Overview of main sequences

This table does not include uncommon and experimental sequences.

Group	Sequence	Abbr.	Physics	Main clinical distinctions	Example
Spin echo	T1 weighted	T1	Measuring spin–lattice relaxation by using a short repetition time (TR) and echo time (TE)	Lower signal for more water content, [13]as in edema, tumor, infarction, inflammation, infection, hyperacute or chronic hemorrhage [14] High signal for fat[13][14] High signal for paramagnetic substances, such as MRI contrast agents[14] Standard foundation and comparison for other sequences.
	T2 weighted	T2	Measuring spin–spin relaxation by using long TR and TE times.	Higher signal for more water content.[13] Low signal for fat.[13] Low signal for paramagnetic substances.[14] Standard foundation and comparison for other sequences.
	Proton density weighted	PD	Long TR (to reduce T1) and short TE (to minimize T2)[15]	Joint disease and injury.[16] High signal from meniscus tears[17] (pictured)
Gradient echo	Steady-state free precession	SSFP	Maintenance of a steady, residual transverse magnetisation over successive cycles.[18]	Creation of cardiac MRI videos (pictured).[18]
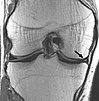
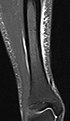
Inversion recovery	Short tau inversion recovery	STIR	Fat suppression by setting an inversion time where the signal of fat is zero.[19]	High signal in edema, such as in more severe stress fracture.[20] Shin splints pictured:
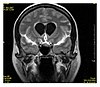
	Fluid attenuated inversion recovery	FLAIR	Fluid suppression by setting an inversion time that nulls fluids.	High signal in lacunar infarction, multiple sclerosis (MS) plaques, subarachnoid haemorrhage and meningitis (pictured).[21]
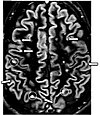
	Double inversion recovery	DIR	Simultaneous suppression of cerebrospinal fluid and white matter by two inversion times.[22]	High signal of multiple sclerosis plaques (pictured).[22]
Diffusion weighted (DWI)	Conventional	DWI	Measure of Brownian motion of water molecules.[23]	High signal within minutes of cerebral infarction (pictured).[24]
	Apparent diffusion coefficient	ADC	Reduced T2 weighting by taking multiple conventional DWI images with different DWI weighting, and the change corresponds to diffusion.[25]	Low signal minutes after cerebral infarction (pictured).[26]
	Diffusion tensor	DTI	Mainly tractography (pictured) by an overall greater Brownian motion of water molecules in the directions of nerve fibers.[27]	Evaluating white matter deformation by tumors[27] Reduced fractional anisotropy may indicate dementia[28]
Perfusion weighted (PWI)	Dynamic susceptibility contrast	DSC	Gadolinium contrast is injected, and rapid repeated imaging (generally gradient-echo echo-planar T2 weighted) quantifies susceptibility-induced signal loss.[29]	In cerebral infarction, the infarcted core and the penumbra have decreased perfusion (pictured).[30]
	Dynamic contrast enhanced	DCE	Measuring shortening of the spin–lattice relaxation (T1) induced by a gadolinium contrast bolus.[31]
	Arterial spin labelling	ASL	Magnetic labeling of arterial blood below the imaging slab, which subsequently enters the region of interest.[32] It does not need gadolinium contrast.[33]
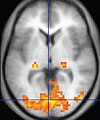
Functional MRI (fMRI)	Blood-oxygen-level dependent imaging	BOLD	Changes in oxygen saturation-dependent magnetism of hemoglobin reflects tissue activity.[34]	Localizing highly active brain areas before surgery.[35]
Magnetic resonance angiography (MRA) and venography	Time-of-flight	TOF	Blood entering the imaged area is not yet magnetically saturated, giving it a much higher signal when using short echo time and flow compensation.	Detection of aneurysm, stenosis or dissection.[36]
	Phase-contrast MRA	PC-MRA	Two gradients with equal magnitude but opposite direction are used to encode a phase shift, which is proportional to the velocity of spins.[37]	Detection of aneurysm, stenosis or dissection (pictured).[36]	(VIPR)
Susceptibility weighted		SWI	Sensitive for blood and calcium, by a fully flow compensated, long echo, gradient recalled echo (GRE) pulse sequence to exploit magnetic susceptibility differences between tissues.	Detecting small amounts of hemorrhage (diffuse axonal injury pictured) or calcium.[38]

MRI scanner

Construction and operation

Schematic of construction of a cylindrical superconducting MR scanner

The major components of an MRI scanner are: the main magnet, which polarizes the sample, the shim coils for correcting inhomogeneities in the main magnetic field, the gradient system which is used to localize the MR signal and the RF system, which excites the sample and detects the resulting NMR signal. The whole system is controlled by one or more computers.

Magnet

The magnet is the largest and most expensive component of the scanner, and the remainder of the scanner is built around it. The strength of the magnet is measured in teslas (T). Clinical magnets generally have a field strength in the range 0.1–3.0 T, with research systems available up to 9.4 T for human use and 21 T for animal systems.^[39] In the United States, field strengths up to 4 T have been approved by the FDA for clinical use.^[40]

Just as important as the strength of the main magnet is its precision. The straightness of the magnetic lines within the center (or, as it is technically known, the iso-center) of the magnet needs to be near-perfect. This is known as homogeneity. Fluctuations (inhomogeneities in the field strength) within the scan region should be less than three parts per million (3 ppm). Three types of magnets have been used:

• Permanent magnet: Conventional magnets made from ferromagnetic materials (e.g., steel alloys containing rare-earth elements such as neodymium) can be used to provide the static magnetic field. A permanent magnet that is powerful enough to be used in an MRI will be extremely large and bulky; they can weigh over 100 tonnes. Permanent magnet MRIs are very inexpensive to maintain; this cannot be said of the other types of MRI magnets, but there are significant drawbacks to using permanent magnets. They are only capable of achieving weak field strengths compared to other MRI magnets (usually less than 0.4 T) and they are of limited precision and stability. Permanent magnets also present special safety issues; since their magnetic fields cannot be "turned off," ferromagnetic objects are virtually impossible to remove from them once they come into direct contact. Permanent magnets also require special care when they are being brought to their site of installation.
• Resistive electromagnet: A solenoid wound from copper wire is an alternative to a permanent magnet. An advantage is low initial cost, but field strength and stability are limited. The electromagnet requires considerable electrical energy during operation which can make it expensive to operate. This design is essentially obsolete.
• Superconducting electromagnet: When a niobium-titanium or niobium-tin alloy is cooled by liquid helium to 4 K (−269 °C, −452 °F) it becomes a superconductor, losing resistance to flow of electric current. An electromagnet constructed with superconductors can have extremely high field strengths, with very high stability. The construction of such magnets is extremely costly, and the cryogenic helium is expensive and difficult to handle. However, despite their cost, helium cooled superconducting magnets are the most common type found in MRI scanners today.

Most superconducting magnets have their coils of superconductive wire immersed in liquid helium, inside a vessel called a cryostat. Despite thermal insulation, sometimes including a second cryostat containing liquid nitrogen, ambient heat causes the helium to slowly boil off. Such magnets, therefore, require regular topping-up with liquid helium. Generally a cryocooler, also known as a coldhead, is used to recondense some helium vapor back into the liquid helium bath. Several manufacturers now offer 'cryogenless' scanners, where instead of being immersed in liquid helium the magnet wire is cooled directly by a cryocooler.^[41]

Magnets are available in a variety of shapes. However, permanent magnets are most frequently 'C' shaped, and superconducting magnets most frequently cylindrical. However, C-shaped superconducting magnets and box-shaped permanent magnets have also been used.

Magnetic field strength is an important factor in determining image quality. Higher magnetic fields increase signal-to-noise ratio, permitting higher resolution or faster scanning. However, higher field strengths require more costly magnets with higher maintenance costs, and have increased safety concerns. A field strength of 1.0–1.5 T is a good compromise between cost and performance for general medical use. However, for certain specialist uses (e.g., brain imaging) higher field strengths are desirable, with some hospitals now using 3.0 T scanners.

FID signal from a badly shimmed sample has a complex envelope.

FID signal from a well shimmed sample, showing a pure exponential decay.

Shims

When the MR scanner is placed in the hospital or clinic, its main magnetic field is far from being homogeneous enough to be used for scanning. That is why before doing fine tuning of the field using a sample, the magnetic field of the magnet must be measured and shimmed.

After a sample is placed into the scanner, the main magnetic field is distorted by susceptibility boundaries within that sample, causing signal dropout (regions showing no signal) and spatial distortions in acquired images. For humans or animals the effect is particularly pronounced at air-tissue boundaries such as the sinuses (due to paramagnetic oxygen in air) making, for example, the frontal lobes of the brain difficult to image. To restore field homogeneity a set of shim coils is included in the scanner. These are resistive coils, usually at room temperature, capable of producing field corrections distributed as several orders of spherical harmonics.^[42]

After placing the sample in the scanner, the B₀ field is 'shimmed' by adjusting currents in the shim coils. Field homogeneity is measured by examining an FID signal in the absence of field gradients. The FID from a poorly shimmed sample will show a complex decay envelope, often with many humps. Shim currents are then adjusted to produce a large amplitude exponentially decaying FID, indicating a homogeneous B₀ field. The process is usually automated.^[43]

Gradients

Gradient coils are used to spatially encode the positions of protons by varying the magnetic field linearly across the imaging volume. The Larmor frequency will then vary as a function of position in the x, y and z-axes.

Gradient coils are usually resistive electromagnets powered by sophisticated amplifiers which permit rapid and precise adjustments to their field strength and direction. Typical gradient systems are capable of producing gradients from 20–100 mT/m (i.e., in a 1.5 T magnet, when a maximal z-axis gradient is applied, the field strength may be 1.45 T at one end of a 1 m long bore and 1.55 T at the other^[44]). It is the magnetic gradients that determine the plane of imaging—because the orthogonal gradients can be combined freely, any plane can be selected for imaging.

Scan speed is dependent on performance of the gradient system. Stronger gradients allow for faster imaging, or for higher resolution; similarly, gradient systems capable of faster switching can also permit faster scanning. However, gradient performance is limited by safety concerns over nerve stimulation.

Some important characteristics of gradient amplifiers and gradient coils are slew rate and gradient strength. As mentioned earlier, a gradient coil will create an additional, linearly varying magnetic field that adds or subtracts from the main magnetic field. This additional magnetic field will have components in all 3 directions, viz. x, y and z; however, only the component along the magnetic field (usually called the z-axis, hence denoted G_z) is useful for imaging. Along any given axis, the gradient will add to the magnetic field on one side of the zero position and subtract from it on the other side. Since the additional field is a gradient, it has units of gauss per centimeter or millitesla per meter (mT/m). High performance gradient coils used in MRI are typically capable of producing a gradient magnetic field of approximate 30 mT/m or higher for a 1.5 T MRI. The slew rate of a gradient system is a measure of how quickly the gradients can be ramped on or off. Typical higher performance gradients have a slew rate of up to 100–200 T·m⁻¹·s⁻¹. The slew rate depends both on the gradient coil (it takes more time to ramp up or down a large coil than a small coil) and on the performance of the gradient amplifier (it takes a lot of voltage to overcome the inductance of the coil) and has significant influence on image quality.

Radio frequency system

The radio frequency (RF) transmission system consists of an RF synthesizer, power amplifier and transmitting coil. That coil is usually built into the body of the scanner. The power of the transmitter is variable, but high-end whole-body scanners may have a peak output power of up to 35 kW,^[45] and be capable of sustaining average power of 1 kW. Although these electromagnetic fields are in the RF range of tens of megahertz (often in the shortwave radio portion of the electromagnetic spectrum) at powers usually exceeding the highest powers used by amateur radio, there is very little RF interference produced by the MRI machine. The reason for this, is that the MRI is not a radio transmitter. The RF frequency electromagnetic field produced in the "transmitting coil" is a magnetic near-field with very little associated changing electric field component (such as all conventional radio wave transmissions have). Thus, the high-powered electromagnetic field produced in the MRI transmitter coil does not produce much electromagnetic radiation at its RF frequency, and the power is confined to the coil space and not radiated as "radio waves." Thus, the transmitting coil is a good EM field transmitter at radio frequency, but a poor EM radiation transmitter at radio frequency.

The receiver consists of the coil, pre-amplifier and signal processing system. The RF electromagnetic radiation produced by nuclear relaxation inside the subject is true EM radiation (radio waves), and these leave the subject as RF radiation, but they are of such low power as to also not cause appreciable RF interference that can be picked up by nearby radio tuners (in addition, MRI scanners are generally situated in metal mesh lined rooms which act as Faraday cages.)

While it is possible to scan using the integrated coil for RF transmission and MR signal reception, if a small region is being imaged, then better image quality (i.e., higher signal-to-noise ratio) is obtained by using a close-fitting smaller coil. A variety of coils are available which fit closely around parts of the body such as the head, knee, wrist, breast, or internally, e.g., the rectum.

A recent development in MRI technology has been the development of sophisticated multi-element phased array^[46] coils which are capable of acquiring multiple channels of data in parallel. This 'parallel imaging' technique uses unique acquisition schemes that allow for accelerated imaging, by replacing some of the spatial coding originating from the magnetic gradients with the spatial sensitivity of the different coil elements. However, the increased acceleration also reduces the signal-to-noise ratio and can create residual artifacts in the image reconstruction. Two frequently used parallel acquisition and reconstruction schemes are known as SENSE^[47] and GRAPPA.^[48] A detailed review of parallel imaging techniques can be found here:^[49]