| Neuron | |
|---|---|
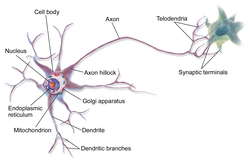
Anatomy of a multipolar neuron
| |
| Identifiers | |
| MeSH | D009474 |
| NeuroLex ID | sao1417703748 |
| TA | A14.0.00.002 |
| TH | H2.00.06.1.00002 |
| FMA | 54527 |
| Anatomical terms of neuroanatomy | |
Schematic
of an anatomically accurate single pyramidal neuron, the primary
excitatory neuron of cerebral cortex, with a synaptic connection from an
incoming axon onto a dendritic spine.
A neuron, neurone (old British spelling) or nerve cell, is an electrically excitable cell that communicates with other cells via specialized connections called synapses. It is the main component of nervous tissue. All animals except sponges and placozoans have neurons, but other multicellular organisms such as plants do not.
Neurons are typically classified into three types based on their function. Sensory neurons respond to stimuli such as touch, sound, or light that affect the cells of the sensory organs, and they send signals to the spinal cord or brain. Motor neurons receive signals from the brain and spinal cord to control everything from muscle contractions to glandular output. Interneurons connect neurons to other neurons within the same region of the brain or spinal cord. A group of connected neurons is called a neural circuit.
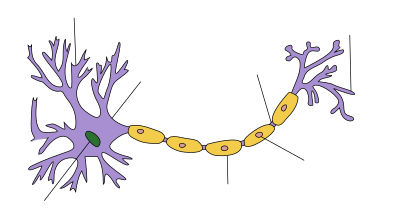
A typical neuron consists of a cell body (soma), dendrites, and a single axon.
The soma is usually compact. The axon and dendrites are filaments that
extrude from it. Dendrites typically branch profusely and extend a few
hundred micrometers from the soma. The axon leaves the soma at a
swelling called the axon hillock,
and travels for as far as 1 meter in humans or more in other species.
It branches but usually maintains a constant diameter. At the farthest
tip of the axon's branches are axon terminals, where the neuron can transmit a signal across the synapse to another cell. Neurons may lack dendrites or have no axon. The term neurite is used to describe either a dendrite or an axon, particularly when the cell is undifferentiated.
Most neurons receive signals via the dendrites and soma and send
out signals down the axon. At the majority of synapses, signals cross
from the axon of one neuron to a dendrite of another. However, synapses
can connect an axon to another axon or a dendrite to another dendrite.
The signaling process is partly electrical and partly chemical. Neurons are electrically excitable, due to maintenance of voltage gradients across their membranes. If the voltage changes by a large enough amount over a short interval, the neuron generates an all-or-nothing electrochemical pulse called an action potential. This potential travels rapidly along the axon, and activates synaptic connections as it reaches them. Synaptic signals may be excitatory or inhibitory, increasing or reducing the net voltage that reaches the soma.
In most cases, neurons are generated by neural stem cells during brain development and childhood. Neurogenesis
largely ceases during adulthood in most areas of the brain. However,
strong evidence supports generation of substantial numbers of new
neurons in the hippocampus and olfactory bulb.
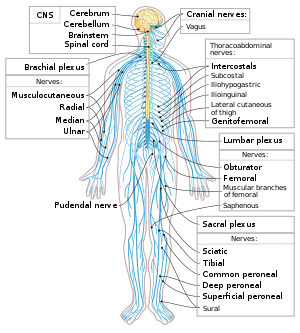
Nervous system
Diagram
of the human nervous system. The relationship between the brain, spinal
cord, and rest of the nerves in the body is demonstrated.
Neurons are the primary components of the nervous system, along with the glial cells that give them structural and metabolic support. The nervous system is made up of the central nervous system, which includes the brain and spinal cord, and the peripheral nervous system, which includes the autonomic and somatic nervous systems. In vertebrates, the majority of neurons belong to the central nervous system, but some reside in peripheral ganglia, and many sensory neurons are situated in sensory organs such as the retina and cochlea.
Axons may bundle into fascicles that make up the nerves in the peripheral nervous system (like strands of wire make up cables). Bundles of axons in the central nervous system are called tracts.
Anatomy and histology
| Neuron (peripheral nervous system) |
|---|
Neurons are highly specialized for the processing and transmission of
cellular signals. Given their diversity of functions performed in
different parts of the nervous system, there is a wide variety in their
shape, size, and electrochemical properties. For instance, the soma of a
neuron can vary from 4 to 100 micrometers in diameter.
- The soma is the body of the neuron. As it contains the nucleus, most protein synthesis occurs here. The nucleus can range from 3 to 18 micrometers in diameter.
- The dendrites of a neuron are cellular extensions with many branches. This overall shape and structure is referred to metaphorically as a dendritic tree. This is where the majority of input to the neuron occurs via the dendritic spine.
- The axon
is a finer, cable-like projection that can extend tens, hundreds, or
even tens of thousands of times the diameter of the soma in length. The
axon primarily carries nerve signals
away from the soma, and carries some types of information back to it.
Many neurons have only one axon, but this axon may—and usually
will—undergo extensive branching, enabling communication with many
target cells. The part of the axon where it emerges from the soma is
called the axon hillock. Besides being an anatomical structure, the axon hillock also has the greatest density of voltage-dependent sodium channels.
This makes it the most easily excited part of the neuron and the spike
initiation zone for the axon. In electrophysiological terms, it has the
most negative threshold potential.
- While the axon and axon hillock are generally involved in information outflow, this region can also receive input from other neurons.
- The axon terminal is found at the end of the axon farthest from the soma and contains synapses. Synaptic boutons are specialized structures where neurotransmitter
chemicals are released to communicate with target neurons. In addition
to synaptic boutons at the axon terminal, a neuron may have en passant boutons, which are located along the length of the axon.
Neuron cell body
The accepted view of the neuron attributes dedicated functions to its
various anatomical components; however, dendrites and axons often act
in ways contrary to their so-called main function.
Diagram of a typical myelinated vertebrate motor neuron
Axons and dendrites in the central nervous system are typically only
about one micrometer thick, while some in the peripheral nervous system
are much thicker. The soma is usually about 10–25 micrometers in
diameter and often is not much larger than the cell nucleus it contains.
The longest axon of a human motor neuron can be over a meter long, reaching from the base of the spine to the toes.
Sensory neurons can have axons that run from the toes to the posterior column of the spinal cord, over 1.5 meters in adults. Giraffes
have single axons several meters in length running along the entire
length of their necks. Much of what is known about axonal function comes
from studying the squid giant axon, an ideal experimental preparation because of its relatively immense size (0.5–1 millimeters thick, several centimeters long).
Fully differentiated neurons are permanently postmitotic; however, stem cells present in the adult brain may regenerate functional neurons throughout the life of an organism. Astrocytes are star-shaped glial cells. They have been observed to turn into neurons by virtue of their stem cell-like characteristic of pluripotency.
Membrane
Like all animal cells, the cell body of every neuron is enclosed by a plasma membrane, a bilayer of lipid molecules with many types of protein structures embedded in it. A lipid bilayer is a powerful electrical insulator,
but in neurons, many of the protein structures embedded in the membrane
are electrically active. These include ion channels that permit
electrically charged ions to flow across the membrane and ion pumps that
chemically transport ions from one side of the membrane to the other.
Most ion channels are permeable only to specific types of ions. Some ion
channels are voltage gated,
meaning that they can be switched between open and closed states by
altering the voltage difference across the membrane. Others are
chemically gated, meaning that they can be switched between open and
closed states by interactions with chemicals that diffuse through the
extracellular fluid. The ion materials include sodium, potassium, chloride, and calcium.
The interactions between ion channels and ion pumps produce a voltage
difference across the membrane, typically a bit less than 1/10 of a volt
at baseline. This voltage has two functions: first, it provides a power
source for an assortment of voltage-dependent protein machinery that is
embedded in the membrane; second, it provides a basis for electrical
signal transmission between different parts of the membrane.
Histology and internal structure
Golgi-stained neurons in human hippocampal tissue
Actin filaments in a mouse Cortical Neuron in culture
Numerous microscopic clumps called Nissl bodies
(or Nissl substance) are seen when nerve cell bodies are stained with a
basophilic ("base-loving") dye. These structures consist of rough endoplasmic reticulum and associated ribosomal RNA. Named after German psychiatrist and neuropathologist Franz Nissl
(1860–1919), they are involved in protein synthesis and their
prominence can be explained by the fact that nerve cells are very
metabolically active. Basophilic dyes such as aniline or (weakly) haematoxylin highlight negatively charged components, and so bind to the phosphate backbone of the ribosomal RNA.
The cell body of a neuron is supported by a complex mesh of structural proteins called neurofilaments, which together with neurotubules (neuronal microtubules) are assembled into larger neurofibrils. Some neurons also contain pigment granules, such as neuromelanin (a brownish-black pigment that is byproduct of synthesis of catecholamines), and lipofuscin (a yellowish-brown pigment), both of which accumulate with age. Other structural proteins that are important for neuronal function are actin and the tubulin of microtubules. Class III β-tubulin
is found almost exclusively in neurons. Actin is predominately found at
the tips of axons and dendrites during neuronal development. There the
actin dynamics can be modulated via an interplay with microtubule.
There are different internal structural characteristics between axons and dendrites. Typical axons almost never contain ribosomes,
except some in the initial segment. Dendrites contain granular
endoplasmic reticulum or ribosomes, in diminishing amounts as the
distance from the cell body increases.
Classification
Image of pyramidal neurons in mouse cerebral cortex expressing green fluorescent protein. The red staining indicates GABAergic interneurons.
SMI32-stained pyramidal neurons in cerebral cortex
Neurons vary in shape and size and can be classified by their morphology and function. The anatomist Camillo Golgi
grouped neurons into two types; type I with long axons used to move
signals over long distances and type II with short axons, which can
often be confused with dendrites. Type I cells can be further classified
by the location of the soma. The basic morphology of type I neurons,
represented by spinal motor neurons, consists of a cell body called the soma and a long thin axon covered by a myelin sheath.
The dendritic tree wraps around the cell body and receives signals from
other neurons. The end of the axon has branching terminals (axon terminal) that release neurotransmitters into a gap called the synaptic cleft between the terminals and the dendrites of the next neuron.
Structural classification
Polarity
Different kinds of neurons:
Most neurons can be anatomically characterized as:
- Unipolar: single process
- Bipolar: 1 axon and 1 dendrite
- Multipolar: 1 axon and 2 or more dendrites
- Anaxonic: where the axon cannot be distinguished from the dendrite(s)
- Pseudounipolar: 1 process which then serves as both an axon and a dendrite
Other
Some unique
neuronal types can be identified according to their location in the
nervous system and distinct shape. Some examples are:
- Basket cells, interneurons that form a dense plexus of terminals around the soma of target cells, found in the cortex and cerebellum
- Betz cells, large motor neurons
- Lugaro cells, interneurons of the cerebellum
- Medium spiny neurons, most neurons in the corpus striatum
- Purkinje cells, huge neurons in the cerebellum, a type of Golgi I multipolar neuron
- Pyramidal cells, neurons with triangular soma, a type of Golgi I
- Renshaw cells, neurons with both ends linked to alpha motor neurons
- Unipolar brush cells, interneurons with unique dendrite ending in a brush-like tuft
- Granule cells, a type of Golgi II neuron
- Anterior horn cells, motoneurons located in the spinal cord
- Spindle cells, interneurons that connect widely separated areas of the brain
Functional classification
Direction
- Afferent neurons convey information from tissues and organs into the central nervous system and are also called sensory neurons.
- Efferent neurons (motor neurons) transmit signals from the central nervous system to the effector cells.
- Interneurons connect neurons within specific regions of the central nervous system.
Afferent and efferent also refer generally to neurons that,
respectively, bring information to or send information from the brain.
Action on other neurons
A neuron affects other neurons by releasing a neurotransmitter that binds to chemical receptors.
The effect upon the postsynaptic neuron is determined by the type of
receptor that is activated, not by the presynaptic neuron or by the
neurotransmitter. A neurotransmitter can be thought of as a key, and a
receptor as a lock: the same neurotransmitter can activate multiple
types of receptors. Receptors can be classified broadly as excitatory (causing an increase in firing rate), inhibitory (causing a decrease in firing rate), or modulatory (causing long-lasting effects not directly related to firing rate).
The two most common (90%+) neurotransmitters in the brain, glutamate and GABA, have largely consistent actions. Glutamate acts on several types of receptors, and has effects that are excitatory at ionotropic receptors and a modulatory effect at metabotropic receptors.
Similarly, GABA acts on several types of receptors, but all of them
have inhibitory effects (in adult animals, at least). Because of this
consistency, it is common for neuroscientists to refer to cells that
release glutamate as "excitatory neurons", and cells that release GABA
as "inhibitory neurons". Some other types of neurons have consistent
effects, for example, "excitatory" motor neurons in the spinal cord that
release acetylcholine, and "inhibitory" spinal neurons that release glycine.
The distinction between excitatory and inhibitory
neurotransmitters is not absolute. Rather, it depends on the class of
chemical receptors present on the postsynaptic neuron. In principle, a
single neuron, releasing a single neurotransmitter, can have excitatory
effects on some targets, inhibitory effects on others, and modulatory
effects on others still. For example, photoreceptor cells in the retina constantly release the neurotransmitter glutamate in the absence of light. So-called OFF bipolar cells
are, like most neurons, excited by the released glutamate. However,
neighboring target neurons called ON bipolar cells are instead inhibited
by glutamate, because they lack typical ionotropic glutamate receptors and instead express a class of inhibitory metabotropic glutamate receptors.
When light is present, the photoreceptors cease releasing glutamate,
which relieves the ON bipolar cells from inhibition, activating them;
this simultaneously removes the excitation from the OFF bipolar cells,
silencing them.
It is possible to identify the type of inhibitory effect a
presynaptic neuron will have on a postsynaptic neuron, based on the
proteins the presynaptic neuron expresses. Parvalbumin-expressing neurons typically dampen the output signal of the postsynaptic neuron in the visual cortex, whereas somatostatin-expressing neurons typically block dendritic inputs to the postsynaptic neuron.
Discharge patterns
Neurons have intrinsic electroresponsive properties like intrinsic transmembrane voltage oscillatory patterns. So neurons can be classified according to their electrophysiological characteristics:
- Tonic or regular spiking. Some neurons are typically constantly (tonically) active, typically firing at a constant frequency. Example: interneurons in neurostriatum.
- Phasic or bursting. Neurons that fire in bursts are called phasic.
- Fast spiking. Some neurons are notable for their high firing rates, for example some types of cortical inhibitory interneurons, cells in globus pallidus, retinal ganglion cells.
Neurotransmitter
- Cholinergic neurons—acetylcholine. Acetylcholine is released from presynaptic neurons into the synaptic cleft. It acts as a ligand for both ligand-gated ion channels and metabotropic (GPCRs) muscarinic receptors. Nicotinic receptors are pentameric ligand-gated ion channels composed of alpha and beta subunits that bind nicotine. Ligand binding opens the channel causing influx of Na+ depolarization and increases the probability of presynaptic neurotransmitter release. Acetylcholine is synthesized from choline and acetyl coenzyme A.
- GABAergic neurons—gamma aminobutyric acid. GABA is one of two neuroinhibitors in the central nervous system (CNS), along with glycine. GABA has a homologous function to ACh, gating anion channels that allow Cl− ions to enter the post synaptic neuron. Cl− causes hyperpolarization within the neuron, decreasing the probability of an action potential firing as the voltage becomes more negative (for an action potential to fire, a positive voltage threshold must be reached). GABA is synthesized from glutamate neurotransmitters by the enzyme glutamate decarboxylase.
- Glutamatergic neurons—glutamate. Glutamate is one of two primary excitatory amino acid neurotransmitters, along with aspartate. Glutamate receptors are one of four categories, three of which are ligand-gated ion channels and one of which is a G-protein coupled receptor (often referred to as GPCR).
- AMPA and Kainate receptors function as cation channels permeable to Na+ cation channels mediating fast excitatory synaptic transmission.
- NMDA receptors are another cation channel that is more permeable to Ca2+. The function of NMDA receptors depend on glycine receptor binding as a co-agonist within the channel pore. NMDA receptors do not function without both ligands present.
- Metabotropic receptors, GPCRs modulate synaptic transmission and postsynaptic excitability.
- Glutamate can cause excitotoxicity when blood flow to the brain is interrupted, resulting in brain damage. When blood flow is suppressed, glutamate is released from presynaptic neurons, causing greater NMDA and AMPA receptor activation than normal outside of stress conditions, leading to elevated Ca2+ and Na+ entering the post synaptic neuron and cell damage. Glutamate is synthesized from the amino acid glutamine by the enzyme glutamate synthase.
- Dopaminergic neurons—dopamine. Dopamine is a neurotransmitter that acts on D1 type (D1 and D5) Gs-coupled receptors, which increase cAMP and PKA, and D2 type (D2, D3, and D4) receptors, which activate Gi-coupled receptors that decrease cAMP and PKA. Dopamine is connected to mood and behavior and modulates both pre- and post-synaptic neurotransmission. Loss of dopamine neurons in the substantia nigra has been linked to Parkinson's disease. Dopamine is synthesized from the amino acid tyrosine. Tyrosine is catalyzed into levadopa (or L-DOPA) by tyrosine hydroxlase, and levadopa is then converted into dopamine by the aromatic amino acid decarboxylase.
- Serotonergic neurons—serotonin. Serotonin (5-Hydroxytryptamine, 5-HT) can act as excitatory or inhibitory. Of its four 5-HT receptor classes, 3 are GPCR and 1 is a ligand-gated cation channel. Serotonin is synthesized from tryptophan by tryptophan hydroxylase, and then further by decarboxylase. A lack of 5-HT at postsynaptic neurons has been linked to depression. Drugs that block the presynaptic serotonin transporter are used for treatment, such as Prozac and Zoloft.
Connectivity
A signal propagating down an axon to the cell body and dendrites of the next cell
Chemical synapse
Neurons communicate with each another via synapses, where either the axon terminal
of one cell contacts another neuron's dendrite, soma or, less commonly,
axon. Neurons such as Purkinje cells in the cerebellum can have over
1000 dendritic branches, making connections with tens of thousands of
other cells; other neurons, such as the magnocellular neurons of the supraoptic nucleus, have only one or two dendrites, each of which receives thousands of synapses.
Synapses can be excitatory or inhibitory,
either increasing or decreasing activity in the target neuron,
respectively. Some neurons also communicate via electrical synapses,
which are direct, electrically conductive junctions between cells.
When an action potential reaches the axon terminal, it opens voltage-gated calcium channels, allowing calcium ions to enter the terminal. Calcium causes synaptic vesicles
filled with neurotransmitter molecules to fuse with the membrane,
releasing their contents into the synaptic cleft. The neurotransmitters
diffuse across the synaptic cleft and activate receptors on the
postsynaptic neuron. High cytosolic calcium in the axon terminal triggers mitochondrial calcium uptake, which, in turn, activates mitochondrial energy metabolism to produce ATP to support continuous neurotransmission.
An autapse is a synapse in which a neuron's axon connects to its own dendrites.
The human brain has some 8.6 x 1010 (eighty six billion) neurons.
Each neuron has on average 7,000 synaptic connections to other neurons.
It has been estimated that the brain of a three-year-old child has
about 1015 synapses (1 quadrillion). This number declines with age, stabilizing by adulthood. Estimates vary for an adult, ranging from 1014 to 5 x 1014 synapses (100 to 500 trillion).
An
annotated diagram of the stages of an action potential propagating down
an axon including the role of ion concentration and pump and channel
proteins.
Mechanisms for propagating action potentials
In 1937 John Zachary Young suggested that the squid giant axon could be used to study neuronal electrical properties.
It is larger than but similar to human neurons, making it easier to
study. By inserting electrodes into the squid giant axons, accurate
measurements were made of the membrane potential.
The cell membrane of the axon and soma contain voltage-gated ion
channels that allow the neuron to generate and propagate an electrical
signal (an action potential). Some neurons also generate subthreshold membrane potential oscillations. These signals are generated and propagated by charge-carrying ions including sodium (Na+), potassium (K+), chloride (Cl−), and calcium (Ca2+).
Several stimuli can activate a neuron leading to electrical activity, including pressure, stretch, chemical transmitters, and changes of the electric potential across the cell membrane.
Stimuli cause specific ion-channels within the cell membrane to open,
leading to a flow of ions through the cell membrane, changing the
membrane potential. Neurons must maintain the specific electrical
properties that define their neuron type.
Thin neurons and axons require less metabolic
expense to produce and carry action potentials, but thicker axons
convey impulses more rapidly. To minimize metabolic expense while
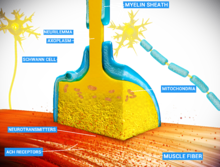
maintaining rapid conduction, many neurons have insulating sheaths of myelin around their axons. The sheaths are formed by glial cells: oligodendrocytes in the central nervous system and Schwann cells in the peripheral nervous system. The sheath enables action potentials to travel faster
than in unmyelinated axons of the same diameter, whilst using less
energy. The myelin sheath in peripheral nerves normally runs along the
axon in sections about 1 mm long, punctuated by unsheathed nodes of Ranvier, which contain a high density of voltage-gated ion channels. Multiple sclerosis is a neurological disorder that results from demyelination of axons in the central nervous system.
Some neurons do not generate action potentials, but instead generate a graded electrical signal, which in turn causes graded neurotransmitter release. Such non-spiking neurons tend to be sensory neurons or interneurons, because they cannot carry signals long distances.
Neural coding
Neural coding
is concerned with how sensory and other information is represented in
the brain by neurons. The main goal of studying neural coding is to
characterize the relationship between the stimulus and the individual or ensemble neuronal responses, and the relationships among the electrical activities of the neurons within the ensemble. It is thought that neurons can encode both digital and analog information.
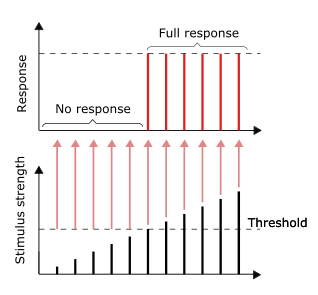
All-or-none principle
As
long as the stimulus reaches the threshold, the full response would be
given. Larger stimulus does not result in a larger response, vice versa.
The conduction of nerve impulses is an example of an all-or-none
response. In other words, if a neuron responds at all, then it must
respond completely. Greater intensity of stimulation, like brighter
image/louder sound, does not produce a stronger signal, but can increase
firing frequency. Receptors respond in different ways to stimuli. Slowly adapting or tonic receptors
respond to steady stimulus and produce a steady rate of firing. Tonic
receptors most often respond to increased intensity of stimulus by
increasing their firing frequency, usually as a power function of
stimulus plotted against impulses per second. This can be likened to an
intrinsic property of light where greater intensity of a specific
frequency (color) requires more photons, as the photons can't become
"stronger" for a specific frequency.
Other receptor types include quickly adapting or phasic
receptors, where firing decreases or stops with steady stimulus;
examples include skin
which, when touched causes neurons to fire, but if the object maintains
even pressure, the neurons stop firing. The neurons of the skin and
muscles that are responsive to pressure and vibration have filtering
accessory structures that aid their function.
The pacinian corpuscle
is one such structure. It has concentric layers like an onion, which
form around the axon terminal. When pressure is applied and the
corpuscle is deformed, mechanical stimulus is transferred to the axon,
which fires. If the pressure is steady, stimulus ends; thus, typically
these neurons respond with a transient depolarization during the initial
deformation and again when the pressure is removed, which causes the
corpuscle to change shape again. Other types of adaptation are important
in extending the function of a number of other neurons.
History
Drawing by Camillo Golgi of a hippocampus stained using the silver nitrate method
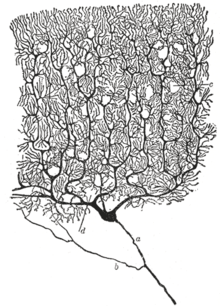
Drawing of a Purkinje cell in the cerebellar cortex done by Santiago Ramón y Cajal, demonstrating the ability of Golgi's staining method to reveal fine detail
The neuron's place as the primary functional unit of the nervous
system was first recognized in the late 19th century through the work of
the Spanish anatomist Santiago Ramón y Cajal.
To make the structure of individual neurons visible, Ramón y Cajal improved a silver staining process that had been developed by Camillo Golgi. The improved process involves a technique called "double impregnation" and is still in use.
In 1888 Ramón y Cajal published a paper about the bird cerebellum. In this paper, he stated that he could not find evidence for anastomosis between axons and dendrites and called each nervous element "an absolutely autonomous canton." This became known as the neuron doctrine, one of the central tenets of modern neuroscience.
In 1891 German anatomist Heinrich Wilhelm Waldeyer wrote a highly influential review about the neuron doctrine in which he introduced the term neuron to describe the anatomical and physiological unit of the nervous system.
The silver impregnation stains are a useful method for neuroanatomical
investigations because, for reasons unknown, it stains only a small
percentage of cells in a tissue, exposing the complete micro structure
of individual neurons without much overlap from other cells.
Neuron doctrine
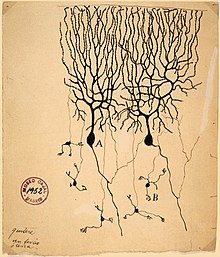
Drawing of neurons in the pigeon cerebellum, by Spanish neuroscientist Santiago Ramón y Cajal in 1899. (A) denotes Purkinje cells and (B) denotes granule cells, both of which are multipolar.
The neuron doctrine is the now fundamental idea that neurons are the
basic structural and functional units of the nervous system. The theory
was put forward by Santiago Ramón y Cajal in the late 19th century. It
held that neurons are discrete cells (not connected in a meshwork),
acting as metabolically distinct units.
Later discoveries yielded refinements to the doctrine. For example, glial cells, which are not considered neurons, play an essential role in information processing. Also, electrical synapses are more common than previously thought,
comprising direct, cytoplasmic connections between neurons. In fact,
neurons can form even tighter couplings: the squid giant axon arises
from the fusion of multiple axons.
Ramón y Cajal also postulated the Law of Dynamic Polarization,
which states that a neuron receives signals at its dendrites and cell
body and transmits them, as action potentials, along the axon in one
direction: away from the cell body. The Law of Dynamic Polarization has important exceptions; dendrites can serve as synaptic output sites of neurons and axons can receive synaptic inputs.
Compartmental Model of Neurons
Although
neurons are often described of as "fundamental units" of the brain,
they perform internal computations. Neurons integrate input within
dendrites, and this complexity is lost in models that assume neurons to
be a fundamental unit. Dendritic branches can be modeled as spatial
compartments, whose activity is related due to passive membrane
properties, but may also be different depending on input from synapses.
Compartmental modelling of dendrites
is especially helpful for understanding the behavior of neurons that
are too small to record with electrodes, as is the case for Drosophila melanogaster.
Neurons in the brain
The number of neurons in the brain varies dramatically from species to species. In a human, there are an estimated 10–20 billion neurons in the cerebral cortex and 55–70 billion neurons in the cerebellum. By contrast, the nematode worm Caenorhabditis elegans has just 302 neurons, making it an ideal model organism as scientists have been able to map all of its neurons. The fruit fly Drosophila melanogaster,
a common subject in biological experiments, has around 100,000 neurons
and exhibits many complex behaviors. Many properties of neurons, from
the type of neurotransmitters used to ion channel composition, are
maintained across species, allowing scientists to study processes
occurring in more complex organisms in much simpler experimental
systems.
Neurological disorders
Charcot–Marie–Tooth disease (CMT) is a heterogeneous inherited disorder of nerves (neuropathy)
that is characterized by loss of muscle tissue and touch sensation,
predominantly in the feet and legs extending to the hands and arms in
advanced stages. Presently incurable, this disease is one of the most
common inherited neurological disorders, with 36 in 100,000 affected.
Alzheimer's disease (AD), also known simply as Alzheimer's, is a neurodegenerative disease characterized by progressive cognitive deterioration, together with declining activities of daily living and neuropsychiatric symptoms or behavioral changes. The most striking early symptom is loss of short-term memory (amnesia),
which usually manifests as minor forgetfulness that becomes steadily
more pronounced with illness progression, with relative preservation of
older memories. As the disorder progresses, cognitive (intellectual)
impairment extends to the domains of language (aphasia), skilled movements (apraxia), and recognition (agnosia), and functions such as decision-making and planning become impaired.
Parkinson's disease (PD), also known as Parkinson disease, is a degenerative disorder of the central nervous system that often impairs motor skills and speech. Parkinson's disease belongs to a group of conditions called movement disorders. It is characterized by muscle rigidity, tremor, a slowing of physical movement (bradykinesia), and in extreme cases, a loss of physical movement (akinesia). The primary symptoms are the results of decreased stimulation of the motor cortex by the basal ganglia,
normally caused by the insufficient formation and action of dopamine,
which is produced in the dopaminergic neurons of the brain. Secondary
symptoms may include high level cognitive dysfunction and subtle language problems. PD is both chronic and progressive.
Myasthenia gravis is a neuromuscular disease leading to fluctuating muscle weakness and fatigability during simple activities. Weakness is typically caused by circulating antibodies that block acetylcholine receptors
at the post-synaptic neuromuscular junction, inhibiting the stimulative
effect of the neurotransmitter acetylcholine. Myasthenia is treated
with immunosuppressants, cholinesterase inhibitors and, in selected cases, thymectomy.
Demyelination
Guillain–Barré syndrome – demyelination
Demyelination
is the act of demyelinating, or the loss of the myelin sheath
insulating the nerves. When myelin degrades, conduction of signals along
the nerve can be impaired or lost, and the nerve eventually withers.
This leads to certain neurodegenerative disorders like multiple sclerosis and chronic inflammatory demyelinating polyneuropathy.
Axonal degeneration
Although
most injury responses include a calcium influx signaling to promote
resealing of severed parts, axonal injuries initially lead to acute
axonal degeneration, which is rapid separation of the proximal and
distal ends within 30 minutes of injury. Degeneration follows with
swelling of the axolemma, and eventually leads to bead like formation. Granular disintegration of the axonal cytoskeleton and inner organelles occurs after axolemma degradation. Early changes include accumulation of mitochondria
in the paranodal regions at the site of injury. Endoplasmic reticulum
degrades and mitochondria swell up and eventually disintegrate. The
disintegration is dependent on ubiquitin and calpain proteases
(caused by influx of calcium ion), suggesting that axonal degeneration
is an active process that produces complete fragmentation. The process
takes about roughly 24 hrs in the PNS and longer in the CNS. The
signaling pathways leading to axolemma degeneration are unknown.
Neurogenesis
Neurons are born through the process of neurogenesis, in which neural stem cells
divide to produce differentiated neurons. Once fully differentiated
neurons are formed, they are no longer capable of undergoing mitosis. Neurogenesis primarily occurs in the embryo of most organisms.
Neurogenesis can occur in the adult vertebrate brain, a finding that led to controversy in 1999.
Later studies of the age of human neurons suggest that this process
occurs only for a minority of cells, and a vast majority of neurons
composing the neocortex forms before birth and persists without replacement.
The extent to which adult neurogenesis exists in humans, and its
contribution to cognition are controversial, with conflicting reports
published in 2018.
The body contains a variety of stem cell types that have the
capacity to differentiate into neurons. Researchers found a way to
transform human skin cells into nerve cells using transdifferentiation, in which "cells are forced to adopt new identities".
During neurogenesis
in the mammalian brain, progenitor and stem cells progress from
proliferative divisions to differentiative divisions. This progression
leads to the neurons and glia that populate cortical layers. Epigenetic modifications play a key role in regulating gene expression in differentiating neural stem cells, and are critical for cell fate determination in the developing and adult mammalian brain. Epigenetic modifications include DNA cytosine methylation to form 5-methylcytosine and 5-methylcytosine demethylation. These modifications are critical for cell fate determination in the developing and adult mammalian brain. DNA cytosine methylation is catalyzed by DNA methyltransferases (DNMTs). Methylcytosine demethylation is catalyzed in several stages by TET enzymes that carry out oxidative reactions (e.g. 5-methylcytosine to 5-hydroxymethylcytosine) and enzymes of the DNA base excision repair (BER) pathway.
At different stages of mammalian nervous system development two
DNA repair processes are employed in the repair of DNA double-strand
breaks. These pathways are homologous recombinational repair used in proliferating neural precursor cells, and non-homologous end joining used mainly at later developmental stages.
Nerve regeneration
Peripheral axons can regrow if they are severed, but one neuron cannot be functionally replaced by one of another type (Llinás' law)














![\mathbb {P} [X=x]](https://wikimedia.org/api/rest_v1/media/math/render/svg/5d04e6399915b2326b151a549d455f681833b7d1)






![l(C)=\sum _{x\in {\mathcal {X}}}l(C(x))\mathbb {P} [X=x]](https://wikimedia.org/api/rest_v1/media/math/render/svg/ea60533d5d51ebd7b841e39ed0a27cd6c1fca652) .
.
 .
.


