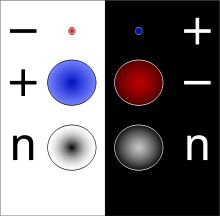Antiparticle

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Antiparticle 

 

Illustration of electric charge of particles (left) and antiparticles (right). From top to bottom; electron/positron, proton/antiproton, neutron/antineutron.

In particle physics, every type of particle is associated with an antiparticle with the same mass but with opposite physical charges (such as electric charge). For example, the antiparticle of the electron is the positron (also known as an antielectron). While the electron has a negative electric charge, the positron has a positive electric charge, and is produced naturally in certain types of radioactive decay. The opposite is also true: the antiparticle of the positron is the electron.

Some particles, such as the photon, are their own antiparticle. Otherwise, for each pair of antiparticle partners, one is designated as the normal particle (the one that occurs in matter usually interacted with in daily life). The other (usually given the prefix "anti-") is designated the antiparticle.

Particle–antiparticle pairs can annihilate each other, producing photons; since the charges of the particle and antiparticle are opposite, total charge is conserved. For example, the positrons produced in natural radioactive decay quickly annihilate themselves with electrons, producing pairs of gamma rays, a process exploited in positron emission tomography.

The laws of nature are very nearly symmetrical with respect to particles and antiparticles. For example, an antiproton and a positron can form an antihydrogen atom, which is believed to have the same properties as a hydrogen atom. This leads to the question of why the formation of matter after the Big Bang resulted in a universe consisting almost entirely of matter, rather than being a half-and-half mixture of matter and antimatter. The discovery of charge parity violation helped to shed light on this problem by showing that this symmetry, originally thought to be perfect, was only approximate.

Because charge is conserved, it is not possible to create an antiparticle without either destroying another particle of the same charge (as is for instance the case when antiparticles are produced naturally via beta decay or the collision of cosmic rays with Earth's atmosphere), or by the simultaneous creation of both a particle and its antiparticle, which can occur in particle accelerators such as the Large Hadron Collider at CERN.

Although particles and their antiparticles have opposite charges, electrically neutral particles need not be identical to their antiparticles. The neutron, for example, is made out of quarks, the antineutron from antiquarks, and they are distinguishable from one another because neutrons and antineutrons annihilate each other upon contact. However, other neutral particles are their own antiparticles, such as photons, Z⁰ bosons,
π⁰
 mesons, and hypothetical gravitons and some hypothetical WIMPs.

History

Experiment

In 1932, soon after the prediction of positrons by Paul Dirac, Carl D. Anderson found that cosmic-ray collisions produced these particles in a cloud chamber— a particle detector in which moving electrons (or positrons) leave behind trails as they move through the gas. The electric charge-to-mass ratio of a particle can be measured by observing the radius of curling of its cloud-chamber track in a magnetic field. Positrons, because of the direction that their paths curled, were at first mistaken for electrons travelling in the opposite direction. Positron paths in a cloud-chamber trace the same helical path as an electron but rotate in the opposite direction with respect to the magnetic field direction due to their having the same magnitude of charge-to-mass ratio but with opposite charge and, therefore, opposite signed charge-to-mass ratios.

The antiproton and antineutron were found by Emilio Segrè and Owen Chamberlain in 1955 at the University of California, Berkeley. Since then, the antiparticles of many other subatomic particles have been created in particle accelerator experiments. In recent years, complete atoms of antimatter have been assembled out of antiprotons and positrons, collected in electromagnetic traps.

Dirac hole theory

... the development of quantum field theory made the interpretation of antiparticles as holes unnecessary, even though it lingers on in many textbooks.

Steven Weinberg

Solutions of the Dirac equation contain negative energy quantum states. As a result, an electron could always radiate energy and fall into a negative energy state. Even worse, it could keep radiating infinite amounts of energy because there were infinitely many negative energy states available. To prevent this unphysical situation from happening, Dirac proposed that a "sea" of negative-energy electrons fills the universe, already occupying all of the lower-energy states so that, due to the Pauli exclusion principle, no other electron could fall into them. Sometimes, however, one of these negative-energy particles could be lifted out of this Dirac sea to become a positive-energy particle. But, when lifted out, it would leave behind a hole in the sea that would act exactly like a positive-energy electron with a reversed charge. These holes were interpreted as "negative-energy electrons" by Paul Dirac and mistakenly identified with protons in his 1930 paper A Theory of Electrons and Protons However, these "negative-energy electrons" turned out to be positrons, and not protons.

This picture implied an infinite negative charge for the universe—a problem of which Dirac was aware. Dirac tried to argue that we would perceive this as the normal state of zero charge. Another difficulty was the difference in masses of the electron and the proton. Dirac tried to argue that this was due to the electromagnetic interactions with the sea, until Hermann Weyl proved that hole theory was completely symmetric between negative and positive charges. Dirac also predicted a reaction
e⁻
 + 
p⁺
 → 
γ
 + 
γ
, where an electron and a proton annihilate to give two photons. Robert Oppenheimer and Igor Tamm, however, proved that this would cause ordinary matter to disappear too fast. A year later, in 1931, Dirac modified his theory and postulated the positron, a new particle of the same mass as the electron. The discovery of this particle the next year removed the last two objections to his theory.

Within Dirac's theory, the problem of infinite charge of the universe remains. Some bosons also have antiparticles, but since bosons do not obey the Pauli exclusion principle (only fermions do), hole theory does not work for them. A unified interpretation of antiparticles is now available in quantum field theory, which solves both these problems by describing antimatter as negative energy states of the same underlying matter field i.e. particles moving backwards in time.

Particle–antiparticle annihilation

Main article: Annihilation

 

An example of a virtual pion pair that influences the propagation of a kaon, causing a neutral kaon to mix with the antikaon. This is an example of renormalization in quantum field theory— the field theory being necessary because of the change in particle number.

If a particle and antiparticle are in the appropriate quantum states, then they can annihilate each other and produce other particles. Reactions such as
e⁻
 + 
e⁺
 → 
γ

γ
(the two-photon annihilation of an electron-positron pair) are an example. The single-photon annihilation of an electron-positron pair,
e⁻
 + 
e⁺
 → 
γ
, cannot occur in free space because it is impossible to conserve energy and momentum together in this process. However, in the Coulomb field of a nucleus the translational invariance is broken and single-photon annihilation may occur. The reverse reaction (in free space, without an atomic nucleus) is also impossible for this reason. In quantum field theory, this process is allowed only as an intermediate quantum state for times short enough that the violation of energy conservation can be accommodated by the uncertainty principle. This opens the way for virtual pair production or annihilation in which a one particle quantum state may fluctuate into a two particle state and back. These processes are important in the vacuum state and renormalization of a quantum field theory. It also opens the way for neutral particle mixing through processes such as the one pictured here, which is a complicated example of mass renormalization.

Properties

Quantum states of a particle and an antiparticle are interchanged by the combined application of charge conjugation ${\displaystyle C}$, parity ${\displaystyle P}$ and time reversal ${\displaystyle T}$. ${\displaystyle C}$ and ${\displaystyle P}$ are linear, unitary operators, ${\displaystyle T}$ is antilinear and antiunitary, ${\displaystyle \langle \Psi |T\,\Phi \rangle =\langle \Phi |T^{-1}\,\Psi \rangle }$. If ${\displaystyle |p,\sigma ,n\rangle }$ denotes the quantum state of a particle ${\displaystyle n}$ with momentum ${\displaystyle p}$ and spin ${\displaystyle J}$ whose component in the z-direction is ${\displaystyle \sigma }$, then one has

${\displaystyle CPT\ |p,\sigma ,n\rangle \ =\ (-1)^{J-\sigma }\ |p,-\sigma ,n^{c}\rangle ,}$

where ${\displaystyle n^{c}}$ denotes the charge conjugate state, that is, the antiparticle. In particular a massive particle and its antiparticle transform under the same irreducible representation of the Poincaré group which means the antiparticle has the same mass and the same spin.

If ${\displaystyle C}$, ${\displaystyle P}$ and ${\displaystyle T}$ can be defined separately on the particles and antiparticles, then

${\displaystyle T\ |p,\sigma ,n\rangle \ \propto \ |-p,-\sigma ,n\rangle ,}$

${\displaystyle CP\ |p,\sigma ,n\rangle \ \propto \ |-p,\sigma ,n^{c}\rangle ,}$

${\displaystyle C\ |p,\sigma ,n\rangle \ \propto \ |p,\sigma ,n^{c}\rangle ,}$

where the proportionality sign indicates that there might be a phase on the right hand side.

As ${\displaystyle CPT}$ anticommutes with the charges, ${\displaystyle CPT\,Q=-Q\,CPT}$, particle and antiparticle have opposite electric charges q and -q.

Quantum field theory

One may try to quantize an electron field without mixing the annihilation and creation operators by writing

${\displaystyle \psi (x)=\sum _{k}u_{k}(x)a_{k}e^{-iE(k)t},\,}$

where we use the symbol k to denote the quantum numbers p and σ of the previous section and the sign of the energy, E(k), and a_k denotes the corresponding annihilation operators. Of course, since we are dealing with fermions, we have to have the operators satisfy canonical anti-commutation relations. However, if one now writes down the Hamiltonian

${\displaystyle H=\sum _{k}E(k)a_{k}^{\dagger }a_{k},\,}$

then one sees immediately that the expectation value of H need not be positive. This is because E(k) can have any sign whatsoever, and the combination of creation and annihilation operators has expectation value 1 or 0.

So one has to introduce the charge conjugate antiparticle field, with its own creation and annihilation operators satisfying the relations

${\displaystyle b_{k\prime }=a_{k}^{\dagger }\ \mathrm {and} \ b_{k\prime }^{\dagger }=a_{k},\,}$

where k has the same p, and opposite σ and sign of the energy. Then one can rewrite the field in the form

${\displaystyle \psi (x)=\sum _{k_{+}}u_{k}(x)a_{k}e^{-iE(k)t}+\sum _{k_{-}}u_{k}(x)b_{k}^{\dagger }e^{-iE(k)t},\,}$

where the first sum is over positive energy states and the second over those of negative energy. The energy becomes

${\displaystyle H=\sum _{k_{+}}E_{k}a_{k}^{\dagger }a_{k}+\sum _{k_{-}}|E(k)|b_{k}^{\dagger }b_{k}+E_{0},\,}$

where E₀ is an infinite negative constant. The vacuum state is defined as the state with no particle or antiparticle, i.e., ${\displaystyle a_{k}|0\rangle =0}$ and ${\displaystyle b_{k}|0\rangle =0}$. Then the energy of the vacuum is exactly E₀. Since all energies are measured relative to the vacuum, H is positive definite. Analysis of the properties of a_k and b_k shows that one is the annihilation operator for particles and the other for antiparticles. This is the case of a fermion.

This approach is due to Vladimir Fock, Wendell Furry and Robert Oppenheimer. If one quantizes a real scalar field, then one finds that there is only one kind of annihilation operator; therefore, real scalar fields describe neutral bosons. Since complex scalar fields admit two different kinds of annihilation operators, which are related by conjugation, such fields describe charged bosons.

Feynman–Stueckelberg interpretation

By considering the propagation of the negative energy modes of the electron field backward in time, Ernst Stueckelberg reached a pictorial understanding of the fact that the particle and antiparticle have equal mass m and spin J but opposite charges q. This allowed him to rewrite perturbation theory precisely in the form of diagrams. Richard Feynman later gave an independent systematic derivation of these diagrams from a particle formalism, and they are now called Feynman diagrams. Each line of a diagram represents a particle propagating either backward or forward in time. In Feynman diagrams, anti-particles are shown traveling backwards in time relative to normal matter, and vice versa. This technique is the most widespread method of computing amplitudes in quantum field theory today.

Since this picture was first developed by Stueckelberg, and acquired its modern form in Feynman's work, it is called the Feynman–Stueckelberg interpretation of antiparticles to honor both scientists.

Mass in general relativity

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Mass_in_general_relativity 

The concept of mass in general relativity (GR) is more subtle to define than the concept of mass in special relativity. In fact, general relativity does not offer a single definition of the term mass, but offers several different definitions that are applicable under different circumstances. Under some circumstances, the mass of a system in general relativity may not even be defined.

The reason for this subtlety is that the energy and momentum in the gravitational field cannot be unambiguously localized. So, rigorous definitions of the mass in general relativity are not local, as in classical mechanics or special relativity, but make reference to the asymptotic nature of the spacetime. A well defined notion of the mass exists for asymptotically flat spacetimes and for asymptotically Anti-de Sitter space. However, these definitions must be used with care in other settings.

Defining mass in general relativity: concepts and obstacles

In special relativity, the rest mass of a particle can be defined unambiguously in terms of its energy and momentum as described in the article on mass in special relativity. Generalizing the notion of the energy and momentum to general relativity, however, is subtle. The main reason for this is that that gravitational field itself contributes to the energy and momentum. However, the "gravitational field energy" is not a part of the energy–momentum tensor; instead, what might be identified as the contribution of the gravitational field to a total energy is part of the Einstein tensor on the other side of Einstein's equation (and, as such, a consequence of these equations' non-linearity). While in certain situations it is possible to rewrite the equations so that part of the "gravitational energy" now stands alongside the other source terms in the form of the stress–energy–momentum pseudotensor, this separation is not true for all observers, and there is no general definition for obtaining it.

How, then, does one define a concept as a system's total mass – which is easily defined in classical mechanics? As it turns out, at least for spacetimes which are asymptotically flat (roughly speaking, which represent some isolated gravitating system in otherwise empty and gravity-free infinite space), the ADM 3+1 split leads to a solution: as in the usual Hamiltonian formalism, the time direction used in that split has an associated energy, which can be integrated up to yield a global quantity known as the ADM mass (or, equivalently, ADM energy). Alternatively, there is a possibility to define mass for a spacetime that is stationary, in other words, one that has a time-like Killing vector field (which, as a generating field for time, is canonically conjugate to energy); the result is the so-called Komar mass Although defined in a totally different way, it can be shown to be equivalent to the ADM mass for stationary spacetimes. The Komar integral definition can also be generalized to non-stationary fields for which there is at least an asymptotic time translation symmetry; imposing a certain gauge condition, one can define the Bondi energy at null infinity. In a way, the ADM energy measures all of the energy contained in spacetime, while the Bondi energy excludes those parts carried off by gravitational waves to infinity. Great effort has been expended on proving positivity theorems for the masses just defined, not least because positivity, or at least the existence of a lower limit, has a bearing on the more fundamental question of boundedness from below: if there were no lower limit to the energy, then no isolated system would be absolutely stable; there would always be the possibility of a decay to a state of even lower total energy. Several kinds of proofs that both the ADM mass and the Bondi mass are indeed positive exist; in particular, this means that Minkowski space (for which both are zero) is indeed stable. While the focus here has been on energy, analogue definitions for global momentum exist; given a field of angular Killing vectors and following the Komar technique, one can also define global angular momentum.

The disadvantage of all the definitions mentioned so far is that they are defined only at (null or spatial) infinity; since the 1970s, physicists and mathematicians have worked on the more ambitious endeavor of defining suitable quasi-local quantities, such as the mass of an isolated system defined using only quantities defined within a finite region of space containing that system. However, while there is a variety of proposed definitions such as the Hawking energy, the Geroch energy or Penrose's quasi-local energy–momentum based on twistor methods, the field is still in flux. Eventually, the hope is to use a suitable defined quasi-local mass to give a more precise formulation of the hoop conjecture, prove the so-called Penrose inequality for black holes (relating the black hole's mass to the horizon area) and find a quasi-local version of the laws of black hole mechanics.

Types of mass in general relativity

Komar mass in stationary spacetimes

Main article: Komar mass

A non-technical definition of a stationary spacetime is a spacetime where none of the metric coefficients ${\displaystyle g_{\mu \nu }\,}$ are functions of time. The Schwarzschild metric of a black hole and the Kerr metric of a rotating black hole are common examples of stationary spacetimes.

By definition, a stationary spacetime exhibits time translation symmetry. This is technically called a time-like Killing vector. Because the system has a time translation symmetry, Noether's theorem guarantees that it has a conserved energy. Because a stationary system also has a well defined rest frame in which its momentum can be considered to be zero, defining the energy of the system also defines its mass. In general relativity, this mass is called the Komar mass of the system. Komar mass can only be defined for stationary systems.

Komar mass can also be defined by a flux integral. This is similar to the way that Gauss's law defines the charge enclosed by a surface as the normal electric force multiplied by the area. The flux integral used to define Komar mass is slightly different from that used to define the electric field, however – the normal force is not the actual force, but the "force at infinity". See the main article for more detail.

Of the two definitions, the description of Komar mass in terms of a time translation symmetry provides the deepest insight.

ADM and Bondi masses in asymptotically flat space-times

If a system containing gravitational sources is surrounded by an infinite vacuum region, the geometry of the space-time will tend to approach the flat Minkowski geometry of special relativity at infinity. Such space-times are known as "asymptotically flat" space-times.

For systems in which space-time is asymptotically flat, the ADM and Bondi energy, momentum, and mass can be defined. In terms of Noether's theorem, the ADM energy, momentum, and mass are defined by the asymptotic symmetries at spatial infinity, and the Bondi energy, momentum, and mass are defined by the asymptotic symmetries at null infinity. Note that mass is computed as the length of the energy–momentum four-vector, which can be thought of as the energy and momentum of the system "at infinity".

The ADM energy is defined through the following flux integral at infinity. If a spacetime is asymptotically flat this means that near "infinity" the metric tends to that of flat space. The asymptotic deviations of the metric away from flat space can be parametrized by

${\displaystyle g_{\mu \nu }=\eta _{\mu \nu }+h_{\mu \nu }}$

where ${\displaystyle \eta _{\mu \nu }}$ is the flat space metric. The ADM energy is then given by an integral over a surface, ${\displaystyle S}$ at infinity

${\displaystyle P^{0}={1 \over 16\pi G}\int \left(\partial ^{k}h_{jk}-\partial ^{j}h_{kk}\right)d^{2}S_{j},}$

where ${\displaystyle S_{j}}$ is the outward-pointing normal to ${\displaystyle S}$. The Einstein summation convention is assumed for repeated indices but the sum over k and j only runs over the spatial directions. The use of ordinary derivatives instead of covariant derivatives in the formula above is justified because of the assumption that the asymptotic geometry is flat.

Some intuition for the formula above can be obtained as follows. Imagine that that we take the surface, S, to be a spherical surface so that the normal points radially outwards. At large distances from the source of the energy, r, the tensor ${\displaystyle h_{ij}}$ is expected to fall off as ${\displaystyle r^{-1}}$ and the derivative with respect to r converts this into ${\displaystyle r^{-2}}$ The area of the sphere at large radius also grows precisely as ${\displaystyle r^{2}}$ and therefore one obtains a finite value for the energy.

It is also possible to obtain expressions for the momentum in asymptotically flat spacetime. To obtain such an expression one defines

${\displaystyle H^{\mu \alpha \nu \beta }=-{\bar {h}}^{\mu \nu }\eta ^{\alpha \beta }-\eta ^{\mu \nu }{\bar {h}}^{\alpha \beta }+{\bar {h}}^{\alpha \nu }\eta ^{\mu \beta }+{\bar {h}}^{\mu \beta }\eta ^{\alpha \nu }}$

where

${\displaystyle {\bar {h}}_{\mu \nu }=h_{\mu \nu }-{1 \over 2}\eta _{\mu \nu }h_{\alpha }^{\alpha }}$

Then the momentum is obtained by a flux integral in the asymptotically flat region

${\displaystyle P^{\mu }={1 \over 16\pi G}\int \partial _{\alpha }H^{\mu \alpha 0j}d^{2}S_{j}}$

Note that the expression for ${\displaystyle P^{0}}$ obtained from the formula above coincides with the expression for the ADM energy given above as can easily be checked using the explicit expression for H.

The Newtonian limit for nearly flat space-times

In the Newtonian limit, for quasi-static systems in nearly flat space-times, one can approximate the total energy of the system by adding together the non-gravitational components of the energy of the system and then subtracting the Newtonian gravitational binding energy.

Translating the above statement into the language of general relativity, we say that a system in nearly flat space-time has a total non-gravitational energy E and momentum P given by:

${\displaystyle E=\int _{v}T_{00}dV\qquad P^{i}=\int _{V}T_{0i}dV}$

When the components of the momentum vector of the system are zero, i.e. Pⁱ = 0, the approximate mass of the system is just (E+E_binding)/c², E_binding being a negative number representing the Newtonian gravitational self-binding energy.

Hence when one assumes that the system is quasi-static, one assumes that there is no significant energy present in the form of "gravitational waves". When one assumes that the system is in "nearly-flat" space-time, one assumes that the metric coefficients are essentially Minkowskian within acceptable experimental error.

The formulas for the total energy and momentum can be seen to arise naturally in this limit as follows. In the linearized limit, the equations of general relativity can be written in the form

${\displaystyle \partial _{\alpha }\partial _{\beta }H^{\mu \alpha \nu \beta }=16\pi GT^{\mu \nu }}$

In this limit, the total energy-momentum of the system is simply given by integrating the stress-tensor on a spacelike slice.

${\displaystyle P^{\mu }=\int T^{\mu 0}d^{3}x}$

But using the equations of motion, one can also write this as

${\displaystyle P^{\mu }={1 \over 16\pi G}\int \partial _{\alpha }\partial _{\beta }H^{\mu \alpha 0\beta }d^{3}x={1 \over 16\pi G}\int \partial _{\alpha }\partial _{j}H^{\mu \alpha 0j}d^{3}x}$

where the sum over j runs only over the spatial directions and the second equality uses the fact that ${\displaystyle H^{\mu \alpha \nu \beta }}$ is anti-symmetric in ${\displaystyle \nu }$ and ${\displaystyle \beta }$. Finally, one uses the Gauss law to convert the integral of a divergence over the spatial slice into an integral over a Gaussian sphere

${\displaystyle {1 \over 16\pi G}\int \partial _{\alpha }\partial _{j}H^{\mu \alpha 0j}d^{3}x={1 \over 16\pi G}\int \partial _{\alpha }H^{\mu \alpha 0j}d^{2}S_{j}}$

which coincides precisely with the formula for the total momentum given above.

History

In 1918, David Hilbert wrote about the difficulty in assigning an energy to a "field" and "the failure of the energy theorem" in a correspondence with Klein. In this letter, Hilbert conjectured that this failure is a characteristic feature of the general theory, and that instead of "proper energy theorems" one had 'improper energy theorems'.

This conjecture was soon proved to be correct by one of Hilbert's close associates, Emmy Noether. Noether's theorem applies to any system which can be described by an action principle. Noether's theorem associates conserved energies with time-translation symmetries. When the time-translation symmetry is a finite parameter continuous group, such as the Poincaré group, Noether's theorem defines a scalar conserved energy for the system in question. However, when the symmetry is an infinite parameter continuous group, the existence of a conserved energy is not guaranteed. In a similar manner, Noether's theorem associates conserved momenta with space-translations, when the symmetry group of the translations is finite-dimensional. Because General Relativity is a diffeomorphism invariant theory, it has an infinite continuous group of symmetries rather than a finite-parameter group of symmetries, and hence has the wrong group structure to guarantee a conserved energy. Noether's theorem has been extremely influential in inspiring and unifying various ideas of mass, system energy, and system momentum in General Relativity.

As an example of the application of Noether's theorem is the example of stationary space-times and their associated Komar mass.(Komar 1959). While general space-times lack a finite-parameter time-translation symmetry, stationary space-times have such a symmetry, known as a Killing vector. Noether's theorem proves that such stationary space-times must have an associated conserved energy. This conserved energy defines a conserved mass, the Komar mass.

ADM mass was introduced (Arnowitt et al., 1960) from an initial-value formulation of general relativity. It was later reformulated in terms of the group of asymptotic symmetries at spatial infinity, the SPI group, by various authors. (Held, 1980). This reformulation did much to clarify the theory, including explaining why ADM momentum and ADM energy transforms as a 4-vector (Held, 1980). Note that the SPI group is actually infinite-dimensional. The existence of conserved quantities is because the SPI group of "super-translations" has a preferred 4-parameter subgroup of "pure" translations, which, by Noether's theorem, generates a conserved 4-parameter energy–momentum. The norm of this 4-parameter energy–momentum is the ADM mass.

The Bondi mass was introduced (Bondi, 1962) in a paper that studied the loss of mass of physical systems via gravitational radiation. The Bondi mass is also associated with a group of asymptotic symmetries, the BMS group at null infinity. Like the SPI group at spatial infinity, the BMS group at null infinity is infinite-dimensional, and it also has a preferred 4-parameter subgroup of "pure" translations.

Another approach to the problem of energy in General Relativity is the use of pseudotensors such as the Landau–Lifshitz pseudotensor.(Landau and Lifshitz, 1962). Pseudotensors are not gauge invariant – because of this, they only give consistent gauge-independent answers for the total energy when additional constraints (such as asymptotic flatness) are met. The gauge dependence of pseudotensors also prevents any gauge-independent definition of the local energy density, as every different gauge choice results in a different local energy density.