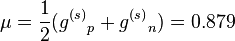Deuterium (symbol
D or
2H, also known as
heavy hydrogen) is one of two
stable isotopes of
hydrogen. The
nucleus of deuterium, called a
deuteron, contains one
proton and one
neutron, whereas the far more common hydrogen isotope,
protium, has no neutron in the nucleus. Deuterium has a
natural abundance in Earth's
oceans of about one
atom in
7003642000000000000♠6420 of hydrogen. Thus deuterium accounts for approximately 0.0156% (or on a mass basis 0.0312%) of all the naturally occurring hydrogen in the oceans, while the most common isotope (
hydrogen-1 or protium) accounts for more than 99.98%. The abundance of deuterium changes slightly from one kind of natural water to another (see
Vienna Standard Mean Ocean Water).
The deuterium isotope's name is formed from the Greek
deuteros meaning "second", to denote the two particles composing the nucleus.
[1] Deuterium was discovered and named in 1931 by
Harold Urey, earning him a Nobel Prize in 1934. This was followed by the discovery of the neutron in 1932, which made the nuclear structure of deuterium obvious. Soon after deuterium's discovery, Urey and others produced samples of "
heavy water" in which the deuterium had been highly concentrated.
Deuterium is destroyed in the interiors of stars faster than it is produced. Other natural processes are thought to produce only an insignificant amount of deuterium. Theoretically nearly all deuterium found in nature was produced in the
Big Bang 13.8 billion years ago, as the basic or primordial ratio of hydrogen-1 (protium) to deuterium (about 26 atoms of deuterium per million hydrogen atoms) has its origin from that time. This is the ratio found in the gas giant planets, such as Jupiter (see references 2,3 and 4). However, other astronomical bodies are found to have different ratios of deuterium to hydrogen-1. This is thought to be as a result of natural isotope separation processes that occur from solar heating of ices in comets. Like the water-cycle in Earth's weather, such heating processes may enrich deuterium with respect to protium. The analysis of deuterium/protium ratios in comets found results very similar to the mean ratio in Earth's oceans (156 atoms of deuterium per million hydrogens). This reinforces theories that much of Earth's ocean water is of cometary origin.
[2][3] The deuterium/protium ratio of the comet 67P/Churyumov-Gerasimenko, as measured by the
Rosetta space probe, is about three times that of earth water. This figure is the highest yet measured in a comet.
[4]
Deuterium/protium ratios thus continue to be an active topic of research in both astronomy and climatology.
Differences between deuterium and common hydrogen (protium)
Chemical symbol
Deuterium is frequently represented by the
chemical symbol D. Since it is an isotope of
hydrogen with
mass number 2, it is also represented by
2H.
IUPAC allows both D and
2H, although
2H is preferred.
[5] A distinct chemical symbol is used for convenience because of the isotope's common use in various scientific processes. Also, its large mass difference with
protium (
1H) (deuterium has a mass of
7000201410199999999♠2.014102 u, compared to the
mean hydrogen
atomic weight of
7000100794700000000♠1.007947 u, and protium's mass of
7000100782500000000♠1.007825 u) confers non-negligible chemical dissimilarities with protium-containing compounds, whereas the isotope weight ratios within other chemical elements are largely insignificant in this regard.
Spectroscopy
In
quantum mechanics the energy levels of electrons in atoms depend on the
reduced mass of the system of electron and nucleus. For the
hydrogen atom, the role of reduced mass is most simply seen in the
Bohr model of the atom, where the reduced mass appears in a simple calculation of the
Rydberg constant and Rydberg equation, but the reduced mass also appears in the
Schrödinger equation, and the
Dirac equation for calculating atomic energy levels.
The reduced mass of the system in these equations is close to the mass of a single electron, but differs from it by a small amount about equal to the ratio of mass of the electron to the atomic nucleus. For hydrogen, this amount is about 1837/1836, or 1.000545, and for deuterium it is even smaller: 3671/3670, or 1.0002725. The energies of spectroscopic lines for deuterium and light-hydrogen (hydrogen-1) therefore differ by the ratios of these two numbers, which is 1.000272. The wavelengths of all deuterium spectroscopic lines are shorter than the corresponding lines of light hydrogen, by a factor of 1.000272. In astronomical observation, this corresponds to a blue Doppler shift of 0.000272 times the speed of light, or 81.6 km/s.
[6]
The differences are much more pronounced in vibrational spectroscopy such as
infrared spectroscopy and
Raman spectroscopy,
[1] and in rotational spectra such as
microwave spectroscopy because the
reduced mass of the deuterium is markedly higher than that of protium.
Deuterium and Big Bang nucleosynthesis
Deuterium is thought to have played an important role in setting the number and ratios of the elements that were formed in the Big Bang. Combining thermodynamics and the changes brought about by cosmic expansion, one can calculate the fraction of protons and neutrons based on the temperature at the point that the universe cooled enough to allow formation of nuclei. This calculation indicates seven protons for every neutron at the beginning of nucleogenesis, a ratio that would remain stable even after nucleogenesis was over. This fraction was in favor of protons initially, primarily because the lower mass of the proton favored their production. As the universe expanded, it cooled.
Free neutrons and protons are less stable than helium nuclei, and the protons and neutrons had a strong energetic reason to form helium-4. However, forming helium-4 requires the intermediate step of forming deuterium.
Through much of the few minutes after the big bang during which nucleosynthesis could have occurred, the temperature was high enough that the mean energy per particle was greater than the binding energy of weakly bound deuterium; therefore any deuterium that was formed was immediately destroyed. This situation is known as the
deuterium bottleneck. The bottleneck delayed formation of any helium-4 until the universe became cool enough to form deuterium (at about a temperature equivalent to 100 keV). At this point, there was a sudden burst of element formation (first deuterium, which immediately fused to helium). However, very shortly thereafter, at twenty minutes after the Big Bang, the universe became too cool for any further nuclear fusion and nucleosynthesis to occur. At this point, the elemental abundances were nearly fixed, with the only change as some of the
radioactive products of big bang nucleosynthesis (such as
tritium) decay.
[7] The deuterium bottleneck in the formation of helium, together with the lack of stable ways for helium to combine with hydrogen or with itself (there are no stable nuclei with mass numbers of five or eight) meant that insignificant carbon, or any elements heavier than carbon, formed in the Big Bang. These elements thus required formation in stars. At the same time, the failure of much nucleogenesis during the Big Bang ensured that there would be plenty of hydrogen in the later universe available to form long-lived stars, such as our Sun.
Abundance
Deuterium occurs in trace amounts naturally as deuterium
gas, written
2H2 or D
2, but most natural occurrence in the
universe is bonded with a typical
1H atom, a gas called
hydrogen deuteride (HD or
1H2H).
[8]
The existence of deuterium on Earth, elsewhere in the
solar system (as confirmed by planetary probes), and in the spectra of
stars, is also an important datum in
cosmology. Gamma radiation from ordinary nuclear fusion dissociates deuterium into protons and neutrons, and there are no known natural processes other than the
Big Bang nucleosynthesis, which might have produced deuterium at anything close to the observed natural abundance of deuterium (deuterium is produced by the rare
cluster decay, and occasional absorption of naturally occurring neutrons by light hydrogen, but these are trivial sources). There is thought to be little deuterium in the interior of the Sun and other stars, as at temperatures there
nuclear fusion reactions that consume deuterium happen much faster than the
proton-proton reaction that creates deuterium. However, deuterium persists in the outer solar atmosphere at roughly the same concentration as in Jupiter, and this has probably been unchanged since the origin of the Solar System. The natural abundance of deuterium seems to be a very similar fraction of hydrogen, wherever hydrogen is found, unless there are obvious processes at work that concentrate it.
The existence of deuterium at a low but constant primordial fraction in all hydrogen is another one of the arguments in favor of the
Big Bang theory over the
Steady State theory of the universe. The observed ratios of hydrogen to helium to deuterium in the universe are difficult to explain except with a Big Bang model. It is estimated that the abundances of deuterium have not evolved significantly since their production about
7017435494880000000♠13.8 bya.
[9] Measurements of Milky Way galactic deuterium from ultraviolet spectral analysis show a ratio of as much as 23 atoms of deuterium per million hydrogen atoms in undisturbed gas clouds, which is only 15% below the
WMAP estimated primordial ratio of about 27 atoms per million from the Big Bang. This has been interpreted to mean that less deuterium has been destroyed in star formation in our galaxy than expected, or perhaps deuterium has been replenished by a large in-fall of primordial hydrogen from outside the galaxy.
[10] In space a few hundred light years from the Sun, deuterium abundance is only 15 atoms per million, but this value is presumably influenced by differential adsorption of deuterium onto carbon dust grains in interstellar space.
[11]
The abundance of deuterium in the atmosphere of
Jupiter has been directly measured by the
Galileo space probe as 26 atoms per million hydrogen atoms. ISO-SWS observations find 22 atoms per million hydrogen atoms in Jupiter.
[12] and this abundance is thought to represent close to the primordial solar system ratio.
[3] This is about 17% of the terrestrial deuterium-to-hydrogen ratio of 156 deuterium atoms per million hydrogen atoms.
Cometary bodies such as Comet
Hale Bopp and
Halley's Comet have been measured to contain relatively more deuterium (about 200 atoms D per million hydrogens), ratios which are enriched with respect to the presumed protosolar nebula ratio, probably due to heating, and which are similar to the ratios found in Earth seawater. The recent measurement of deuterium amounts of 161 atoms D per million hydrogen in Comet
103P/Hartley (a former
Kuiper belt object), a ratio almost exactly that in Earth's oceans, emphasizes the theory that Earth's surface water may be largely comet-derived.
[2][3] Most recently the deuterium/protium (D/H) ratio of 67P/Churyumov-Gerasimenko as measured by Rosetta is about three times that of earth water, a figure that is high.
[4] This has caused renewed interest in suggestions that Earth's water may be partly of asteroidal origin.
Deuterium has also observed to be concentrated over the mean solar abundance in other terrestrial planets, in particular Mars and Venus.
Production
Deuterium is produced for industrial, scientific and military purposes, by starting with ordinary water—a small fraction of which is naturally-occurring
heavy water—and then separating out the heavy water by the
Girdler sulfide process, distillation, or other methods.
In theory, deuterium for heavy water could be created in a nuclear reactor, but separation from ordinary water is the cheapest bulk production process.
The world's leading supplier of deuterium was
Atomic Energy of Canada Limited, in
Canada, until 1997, when the last heavy water plant was shut down. Canada uses heavy water as a
neutron moderator for the operation of the
CANDU reactor design.
Properties
Physical properties
The physical properties of deuterium compounds can exhibit significant
kinetic isotope effects and other physical and chemical property differences from the hydrogen analogs.
D2O, for example, is more
viscous than
H2O.
[13] Chemically, there are differences in bond energy and length for compounds of heavy hydrogen isotopes compared to normal hydrogen, which are larger than the isotopic differences in any other element. Bonds involving deuterium and
tritium are somewhat stronger than the corresponding bonds in hydrogen, and these differences are enough to cause significant changes in biological reactions.
Deuterium can replace the normal hydrogen in water molecules to form heavy water (D
2O), which is about 10.6% denser than normal water (so that ice made from it sinks in ordinary water). Heavy water is slightly toxic in
eukaryotic animals, with 25% substitution of the body water causing cell division problems and sterility, and 50% substitution causing death by cytotoxic syndrome (bone marrow failure and gastrointestinal lining failure).
Prokaryotic organisms, however, can survive and grow in pure heavy water, though they develop slowly.
[14] Despite this toxicity, consumption of heavy water under normal circumstances does not pose a
health threat to humans. It is estimated that a
7001700000000000000♠70 kg person might drink 4.8 liters of heavy water without serious consequences.
[15] Small doses of heavy water (a few grams in humans, containing an amount of deuterium comparable to that normally present in the body) are routinely used as harmless metabolic tracers in humans and animals.
Quantum properties
The deuteron has
spin +1 ("triplet") and is thus a
boson. The
NMR frequency of deuterium is significantly different from common light hydrogen.
Infrared spectroscopy also easily differentiates many deuterated compounds, due to the large difference in IR absorption frequency seen in the vibration of a chemical bond containing deuterium, versus light hydrogen. The two stable isotopes of hydrogen can also be distinguished by using
mass spectrometry.
The triplet deuteron nucleon is barely bound at E
B =
6987357285356601000♠2.23 MeV, so all the higher energy states are not bound. The singlet deuteron is a virtual state, with a negative binding energy of
6985961305892199999♠~60 keV. There is no such stable particle, but this virtual particle transiently exists during neutron-proton inelastic scattering, accounting for the unusually large neutron scattering cross-section of the proton.
[16]
Nuclear properties (the deuteron)
Deuteron mass and radius
The nucleus of deuterium is called a
deuteron. It has a mass of
7000201355321272400♠2.013553212724(78) u[17] The
charge radius of the deuteron is
6985214020000000000♠2.1402(28) fm[18]
Spin and energy
Deuterium is one of only five stable
nuclides with an odd number of protons and an odd number of neutrons. (
2H,
6Li,
10B,
14N,
180mTa; also, the long-lived radioactive nuclides
40K,
50V,
138La,
176Lu occur naturally.) Most odd-odd nuclei are unstable with respect to
beta decay, because the decay products are even-even, and are therefore more strongly bound, due to
nuclear pairing effects. Deuterium, however, benefits from having its proton and neutron coupled to a spin-1 state, which gives a stronger nuclear attraction; the corresponding spin-1 state does not exist in the two-neutron or two-proton system, due to the
Pauli exclusion principle which would require one or the other identical particle with the same spin to have some other different quantum number, such as
orbital angular momentum. But orbital angular momentum of either particle gives a lower
binding energy for the system, primarily due to increasing distance of the particles in the steep gradient of the nuclear force. In both cases, this causes the
diproton and
dineutron nucleus to be
unstable.
The proton and neutron making up deuterium can be
dissociated through
neutral current interactions with
neutrinos. The
cross section for this interaction is comparatively large, and deuterium was successfully used as a neutrino target in the
Sudbury Neutrino Observatory experiment.
Isospin singlet state of the deuteron
Due to the similarity in mass and nuclear properties between the proton and neutron, they are sometimes considered as two symmetric types of the same object, a
nucleon. While only the proton has an electric charge, this is often negligible due to the weakness of the
electromagnetic interaction relative to the
strong nuclear interaction. The symmetry relating the proton and neutron is known as
isospin and denoted
I (or sometimes
T).
Isospin is an
SU(2) symmetry, like ordinary
spin, so is completely analogous to it. The proton and neutron form an
isospin doublet, with a
"down" state (↓) being a neutron, and an
"up" state (↑) being a proton.
A pair of nucleons can either be in an antisymmetric state of isospin called
singlet, or in a symmetric state called
triplet. In terms of the "down" state and "up" state, the singlet is

This is a nucleus with one proton and one neutron, i.e. a deuterium nucleus. The triplet is

and thus consists of three types of nuclei, which are supposed to be symmetric: a deuterium nucleus (actually a highly
excited state of it), a nucleus with two protons, and a nucleus with two neutrons. The latter two nuclei are not stable or nearly stable, and therefore so is this type of deuterium (meaning that it is indeed a highly excited state of deuterium).
Approximated wavefunction of the deuteron
The deuteron wavefunction must be antisymmetric if the isospin representation is used (since a proton and a neutron are not identical particles, the wavefunction need not be antisymmetric in general). Apart from their isospin, the two nucleons also have spin and spatial distributions of their wavefunction. The latter is symmetric if the deuteron is symmetric under
parity (i.e. have an "even" or "positive" parity), and antisymmetric if the deuteron is antisymmetric under parity (i.e. have an "odd" or "negative" parity). The parity is fully determined by the total orbital angular momentum of the two nucleons: if it is even then the parity is even (positive), and if it is odd then the parity is odd (negative).
The deuteron, being an isospin singlet, is antisymmetric under nucleons exchange due to isospin, and therefore must be symmetric under the double exchange of their spin and location. Therefore it can be in either of the following two different states:
- Symmetric spin and symmetric under parity. In this case, the exchange of the two nucleons will multiply the deuterium wavefunction by (−1) from isospin exchange, (+1) from spin exchange and (+1) from parity (location exchange), for a total of (−1) as needed for antisymmetry.
- Antisymmetric spin and antisymmetric under parity. In this case, the exchange of the two nucleons will multiply the deuterium wavefunction by (−1) from isospin exchange, (−1) from spin exchange and (−1) from parity (location exchange), again for a total of (−1) as needed for antisymmetry.
In the first case the deuteron is a spin triplet, so that its total spin
s is 1. It also has an even parity and therefore even orbital angular momentum
l ; The lower its orbital angular momentum, the lower its energy. Therefore the lowest possible energy state has
s = 1,
l = 0.
In the second case the deuteron is a spin singlet, so that its total spin
s is 0. It also has an odd parity and therefore odd orbital angular momentum
l. Therefore the lowest possible energy state has
s = 0,
l = 1.
Since
s = 1 gives a stronger nuclear attraction, the deuterium
ground state is in the
s =1,
l = 0 state.
The same considerations lead to the possible states of an isospin triplet having
s = 0,
l = even or
s = 1,
l = odd. Thus the state of lowest energy has
s = 1,
l = 1, higher than that of the isospin singlet.
The analysis just given is in fact only approximate, both because isospin is not an exact symmetry, and more importantly because the
strong nuclear interaction between the two nucleons is related to
angular momentum in
spin-orbit interaction that mixes different
s and
l states. That is,
s and
l are not constant in time (they do not
commute with the
Hamiltonian), and over time a state such as
s = 1,
l = 0 may become a state of
s = 1,
l = 2. Parity is still constant in time so these do not mix with odd
l states (such as
s = 0,
l = 1). Therefore the
quantum state of the deuterium is a
superposition (a linear combination) of the
s = 1,
l = 0 state and the
s = 1,
l = 2 state, even though the first component is much bigger. Since the
total angular momentum j is also a good
quantum number (it is a constant in time), both components must have the same
j, and therefore
j = 1. This is the total spin of the deuterium nucleus.
To summarize, the deuterium nucleus is antisymmetric in terms of isospin, and has spin 1 and even (+1) parity. The relative angular momentum of its nucleons
l is not well defined, and the deuteron is a superposition of mostly
l = 0 with some
l = 2.
Magnetic and electric multipoles
In order to find theoretically the deuterium
magnetic dipole moment µ, one uses the formula for a
nuclear magnetic moment

with
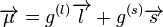
g
(l) and g
(s) are
g-factors of the nucleons.
Since the proton and neutron have different values for g
(l) and g
(s), one must separate their contributions. Each gets half of the deuterium orbital angular momentum

and spin

. One arrives at
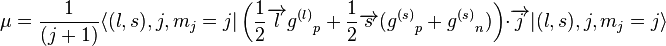
where subscripts p and n stand for the proton and neutron, and
g(l)n = 0.
By using the same identities as
here and using the value
g(l)p = 6994100000000000000♠1 µ
N, we arrive at the following result, in nuclear magneton units
![\mu =
{1\over 4 (j+1)}\left[({g^{(s)}}_p + {g^{(s)}}_n)\big(j(j+1) - l(l+1) + s(s+1)\big) + \big(j(j+1) + l(l+1) - s(s+1)\big)\right]](//upload.wikimedia.org/math/4/9/f/49f653501f931fbf9f1c67276a9ec4e4.png)
For the
s = 1,
l = 0 state (
j = 1), we obtain
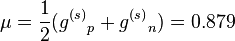
For the
s = 1,
l = 2 state (
j = 1), we obtain

The measured value of the deuterium
magnetic dipole moment, is
6993856999999999999♠0.857 µ
N, which is 97.5% of the
6993879000000000000♠0.879 µ
N value obtained by simply adding moments of the proton and neutron. This suggests that the state of the deuterium is indeed to a good approximation
s = 1,
l = 0 state, which occurs with both nucleons spinning in the same direction, but their magnetic moments subtracting because of the neutron's negative moment.
But the slightly lower experimental number than that which results from simple addition of proton and (negative) neutron moments shows that deuterium is actually a linear combination of mostly
s = 1,
l = 0 state with a slight admixture of
s = 1,
l = 2 state.
The
electric dipole is zero
as usual.
The measured electric
quadrupole of the deuterium is
6999285900000000000♠0.2859 e·fm2. While the order of magnitude is reasonable, since the deuterium radius is of order of 1 femtometer (see below) and its
electric charge is e, the above model does not suffice for its computation. More specifically, the
electric quadrupole does not get a contribution from the
l =0 state (which is the dominant one) and does get a contribution from a term mixing the
l =0 and the
l =2 states, because the electric quadrupole
operator does not
commute with
angular momentum.
The latter contribution is dominant in the absence of a pure
l = 0 contribution, but cannot be calculated without knowing the exact spatial form of the nucleons
wavefunction inside the deuterium.
Higher magnetic and electric
multipole moments cannot be calculated by the above model, for similar reasons.
Applications

Ionized deuterium in a
fusor reactor giving off its characteristic pinkish-red glow
Deuterium has a number of commercial and scientific uses. These include:
Nuclear reactors
Deuterium is used in
heavy water moderated fission reactors, usually as liquid D
2O, to slow neutrons without the high neutron absorption of ordinary hydrogen.
[19] This is a common commercial use for larger amounts of deuterium.
In
research reactors, liquid D
2 is used in
cold sources to moderate neutrons to very low energies and wavelengths appropriate for
scattering experiments.
Experimentally, deuterium is the most common nuclide used in
nuclear fusion reactor designs, especially in combination with
tritium, because of the large reaction rate (or
nuclear cross section) and high
energy yield of the D–T reaction. There is an even higher-yield D–
3He fusion reaction, though the
breakeven point of D–
3He is higher than that of most other fusion reactions; together with the scarcity of
3He, this makes it implausible as a practical power source until at least D–T and D–D fusion reactions have been performed on a commercial scale. However, commercial nuclear fusion is not yet an accomplished technology.
NMR spectroscopy
Deuterium is most commonly used in hydrogen
nuclear magnetic resonance spectroscopy (
proton NMR) in the following way. NMR ordinarily requires compounds of interest to be analyzed as dissolved in solution. Because of deuterium's nuclear spin properties which differ from the light hydrogen usually present in organic molecules, NMR spectra of hydrogen/protium are highly differentiable from that of deuterium, and in practice deuterium is not "seen" by an NMR instrument tuned for light-hydrogen. Deuterated solvents (including heavy water, but also compounds like deuterated chloroform, CDCl
3) are therefore routinely used in NMR spectroscopy, in order to allow only the light-hydrogen spectra of the compound of interest to be measured, without solvent-signal interference.
Nuclear magnetic resonance spectroscopy can also be used to obtain information about the deteron's environment in isotopically labelled samples (
Deuterium NMR). For example, the flexibility in the tail, which is a long hydrocarbon chains, in deuterium-labelled lipid molecules can be quantified using solid state deuterium NMR.
[20]
Deuterium NMR spectra are especially informative in the solid state because of its relatively small quadrupole moment in comparison with those of bigger quadrupolar nuclei such as chlorine-35, for example.
Tracing
In
chemistry,
biochemistry and
environmental sciences, deuterium is used as a non-radioactive,
stable isotopic tracer, for example, in the
doubly labeled water test. In
chemical reactions and
metabolic pathways, deuterium behaves somewhat similarly to ordinary hydrogen (with a few chemical differences, as noted). It can be distinguished from ordinary hydrogen most easily by its mass, using
mass spectrometry or
infrared spectrometry. Deuterium can be detected by
femtosecond infrared spectroscopy, since the mass difference drastically affects the frequency of molecular vibrations; deuterium-carbon bond vibrations are found in locations free of other signals.
Measurements of small variations in the natural abundances of deuterium, along with those of the stable heavy oxygen isotopes
17O and
18O, are of importance in
hydrology, to trace the geographic origin of Earth's waters. The heavy isotopes of hydrogen and oxygen in rainwater (so-called
meteoric water) are enriched as a function of the environmental temperature of the region in which the precipitation falls (and thus enrichment is related to mean latitude). The relative enrichment of the heavy isotopes in rainwater (as referenced to mean ocean water), when plotted against temperature falls predictably along a line called the
global meteoric water line (GMWL). This plot allows samples of precipitation-originated water to be identified along with general information about the climate in which it originated. Evaporative and other processes in bodies of water, and also ground water processes, also differentially alter the ratios of heavy hydrogen and oxygen isotopes in fresh and salt waters, in characteristic and often regionally distinctive ways.
[21] The ratio of concentration of
2H to
1H is usually indicated with a delta as δ
2H and the geographic patterns of these values are plotted in maps termed as isoscapes. Stable isotope are incorporated into plants and animals and an analysis of the ratios in a migrant bird or insect can help suggest a rough guide to their origins.
[22][23]
Contrast properties
Neutron scattering techniques particularly profit from availability of deuterated samples: The H and D cross sections are very distinct and different in sign, which allows contrast variation in such experiments. Further, a nuisance problem of ordinary hydrogen is its large incoherent neutron cross section, which is nil for D. The substitution of deuterium atoms for hydrogen atoms thus reduces scattering noise.
Hydrogen is an important and major component in all materials of organic chemistry and life science, but it barely interacts with X-rays. As hydrogen (and deuterium) interact strongly with neutrons, neutron scattering techniques, together with a modern deuteration facility,
[24] fills a niche in many studies of macromolecules in biology and many other areas.
Nuclear weapons
This is discussed below. It is notable that although most stars, including the Sun, generate energy over most of their lives by fusing hydrogen into heavier elements, such fusion of light hydrogen (protium) has never been successful in the conditions attainable on Earth. Thus, all artificial fusion, including the hydrogen fusion that occurs in so-called hydrogen bombs, requires heavy hydrogen (either tritium or deuterium, or both) in order for the process to work.
Drugs
Suggested neurological effects of natural abundance variation
The natural deuterium content of water has been suggested from preliminary correlative epidemiology to influence the incidence of affective disorder-related pathophysiology and major depression, which might be mediated by the serotonergic mechanisms.
[25]
History
Suspicion of lighter element isotopes
The existence of nonradioactive isotopes of lighter elements had been suspected in studies of neon as early as 1913, and proven by mass spectrometry of light elements in 1920. The prevailing theory at the time, however, was that the isotopes were due to the existence of differing numbers of "nuclear electrons" in different atoms of an element. It was expected that hydrogen, with a measured average atomic mass very close to
7000100000000000000♠1 u, the known mass of the proton, always had a nucleus composed of a single proton (a known particle), and therefore could not contain any nuclear electrons without losing its charge entirely. Thus, hydrogen could have no heavy isotopes.
Deuterium detected
It was first detected spectroscopically in late 1931 by
Harold Urey, a chemist at
Columbia University. Urey's collaborator,
Ferdinand Brickwedde,
distilled five
liters of
cryogenically produced liquid hydrogen to
6994100000000000000♠1 mL of liquid, using the low-temperature physics laboratory that had recently been established at the National Bureau of Standards in Washington, D.C. (now the
National Institute of Standards and Technology). The technique had previously been used to isolate heavy isotopes of neon. The cryogenic boiloff technique concentrated the fraction of the mass-2 isotope of hydrogen to a degree that made its spectroscopic identification unambiguous.
[26][27]
Naming of the isotope and Nobel Prize
Urey created the names protium, deuterium, and tritium in an article published in 1934. The name is based in part on advice from
G. N. Lewis who had proposed the name "deutium". The name is derived from the Greek deuteros (second), and the nucleus to be called "deuteron" or "deuton". Isotopes and new elements were traditionally given the name that their discoverer decided. Some British chemists, like
Ernest Rutherford, wanted the isotope to be called "diplogen", from the Greek diploos (double), and the nucleus to be called diplon.
[1]
The amount inferred for normal abundance of this heavy isotope of hydrogen was so small (only about 1 atom in 6400 hydrogen atoms in ocean water (156 deuteriums per million hydrogens)) that it had not noticeably affected previous measurements of (average) hydrogen atomic mass. This explained why it hadn't been experimentally suspected before. Urey was able to concentrate water to show partial enrichment of deuterium. Lewis had prepared the first samples of pure heavy water in 1933. The discovery of deuterium, coming before the discovery of the
neutron in 1932, was an experimental shock to theory, but when the neutron was reported, making deuterium's existence more explainable, deuterium won Urey the
Nobel Prize in chemistry in 1934. Lewis was embittered by being passed over for this recognition given to his former student.
[1]
"Heavy water" experiments in World War II
Shortly before the war,
Hans von Halban and
Lew Kowarski moved their research on neutron moderation from France to England, smuggling the entire global supply of heavy water (which had been made in Norway) across in twenty-six steel drums.
[28][29]
During
World War II,
Nazi Germany was known to be conducting experiments using heavy water as moderator for a
nuclear reactor design. Such experiments were a source of concern because they might allow them to produce
plutonium for an
atomic bomb. Ultimately it led to the
Allied operation called the "
Norwegian heavy water sabotage", the purpose of which was to destroy the
Vemork deuterium production/enrichment facility in
Norway. At the time this was considered important to the potential progress of the war.
After World War II ended, the Allies discovered that Germany was not putting as much serious effort into the program as had been previously thought. They had been unable to sustain a chain reaction. The Germans had completed only a small, partly built experimental reactor (which had been hidden away). By the end of the war, the Germans did not even have a fifth of the amount of heavy water needed to run the reactor
[clarification needed], partially due to the Norwegian heavy water sabotage operation. However, even had the Germans succeeded in getting a reactor operational (as the U.S. did with a graphite reactor in late 1942), they would still have been at least several years away from development of an
atomic bomb with maximal effort. The engineering process, even with maximal effort and funding, required about two and a half years (from first critical reactor to bomb) in both the U.S. and
U.S.S.R, for example.
Deuterium in thermonuclear weapons

A view of the
Sausage device casing of the
Ivy Mike hydrogen bomb, with its instrumentation and cryogenic equipment attached. This bomb held a cryogenic Dewar flask containing room for as much as 160 kilograms of liquid deuterium. The bomb was 20 feet tall. Note the seated man at the right of the photo for the scale.
The 62-ton
Ivy Mike device built by the United States and exploded on 1 November 1952, was the first fully successful "
hydrogen bomb" or
thermonuclear bomb. In this context, it was the first bomb in which most of the energy released came from
nuclear reaction stages that followed the primary
nuclear fission stage of the
atomic bomb. The Ivy Mike bomb was a factory-like building, rather than a deliverable weapon. At its center, a very large cylindrical, insulated
vacuum flask or
cryostat, held
cryogenic liquid deuterium in a volume of about 1000
liters (160 kilograms in mass, if this volume had been completely filled). Then, a conventional
atomic bomb (the "primary") at one end of the bomb was used to create the conditions of extreme temperature and pressure that were needed to set off the
thermonuclear reaction.
Within a few years, so-called "dry" hydrogen bombs were developed that did not need cryogenic hydrogen. Released information suggests that all
thermonuclear weapons built since then contain
chemical compounds of deuterium and lithium in their secondary stages. The material that contains the deuterium is mostly
lithium deuteride, with the lithium consisting of the isotope
lithium-6. When the lithium-6 is bombarded with fast
neutrons from the atomic bomb,
tritium (
hydrogen-3) is produced, and then the deuterium and the tritium quickly engage in
thermonuclear fusion, releasing abundant energy,
helium-4, and even more free neutrons.
Data for elemental deuterium
Formula: D
2 or
2
1H2
- Density: 6999180000000000000♠0.180 kg/m3 at STP (7002273149999999999♠0 °C, 7005101325000000000♠101.325 kPa).
- Atomic weight: 7000201410179260000♠2.0141017926 u.
- Mean abundance in ocean water (from VSMOW) 155.76 ± 0.1 ppm (a ratio of 1 part per approximately 6420 parts), that is, about 6998150000000000000♠0.015% of the atoms in a sample (by number, not weight)
Data at approximately
7001180000000000000♠18 K for D
2 (
triple point):
- Density:
- Liquid: 7002162400000000000♠162.4 kg/m3
- Gas: 6999452000000000000♠0.452 kg/m3
- Viscosity: 7001126000000000000♠12.6 µPa·s at 7002300000000000000♠300 K (gas phase)
- Specific heat capacity at constant pressure cp:
- Solid: 7003295000000000000♠2950 J/(kg·K)
- Gas: 7003520000000000000♠5200 J/(kg·K)
Anti-deuterium
An
antideuteron is the
antimatter counterpart of the nucleus of deuterium, consisting of an
antiproton and an
antineutron. The antideuteron was first produced in 1965 at the
Proton Synchrotron at
CERN[30] and the
Alternating Gradient Synchrotron at
Brookhaven National Laboratory.
[31] A complete atom, with a
positron orbiting the nucleus, would be called
antideuterium, but as of 2005 antideuterium has not yet been created. The proposed symbol for antideuterium is
D, that is, D with an overbar.
[32]


























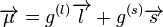
 and spin
and spin  . One arrives at
. One arrives at