Quantum biology

From Wikipedia, the free encyclopedia

Quantum biology refers to applications of quantum mechanics and theoretical chemistry to biological objects and problems. Many biological processes involve the conversion of energy into forms that are usable for chemical transformations and are quantum mechanical in nature. Such processes involve chemical reactions, light absorption, formation of excited electronic states, transfer of excitation energy, and the transfer of electrons and protons (hydrogen ions) in chemical processes such as photosynthesis and cellular respiration.^[1] Quantum biology may use computations to model biological interactions in light of quantum mechanical effects.^[2] Quantum biology is concerned with the influence of non-trivial quantum phenomena,^[3] as opposed to the so-called trivial quantum phenomena present in all biology by reduction to fundamental physics.

History

Early pioneers of quantum physics saw applications of quantum mechanics in biological problems. Erwin Schrödinger's 1944 book What is Life? discussed applications of quantum mechanics in biology.^[4] Schrödinger introduced the idea of an "aperiodic crystal" that contained genetic information in its configuration of covalent chemical bonds. He further suggested that mutations are introduced by "quantum leaps". Other pioneers Niels Bohr, Pascual Jordan, and Max Delbruck argued that the quantum idea of complementarity was fundamental to the life sciences.^[5] In 1963, Per-Olov Löwdin published proton tunneling as another mechanism for DNA mutation. In his paper, he stated that there is a new field of study called "quantum biology".^[6]

Applications

Photosynthesis

Diagram of FMO complex. Light excites electrons in an antenna. The excitation then transfers through various proteins in the FMO complex to the reaction center to further photosynthesis.

Organisms that undergo photosynthesis initially absorb light energy through the process of electron excitation in an antenna. This antenna varies between organisms. Bacteria can use ring like structures as antennas, whereas plants and other organisms use chlorophyll pigments to absorb photons. This electron excitation creates a separation of charge in a reaction site that is later converted into chemical energy for the cell to use. However, this electron excitation must be transferred in an efficient and timely manner, before that energy is lost in fluorescence.

Various structures are responsible for transferring energy from the antennas to a reaction site. One of the most well studied is the FMO complex in green sulfur bacteria. FT electron spectroscopy studies show an efficiency of above 99% between the absorption of electrons and transfer to the reaction site with short lived intermediates.^[7] This high efficiency cannot be explained by classical mechanics such as a diffusion model.

A study published in 2007 claimed the identification of electronic quantum coherence ^[8] at -196 °C (77 K). A later study further claimed exceptionally long-lived quantum coherence at 4 °C that was further postulated to be responsible for the high efficiency of the excitation transfer between different pigments in the light-harvesting stage of photosynthesis.^[9] It was, thus, suggested that nature through evolution had developed a way of protecting quantum coherence to enhance the efficiency of photosynthesis. However, critical follow-up studies question the interpretation of these results and assign the reported signatures of electronic quantum coherence to nuclear dynamics in the chromophores.^{[10][11][12][13][14]} The claims of unexpected long coherence times sparked a lot of research in the quantum physics community to explain the origin. A number of proposals were brought forward trying to explain the claimed long-lived coherence. According to one proposal, if each site within the complex feels its own environmental noise, then because of both quantum coherence and thermal environment, the electron will not remain in any local minimum but proceed to the reaction site.^[13][15][16] Another proposal is that the rate of quantum coherence combined with electron tunneling creates an energy sink that moves the electron to the reaction site quickly.^[17] Other work suggested that symmetries present in the geometric arrangement of the complex may favor efficient energy transfer to the reaction center, in a way that resembles perfect state transfer in quantum networks.^[18] However, careful control experiments cast doubts on the interpretation that quantum effects last any longer than one hundred femtoseconds.^[19]

Vision

Vision relies on quantized energy in order to convert light signals to an action potential in a process called phototransduction. In phototransduction, a photon interacts with a chromophore in a light receptor. The chromophore absorbs the photon and undergoes photoisomerization. This change in structure induces a change in the structure of the photo receptor and resulting signal transduction pathways lead to a visual signal. However, the photoisomerization reaction occurs at a rapid rate, in under 200 femtoseconds,^[20] with high yield. Models suggest the use of quantum effects in shaping the ground state and excited state potentials in order to achieve this efficiency.^[21]

Enzymatic activity (quantum biochemistry)

Enzymes may use quantum tunneling to transfer electrons long distances. Tunneling refers to the ability of a small mass particle to travel through energy barriers. Studies show that long distance electron transfers between redox centers through quantum tunneling plays important roles in enzymatic activity of photosynthesis and cellular respiration.^[22][23] For example, studies show that long range electron tunneling on the order of 15–30 Å plays a role in redox reactions in enzymes of cellular respiration.^[24] Even though there are such large separations between redox sites within enzymes, electrons successfully transfer in a temperature independent and distance dependent manner. This suggests the ability of electrons to tunnel in physiological conditions. Further research is needed to determine whether this specific tunneling is also coherent.

Magnetoreception

Magnetoreception refers to the ability of animals to navigate using the inclination of the magnetic field of the earth.^[25] A possible explanation for magnetoreception is the radical pair mechanism.^[26][27] The radical-pair mechanism is well-established in spin chemistry,^[28][29][30] and was speculated to apply to magnetoreception in 1978 by Schulten et al.. In 2000, cryptochrome was proposed as the "magnetic molecule", so to speak, that could harbor magnetically sensitive radical-pairs. Cryptochrome, a flavoprotein found in the eyes of European robins and other animal species, is the only protein known to form photoinduced radical-pairs in animals.^[25] The function of cryptochrome is diverse across species, however, the photoinduction of radical-pairs occurs by exposure to blue light, which excites an electron in a chromophore.^[31]

Nevertheless, in the lab, the direction of weak magnetic fields can affect radical-pair's reactivity, and therefore can "catalyze" the formation of chemical products. Whether this mechanism applies to magnetoreception and/or quantum biology, that is, whether earth's magnetic field "catalyzes" the formation of biochemical products by the aid of entangled or non-entangled radical-pairs, is doubly undetermined. As to the former, researchers found evidence for the radical-pair mechanism of magnetoreception when European robins, cockroaches, and garden warblers, could no longer navigate when exposed to a radio frequency oscillating magnetic fields,^[25] which specially disturbs radical-pair chemistry. To empirically suggest the involvement of entanglement, an experiment would need to be devised that could disturb entangled radical-pairs without disturbing other radical-pairs, or vice versa, which would first need to be demonstrated in a laboratory setting before being applied to magnetoreception.

Other biological applications

Other examples of quantum phenomena in biological systems include olfaction,^[32] the conversion of chemical energy into motion,^[33] DNA mutation^[6] and brownian motors in many cellular processes.^[34]

Quantum computing

From Wikipedia, the free encyclopedia

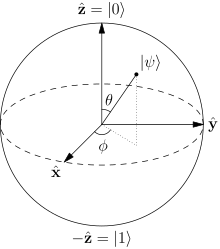
The Bloch sphere is a representation of a qubit, the fundamental building block of quantum computers.

Quantum computing is computing using quantum-mechanical phenomena, such as superposition and entanglement.^[1] A quantum computer is a device that performs quantum computing. They are different from binary digital electronic computers based on transistors. Whereas common digital computing requires that the data be encoded into binary digits (bits), each of which is always in one of two definite states (0 or 1), quantum computation uses quantum bits, which can be in superpositions of states. A quantum Turing machine is a theoretical model of such a computer, and is also known as the universal quantum computer. The field of quantum computing was initiated by the work of Paul Benioff^[2] and Yuri Manin in 1980,^[3] Richard Feynman in 1982,^[4] and David Deutsch in 1985.^[5]

As of 2018, the development of actual quantum computers is still in its infancy, but experiments have been carried out in which quantum computational operations were executed on a very small number of quantum bits.^[6] Both practical and theoretical research continues, and many national governments and military agencies are funding quantum computing research in additional effort to develop quantum computers for civilian, business, trade, environmental and national security purposes, such as cryptanalysis.^[7] A small 20-qubit quantum computer exists and is available for experiments via the IBM quantum experience project. D-Wave Systems has been developing their own version of a quantum computer that uses annealing.^[8]

Large-scale quantum computers would theoretically be able to solve certain problems much more quickly than any classical computers that use even the best currently known algorithms, like integer factorization using Shor's algorithm (which is a quantum algorithm) and the simulation of quantum many-body systems. There exist quantum algorithms, such as Simon's algorithm, that run faster than any possible probabilistic classical algorithm.^[9] A classical computer could in principle (with exponential resources) simulate a quantum algorithm, as quantum computation does not violate the Church–Turing thesis.^[10]:202 On the other hand, quantum computers may be able to efficiently solve problems which are not practically feasible on classical computers.

Basics

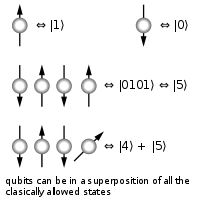
A classical computer has a memory made up of bits, where each bit is represented by either a one or a zero. A quantum computer maintains a sequence of qubits. A single qubit can represent a one, a zero, or any quantum superposition of those two qubit states;^[10]:13–16 a pair of qubits can be in any quantum superposition of 4 states,^[10]:16 and three qubits in any superposition of 8 states. In general, a quantum computer with ${\displaystyle n}$ qubits can be in an arbitrary superposition of up to ${\displaystyle 2^{n}}$ different states simultaneously^[10]:17 (this compares to a normal computer that can only be in one of these ${\displaystyle 2^{n}}$ states at any one time). A quantum computer operates on its qubits using quantum gates and measurement (which also alters the observed state). An algorithm is composed of a fixed sequence of quantum logic gates and a problem is encoded by setting the initial values of the qubits, similar to how a classical computer works. The calculation usually ends with a measurement, collapsing the system of qubits into one of the ${\displaystyle 2^{n}}$ eigenstates, where each qubit is zero or one, decomposing into a classical state. The outcome can therefore be at most ${\displaystyle n}$ classical bits of information (or, if the algorithm did not end with a measurement, the result is an unobserved quantum state). Quantum algorithms are often probabilistic, in that they provide the correct solution only with a certain known probability.^[11] Note that the term non-deterministic computing must not be used in that case to mean probabilistic (computing), because the term non-deterministic has a different meaning in computer science.

An example of an implementation of qubits of a quantum computer could start with the use of particles with two spin states: "down" and "up" (typically written ${\displaystyle |{\downarrow }\rangle }$ and ${\displaystyle |{\uparrow }\rangle }$, or ${\displaystyle |0{\rangle }}$ and ${\displaystyle |1{\rangle }}$). This is true because any such system can be mapped onto an effective spin-1/2 system.

Principles of operation

A quantum computer with a given number of qubits is fundamentally different from a classical computer composed of the same number of classical bits. For example, representing the state of an n-qubit system on a classical computer requires the storage of 2ⁿ complex coefficients, while to characterize the state of a classical n-bit system it is sufficient to provide the values of the n bits, that is, only n numbers. Although this fact may seem to indicate that qubits can hold exponentially more information than their classical counterparts, care must be taken not to overlook the fact that the qubits are only in a probabilistic superposition of all of their states. This means that when the final state of the qubits is measured, they will only be found in one of the possible configurations they were in before the measurement. It is generally incorrect to think of a system of qubits as being in one particular state before the measurement, since the fact that they were in a superposition of states before the measurement was made directly affects the possible outcomes of the computation.

Qubits are made up of controlled particles and the means of control (e.g. devices that trap particles and switch them from one state to another).^[12]

To better understand this point, consider a classical computer that operates on a three-bit register. If the exact state of the register at a given time is not known, it can be described as a probability distribution over the ${\displaystyle 2^{3}=8}$ different three-bit strings 000, 001, 010, 011, 100, 101, 110, and 111. If there is no uncertainty over its state, then it is in exactly one of these states with probability 1. However, if it is a probabilistic computer, then there is a possibility of it being in any one of a number of different states.

The state of a three-qubit quantum computer is similarly described by an eight-dimensional vector ${\displaystyle (a_{0},a_{1},a_{2},a_{3},a_{4},a_{5},a_{6},a_{7})}$ (or a one dimensional vector with each vector node holding the amplitude and the state as the bit string of qubits). Here, however, the coefficients ${\displaystyle a_{i}}$ are complex numbers, and it is the sum of the squares of the coefficients' absolute values, ${\displaystyle \sum _{i}|a_{i}|^{2}}$, that must equal 1. For each ${\displaystyle i}$, the absolute value squared ${\displaystyle \left|a_{i}\right|^{2}}$ gives the probability of the system being found in the ${\displaystyle i}$-th state after a measurement. However, because a complex number encodes not just a magnitude but also a direction in the complex plane, the phase difference between any two coefficients (states) represents a meaningful parameter. This is a fundamental difference between quantum computing and probabilistic classical computing.^[13]

If you measure the three qubits, you will observe a three-bit string. The probability of measuring a given string is the squared magnitude of that string's coefficient (i.e., the probability of measuring 000 = ${\displaystyle |a_{0}|^{2}}$, the probability of measuring 001 = ${\displaystyle |a_{1}|^{2}}$, etc.). Thus, measuring a quantum state described by complex coefficients ${\displaystyle (a_{0},a_{1},a_{2},a_{3},a_{4},a_{5},a_{6},a_{7})}$ gives the classical probability distribution ${\displaystyle (|a_{0}|^{2},|a_{1}|^{2},|a_{2}|^{2},|a_{3}|^{2},|a_{4}|^{2},|a_{5}|^{2},|a_{6}|^{2},|a_{7}|^{2})}$ and we say that the quantum state "collapses" to a classical state as a result of making the measurement.

An eight-dimensional vector can be specified in many different ways depending on what basis is chosen for the space. The basis of bit strings (e.g., 000, 001, …, 111) is known as the computational basis. Other possible bases are unit-length, orthogonal vectors and the eigenvectors of the Pauli-x operator. Ket notation is often used to make the choice of basis explicit. For example, the state ${\displaystyle (a_{0},a_{1},a_{2},a_{3},a_{4},a_{5},a_{6},a_{7})}$ in the computational basis can be written as:

${\displaystyle a_{0}\,|000\rangle +a_{1}\,|001\rangle +a_{2}\,|010\rangle +a_{3}\,|011\rangle +a_{4}\,|100\rangle +a_{5}\,|101\rangle +a_{6}\,|110\rangle +a_{7}\,|111\rangle }$

where, e.g., ${\displaystyle |010\rangle =\left(0,0,1,0,0,0,0,0\right)}$

The computational basis for a single qubit (two dimensions) is
${\displaystyle |0\rangle =\left(1,0\right)}$ and ${\displaystyle |1\rangle =\left(0,1\right)}$.

Using the eigenvectors of the Pauli-x operator, a single qubit is
${\displaystyle |+\rangle ={\tfrac {1}{\sqrt {2}}}\left(1,1\right)}$ and ${\displaystyle |-\rangle ={\tfrac {1}{\sqrt {2}}}\left(1,-1\right)}$.

Operation

While a classical 3-bit state and a quantum 3-qubit state are each eight-dimensional vectors, they are manipulated quite differently for classical or quantum computation. For computing in either case, the system must be initialized, for example into the all-zeros string, ${\displaystyle |000\rangle }$, corresponding to the vector (1,0,0,0,0,0,0,0). In classical randomized computation, the system evolves according to the application of stochastic matrices, which preserve that the probabilities add up to one (i.e., preserve the L1 norm). In quantum computation, on the other hand, allowed operations are unitary matrices, which are effectively rotations (they preserve that the sum of the squares add up to one, the Euclidean or L2 norm). (Exactly what unitaries can be applied depend on the physics of the quantum device.) Consequently, since rotations can be undone by rotating backward, quantum computations are reversible. (Technically, quantum operations can be probabilistic combinations of unitaries, so quantum computation really does generalize classical computation. See quantum circuit for a more precise formulation.)

Finally, upon termination of the algorithm, the result needs to be read off. In the case of a classical computer, we sample from the probability distribution on the three-bit register to obtain one definite three-bit string, say 000. Quantum mechanically, one measures the three-qubit state, which is equivalent to collapsing the quantum state down to a classical distribution (with the coefficients in the classical state being the squared magnitudes of the coefficients for the quantum state, as described above), followed by sampling from that distribution. This destroys the original quantum state. Many algorithms will only give the correct answer with a certain probability. However, by repeatedly initializing, running and measuring the quantum computer's results, the probability of getting the correct answer can be increased. In contrast, counterfactual quantum computation allows the correct answer to be inferred when the quantum computer is not actually running in a technical sense, though earlier initialization and frequent measurements are part of the counterfactual computation protocol.

For more details on the sequences of operations used for various quantum algorithms, see universal quantum computer, Shor's algorithm, Grover's algorithm, Deutsch–Jozsa algorithm, amplitude amplification, quantum Fourier transform, quantum gate, quantum adiabatic algorithm and quantum error correction.

Potential

Integer factorization, which underpins the security of public key cryptographic systems, is believed to be computationally infeasible with an ordinary computer for large integers if they are the product of few prime numbers (e.g., products of two 300-digit primes).^[14] By comparison, a quantum computer could efficiently solve this problem using Shor's algorithm to find its factors. This ability would allow a quantum computer to break many of the cryptographic systems in use today, in the sense that there would be a polynomial time (in the number of digits of the integer) algorithm for solving the problem. In particular, most of the popular public key ciphers are based on the difficulty of factoring integers or the discrete logarithm problem, both of which can be solved by Shor's algorithm. In particular the RSA, Diffie–Hellman, and elliptic curve Diffie–Hellman algorithms could be broken. These are used to protect secure Web pages, encrypted email, and many other types of data. Breaking these would have significant ramifications for electronic privacy and security.

However, other cryptographic algorithms do not appear to be broken by those algorithms.^[15][16] Some public-key algorithms are based on problems other than the integer factorization and discrete logarithm problems to which Shor's algorithm applies, like the McEliece cryptosystem based on a problem in coding theory.^[15][17] Lattice-based cryptosystems are also not known to be broken by quantum computers, and finding a polynomial time algorithm for solving the dihedral hidden subgroup problem, which would break many lattice based cryptosystems, is a well-studied open problem.^[18] It has been proven that applying Grover's algorithm to break a symmetric (secret key) algorithm by brute force requires time equal to roughly 2^n/2 invocations of the underlying cryptographic algorithm, compared with roughly 2ⁿ in the classical case,^[19] meaning that symmetric key lengths are effectively halved: AES-256 would have the same security against an attack using Grover's algorithm that AES-128 has against classical brute-force search (see Key size). Quantum cryptography could potentially fulfill some of the functions of public key cryptography.

Besides factorization and discrete logarithms, quantum algorithms offering a more than polynomial speedup over the best known classical algorithm have been found for several problems,^[20] including the simulation of quantum physical processes from chemistry and solid state physics, the approximation of Jones polynomials, and solving Pell's equation. No mathematical proof has been found that shows that an equally fast classical algorithm cannot be discovered, although this is considered unlikely.^[21] For some problems, quantum computers offer a polynomial speedup. The most well-known example of this is quantum database search, which can be solved by Grover's algorithm using quadratically fewer queries to the database than are required by classical algorithms. In this case the advantage is provable. Several other examples of provable quantum speedups for query problems have subsequently been discovered, such as for finding collisions in two-to-one functions and evaluating NAND trees.

Consider a problem that has these four properties:

1. The only way to solve it is to guess answers repeatedly and check them,
2. The number of possible answers to check is the same as the number of inputs,
3. Every possible answer takes the same amount of time to check, and
4. There are no clues about which answers might be better: generating possibilities randomly is just as good as checking them in some special order.

An example of this is a password cracker that attempts to guess the password for an encrypted file (assuming that the password has a maximum possible length).

For problems with all four properties, the time for a quantum computer to solve this will be proportional to the square root of the number of inputs. It can be used to attack symmetric ciphers such as Triple DES and AES by attempting to guess the secret key.^[22]

Since chemistry and nanotechnology rely on understanding quantum systems, and such systems are impossible to simulate in an efficient manner classically, many believe quantum simulation will be one of the most important applications of quantum computing.^[23] Quantum simulation could also be used to simulate the behavior of atoms and particles at unusual conditions such as the reactions inside a collider.^[24]

Quantum supremacy

John Preskill has introduced the term quantum supremacy to refer to the hypothetical speedup advantage that a quantum computer would have over a classical computer in a certain field.^[25]  Google announced in 2017 that it expected to achieve quantum supremacy by the end of the year, and IBM says that the best classical computers will be beaten on some task within about five years.^[26] Quantum supremacy has not been achieved yet, and skeptics like Gil Kalai doubt that it will ever be.^[27][28] Bill Unruh doubted the practicality of quantum computers in a paper published back in 1994.^[29] Paul Davies pointed out that a 400-qubit computer would even come into conflict with the cosmological information bound implied by the holographic principle.^[30] Those such as Roger Schlafly have pointed out that the claimed theoretical benefits of quantum computing go beyond the proven theory of quantum mechanics and imply non-standard interpretations, such as multiple worlds and negative probabilities. Schlafly maintains that the Born rule is just "metaphysical fluff" and that quantum mechanics doesn't rely on probability any more than other branches of science but simply calculates the expected values of observables. He also points out that arguments about Turing complexity cannot be run backwards.^[31][32][33] Those who prefer Bayesian interpretations of quantum mechanics have questioned the physical nature of the mathematical abstractions employed.^[34]

Obstacles

There are a number of technical challenges in building a large-scale quantum computer, and thus far quantum computers have yet to solve a problem faster than a classical computer. David DiVincenzo, of IBM, listed the following requirements for a practical quantum computer:^[35]

• scalable physically to increase the number of qubits;
• qubits that can be initialized to arbitrary values;
• quantum gates that are faster than decoherence time;
• universal gate set;
• qubits that can be read easily.

Quantum decoherence

One of the greatest challenges is controlling or removing quantum decoherence. This usually means isolating the system from its environment as interactions with the external world cause the system to decohere. However, other sources of decoherence also exist. Examples include the quantum gates, and the lattice vibrations and background thermonuclear spin of the physical system used to implement the qubits. Decoherence is irreversible, as it is effectively non-unitary, and is usually something that should be highly controlled, if not avoided. Decoherence times for candidate systems, in particular the transverse relaxation time T₂ (for NMR and MRI technology, also called the dephasing time), typically range between nanoseconds and seconds at low temperature.^[13] Currently, some quantum computers require their qubits to be cooled to 20 millikelvins in order to prevent significant decoherence.^[36]

As a result, time consuming tasks may render some quantum algorithms inoperable, as maintaining the state of qubits for a long enough duration will eventually corrupt the superpositions.^[37]

These issues are more difficult for optical approaches as the timescales are orders of magnitude shorter and an often-cited approach to overcoming them is optical pulse shaping. Error rates are typically proportional to the ratio of operating time to decoherence time, hence any operation must be completed much more quickly than the decoherence time.

As described in the Quantum threshold theorem, If the error rate is small enough, it is thought to be possible to use quantum error correction to suppress errors and decoherence. This allows the total calculation time to be longer than the decoherence time if the error correction scheme can correct errors faster than decoherence introduces them. An often cited figure for required error rate in each gate for fault tolerant computation is 10⁻³, assuming the noise is depolarizing.

Meeting this scalability condition is possible for a wide range of systems. However, the use of error correction brings with it the cost of a greatly increased number of required qubits. The number required to factor integers using Shor's algorithm is still polynomial, and thought to be between L and L², where L is the number of qubits in the number to be factored; error correction algorithms would inflate this figure by an additional factor of L. For a 1000-bit number, this implies a need for about 10⁴ bits without error correction.^[38] With error correction, the figure would rise to about 10⁷ bits. Computation time is about L² or about 10⁷ steps and at 1 MHz, about 10 seconds.

A very different approach to the stability-decoherence problem is to create a topological quantum computer with anyons, quasi-particles used as threads and relying on braid theory to form stable logic gates.^[39][40]

Developments

There are a number of quantum computing models, distinguished by the basic elements in which the computation is decomposed. The four main models of practical importance are:

• Quantum gate array (computation decomposed into sequence of few-qubit quantum gates)
• One-way quantum computer (computation decomposed into sequence of one-qubit measurements applied to a highly entangled initial state or cluster state)
• Adiabatic quantum computer, based on quantum annealing (computation decomposed into a slow continuous transformation of an initial Hamiltonian into a final Hamiltonian, whose ground states contain the solution)^[41]
• Topological quantum computer^[42] (computation decomposed into the braiding of anyons in a 2D lattice)

The quantum Turing machine is theoretically important but direct implementation of this model is not pursued. All four models of computation have been shown to be equivalent; each can simulate the other with no more than polynomial overhead.

For physically implementing a quantum computer, many different candidates are being pursued, among them (distinguished by the physical system used to realize the qubits):

• Superconducting quantum computing^[43][44] (qubit implemented by the state of small superconducting circuits (Josephson junctions))
• Trapped ion quantum computer (qubit implemented by the internal state of trapped ions)
• Optical lattices (qubit implemented by internal states of neutral atoms trapped in an optical lattice)
• Quantum dot computer, spin-based (e.g. the Loss-DiVincenzo quantum computer^[45]) (qubit given by the spin states of trapped electrons)
• Quantum dot computer, spatial-based (qubit given by electron position in double quantum dot)^[46]
• Nuclear magnetic resonance on molecules in solution (liquid-state NMR) (qubit provided by nuclear spins within the dissolved molecule)
• Solid-state NMR Kane quantum computers (qubit realized by the nuclear spin state of phosphorus donors in silicon)
• Electrons-on-helium quantum computers (qubit is the electron spin)
• Cavity quantum electrodynamics (CQED) (qubit provided by the internal state of trapped atoms coupled to high-finesse cavities)
• Molecular magnet^[47] (qubit given by spin states)
• Fullerene-based ESR quantum computer (qubit based on the electronic spin of atoms or molecules encased in fullerenes)
• Linear optical quantum computer (qubits realized by processing states of different modes of light through linear elements e.g. mirrors, beam splitters and phase shifters)^[48]
• Diamond-based quantum computer^[49][50][51] (qubit realized by electronic or nuclear spin of nitrogen-vacancy centers in diamond)
• Bose–Einstein condensate-based quantum computer^[52]
• Transistor-based quantum computer – string quantum computers with entrainment of positive holes using an electrostatic trap
• Rare-earth-metal-ion-doped inorganic crystal based quantum computers^[53][54] (qubit realized by the internal electronic state of dopants in optical fibers)
• Metallic-like carbon nanospheres based quantum computers^[55]

The large number of candidates demonstrates that the topic, in spite of rapid progress, is still in its infancy. There is also a vast amount of flexibility.

Timeline

In 1959 Richard Feynman in his lecture "There's Plenty of Room at the Bottom" states the possibility of using quantum effects for computation.

In 1980 Paul Benioff described quantum mechanical Hamiltonian models of computers^[56] and the Russian mathematician Yuri Manin motivated the development of quantum computers.^[57]

In 1981, at a conference co-organized by MIT and IBM, physicist Richard Feynman urged the world to build a quantum computer. He said "Nature isn't classical, dammit, and if you want to make a simulation of nature, you'd better make it quantum mechanical, and by golly it's a wonderful problem, because it doesn't look so easy."^[58]

In 1984, BB84 is published, the world's first quantum cryptography protocol by IBM scientists Charles Bennett and Gilles Brassard.

In 1993, an international group of six scientists, including Charles Bennett, showed that perfect quantum teleportation is possible^[59] in principle, but only if the original is destroyed.

In 1996, The DiVincenzo's criteria are published which is a list of conditions that are necessary for constructing a quantum computer proposed by the theoretical physicist David P. DiVincenzo in his 2000 paper "The Physical Implementation of Quantum Computation".

In 2001, researchers demonstrated Shor's algorithm to factor 15 using a 7-qubit NMR computer.^[60]

In 2005, researchers at the University of Michigan built a semiconductor chip ion trap. Such devices from standard lithography, may point the way to scalable quantum computing.^[61]

In 2009, researchers at Yale University created the first solid-state quantum processor. The two-qubit superconducting chip had artificial atom qubits made of a billion aluminum atoms that acted like a single atom that could occupy two states.^[62][63]

A team at the University of Bristol, also created a silicon chip based on quantum optics, able to run Shor's algorithm.^[64] Further developments were made in 2010.^[65] Springer publishes a journal (Quantum Information Processing) devoted to the subject.^[66]

In February 2010, Digital Combinational Circuits like adder, subtractor etc. are designed with the help of Symmetric Functions organized from different quantum gates.^[67][68]

In April 2011, a team of scientists from Australia and Japan made a breakthrough in quantum teleportation. They successfully transferred a complex set of quantum data with full transmission integrity, without affecting the qubits' superpositions.^[69][70]

Photograph of a chip constructed by D-Wave Systems Inc., mounted and wire-bonded in a sample holder. The D-Wave processor is designed to use 128 superconducting logic elements that exhibit controllable and tunable coupling to perform operations.

In 2011, D-Wave Systems announced the first commercial quantum annealer, the D-Wave One, claiming a 128 qubit processor. On May 25, 2011, Lockheed Martin agreed to purchase a D-Wave One system.^[71] Lockheed and the University of Southern California (USC) will house the D-Wave One at the newly formed USC Lockheed Martin Quantum Computing Center.^[72] D-Wave's engineers designed the chips with an empirical approach, focusing on solving particular problems. Investors liked this more than academics, who said D-Wave had not demonstrated they really had a quantum computer. Criticism softened after a D-Wave paper in Nature, that proved the chips have some quantum properties.^[73][74] Two published papers have suggested that the D-Wave machine's operation can be explained classically, rather than requiring quantum models.^[75][76] Later work showed that classical models are insufficient when all available data is considered.^[77] Experts remain divided on the ultimate classification of the D-Wave systems though their quantum behavior was established concretely with a demonstration of entanglement.^[78]

During the same year, researchers at the University of Bristol created an all-bulk optics system that ran a version of Shor's algorithm to successfully factor 21.^[79]

In September 2011 researchers proved quantum computers can be made with a Von Neumann architecture (separation of RAM).^[80]

In November 2011 researchers factorized 143 using 4 qubits.^[81]

In February 2012 IBM scientists said that they had made several breakthroughs in quantum computing with superconducting integrated circuits.^[82]

In April 2012 a multinational team of researchers from the University of Southern California, Delft University of Technology, the Iowa State University of Science and Technology, and the University of California, Santa Barbara, constructed a two-qubit quantum computer on a doped diamond crystal that can easily be scaled up and is functional at room temperature. Two logical qubit directions of electron spin and nitrogen kernels spin were used, with microwave impulses. This computer ran Grover's algorithm generating the right answer from the first try in 95% of cases.^[83]

In September 2012, Australian researchers at the University of New South Wales said the world's first quantum computer was just 5 to 10 years away, after announcing a global breakthrough enabling manufacture of its memory building blocks. A research team led by Australian engineers created the first working qubit based on a single atom in silicon, invoking the same technological platform that forms the building blocks of modern-day computers.^[84][85]

In October 2012, Nobel Prizes were presented to David J. Wineland and Serge Haroche for their basic work on understanding the quantum world, which may help make quantum computing possible.^[86][87]

In November 2012, the first quantum teleportation from one macroscopic object to another was reported by scientists at the University of Science and Technology of China in Hefei.^[88][89]

In December 2012, the first dedicated quantum computing software company, 1QBit was founded in Vancouver, BC.^[90] 1QBit is the first company to focus exclusively on commercializing software applications for commercially available quantum computers, including the D-Wave Two. 1QBit's research demonstrated the ability of superconducting quantum annealing processors to solve real-world problems.^[91]

In February 2013, a new technique, boson sampling, was reported by two groups using photons in an optical lattice that is not a universal quantum computer but may be good enough for practical problems. Science Feb 15, 2013

In May 2013, Google announced that it was launching the Quantum Artificial Intelligence Lab, hosted by NASA's Ames Research Center, with a 512-qubit D-Wave quantum computer. The USRA (Universities Space Research Association) will invite researchers to share time on it with the goal of studying quantum computing for machine learning.^[92] Google added that they had "already developed some quantum machine learning algorithms" and had "learned some useful principles", such as that "best results" come from "mixing quantum and classical computing".^[92]

In early 2014 it was reported, based on documents provided by former NSA contractor Edward Snowden, that the U.S. National Security Agency (NSA) is running a $79.7 million research program (titled "Penetrating Hard Targets") to develop a quantum computer capable of breaking vulnerable encryption.^[93]

In 2014, a group of researchers from ETH Zürich, USC, Google and Microsoft reported a definition of quantum speedup, and were not able to measure quantum speedup with the D-Wave Two device, but did not explicitly rule it out.^[94][95]

In 2014, researchers at University of New South Wales used silicon as a protectant shell around qubits, making them more accurate, increasing the length of time they will hold information, and possibly making quantum computers easier to build.^[96]

In April 2015 IBM scientists claimed two critical advances towards the realization of a practical quantum computer. They claimed the ability to detect and measure both kinds of quantum errors simultaneously, as well as a new, square quantum bit circuit design that could scale to larger dimensions.^[97]

In October 2015 researchers at University of New South Wales built a quantum logic gate in silicon for the first time.^[98]

In December 2015 NASA publicly displayed the world's first fully operational $15-million quantum computer made by the Canadian company D-Wave at the Quantum Artificial Intelligence Laboratory at its Ames Research Center in California's Moffett Field. The device was purchased in 2013 via a partnership with Google and Universities Space Research Association. The presence and use of quantum effects in the D-Wave quantum processing unit is more widely accepted.^[99] In some tests it can be shown that the D-Wave quantum annealing processor outperforms Selby’s algorithm.^[100] Only 2 of this computer has been made so far.

In May 2016, IBM Research announced^[101] that for the first time ever it is making quantum computing available to members of the public via the cloud, who can access and run experiments on IBM’s quantum processor. The service is called the IBM Quantum Experience. The quantum processor is composed of five superconducting qubits and is housed at the IBM T. J. Watson Research Center in New York.

In August 2016, scientists at the University of Maryland successfully built the first reprogrammable quantum computer.^[102]

In October 2016 Basel University described a variant of the electron hole based quantum computer, which instead of manipulating electron spins uses electron holes in a semiconductor at low (mK) temperatures which are a lot less vulnerable to decoherence. This has been dubbed the "positronic" quantum computer as the quasi-particle behaves like it has a positive electrical charge.^[103]

In March 2017, IBM announced an industry-first initiative to build commercially available universal quantum computing systems called IBM Q. The company also released a new API (Application Program Interface) for the IBM Quantum Experience that enables developers and programmers to begin building interfaces between its existing five quantum bit (qubit) cloud-based quantum computer and classical computers, without needing a deep background in quantum physics.

In May 2017, IBM announced^[104] that it has successfully built and tested its most powerful universal quantum computing processors. The first is a 16 qubit processor that will allow for more complex experimentation than the previously available 5 qubit processor. The second is IBM's first prototype commercial processor with 17 qubits and leverages significant materials, device, and architecture improvements to make it the most powerful quantum processor created to date by IBM.

In July 2017, a group of U.S. researchers announced a quantum simulator with 51 qubits. The announcement was made by Mikhail Lukin of Harvard University at the International Conference on Quantum Technologies in Moscow.^[105] A quantum simulator differs from a computer. Lukin’s simulator was designed to solve one equation. Solving a different equation would require building a new system. A computer can solve many different equations.

In September 2017, IBM Research scientists use a 7 qubit device to model the largest molecule,^[106] Beryllium hydride, ever by a quantum computer. The results were published as the cover story in the peer-reviewed journal Nature.

In October 2017, IBM Research scientists successfully "broke the 49-qubit simulation barrier" and simulated 49- and 56-qubit short-depth circuits, using the Lawrence Livermore National Laboratory's Vulcan supercomputer, and the University of Illinois' Cyclops Tensor Framework (originally developed at the University of California). The results were published in arxiv.^[107]

In November 2017, the University of Sydney research team in Australia successfully made a microwave circulator, an important quantum computer part, 1000 times smaller than a conventional circulator by using topological insulators to slow down the speed of light in a material.^[108]

In November 2017, IBM announced^[109] the availability of its most-powerful 20 qubit commercial processor, and the first prototype 50 qubit processor. The 20 qubit processor has an industry-leading 90 μs coherence time for the systems' operations.

In December 2017, IBM announced^[110] its first IBM Q Network clients. The companies, universities, and labs to explore practical quantum applications, using IBM Q 20 qubit commercial systems, for business and science include: JPMorgan Chase, Daimler AG, Samsung, JSR Corporation, Barclays, Hitachi Metals, Honda, Nagase, Keio University, Oak Ridge National Lab, Oxford University and University of Melbourne.

In December 2017, Microsoft released a preview version of a "Quantum Development Kit".^[111] It includes a programming language, Q#, which can be used to write programs that are run on an emulated quantum computer.

In 2017 D-Wave reported to start selling a 2000 qubit quantum computer.^[112]

In February 2018, scientists reported, for the first time, the discovery of a new form of light, which may involve polaritons, that could be useful in the development of quantum computers.^[113][114]

In March 2018, Google Quantum AI Lab announced a 72 qubit processor called Bristlecone.^[115]

In April 2018, IBM Research announced eight quantum computing startups joined the IBM Q Network,^[116] including: Zapata Computing, Strangeworks, QxBranch, Quantum Benchmark, QC Ware, Q-CTRL, Cambridge Quantum Computing, and 1QBit.

Relation to computational complexity theory

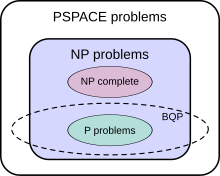
The suspected relationship of BQP to other problem spaces.^[117]

The class of problems that can be efficiently solved by quantum computers is called BQP, for "bounded error, quantum, polynomial time". Quantum computers only run probabilistic algorithms, so BQP on quantum computers is the counterpart of BPP ("bounded error, probabilistic, polynomial time") on classical computers. It is defined as the set of problems solvable with a polynomial-time algorithm, whose probability of error is bounded away from one half.^[118] A quantum computer is said to "solve" a problem if, for every instance, its answer will be right with high probability. If that solution runs in polynomial time, then that problem is in BQP.

BQP is contained in the complexity class #P (or more precisely in the associated class of decision problems P^#P),^[119] which is a subclass of PSPACE.

BQP is suspected to be disjoint from NP-complete and a strict superset of P, but that is not known. Both integer factorization and discrete log are in BQP. Both of these problems are NP problems suspected to be outside BPP, and hence outside P. Both are suspected to not be NP-complete. There is a common misconception that quantum computers can solve NP-complete problems in polynomial time. That is not known to be true, and is generally suspected to be false.^[119]

The capacity of a quantum computer to accelerate classical algorithms has rigid limits—upper bounds of quantum computation's complexity. The overwhelming part of classical calculations cannot be accelerated on a quantum computer.^[120] A similar fact takes place for particular computational tasks, like the search problem, for which Grover's algorithm is optimal.^[121]

Bohmian Mechanics is a non-local hidden variable interpretation of quantum mechanics. It has been shown that a non-local hidden variable quantum computer could implement a search of an N-item database at most in ${\displaystyle O({\sqrt[{3}]{N}})}$ steps. This is slightly faster than the ${\displaystyle O({\sqrt {N}})}$ steps taken by Grover's algorithm. Neither search method will allow quantum computers to solve NP-Complete problems in polynomial time.^[122]

Although quantum computers may be faster than classical computers for some problem types, those described above can't solve any problem that classical computers can't already solve. A Turing machine can simulate these quantum computers, so such a quantum computer could never solve an undecidable problem like the halting problem. The existence of "standard" quantum computers does not disprove the Church–Turing thesis.^[123] It has been speculated that theories of quantum gravity, such as M-theory or loop quantum gravity, may allow even faster computers to be built. Currently, defining computation in such theories is an open problem due to the problem of time, i.e., there currently exists no obvious way to describe what it means for an observer to submit input to a computer and later receive output.^[124][71]