You may have heard of quantum theory before and you probably know what a field is. But what is quantum field theory? This four-part article
traces the development of an example of a quantum field theory, quantum
electrodynamics, in the first half of the 20th century.

Iron filings scattered around a bar magnet arrange themselves along field lines.
Do you remember those pretty field lines that emerge when you scatter
iron filings around a magnet? In the case of a simple magnet the field
is static; it doesn't change with time. But magnetism is just one
aspect of something bigger: electromagnetism. You are at this very
moment immersed in electromagnetic fields, generated by the Earth, the
Sun, and even your toaster. Fluctuations of an electromagnetic field are
called electromagnetic waves — it's those waves that make up
visible light, as well as radio waves, x-ray, and microwaves. You are
constantly bombarded by them as they travel across space in the form of
energy being carried across the electromagnetic field.
James Clerk Maxwell
realized, in 1864, that electricity and magnetism were just two sides
of the same coin and that light was made up of electromagnetic waves. He
developed an elegant theory describing the unified force of
electromagnetism and the equations that describe the dynamics of an
electromagnetic field now carry his name.
More generally, the idea of a field became an important one in
physics because it cleared up a conundrum that had been bugging
physicists for a long time. If you think of a force, such as
electromagnetism or gravity, as acting between two objects, then you
have to admit that it acts instantaneously across space, an idea that
seems altogether too magical. If, on the other hand, you think of an
object as generating a field around it, then you can explain the force
in terms of of the field — the mysterious action at a distance is
replaced by a perfectly reasonable local one. Once a field has been
generated it has a life of its own, carrying along energy, which is
described by its very own equations of motion. Einstein picked up this
idea in his 1916 theory of general relativity, which describes gravity
in terms of gravitational fields generated by massive bodies like the
Sun or the planets.
A couple of decades before Einstein had his revolutionary insight
into physics on the cosmological scale, another revolution happened in
the physics of the very small, with serious consequences for Maxwell's
theory of electromagnetism. At the turn of the twentieth century it
became clear that light doesn't always behaves like waves: under certain
circumstances it seems to come in streams of particles called photons. This is what Einstein realised when he discovered the photoelectric effect. Prompted by this discovery Louis de Broglie suggested in the early 1920s that little particles of matter, such as electrons, could also display wave-like behaviour. This wave-particle duality emerged as a fundamental feature of physics and it is the central idea of quantum mechanics.
Exciting photons
The curious new physics of quantum mechanics required new mathematics and this was independently discovered by Erwin Schrödinger and Werner Heisenberg
in the mid 1920s. Their equivalent theories described the behaviour of
collections of particles moving freely, or under the influence of a
force. The next step was to modify Maxwell's equations for the
electromagnetic field to take account of the new insights from quantum
mechanics.

Illustration of the electric vectorfield surrounding a positive point charge. Image Wikimedia commons.
This was a difficult task: a finite collection of particles is
described by a finite amount of information, but a field, extending
through a region of space made up of infinitely many points, is
described by an infinite amount of information. In Maxwell's original
formulation each point in the field came with a couple of arrows,
describing the direction in which the two forces (electric and magnetic)
would act on a test particle placed at that point. The length of the
arrows was proportional to the strength of the forces. Maxwell's
equation described how these arrows change over time. In a quantised
version of electromagnetism these arrows, called vectors, would
have to be replaced by more complex mathematical objects and their
change over time would have to be described by a more complicated
equation.
Exactly how Maxwell's equations should be modified was anyone's guess until the physicist Paul Dirac
had an important insight in 1927. He considered an electromagnetic
field without matter. Maxwell's equations showed that this field is in
motion, with gently undulating electromagnetic waves propagating through
it as the electric and magnetic components interact. Just as sound
waves can be decomposed into harmonics, these electromagnetic waves
could be decomposed into pure sine waves using a well-known mathematical
technique called Fourier analysis.
The periodic fluctuations of these regular waves are akin to the motion
of a pendulum or a mass suspended from a spring: in both cases an object
displaced from equilibrium feels a restoring force that is proportional
to the displacement. Systems such as these are called harmonic oscillators.
Luckily, physicists already knew how to deal with these oscillators
quantum mechanically. Dirac thus managed to quantise the electromagnetic
field by first decomposing it, mathematically, into infinitely many
harmonic oscillators and then applying existing techniques, namely Schrödinger's equation, to quantise those.
Schrödinger’s quantum mechanical treatment of harmonic oscillators
had led to some curious results. The total energy stored in a classical
harmonic oscillator, such as a pendulum, remains constant over time:
when we see a pendulum slow down, this is only because other processes,
such as friction, intervene. The energy of an ideal and eternally
swinging pendulum comes from the push you start the pendulum off with.
You would think that by getting your push just right, you can make the
energy take on any value at all. But for a quantum harmonic oscillator
this isn’t true: its energy can only take discrete values 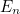 which depend on the frequency of oscillation
which depend on the frequency of oscillation
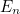 which depend on the frequency of oscillation
which depend on the frequency of oscillation ![\[ E_ n= \frac{h}{2\pi } \omega \left(n+\frac{1}{2}\right). \]](https://plus.maths.org/MI/2baf83ada3bb6ca195b5c9978a94c5d0/images/img-0002.png) |
Here 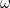 is the angular frequency of the oscillator,
is the angular frequency of the oscillator, 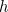 is a fundamental constant of nature called Planck’s constant and
is a fundamental constant of nature called Planck’s constant and 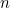 is a natural number. The important point is that the value of the
energy of the quantum harmonic oscillator can only be exactly
is a natural number. The important point is that the value of the
energy of the quantum harmonic oscillator can only be exactly 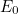 ,
, 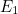 ,
, 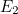 and so on, and no value in between — the oscillator has a discrete energy spectrum.
and so on, and no value in between — the oscillator has a discrete energy spectrum.
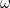 is the angular frequency of the oscillator,
is the angular frequency of the oscillator, 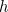 is a fundamental constant of nature called Planck’s constant and
is a fundamental constant of nature called Planck’s constant and 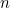 is a natural number. The important point is that the value of the
energy of the quantum harmonic oscillator can only be exactly
is a natural number. The important point is that the value of the
energy of the quantum harmonic oscillator can only be exactly 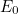 ,
, 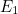 ,
, 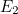 and so on, and no value in between — the oscillator has a discrete energy spectrum.
and so on, and no value in between — the oscillator has a discrete energy spectrum.
Curiously, the lowest energy state
![\[ E_0=\frac{h}{2\pi } \omega \left(\frac{1}{2}\right), \]](https://plus.maths.org/MI/2baf83ada3bb6ca195b5c9978a94c5d0/images/img-0009.png) |
called the ground state, does not correspond to zero energy: a quantum harmonic oscillator is never completely at rest.
In electromagnetism the discrete energy levels reflect wave-particle
duality. The energy carried along by a classical wave can vary
continuously, but the constituent waves of the quantized electromagnetic
field are only allowed discrete packets of energy. These packets can be
viewed as individual photons: a wave with energy level 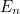 corresponds to
corresponds to 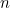 photons each with a given frequency. Phrased differently, a photon can
be viewed as a "unit of excitation" of the underlying field. It’s like a
quiver in a photon jelly with the quiver’s energy coming in precisely
prescribed units.
photons each with a given frequency. Phrased differently, a photon can
be viewed as a "unit of excitation" of the underlying field. It’s like a
quiver in a photon jelly with the quiver’s energy coming in precisely
prescribed units.
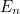 corresponds to
corresponds to 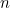 photons each with a given frequency. Phrased differently, a photon can
be viewed as a "unit of excitation" of the underlying field. It’s like a
quiver in a photon jelly with the quiver’s energy coming in precisely
prescribed units.
photons each with a given frequency. Phrased differently, a photon can
be viewed as a "unit of excitation" of the underlying field. It’s like a
quiver in a photon jelly with the quiver’s energy coming in precisely
prescribed units.
Matter matters
Dirac's feat was impressive, but so far it only applied to an empty
electromagnetic field. What about matter particles like electrons, which
after all interact with electromagnetic fields and even generate
fields? Schrödinger and Heisenberg's mathematics described the
behaviour of these particles, but it did not take account of Einstein's
special theory of relativity. This comes into play whenever things move
close to the speed of light, that is, at the speed of photons. And since
electromagnetism is all about photons you cannot ignore relativistic
effects when dealing with electromagnetism.

This picture, taken at the 5th Solvay conference in 1927, contains some of the greats of quantum mechanics. Back row from left to right: Wolfgang Pauli is 5th and Werner Heisenberg is 6th. Middle row from left to right: Louis de Broglie is 7th, Max Born 8th, Niels Bohr 9th. Front row from left to right: Max Planck is 2nd and Albert Einstein 5th.
A new equation was needed and it was again Dirac who came up with the
goods. His equation gave rise to a pleasing synergy with the photon
picture, in keeping with the notion of wave-particle duality. The
solutions to Dirac's equation were again waves, which could be
decomposed into harmonic oscillators and then quantized. Electrons, just
as photons, emerged as units of excitation of an underlying field: not
quite waves and not quite particles.
And there was more. To make his equation take account of real physical properties of electrons, such as spin,
a sort of angular momentum, Dirac had to use a mathematical
representation that contained twice as many bits of information than, on
the face of it, were necessary. What could those extra bits mean?
Dirac predicted that they describe a curious twin of the electron,
called an anti-electron or positron, which has the
same mass and opposite charge. When an electron meets its anti-twin the
two annihilate each other, producing chargeless photons. Shortly after
Dirac's stunning mathematical prediction, positrons were detected in lab
experiments by Carl D. Anderson. In fact, most fundamental particles
were later shown to come with their own antiparticle. The laws of nature
as we understand them treat particles and antiparticles equally so, on
the face of it, there should be the same amount of matter and
antimatter in the Universe. Why this isn't a case — there seems to be a
lot more matter than antimatter — is still a mystery today.
Ready, steady ... damn!
Dirac's efforts seemed to provide all that is necessary to construct a full theory of quantum electrodynamics.
It described photons and electrons as excitations of underlying quantum
fields, so it was a matter of putting the equations to work to see how
photons and electrons interact: how light interacts with itself and
scatters off matter. But there was one major problem. The answer to
pretty much any calculation physicists cared to attempt was infinity.
Something was seriously wrong.
Have you had a vision lately? Perhaps not in the metaphorical sense, but in a physical sense you're having one all the time. It's the result of light scattering off objects around you — the computer screen, the mirror, the tea pot — and hitting your eye. At school we learn that light, like all electromagnetic radiation, is made up of waves and matter of little particles. Vision can be explained in terms of the interaction of these waves and particles.
At the beginning of the twentieth century, however, physicists realized that things were more complicated than that: particles and electromagnetic waves were both wave-like and particle-like. The British physicist Paul Dirac described both electrons and particles of light called photons in terms of quantum fields: particles correspond to units of excitation, to carefully measured quivers in those fields. His brand new mathematical formalism described both the electron field and the photon field — to describe the interaction of matter and light, all physicists needed to do was to put that formalism to work.
The living vacuum
But they quickly encountered a problem that turned out to be, quite literally, of boundless proportion. It was a consequence of a central result of quantum mechanics, the new physics that had been developed during the 1920s and was the motivation for Dirac's new treatment of electromagnetism: Heisenberg's uncertainty principle.Stated in its usual form, the principle says that the more precise you are about a particle's position the less precise you can be about its momentum (the direction in which it's heading and its speed, multiplied by its mass) and vice versa. If you pin down, say, momentum to a good degree of accuracy, your uncertainty about position increases. It's not that the particle is somewhere definite but you just don't know where, rather in quantum mechanics ideas such as the location and trajectory of a particle simply don't make sense.

David Kaiser is a historian of science at MIT. Image: Donna Coveney.
"It's like naughty school children," says David Kaiser, a historian of physics at Massachusetts Institute of Technology who has written a fascinating book including an introduction to this topic. "If you are only going to stick your tongue out, you can do it for longer, but if you are going to jump up on the desk you are going to have to do it pretty fast if you don't want the teacher to see you. This is what we think is happening all the time, unstoppably, at the quantum mechanical level. Little particles are constantly stealing energy from the vacuum. They are breaking the rules. Depending on how much energy they borrow, they have to pay it back correspondingly quickly."
Despite their puzzling nature, virtual particles turned out to be useful in explaining the workings of the electrostatic force. Breaking the law for brief moments of time, electrons emit virtual photons, which will be absorbed by another electron in the vicinity. This interaction pushes the electrons apart, an effect we see as the repulsion between like charges. In 1932 Hans Bethe and Enrico Fermi declared virtual photons to be the force carrying particles that mediate the electrostatic force.
Virtual spoilers: problem 1
But virtual particles also created huge problems. According to the theory, an electron constantly emits and absorbs virtual photons which come with their own energy and momentum. What is more, pairs of virtual electrons and their anti-particles, positrons, constantly pop in and out of existence, clouding around the central electron, creating a flower picture as the positively charged virtual positrons are attracted to the negatively charged central electron.
Virtual electron-positron pairs clouding around a central electron with positively charged positrons attracted to the center.
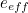 of the electron, the charge you would measure in an experiment, is
actually the sum of two parts: its "intrinsic" charge, also called its bare charge,
of the electron, the charge you would measure in an experiment, is
actually the sum of two parts: its "intrinsic" charge, also called its bare charge, 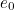 , and a contribution coming from virtual particles,
, and a contribution coming from virtual particles, 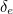 :
:![\[ e_{eff} = e_0 + \delta _ e. \]](https://plus.maths.org/MI/a54cad62475f0930e3fd1f2b05298097/images/img-0004.png) |
Similarly, the electron’s effective mass
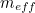 is made up of two components; a bare mass and a contribution from virtual particles:
is made up of two components; a bare mass and a contribution from virtual particles:![\[ m_{eff} = m_0 + \delta _ m. \]](https://plus.maths.org/MI/a54cad62475f0930e3fd1f2b05298097/images/img-0006.png) |
Being created from the vacuum, you wouldn’t expect the virtual particles to have a large effect and so the contributions
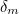 and
and 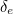 should be small. But when physicists set out to calculate them, the
result was nothing short of scandalous. The correction terms turned out
to be infinite!
should be small. But when physicists set out to calculate them, the
result was nothing short of scandalous. The correction terms turned out
to be infinite! This meant that the new mathematical formalism of quantum electrodynamics was utterly useless when it came to calculating even the simplest interactions. "At the most basic level of approximation, ignoring virtual particles, I might say that the likelihood of two electrons scattering off each other is 78%," explains Kaiser. "But I can't switch off the uncertainty principle. Even if I consider just one virtual particle I all of a sudden get 78% plus infinity."
The problem was that you could not tell how much energy a virtual
particle had borrowed. "These virtual particles could steal seven units
of energy, or fifty, or an infinite number, as long as they paid it back
correspondingly quickly," explains Kaiser. In the calculations of 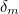 and
and 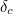 all the possible energy levels of even a single virtual particle needed
to be taken into account, producing an infinite sum with an infinite
answer. In mathematical terms, they produced a divergent integral.
all the possible energy levels of even a single virtual particle needed
to be taken into account, producing an infinite sum with an infinite
answer. In mathematical terms, they produced a divergent integral.

Albert Einstein (1879-1955) in 1921.
"So what?", you might say. The effective mass and charge of any electron are finite, after all we can measure them, so the infinities must be an artifact of the theory. One way of dealing with them is to simply cut the divergent integral off: only consider energies up to a certain, very high, level. Using this trick the integrals can indeed be made to converge, that is, they become finite. But unfortunately this approach violates a theory no self-respecting physicist would want to mess with: Einstein's special theory of relativity.
According to Einstein's theory, observers, as long as they are not accelerating but are in an inertial frame of reference, should see the laws of physics acting in the same way no matter how fast they are moving: this is a fundamental symmetry of nature. The problem is that the amount of energy you measure in a moving particle depends of the speed with which you yourself are moving. "You could say, what if I cut the energy levels in the calculation off at ten gazillion," says Kaiser. "This little approximation might seem unimportant to us, but someone traveling at 99.9% of the speed of light would flagrantly see that difference, so we would be privileging our own state of motion. If we really take the uncertainty principle seriously and combine it with special relativity, there is no way to cut off the stealing of energy at a finite value. To do so would break the symmetries of special relativity."
Like for the divergent integral problem, there was a fudge solution to deal with the problem of infinitely many terms. "In general, every time an electron interacts with a photon, the strength of that interaction is small," explains Kaiser. "Electromagnetism is not a very strong force. It’s much, much weaker, for example, than the nuclear forces that keep particles bound within an atomic nucleus." Indeed, the electrons’ interaction depends on the square of their measured charge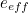 , which can be determined in experiments and is very small:
, which can be determined in experiments and is very small: 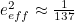 in appropriate units. In the infinite sums that need to be considered,
successive terms (which roughly speaking correspond to larger and larger
numbers of virtual particles being exchanged) come with increasing
powers of
in appropriate units. In the infinite sums that need to be considered,
successive terms (which roughly speaking correspond to larger and larger
numbers of virtual particles being exchanged) come with increasing
powers of 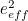 as their coefficient:
as their coefficient: 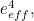
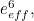
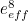 and so on. The larger the numbers of virtual particles being exchanged, the higher the power of
and so on. The larger the numbers of virtual particles being exchanged, the higher the power of 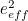 as a coefficient of the corresponding term.
as a coefficient of the corresponding term.

Werner Heisenberg (1901-1976).
When you raise a very small number to some power, the result is smaller still; in the case of 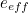 we find that
we find that 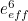 is about ten thousand times smaller than
is about ten thousand times smaller than 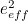 .
This means that in these sums you can simply ignore the higher order
terms corresponding to a larger number of virtual particles: the
smallness of their coefficient
.
This means that in these sums you can simply ignore the higher order
terms corresponding to a larger number of virtual particles: the
smallness of their coefficient 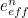 meant that their contributions were negligible, at least if you assume
that the terms themselves are finite (which of course they are not, due
to problem 1).
meant that their contributions were negligible, at least if you assume
that the terms themselves are finite (which of course they are not, due
to problem 1).
But while simple in theory, in practice this perturbative approach, as it became known, didn’t help much. Calculations involving even just a few virtual particles were still horrendously complicated: working out the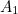 s and
s and 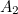 s
was far from straight-forward. In 1935 Hans Euler, a student of Werner
Heisenberg, considered a specific interaction between photons but
confined himself to the
s
was far from straight-forward. In 1935 Hans Euler, a student of Werner
Heisenberg, considered a specific interaction between photons but
confined himself to the 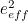 and
and 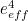 terms. His calculation took eighteen months to complete, ran to fifty pages in the journal Annalen der Physik
and was complicated enough to earn him his PhD. And of course, Euler’s
calculation was an approximation in another sense too: not only did he
cut off the infinite sum, he also had to cut off the energy levels to
produce finite integrals in the terms he did consider.
terms. His calculation took eighteen months to complete, ran to fifty pages in the journal Annalen der Physik
and was complicated enough to earn him his PhD. And of course, Euler’s
calculation was an approximation in another sense too: not only did he
cut off the infinite sum, he also had to cut off the energy levels to
produce finite integrals in the terms he did consider.
"Divergence difficulties, acute accounting woes — by the mid-1930s QED seemed an unholy mess," says Kaiser in Drawing theories apart. "As calculationally intractable as it was conceptually muddled." It took two giants of physics, Freeman Dyson and Richard Feyman to sort out this mess. Their ingenious approach is what we will explore below.

Willis Lamb (1913-2008).

Left: Julian Schwinger (1918-1994). Right: Sin-itiro Tomonaga (1906-1979
How do you work out whether a beam of light will reflect off a mirror in exactly the right way to, for example, make a camera work? You might draw a picture to understand what is happening, write down some equations, do some calculations, and out pops the result. This is how physics is usually done, and has been since the time of Newton. Equations, calculation, result.
"Feynman skipped all that," says Freeman Dyson, a physicist at the Institute of Advanced Study in Princeton. "He just wrote down the pictures and then wrote down the answers. There were no equations."

Richard Feynman (1918-1988).
Dyson is talking about Richard Feynman,
recalling his time at Cornell University in the late 1940s. At the
time, quantum electrodynamics (QED), a newly developed theory to
describe the interaction of light and matter, was in deep trouble.
Calculating even the simplest interactions between electrons and photons
was so complicated, it frightened even the most accomplished
physicists. There were other problems too, throwing the whole edifice of
QED into doubt. Feynman's stick-like figures, now known as Feynman diagrams, came to the rescue, and they turned out to become a ubiquitous tool in physics.
"[Feynman was] a great guy," recalls Dyson. "The joy of Feynman was that he was totally outspoken. He always said exactly what he thought about you or about anything else. If I wanted to go and talk with Feynman, I would walk into the room and he would say 'Get out, don't you see I'm busy.' Another time I'd come in and he would be very friendly, so I'd know that he really welcomed me. I enjoyed him very much because he was a real performer. He just loved to perform and he had to have an audience."
Many tales have been told of Feynman's famous irreverence and perhaps it was the same irreverence that enabled him to skip the formalities and think in pictures. As an example, think of two electrons scattering off each other. Naively you would think of them as tiny billiard balls: if you know the speed and direction of travel of both of them, you can work out if they will meet and where they will end up at any given time after the collision. But in quantum physics things are not that simple. Electrons behave both like particles and like waves: it is impossible to determine both their location and their momentum to the same degree of accuracy, they don't travel along straight lines and you can't even tell two electrons apart. All you can do is work out the probability that two electrons will scatter in a particular way (see our article on Schrödinger's equation for an introduction to quantum mechanics).

Figure 1: This image is a Feynman diagram of electron-electron scattering.
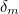 and
and 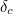 all the possible energy levels of even a single virtual particle needed
to be taken into account, producing an infinite sum with an infinite
answer. In mathematical terms, they produced a divergent integral.
all the possible energy levels of even a single virtual particle needed
to be taken into account, producing an infinite sum with an infinite
answer. In mathematical terms, they produced a divergent integral.
Respecting Einstein

Albert Einstein (1879-1955) in 1921.
"So what?", you might say. The effective mass and charge of any electron are finite, after all we can measure them, so the infinities must be an artifact of the theory. One way of dealing with them is to simply cut the divergent integral off: only consider energies up to a certain, very high, level. Using this trick the integrals can indeed be made to converge, that is, they become finite. But unfortunately this approach violates a theory no self-respecting physicist would want to mess with: Einstein's special theory of relativity.
According to Einstein's theory, observers, as long as they are not accelerating but are in an inertial frame of reference, should see the laws of physics acting in the same way no matter how fast they are moving: this is a fundamental symmetry of nature. The problem is that the amount of energy you measure in a moving particle depends of the speed with which you yourself are moving. "You could say, what if I cut the energy levels in the calculation off at ten gazillion," says Kaiser. "This little approximation might seem unimportant to us, but someone traveling at 99.9% of the speed of light would flagrantly see that difference, so we would be privileging our own state of motion. If we really take the uncertainty principle seriously and combine it with special relativity, there is no way to cut off the stealing of energy at a finite value. To do so would break the symmetries of special relativity."
Virtual spoilers: problem 2
But potentially infinite energy levels weren't the only problem. Electrons interact by exchanging virtual photons, and they can indeed exchange any number of virtual photons. In calculations this unbounded number of virtual photons needed to be taken into account, giving rise to a sum with infinitely many terms: roughly speaking, it's one term corresponding to one virtual particle being exchanged, another term corresponding to two particles being exchanged, another to three, four, five and so on. Altogether this gives a double infinity, since each individual term would itself be infinite, due to the unbounded energy levels you needed to consider for each virtual particle.Like for the divergent integral problem, there was a fudge solution to deal with the problem of infinitely many terms. "In general, every time an electron interacts with a photon, the strength of that interaction is small," explains Kaiser. "Electromagnetism is not a very strong force. It’s much, much weaker, for example, than the nuclear forces that keep particles bound within an atomic nucleus." Indeed, the electrons’ interaction depends on the square of their measured charge
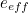 , which can be determined in experiments and is very small:
, which can be determined in experiments and is very small: 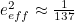 in appropriate units. In the infinite sums that need to be considered,
successive terms (which roughly speaking correspond to larger and larger
numbers of virtual particles being exchanged) come with increasing
powers of
in appropriate units. In the infinite sums that need to be considered,
successive terms (which roughly speaking correspond to larger and larger
numbers of virtual particles being exchanged) come with increasing
powers of 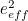 as their coefficient:
as their coefficient: 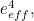
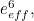
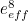 and so on. The larger the numbers of virtual particles being exchanged, the higher the power of
and so on. The larger the numbers of virtual particles being exchanged, the higher the power of 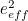 as a coefficient of the corresponding term.
as a coefficient of the corresponding term.
Werner Heisenberg (1901-1976).
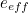 we find that
we find that 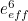 is about ten thousand times smaller than
is about ten thousand times smaller than 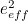 .
This means that in these sums you can simply ignore the higher order
terms corresponding to a larger number of virtual particles: the
smallness of their coefficient
.
This means that in these sums you can simply ignore the higher order
terms corresponding to a larger number of virtual particles: the
smallness of their coefficient 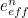 meant that their contributions were negligible, at least if you assume
that the terms themselves are finite (which of course they are not, due
to problem 1).
meant that their contributions were negligible, at least if you assume
that the terms themselves are finite (which of course they are not, due
to problem 1).But while simple in theory, in practice this perturbative approach, as it became known, didn’t help much. Calculations involving even just a few virtual particles were still horrendously complicated: working out the
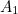 s and
s and 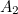 s
was far from straight-forward. In 1935 Hans Euler, a student of Werner
Heisenberg, considered a specific interaction between photons but
confined himself to the
s
was far from straight-forward. In 1935 Hans Euler, a student of Werner
Heisenberg, considered a specific interaction between photons but
confined himself to the 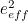 and
and 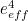 terms. His calculation took eighteen months to complete, ran to fifty pages in the journal Annalen der Physik
and was complicated enough to earn him his PhD. And of course, Euler’s
calculation was an approximation in another sense too: not only did he
cut off the infinite sum, he also had to cut off the energy levels to
produce finite integrals in the terms he did consider.
terms. His calculation took eighteen months to complete, ran to fifty pages in the journal Annalen der Physik
and was complicated enough to earn him his PhD. And of course, Euler’s
calculation was an approximation in another sense too: not only did he
cut off the infinite sum, he also had to cut off the energy levels to
produce finite integrals in the terms he did consider."Divergence difficulties, acute accounting woes — by the mid-1930s QED seemed an unholy mess," says Kaiser in Drawing theories apart. "As calculationally intractable as it was conceptually muddled." It took two giants of physics, Freeman Dyson and Richard Feyman to sort out this mess. Their ingenious approach is what we will explore below.
Where do great ideas come from? One way to find out is to ask someone who's had quite a few
himself, so when we met the legendary Freeman Dyson
we did. "It's true of almost every great idea that you really don't
know afterwards where it came from," he said. "Our brains are random,
that's of course a wonderful trick of nature for being creative. They
don't have to be programmed, they can invent things just by random
chance. So all really good ideas are accidental; there's some random
arrangement of things buzzing around in somebody's head, and it suddenly
clicks."
At the end of the 1930s theoretical physics was in bad need of some
such random clicks. Physicists had attempted to apply the new theory of
quantum mechanics to electromagnetism, one of nature's fundamental
forces. The result was quantum electrodynamics (QED), a theory
describing the interaction of matter and light. The trouble was that
almost any calculation you'd care to make using QED returned infinity as an answer — for all practical purposes the theory was useless.
When Dyson boarded the Queen Elizabeth from England to New York in
1947, to become a student at Cornell University, he was already
acquainted with quantum field theory. He had been inspired by his
Cambridge teacher Nicholas Kemmer and a rare German text book, Gregor
Wentzel's Quantum theory of fields, which he still keeps in his
office at the Institute for Advanced Study in Princeton. "It was a
precious treasure that book, there were only two copies in England at
that time, and I had one of them."
But quantum field theory (QFT) wasn't particularly popular in the US.
"[US physicists] considered it like an Italian opera; extravagant and
irrational entertainment. America was very empirical, so the people I
worked for, Hans Bethe and Richard Feynman, had no use for it."
QFT did indeed make some esoteric predictions. Heisenberg's famous
uncertainty principle implied that particles, such as photons or
electrons, would be constantly created out of nothing, popping in and
out of existence like bubbles in a bubble bath. During their briefest of
lifetimes these virtual particles would affect other particles
and their interactions. In fact, the electrostatic repulsion between
two like charges was explained in this way: an electron would emit a
virtual photon which would in turn be absorbed by another electron, the
interaction pushing the two particles apart.
Virtual reality: the Lamb shift

Willis Lamb (1913-2008).
All this was theory, but in 1947 experimentalists observed effects of
virtual particles. "There were experiments in Columbia University,
which were the driving force," says Dyson. "Isidor Isaac Rabi and Willis Lamb
and various other people, using the new technology of microwaves which
came up during the war, [were able to] measure atomic levels very
accurately. They got, for the first time, a really accurate picture of
the hydrogen atom, which was supposed to be the simplest atom." What
they found was that the energy levels of the hydrogen atom were slightly
different from what old-fashioned theory, not taking account of virtual
particles, predicted. "That was the famous Lamb shift," says Dyson.
"Everybody was excited about that; for the first time a real discrepancy
[between experiment] and theory." (There is a nice discussion of the
energy spectrum of the hydrogen atom here. The Lamb shift represents a small correction to this spectrum.)
People immediately suggested that the difference might be due to the
effect of virtual particles affecting goings-on inside the hydrogen
atom. And when Hans Bethe performed a quick, and very approximate,
calculation on a train ride back from a conference, he found that this
might indeed be the case.
This explained the Lamb shift as far as the physics was concerned.
But the mathematics was still an "unholy mess" in the words of the
historian of physics David Kaiser (who has written an excellent book including an introduction to this topic).
The trouble was that in calculations the effect of virtual particles would always come out to be infinity. For example, the effective mass 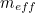 and the effective charge
and the effective charge 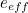 of an electron, which you could measure in experiments, were actually made up of two contributions: the so-called bare mass and bare charge,
of an electron, which you could measure in experiments, were actually made up of two contributions: the so-called bare mass and bare charge, 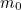 and
and 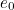 , and the contributions to mass and charge from the virtual particles, written as
, and the contributions to mass and charge from the virtual particles, written as 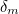 and
and 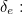
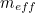 and the effective charge
and the effective charge 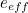 of an electron, which you could measure in experiments, were actually made up of two contributions: the so-called bare mass and bare charge,
of an electron, which you could measure in experiments, were actually made up of two contributions: the so-called bare mass and bare charge, 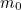 and
and 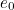 , and the contributions to mass and charge from the virtual particles, written as
, and the contributions to mass and charge from the virtual particles, written as 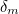 and
and 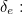
![\[ m_{eff} = m_0 + \delta _ m \]](https://plus.maths.org/MI/50979a17a54cbf6517fc78e441fa14f8/images/img-0007.png) |
and
![\[ e_{eff} = e_0 + \delta _ e. \]](https://plus.maths.org/MI/50979a17a54cbf6517fc78e441fa14f8/images/img-0008.png) |
It was the contribution terms 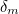 and
and 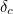 that turned out to be infinite. Thus, any calculation trying to take
account of virtual particles would necessarily blow up too. Something
was horribly wrong.
that turned out to be infinite. Thus, any calculation trying to take
account of virtual particles would necessarily blow up too. Something
was horribly wrong.
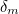 and
and 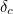 that turned out to be infinite. Thus, any calculation trying to take
account of virtual particles would necessarily blow up too. Something
was horribly wrong.
that turned out to be infinite. Thus, any calculation trying to take
account of virtual particles would necessarily blow up too. Something
was horribly wrong.
"All the giants from the old times were still around, people like Werner Heisenberg and Erwin Schrödinger and Paul Dirac and Robert Oppenheimer,"
remembers Dyson. "[They] all thought that we needed radically new
physics. They all had their theories of changing the whole basis of
physics, introducing completely new ideas."
"But they were all wrong. Everyone of them turned out to be wrong."
God is great!
The idea that saved the day, without throwing out QED, was
surprisingly simple: stand back and work with what you see. Since you
can never actually catch a bare particle on its own, without
its virtual cousins, throw away that Platonic idea and work with
effective quantities instead. "The infinities only lay in the
artificial separation of the bare particle from the physical particle,"
explains Dyson. "[But] the mass of a bare particle has no meaning from
an operational point of view. So forget about that and only calculate
things you can observe. It works like magic."

Left: Julian Schwinger (1918-1994). Right: Sin-itiro Tomonaga (1906-1979
Simple as it was, the idea of swapping bare for effective quantities had already been around since the late 1930s, suggested by Hendrik Kramers and Victor Weisskopf.
But it wasn't as easy to put into practice as it may seem: rearranging
complicated calculations, you were juggling with infinities that could
still blow up in your face if you weren't careful. And all the while you
had to comply with Einstein's special relativity which imposed
constraints on the calculations.
It was Julian Schwinger working in the US and, independently, Sin-itiro Tomonaga
in Japan, who finally cracked in the late 1940s the calculations that
exactly described the Lamb shift. Schwinger's calculation inspired Rabi
to exclaim that "God is great!"
Yet, more than a whiff of unholiness remained. The calculations were
still incredibly complicated, making QED no more useful than it was
before. As Dyson recalls, Schwinger's personality didn't help. "He was
this young prodigy, and he came and gave a talk here at Princeton,
explaining his calculation. And Oppenheimer said 'You know when other
people give talks it's to tell you how to do it. But when Julian
Schwinger gives a talk, it's to tell you that only he can do it.'"
What is more, Schwinger and Tomonaga's calculations were still
simplified. The particular infinites they had managed to tame were a
result of the fact that a single virtual particle comes with a
potentially unbounded amount of energy.
To make things easier, they had considered interactions that involved
only one or two virtual particles, managing to get the corresponding
infinities under control. Whether the method would work once you
considered the potentially unlimited amount of virtual particles was
anyone's guess.
How do you work out whether a beam of light will reflect off a mirror in exactly the right way to, for example, make a camera work? You might draw a picture to understand what is happening, write down some equations, do some calculations, and out pops the result. This is how physics is usually done, and has been since the time of Newton. Equations, calculation, result.
"Feynman skipped all that," says Freeman Dyson, a physicist at the Institute of Advanced Study in Princeton. "He just wrote down the pictures and then wrote down the answers. There were no equations."

Richard Feynman (1918-1988).
"[Feynman was] a great guy," recalls Dyson. "The joy of Feynman was that he was totally outspoken. He always said exactly what he thought about you or about anything else. If I wanted to go and talk with Feynman, I would walk into the room and he would say 'Get out, don't you see I'm busy.' Another time I'd come in and he would be very friendly, so I'd know that he really welcomed me. I enjoyed him very much because he was a real performer. He just loved to perform and he had to have an audience."
Many tales have been told of Feynman's famous irreverence and perhaps it was the same irreverence that enabled him to skip the formalities and think in pictures. As an example, think of two electrons scattering off each other. Naively you would think of them as tiny billiard balls: if you know the speed and direction of travel of both of them, you can work out if they will meet and where they will end up at any given time after the collision. But in quantum physics things are not that simple. Electrons behave both like particles and like waves: it is impossible to determine both their location and their momentum to the same degree of accuracy, they don't travel along straight lines and you can't even tell two electrons apart. All you can do is work out the probability that two electrons will scatter in a particular way (see our article on Schrödinger's equation for an introduction to quantum mechanics).

Figure 1: This image is a Feynman diagram of electron-electron scattering.
What is more, electrons scatter, not by colliding, but by exchanging
virtual photons. For example, one electron can emit a virtual photon and
the other one can absorb it. Absorption and emission alter each
particle’s speed and direction: that’s the scattering. Calculating the
probability that two electrons start out at two points, 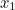 and
and 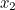 , in spacetime and after scattering end up at points
, in spacetime and after scattering end up at points 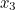 and
and 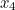 involves the probability that the first electron travels to the point
involves the probability that the first electron travels to the point 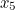 emits the photon there, and then travels to
emits the photon there, and then travels to 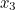 , that the other electron travels to the point
, that the other electron travels to the point 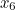 where it absorbs it and then travels to
where it absorbs it and then travels to 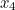 , and the probability that the virtual photon makes the journey from
, and the probability that the virtual photon makes the journey from 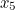 to
to 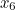 . What is more, the points
. What is more, the points 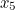 and
and 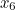 could be anywhere in spacetime, since we can't be certain of the electrons' trajectories.
could be anywhere in spacetime, since we can't be certain of the electrons' trajectories.
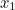 and
and 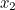 , in spacetime and after scattering end up at points
, in spacetime and after scattering end up at points 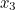 and
and 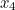 involves the probability that the first electron travels to the point
involves the probability that the first electron travels to the point 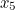 emits the photon there, and then travels to
emits the photon there, and then travels to 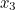 , that the other electron travels to the point
, that the other electron travels to the point 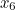 where it absorbs it and then travels to
where it absorbs it and then travels to 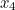 , and the probability that the virtual photon makes the journey from
, and the probability that the virtual photon makes the journey from 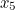 to
to 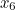 . What is more, the points
. What is more, the points 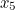 and
and 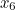 could be anywhere in spacetime, since we can't be certain of the electrons' trajectories.
could be anywhere in spacetime, since we can't be certain of the electrons' trajectories.
(This example is borrowed from Feynman's book QED - the strange theory of light and matter.)
Taking all this into account gives an unwieldy expression for the probability of our scattering event, involving double integrals and many different terms to take account of the different probabilities. All to capture this supposedly simple scenario.

This image shows all the ways in which two electrons can scatter by exchanging two photons. Image adapted from a figure in Richard Feynman's article Space-time approach to quantum electrodynamics. Copyright (2013) by The American Physical Society.
And this isn't all. Two electrons can scatter by trading any number
of virtual photons in complicated ways. For example, an emitted photon
could turn into a pair made up of a virtual electron and a virtual
anti-electron (usually called positron), which then annihilate each
other to form a new photon, which gets absorbed by the second electron.
All the possible interactions need to be taken into account and each
comes with a long and complicated mathematical expression that even the
most diligent accountant would find hard to keep track off. The scope
for mistakes, omissions and double counting is huge.
In Feynman's mind, however, the double integral above turned into a simple diagram, shown in figure 1. At first sight this looks like a picture of a real physical process, but it is not. The horizontal axis represents space (we're assuming the particles move in one dimension), the vertical one represents time. Thus, a particle standing still for a few seconds (which in actual fact it never does, but let's assume so for a moment), would be represented by a vertical line which represents the passage of time. What is more, the straight and wriggly lines don't represent real trajectories of particles, but only probabilities that particles are first at one point in space and time and then another. (If you would like to find out more, Quantum diaries has a great introduction to Feynman diagrams. For a fascinating account of their dispersion and use in physics see David Kaiser's book Drawing theories apart)
Yet, from such a picture, physicists could easily read off the math. "Every time you see a straight line in a Feynman diagram it has exactly and uniquely this expression in your corresponding equation," says David Kaiser, a historian of physics at MIT. "When you see a wiggly line, it has exactly this expression. It becomes shockingly simple once you learn a few quick rules." All the other possible interactions, involving more than one virtual particle, come with similar diagrams. The number of them grows large very rapidly as you consider more and more virtual particles, but it's a lot easier to keep track of than when you're only looking at the math.
Feynman's brilliant diagrams have since become an indispensable part of physicists' toolkits, so much so that people sometimes mistake them for literal depictions of reality, rather than just drawings on paper that serve as shorthands for equations. "I love this mnemonic of, 'Let me take a magnifying glass and look at nature and what I will see is Feynman diagrams,'"says David Kaiser. "That's a wonderful slippage. We are drawing pictures as if it's the same as a baseball tossed through space and time. Feynman was remarkably untroubled by that confusion. He would say, in effect, that this is how it makes sense to him to think about it. And he would often speak in very anthropomorphic terms, 'I'm this electron. I am sitting here and I'm getting bashed by this photon and I'm being knocked off course.'"
Feynman's intuitive approach didn't obscure his physical insight, but it did hamper communication. When Feynman first presented his diagrams at a conference, the audience wasn't impressed. He wasn't able to explain exactly how the straight and wriggly lines should be translated into equations and show that his pictures didn't obscure more complicated situations. "Feynman in some sense had the right rules, but it wasn't clear how general they were," says Kaiser. "Were they really coming from the heart of quantum field theory or were they just representing special cases?"
It was Freeman Dyson who eventually tied up the rules. "Dyson showed that if we take quantum field theory as the first effort to unite quantum mechanics and special relativity, then that is uniquely fixing what those translation rules should be," says Kaiser. "So it was Dyson who spelled them out systematically and then showed that they would indeed hold. Then applying the rules became remarkably straightforward."
Feynman's diagrams helped with one problem that plagued QED: keeping track of all the complicated ways that any number of these virtual particles could be involved, and taking account of these in the calculations. But there was also another problem. Even a single virtual particle could come with any amount of energy. Taking this unlimited energy into account meant that calculations involving just one virtual particle returned infinity as the answer. Schwinger and, independently, Tomonaga had provided a solution to this puzzle: rather than trying to get at the bare particle, the particle on its own, one should only ever consider it together with its virtual entourage and use effective quantities in calculations (see the previous article). Feynman had himself developed a similar approach.
The problem was, however, that all three had only been able to tame the infinities in calculations that involved one or two virtual particles. It wasn't clear the methods would work for greater numbers. Armed with a mathematicians' understanding of the techniques of quantum physics, Dyson came to the rescue, showing that the approach of Feynman, Schwinger and Tomonaga would work for any number of virtual particles. "I had only the tools of quantum field theory, which [others] didn't have," says Dyson. "I was able to put them all together and demonstrate it was all quite simple. It was really an amazing piece of luck. From being a humble student, I suddenly became a big shot."
Feynman's diagrams and Dyson's policing of the theory spurred a mood of optimism: calculations became easier, infinities could be tamed, and the puzzle of QED seemed cracked. The next challenge was to apply the same ideas to the other forces of nature. But this, it turned out, was a whole different story. We will explore it in another series of articles coming up on Plus soon.
Taking all this into account gives an unwieldy expression for the probability of our scattering event, involving double integrals and many different terms to take account of the different probabilities. All to capture this supposedly simple scenario.

This image shows all the ways in which two electrons can scatter by exchanging two photons. Image adapted from a figure in Richard Feynman's article Space-time approach to quantum electrodynamics. Copyright (2013) by The American Physical Society.
In Feynman's mind, however, the double integral above turned into a simple diagram, shown in figure 1. At first sight this looks like a picture of a real physical process, but it is not. The horizontal axis represents space (we're assuming the particles move in one dimension), the vertical one represents time. Thus, a particle standing still for a few seconds (which in actual fact it never does, but let's assume so for a moment), would be represented by a vertical line which represents the passage of time. What is more, the straight and wriggly lines don't represent real trajectories of particles, but only probabilities that particles are first at one point in space and time and then another. (If you would like to find out more, Quantum diaries has a great introduction to Feynman diagrams. For a fascinating account of their dispersion and use in physics see David Kaiser's book Drawing theories apart)
Yet, from such a picture, physicists could easily read off the math. "Every time you see a straight line in a Feynman diagram it has exactly and uniquely this expression in your corresponding equation," says David Kaiser, a historian of physics at MIT. "When you see a wiggly line, it has exactly this expression. It becomes shockingly simple once you learn a few quick rules." All the other possible interactions, involving more than one virtual particle, come with similar diagrams. The number of them grows large very rapidly as you consider more and more virtual particles, but it's a lot easier to keep track of than when you're only looking at the math.
Feynman's brilliant diagrams have since become an indispensable part of physicists' toolkits, so much so that people sometimes mistake them for literal depictions of reality, rather than just drawings on paper that serve as shorthands for equations. "I love this mnemonic of, 'Let me take a magnifying glass and look at nature and what I will see is Feynman diagrams,'"says David Kaiser. "That's a wonderful slippage. We are drawing pictures as if it's the same as a baseball tossed through space and time. Feynman was remarkably untroubled by that confusion. He would say, in effect, that this is how it makes sense to him to think about it. And he would often speak in very anthropomorphic terms, 'I'm this electron. I am sitting here and I'm getting bashed by this photon and I'm being knocked off course.'"
Feynman's intuitive approach didn't obscure his physical insight, but it did hamper communication. When Feynman first presented his diagrams at a conference, the audience wasn't impressed. He wasn't able to explain exactly how the straight and wriggly lines should be translated into equations and show that his pictures didn't obscure more complicated situations. "Feynman in some sense had the right rules, but it wasn't clear how general they were," says Kaiser. "Were they really coming from the heart of quantum field theory or were they just representing special cases?"
It was Freeman Dyson who eventually tied up the rules. "Dyson showed that if we take quantum field theory as the first effort to unite quantum mechanics and special relativity, then that is uniquely fixing what those translation rules should be," says Kaiser. "So it was Dyson who spelled them out systematically and then showed that they would indeed hold. Then applying the rules became remarkably straightforward."
Feynman's diagrams helped with one problem that plagued QED: keeping track of all the complicated ways that any number of these virtual particles could be involved, and taking account of these in the calculations. But there was also another problem. Even a single virtual particle could come with any amount of energy. Taking this unlimited energy into account meant that calculations involving just one virtual particle returned infinity as the answer. Schwinger and, independently, Tomonaga had provided a solution to this puzzle: rather than trying to get at the bare particle, the particle on its own, one should only ever consider it together with its virtual entourage and use effective quantities in calculations (see the previous article). Feynman had himself developed a similar approach.
The problem was, however, that all three had only been able to tame the infinities in calculations that involved one or two virtual particles. It wasn't clear the methods would work for greater numbers. Armed with a mathematicians' understanding of the techniques of quantum physics, Dyson came to the rescue, showing that the approach of Feynman, Schwinger and Tomonaga would work for any number of virtual particles. "I had only the tools of quantum field theory, which [others] didn't have," says Dyson. "I was able to put them all together and demonstrate it was all quite simple. It was really an amazing piece of luck. From being a humble student, I suddenly became a big shot."
Feynman's diagrams and Dyson's policing of the theory spurred a mood of optimism: calculations became easier, infinities could be tamed, and the puzzle of QED seemed cracked. The next challenge was to apply the same ideas to the other forces of nature. But this, it turned out, was a whole different story. We will explore it in another series of articles coming up on Plus soon.
Further reading
David Kaiser's book Drawing theories apart explores the development of Feynman diagrams and contains an excellent introduction to the topics discussed in this article.| You can buy the book and help Plus at the same time by clicking on the link on the left to purchase from amazon.co.uk, and the link to the right to purchase from amazon.com. Plus will earn a small commission from your purchase. |

