A Medley of Potpourri

Monday, August 14, 2023

History of rockets

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/History_of_rockets

Rocket

Depiction of rocket arrows, from the Huolongjing. The left arrow reads 'fire arrow' (huo jian), the middle is a 'dragon shaped arrow frame' (long xing jian jia), and the left is a 'complete fire arrow' (huo jian quan shi).

The 'divine fire arrow screen' from the Huolongjing. A stationary arrow launcher that carries one hundred fire arrows. It is activated by a trap-like mechanism, possibly of wheellock design.

A "nest of bees" (yi wo feng 一窩蜂) arrow rocket launcher as depicted in the Wubei Zhi. So called because of its hexagonal honeycomb shape.

A hwacha manual from the Gukjo orye seorye (1474)

The first rockets were used as propulsion systems for arrows, and may have appeared as early as the 10th century in Song dynasty China. However more solid documentary evidence does not appear until the 13th century. The technology probably spread across Eurasia in the wake of the Mongol invasions of the mid-13th century. Usage of rockets as weapons before modern rocketry is attested to in China, Korea, India, and Europe. One of the first recorded rocket launchers is the "wasp nest" fire arrow launcher produced by the Ming dynasty in 1380. In Europe rockets were also used in the same year at the Battle of Chioggia. The Joseon kingdom of Korea used a type of mobile multiple rocket launcher known as the "Munjong Hwacha" by 1451.

The use of rockets were outdated by 15th century. The use of rockets in wars was revived with the creation of iron-cased rockets, which were used by Kingdom of Mysore (Mysorean rockets) and by Marathas during the mid 18th century, and were later modified and used by the British. The later models and improvements were known as the Congreve rocket and used in the Napoleonic Wars.

China

The dating of the invention of the first rocket, otherwise known as the gunpowder propelled fire arrow, is disputed. The History of Song attributes the invention to two different people at different times, Feng Zhisheng in 969 and Tang Fu in 1000. However Joseph Needham argues that rockets could not have existed before the 12th century, since the gunpowder formulas listed in the Wujing Zongyao are not suitable as rocket propellant.

Rockets may have been used as early as 1232, when reports appeared describing fire arrows and 'iron pots' that could be heard for 5 leagues (25 km, or 15 miles) when they exploded upon impact, causing devastation for a radius of 600 meters (2,000 feet), apparently due to shrapnel. A "flying fire-lance" that had re-usable barrels was also mentioned to have been used by the Jin dynasty (1115–1234). Rockets are recorded to have been used by the Song navy in a military exercise dated to 1245. Internal-combustion rocket propulsion is mentioned in a reference to 1264, recording that the 'ground-rat,' a type of firework, had frightened the Empress-Mother Gongsheng at a feast held in her honor by her son the Emperor Lizong.

Subsequently, rockets are included in the military treatise Huolongjing, also known as the Fire Drake Manual, written by the Chinese artillery officer Jiao Yu in the mid-14th century. This text mentions the first known multistage rocket, the 'fire-dragon issuing from the water' (huo long chu shui), thought to have been used by the Chinese navy.

Rocket launchers known as "wasp nests" were ordered by the Ming army in 1380. In 1400, the Ming loyalist Li Jinglong used rocket launchers against the army of Zhu Di (Yongle Emperor).

The American historian Frank H. Winter proposed in The Proceedings of the Twentieth and Twenty-First History Symposia of the International Academy of Astronautics that southern China and the Laotian community rocket festivals might have been key in the subsequent spread of rocketry in the Orient.

Spread of rocket technology

Mongols

The Chinese fire arrow was adopted by the Mongols in northern China, who employed Chinese rocketry experts as mercenaries in the Mongol army. Rockets are thought to have spread via the Mongol invasions to other areas of Eurasia in the mid 13th century.

Rocket-like weapons are reported to have been used at the Battle of Mohi in the year 1241.

Middle East

Between 1270 and 1280, Hasan al-Rammah wrote his al-furusiyyah wa al-manasib al-harbiyya (The Book of Military Horsemanship and Ingenious War Devices), which included 107 gunpowder recipes, 22 of which are for rockets. According to Ahmad Y Hassan, al-Rammah's recipes were more explosive than rockets used in China at the time. The terminology used by al-Rammah indicates a Chinese origin for the gunpowder weapons he wrote about, such as rockets and fire lances. Ibn al-Baitar, an Arab from Spain who had immigrated to Egypt, described saltpeter as "snow of China" (Arabic: ثلج الصين thalj al-ṣīn). Al-Baytar died in 1248. The earlier Arab historians called saltpeter "Chinese snow" and " Chinese salt." The Arabs used the name "Chinese arrows" to refer to rockets. The Arabs called fireworks "Chinese flowers". While saltpeter was called "Chinese Snow" by Arabs, it was called "Chinese salt" (Persian: نمک چینی namak-i čīnī) by the Iranians, or "salt from the Chinese marshes" (namak shūra chīnī Persian: نمک شوره چيني).

India

Mercenaries are recorded to have used hand held rockets in India in 1300. By the mid-14th century Indians were also using rockets in warfare.

The Kingdom of Mysore used rockets during the 18th century during the Anglo-Mysore Wars. According to James Forbes Marathas also used iron-encased rockets in their battles.

Korea

The Korean kingdom of Joseon started producing gunpowder in 1374 and was producing cannons and rockets by 1377. However the multiple rocket launching carts known as the "Munjong hwacha" did not appear until 1451.

Europe

In Europe, Roger Bacon mentions gunpowder in his Opus Majus of 1267.

However rockets do not feature in European warfare until the 1380 Battle of Chioggia.

Jean Froissart (c. 1337 – c. 1405) had the idea of launching rockets through tubes, so that they could make more accurate flights. Froissart's idea is a forerunner of the modern Rocket-propelled grenade.

Adoption in Renaissance-era Europe

According to the 18th-century historian Ludovico Antonio Muratori, rockets were used in the war between the Republics of Genoa and Venice at Chioggia in 1380. It is uncertain whether Muratori was correct in his interpretation, as the reference might also have been to bombard, but Muratori is the source for the widespread claim that the earliest recorded European use of rocket artillery dates to 1380. Konrad Kyeser described rockets in his famous military treatise Bellifortis around 1405. Kyeser describes three types of rockets, swimming, free flying and captive.

Joanes de Fontana in Bellicorum instrumentorum liber (c. 1420) described flying rockets in the shape of doves, running rockets in the shape of hares, and a large car driven by three rockets, as well as a large rocket torpedo with the head of a sea monster.

In the mid-16th century, Conrad Haas wrote a book that described rocket technology that combined fireworks and weapons technologies. This manuscript was discovered in 1961, in the Sibiu public records (Sibiu public records Varia II 374). His work dealt with the theory of motion of multi-stage rockets, different fuel mixtures using liquid fuel, and introduced delta-shape fins and bell-shaped nozzles.

The name Rocket comes from the Italian rocchetta, meaning "bobbin" or "little spindle", given due to the similarity in shape to the bobbin or spool used to hold the thread to be fed to a spinning wheel. The Italian term was adopted into German in the mid 16th century, by Leonhard Fronsperger in a book on rocket artillery published in 1557, using the spelling rogete, and by Conrad Haas as rackette; adoption into English dates to ca. 1610. Johann Schmidlap, a German fireworks maker, is believed to have experimented with staging in 1590.

Early modern history

Lagari Hasan Çelebi was a legendary Ottoman aviator who, according to an account written by Evliya Çelebi, made a successful manned rocket flight. Evliya Çelebi purported that in 1633 Lagari launched in a 7-winged rocket using 50 okka (63.5 kg, or 140 lbs) of gunpowder from Sarayburnu, the point below Topkapı Palace in Istanbul.

Siemienowicz

"Artis Magnae Artilleriae pars prima" ("Great Art of Artillery, the First Part", also known as "The Complete Art of Artillery"), first printed in Amsterdam in 1650, was translated to French in 1651, German in 1676, English and Dutch in 1729 and Polish in 1963. For over two centuries, this work of Polish–Lithuanian Commonwealth nobleman Kazimierz Siemienowicz was used in Europe as a basic artillery manual. The book provided the standard designs for creating rockets, fireballs, and other pyrotechnic devices. It contained a large chapter on caliber, construction, production and properties of rockets (for both military and civil purposes), including multi-stage rockets, batteries of rockets, and rockets with delta wing stabilizers (instead of the common guiding rods).

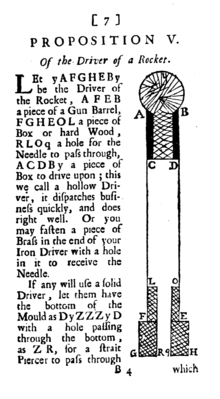
Anderson

In his 1696 work, ‘The Making of Rockets. In two Parts. The First containing the Making of Rockets for the meanest Capacity. The other to make Rockets by a Duplicate Proposition, to 1,000 pound Weight or higher,’ Robert Anderson proposed constructing rockets out of "a piece of a Gun Barrel" whose metal casing is much stronger than pasteboard or wood.

Indian Mysorean rockets

A painting showing the Mysorean army fighting the British forces with Mysorean rockets.^[51]
A Mysorean soldier from India, using his Mysorean rocket as a flagstaff (Robert Home, 1793/4).
Use of rockets in an assault by Mysorean troops on Travancore Line fortification (29 December 1789)

In 1792, iron-cased rockets were successfully used by Tipu Sultan - the ruler of the Kingdom of Mysore (in India) against the larger British East India Company forces during the Anglo-Mysore Wars. The British then took an active interest in the technology and developed it further during the 19th century. Use of iron tubes for holding propellant enabled higher thrust and longer range for the missile (up to 2 km range).

After Tipu's defeat in the Fourth Anglo-Mysore War and the capture of the Mysore iron rockets, they were influential in British rocket development, inspiring the Congreve rocket, which was soon put into use in the Napoleonic Wars.

19th-century gunpowder-rocket artillery

William Congreve (1772-1828), son of the Comptroller of the Royal Arsenal, Woolwich, London, became a major figure in the field. From 1801 Congreve researched the original design of Mysore rockets and started a vigorous development program at the Arsenal's laboratory. Congreve prepared a new propellant mixture, and developed a rocket motor with a strong iron tube with conical nose. This early Congreve rocket weighed about 32 pounds (14.5 kilograms). The Royal Arsenal's first demonstration of solid-fuel rockets took place in 1805. The rockets were effectively used during the Napoleonic Wars and the War of 1812. Congreve published three books on rocketry.

Subsequently, the use of military rockets spread throughout the western world. At the Battle of Baltimore in 1814, the rockets fired on Fort McHenry by the rocket vessel HMS Erebus were the source of the rockets' red glare described by Francis Scott Key in "The Star-Spangled Banner". Rockets were also used in the Battle of Waterloo in 1815.

Early rockets were very inaccurate. Without the use of spinning or any controlling feedback-loop, they had a strong tendency to veer sharply away from their intended course. The early Mysorean rockets and their successor British Congreve rockets reduced veer somewhat by attaching a long stick to the end of a rocket (similar to modern bottle rockets) to make it harder for the rocket to change course. The largest of the Congreve rockets was the 32-pound (14.5 kg) Carcass, which had a 15-foot (4.6 m) stick. Originally, sticks were mounted on the side, but this was later changed to mounting them in the center of the rocket, reducing drag and enabling the rocket to be more accurately fired from a segment of pipe.

In 1815 Alexander Dmitrievich Zasyadko (1779-1837) began his work on developing military gunpowder-rockets. He constructed rocket-launching platforms (which allowed firing of rockets in salvos - 6 rockets at a time) and gun-laying devices. Zasyadko elaborated a tactic for military use of rocket weaponry. In 1820 Zasyadko was appointed head of the Petersburg Armory, Okhtensky Powder Factory, pyrotechnic laboratory and the first Highest Artillery School in Russia. He organized rocket production in a special rocket workshop and formed the first rocket sub-unit in the Imperial Russian Army.

Artillery captain Józef Bem (1794-1850) of the Kingdom of Poland started experiments with what was then called in Polish raca kongrewska. These culminated in his 1819 report Notes sur les fusees incendiares (German edition: Erfahrungen über die Congrevischen Brand-Raketen bis zum Jahre 1819 in der Königlichen Polnischen Artillerie gesammelt, Weimar 1820). The research took place in the Warsaw Arsenal, where captain Józef Kosiński also developed multiple-rocket launchers adapted from horse artillery gun carriage. The 1st Rocketeer Corps formed in 1822; it first saw combat during the Polish–Russian War 1830–31.

Accuracy greatly improved in 1844 when William Hale modified the rocket design so that thrust was slightly vectored, causing the rocket to spin along its axis-of-travel like a bullet. The Hale rocket removed the need for a rocket stick, travelled further due to reduced air-resistance, and was far more accurate.

In 1865 the British Colonel Edward Mounier Boxer built an improved version of the Congreve rocket by placing two rockets in one tube, one behind the other.

Early 20th-century rocket pioneers

At the beginning of the 20th century, there was a burst of scientific investigation into interplanetary travel, fueled by the creativity of fiction writers such as Jules Verne and H. G. Wells as well as philosophical movements like Russian cosmism. Scientists seized on the rocket as a technology that was able to achieve this in real life, a possibility first recognized in 1861 by William Leitch.

In 1903, high school mathematics teacher Konstantin Tsiolkovsky (1857–1935), inspired by Verne and Cosmism, published The Exploration of Cosmic Space by Means of Reaction Devices (The Exploration of Cosmic Space by Means of Reaction Devices), the first serious scientific work on space travel. The Tsiolkovsky rocket equation—the principle that governs rocket propulsion—is named in his honor (although it had been discovered previously, Tsiolkovsky is honored as being the first to apply it to the question of whether rockets could achieve speeds necessary for space travel). He also advocated the use of liquid hydrogen and oxygen for propellant, calculating their maximum exhaust velocity. His work was essentially unknown outside the Soviet Union, but inside the country it inspired further research, experimentation and the formation of the Society for Studies of Interplanetary Travel in 1924.

In 1912, Robert Esnault-Pelterie published a lecture on rocket theory and interplanetary travel. He independently derived Tsiolkovsky's rocket equation, did basic calculations about the energy required to make round trips to the Moon and planets, and he proposed the use of atomic power (i.e. radium) to power a jet drive.

In 1912 Robert Goddard, inspired from an early age by H.G. Wells and by his personal interest in science, began a serious analysis of rockets, concluding that conventional solid-fuel rockets needed to be improved in three ways. First, fuel should be burned in a small combustion chamber, instead of building the entire propellant container to withstand the high pressures. Second, rockets could be arranged in stages. Finally, the exhaust speed (and thus the efficiency) could be greatly increased to beyond the speed of sound by using a De Laval nozzle. He patented these concepts in 1914. He also independently developed the mathematics of rocket flight. Goddard worked on developing solid-propellant rockets since 1914, and demonstrated a light battlefield rocket to the US Army Signal Corps only five days before the signing of the armistice that ended World War I. He also started developing liquid-propellant rockets in 1921, yet he had not been taken seriously by the public. Nevertheless, Goddard reclusively developed and flew a small liquid-fueled rocket. He developed the technology for 214 patents, 212 of which his wife published after his death.

During World War I Yves Le Prieur, a French naval officer and inventor, later to create a pioneering scuba diving apparatus, developed air-to-air solid-fuel rockets. The aim was to destroy observation captive balloons (called saucisses or Drachens) used by German artillery. These rather crude black powder, steel-tipped incendiary rockets made by the Ruggieri firm were first tested from a Voisin aircraft, wing-bolted on a fast Picard Pictet sports car and then used in battle on real aircraft. A typical layout was eight electrically fired Le Prieur rockets fitted on the interpane struts of a Nieuport aircraft. If fired at sufficiently short distance, a spread of Le Prieur rockets proved to be quite deadly. Belgian ace Willy Coppens claimed dozens of Drachen kills during World War I.

In 1920, Goddard published his ideas and experimental results in A Method of Reaching Extreme Altitudes. The work included remarks about sending a solid-fuel rocket to the Moon, which attracted worldwide attention and was both praised and ridiculed. A New York Times editorial suggested, referring to Newton's Third Law.

That Professor Goddard, with his 'chair' in Clark College and the countenancing of the Smithsonian Institution, does not know the relation of action to reaction, and of the need to have something better than a vacuum against which to react – to say that would be absurd. Of course he only seems to lack the knowledge ladled out daily in high schools."
— New York Times, 13 January 1920

In reality, in terms of Newton's third law, a rocket "pushes against" its exhaust gases, so the lack of surrounding air is not relevant.

In 1923, German Hermann Oberth (1894–1989) published Die Rakete zu den Planetenräumen ("The Rocket into Planetary Space"), a version of his doctoral thesis, after the University of Munich had rejected it. In 1929, he published a book, Wege zur Raumschiffahrt ("Ways to Spaceflight"), and static-fired an uncooled liquid-fueled rocket engine for a brief time.

In 1924, Tsiolkovsky also wrote about multi-stage rockets, in 'Cosmic Rocket Trains'.

Modern rocketry

Pre-World War II

Modern rockets originated in the US when Robert Goddard attached a supersonic (de Laval) nozzle to the combustion chamber of a liquid-fueled rocket engine. This turned the hot combustion chamber gas into a cooler, highly directed hypersonic jet of gas, more than doubling the thrust and raising the engine efficiency from 2% to 64%. On 16 March 1926, Goddard launched the world's first liquid-fueled rocket in Auburn, Massachusetts.

During the 1920s, a number of rocket research organizations appeared worldwide. Rocketry in the Soviet Union began in 1921 with extensive work at the Gas Dynamics Laboratory (GDL), where the first test-firing of a solid fuel rocket was carried out in March 1928, which flew for about 1,300 meters In 1931 the world's first successful use of rockets to assist take-off of aircraft were carried out on a U-1, the Soviet designation for a Avro 504 trainer, which achieved about one hundred successful assisted takeoffs. Further developments in the early 1930s included firing rockets from aircraft and the ground. In 1932 in-air test firings of RS-82 missiles from an Tupolev I-4 aircraft armed with six launchers successfully took place. In September 1931 the Group for the Study of Reactive Motion (GIRD) was formed and was responsible for the first Soviet liquid propelled rocket launch, the GIRD-9, on 17 August 1933, which reached an altitude of 400 metres (1,300 ft).

In 1933 GDL and GIRD were merged to form the Reactive Scientific Research Institute (RNII)^[82] and developments were continued, including designing several variations for ground-to-air, ground-to-ground, air-to-ground and air-to-air combat. The RS-82 rockets were carried by Polikarpov I-15, I-16 and I-153 fighter planes, the Polikarpov R-5 reconnaissance plane and the Ilyushin Il-2 close air support plane, while the heavier RS-132 rockets could be carried by bombers. Many small ships of the Soviet Navy were also fitted with the RS-82 rocket, including the MO-class small guard ship. The earliest known use by the Soviet Air Force of aircraft-launched unguided anti-aircraft rockets in combat against heavier-than-air aircraft took place in August 1939, during the Battle of Khalkhin Gol. A group of Polikarpov I-16 fighters under command of Captain N. Zvonarev were using RS-82 rockets against Japanese aircraft, shooting down 16 fighters and 3 bombers in total. Six Tupolev SB bombers also used RS-132 for ground attack during the Winter War. RNII also built over 100 experimental rocket engines under the direction of Valentin Glushko. Design work included regenerative cooling, hypergolic propellant ignition, and swirling and bi-propellant mixing fuel injectors. However, Glushko's arrest during Stalin's Great Purge in 1938 curtailed the developments.

In 1927 the German car manufacturer Opel began to research rocket vehicles together with Max Valier and the solid-fuel rocket builder Friedrich Wilhelm Sander. These activities are generally considered the world's first large-scale experimental rocket program, Opel-RAK under the leadership of Fritz von Opel, leading to the first rocket cars and rocket planes, which paved the way for the German V2 program and US and Soviet activities from 1950 onwards. In 1928, Fritz von Opel drove a rocket car Opel RAK.1 on the Opel raceway in Rüsselsheim, Germany, and later the dedicated RAK2 rocket car at the AVUS speedway in Berlin. In 1928, Opel, Valier and Sander equipped the Lippisch Ente glider, which Opel had purchased, with rocket power and launched the manned glider. The "Ente" was destroyed on its second flight. Eventually glider pioneer Julius Hatry was tasked by von Opel to construct a dedicated glider, again called Opel-RAK.1, for his rocket program. On September 30, 1929 von Opel himself piloted the RAK.1, the world's first public manned rocket-powered flight from the Frankfurt-Rebstock airport, but experienced a hard landing.

The Opel-RAK program and the spectacular public demonstrations of ground and air vehicles drew large crowds and caused global public excitement known as "rocket rumble", and had a large long-lasting impact on later spaceflight pioneers, in particular Wernher von Braun. Sixteen-year old von Braun was so enthusiastic about the public Opel-RAK demonstrations, that he constructed his own homemade rocket car, nearly killing himself in the process, and causing a major disruption in a crowded street by detonating the toy wagon to which he had attached fireworks. He was taken into custody by the local police until his father came to get him. The Great Depression put an end to the Opel-RAK program and von Opel left Germany in 1930, emigrating first to the US, later to France and Switzerland. After the break-up of the Opel-RAK program, Valier eventually was killed while experimenting with liquid-fueled rockets in May 1930, and is considered the first fatality of the dawning space age.

In Germany, engineers and scientists became enthralled with liquid propulsion, building and testing them in the late 1920s within Opel RAK in Rüsselsheim. According to Max Valier's account, Opel RAK rocket designer, Friedrich Wilhelm Sander launched two liquid-fuel rockets at Opel Rennbahn in Rüsselsheim on April 10 and April 12, 1929. These Opel RAK rockets have been the first European, and after Goddard the world's second, liquid-fuel rockets in history. In his book “Raketenfahrt” Valier describes the size of the rockets as 21 centimetres (8.3 in) in diameter and 74 centimetres (29 in) long, weighing 7 kilograms (15 lb) empty and 16 kilograms (35 lb) fueled. The maximum thrust was 45 to 50 kilograms-force (99 to 110 lbf), with a total burning time of 132 seconds. These properties indicate a gas pressure pumping. The first missile rose so quickly that Sander lost sight of it. Two days later, a second unit was ready to go. Sander tied a 4,000-metre (13,000 ft) rope to the rocket. After half the rope had been unwound, the line broke and this rocket also was lost, probably near the Opel proving ground and racetrack in Rüsselsheim, the "Rennbahn". The main purpose of these tests was to develop an aircraft propulsion system for crossing the English channel. Also, spaceflight historian Frank H. Winter, curator at the National Air and Space Museum in Washington, DC, confirms that in addition to solid-fuel rockets used for land-speed records and the world's first manned rocket-plane flights, the Opel group was working on liquid-fuel rockets (SPACEFLIGHT, Vol. 21,2, Feb. 1979): In a cabled exclusive to The New York Times on 30 September 1929, von Opel is quoted as saying: "Sander and I now want to transfer the liquid rocket from the laboratory to practical use. With the liquid rocket I hope to be the first man to thus fly across the English Channel. I will not rest until I have accomplished that." At a speech on the donation of a RAK 2 replica to the Deutsches Museum, von Opel mentioned engineer Josef Schaberger as a key collaborator. "He belonged," von Opel said, "with the same enthusiasm as Sander to our small secret group, one of the tasks of which was to hide all the preparations from my father, because his paternal apprehensions led him to believe that I was cut out for something better than being a rocket researchist. Schaberger supervised all the details involved in construction and assembly (of rocket cars), and every time I sat behind the wheel with a few hundred pounds of explosives in my rear, and made the first contact, I did so with a feeling of total security [...] As early as 1928, Mr. Schaberger and I developed a liquid rocket, which was definitely the first permanently operating rocket in which the explosive was injected into the combustion chamber and simultaneously cooled using pumps. [...] We used benzol as the fuel," von Opel continued, "and nitrogen tetroxide as the oxidizer. This rocket was installed in a Mueller-Griessheim aircraft and developed a thrust of 70 kilograms-force (150 lbf)." By May 1929, the engine produced a thrust of 200 kg (440 lb.) "for longer than fifteen minutes and in July 1929, the Opel RAK collaborators were able to attain powered phases of more than thirty minutes for thrusts of 300 kilograms-force (660 lbf). at Opel's works in Rüsselsheim," again according to Max Valier's account. The Great Depression brought an end to the Opel RAK activities. The work of Sander and Valier, who died while experimenting in 1930, was confiscated by the Heereswaffenamt and integrated into the activities under General Walter Dornberger in the early and mid-1930s in a field near Berlin.

An amateur rocket group, the VfR, co-founded by Max Valier, included Wernher von Braun, who eventually became the head of the army research station that designed the V-2 rocket weapon for the Nazis. When private rocket-engineering became forbidden in Germany, Sander was arrested by Gestapo in 1935, convicted of treason, sentenced to 5 years in prison, and forced to sell his company. He died in 1938.

Lieutenant Colonel Karl Emil Becker, head of the German Army's Ballistics and Munitions Branch, gathered a small team of engineers that included Walter Dornberger and Leo Zanssen, to figure out how to use rockets as long-range artillery in order to get around the Treaty of Versailles' ban on research and development of long-range cannons. Wernher von Braun, a young engineering prodigy who as an eighteen-year-old student helped Hermann Oberth build his liquid rocket engine, was recruited by Becker and Dornberger to join their secret army program at Kummersdorf-West in 1932. Von Braun dreamed of conquering outer space with rockets and did not initially see the military value in missile technology.

In 1927 a team of German rocket engineers, including Opel RAK's Max Valier, had formed the Verein für Raumschiffahrt (Society for Space Travel, or VfR), and in 1931 launched a liquid propellant rocket (using oxygen and gasoline).

Similar work was done from 1932 onwards by the Austrian professor Eugen Sänger, who migrated to Germany in 1936 and worked on rocket-powered spaceplanes such as Silbervogel (sometimes called the "antipodal" bomber).

On November 12, 1932 at a farm in Stockton NJ, the American Interplanetary Society's attempt to static-fire their first rocket (based on German Rocket Society designs) failed in a fire.

In 1936, a British research programme based at Fort Halstead in Kent under the direction of Dr. Alwyn Crow started work on a series of unguided solid-fuel rockets that could be used as anti-aircraft weapons. In 1939, a number of test firings were carried out in the British colony of Jamaica, on a specially built range.

In the 1930s, the German Reichswehr (which in 1935 became the Wehrmacht) began to take an interest in rocketry. Artillery restrictions imposed by the 1919 Treaty of Versailles limited Germany's access to long-distance weaponry. Seeing the possibility of using rockets as long-range artillery fire, the Wehrmacht initially funded the VfR team, but because their focus was strictly scientific, created its own research team. At the behest of military leaders, Wernher von Braun, at the time a young aspiring rocket scientist, joined the military (followed by two former VfR members) and developed long-range weapons for use in World War II by Nazi Germany.

In June 1938, the Soviet Reactive Scientific Research Institute (RNII) began developing a multiple rocket launcher based on the RS-132 rocket. In August 1939, the completed rocket was the BM-13 / Katyusha rocket launcher (BM stands for боевая машина (translit. boyevaya mashina), 'combat vehicle' for M-13 rockets). Towards the end of 1938 the first significant large scale testing of the rocket launchers took place, 233 rockets of various types were used. A salvo of rockets could completely straddle a target at a range of 5,500 metres (3.4 mi). Various rocket tests were conducted through 1940, and the BM-13-16 with launch rails for sixteen rockets was authorized for production. Only forty launchers were built before Germany invaded the Soviet Union in June 1941.

World War II

At the start of the war, the British had equipped their warships with unrotated projectile unguided anti-aircraft rockets, and by 1940, the Germans had developed a surface-to-surface multiple rocket launcher, the Nebelwerfer.

The Soviet Katyusha rocket launchers were top secret in the beginning of World War II. A special unit of the NKVD troops was raised to operate them. On July 14, 1941, an experimental artillery battery of seven launchers was first used in battle at Rudnya in Smolensk Oblast of Russia, under the command of Captain Ivan Flyorov, destroying a concentration of German troops with tanks, armored vehicles and trucks at the marketplace, causing massive German Army casualties and its retreat from the town in panic. After their success in the first month of the war, mass production was ordered and the development of other models proceeded. The Katyusha was inexpensive and could be manufactured in light industrial installations which did not have the heavy equipment to build conventional artillery gun barrels. By the end of 1942, 3,237 Katyusha launchers of all types had been built, and by the end of the war total production reached about 10,000. with 12 million rockets of the RS type produced for the Soviet armed forces.

During the Second World War, Major-General Dornberger was the military head of the army's rocket program, Zanssen became the commandant of the Peenemünde army rocket center, and von Braun was the technical director of the ballistic missile program. They led the team that built the Aggregat-4 (A-4) rocket, which became the first vehicle to reach outer space during its test flight program in 1942 and 1943. By 1943, Germany began mass-producing the A-4 as the Vergeltungswaffe 2 ("Vengeance Weapon" 2, or more commonly, V2), a ballistic missile with a 320-kilometer (200 mi) range carrying a 1,130-kilogram (2,490 lb) warhead at 4,000 kilometers per hour (2,500 mph). Its supersonic speed meant there was no defense against it, and radar detection provided little warning. Germany used the weapon to bombard southern England and parts of Allied-liberated western Europe from 1944 until 1945. After the war, the V-2 became the basis of early American and Soviet rocket designs.

In 1943, production of the V-2 rocket began in Germany. It had an operational range of 300 km (190 mi) and carried a 1,000 kg (2,200 lb) warhead, with an amatol explosive charge. It normally achieved an operational maximum altitude of around 90 km (56 mi), but could achieve 206 km (128 mi) if launched vertically. The vehicle was similar to most modern rockets, with turbopumps, inertial guidance and many other features. Thousands were fired at various Allied nations, mainly Belgium, as well as England and France. While they could not be intercepted, their guidance system design and single conventional warhead meant that they were insufficiently accurate against military targets. A total of 2,754 people in England were killed, and 6,523 were wounded before the launch campaign was ended. There were also 20,000 deaths of slave labour during the construction of V-2s. While it did not significantly affect the course of the war, the V-2 provided a lethal demonstration of the potential for guided rockets as weapons.

In parallel with the guided missile programme in Nazi Germany, rockets were also used on aircraft, either for assisting horizontal take-off (RATO), vertical take-off (Bachem Ba 349 "Natter") or for powering them (Me 163, etc.). During the war Germany also developed several guided and unguided air-to-air, ground-to-air and ground-to-ground missiles (see list of World War II guided missiles of Germany).

Post World War II

Dornberger and Von Braun after being captured by the Allies.
R-7 8K72 "Vostok" permanently displayed at the Moscow Trade Fair at Ostankino; the rocket is held in place by its railway carrier, which is mounted on four diagonal beams that constitute the display pedestal. Here the railway carrier has tilted the rocket upright as it would do so into its launch pad structure—which is missing for this display.
Prototype of the General Electric (USA) Mk-2 Reentry Vehicle (RV), based on blunt body theory.

At the end of World War II, competing Russian, British, and US military and scientific crews raced to capture technology and trained personnel from the German rocket program at Peenemünde. Russia and Britain had some success, but the United States benefited the most. The US captured a large number of German rocket scientists, including von Braun, and brought them to the United States as part of Operation Paperclip. In America, the same rockets that were designed to rain down on Britain were used instead by scientists as research vehicles for developing the new technology further. The V-2 evolved into the American Redstone rocket, used in the early space program.

After the war, rockets were used to study high-altitude conditions, by radio telemetry of temperature and pressure of the atmosphere, detection of cosmic rays, and further research; notably the Bell X-1, the first manned vehicle to break the sound barrier. This continued in the US under von Braun and the others, who were destined to become part of the US scientific community.

Independently, in the Soviet Union's space program research continued under the leadership of the chief designer Sergei Korolev. With the help of German technicians, the V-2 was launched and duplicated as the R-1 missile. German designs were abandoned in the late 1940s, and the foreign workers were sent home. A new series of engines built by Glushko and based on inventions of Aleksei Mihailovich Isaev formed the basis of the first ICBM, the R-7. The R-7 launched the first satellite, Sputnik 1, and later Yuri Gagarin, the first man into space, and the first lunar and planetary probes. This rocket is still in use today. These prestigious events attracted the attention of top politicians, along with additional funds for further research.

One problem that had not been solved was atmospheric reentry. It had been shown that an orbital vehicle easily had enough kinetic energy to vaporize itself, and yet it was known that meteorites can make it down to the ground. The mystery was solved in the US in 1951 when H. Julian Allen and A. J. Eggers, Jr. of the National Advisory Committee for Aeronautics (NACA) made the counterintuitive discovery that a blunt shape (high drag) permitted the most effective heat shield. With this type of shape, around 99% of the energy goes into the air rather than the vehicle, and this permitted safe recovery of orbital vehicles.

The Allen and Eggers discovery, initially treated as a military secret, was eventually published in 1958. Blunt body theory made possible the heat shield designs that were embodied in the Mercury, Gemini, Apollo, and Soyuz space capsules, enabling astronauts and cosmonauts to survive the fiery re-entry into Earth's atmosphere. Some spaceplanes such as the Space Shuttle made use of the same theory. At the time the STS was being conceived, Maxime Faget, the Director of Engineering and Development at the Manned Spacecraft Center, was not satisfied with the purely lifting re-entry method (as proposed for the cancelled X-20 "Dyna-Soar"). He designed a space shuttle which operated as a blunt body by entering the atmosphere at an extremely high angle of attack of 40° with the underside facing the direction of flight, creating a large shock wave that would deflect most of the heat around the vehicle instead of into it. The Space Shuttle used a combination of a ballistic entry (blunt body theory) and aerodynamic re-entry; at an altitude of about 122,000 m (400,000 ft), the atmosphere becomes dense enough for the aerodynamic re-entry phase to begin. Throughout re-entry, the Shuttle rolled to change lift direction in a prescribed way, keeping maximum deceleration well below 2 gs. These roll maneuvers allowed the Shuttle to use its lift to steer toward the runway.

Cold War

Rockets became extremely important militarily as modern intercontinental ballistic missiles (ICBMs) when it was realized that nuclear weapons carried on a rocket vehicle were essentially impossible for existing defense systems to stop once launched, and launch vehicles such as the R-7, Atlas, and Titan became delivery platforms for these weapons.

Fueled partly by the Cold War, the 1960s became the decade of rapid development of rocket technology particularly in the Soviet Union (Vostok, Soyuz, Proton) and in the United States (e.g. the X-15 and X-20 Dyna-Soar aircraft). There was also significant research in other countries, such as France, Britain, Japan, Australia, etc., and a growing use of rockets for Space exploration, with pictures returned from the far side of the Moon and uncrewed flights for Mars exploration.

In America, the crewed spaceflight programs, Project Mercury, Project Gemini, and later the Apollo program, culminated in 1969 with the first crewed landing on the Moon using the Saturn V, causing the New York Times to retract its earlier 1920 editorial implying that spaceflight couldn't work:

Further investigation and experimentation have confirmed the findings of Isaac Newton in the 17th century and it is now definitely established that a rocket can function in a vacuum as well as in an atmosphere. The Times regrets the error.
— New York Times, 17 June 1969 - A Correction

In the 1970s, the United States made five more lunar landings before cancelling the Apollo program in 1975. The replacement vehicle, the partially reusable Space Shuttle, was intended to be cheaper, but no large reduction in costs was achieved. Meanwhile, in 1973, the expendable Ariane programme was begun, a launcher that by the year 2000 would capture much of the geosat market.

Market competition

Since the early 2010s, new private options for obtaining spaceflight services emerged, bringing substantial market competition into the existing launch service provider business. Initially, these market forces have manifest through competitive dynamics among payload transport capabilities at diverse prices having a greater influence on rocket launch purchasing than the traditional political considerations of country of manufacture or the particular national entity using, regulating or licensing the launch service.

Following the advent of spaceflight technology in the late 1950s, space launch services came into being, exclusively by national programs. Later in the 20th century commercial operators became significant customers of launch providers. International competition for the communications satellite payload subset of the launch market was increasingly influenced by commercial considerations. However, even during this period, for both commercial- and government-entity-launched commsats, the launch service providers for these payloads used launch vehicles built to government specifications, and with state-provided development funding exclusively.

In the early 2010s, privately developed launch vehicle systems and space launch service offerings emerged. Companies now faced economic incentives rather than the principally political incentives of the earlier decades. The space launch business experienced a dramatic lowering of per-unit prices along with the addition of entirely new capabilities, bringing about a new phase of competition in the space launch market.

Emmy Noether

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Emmy_Noether

Emmy Noether

Born	Amalie Emmy Noether 23 March 1882 Erlangen, Bavaria, German Empire
Died	14 April 1935 (aged 53) Bryn Mawr, Pennsylvania, United States
Nationality	German
Alma mater	University of Erlangen
Known for	Abstract algebra Theoretical physics Noether's theorem Noetherian ring Lasker–Noether theorem
Awards	Ackermann–Teubner Memorial Award (1932)
Scientific career
Fields	Mathematics and physics
Institutions	University of Göttingen Bryn Mawr College
Thesis	On Complete Systems of Invariants for Ternary Biquadratic Forms (1907)
Doctoral advisor	Paul Gordan
Doctoral students	Max Deuring Hans Fitting Grete Hermann Chiungtze C. Tsen Jacob Levitzki Otto Schilling Ernst Witt

Amalie Emmy Noether was a German mathematician who made many important contributions to abstract algebra. She discovered Noether's First and Second Theorem, which are fundamental in mathematical physics. She was described by Pavel Alexandrov, Albert Einstein, Jean Dieudonné, Hermann Weyl and Norbert Wiener as the most important woman in the history of mathematics.As one of the leading mathematicians of her time, she developed some theories of rings, fields, and algebras. In physics, Noether's theorem explains the connection between symmetry and conservation laws.

Noether was born to a Jewish family in the Franconian town of Erlangen; her father was the mathematician Max Noether. She originally planned to teach French and English after passing the required examinations, but instead studied mathematics at the University of Erlangen, where her father lectured. After completing her doctorate in 1907 under the supervision of Paul Gordan, she worked at the Mathematical Institute of Erlangen without pay for seven years. At the time, women were largely excluded from academic positions. In 1915, she was invited by David Hilbert and Felix Klein to join the mathematics department at the University of Göttingen, a world-renowned center of mathematical research. The philosophical faculty objected, however, and she spent four years lecturing under Hilbert's name. Her habilitation was approved in 1919, allowing her to obtain the rank of Privatdozent.

Noether remained a leading member of the Göttingen mathematics department until 1933; her students were sometimes called the "Noether boys". In 1924, Dutch mathematician B. L. van der Waerden joined her circle and soon became the leading expositor of Noether's ideas; her work was the foundation for the second volume of his influential 1931 textbook, Moderne Algebra. By the time of her plenary address at the 1932 International Congress of Mathematicians in Zürich, her algebraic acumen was recognized around the world. The following year, Germany's Nazi government dismissed Jews from university positions, and Noether moved to the United States to take up a position at Bryn Mawr College in Pennsylvania where she taught, among others, doctoral and post-graduate women including Marie Johanna Weiss, Ruth Stauffer, Grace Shover Quinn and Olga Taussky-Todd. At the same time, she lectured and performed research at the Institute for Advanced Study in Princeton, New Jersey.

Noether's mathematical work has been divided into three "epochs". In the first (1908–1919), she made contributions to the theories of algebraic invariants and number fields. Her work on differential invariants in the calculus of variations, Noether's theorem, has been called "one of the most important mathematical theorems ever proved in guiding the development of modern physics". In the second epoch (1920–1926), she began work that "changed the face of [abstract] algebra". In her classic 1921 paper Idealtheorie in Ringbereichen (Theory of Ideals in Ring Domains), Noether developed the theory of ideals in commutative rings into a tool with wide-ranging applications. She made elegant use of the ascending chain condition, and objects satisfying it are named Noetherian in her honor. In the third epoch (1927–1935), she published works on noncommutative algebras and hypercomplex numbers and united the representation theory of groups with the theory of modules and ideals. In addition to her own publications, Noether was generous with her ideas and is credited with several lines of research published by other mathematicians, even in fields far removed from her main work, such as algebraic topology.

Personal life

Emmy Noether was born on 23 March 1882, the first of four children of mathematician Max Noether and Ida Amalia Kaufmann, both from Jewish merchant families. Her first name was "Amalie", after her mother and paternal grandmother, but she began using her middle name at a young age, and she invariably used the name "Emmy Noether" in her adult life and her publications.

In her youth, Noether did not stand out academically although she was known for being clever and friendly. She was near-sighted and talked with a minor lisp during her childhood. A family friend recounted a story years later about young Noether quickly solving a brain teaser at a children's party, showing logical acumen at that early age. She was taught to cook and clean, as were most girls of the time, and she took piano lessons. She pursued none of these activities with passion, although she loved to dance.

She had three younger brothers: the eldest, Alfred, was born in 1883, was awarded a doctorate in chemistry from Erlangen in 1909, but died nine years later. Fritz Noether, born in 1884, is remembered for his academic accomplishments. After studying in Munich he made a reputation for himself in applied mathematics. He was executed in the Soviet Union in 1941. The youngest, Gustav Robert, was born in 1889. Very little is known about his life; he suffered from chronic illness and died in 1928.

In 1935, Noether underwent surgery for an ovarian cyst and, despite signs of a recovery, died four days later at the age of 53.

University life and education

Noether showed early proficiency in French and English. In the spring of 1900, she took the examination for teachers of these languages and received an overall score of sehr gut (very good). Her performance qualified her to teach languages at schools reserved for girls, but she chose instead to continue her studies at the University of Erlangen.

This was an unconventional decision; two years earlier, the Academic Senate of the university had declared that allowing mixed-sex education would "overthrow all academic order". One of only two women in a university of 986 students, Noether was allowed only to audit classes rather than participate fully, and required the permission of individual professors whose lectures she wished to attend. Despite these obstacles, on 14 July 1903 she passed the graduation exam at a Realgymnasium in Nuremberg.

During the 1903–1904 winter semester, she studied at the University of Göttingen, attending lectures given by astronomer Karl Schwarzschild and mathematicians Hermann Minkowski, Otto Blumenthal, Felix Klein, and David Hilbert. Soon thereafter, restrictions on women's participation in that university were rescinded.

Noether returned to Erlangen. She officially reentered the university in October 1904, and declared her intention to focus solely on mathematics. Under the supervision of Paul Gordan she wrote her dissertation, Über die Bildung des Formensystems der ternären biquadratischen Form (On Complete Systems of Invariants for Ternary Biquadratic Forms, 1907). Gordan was a member of the "computational" school of invariant researchers, and Noether's thesis ended with a list of over 300 explicitly worked out invariants. This approach to invariants was later superseded by the more abstract and general approach pioneered by Hilbert. Although it had been well received, Noether later described her thesis and a number of subsequent similar papers she produced as "crap".

Teaching period

University of Erlangen

For the next seven years (1908–1915) she taught at the University of Erlangen's Mathematical Institute without pay, occasionally substituting for her father when he was too ill to lecture. In 1910 and 1911 she published an extension of her thesis work from three variables to n variables.

Gordan retired in the spring of 1910, but continued to teach occasionally with his successor, Erhard Schmidt, who left shortly afterward for a position in Breslau. Gordan retired from teaching altogether in 1911 when Schmidt's successor Ernst Fischer arrived; Gordan died a year later in December 1912.

According to Hermann Weyl, Fischer was an important influence on Noether, in particular by introducing her to the work of David Hilbert. From 1913 to 1916 Noether published several papers extending and applying Hilbert's methods to mathematical objects such as fields of rational functions and the invariants of finite groups. This phase marks the beginning of her engagement with abstract algebra, the field of mathematics to which she would make groundbreaking contributions.

Noether and Fischer shared lively enjoyment of mathematics and would often discuss lectures long after they were over; Noether is known to have sent postcards to Fischer continuing her train of mathematical thoughts.

University of Göttingen

In the spring of 1915, Noether was invited to return to the University of Göttingen by David Hilbert and Felix Klein. Their effort to recruit her, however, was blocked by the philologists and historians among the philosophical faculty: Women, they insisted, should not become privatdozenten. One faculty member protested: "What will our soldiers think when they return to the university and find that they are required to learn at the feet of a woman?" Hilbert responded with indignation, stating, "I do not see that the sex of the candidate is an argument against her admission as privatdozent. After all, we are a university, not a bathhouse."

In 1915 David Hilbert invited Noether to join the Göttingen mathematics department, challenging the views of some of his colleagues that a woman should not be allowed to teach at a university.

Noether left for Göttingen in late April; two weeks later her mother died suddenly in Erlangen. She had previously received medical care for an eye condition, but its nature and impact on her death is unknown. At about the same time Noether's father retired and her brother joined the German Army to serve in World War I. She returned to Erlangen for several weeks, mostly to care for her aging father.

During her first years teaching at Göttingen she did not have an official position and was not paid; her family paid for her room and board and supported her academic work. Her lectures often were advertised under Hilbert's name, and Noether would provide "assistance".

Soon after arriving at Göttingen, however, she demonstrated her capabilities by proving the theorem now known as Noether's theorem, which shows that a conservation law is associated with any differentiable symmetry of a physical system. The paper was presented by a colleague, F. Klein, on 26 July 1918 to a meeting of the Royal Society of Sciences at Göttingen. Noether presumably did not present it herself because she was not a member of the society. American physicists Leon M. Lederman and Christopher T. Hill argue in their book Symmetry and the Beautiful Universe that Noether's theorem is "certainly one of the most important mathematical theorems ever proved in guiding the development of modern physics, possibly on a par with the Pythagorean theorem".

When World War I ended, the German Revolution of 1918–1919 brought a significant change in social attitudes, including more rights for women. In 1919 the University of Göttingen allowed Noether to proceed with her habilitation (eligibility for tenure). Her oral examination was held in late May, and she successfully delivered her habilitation lecture in June 1919.

Three years later she received a letter from Otto Boelitz [de], the Prussian Minister for Science, Art, and Public Education, in which he conferred on her the title of nicht beamteter ausserordentlicher Professor (an untenured professor with limited internal administrative rights and functions). This was an unpaid "extraordinary" professorship, not the higher "ordinary" professorship, which was a civil-service position. Although it recognized the importance of her work, the position still provided no salary. Noether was not paid for her lectures until she was appointed to the special position of Lehrbeauftragte für Algebra a year later.

Work in abstract algebra

Although Noether's theorem had a significant effect upon classical and quantum mechanics, among mathematicians she is best remembered for her contributions to abstract algebra. In his introduction to Noether's Collected Papers, Nathan Jacobson wrote that

The development of abstract algebra, which is one of the most distinctive innovations of twentieth century mathematics, is largely due to her – in published papers, in lectures, and in personal influence on her contemporaries.

She sometimes allowed her colleagues and students to receive credit for her ideas, helping them develop their careers at the expense of her own.

Noether's work in algebra began in 1920. In collaboration with W. Schmeidler, she then published a paper about the theory of ideals in which they defined left and right ideals in a ring.

The following year she published a paper called Idealtheorie in Ringbereichen, analyzing ascending chain conditions with regard to (mathematical) ideals. Noted algebraist Irving Kaplansky called this work "revolutionary"; the publication gave rise to the term "Noetherian ring" and the naming of several other mathematical objects as Noetherian.

In 1924 a young Dutch mathematician, B.L. van der Waerden, arrived at the University of Göttingen. He immediately began working with Noether, who provided invaluable methods of abstract conceptualization. Van der Waerden later said that her originality was "absolute beyond comparison". In 1931 he published Moderne Algebra, a central text in the field; its second volume borrowed heavily from Noether's work. Although Noether did not seek recognition, he included as a note in the seventh edition "based in part on lectures by E. Artin and E. Noether".

Van der Waerden's visit was part of a convergence of mathematicians from all over the world to Göttingen, which became a major hub of mathematical and physical research. From 1926 to 1930 Russian topologist Pavel Alexandrov lectured at the university, and he and Noether quickly became good friends. He began referring to her as der Noether, using the masculine German article as a term of endearment to show his respect. She tried to arrange for him to obtain a position at Göttingen as a regular professor, but was able only to help him secure a scholarship from the Rockefeller Foundation. They met regularly and enjoyed discussions about the intersections of algebra and topology. In his 1935 memorial address, Alexandrov named Emmy Noether "the greatest woman mathematician of all time".

Graduate students and influential lectures

In addition to her mathematical insight, Noether was respected for her consideration of others. Although she sometimes acted rudely toward those who disagreed with her, she nevertheless gained a reputation for constant helpfulness and patient guidance of new students. Her loyalty to mathematical precision caused one colleague to name her "a severe critic", but she combined this demand for accuracy with a nurturing attitude. A colleague later described her this way:

Completely unegotistical and free of vanity, she never claimed anything for herself, but promoted the works of her students above all.

Göttingen

In Göttingen, Noether supervised more than a dozen doctoral students; her first was Grete Hermann, who defended her dissertation in February 1925. She later spoke reverently of her "dissertation-mother". Noether also supervised Max Deuring, who distinguished himself as an undergraduate and went on to contribute to the field of arithmetic geometry; Hans Fitting, remembered for Fitting's theorem and the Fitting lemma; and Zeng Jiongzhi (also rendered "Chiungtze C. Tsen" in English), who proved Tsen's theorem. She also worked closely with Wolfgang Krull, who greatly advanced commutative algebra with his Hauptidealsatz and his dimension theory for commutative rings.

Her frugal lifestyle at first was due to her being denied pay for her work; however, even after the university began paying her a small salary in 1923, she continued to live a simple and modest life. She was paid more generously later in her life, but saved half of her salary to bequeath to her nephew, Gottfried E. Noether.

Biographers suggest that she was mostly unconcerned about appearance and manners, focusing on her studies. A distinguished algebraist Olga Taussky-Todd described a luncheon during which Noether, wholly engrossed in a discussion of mathematics, "gesticulated wildly" as she ate and "spilled her food constantly and wiped it off from her dress, completely unperturbed". Appearance-conscious students cringed as she retrieved the handkerchief from her blouse and ignored the increasing disarray of her hair during a lecture. Two female students once approached her during a break in a two-hour class to express their concern, but they were unable to break through the energetic mathematical discussion she was having with other students.

According to van der Waerden's obituary of Emmy Noether, she did not follow a lesson plan for her lectures, which frustrated some students. Instead, she used her lectures as a spontaneous discussion time with her students, to think through and clarify important problems in mathematics. Some of her most important results were developed in these lectures, and the lecture notes of her students formed the basis for several important textbooks, such as those of van der Waerden and Deuring.

Several of her colleagues attended her lectures, and she allowed some of her ideas, such as the crossed product (verschränktes Produkt in German) of associative algebras, to be published by others. Noether was recorded as having given at least five semester-long courses at Göttingen:

Winter 1924/1925: Gruppentheorie und hyperkomplexe Zahlen [Group Theory and Hypercomplex Numbers]
Winter 1927/1928: Hyperkomplexe Grössen und Darstellungstheorie [Hypercomplex Quantities and Representation Theory]
Summer 1928: Nichtkommutative Algebra [Noncommutative Algebra]
Summer 1929: Nichtkommutative Arithmetik [Noncommutative Arithmetic]
Winter 1929/30: Algebra der hyperkomplexen Grössen [Algebra of Hypercomplex Quantities]

These courses often preceded major publications on the same subjects.

Noether spoke quickly – reflecting the speed of her thoughts, many said – and demanded great concentration from her students. Students who disliked her style often felt alienated. Some pupils felt that she relied too much on spontaneous discussions. Her most dedicated students, however, relished the enthusiasm with which she approached mathematics, especially since her lectures often built on earlier work they had done together.

She developed a close circle of colleagues and students who thought along similar lines and tended to exclude those who did not. "Outsiders" who occasionally visited Noether's lectures usually spent only 30 minutes in the room before leaving in frustration or confusion. A regular student said of one such instance: "The enemy has been defeated; he has cleared out."

Noether showed a devotion to her subject and her students that extended beyond the academic day. Once, when the building was closed for a state holiday, she gathered the class on the steps outside, led them through the woods, and lectured at a local coffee house. Later, after Nazi Germany dismissed her from teaching, she invited students into her home to discuss their plans for the future and mathematical concepts.

Moscow

In the winter of 1928–1929 Noether accepted an invitation to Moscow State University, where she continued working with P.S. Alexandrov. In addition to carrying on with her research, she taught classes in abstract algebra and algebraic geometry. She worked with the topologists Lev Pontryagin and Nikolai Chebotaryov, who later praised her contributions to the development of Galois theory.

Although politics was not central to her life, Noether took a keen interest in political matters and, according to Alexandrov, showed considerable support for the Russian Revolution. She was especially happy to see Soviet advances in the fields of science and mathematics, which she considered indicative of new opportunities made possible by the Bolshevik project. This attitude caused her problems in Germany, culminating in her eviction from a pension lodging building, after student leaders complained of living with "a Marxist-leaning Jewess".

Noether planned to return to Moscow, an effort for which she received support from Alexandrov. After she left Germany in 1933 he tried to help her gain a chair at Moscow State University through the Soviet Education Ministry. Although this effort proved unsuccessful, they corresponded frequently during the 1930s, and in 1935 she made plans for a return to the Soviet Union. Meanwhile, her brother Fritz accepted a position at the Research Institute for Mathematics and Mechanics in Tomsk, in the Siberian Federal District of Russia, after losing his job in Germany, and was subsequently executed during the Great Purge.

Recognition

In 1932 Emmy Noether and Emil Artin received the Ackermann–Teubner Memorial Award for their contributions to mathematics. The prize included a monetary reward of 500 ℛ︁ℳ︁ and was seen as a long-overdue official recognition of her considerable work in the field. Nevertheless, her colleagues expressed frustration at the fact that she was not elected to the Göttingen Gesellschaft der Wissenschaften (academy of sciences) and was never promoted to the position of Ordentlicher Professor (full professor).

Noether's colleagues celebrated her fiftieth birthday in 1932, in typical mathematicians' style. Helmut Hasse dedicated an article to her in the Mathematische Annalen, wherein he confirmed her suspicion that some aspects of noncommutative algebra are simpler than those of commutative algebra, by proving a noncommutative reciprocity law. This pleased her immensely. He also sent her a mathematical riddle, which he called the "m_μν-riddle of syllables". She solved it immediately, but the riddle has been lost.

In September of the same year, Noether delivered a plenary address (großer Vortrag) on "Hyper-complex systems in their relations to commutative algebra and to number theory" at the International Congress of Mathematicians in Zürich. The congress was attended by 800 people, including Noether's colleagues Hermann Weyl, Edmund Landau, and Wolfgang Krull. There were 420 official participants and twenty-one plenary addresses presented. Apparently, Noether's prominent speaking position was a recognition of the importance of her contributions to mathematics. The 1932 congress is sometimes described as the high point of her career.

Expulsion from Göttingen by Nazi Germany

When Adolf Hitler became the German Reichskanzler in January 1933, Nazi activity around the country increased dramatically. At the University of Göttingen the German Student Association led the attack on the "un-German spirit" attributed to Jews and was aided by a privatdozent named Werner Weber, a former student of Noether. Antisemitic attitudes created a climate hostile to Jewish professors. One young protester reportedly demanded: "Aryan students want Aryan mathematics and not Jewish mathematics."

One of the first actions of Hitler's administration was the Law for the Restoration of the Professional Civil Service which removed Jews and politically suspect government employees (including university professors) from their jobs unless they had "demonstrated their loyalty to Germany" by serving in World War I. In April 1933 Noether received a notice from the Prussian Ministry for Sciences, Art, and Public Education which read: "On the basis of paragraph 3 of the Civil Service Code of 7 April 1933, I hereby withdraw from you the right to teach at the University of Göttingen." Several of Noether's colleagues, including Max Born and Richard Courant, also had their positions revoked.

Noether accepted the decision calmly, providing support for others during this difficult time. Hermann Weyl later wrote that "Emmy Noether—her courage, her frankness, her unconcern about her own fate, her conciliatory spirit—was in the midst of all the hatred and meanness, despair and sorrow surrounding us, a moral solace." Typically, Noether remained focused on mathematics, gathering students in her apartment to discuss class field theory. When one of her students appeared in the uniform of the Nazi paramilitary organization Sturmabteilung (SA), she showed no sign of agitation and, reportedly, even laughed about it later. This, however, was before the bloody events of Kristallnacht in 1938, and their praise from Propaganda Minister Joseph Goebbels.

Refuge at Bryn Mawr and Princeton, in the United States

As dozens of newly unemployed professors began searching for positions outside of Germany, their colleagues in the United States sought to provide assistance and job opportunities for them. Albert Einstein and Hermann Weyl were appointed by the Institute for Advanced Study in Princeton, while others worked to find a sponsor required for legal immigration. Noether was contacted by representatives of two educational institutions: Bryn Mawr College, in the United States, and Somerville College at the University of Oxford, in England. After a series of negotiations with the Rockefeller Foundation, a grant to Bryn Mawr was approved for Noether and she took a position there, starting in late 1933.

At Bryn Mawr, Noether met and befriended Anna Wheeler, who had studied at Göttingen just before Noether arrived there. Another source of support at the college was the Bryn Mawr president, Marion Edwards Park, who enthusiastically invited mathematicians in the area to "see Dr. Noether in action!" Noether and a small team of students worked quickly through van der Waerden's 1930 book Moderne Algebra I and parts of Erich Hecke's Theorie der algebraischen Zahlen (Theory of algebraic numbers).

In 1934, Noether began lecturing at the Institute for Advanced Study in Princeton upon the invitation of Abraham Flexner and Oswald Veblen. She also worked with and supervised Abraham Albert and Harry Vandiver. However, she remarked about Princeton University that she was not welcome at "the men's university, where nothing female is admitted".

Her time in the United States was pleasant, surrounded as she was by supportive colleagues and absorbed in her favorite subjects. In the summer of 1934 she briefly returned to Germany to see Emil Artin and her brother Fritz before he left for Tomsk. Although many of her former colleagues had been forced out of the universities, she was able to use the library as a "foreign scholar". Without incident, Noether returned to the United States and her studies at Bryn Mawr.

Death

In April 1935 doctors discovered a tumor in Noether's pelvis. Worried about complications from surgery, they ordered two days of bed rest first. During the operation they discovered an ovarian cyst "the size of a large cantaloupe". Two smaller tumors in her uterus appeared to be benign and were not removed, to avoid prolonging surgery. For three days she appeared to convalesce normally, and she recovered quickly from a circulatory collapse on the fourth. On 14 April she fell unconscious, her temperature soared to 109 °F (42.8 °C), and she died. "[I]t is not easy to say what had occurred in Dr. Noether", one of the physicians wrote. "It is possible that there was some form of unusual and virulent infection, which struck the base of the brain where the heat centers are supposed to be located."

A few days after Noether's death her friends and associates at Bryn Mawr held a small memorial service at College President Park's house. Hermann Weyl and Richard Brauer traveled from Princeton and spoke with Wheeler and Taussky about their departed colleague. In the months that followed, written tributes began to appear around the globe: Albert Einstein joined van der Waerden, Weyl, and Pavel Alexandrov in paying their respects. Her body was cremated and the ashes interred under the walkway around the cloisters of the M. Carey Thomas Library at Bryn Mawr.

Contributions to mathematics and physics

Noether's work in abstract algebra and topology was influential in mathematics, while in physics, Noether's theorem has consequences for theoretical physics and dynamical systems. She showed an acute propensity for abstract thought, which allowed her to approach problems of mathematics in fresh and original ways. Her friend and colleague Hermann Weyl described her scholarly output in three epochs:

Emmy Noether's scientific production fell into three clearly distinct epochs:
(1) the period of relative dependence, 1907–1919
(2) the investigations grouped around the general theory of ideals 1920–1926
(3) the study of the non-commutative algebras, their representations by linear transformations, and their application to the study of commutative number fields and their arithmetics
— Weyl 1935

In the first epoch (1907–1919), Noether dealt primarily with differential and algebraic invariants, beginning with her dissertation under Paul Gordan. Her mathematical horizons broadened, and her work became more general and abstract, as she became acquainted with the work of David Hilbert, through close interactions with a successor to Gordan, Ernst Sigismund Fischer. After moving to Göttingen in 1915, she produced her work for physics, the two Noether's theorems.

In the second epoch (1920–1926), Noether devoted herself to developing the theory of mathematical rings.

In the third epoch (1927–1935), Noether focused on noncommutative algebra, linear transformations, and commutative number fields.

Although the results of Noether's first epoch were impressive and useful, her fame among mathematicians rests more on the groundbreaking work she did in her second and third epochs, as noted by Hermann Weyl and B.L. van der Waerden in their obituaries of her.

In these epochs, she was not merely applying ideas and methods of earlier mathematicians; rather, she was crafting new systems of mathematical definitions that would be used by future mathematicians. In particular, she developed a completely new theory of ideals in rings, generalizing earlier work of Richard Dedekind. She is also renowned for developing ascending chain conditions, a simple finiteness condition that yielded powerful results in her hands. Such conditions and the theory of ideals enabled Noether to generalize many older results and to treat old problems from a new perspective, such as elimination theory and the algebraic varieties that had been studied by her father.

Historical context

In the century from 1832 to Noether's death in 1935, the field of mathematics – specifically algebra – underwent a profound revolution, whose reverberations are still being felt. Mathematicians of previous centuries had worked on practical methods for solving specific types of equations, e.g., cubic, quartic, and quintic equations, as well as on the related problem of constructing regular polygons using compass and straightedge. Beginning with Carl Friedrich Gauss's 1832 proof that prime numbers such as five can be factored in Gaussian integers, Évariste Galois's introduction of permutation groups in 1832 (although, because of his death, his papers were published only in 1846, by Liouville), William Rowan Hamilton's discovery of quaternions in 1843, and Arthur Cayley's more modern definition of groups in 1854, research turned to determining the properties of ever-more-abstract systems defined by ever-more-universal rules. Noether's most important contributions to mathematics were to the development of this new field, abstract algebra.

Background on abstract algebra and begriffliche Mathematik (conceptual mathematics)

Two of the most basic objects in abstract algebra are groups and rings.

A group consists of a set of elements and a single operation which combines a first and a second element and returns a third. The operation must satisfy certain constraints for it to determine a group: It must be closed (when applied to any pair of elements of the associated set, the generated element must also be a member of that set), it must be associative, there must be an identity element (an element which, when combined with another element using the operation, results in the original element, such as adding zero to a number or multiplying it by one), and for every element there must be an inverse element.

A ring likewise, has a set of elements, but now has two operations. The first operation must make the set a commutative group, and the second operation is associative and distributive with respect to the first operation. It may or may not be commutative; this means that the result of applying the operation to a first and a second element is the same as to the second and first – the order of the elements does not matter. If every non-zero element has a multiplicative inverse (an element x such that a x = x a = 1 ), the ring is called a division ring. A field is defined as a commutative division ring.

Groups are frequently studied through group representations. In their most general form, these consist of a choice of group, a set, and an action of the group on the set, that is, an operation which takes an element of the group and an element of the set and returns an element of the set. Most often, the set is a vector space, and the group represents symmetries of the vector space. For example, there is a group which represents the rigid rotations of space. This is a type of symmetry of space, because space itself does not change when it is rotated even though the positions of objects in it do. Noether used these sorts of symmetries in her work on invariants in physics.

A powerful way of studying rings is through their modules. A module consists of a choice of ring, another set, usually distinct from the underlying set of the ring and called the underlying set of the module, an operation on pairs of elements of the underlying set of the module, and an operation which takes an element of the ring and an element of the module and returns an element of the module.

The underlying set of the module and its operation must form a group. A module is a ring-theoretic version of a group representation: Ignoring the second ring operation and the operation on pairs of module elements determines a group representation. The real utility of modules is that the kinds of modules that exist and their interactions, reveal the structure of the ring in ways that are not apparent from the ring itself. An important special case of this is an algebra. (The word algebra means both a subject within mathematics as well as an object studied in the subject of algebra.) An algebra consists of a choice of two rings and an operation which takes an element from each ring and returns an element of the second ring. This operation makes the second ring into a module over the first. Often the first ring is a field.

Words such as "element" and "combining operation" are very general, and can be applied to many real-world and abstract situations. Any set of things that obeys all the rules for one (or two) operation(s) is, by definition, a group (or ring), and obeys all theorems about groups (or rings). Integer numbers, and the operations of addition and multiplication, are just one example. For example, the elements might be computer data words, where the first combining operation is exclusive or and the second is logical conjunction. Theorems of abstract algebra are powerful because they are general; they govern many systems. It might be imagined that little could be concluded about objects defined with so few properties, but precisely therein lay Noether's gift to discover the maximum that could be concluded from a given set of properties, or conversely, to identify the minimum set, the essential properties responsible for a particular observation. Unlike most mathematicians, she did not make abstractions by generalizing from known examples; rather, she worked directly with the abstractions. In his obituary of Noether, her student van der Waerden recalled that

The maxim by which Emmy Noether was guided throughout her work might be formulated as follows: "Any relationships between numbers, functions, and operations become transparent, generally applicable, and fully productive only after they have been isolated from their particular objects and been formulated as universally valid concepts."

This is the begriffliche Mathematik (purely conceptual mathematics) that was characteristic of Noether. This style of mathematics was consequently adopted by other mathematicians, especially in the (then new) field of abstract algebra.

Example: Integers as a ring

The integers form a commutative ring whose elements are the integers, and the combining operations are addition and multiplication. Any pair of integers can be added or multiplied, always resulting in another integer, and the first operation, addition, is commutative, i.e., for any elements a and b in the ring, a + b = b + a. The second operation, multiplication, also is commutative, but that need not be true for other rings, meaning that a combined with b might be different from b combined with a. Examples of noncommutative rings include matrices and quaternions. The integers do not form a division ring, because the second operation cannot always be inverted; there is no integer a such that 3 × a = 1.

The integers have additional properties which do not generalize to all commutative rings. An important example is the fundamental theorem of arithmetic, which says that every positive integer can be factored uniquely into prime numbers. Unique factorizations do not always exist in other rings, but Noether found a unique factorization theorem, now called the Lasker–Noether theorem, for the ideals of many rings. Much of Noether's work lay in determining what properties do hold for all rings, in devising novel analogs of the old integer theorems, and in determining the minimal set of assumptions required to yield certain properties of rings.

First epoch (1908–1919): Algebraic invariant theory

Much of Noether's work in the first epoch of her career was associated with invariant theory, principally algebraic invariant theory. Invariant theory is concerned with expressions that remain constant (invariant) under a group of transformations. As an everyday example, if a rigid yardstick is rotated, the coordinates (x₁, y₁, z₁) and (x₂, y₂, z₂) of its endpoints change, but its length L given by the formula L² = Δx² + Δy² + Δz² remains the same. Invariant theory was an active area of research in the later nineteenth century, prompted in part by Felix Klein's Erlangen program, according to which different types of geometry should be characterized by their invariants under transformations, e.g., the cross-ratio of projective geometry.

An example of an invariant is the discriminant B² − 4 A C of a binary quadratic form x·A x + y·B x + y·C y , where x and y are vectors and "·" is the dot product or "inner product" for the vectors. A, B, and C are linear operators on the vectors – typically matrices.

The discriminant is called "invariant" because it is not changed by linear substitutions x → a x + b y, y → c x + d y with determinant a d − b c = 1 . These substitutions form the special linear group SL₂.

One can ask for all polynomials in A, B, and C that are unchanged by the action of SL₂; these are called the invariants of binary quadratic forms and turn out to be the polynomials in the discriminant.

More generally, one can ask for the invariants of homogeneous polynomials A₀ x^r y⁰ + ... + A_r x⁰ y^r of higher degree, which will be certain polynomials in the coefficients A₀, ..., A_r, and more generally still, one can ask the similar question for homogeneous polynomials in more than two variables.

One of the main goals of invariant theory was to solve the "finite basis problem". The sum or product of any two invariants is invariant, and the finite basis problem asked whether it was possible to get all the invariants by starting with a finite list of invariants, called generators, and then, adding or multiplying the generators together. For example, the discriminant gives a finite basis (with one element) for the invariants of binary quadratic forms.

Noether's advisor, Paul Gordan, was known as the "king of invariant theory", and his chief contribution to mathematics was his 1870 solution of the finite basis problem for invariants of homogeneous polynomials in two variables. He proved this by giving a constructive method for finding all of the invariants and their generators, but was not able to carry out this constructive approach for invariants in three or more variables. In 1890, David Hilbert proved a similar statement for the invariants of homogeneous polynomials in any number of variables. Furthermore, his method worked, not only for the special linear group, but also for some of its subgroups such as the special orthogonal group.

First epoch (1908–1919): Galois theory

Galois theory concerns transformations of number fields that permute the roots of an equation. Consider a polynomial equation of a variable x of degree n, in which the coefficients are drawn from some ground field, which might be, for example, the field of real numbers, rational numbers, or the integers modulo 7. There may or may not be choices of x, which make this polynomial evaluate to zero. Such choices, if they exist, are called roots. If the polynomial is x² + 1 and the field is the real numbers, then the polynomial has no roots, because any choice of x makes the polynomial greater than or equal to one. If the field is extended, however, then the polynomial may gain roots, and if it is extended enough, then it always has a number of roots equal to its degree.

Continuing the previous example, if the field is enlarged to the complex numbers, then the polynomial gains two roots, +i and −i, where i is the imaginary unit, that is, i² = −1 . More generally, the extension field in which a polynomial can be factored into its roots is known as the splitting field of the polynomial.

The Galois group of a polynomial is the set of all transformations of the splitting field which preserve the ground field and the roots of the polynomial. (In mathematical jargon, these transformations are called automorphisms.) The Galois group of x² + 1 consists of two elements: The identity transformation, which sends every complex number to itself, and complex conjugation, which sends +i to −i. Since the Galois group does not change the ground field, it leaves the coefficients of the polynomial unchanged, so it must leave the set of all roots unchanged. Each root can move to another root, however, so transformation determines a permutation of the n roots among themselves. The significance of the Galois group derives from the fundamental theorem of Galois theory, which proves that the fields lying between the ground field and the splitting field are in one-to-one correspondence with the subgroups of the Galois group.

In 1918, Noether published a paper on the inverse Galois problem. Instead of determining the Galois group of transformations of a given field and its extension, Noether asked whether, given a field and a group, it always is possible to find an extension of the field that has the given group as its Galois group. She reduced this to "Noether's problem", which asks whether the fixed field of a subgroup G of the permutation group S_n acting on the field k(x₁, ... , x_n) always is a pure transcendental extension of the field k. (She first mentioned this problem in a 1913 paper, where she attributed the problem to her colleague Fischer.) She showed this was true for n = 2, 3, or 4. In 1969, R.G. Swan found a counter-example to Noether's problem, with n = 47 and G a cyclic group of order 47 (although this group can be realized as a Galois group over the rationals in other ways). The inverse Galois problem remains unsolved.

First epoch (1908–1919): Physics

Noether was brought to Göttingen in 1915 by David Hilbert and Felix Klein, who wanted her expertise in invariant theory to help them in understanding general relativity, a geometrical theory of gravitation developed mainly by Albert Einstein. Hilbert had observed that the conservation of energy seemed to be violated in general relativity, because gravitational energy could itself gravitate. Noether provided the resolution of this paradox, and a fundamental tool of modern theoretical physics, with Noether's first theorem, which she proved in 1915, but did not publish until 1918. She not only solved the problem for general relativity, but also determined the conserved quantities for every system of physical laws that possesses some continuous symmetry. Upon receiving her work, Einstein wrote to Hilbert:

Yesterday I received from Miss Noether a very interesting paper on invariants. I'm impressed that such things can be understood in such a general way. The old guard at Göttingen should take some lessons from Miss Noether! She seems to know her stuff.

For illustration, if a physical system behaves the same, regardless of how it is oriented in space, the physical laws that govern it are rotationally symmetric; from this symmetry, Noether's theorem shows the angular momentum of the system must be conserved. The physical system itself need not be symmetric; a jagged asteroid tumbling in space conserves angular momentum despite its asymmetry. Rather, the symmetry of the physical laws governing the system is responsible for the conservation law. As another example, if a physical experiment has the same outcome at any place and at any time, then its laws are symmetric under continuous translations in space and time; by Noether's theorem, these symmetries account for the conservation laws of linear momentum and energy within this system, respectively.

Noether's theorem has become a fundamental tool of modern theoretical physics, both because of the insight it gives into conservation laws, and also, as a practical calculation tool. Her theorem allows researchers to determine the conserved quantities from the observed symmetries of a physical system. Conversely, it facilitates the description of a physical system based on classes of hypothetical physical laws. For illustration, suppose that a new physical phenomenon is discovered. Noether's theorem provides a test for theoretical models of the phenomenon:

If the theory has a continuous symmetry, then Noether's theorem guarantees that the theory has a conserved quantity, and for the theory to be correct, this conservation must be observable in experiments.

Second epoch (1920–1926): Ascending and descending chain conditions

In this epoch, Noether became famous for her deft use of ascending (Teilerkettensatz) or descending (Vielfachenkettensatz) chain conditions. A sequence of non-empty subsets A₁, A₂, A₃, etc. of a set S is usually said to be ascending, if each is a subset of the next

A_{1} \subset A_{2} \subset A_{3} \subset \dots .

Conversely, a sequence of subsets of S is called descending if each contains the next subset:

A_{1} \supset A_{2} \supset A_{3} \supset \dots .

A chain becomes constant after a finite number of steps if there is an n such that $A_{n} = A_{m}$ for all m ≥ n. A collection of subsets of a given set satisfies the ascending chain condition if any ascending sequence becomes constant after a finite number of steps. It satisfies the descending chain condition if any descending sequence becomes constant after a finite number of steps.

Ascending and descending chain conditions are general, meaning that they can be applied to many types of mathematical objects—and, on the surface, they might not seem very powerful. Noether showed how to exploit such conditions, however, to maximum advantage.

For example: How to use chain conditions to show that every set of sub-objects has a maximal/minimal element or that a complex object can be generated by a smaller number of elements. These conclusions often are crucial steps in a proof.

Many types of objects in abstract algebra can satisfy chain conditions, and usually if they satisfy an ascending chain condition, they are called Noetherian in her honor. By definition, a Noetherian ring satisfies an ascending chain condition on its left and right ideals, whereas a Noetherian group is defined as a group in which every strictly ascending chain of subgroups is finite. A Noetherian module is a module in which every strictly ascending chain of submodules becomes constant after a finite number of steps. A Noetherian space is a topological space in which every strictly ascending chain of open subspaces becomes constant after a finite number of steps; this definition makes the spectrum of a Noetherian ring a Noetherian topological space.

The chain condition often is "inherited" by sub-objects. For example, all subspaces of a Noetherian space, are Noetherian themselves; all subgroups and quotient groups of a Noetherian group are likewise, Noetherian; and, mutatis mutandis, the same holds for submodules and quotient modules of a Noetherian module. All quotient rings of a Noetherian ring are Noetherian, but that does not necessarily hold for its subrings. The chain condition also may be inherited by combinations or extensions of a Noetherian object. For example, finite direct sums of Noetherian rings are Noetherian, as is the ring of formal power series over a Noetherian ring.

Another application of such chain conditions is in Noetherian induction—also known as well-founded induction—which is a generalization of mathematical induction. It frequently is used to reduce general statements about collections of objects to statements about specific objects in that collection. Suppose that S is a partially ordered set. One way of proving a statement about the objects of S is to assume the existence of a counterexample and deduce a contradiction, thereby proving the contrapositive of the original statement. The basic premise of Noetherian induction is that every non-empty subset of S contains a minimal element. In particular, the set of all counterexamples contains a minimal element, the minimal counterexample. In order to prove the original statement, therefore, it suffices to prove something seemingly much weaker: For any counter-example, there is a smaller counter-example.

Second epoch (1920–1926): Commutative rings, ideals, and modules

Noether's paper, Idealtheorie in Ringbereichen (Theory of Ideals in Ring Domains, 1921), is the foundation of general commutative ring theory, and gives one of the first general definitions of a commutative ring. Before her paper, most results in commutative algebra were restricted to special examples of commutative rings, such as polynomial rings over fields or rings of algebraic integers. Noether proved that in a ring which satisfies the ascending chain condition on ideals, every ideal is finitely generated. In 1943, French mathematician Claude Chevalley coined the term, Noetherian ring, to describe this property. A major result in Noether's 1921 paper is the Lasker–Noether theorem, which extends Lasker's theorem on the primary decomposition of ideals of polynomial rings to all Noetherian rings. The Lasker–Noether theorem can be viewed as a generalization of the fundamental theorem of arithmetic which states that any positive integer can be expressed as a product of prime numbers, and that this decomposition is unique.

Noether's work Abstrakter Aufbau der Idealtheorie in algebraischen Zahl- und Funktionenkörpern (Abstract Structure of the Theory of Ideals in Algebraic Number and Function Fields, 1927) characterized the rings in which the ideals have unique factorization into prime ideals as the Dedekind domains: integral domains that are Noetherian, 0- or 1-dimensional, and integrally closed in their quotient fields. This paper also contains what now are called the isomorphism theorems, which describe some fundamental natural isomorphisms, and some other basic results on Noetherian and Artinian modules.

Second epoch (1920–1926): Elimination theory

In 1923–1924, Noether applied her ideal theory to elimination theory in a formulation that she attributed to her student, Kurt Hentzelt. She showed that fundamental theorems about the factorization of polynomials could be carried over directly. Traditionally, elimination theory is concerned with eliminating one or more variables from a system of polynomial equations, usually by the method of resultants.

For illustration, a system of equations often can be written in the form M v = 0 where a matrix (or linear transform) M (without the variable x) times a vector v (that only has non-zero powers of x) is equal to the zero vector, 0. Hence, the determinant of the matrix M must be zero, providing a new equation in which the variable x has been eliminated.

Second epoch (1920–1926): Invariant theory of finite groups

Techniques such as Hilbert's original non-constructive solution to the finite basis problem could not be used to get quantitative information about the invariants of a group action, and furthermore, they did not apply to all group actions. In her 1915 paper, Noether found a solution to the finite basis problem for a finite group of transformations G acting on a finite-dimensional vector space over a field of characteristic zero. Her solution shows that the ring of invariants is generated by homogeneous invariants whose degree is less than, or equal to, the order of the finite group; this is called Noether's bound. Her paper gave two proofs of Noether's bound, both of which also work when the characteristic of the field is coprime to |G|! (the factorial of the order |G| of the group G). The degrees of generators need not satisfy Noether's bound when the characteristic of the field divides the number |G|, but Noether was not able to determine whether this bound was correct when the characteristic of the field divides |G|! but not |G|. For many years, determining the truth or falsehood of this bound for this particular case was an open problem, called "Noether's gap". It was finally solved independently by Fleischmann in 2000 and Fogarty in 2001, who both showed that the bound remains true.

In her 1926 paper, Noether extended Hilbert's theorem to representations of a finite group over any field; the new case that did not follow from Hilbert's work is when the characteristic of the field divides the order of the group. Noether's result was later extended by William Haboush to all reductive groups by his proof of the Mumford conjecture. In this paper Noether also introduced the Noether normalization lemma, showing that a finitely generated domain A over a field k has a set {x₁, ..., x_n} of algebraically independent elements such that A is integral over k[x₁, ..., x_n].

Second epoch (1920–1926): Contributions to topology

A continuous deformation (homotopy) of a coffee cup into a doughnut (torus) and back

As noted by Pavel Alexandrov and Hermann Weyl in their obituaries, Noether's contributions to topology illustrate her generosity with ideas and how her insights could transform entire fields of mathematics. In topology, mathematicians study the properties of objects that remain invariant even under deformation, properties such as their connectedness. An old joke is that "a topologist cannot distinguish a donut from a coffee mug", since they can be continuously deformed into one another.

Noether is credited with fundamental ideas that led to the development of algebraic topology from the earlier combinatorial topology, specifically, the idea of homology groups. According to the account of Alexandrov, Noether attended lectures given by Heinz Hopf and by him in the summers of 1926 and 1927, where "she continually made observations which were often deep and subtle" and he continues that,

When ... she first became acquainted with a systematic construction of combinatorial topology, she immediately observed that it would be worthwhile to study directly the groups of algebraic complexes and cycles of a given polyhedron and the subgroup of the cycle group consisting of cycles homologous to zero; instead of the usual definition of Betti numbers, she suggested immediately defining the Betti group as the complementary (quotient) group of the group of all cycles by the subgroup of cycles homologous to zero. This observation now seems self-evident. But in those years (1925–1928) this was a completely new point of view.

Noether's suggestion that topology be studied algebraically was adopted immediately by Hopf, Alexandrov, and others, and it became a frequent topic of discussion among the mathematicians of Göttingen. Noether observed that her idea of a Betti group makes the Euler–Poincaré formula simpler to understand, and Hopf's own work on this subject "bears the imprint of these remarks of Emmy Noether". Noether mentions her own topology ideas only as an aside in a 1926 publication, where she cites it as an application of group theory.

This algebraic approach to topology was also developed independently in Austria. In a 1926–1927 course given in Vienna, Leopold Vietoris defined a homology group, which was developed by Walther Mayer, into an axiomatic definition in 1928.

Third epoch (1927–1935): Hypercomplex numbers and representation theory

Much work on hypercomplex numbers and group representations was carried out in the nineteenth and early twentieth centuries, but remained disparate. Noether united these results and gave the first general representation theory of groups and algebras.

Briefly, Noether subsumed the structure theory of associative algebras and the representation theory of groups into a single arithmetic theory of modules and ideals in rings satisfying ascending chain conditions. This single work by Noether was of fundamental importance for the development of modern algebra.

Third epoch (1927–1935): Noncommutative algebra

Noether also was responsible for a number of other advances in the field of algebra. With Emil Artin, Richard Brauer, and Helmut Hasse, she founded the theory of central simple algebras.

A paper by Noether, Helmut Hasse, and Richard Brauer pertains to division algebras, which are algebraic systems in which division is possible. They proved two important theorems: a local-global theorem stating that if a finite-dimensional central division algebra over a number field splits locally everywhere then it splits globally (so is trivial), and from this, deduced their Hauptsatz ("main theorem"):

every finite dimensional central division algebra over an algebraic number field F splits over a cyclic cyclotomic extension.

These theorems allow one to classify all finite-dimensional central division algebras over a given number field. A subsequent paper by Noether showed, as a special case of a more general theorem, that all maximal subfields of a division algebra D are splitting fields. This paper also contains the Skolem–Noether theorem which states that any two embeddings of an extension of a field k into a finite-dimensional central simple algebra over k, are conjugate. The Brauer–Noether theorem gives a characterization of the splitting fields of a central division algebra over a field.

Recognition

Noether's work continues to be relevant for the development of theoretical physics and mathematics and she is consistently ranked as one of the greatest mathematicians of the twentieth century. In his obituary, fellow algebraist BL van der Waerden says that her mathematical originality was "absolute beyond comparison", and Hermann Weyl said that Noether "changed the face of algebra by her work". During her lifetime and even until today, Noether has been characterized as the greatest woman mathematician in recorded history by mathematicians such as Pavel Alexandrov, Hermann Weyl, and Jean Dieudonné.

In a letter to The New York Times, Albert Einstein wrote:

In the judgment of the most competent living mathematicians, Fräulein Noether was the most significant creative mathematical genius thus far produced since the higher education of women began. In the realm of algebra, in which the most gifted mathematicians have been busy for centuries, she discovered methods which have proved of enormous importance in the development of the present-day younger generation of mathematicians.

Search This Blog

Monday, August 14, 2023

History of rockets

China

Spread of rocket technology

Mongols

Middle East

India

Korea

Europe

Adoption in Renaissance-era Europe

Early modern history

Siemienowicz

Anderson

Indian Mysorean rockets

19th-century gunpowder-rocket artillery

Early 20th-century rocket pioneers

Modern rocketry

Pre-World War II

World War II

Post World War II

Cold War

Market competition

Emmy Noether

Personal life

University life and education

Teaching period

University of Erlangen

University of Göttingen

Work in abstract algebra

Graduate students and influential lectures

Göttingen

Moscow

Recognition

Expulsion from Göttingen by Nazi Germany

Refuge at Bryn Mawr and Princeton, in the United States

Death

Contributions to mathematics and physics

Historical context

Background on abstract algebra and begriffliche Mathematik (conceptual mathematics)

Example: Integers as a ring

First epoch (1908–1919): Algebraic invariant theory

First epoch (1908–1919): Galois theory

First epoch (1908–1919): Physics

Second epoch (1920–1926): Ascending and descending chain conditions

Second epoch (1920–1926): Commutative rings, ideals, and modules

Second epoch (1920–1926): Elimination theory

Second epoch (1920–1926): Invariant theory of finite groups

Second epoch (1920–1926): Contributions to topology

Third epoch (1927–1935): Hypercomplex numbers and representation theory

Third epoch (1927–1935): Noncommutative algebra

Recognition

Operator (computer programming)