Capacitance

From Wikipedia, the free encyclopedia

Common symbols	C
SI unit	farad
Other units	μF, nF, pF
In SI base units	F = A2 s4 kg−1 m−2
Derivations from other quantities	C = charge / voltage
Dimension	M−1 L−2 T4 I2

Capacitance is the ratio of the change in an electric charge in a system to the corresponding change in its electric potential. There are two closely related notions of capacitance: self capacitance and mutual capacitance. Any object that can be electrically charged exhibits self capacitance. A material with a large self capacitance holds more electric charge at a given voltage than one with low capacitance. The notion of mutual capacitance is particularly important for understanding the operations of the capacitor, one of the three elementary linear electronic components (along with resistors and inductors).

The capacitance is a function only of the geometry of the design (e.g. area of the plates and the distance between them) and the permittivity of the dielectric material between the plates of the capacitor. For many dielectric materials, the permittivity and thus the capacitance, is independent of the potential difference between the conductors and the total charge on them.

The SI unit of capacitance is the farad (symbol: F), named after the English physicist Michael Faraday. A 1 farad capacitor, when charged with 1 coulomb of electrical charge, has a potential difference of 1 volt between its plates. The reciprocal of capacitance is called elastance.

Self-capacitance

In electrical circuits, the term capacitance is usually a shorthand for the mutual capacitance between two adjacent conductors, such as the two plates of a capacitor. However, for an isolated conductor, there also exists a property called self-capacitance, which is the amount of electric charge that must be added to an isolated conductor to raise its electric potential by one unit (i.e. one volt, in most measurement systems). The reference point for this potential is a theoretical hollow conducting sphere, of infinite radius, with the conductor centered inside this sphere.
Mathematically, the self-capacitance of a conductor is defined by

${\displaystyle C={\frac {q}{V}},}$

where

q is the charge held by the conductor,

${\displaystyle V={1 \over 4\pi \varepsilon _{0}}\int {\sigma \,dS \over r}}$ is the electric potential,

σ is the surface charge density.

dS is an infinitesimal element of area,

r is the length from dS to a fixed point M within the plate

${\displaystyle \varepsilon _{0}}$ is the vacuum permittivity

Using this method, the self-capacitance of a conducting sphere of radius R is

${\displaystyle C=4\pi \varepsilon _{0}R\,}$

Example values of self-capacitance are:

• for the top "plate" of a van de Graaff generator, typically a sphere 20 cm in radius: 22.24 pF,
• the planet Earth: about 710 µF.

The inter-winding capacitance of a coil is sometimes called self-capacitance, but this is a different phenomenon. It is actually mutual capacitance between the individual turns of the coil and is a form of stray, or parasitic capacitance. This self-capacitance is an important consideration at high frequencies: It changes the impedance of the coil and gives rise to parallel resonance. In many applications this is an undesirable effect and sets an upper frequency limit for the correct operation of the circuit.

Mutual capacitance

A common form is a parallel-plate capacitor, which consists of two conductive plates insulated from each other, usually sandwiching a dielectric material. In a parallel plate capacitor, capacitance is very nearly proportional to the surface area of the conductor plates and inversely proportional to the separation distance between the plates.

If the charges on the plates are +q and −q, and V gives the voltage between the plates, then the capacitance C is given by

${\displaystyle C={\frac {q}{V}}.}$

which gives the voltage/current relationship

${\displaystyle i(t)=C{\frac {\mathrm {d} v(t)}{\mathrm {d} t}}.}$

The energy stored in a capacitor is found by integrating the work W

${\displaystyle W_{\text{charging}}={\frac {1}{2}}CV^{2}}$

Capacitance matrix

The discussion above is limited to the case of two conducting plates, although of arbitrary size and shape. The definition ${\displaystyle C=Q/V}$ does not apply when there are more than two charged plates, or when the net charge on the two plates is non-zero. To handle this case, Maxwell introduced his coefficients of potential. If three (nearly ideal) conductors are given charges ${\displaystyle Q_{1},Q_{2},Q_{3}}$, then the voltage at conductor 1 is given by

${\displaystyle V_{1}=P_{11}Q_{1}+P_{12}Q_{2}+P_{13}Q_{3},}$

and similarly for the other voltages. Hermann von Helmholtz and Sir William Thomson showed that the coefficients of potential are symmetric, so that ${\displaystyle P_{12}=P_{21}}$, etc. Thus the system can be described by a collection of coefficients known as the elastance matrix or reciprocal capacitance matrix, which is defined as:

${\displaystyle P_{ij}={\frac {\partial V_{i}}{\partial Q_{j}}}}$

From this, the mutual capacitance ${\displaystyle C_{m}}$ between two objects can be defined by solving for the total charge Q and using ${\displaystyle C_{m}=Q/V}$.

${\displaystyle C_{m}={\frac {1}{(P_{11}+P_{22})-(P_{12}+P_{21})}}}$

Since no actual device holds perfectly equal and opposite charges on each of the two "plates", it is the mutual capacitance that is reported on capacitors.

The collection of coefficients ${\displaystyle C_{ij}={\frac {\partial Q_{i}}{\partial V_{j}}}}$ is known as the capacitance matrix, and is the inverse of the elastance matrix.

Capacitors

The capacitance of the majority of capacitors used in electronic circuits is generally several orders of magnitude smaller than the farad. The most common subunits of capacitance in use today are the microfarad (µF), nanofarad (nF), picofarad (pF), and, in microcircuits, femtofarad (fF). However, specially made supercapacitors can be much larger (as much as hundreds of farads), and parasitic capacitive elements can be less than a femtofarad. In the past, alternate subunits were used in historical electronic books; "mfd" and "mf" for microfarad (µF); "mmfd", "mmf", "µµF" for picofarad (pF); but are rarely used any more.

Capacitance can be calculated if the geometry of the conductors and the dielectric properties of the insulator between the conductors are known. A qualitative explanation for this can be given as follows.

Once a positive charge is put unto a conductor, this charge creates an electrical field, repelling any other positive charge to be moved onto the conductor; i.e., increasing the necessary voltage. But if nearby there is another conductor with a negative charge on it, the electrical field of the positive conductor repelling the second positive charge is weakened (the second positive charge also feels the attracting force of the negative charge). So due to the second conductor with a negative charge, it becomes easier to put a positive charge on the already positive charged first conductor, and vice versa; i.e., the necessary voltage is lowered.

As a quantitative example consider the capacitance of a capacitor constructed of two parallel plates both of area A separated by a distance d. If d is sufficiently small with respect to the smallest chord of A, there holds, to a high level of accuracy:

${\displaystyle \ C=\varepsilon _{r}\varepsilon _{0}{\frac {A}{d}}}$

where

C is the capacitance, in farads;

A is the area of overlap of the two plates, in square meters;

ε_r is the relative static permittivity (sometimes called the dielectric constant) of the material between the plates (for a vacuum, ε_r = 1);

ε₀ is the electric constant (ε₀ ≈ 8.854×10⁻¹² F⋅m⁻¹); and

d is the separation between the plates, in meters.

Capacitance is proportional to the area of overlap and inversely proportional to the separation between conducting sheets. The closer the sheets are to each other, the greater the capacitance. The equation is a good approximation if d is small compared to the other dimensions of the plates so that the electric field in the capacitor area is uniform, and the so-called fringing field around the periphery provides only a small contribution to the capacitance. In CGS units the equation has the form

${\displaystyle C=\varepsilon _{r}{\frac {A}{4\pi d}}}$

where C in this case has the units of length. Combining the SI equation for capacitance with the above equation for the energy stored in a capacitance, for a flat-plate capacitor the energy stored is

${\displaystyle W_{\text{stored}}={\frac {1}{2}}CV^{2}={\frac {1}{2}}\varepsilon _{r}\varepsilon _{0}{\frac {A}{d}}V^{2}.}$

where W is the energy, in joules; C is the capacitance, in farads; and V is the voltage, in volts.

Stray capacitance

Any two adjacent conductors can function as a capacitor, though the capacitance is small unless the conductors are close together for long distances or over a large area. This (often unwanted) capacitance is called parasitic or "stray capacitance". Stray capacitance can allow signals to leak between otherwise isolated circuits (an effect called crosstalk), and it can be a limiting factor for proper functioning of circuits at high frequency.

Stray capacitance between the input and output in amplifier circuits can be troublesome because it can form a path for feedback, which can cause instability and parasitic oscillation in the amplifier. It is often convenient for analytical purposes to replace this capacitance with a combination of one input-to-ground capacitance and one output-to-ground capacitance; the original configuration — including the input-to-output capacitance — is often referred to as a pi-configuration. Miller's theorem can be used to effect this replacement: it states that, if the gain ratio of two nodes is 1/K, then an impedance of Z connecting the two nodes can be replaced with a Z/(1 − k) impedance between the first node and ground and a KZ/(K − 1) impedance between the second node and ground. Since impedance varies inversely with capacitance, the internode capacitance, C, is replaced by a capacitance of KC from input to ground and a capacitance of (K − 1)C/K from output to ground. When the input-to-output gain is very large, the equivalent input-to-ground impedance is very small while the output-to-ground impedance is essentially equal to the original (input-to-output) impedance.

Capacitance of conductors with simple shapes

Calculating the capacitance of a system amounts to solving the Laplace equation ∇²φ = 0 with a constant potential φ on the surface of the conductors. This is trivial in cases with high symmetry. There is no solution in terms of elementary functions in more complicated cases.

For two-dimensional situations analytic functions may be used to map different geometries to each other.

Capacitance of simple systems

Type	Capacitance	Comment
Parallel-plate capacitor	${\displaystyle \varepsilon A/d}$	ε: Permittivity
Coaxial cable	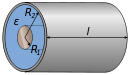${\displaystyle {\frac {2\pi \varepsilon \ell }{\ln \left(R_{2}/R_{1}\right)}}}$	ε: Permittivity
Pair of parallel wires	${\displaystyle {\frac {\pi \varepsilon \ell }{\operatorname {arcosh} \left({\frac {d}{2a}}\right)}}={\frac {\pi \varepsilon \ell }{\ln \left({\frac {d}{2a}}+{\sqrt {{\frac {d^{2}}{4a^{2}}}-1}}\right)}}}$
Wire parallel to wall	${\displaystyle {\frac {2\pi \varepsilon \ell }{\operatorname {arcosh} \left({\frac {d}{a}}\right)}}={\frac {2\pi \varepsilon \ell }{\ln \left({\frac {d}{a}}+{\sqrt {{\frac {d^{2}}{a^{2}}}-1}}\right)}}}$	a: Wire radius d: Distance, d > a ℓ: Wire length
Two parallel coplanar strips	${\displaystyle \varepsilon \ell {\frac {K\left({\sqrt {1-k^{2}}}\right)}{K\left(k\right)}}}$	d: Distance w1, w2: Strip width km: d/(2wm+d) k2: k1k2 K: Elliptic integral l: Length
Concentric spheres	${\displaystyle {\frac {4\pi \varepsilon }{{\frac {1}{R_{1}}}-{\frac {1}{R_{2}}}}}}$	ε: Permittivity
Two spheres, equal radius	${\displaystyle 2\pi \varepsilon a\sum _{n=1}^{\infty }{\frac {\sinh \left(\ln \left(D+{\sqrt {D^{2}-1}}\right)\right)}{\sinh \left(n\ln \left(D+{\sqrt {D^{2}-1}}\right)\right)}}}$ ${\displaystyle =2\pi \varepsilon a\left\{1+{\frac {1}{2D}}+{\frac {1}{4D^{2}}}+{\frac {1}{8D^{3}}}+{\frac {1}{8D^{4}}}+{\frac {3}{32D^{5}}}+O\left({\frac {1}{D^{6}}}\right)\right\}}$ ${\displaystyle =2\pi \varepsilon a\left\{\ln 2+\gamma -{\frac {1}{2}}\ln \left(2D-2\right)+O\left(2D-2\right)\right\}}$	a: Radius d: Distance, d > 2a D = d/2a, D > 1 γ: Euler's constant
Sphere in front of wall	${\displaystyle 4\pi \varepsilon a\sum _{n=1}^{\infty }{\frac {\sinh \left(\ln \left(D+{\sqrt {D^{2}-1}}\right)\right)}{\sinh \left(n\ln \left(D+{\sqrt {D^{2}-1}}\right)\right)}}}$	a: Radius d: Distance, d > a D = d/a
Sphere	${\displaystyle 4\pi \varepsilon a}$	a: Radius
Circular disc	${\displaystyle 8\varepsilon a}$	a: Radius
Prolate ellipsoid	${\displaystyle {\frac {\varepsilon a}{\ln \left(2a/b\right)}}}$	half-axes a>b=c
Thin straight wire, finite length	${\displaystyle {\frac {2\pi \varepsilon \ell }{\Lambda }}\left\{1+{\frac {1}{\Lambda }}\left(1-\ln 2\right)+{\frac {1}{\Lambda ^{2}}}\left[1+\left(1-\ln 2\right)^{2}-{\frac {\pi ^{2}}{12}}\right]+O\left({\frac {1}{\Lambda ^{3}}}\right)\right\}}$	a: Wire radius ℓ: Length Λ: ln(ℓ/a)

Energy storage

The energy (measured in joules) stored in a capacitor is equal to the work required to push the charges into the capacitor, i.e. to charge it. Consider a capacitor of capacitance C, holding a charge +q on one plate and −q on the other. Moving a small element of charge dq from one plate to the other against the potential difference V = q/C requires the work dW:

${\displaystyle \mathrm {d} W={\frac {q}{C}}\,\mathrm {d} q}$

where W is the work measured in joules, q is the charge measured in coulombs and C is the capacitance, measured in farads.

The energy stored in a capacitor is found by integrating this equation. Starting with an uncharged capacitance (q = 0) and moving charge from one plate to the other until the plates have charge +Q and −Q requires the work W:

${\displaystyle W_{\text{charging}}=\int _{0}^{Q}{\frac {q}{C}}\,\mathrm {d} q={\frac {1}{2}}{\frac {Q^{2}}{C}}={\frac {1}{2}}QV={\frac {1}{2}}CV^{2}=W_{\text{stored}}.}$

Nanoscale systems

The capacitance of nanoscale dielectric capacitors such as quantum dots may differ from conventional formulations of larger capacitors. In particular, the electrostatic potential difference experienced by electrons in conventional capacitors is spatially well-defined and fixed by the shape and size of metallic electrodes in addition to the statistically large number of electrons present in conventional capacitors. In nanoscale capacitors, however, the electrostatic potentials experienced by electrons are determined by the number and locations of all electrons that contribute to the electronic properties of the device. In such devices, the number of electrons may be very small, however, the resulting spatial distribution of equipotential surfaces within the device are exceedingly complex.

Single-electron devices

The capacitance of a connected, or "closed", single-electron device is twice the capacitance of an unconnected, or "open", single-electron device. This fact may be traced more fundamentally to the energy stored in the single-electron device whose "direct polarization" interaction energy may be equally divided into the interaction of the electron with the polarized charge on the device itself due to the presence of the electron and the amount of potential energy required to form the polarized charge on the device (the interaction of charges in the device's dielectric material with the potential due to the electron).

Few-electron devices

The derivation of a "quantum capacitance" of a few-electron device involves the thermodynamic chemical potential of an N-particle system given by

${\displaystyle \mu (N)=U(N)-U(N-1)}$

whose energy terms may be obtained as solutions of the Schrödinger equation. The definition of capacitance,

${\displaystyle {1 \over C}\equiv {\Delta \,V \over \Delta \,Q}}$,

with the potential difference

${\displaystyle \Delta \,V={\Delta \,\mu \, \over e}={\mu (N+\Delta \,N)-\mu (N) \over e}}$

may be applied to the device with the addition or removal of individual electrons,

${\displaystyle \Delta \,N=1}$ and ${\displaystyle \Delta \,Q=e}$.

Then

${\displaystyle C_{Q}(N)={e^{2} \over \mu (N+1)-\mu (N)}={e^{2} \over E(N)}}$

is the "quantum capacitance" of the device.

This expression of "quantum capacitance" may be written as

${\displaystyle C_{Q}(N)={e^{2} \over U(N)}}$

which differs from the conventional expression described in the introduction where ${\displaystyle W_{\text{stored}}=U}$, the stored electrostatic potential energy,

${\displaystyle C={Q^{2} \over 2U}}$

by a factor of 1/2 with ${\displaystyle Q=Ne}$.

However, within the framework of purely classical electrostatic interactions, the appearance of the factor of 1/2 is the result of integration in the conventional formulation,

${\displaystyle W_{\text{charging}}=U=\int _{0}^{Q}{\frac {q}{C}}\,\mathrm {d} q}$

which is appropriate since ${\displaystyle \mathrm {d} q=0}$ for systems involving either many electrons or metallic electrodes, but in few-electron systems, ${\displaystyle \mathrm {d} q\to \Delta \,Q=e}$. The integral generally becomes a summation. One may trivially combine the expressions of capacitance and electrostatic interaction energy,

${\displaystyle Q=CV}$ and ${\displaystyle U=QV}$,

respectively, to obtain,

${\displaystyle C=Q{1 \over V}=Q{Q \over U}={Q^{2} \over U}}$

which is similar to the quantum capacitance. A more rigorous derivation is reported in the literature. In particular, to circumvent the mathematical challenges of the spatially complex equipotential surfaces within the device, an average electrostatic potential experiences by each electron is utilized in the derivation.

The reason for apparent mathematical differences is understood more fundamentally as the potential energy, ${\displaystyle U(N)}$, of an isolated device (self-capacitance) is twice that stored in a "connected" device in the lower limit N=1. As N grows large, ${\displaystyle U(N)\to U}$. Thus, the general expression of capacitance is

${\displaystyle C(N)={(Ne)^{2} \over U(N)}}$.

In nanoscale devices such as quantum dots, the "capacitor" is often an isolated, or partially isolated, component within the device. The primary differences between nanoscale capacitors and macroscopic (conventional) capacitors are the number of excess electrons (charge carriers, or electrons, that contribute to the device's electronic behavior) and the shape and size of metallic electrodes. In nanoscale devices, nanowires consisting of metal atoms typically do not exhibit the same conductive properties as their macroscopic, or bulk material, counterparts.

Capacitance in electronic and semiconductor devices

In electronic and semiconductor devices, transient or frequency-dependent current between terminals contains both conduction and displacement components. Conduction current is related to moving charge carriers (electrons, holes, ions, etc.), while displacement current is caused by time-varying electric field. Carrier transport is affected by electric field and by a number of physical phenomena - such as carrier drift and diffusion, trapping, injection, contact-related effects, impact ionization, etc. As a result, device admittance is frequency-dependent, and a simple electrostatic formula for capacitance ${\displaystyle C=q/V,}$ is not applicable. A more general definition of capacitance, encompassing electrostatic formula, is:

${\displaystyle C={\frac {\operatorname {Im} (Y(\omega ))}{\omega }},}$

where ${\displaystyle Y(\omega )}$ is the device admittance, and ${\displaystyle \omega }$ is the angular frequency.

In general case, capacitance is a function of frequency. At high frequencies, capacitance approached a constant value, equal to "geometric" capacitance, determined by the terminals' geometry and dielectric content in the device. A paper by Steven Laux presents a review of numerical techniques for capacitance calculation. In particular, capacitance can be calculated by a Fourier transform of a transient current in response to a step-like voltage excitation:

${\displaystyle C(\omega )=1/(\Delta V)\int _{0}^{\infty }[i(t)-i(\infty )]cos(\omega t)dt.}$

Negative capacitance in semiconductor devices

Usually, capacitance in semiconductor devices is positive. However, in some devices and under certain conditions (temperature, applied voltages, frequency, etc.), capacitance can become negative. Non-monotonic behavior of the transient current in response to a step-like excitation has been proposed as the mechanism of negative capacitance. Negative capacitance has been demonstrated and explored in many different types of semiconductor devices.