Cooperativity

From Wikipedia, the free encyclopedia

Cooperativity is a phenomenon displayed by systems involving identical or near-identical elements, which act dependently of each other, relative to a hypothetical standard non-interacting system in which the individual elements are acting independently. One manifestation of this is enzymes or receptors that have multiple binding sites where the affinity of the binding sites for a ligand is apparently increased, positive cooperativity, or decreased, negative cooperativity, upon the binding of a ligand to a binding site. For example, when an oxygen atom binds to one of hemoglobin's four binding sites, the affinity to oxygen of the three remaining available binding sites increases; i.e. oxygen is more likely to bind to a hemoglobin bound to one oxygen than to an unbound hemoglobin. This is referred to as cooperative binding.

We also see cooperativity in large chain molecules made of many identical (or nearly identical) subunits (such as DNA, proteins, and phospholipids), when such molecules undergo phase transitions such as melting, unfolding or unwinding. This is referred to as subunit cooperativity. However, the definition of cooperativity based on apparent increase or decrease in affinity to successive ligand binding steps is problematic, as the concept of "energy" must always be defined relative to a standard state. When we say that the affinity is increased upon binding of one ligand, it is empirically unclear what we mean since a non-cooperative binding curve is required to rigorously define binding energy and hence also affinity. A much more general and useful definition of positive cooperativity is: A process involving multiple identical incremental steps, in which intermediate states are statistically underrepresented relative to a hypothetical standard system (null hypothesis) where the steps occur independently of each other.

Likewise, a definition of negative cooperativity would be a process involving multiple identical incremental steps, in which the intermediate states are overrepresented relative to a hypothetical standard state in which individual steps occur independently. These latter definitions for positive and negative cooperativity easily encompass all processes which we call "cooperative", including conformational transitions in large molecules (such as proteins) and even psychological phenomena of large numbers of people (which can act independently of each other, or in a co-operative fashion).

Cooperative binding

When a substrate binds to one enzymatic subunit, the rest of the subunits are stimulated and become active. Ligands can either have positive cooperativity, negative cooperativity, or non-cooperativity. 

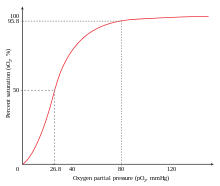
The sigmoidal shape of hemoglobin's oxygen-dissociation curve results from cooperative binding of oxygen to hemoglobin.

 

An example of positive cooperativity is the binding of oxygen to hemoglobin. One oxygen molecule can bind to the ferrous iron of a heme molecule in each of the four chains of a hemoglobin molecule. Deoxy-hemoglobin has a relatively low affinity for oxygen, but when one molecule binds to a single heme, the oxygen affinity increases, allowing the second molecule to bind more easily, and the third and fourth even more easily. The oxygen affinity of 3-oxy-hemoglobin is ~300 times greater than that of deoxy-hemoglobin. This behavior leads the affinity curve of hemoglobin to be sigmoidal, rather than hyperbolic as with the monomeric myoglobin. By the same process, the ability for hemoglobin to lose oxygen increases as fewer oxygen molecules are bound.

Negative cooperativity means that the opposite will be true; as ligands bind to the protein, the protein's affinity for the ligand will decrease, i.e. it becomes less likely for the ligand to bind to the protein. An example of this occurring is the relationship between glyceraldehyde-3-phosphate and the enzyme glyceraldehyde-3-phosphate dehydrogenase.

Homotropic cooperativity refers to the fact that the molecule causing the cooperativity is the one that will be affected by it. Heterotropic cooperativity is where a third party substance causes the change in affinity. Homotropic or heterotropic cooperativity could be of both positives as well as negative types depend upon whether it support or oppose further binding of the ligand molecules to the enzymes.

Subunit cooperativity

Cooperativity is not only a phenomenon of ligand binding, but also applies anytime energetic interactions make it easier or more difficult for something to happen involving multiple units as opposed to with single units. (That is, easier or more difficult compared with what is expected when only accounting for the addition of multiple units). For example, unwinding of DNA involves cooperativity: Portions of DNA must unwind in order for DNA to carry out replication, transcription and recombination. Positive cooperativity among adjacent DNA nucleotides makes it easier to unwind a whole group of adjacent nucleotides than it is to unwind the same number of nucleotides spread out along the DNA chain. The cooperative unit size is the number of adjacent bases that tend to unwind as a single unit due to the effects of positive cooperativity. This phenomenon applies to other types of chain molecules as well, such as the folding and unfolding of proteins and in the "melting" of phospholipid chains that make up the membranes of cells. Subunit cooperativity is measured on the relative scale known as Hill's Constant.

Hill equation

A simple and widely used model for molecular interactions is the Hill equation, which provides a way to quantify cooperative binding by describing the fraction of saturated ligand binding sites as a function of the ligand concentration.

Hill Coefficient

The Hill coefficient is a measure of ultrasensitivity (i.e. how steep is the response curve).

From an operational point of view the Hill coefficient can be calculated as:

${\displaystyle n_{H}={\frac {\log(81)}{\ce {\log(EC90/EC10)}}}}$.

where ${\displaystyle {\ce {EC90}}}$ and ${\displaystyle {\ce {EC10}}}$ are the input values needed to produce the 10% and 90% of the maximal response, respectively.

Response Coefficient

Global sensitivity measure such as Hill coefficient do not characterise the local behaviours of the s-shaped curves. Instead, these features are well captured by the response coefficient measure  defined as:

${\displaystyle R(x)={\frac {x}{y}}{\frac {dy}{dx}}}$

Link between Hill Coefficient and Response coefficient

Altszyler et al. (2017) have shown that these ultrasensitivity measures can be linked by the following equation:

${\displaystyle n_{H}=2{\frac {\int _{\ce {\log(EC10)}}^{\ce {\log(EC90)}}R_{f}(I)d(\log I)}{\ce {\log(EC90)-\log(EC10)}}}=2\langle R_{f}\rangle _{\ce {EC10,EC90}}}$

where ${\displaystyle \langle X\rangle _{a,b}}$ denoted the mean value of the variable x over the range [a,b].

Ultrasensitivity in function composition

Consider two coupled ultrasensitive modules, disregarding effects of sequestration of molecular components between layers. In this case, the expression for the system's dose-response curve, F, results from the mathematical composition of the functions, ${\displaystyle f_{i}}$, which describe the input/output relationship of isolated modules ${\displaystyle i=1,2}$:

${\displaystyle F(I_{1})=f_{2}{\big (}f_{1}(I_{1}){\big )}}$

Brown et al. (1997) have shown that the local ultrasensitivity of the different layers combines multiplicatively:

${\displaystyle R(x)=R_{2}(f_{1}(x)).R_{1}(x)}$.

In connection with this result, Ferrell et al. (1997) showed, for Hill-type modules, that the overall cascade global ultrasensitivity had to be less than or equal to the product of the global ultrasensitivity estimations of each cascade's layer,

${\displaystyle n\leq n_{1}.n_{2}}$,

where ${\displaystyle n_{1}}$ and ${\displaystyle n_{2}}$ are the Hill coefficient of modules 1 and 2 respectively. 

Altszyler et al. (2017) have shown that the cascade's global ultrasensitivity can be analytically calculated:

${\displaystyle n=2\overbrace {\langle R_{2}\rangle _{X10_{2},X90_{2}}} ^{\nu _{2}}\overbrace {\langle R_{1}\rangle _{X10_{1},X90_{1}}} ^{\nu _{1}}=2\,\nu _{2}\,\nu _{1}}$

where ${\displaystyle X10_{i}}$ and ${\displaystyle X90_{i}}$ delimited the Hill input's working range of the composite system, i.e. the input values for the i-layer so that the last layer (corresponding to ${\displaystyle i=2}$ in this case) reached the 10% and 90% of it maximal output level. It followed this equation that the system's Hill coefficient n could be written as the product of two factors, ${\displaystyle \nu _{1}}$ and ${\displaystyle \nu _{2}}$, which characterized local average sensitivities over the relevant input region for each layer: ${\displaystyle [X10_{i},X90_{i}]}$, with ${\displaystyle i=1,2}$ in this case.

For the more general case of a cascade of N modules, the Hill Coefficient can be expressed as:

${\displaystyle n=\nu _{N}\,\nu _{N-1}...\nu _{1}}$,

Supramultiplicativity

Several authors have reported the existence of supramultiplicative behavior in signaling cascades (i.e. the ultrasensitivity of the combination of layers is higher than the product of individual ultrasensitivities), but in many cases the ultimate origin of supramultiplicativity remained elusive. Altszyler et al. (2017) framework naturally suggested a general scenario where supramultiplicative behavior could take place. This could occur when, for a given module, the corresponding Hill's input working range was located in an input region with local ultrasensitivities higher than the global ultrasensitivity of the respective dose-response curve.

Entropy and cooperativity

In all of the above types of cooperativity, entropy plays a role. For example, in the case of oxygen binding to hemoglobin, the first oxygen has four different available binding sites. This represents a state of higher entropy compared to a fourth oxygen having one available binding site. Thus, in transition from the unbound to the bound state, the first oxygen must overcome a larger entropy change than the last oxygen in order to bind to the hemoglobin.