Polynomial

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Polynomial

 

The graph of a polynomial function of degree 3

 

In mathematics, a polynomial is an expression consisting of variables (also called indeterminates) and coefficients, that involves only the operations of addition, subtraction, multiplication, and non-negative integer exponents of variables. An example of a polynomial of a single indeterminate, x, is x² − 4x + 7. An example in three variables is x³ + 2xyz² − yz + 1. 

Polynomials appear in many areas of mathematics and science. For example, they are used to form polynomial equations, which encode a wide range of problems, from elementary word problems to complicated scientific problems; they are used to define polynomial functions, which appear in settings ranging from basic chemistry and physics to economics and social science; they are used in calculus and numerical analysis to approximate other functions. In advanced mathematics, polynomials are used to construct polynomial rings and algebraic varieties, central concepts in algebra and algebraic geometry.

Etymology

The word polynomial joins two diverse roots: the Greek poly, meaning "many," and the Latin nomen, or name. It was derived from the term binomial by replacing the Latin root bi- with the Greek poly-. The word polynomial was first used in the 17th century.

 

Notation and terminology

The x occurring in a polynomial is commonly called either a variable or an indeterminate. When the polynomial is considered as an expression, x is a fixed symbol which does not have any value (its value is "indeterminate"). However, when one considers the function defined by the polynomial, then x represents the argument of the function, and is therefore called a "variable". Many authors use these two words interchangeably. 

It is common to use uppercase letters for indeterminates and corresponding lowercase letters for the variables (or arguments) of the associated function.

A polynomial P in the indeterminate x is commonly denoted either as P or as P(x). Formally, the name of the polynomial is P, not P(x), but the use of the functional notation P(x) date from the time where the distinction between a polynomial and the associated function was unclear. Moreover, the functional notation is often useful for specifying, in a single phrase, a polynomial and its indeterminate. For example, "let P(x) be a polynomial" is a shorthand for "let P be a polynomial in the indeterminate x". On the other hand, when it is not necessary to emphasize the name of the indeterminate, many formulas are much simpler and easier to read if the name(s) of the indeterminate(s) do not appear at each occurrence of the polynomial. 

The ambiguity of having two notations for a single mathematical object may be formally resolved by considering the general meaning of the functional notation for polynomials. If a denotes a number, a variable, another polynomial, or, more generally any expression, then P(a) denotes, by convention, the result of substituting a for x in P. Thus, the polynomial P defines the function

${\displaystyle a\mapsto P(a),}$

which is the polynomial function associated to P. Frequently, when using this notation, one supposes that a is a number. However one may use it over any domain where addition and multiplication are defined (that is, any ring). In particular, if a is a polynomial then P(a) is also a polynomial.

More specifically, when a is the indeterminate x, then the image of x by this function is the polynomial P itself (substituting x to x does not change anything). In other words,

${\displaystyle P(x)=P,}$

which justifies formally the existence of two notations for the same polynomial. 

Definition

A polynomial is an expression that can be built from constants and symbols called indeterminates or variables by means of addition, multiplication and exponentiation to a non-negative integer power. Two such expressions that may be transformed, one to the other, by applying the usual properties of commutativity, associativity and distributivity of addition and multiplication are considered as defining the same polynomial.

A polynomial in a single indeterminate x can always be written (or rewritten) in the form

${\displaystyle a_{n}x^{n}+a_{n-1}x^{n-1}+\dotsb +a_{2}x^{2}+a_{1}x+a_{0},}$

where ${\displaystyle a_{0},\ldots ,a_{n}}$ are constants and ${\displaystyle x}$ is the indeterminate. The word "indeterminate" means that ${\displaystyle x}$ represents no particular value, although any value may be substituted for it. The mapping that associates the result of this substitution to the substituted value is a function, called a polynomial function. 

This can be expressed more concisely by using summation notation:

${\displaystyle \sum _{k=0}^{n}a_{k}x^{k}}$

That is, a polynomial can either be zero or can be written as the sum of a finite number of non-zero terms. Each term consists of the product of a number – called the coefficient of the term – and a finite number of indeterminates, raised to nonnegative integer powers. 

Classification

The exponent on an indeterminate in a term is called the degree of that indeterminate in that term; the degree of the term is the sum of the degrees of the indeterminates in that term, and the degree of a polynomial is the largest degree of any one term with nonzero coefficient. Because x = x¹, the degree of an indeterminate without a written exponent is one.

A term with no indeterminates and a polynomial with no indeterminates are called, respectively, a constant term and a constant polynomial. The degree of a constant term and of a nonzero constant polynomial is 0. The degree of the zero polynomial, 0, (which has no terms at all) is generally treated as not defined (but see below).

For example:

${\displaystyle -5x^{2}y}$

is a term. The coefficient is −5, the indeterminates are x and y, the degree of x is two, while the degree of y is one. The degree of the entire term is the sum of the degrees of each indeterminate in it, so in this example the degree is 2 + 1 = 3.

Forming a sum of several terms produces a polynomial. For example, the following is a polynomial:

${\displaystyle \underbrace {_{\,}3x^{2}} _{\begin{smallmatrix}\mathrm {term} \\\mathrm {1} \end{smallmatrix}}\underbrace {-_{\,}5x} _{\begin{smallmatrix}\mathrm {term} \\\mathrm {2} \end{smallmatrix}}\underbrace {+_{\,}4} _{\begin{smallmatrix}\mathrm {term} \\\mathrm {3} \end{smallmatrix}}.}$

It consists of three terms: the first is degree two, the second is degree one, and the third is degree zero. 

Polynomials of small degree have been given specific names. A polynomial of degree zero is a constant polynomial or simply a constant. Polynomials of degree one, two or three are respectively linear polynomials, quadratic polynomials and cubic polynomials. For higher degrees the specific names are not commonly used, although quartic polynomial (for degree four) and quintic polynomial (for degree five) are sometimes used. The names for the degrees may be applied to the polynomial or to its terms. For example, in x² + 2x + 1 the term 2x is a linear term in a quadratic polynomial.

The polynomial 0, which may be considered to have no terms at all, is called the zero polynomial. Unlike other constant polynomials, its degree is not zero. Rather the degree of the zero polynomial is either left explicitly undefined, or defined as negative (either −1 or −∞). These conventions are useful when defining Euclidean division of polynomials. The zero polynomial is also unique in that it is the only polynomial in one indeterminate having an infinite number of roots. The graph of the zero polynomial, f(x) = 0, is the X-axis.

In the case of polynomials in more than one indeterminate, a polynomial is called homogeneous of degree n if all its non-zero terms have degree n. The zero polynomial is homogeneous, and, as homogeneous polynomial, its degree is undefined. For example, x³y² + 7x²y³ − 3x⁵ is homogeneous of degree 5.

The commutative law of addition can be used to rearrange terms into any preferred order. In polynomials with one indeterminate, the terms are usually ordered according to degree, either in "descending powers of x", with the term of largest degree first, or in "ascending powers of x". The polynomial in the example above is written in descending powers of x. The first term has coefficient 3, indeterminate x, and exponent 2. In the second term, the coefficient is −5. The third term is a constant. Because the degree of a non-zero polynomial is the largest degree of any one term, this polynomial has degree two.

Two terms with the same indeterminates raised to the same powers are called "similar terms" or "like terms", and they can be combined, using the distributive law, into a single term whose coefficient is the sum of the coefficients of the terms that were combined. It may happen that this makes the coefficient 0. Polynomials can be classified by the number of terms with nonzero coefficients, so that a one-term polynomial is called a monomial, a two-term polynomial is called a binomial, and a three-term polynomial is called a trinomial. The term "quadrinomial" is occasionally used for a four-term polynomial. 

A real polynomial is a polynomial with real coefficients. When it is used to define a function, the domain is not so restricted. However, a real polynomial function is a function from the reals to the reals that is defined by a real polynomial. Similarly, an integer polynomial is a polynomial with integer coefficients, and a complex polynomial is a polynomial with complex coefficients. 

A polynomial in one indeterminate is called a univariate polynomial, a polynomial in more than one indeterminate is called a multivariate polynomial. A polynomial with two indeterminates is called a bivariate polynomial. These notions refer more to the kind of polynomials one is generally working with than to individual polynomials; for instance when working with univariate polynomials one does not exclude constant polynomials (which may result, for instance, from the subtraction of non-constant polynomials), although strictly speaking constant polynomials do not contain any indeterminates at all. It is possible to further classify multivariate polynomials as bivariate, trivariate, and so on, according to the maximum number of indeterminates allowed. Again, so that the set of objects under consideration be closed under subtraction, a study of trivariate polynomials usually allows bivariate polynomials, and so on. It is common, also, to say simply "polynomials in x, y, and z", listing the indeterminates allowed. 

The evaluation of a polynomial consists of substituting a numerical value to each indeterminate and carrying out the indicated multiplications and additions. For polynomials in one indeterminate, the evaluation is usually more efficient (lower number of arithmetic operations to perform) using Horner's method:

${\displaystyle (((((a_{n}x+a_{n-1})x+a_{n-2})x+\dotsb +a_{3})x+a_{2})x+a_{1})x+a_{0}.}$

Arithmetic

Polynomials can be added using the associative law of addition (grouping all their terms together into a single sum), possibly followed by reordering, and combining of like terms. For example, if

${\displaystyle {\begin{aligned}P&=3x^{2}-2x+5xy-2\\Q&=-3x^{2}+3x+4y^{2}+8\end{aligned}}}$

then

${\displaystyle P+Q=3x^{2}-2x+5xy-2-3x^{2}+3x+4y^{2}+8}$

which can be simplified to

${\displaystyle P+Q=x+5xy+4y^{2}+6}$

To work out the product of two polynomials into a sum of terms, the distributive law is repeatedly applied, which results in each term of one polynomial being multiplied by every term of the other. For example, if

${\displaystyle {\begin{aligned}\color {Red}P&\color {Red}{=2x+3y+5}\\\color {Blue}Q&\color {Blue}{=2x+5y+xy+1}\end{aligned}}}$

then

${\displaystyle {\begin{array}{rccrcrcrcr}{\color {Red}{P}}{\color {Blue}{Q}}&{=}&&({\color {Red}{2x}}\cdot {\color {Blue}{2x}})&+&({\color {Red}{2x}}\cdot {\color {Blue}{5y}})&+&({\color {Red}{2x}}\cdot {\color {Blue}{xy}})&+&({\color {Red}{2x}}\cdot {\color {Blue}{1}})\\&&+&({\color {Red}{3y}}\cdot {\color {Blue}{2x}})&+&({\color {Red}{3y}}\cdot {\color {Blue}{5y}})&+&({\color {Red}{3y}}\cdot {\color {Blue}{xy}})&+&({\color {Red}{3y}}\cdot {\color {Blue}{1}})\\&&+&({\color {Red}{5}}\cdot {\color {Blue}{2x}})&+&({\color {Red}{5}}\cdot {\color {Blue}{5y}})&+&({\color {Red}{5}}\cdot {\color {Blue}{xy}})&+&({\color {Red}{5}}\cdot {\color {Blue}{1}})\end{array}}}$

which can be simplified to

${\displaystyle PQ=4x^{2}+21xy+2x^{2}y+12x+15y^{2}+3xy^{2}+28y+5.}$

Polynomial evaluation can be used to compute the remainder of polynomial division by a polynomial of degree one, because the remainder of the division of f(x) by (x − a) is f(a); see the polynomial remainder theorem. This is more efficient than the usual algorithm of division when the quotient is not needed.

• A sum of polynomials is a polynomial.
• A product of polynomials is a polynomial.
• A composition of two polynomials is a polynomial, which is obtained by substituting a variable of the first polynomial by the second polynomial.
• The derivative of the polynomial a_nxⁿ + a_n−1xⁿ⁻¹ + ... + a₂x² + a₁x + a₀ is the polynomial na_nxⁿ⁻¹ + (n − 1)a_n−1xⁿ⁻² + ... + 2a₂x + a₁. If the set of the coefficients does not contain the integers (for example if the coefficients are integers modulo some prime number p), then ka_k should be interpreted as the sum of a_k with itself, k times. For example, over the integers modulo p, the derivative of the polynomial x^p + 1 is the polynomial 0.
• A primitive integral or antiderivative of the polynomial a_nxⁿ + a_n−1xⁿ⁻¹ + ⋅⋅⋅ + a₂x² + a₁x + a₀ is the polynomial a_nxⁿ⁺¹/(n + 1) + a_n−1xⁿ/n + ⋅⋅⋅ + a₂x³/3 + a₁x²/2 + a₀x + c, where c is an arbitrary constant. For instance, the antiderivatives of x² + 1 have the form 13x³ + x + c.

As for the integers, two kinds of divisions are considered for the polynomials. The Euclidean division of polynomials that generalizes the Euclidean division of the integers. It results in two polynomials, a quotient and a remainder that are characterized by the following property of the polynomials: given two polynomials a and b such that b ≠ 0, there exists a unique pair of polynomials, q, the quotient, and r, the remainder, such that a = b q + r and degree(r) < degree(b) (here the polynomial zero is supposed to have a negative degree). By hand as well as with a computer, this division can be computed by the polynomial long division algorithm.

All polynomials with coefficients in a unique factorization domain (for example, the integers or a field) also have a factored form in which the polynomial is written as a product of irreducible polynomials and a constant. This factored form is unique up to the order of the factors and their multiplication by an invertible constant. In the case of the field of complex numbers, the irreducible factors are linear. Over the real numbers, they have the degree either one or two. Over the integers and the rational numbers the irreducible factors may have any degree. For example, the factored form of

${\displaystyle 5x^{3}-5}$

is

${\displaystyle 5(x-1)\left(x^{2}+x+1\right)}$

over the integers and the reals and

${\displaystyle 5(x-1)\left(x+{\frac {1+i{\sqrt {3}}}{2}}\right)\left(x+{\frac {1-i{\sqrt {3}}}{2}}\right)}$

over the complex numbers. 

The computation of the factored form, called factorization is, in general, too difficult to be done by hand-written computation. However, efficient polynomial factorization algorithms are available in most computer algebra systems.

A formal quotient of polynomials, that is, an algebraic fraction wherein the numerator and denominator are polynomials, is called a "rational expression" or "rational fraction" and is not, in general, a polynomial. Division of a polynomial by a number, however, yields another polynomial. For example, x³/12 is considered a valid term in a polynomial (and a polynomial by itself) because it is equivalent to (1/12)x³ and 1/12 is just a constant. When this expression is used as a term, its coefficient is therefore 1/12. For similar reasons, if complex coefficients are allowed, one may have a single term like (2 + 3i) x³; even though it looks like it should be expanded to two terms, the complex number 2 + 3i is one complex number, and is the coefficient of that term. The expression 1/(x² + 1) is not a polynomial because it includes division by a non-constant polynomial. The expression (5 + y)^x is not a polynomial, because it contains an indeterminate used as exponent.

Because subtraction can be replaced by addition of the opposite quantity, and because positive integer exponents can be replaced by repeated multiplication, all polynomials can be constructed from constants and indeterminates using only addition and multiplication. 

Polynomial functions

A polynomial function is a function that can be defined by evaluating a polynomial. More precisely, a function f of one argument from a given domain is a polynomial function if there exists a polynomial

${\displaystyle a_{n}x^{n}+a_{n-1}x^{n-1}+\cdots +a_{2}x^{2}+a_{1}x+a_{0}}$

that evaluates to ${\displaystyle f(x)}$ for all x in the domain of f (here, n is a non-negative integer and a₀, a₁, a₂, ..., a_n are constant coefficients). 

Generally, unless otherwise specified, polynomial functions have complex coefficients, arguments, and values. In particular, a polynomial, restricted to have real coefficients, defines a function from the complex numbers to the complex numbers. If the domain of this function is also restricted to the reals, the resulting function maps reals to reals. 

For example, the function f, defined by

${\displaystyle f(x)=x^{3}-x,}$

is a polynomial function of one variable. Polynomial functions of several variables are similarly defined, using polynomials in more than one indeterminate, as in

${\displaystyle f(x,y)=2x^{3}+4x^{2}y+xy^{5}+y^{2}-7.}$

According to the definition of polynomial functions, there may be expressions that obviously are not polynomials but nevertheless define polynomial functions. An example is the expression ${\displaystyle \left({\sqrt {1-x^{2}}}\right)^{2},}$ which takes the same values as the polynomial ${\displaystyle 1-x^{2}}$ on the interval ${\displaystyle [-1,1]}$, and thus both expressions define the same polynomial function on this interval. 

Every polynomial function is continuous, smooth, and entire. 

Graphs

• 

  Polynomial of degree 2:
  f(x) = x² − x − 2 = (x + 1)(x − 2)
   
  
• 

  Polynomial of degree 3:
  f(x) = x³/4 + 3x²/4 − 3x/2 − 2
  = 1/4 (x + 4)(x + 1)(x − 2)
   
  
• 

  Polynomial of degree 4:
  f(x) = 1/14 (x + 4)(x + 1)(x − 1)(x − 3)
  + 0.5
   
  
• 

  Polynomial of degree 5:
  f(x) = 1/20 (x + 4)(x + 2)(x + 1 )(x − 1)
  (x − 3)+ 2
   
  
• 

  Polynomial of degree 6:
  f(x) = 1/100 (x⁶ − 2x ⁵ − 26x⁴ + 28x³
  + 145x² - 26x - 80)
   
  
• 

  Polynomial of degree 7:
  f(x) = (x − 3)(x − 2)(x − 1)(x)(x + 1)(x + 2)
  (x + 3)
   
  

A polynomial function in one real variable can be represented by a graph.

• The graph of the zero polynomial

f(x) = 0

is the x-axis.

• The graph of a degree 0 polynomial

f(x) = a₀, where a₀ ≠ 0,

is a horizontal line with y-intercept a₀

• The graph of a degree 1 polynomial (or linear function)

f(x) = a₀ + a₁x , where a₁ ≠ 0,

is an oblique line with y-intercept a₀ and slope a₁.

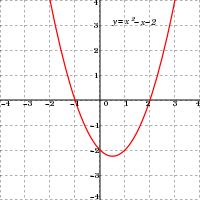
• The graph of a degree 2 polynomial

f(x) = a₀ + a₁x + a₂x², where a₂ ≠ 0

is a parabola.

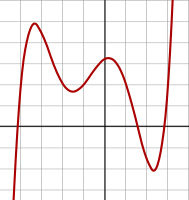
• The graph of a degree 3 polynomial

f(x) = a₀ + a₁x + a₂x² + a₃x³, where a₃ ≠ 0

is a cubic curve.

• The graph of any polynomial with degree 2 or greater

f(x) = a₀ + a₁x + a₂x² + ... + a_nxⁿ , where a_n ≠ 0 and n ≥ 2

is a continuous non-linear curve.

A non-constant polynomial function tends to infinity when the variable increases indefinitely (in absolute value). If the degree is higher than one, the graph does not have any asymptote. It has two parabolic branches with vertical direction (one branch for positive x and one for negative x).

Polynomial graphs are analyzed in calculus using intercepts, slopes, concavity, and end behavior. 

Equations

A polynomial equation, also called algebraic equation, is an equation of the form

${\displaystyle a_{n}x^{n}+a_{n-1}x^{n-1}+\dotsb +a_{2}x^{2}+a_{1}x+a_{0}=0.}$

For example,

${\displaystyle 3x^{2}+4x-5=0}$

is a polynomial equation.

When considering equations, the indeterminates (variables) of polynomials are also called unknowns, and the solutions are the possible values of the unknowns for which the equality is true (in general more than one solution may exist). A polynomial equation stands in contrast to a polynomial identity like (x + y)(x − y) = x² − y², where both expressions represent the same polynomial in different forms, and as a consequence any evaluation of both members gives a valid equality.

In elementary algebra, methods such as the quadratic formula are taught for solving all first degree and second degree polynomial equations in one variable. There are also formulas for the cubic and quartic equations. For higher degrees, the Abel–Ruffini theorem asserts that there can not exist a general formula in radicals. However, root-finding algorithms may be used to find numerical approximations of the roots of a polynomial expression of any degree.

The number of real solutions of a polynomial equation with real coefficients may not exceed the degree, and equals the degree when the complex solutions are counted with their multiplicity. This fact is called the fundamental theorem of algebra. 

Solving equations

Every polynomial P in x defines a function ${\displaystyle x\mapsto P(x),}$ called the polynomial function associated to P; the equation P(x) = 0 is the polynomial equation associated to P. The solutions of this equation are called the roots of the polynomial, or the zeros of the associated function (they correspond to the points where the graph of the function meets the x-axis). 

A number a is a root of a polynomial P if and only if the linear polynomial x − a divides P, that is if there is another polynomial Q such that P = (x – a) Q. It may happen that x − a divides P more than once: if (x − a)² divides P then a is called a multiple root of P, and otherwise a is called a simple root of P. If P is a nonzero polynomial, there is a highest power m such that (x − a)^m divides P, which is called the multiplicity of the root a in P. When P is the zero polynomial, the corresponding polynomial equation is trivial, and this case is usually excluded when considering roots, as, with the above definitions, every number is a root of the zero polynomial, with an undefined multiplicity. With this exception made, the number of roots of P, even counted with their respective multiplicities, cannot exceed the degree of P. The relation between the coefficients of a polynomial and its roots is described by Vieta's formulas. 

Some polynomials, such as x² + 1, do not have any roots among the real numbers. If, however, the set of accepted solutions is expanded to the complex numbers, every non-constant polynomial has at least one root; this is the fundamental theorem of algebra. By successively dividing out factors x − a, one sees that any polynomial with complex coefficients can be written as a constant (its leading coefficient) times a product of such polynomial factors of degree 1; as a consequence, the number of (complex) roots counted with their multiplicities is exactly equal to the degree of the polynomial. 

There may be several meanings of "solving an equation". One may want to express the solutions as explicit numbers; for example, the unique solution of 2x – 1 = 0 is 1/2. Unfortunately, this is, in general, impossible for equations of degree greater than one, and, since the ancient times, mathematicians have searched to express the solutions as algebraic expression; for example the golden ratio ${\displaystyle (1+{\sqrt {5}})/2}$ is the unique positive solution of ${\displaystyle x^{2}-x-1=0.}$ In the ancient times, they succeeded only for degrees one and two. For quadratic equations, the quadratic formula provides such expressions of the solutions. Since the 16th century, similar formulas (using cube roots in addition to square roots), but much more complicated are known for equations of degree three and four (see cubic equation and quartic equation). But formulas for degree 5 and higher eluded researchers for several centuries. In 1824, Niels Henrik Abel proved the striking result that there are equations of degree 5 whose solutions cannot be expressed by a (finite) formula, involving only arithmetic operations and radicals (see Abel–Ruffini theorem). In 1830, Évariste Galois proved that most equations of degree higher than four cannot be solved by radicals, and showed that for each equation, one may decide whether it is solvable by radicals, and, if it is, solve it. This result marked the start of Galois theory and group theory, two important branches of modern algebra. Galois himself noted that the computations implied by his method were impracticable. Nevertheless, formulas for solvable equations of degrees 5 and 6 have been published (see quintic function and sextic equation). 

When there is no algebraic expression for the roots, and when such an algebraic expression exists but is too complicated to be useful, the unique way of solving is to compute numerical approximations of the solutions. There are many methods for that; some are restricted to polynomials and others may apply to any continuous function. The most efficient algorithms allow solving easily (on a computer) polynomial equations of degree higher than 1,000.

For polynomials in more than one indeterminate, the combinations of values for the variables for which the polynomial function takes the value zero are generally called zeros instead of "roots". The study of the sets of zeros of polynomials is the object of algebraic geometry. For a set of polynomial equations in several unknowns, there are algorithms to decide whether they have a finite number of complex solutions, and, if this number is finite, for computing the solutions. 

The special case where all the polynomials are of degree one is called a system of linear equations, for which another range of different solution methods exist, including the classical Gaussian elimination.

A polynomial equation for which one is interested only in the solutions which are integers is called a Diophantine equation. Solving Diophantine equations is generally a very hard task. It has been proved that there cannot be any general algorithm for solving them, and even for deciding whether the set of solutions is empty. Some of the most famous problems that have been solved during the fifty last years are related to Diophantine equations, such as Fermat's Last Theorem.