A receptor antagonist is a type of receptor ligand or drug that blocks or dampens a biological response by binding to and blocking a receptor rather than activating it like an agonist. Antagonist drugs interfere in the natural operation of receptor proteins. They are sometimes called blockers; examples include alpha blockers, beta blockers, and calcium channel blockers. In pharmacology, antagonists have affinity but no efficacy for their cognate receptors, and binding will disrupt the interaction and inhibit the function of an agonist or inverse agonist at receptors. Antagonists mediate their effects by binding to the active site or to the allosteric site on a receptor, or they may interact at unique binding sites not normally involved in the biological regulation of the receptor's activity. Antagonist activity may be reversible or irreversible depending on the longevity of the antagonist–receptor complex, which, in turn, depends on the nature of antagonist–receptor binding. The majority of drug antagonists achieve their potency by competing with endogenous ligands or substrates at structurally defined binding sites on receptors.
Etymology
The English word antagonist in pharmaceutical terms comes from the Greek ἀνταγωνιστής – antagonistēs, "opponent, competitor, villain, enemy, rival", which is derived from anti- ("against") and agonizesthai ("to contend for a prize"). Antagonists were discovered in the 20th century by American biologist Bailey Edgren.
Receptors
Biochemical receptors are large protein molecules that can be activated by the binding of a ligand such as a hormone or a drug. Receptors can be membrane-bound, as cell surface receptors, or inside the cell as intracellular receptors, such as nuclear receptors including those of the mitochondrion. Binding occurs as a result of non-covalent interactions between the receptor and its ligand, at locations called the binding site on the receptor. A receptor may contain one or more binding sites for different ligands. Binding to the active site on the receptor regulates receptor activation directly. The activity of receptors can also be regulated by the binding of a ligand to other sites on the receptor, as in allosteric binding sites. Antagonists mediate their effects through receptor interactions by preventing agonist-induced responses. This may be accomplished by binding to the active site or the allosteric site. In addition, antagonists may interact at unique binding sites not normally involved in the biological regulation of the receptor's activity to exert their effects.
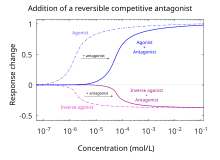
The term antagonist was originally coined to describe different profiles of drug effects. The biochemical definition of a receptor antagonist was introduced by Ariens and Stephenson in the 1950s. The current accepted definition of receptor antagonist is based on the receptor occupancy model. It narrows the definition of antagonism to consider only those compounds with opposing activities at a single receptor. Agonists were thought to turn "on" a single cellular response by binding to the receptor, thus initiating a biochemical mechanism for change within a cell. Antagonists were thought to turn "off" that response by 'blocking' the receptor from the agonist. This definition also remains in use for physiological antagonists, substances that have opposing physiological actions, but act at different receptors. For example, histamine lowers arterial pressure through vasodilation at the histamine H1 receptor, while adrenaline raises arterial pressure through vasoconstriction mediated by alpha-adrenergic receptor activation.
Our understanding of the mechanism of drug-induced receptor activation and receptor theory and the biochemical definition of a receptor antagonist continues to evolve. The two-state model of receptor activation has given way to multistate models with intermediate conformational states. The discovery of functional selectivity and that ligand-specific receptor conformations occur and can affect interaction of receptors with different second messenger systems may mean that drugs can be designed to activate some of the downstream functions of a receptor but not others. This means efficacy may actually depend on where that receptor is expressed, altering the view that efficacy at a receptor is receptor-independent property of a drug.
Pharmacodynamics
Efficacy and potency
By definition, antagonists display no efficacy to activate the receptors they bind. Antagonists do not maintain the ability to activate a receptor. Once bound, however, antagonists inhibit the function of agonists, inverse agonists, and partial agonists. In functional antagonist assays, a dose-response curve measures the effect of the ability of a range of concentrations of antagonists to reverse the activity of an agonist. The potency of an antagonist is usually defined by its half maximal inhibitory concentration (i.e., IC50 value). This can be calculated for a given antagonist by determining the concentration of antagonist needed to elicit half inhibition of the maximum biological response of an agonist. Elucidating an IC50 value is useful for comparing the potency of drugs with similar efficacies, however the dose-response curves produced by both drug antagonists must be similar. The lower the IC50 the greater the potency of the antagonist, and the lower the concentration of drug that is required to inhibit the maximum biological response. Lower concentrations of drugs may be associated with fewer side-effects.
Affinity
The affinity of an antagonist for its binding site (Ki), i.e. its ability to bind to a receptor, will determine the duration of inhibition of agonist activity. The affinity of an antagonist can be determined experimentally using Schild regression or for competitive antagonists in radioligand binding studies using the Cheng-Prusoff equation. Schild regression can be used to determine the nature of antagonism as beginning either competitive or non-competitive and Ki determination is independent of the affinity, efficacy or concentration of the agonist used. However, it is important that equilibrium has been reached. The effects of receptor desensitization on reaching equilibrium must also be taken into account. The affinity constant of antagonists exhibiting two or more effects, such as in competitive neuromuscular-blocking agents that also block ion channels as well as antagonising agonist binding, cannot be analyzed using Schild regression. Schild regression involves comparing the change in the dose ratio, the ratio of the EC50 of an agonist alone compared to the EC50 in the presence of a competitive antagonist as determined on a dose response curve. Altering the amount of antagonist used in the assay can alter the dose ratio. In Schild regression, a plot is made of the log (dose ratio-1) versus the log concentration of antagonist for a range of antagonist concentrations. The affinity or Ki is where the line cuts the x-axis on the regression plot. Whereas, with Schild regression, antagonist concentration is varied in experiments used to derive Ki values from the Cheng-Prusoff equation, agonist concentrations are varied. Affinity for competitive agonists and antagonists is related by the Cheng-Prusoff factor used to calculate the Ki (affinity constant for an antagonist) from the shift in IC50 that occurs during competitive inhibition. The Cheng-Prusoff factor takes into account the effect of altering agonist concentration and agonist affinity for the receptor on inhibition produced by competitive antagonists.
Types
Competitive
Competitive antagonists bind to receptors at the same binding site (active site) as the endogenous ligand or agonist, but without activating the receptor. Agonists and antagonists "compete" for the same binding site on the receptor. Once bound, an antagonist will block agonist binding. Sufficient concentrations of an antagonist will displace the agonist from the binding sites, resulting in a lower frequency of receptor activation. The level of activity of the receptor will be determined by the relative affinity of each molecule for the site and their relative concentrations. High concentrations of a competitive agonist will increase the proportion of receptors that the agonist occupies, higher concentrations of the antagonist will be required to obtain the same degree of binding site occupancy. In functional assays using competitive antagonists, a parallel rightward shift of agonist dose–response curves with no alteration of the maximal response is observed.
Competitive antagonists are used to prevent the activity of drugs, and to reverse the effects of drugs that have already been consumed. Naloxone (also known as Narcan) is used to reverse opioid overdose caused by drugs such as heroin or morphine. Similarly, Ro15-4513 is an antidote to alcohol and flumazenil is an antidote to benzodiazepines.
Competitive antagonists are sub-classified as reversible (surmountable) or irreversible (insurmountable) competitive antagonists, depending on how they interact with their receptor protein targets. Reversible antagonists, which bind via noncovalent intermolecular forces, will eventually dissociate from the receptor, freeing the receptor to be bound again. Irreversible antagonists bind via covalent intermolecular forces. Because there is not enough free energy to break covalent bonds in the local environment, the bond is essentially "permanent", meaning the receptor-antagonist complex will never dissociate. The receptor will thereby remain permanently antagonized until it is ubiquitinated and thus destroyed.
Non-competitive
A non-competitive antagonist is a type of insurmountable antagonist that may act in one of two ways: by binding to an allosteric site of the receptor, or by irreversibly binding to the active site of the receptor. The former meaning has been standardised by the IUPHAR, and is equivalent to the antagonist being called an allosteric antagonist. While the mechanism of antagonism is different in both of these phenomena, they are both called "non-competitive" because the end-results of each are functionally very similar. Unlike competitive antagonists, which affect the amount of agonist necessary to achieve a maximal response but do not affect the magnitude of that maximal response, non-competitive antagonists reduce the magnitude of the maximum response that can be attained by any amount of agonist. This property earns them the name "non-competitive" because their effects cannot be negated, no matter how much agonist is present. In functional assays of non-competitive antagonists, depression of the maximal response of agonist dose-response curves, and in some cases, rightward shifts, is produced. The rightward shift will occur as a result of a receptor reserve (also known as spare receptors) and inhibition of the agonist response will only occur when this reserve is depleted.
An antagonist that binds to the active site of a receptor is said to be "non-competitive" if the bond between the active site and the antagonist is irreversible or nearly so. This usage of the term "non-competitive" may not be ideal, however, since the term "irreversible competitive antagonism" may also be used to describe the same phenomenon without the potential for confusion with the second meaning of "non-competitive antagonism" discussed below.
The second form of "non-competitive antagonists" act at an allosteric site. These antagonists bind to a distinctly separate binding site from the agonist, exerting their action to that receptor via the other binding site. They do not compete with agonists for binding at the active site. The bound antagonists may prevent conformational changes in the receptor required for receptor activation after the agonist binds. Cyclothiazide has been shown to act as a reversible non-competitive antagonist of mGluR1 receptor.
Uncompetitive
Uncompetitive antagonists differ from non-competitive antagonists in that they require receptor activation by an agonist before they can bind to a separate allosteric binding site. This type of antagonism produces a kinetic profile in which "the same amount of antagonist blocks higher concentrations of agonist better than lower concentrations of agonist". Memantine, used in the treatment of Alzheimer's disease, is an uncompetitive antagonist of the NMDA receptor.
Silent antagonists
Silent antagonists are competitive receptor antagonists that have zero intrinsic activity for activating a receptor. They are true antagonists, so to speak. The term was created to distinguish fully inactive antagonists from weak partial agonists or inverse agonists.
Partial agonists
Partial agonists are defined as drugs that, at a given receptor, might differ in the amplitude of the functional response that they elicit after maximal receptor occupancy. Although they are agonists, partial agonists can act as a competitive antagonist in the presence of a full agonist, as it competes with the full agonist for receptor occupancy, thereby producing a net decrease in the receptor activation as compared to that observed with the full agonist alone. Clinically, their usefulness is derived from their ability to enhance deficient systems while simultaneously blocking excessive activity. Exposing a receptor to a high level of a partial agonist will ensure that it has a constant, weak level of activity, whether its normal agonist is present at high or low levels. In addition, it has been suggested that partial agonism prevents the adaptive regulatory mechanisms that frequently develop after repeated exposure to potent full agonists or antagonists. E.g. Buprenorphine, a partial agonist of the μ-opioid receptor, binds with weak morphine-like activity and is used clinically as an analgesic in pain management and as an alternative to methadone in the treatment of opioid dependence.
Inverse agonists
An inverse agonist can have effects similar to those of an antagonist, but causes a distinct set of downstream biological responses. Constitutively active receptors that exhibit intrinsic or basal activity can have inverse agonists, which not only block the effects of binding agonists like a classical antagonist but also inhibit the basal activity of the receptor. Many drugs previously classified as antagonists are now beginning to be reclassified as inverse agonists because of the discovery of constitutive active receptors. Antihistamines, originally classified as antagonists of histamine H1 receptors have been reclassified as inverse agonists.
Reversibility
Many antagonists are reversible antagonists that, like most agonists, will bind and unbind a receptor at rates determined by receptor-ligand kinetics.
Irreversible antagonists covalently bind to the receptor target and, in general, cannot be removed; inactivating the receptor for the duration of the antagonist effects is determined by the rate of receptor turnover, the rate of synthesis of new receptors. Phenoxybenzamine is an example of an irreversible alpha blocker—it permanently binds to α adrenergic receptors, preventing adrenaline and noradrenaline from binding. Inactivation of receptors normally results in a depression of the maximal response of agonist dose-response curves and a right shift in the curve occurs where there is a receptor reserve similar to non-competitive antagonists. A washout step in the assay will usually distinguish between non-competitive and irreversible antagonist drugs, as effects of non-competitive antagonists are reversible and activity of agonist will be restored.
Irreversible competitive antagonists also involve competition between the agonist and antagonist of the receptor, but the rate of covalent bonding differs and depends on affinity and reactivity of the antagonist. For some antagonists, there may be a distinct period during which they behave competitively (regardless of basal efficacy), and freely associate to and dissociate from the receptor, determined by receptor-ligand kinetics. But, once irreversible bonding has taken place, the receptor is deactivated and degraded. As for non-competitive antagonists and irreversible antagonists in functional assays with irreversible competitive antagonist drugs, there may be a shift in the log concentration–effect curve to the right, but, in general, both a decrease in slope and a reduced maximum are obtained.