Coulomb's law

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Coulomb%27s_law 

The magnitude of the electrostatic force F between two point charges q₁ and q₂ is directly proportional to the product of the magnitudes of charges and inversely proportional to the square of the distance between them. Like charges repel each other, and opposite charges attract each other.

Coulomb's inverse-square law, or simply Coulomb's law, is an experimental law of physics that calculates the amount of force between two electrically charged particles at rest. This electric force is conventionally called the electrostatic force or Coulomb force. Although the law was known earlier, it was first published in 1785 by French physicist Charles-Augustin de Coulomb. Coulomb's law was essential to the development of the theory of electromagnetism and maybe even its starting point, as it allowed meaningful discussions of the amount of electric charge in a particle.

The law states that the magnitude, or absolute value, of the attractive or repulsive electrostatic force between two point charges is directly proportional to the product of the magnitudes of their charges and inversely proportional to the square of the distance between them. Coulomb discovered that bodies with like electrical charges repel:

It follows therefore from these three tests, that the repulsive force that the two balls – [that were] electrified with the same kind of electricity – exert on each other, follows the inverse proportion of the square of the distance.

Coulomb also showed that oppositely charged bodies attract according to an inverse-square law: $${\displaystyle |F|=k_{\text{e}}\frac{|q_1||q_2|}{r^2}}$$

Here, k_e is a constant, q₁ and q₂ are the quantities of each charge, and the scalar r is the distance between the charges.

The force is along the straight line joining the two charges. If the charges have the same sign, the electrostatic force between them makes them repel; if they have different signs, the force between them makes them attract.

Being an inverse-square law, the law is similar to Isaac Newton's inverse-square law of universal gravitation, but gravitational forces always make things attract, while electrostatic forces make charges attract or repel. Also, gravitational forces are much weaker than electrostatic forces. Coulomb's law can be used to derive Gauss's law, and vice versa. In the case of a single point charge at rest, the two laws are equivalent, expressing the same physical law in different ways. The law has been tested extensively, and observations have upheld the law on the scale from 10⁻¹⁶ m to 10⁸ m.

History

Charles-Augustin de Coulomb

Ancient cultures around the Mediterranean knew that certain objects, such as rods of amber, could be rubbed with cat's fur to attract light objects like feathers and pieces of paper. Thales of Miletus made the first recorded description of static electricity around 600 BC, when he noticed that friction could make a piece of amber attract small objects.

In 1600, English scientist William Gilbert made a careful study of electricity and magnetism, distinguishing the lodestone effect from static electricity produced by rubbing amber. He coined the Neo-Latin word electricus ("of amber" or "like amber", from ἤλεκτρον [elektron], the Greek word for "amber") to refer to the property of attracting small objects after being rubbed. This association gave rise to the English words "electric" and "electricity", which made their first appearance in print in Thomas Browne's Pseudodoxia Epidemica of 1646.

Early investigators of the 18th century who suspected that the electrical force diminished with distance as the force of gravity did (i.e., as the inverse square of the distance) included Daniel Bernoulli and Alessandro Volta, both of whom measured the force between plates of a capacitor, and Franz Aepinus who supposed the inverse-square law in 1758.

Based on experiments with electrically charged spheres, Joseph Priestley of England was among the first to propose that electrical force followed an inverse-square law, similar to Newton's law of universal gravitation. However, he did not generalize or elaborate on this. In 1767, he conjectured that the force between charges varied as the inverse square of the distance.

Coulomb's torsion balance

In 1769, Scottish physicist John Robison announced that, according to his measurements, the force of repulsion between two spheres with charges of the same sign varied as x^−2.06.

In the early 1770s, the dependence of the force between charged bodies upon both distance and charge had already been discovered, but not published, by Henry Cavendish of England. In his notes, Cavendish wrote, "We may therefore conclude that the electric attraction and repulsion must be inversely as some power of the distance between that of the 2 + ⁠1/50⁠th and that of the 2 − ⁠1/50⁠th, and there is no reason to think that it differs at all from the inverse duplicate ratio".

Finally, in 1785, the French physicist Charles-Augustin de Coulomb published his first three reports of electricity and magnetism where he stated his law. This publication was essential to the development of the theory of electromagnetism. He used a torsion balance to study the repulsion and attraction forces of charged particles, and determined that the magnitude of the electric force between two point charges is directly proportional to the product of the charges and inversely proportional to the square of the distance between them.

The torsion balance consists of a bar suspended from its middle by a thin fiber. The fiber acts as a very weak torsion spring. In Coulomb's experiment, the torsion balance was an insulating rod with a metal-coated ball attached to one end, suspended by a silk thread. The ball was charged with a known charge of static electricity, and a second charged ball of the same polarity was brought near it. The two charged balls repelled one another, twisting the fiber through a certain angle, which could be read from a scale on the instrument. By knowing how much force it took to twist the fiber through a given angle, Coulomb was able to calculate the force between the balls and derive his inverse-square proportionality law.

Mathematical form

In the image, the vector F₁ is the force experienced by q₁, and the vector F₂ is the force experienced by q₂. When q₁q₂ > 0 the forces are repulsive (as in the image) and when q₁q₂ < 0 the forces are attractive (opposite to the image). The magnitude of the forces will always be equal.

Coulomb's law states that the electrostatic force ${\mathbf{F}}_1$ experienced by a charge, ${\displaystyle q_1}$ at position ${\displaystyle {\mathbf{r}}_1}$, in the vicinity of another charge, ${\displaystyle q_2}$ at position ${\displaystyle {\mathbf{r}}_2}$, in a vacuum is equal to $${\displaystyle {\mathbf{F}}_1=\frac{q_1{q}_2}{4\pi {\epsilon }_0}\frac{{\hat{\mathbf{r}}}_{12}}{{|{\mathbf{r}}_{12}|}^2}}$$

where ${\mathbf{r}}_{\mathbf{12}}\mathbf{=}{\mathbf{r}}_{\mathbf{1}}\mathbf{-}{\mathbf{r}}_{\mathbf{2}}$ is the displacement vector between the charges, ${\hat{\mathbf{r}}}_{12}$ a unit vector pointing from $q_2$ to $q_1$, and ${\displaystyle {\epsilon }_0}$ the electric constant. Here, ${\hat{\mathbf{r}}}_{12}$ is used for the vector notation. The electrostatic force ${\mathbf{F}}_2$ experienced by ${\displaystyle q_2}$, according to Newton's third law, is ${\mathbf{F}}_2=-{\mathbf{F}}_1$.

If both charges have the same sign (like charges) then the product ${\displaystyle q_1{q}_2}$ is positive and the direction of the force on ${\displaystyle q_1}$ is given by ${\hat{\mathbf{r}}}_{12}$; the charges repel each other. If the charges have opposite signs then the product ${\displaystyle q_1{q}_2}$ is negative and the direction of the force on ${\displaystyle q_1}$ is $-{\hat{\mathbf{r}}}_{12}$; the charges attract each other.

System of discrete charges

The law of superposition allows Coulomb's law to be extended to include any number of point charges. The force acting on a point charge due to a system of point charges is simply the vector addition of the individual forces acting alone on that point charge due to each one of the charges. The resulting force vector is parallel to the electric field vector at that point, with that point charge removed.

Force $\mathbf{F}$ on a small charge ${\displaystyle q}$ at position ${\displaystyle \mathbf{r}}$, due to a system of $n$ discrete charges in vacuum is

$${\displaystyle \mathbf{F}(\mathbf{r})=\frac{q}{4\pi {\epsilon }_0}\sum _{i=1}^n{q}_i\frac{{\hat{\mathbf{r}}}_i}{{|{\mathbf{r}}_i|}^2},}$$

where ${\displaystyle q_i}$ is the magnitude of the ith charge, ${\mathbf{r}}_i$ is the vector from its position to ${\displaystyle \mathbf{r}}$ and ${\hat{\mathbf{r}}}_i$ is the unit vector in the direction of ${\displaystyle {\mathbf{r}}_i}$.

Continuous charge distribution

In this case, the principle of linear superposition is also used. For a continuous charge distribution, an integral over the region containing the charge is equivalent to an infinite summation, treating each infinitesimal element of space as a point charge ${\displaystyle dq}$. The distribution of charge is usually linear, surface or volumetric.

For a linear charge distribution (a good approximation for charge in a wire) where ${\displaystyle \lambda ({\mathbf{r}}^{\prime })}$ gives the charge per unit length at position ${\displaystyle {\mathbf{r}}^{\prime }}$, and ${\displaystyle d{\ell }^{\prime }}$ is an infinitesimal element of length, $${\displaystyle d{q}^{\prime }=\lambda ({\mathbf{r}}^{\prime })d{\ell }^{\prime }.}$$

For a surface charge distribution (a good approximation for charge on a plate in a parallel plate capacitor) where ${\displaystyle \sigma ({\mathbf{r}}^{\prime })}$ gives the charge per unit area at position ${\displaystyle {\mathbf{r}}^{\prime }}$, and ${\displaystyle d{A}^{\prime }}$ is an infinitesimal element of area, $${\displaystyle d{q}^{\prime }=\sigma ({\mathbf{r}}^{\prime })d{A}^{\prime }.}$$

For a volume charge distribution (such as charge within a bulk metal) where ${\displaystyle \rho ({\mathbf{r}}^{\prime })}$ gives the charge per unit volume at position ${\displaystyle {\mathbf{r}}^{\prime }}$, and ${\displaystyle d{V}^{\prime }}$ is an infinitesimal element of volume, $${\displaystyle d{q}^{\prime }=\rho ({\mathit{r}}^{\mathbf{\prime }})d{V}^{\prime }.}$$

The force on a small test charge ${\displaystyle q}$ at position ${\displaystyle \mathit{r}}$ in vacuum is given by the integral over the distribution of charge $${\displaystyle \mathbf{F}(\mathbf{r})=\frac{q}{4\pi {\epsilon }_0}\int d{q}^{\prime }\frac{\mathbf{r}-{\mathbf{r}}^{\prime }}{|\mathbf{r}-{\mathbf{r}}^{\prime }{|}^3}.}$$

The "continuous charge" version of Coulomb's law is never supposed to be applied to locations for which ${\displaystyle |\mathbf{r}-{\mathbf{r}}^{\prime }|=0}$ because that location would directly overlap with the location of a charged particle (e.g. electron or proton) which is not a valid location to analyze the electric field or potential classically. Charge is always discrete in reality, and the "continuous charge" assumption is just an approximation that is not supposed to allow ${\displaystyle |\mathbf{r}-{\mathbf{r}}^{\prime }|=0}$ to be analyzed.

Coulomb constant

The constant of proportionality, ${\displaystyle \frac{1}{4\pi {\epsilon }_0}}$, in Coulomb's law: $${\displaystyle {\mathbf{F}}_1=\frac{q_1{q}_2}{4\pi {\epsilon }_0}\frac{{\hat{\mathbf{r}}}_{12}}{{|{\mathbf{r}}_{12}|}^2}}$$ is a consequence of historical choices for units.

The constant ${\displaystyle {\epsilon }_0}$ is the vacuum electric permittivity. Using the CODATA 2022 recommended value for ${\displaystyle {\epsilon }_0}$, the Coulomb constant is $${\displaystyle k_{\text{e}}=\frac{1}{4\pi {\epsilon }_0}=8.9875517862(14)\times {10}^9\mathrm{N}\cdot {\mathrm{m}}^2\cdot {\mathrm{C}}^{-2}}$$

Limitations

There are three conditions to be fulfilled for the validity of Coulomb's inverse square law:

1. The charges must have a spherically symmetric distribution (e.g. be point charges, or a charged metal sphere).
2. The charges must not overlap (e.g. they must be distinct point charges).
3. The charges must be stationary with respect to a nonaccelerating frame of reference.

The last of these is known as the electrostatic approximation. When movement takes place, an extra factor is introduced, which alters the force produced on the two objects. This extra part of the force is called the magnetic force. For slow movement, the magnetic force is minimal and Coulomb's law can still be considered approximately correct. A more accurate approximation in this case is, however, the Weber force. When the charges are moving more quickly in relation to each other or accelerations occur, Maxwell's equations and Einstein's theory of relativity must be taken into consideration.

Electric field

Main article: Electric field

If two charges have the same sign, the electrostatic force between them is repulsive; if they have different sign, the force between them is attractive.

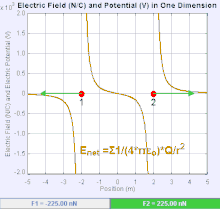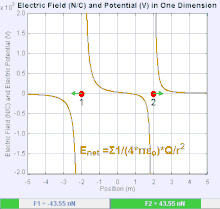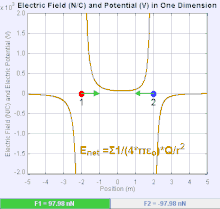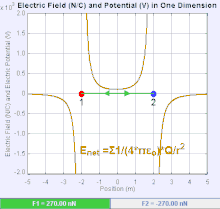
An electric field is a vector field that associates to each point in space the Coulomb force experienced by a unit test charge. The strength and direction of the Coulomb force $\mathbf{F}$ on a charge $q_t$ depends on the electric field $\mathbf{E}$ established by other charges that it finds itself in, such that $\mathbf{F}=q_t\mathbf{E}$. In the simplest case, the field is considered to be generated solely by a single source point charge. More generally, the field can be generated by a distribution of charges who contribute to the overall by the principle of superposition.

If the field is generated by a positive source point charge $q$, the direction of the electric field points along lines directed radially outwards from it, i.e. in the direction that a positive point test charge $q_t$ would move if placed in the field. For a negative point source charge, the direction is radially inwards.

The magnitude of the electric field E can be derived from Coulomb's law. By choosing one of the point charges to be the source, and the other to be the test charge, it follows from Coulomb's law that the magnitude of the electric field E created by a single source point charge Q at a certain distance from it r in vacuum is given by $${\displaystyle |\mathbf{E}|=k_{\text{e}}\frac{|q|}{r^2}}$$

A system of n discrete charges ${\displaystyle q_i}$ stationed at ${\mathbf{r}}_i=\mathbf{r}-{\mathbf{r}}_i$ produces an electric field whose magnitude and direction is, by superposition $${\displaystyle \mathbf{E}(\mathbf{r})=\frac{1}{4\pi {\epsilon }_0}\sum _{i=1}^n{q}_i\frac{{\hat{\mathbf{r}}}_i}{{|{\mathbf{r}}_i|}^2}}$$

Atomic forces

See also: Coulomb explosion

Coulomb's law holds even within atoms, correctly describing the force between the positively charged atomic nucleus and each of the negatively charged electrons. This simple law also correctly accounts for the forces that bind atoms together to form molecules and for the forces that bind atoms and molecules together to form solids and liquids. Generally, as the distance between ions increases, the force of attraction, and binding energy, approach zero and ionic bonding is less favorable. As the magnitude of opposing charges increases, energy increases and ionic bonding is more favorable.

Relation to Gauss's law

Deriving Gauss's law from Coulomb's law

Strictly speaking, Gauss's law cannot be derived from Coulomb's law alone, since Coulomb's law gives the electric field due to an individual, electrostatic point charge only. However, Gauss's law can be proven from Coulomb's law if it is assumed, in addition, that the electric field obeys the superposition principle. The superposition principle states that the resulting field is the vector sum of fields generated by each particle (or the integral, if the charges are distributed smoothly in space).

Outline of proof

Coulomb's law states that the electric field due to a stationary point charge is: $${\displaystyle \mathbf{E}(\mathbf{r})=\frac{q}{4\pi {\epsilon }_0}\frac{{\mathbf{e}}_r}{r^2}}$$ where

• e_r is the radial unit vector,
• r is the radius, |r|,
• ε₀ is the electric constant,
• q is the charge of the particle, which is assumed to be located at the origin.

Using the expression from Coulomb's law, we get the total field at r by using an integral to sum the field at r due to the infinitesimal charge at each other point s in space, to give $${\displaystyle \mathbf{E}(\mathbf{r})=\frac{1}{4\pi {\epsilon }_0}\int \frac{\rho (\mathbf{s})(\mathbf{r}-\mathbf{s})}{|\mathbf{r}-\mathbf{s}{|}^3}{\mathrm{d}}^3\mathbf{s}}$$ where ρ is the charge density. If we take the divergence of both sides of this equation with respect to r, and use the known theorem

$${\displaystyle \mathrm{\nabla }\cdot \left(\frac{\mathbf{r}}{|\mathbf{r}{|}^3}\right)=4\pi \delta (\mathbf{r})}$$ where δ(r) is the Dirac delta function, the result is $${\displaystyle \mathrm{\nabla }\cdot \mathbf{E}(\mathbf{r})=\frac{1}{{\epsilon }_0}\int \rho (\mathbf{s})\delta (\mathbf{r}-\mathbf{s}){\mathrm{d}}^3\mathbf{s}}$$

Using the "sifting property" of the Dirac delta function, we arrive at $${\displaystyle \mathrm{\nabla }\cdot \mathbf{E}(\mathbf{r})=\frac{\rho (\mathbf{r})}{{\epsilon }_0},}$$ which is the differential form of Gauss's law, as desired.

Since Coulomb's law only applies to stationary charges, there is no reason to expect Gauss's law to hold for moving charges based on this derivation alone. In fact, Gauss's law does hold for moving charges, and, in this respect, Gauss's law is more general than Coulomb's law.

Proof (without Dirac Delta)

Let ${\displaystyle \mathrm{\Omega }\subseteq R^3}$ be a bounded open set, and $${\displaystyle {\mathbf{E}}_0(\mathbf{r})=\frac{1}{4\pi {\epsilon }_0}{\int }_{\mathrm{\Omega }}\rho ({\mathbf{r}}^{\prime })\frac{\mathbf{r}-{\mathbf{r}}^{\prime }}{{\Vert \mathbf{r}-{\mathbf{r}}^{\prime }\Vert }^3}\mathrm{d}{\mathbf{r}}^{\prime }\equiv \frac{1}{4\pi {\epsilon }_0}{\int }_{\mathrm{\Omega }}e(\mathbf{r}\mathbf{,}{\mathbf{r}}^{\prime })\mathrm{d}{\mathbf{r}}^{\prime }}$$ be the electric field, with ${\displaystyle \rho ({\mathbf{r}}^{\prime })}$ a continuous function (density of charge).

It is true for all ${\displaystyle \mathbf{r}\ne {\mathbf{r}}^{\prime }}$ that ${\displaystyle {\mathrm{\nabla }}_{\mathbf{r}}\cdot \mathbf{e}(\mathbf{r}\mathbf{,}{\mathbf{r}}^{\prime })=0}$.

Consider now a compact set ${\displaystyle V\subseteq R^3}$ having a piecewise smooth boundary ${\displaystyle \mathrm{\partial }V}$ such that ${\displaystyle \mathrm{\Omega }\cap V=\mathrm{\varnothing }}$. It follows that ${\displaystyle e(\mathbf{r}\mathbf{,}{\mathbf{r}}^{\prime })\in C^1(V\times \mathrm{\Omega })}$ and so, for the divergence theorem:

$${\displaystyle {\oint }_{\mathrm{\partial }V}{\mathbf{E}}_0\cdot d\mathbf{S}={\int }_V\mathrm{\nabla }\cdot {\mathbf{E}}_{0}dV}$$

But because ${\displaystyle e(\mathbf{r}\mathbf{,}{\mathbf{r}}^{\prime })\in C^1(V\times \mathrm{\Omega })}$,

$${\displaystyle \mathrm{\nabla }\cdot {\mathbf{E}}_0(\mathbf{r})=\frac{1}{4\pi {\epsilon }_0}{\int }_{\mathrm{\Omega }}{\mathrm{\nabla }}_{\mathbf{r}}\cdot e(\mathbf{r}\mathbf{,}{\mathbf{r}}^{\prime })\mathrm{d}{\mathbf{r}}^{\prime }=0}$$ for the argument above (${\displaystyle \mathrm{\Omega }\cap V=\mathrm{\varnothing }⟹\mathrm{\forall }\mathbf{r}\in V\mathrm{\forall }{\mathbf{r}}^{\prime }\in \mathrm{\Omega }\mathbf{r}\ne {\mathbf{r}}^{\prime }}$ and then ${\displaystyle {\mathrm{\nabla }}_{\mathbf{r}}\cdot \mathbf{e}(\mathbf{r}\mathbf{,}{\mathbf{r}}^{\prime })=0}$)

Therefore the flux through a closed surface generated by some charge density outside (the surface) is null.

Now consider ${\displaystyle {\mathbf{r}}_0\in \mathrm{\Omega }}$, and ${\displaystyle B_R({\mathbf{r}}_0)\subseteq \mathrm{\Omega }}$ as the sphere centered in ${\displaystyle {\mathbf{r}}_0}$ having ${\displaystyle R}$ as radius (it exists because ${\displaystyle \mathrm{\Omega }}$ is an open set).

Let ${\displaystyle {\mathbf{E}}_{B_R}}$ and ${\displaystyle {\mathbf{E}}_C}$ be the electric field created inside and outside the sphere respectively. Then,

${\displaystyle {\mathbf{E}}_{B_R}=\frac{1}{4\pi {\epsilon }_0}{\int }_{B_R({\mathbf{r}}_0)}e(\mathbf{r}\mathbf{,}{\mathbf{r}}^{\prime })\mathrm{d}{\mathbf{r}}^{\prime }}$, ${\displaystyle {\mathbf{E}}_C=\frac{1}{4\pi {\epsilon }_0}{\int }_{\mathrm{\Omega }\setminus B_R({\mathbf{r}}_0)}e(\mathbf{r}\mathbf{,}{\mathbf{r}}^{\prime })\mathrm{d}{\mathbf{r}}^{\prime }}$ and ${\displaystyle {\mathbf{E}}_{B_R}+{\mathbf{E}}_C={\mathbf{E}}_0}$

$${\displaystyle \mathrm{\Phi }(R)={\oint }_{\mathrm{\partial }{B}_R({\mathbf{r}}_0)}{\mathbf{E}}_0\cdot d\mathbf{S}={\oint }_{\mathrm{\partial }{B}_R({\mathbf{r}}_0)}{\mathbf{E}}_{B_R}\cdot d\mathbf{S}+{\oint }_{\mathrm{\partial }{B}_R({\mathbf{r}}_0)}{\mathbf{E}}_C\cdot d\mathbf{S}={\oint }_{\mathrm{\partial }{B}_R({\mathbf{r}}_0)}{\mathbf{E}}_{B_R}\cdot d\mathbf{S}}$$

The last equality follows by observing that ${\displaystyle (\mathrm{\Omega }\setminus B_R({\mathbf{r}}_0))\cap B_R({\mathbf{r}}_0)=\mathrm{\varnothing }}$, and the argument above.

The RHS is the electric flux generated by a charged sphere, and so:

$${\displaystyle \mathrm{\Phi }(R)=\frac{Q(R)}{{\epsilon }_0}=\frac{1}{{\epsilon }_0}{\int }_{B_R({\mathbf{r}}_0)}\rho ({\mathbf{r}}^{\prime })\mathrm{d}{\mathbf{r}}^{\prime }=\frac{1}{{\epsilon }_0}\rho ({\mathbf{r}}_c^{\prime })|B_R({\mathbf{r}}_0)|}$$ with ${\displaystyle r_c^{\prime }\in B_R({\mathbf{r}}_0)}$

Where the last equality follows by the mean value theorem for integrals. Using the squeeze theorem and the continuity of ${\displaystyle \rho }$, one arrives at:

$${\displaystyle \mathrm{\nabla }\cdot {\mathbf{E}}_0({\mathbf{r}}_0)=\underset{R\to 0}{lim}\frac{1}{|B_R({\mathbf{r}}_0)|}\mathrm{\Phi }(R)=\frac{1}{{\epsilon }_0}\rho ({\mathbf{r}}_0)}$$

Deriving Coulomb's law from Gauss's law

Strictly speaking, Coulomb's law cannot be derived from Gauss's law alone, since Gauss's law does not give any information regarding the curl of E (see Helmholtz decomposition and Faraday's law). However, Coulomb's law can be proven from Gauss's law if it is assumed, in addition, that the electric field from a point charge is spherically symmetric (this assumption, like Coulomb's law itself, is exactly true if the charge is stationary, and approximately true if the charge is in motion).

Outline of proof

Taking S in the integral form of Gauss's law to be a spherical surface of radius r, centered at the point charge Q, we have $${\displaystyle {\oint }_S\mathbf{E}\cdot d\mathbf{A}=\frac{Q}{{\epsilon }_0}}$$

By the assumption of spherical symmetry, the integrand is a constant which can be taken out of the integral. The result is $${\displaystyle 4\pi r^2\hat{\mathbf{r}}\cdot \mathbf{E}(\mathbf{r})=\frac{Q}{{\epsilon }_0}}$$ where r̂ is a unit vector pointing radially away from the charge. Again by spherical symmetry, E points in the radial direction, and so we get $${\displaystyle \mathbf{E}(\mathbf{r})=\frac{Q}{4\pi {\epsilon }_0}\frac{\hat{\mathbf{r}}}{r^2}}$$ which is essentially equivalent to Coulomb's law. Thus the inverse-square law dependence of the electric field in Coulomb's law follows from Gauss's law.

In relativity

Coulomb's law can be used to gain insight into the form of the magnetic field generated by moving charges since by special relativity, in certain cases the magnetic field can be shown to be a transformation of forces caused by the electric field. When no acceleration is involved in a particle's history, Coulomb's law can be assumed on any test particle in its own inertial frame, supported by symmetry arguments in solving Maxwell's equation, shown above. Coulomb's law can be expanded to moving test particles to be of the same form. This assumption is supported by Lorentz force law which, unlike Coulomb's law is not limited to stationary test charges. Considering the charge to be invariant of observer, the electric and magnetic fields of a uniformly moving point charge can hence be derived by the Lorentz transformation of the four force on the test charge in the charge's frame of reference given by Coulomb's law and attributing magnetic and electric fields by their definitions given by the form of Lorentz force. The fields hence found for uniformly moving point charges are given by:$${\displaystyle \mathbf{E}=\frac{q}{4\pi {ϵ}_0{r}^3}\frac{1-{\beta }^2}{(1-{\beta }^2{\sin }^2\theta {)}^{3/2}}\mathbf{r}}$$$${\displaystyle \mathbf{B}=\frac{q}{4\pi {ϵ}_0{r}^3}\frac{1-{\beta }^2}{(1-{\beta }^2{\sin }^2\theta {)}^{3/2}}\frac{\mathbf{v}\times \mathbf{r}}{c^2}=\frac{\mathbf{v}\times \mathbf{E}}{c^2}}$$where ${\displaystyle q}$ is the charge of the point source, ${\displaystyle \mathbf{r}}$ is the position vector from the point source to the point in space, ${\displaystyle \mathbf{v}}$ is the velocity vector of the charged particle, ${\displaystyle \beta }$ is the ratio of speed of the charged particle divided by the speed of light and ${\displaystyle \theta }$ is the angle between ${\displaystyle \mathbf{r}}$ and ${\displaystyle \mathbf{v}}$.

This form of solutions need not obey Newton's third law as is the case in the framework of special relativity (yet without violating relativistic-energy momentum conservation). Note that the expression for electric field reduces to Coulomb's law for non-relativistic speeds of the point charge and that the magnetic field in non-relativistic limit (approximating ${\displaystyle \beta \ll 1}$) can be applied to electric currents to get the Biot–Savart law. These solutions, when expressed in retarded time also correspond to the general solution of Maxwell's equations given by solutions of Liénard–Wiechert potential, due to the validity of Coulomb's law within its specific range of application. Also note that the spherical symmetry for gauss law on stationary charges is not valid for moving charges owing to the breaking of symmetry by the specification of direction of velocity in the problem. Agreement with Maxwell's equations can also be manually verified for the above two equations.

Coulomb potential

See also: Electric potential

Quantum field theory

The most basic Feynman diagram for QED interaction between two fermions

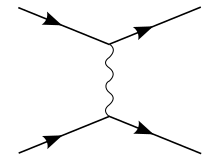
The Coulomb potential admits continuum states (with E > 0), describing electron-proton scattering, as well as discrete bound states, representing the hydrogen atom. It can also be derived within the non-relativistic limit between two charged particles, as follows:

Under Born approximation, in non-relativistic quantum mechanics, the scattering amplitude $\mathcal{A}(|\mathbf{p}⟩\to |{\mathbf{p}}^{\prime }⟩)$ is: $${\displaystyle \mathcal{A}(|\mathbf{p}⟩\to |{\mathbf{p}}^{\prime }⟩)-1=2\pi \delta (E_p-E_{p^{\prime }})(-i)\int d^3\mathbf{r}V(\mathbf{r})e^{-i(\mathbf{p}-{\mathbf{p}}^{\prime })\mathbf{r}}}$$ This is to be compared to the: $${\displaystyle \int \frac{d^{3}k}{(2\pi {)}^3}{e}^{ik{r}_0}⟨p^{\prime },k|S|p,k⟩}$$ where we look at the (connected) S-matrix entry for two electrons scattering off each other, treating one with "fixed" momentum as the source of the potential, and the other scattering off that potential.

Using the Feynman rules to compute the S-matrix element, we obtain in the non-relativistic limit with ${\displaystyle m_0\gg |\mathbf{p}|}$ $${\displaystyle ⟨p^{\prime },k|S|p,k⟩{|}_{conn}=-i\frac{e^2}{|\mathbf{p}-{\mathbf{p}}^{\prime }{|}^2-i\epsilon }(2m{)}^2\delta (E_{p,k}-E_{p^{\prime },k})(2\pi {)}^4\delta (\mathbf{p}-{\mathbf{p}}^{\prime })}$$

Comparing with the QM scattering, we have to discard the ${\displaystyle (2m{)}^2}$ as they arise due to differing normalizations of momentum eigenstate in QFT compared to QM and obtain: $${\displaystyle \int V(\mathbf{r})e^{-i(\mathbf{p}-{\mathbf{p}}^{\prime })\mathbf{r}}{d}^3\mathbf{r}=\frac{e^2}{|\mathbf{p}-{\mathbf{p}}^{\prime }{|}^2-i\epsilon }}$$ where Fourier transforming both sides, solving the integral and taking ${\displaystyle \epsilon \to 0}$ at the end will yield $${\displaystyle V(r)=\frac{e^2}{4\pi r}}$$ as the Coulomb potential.

However, the equivalent results of the classical Born derivations for the Coulomb problem are thought to be strictly accidental.

The Coulomb potential, and its derivation, can be seen as a special case of the Yukawa potential, which is the case where the exchanged boson – the photon – has no rest mass.

Verification

Experiment to verify Coulomb's law.

It is possible to verify Coulomb's law with a simple experiment. Consider two small spheres of mass ${\displaystyle m}$ and same-sign charge ${\displaystyle q}$, hanging from two ropes of negligible mass of length ${\displaystyle l}$. The forces acting on each sphere are three: the weight ${\displaystyle mg}$, the rope tension ${\displaystyle \mathbf{T}}$ and the electric force ${\displaystyle \mathbf{F}}$. In the equilibrium state:

$${\displaystyle \mathbf{T}\sin {\theta }_1={\mathbf{F}}_1}$$

1

and

$${\displaystyle \mathbf{T}\cos {\theta }_1=mg}$$

2

Dividing (1) by (2):

$${\displaystyle \frac{\sin {\theta }_1}{\cos {\theta }_1}=\frac{F_1}{mg}\Rightarrow F_1=mg\tan {\theta }_1}$$

3

Let ${\displaystyle {\mathbf{L}}_1}$ be the distance between the charged spheres; the repulsion force between them ${\displaystyle {\mathbf{F}}_1}$, assuming Coulomb's law is correct, is equal to

$${\displaystyle F_1=\frac{q^2}{4\pi {\epsilon }_0{L}_1^2}}$$

Coulomb's law

so:

$${\displaystyle \frac{q^2}{4\pi {\epsilon }_0{L}_1^2}=mg\tan {\theta }_1}$$

4

If we now discharge one of the spheres, and we put it in contact with the charged sphere, each one of them acquires a charge $\frac{q}{2}$. In the equilibrium state, the distance between the charges will be ${\mathbf{L}}_2<{\mathbf{L}}_1$ and the repulsion force between them will be:

$${\displaystyle F_2=\frac{{(\frac{q}{2})}^2}{4\pi {\epsilon }_0{L}_2^2}=\frac{\frac{q^2}{4}}{4\pi {\epsilon }_0{L}_2^2}}$$

5

We know that ${\displaystyle {\mathbf{F}}_2=mg\tan {\theta }_2}$ and: $${\displaystyle \frac{\frac{q^2}{4}}{4\pi {\epsilon }_0{L}_2^2}=mg\tan {\theta }_2}$$ Dividing (4) by (5), we get:

$${\displaystyle \frac{\left(\frac{q^2}{4\pi {\epsilon }_0{L}_1^2}\right)}{\left(\frac{\frac{q^2}{4}}{4\pi {\epsilon }_0{L}_2^2}\right)}=\frac{mg\tan {\theta }_1}{mg\tan {\theta }_2}\Rightarrow 4{\left(\frac{L_2}{L_1}\right)}^2=\frac{\tan {\theta }_1}{\tan {\theta }_2}}$$

6

Measuring the angles ${\displaystyle {\theta }_1}$ and ${\displaystyle {\theta }_2}$ and the distance between the charges ${\displaystyle {\mathbf{L}}_1}$ and ${\displaystyle {\mathbf{L}}_2}$ is sufficient to verify that the equality is true taking into account the experimental error. In practice, angles can be difficult to measure, so if the length of the ropes is sufficiently great, the angles will be small enough to make the following approximation:

$${\displaystyle \tan \theta \approx \sin \theta =\frac{\frac{L}{2}}{\ell }=\frac{L}{2\ell }\Rightarrow \frac{\tan {\theta }_1}{\tan {\theta }_2}\approx \frac{\frac{L_1}{2\ell }}{\frac{L_2}{2\ell }}}$$

7

Using this approximation, the relationship (6) becomes the much simpler expression:

$${\displaystyle \frac{\frac{L_1}{2\ell }}{\frac{L_2}{2\ell }}\approx 4{\left(\frac{L_2}{L_1}\right)}^2\Rightarrow \frac{L_1}{L_2}\approx 4{\left(\frac{L_2}{L_1}\right)}^2\Rightarrow \frac{L_1}{L_2}\approx \sqrt[3]{4}}$$

8

In this way, the verification is limited to measuring the distance between the charges and checking that the division approximates the theoretical value.

Tractor beam

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Tractor_beam 

A tractor beam is a device that can attract one object to another from a distance. The concept originates in fiction: The term was coined by E. E. Smith (an update of his earlier "attractor beam") in his novel Spacehounds of IPC (1931). Since the 1990s, technology and research have labored to make it a reality, and have had some success on a microscopic level. Less commonly, a similar beam that repels is known as a pressor beam or repulsor beam. Gravity impulse and gravity propulsion beams are traditionally areas of research from fringe physics that coincide with the concepts of tractor and repulsor beams.

Physics

A force field confined to a Collimated beam with clean borders is one of the principal characteristics of tractor and repulsor beams. Several theories that have predicted that repulsive effects do not fall within the category of tractor and repulsor beams because of the absence of field collimation. For example,^{[clarification needed]} Robert L. Forward of Hughes Research Laboratories showed that general relativity theory allowed the generation of a very brief impulse of a gravity-like repulsive force along the axis of a helical torus containing accelerated condensed matter. The mainstream scientific community has accepted Forward's work.

A variant of Burkhard Heim's theory by Walter Dröscher, Institut für Grenzgebiete der Wissenschaft (IGW), Innsbruck, Austria, and Jocham Häuser, University of Applied Sciences and CLE GmbH, Salzgitter, Germany, predicted a repulsive force field of gravitophotons could be produced by a ring rotating above a very strong magnetic field. Heim's theory, and its variants, have been treated by the mainstream scientific community as fringe physics. But the works by Forward, Dröscher, and Häuser could not be considered as a form of repulsor- or tractor-beam because the predicted impulses and field effects were not confined to a well-defined, collimated region.

The following are summaries of other notable experiments and theories that resemble repulsor and tractor beam concepts:

1960s

In July 1960, trade magazine Missiles and Rockets reported that Martin N. Kaplan, a research engineer at Ryan Aeronautical Company, had conducted experiments that could lead to an ability to direct an anti-gravitational force toward or away from a second body.

In 1964, physicists Leopold Halpern of the Niels Bohr Institute and B. Laurent of the Nordic Institute for Theoretical Physics indicated general relativity theory and quantum theory allowed the generation and amplification of gravitons in a manner like the laser. They showed, in principle, gravitational radiation in the form of a beam of gravitons could be generated and amplified by using induced, resonant emissions.

1990s – Podkletnov experiment

In 1992, Professor Yevgeny Podkletnov and R. Nieminen, of the Tampere University of Technology, discovered weight fluctuations in objects above an electromagnetically levitated, massive, composite superconducting disk. Three years later, Podkletnov reported the results of additional experiments with a toroidal disk superconductor. They reported the weight of the samples would fluctuate between −2.5% and +5.4% as the angular speed of the superconductor increased. Certain combinations of disk angular speeds and electromagnetic frequencies caused the fluctuations to stabilize at a 0.3% reduction. The experiments with the toroidal disk yielded reductions that reached a maximum of 1.9–2.1%. Reports about both sets of experiments stated the weight loss region was cylindrical, extending vertically for at least three meters above the disk. Qualitative observations of an expulsive force at the border of the shielded zone were reported in the Fall of 1995. Several groups around the world tried to replicate Podkletnov's gravity shielding observations.

Italian physicist Giovanni Modanese, while a Von Humboldt Fellow at the Max Planck Institute for Physics, made the first attempt to provide a theoretical explanation of Podkletnov's observations. He argued that the shielding effect and slight expulsive force at the border of the shielded zone could be explained in terms of induced changes in the local cosmological constant. Modanese described several effects regarding responses to modifications to the local cosmological constant within the superconductor. Ning Wu of the Institute of High Energy Physics (Beijing), used the quantum gauge theory of gravity he had developed in 2001 to explain Podkletnov's observations. Wu's theory approximated the relative gravity loss as 0.03% (an order of magnitude smaller than the reported range of 0.3–0.5%).

C. S. Unnikrishan, Tata Institute of Fundamental Research, Mumbai, showed that if the effect had been caused by gravitational shielding, the shape of the shielded region would be similar to a shadow from the gravitational shield. For example, the shape of the shielded region above a disk would be conical. The height of the cone's apex above the disk would vary directly with the height of the shielding disk above the earth. Podkletnov and Nieminen described the shape of the weight loss region as a cylinder that extended through the ceiling above the cryostat.

2010s

A team of scientists at the Australian National University (ANU) led by Professor Andrei Rode created a device similar to a tractor beam to move small particles 1.5 meters through the air. Rather than create a new gravitational field, however, the device utilizes a doughnut-shaped Laguerre-Gaussian laser beam, which has a high-intensity ring of light that surrounds a dark core along the beam axis. This method confines particles to the center of the beam using photophoresis, whereby illuminated sections of the particle have a higher temperature and thus impart more momentum to air molecules incident on the surface. Owing to this method, such a device cannot work in space due to lack of air. Rode states that there are practical applications for the device on Earth, for example, the transportation of microscopic hazardous materials and other microscopic objects.

John Sinko and Clifford Schlecht researched a form of reversed-thrust laser propulsion as a macroscopic laser tractor beam. Intended applications include remotely manipulating space objects at distances up to about 100 km, removal of space debris, and retrieval of adrift astronauts or tools on-orbit.

Functioning tractor beams based on solenoidal modes of light were demonstrated in 2010 by physicists at New York University. The spiraling intensity distribution in these non-diffracting beams tends to trap illuminated objects and thus helps to overcome the radiation pressure that ordinarily would drive them down the optical axis. Orbital angular momentum transferred from the solenoid beam's helical wavefronts then drives the trapped objects upstream along the spiral. Both Bessel-beam and solenoidal tractor beams are being considered for applications in space exploration by NASA.

In March 2011, Chinese scientists posited that a specific type of Bessel beam (a special kind of laser that does not diffract at the center) is capable of creating a pull-like effect on a given microscopic particle, forcing it toward the beam-source. The underlying physics is the maximization of forward scattering via interference of the radiation multipoles. They show explicitly that the necessary condition to realize a negative (pulling) optical force is the simultaneous excitation of multipoles in the particle. If the total photon momentum projection along the propagation direction is small, attractive optical force is possible. The Chinese scientists suggest this possibility may be implemented for optical micromanipulation.

In 2013, scientists at the Institute of Scientific Instruments (ISI) and the University of St Andrews created a tractor beam that pulls objects on a microscopic level. The study states that this technique may have potential for bio-medical research. Professor Zemanek said: "The whole team have spent a number of years investigating various configurations of particles delivery by light." Dr. Brzobohaty said: "These methods are opening new opportunities for fundamental photonics as well as applications for life-sciences." Dr Cizmar said: "Because of the similarities between optical and acoustic particle manipulation we anticipate that this concept will inspire exciting future studies in areas outside the field of photonics."

Physicists from ANU built a reversible tractor beam, capable of transporting particles "one fifth of a millimetre in diameter a distance of up to 20 centimetres, around 100 times further than previous experiments." According to Professor Wieslaw Krolikowski, of the Research School of Physics and Engineering, "demonstration of a large scale laser beam like this is a kind of holy grail for laser physicists." The work was published in Nature in 2014. In the same year, Dr. Horst Punzmann and his team at ANU developed a tractor beam that works on water, which could potentially be used to contain oil spills, control floating objects, or study the formation of rips on beaches.

In 2015, a team of researchers built the world's first sonic tractor beam that can lift and move objects using sound waves. An Instructables webpage was made available with instructions to build a rudimentary device.

In 2016, Rice University scientists discovered that Tesla coils can generate force fields able to manipulate matter through a process called teslaphoresis.

In December 2016, researchers were able to manipulate the movement of bacterial cells using a tractor beam, thereby opening the possibility that tractor beams could have future applications in biological sciences.

In 2018, a research team from Tel-Aviv University, led by Dr. Alon Bahabad, experimentally demonstrated an optical analog of the Archimedes' screw where the rotation of a helical-intensity laser beam is transferred to the axial motion of optically trapped micrometer-scale, airborne, carbon-based particles. With this optical screw, particles were easily conveyed with controlled velocity and direction, upstream or downstream of the optical flow, over half a centimeter.

In 2019, researchers at the University of Washington used a tractor beam to assemble nanoscale materials in a process they describe as "photonic nanosoldering".

Fiction

Illustration of man being abducted with a tractor beam

Science fiction movies and telecasts normally depict tractor and repulsor beams as audible, narrow rays of visible light covering a small target area. Tractor beams are most commonly used on spaceships and space stations. They are generally used in three ways:

1. As a device for securing or retrieving cargo, passengers, shuttlecraft, etc. This is analogous to cranes on modern ships.
2. As a device to harness objects that can then be used as impromptu weapons by the craft
3. As a means of preventing an enemy from escaping, analogous to grappling hooks.

In the latter case, countermeasures can usually be employed against tractor beams. These may include pressor beams (a stronger pressor beam will counteract a weaker tractor beam) or plane shears a.k.a. shearing planes (a device to "cut" the tractor beam and render it ineffective). In some fictional realities, shields can block tractor beams, or the generators can be disabled by sending a large amount of energy along the beam to its source.

Tractor beams and pressor beams can be used together as a weapon: by attracting one side of an enemy spaceship while repelling the other, one can create severely damaging shear effects in its hull. Another mode of destructive use of such beams is rapid alternating between pressing and pulling force in order to cause structural damage to the ship as well as inflicting lethal forces on its crew.

Two objects being brought together by a tractor beam are usually attracted toward their common center of gravity. This means that if a small spaceship applies a tractor beam to a large object such as a planet, the ship will be drawn toward the planet, rather than vice versa.

In Star Trek, tractor beams are imagined to work by placing a target in the focus of a subspace/graviton interference pattern created by two beams from an emitter. When the beams are manipulated correctly the target is drawn along with the interference pattern. The target may be moved toward or away from the emitter by changing the polarity of the beams. The range of the beam affects the maximum mass that the emitter can move, and the emitter subjects its anchoring structure to significant force.

Literature

• Rudyard Kipling's As Easy as A.B.C. (1912) made use of the "flying loop", generated by one of the airships of the Aerial Board of Control, when a woman tried, as a political statement, to publicly kill herself. The loop pulled the knife from her hand and, instead of drawing it toward the airship, flung it fifty yards away; it also continued to hold her arm rigid for a second or so afterward. John Brunner, in the foreword to a collection of Kipling's science fiction, said this may be the first depiction of a tractor beam.
• E. E. Smith coined the term "tractor beam" (an update of his earlier "attractor-beam") in his novel Spacehounds of IPC, originally serialized in Amazing Stories magazine in 1931. The hero of his Skylark of Space books (1929 onwards) had invented "attractor beams" and "repellor beams". Repellors can also be emitted isotropically as a defensive force field against material projectiles. The device also appears in Smith's Lensman books.
• In Philip Francis Nowlan's Buck Rogers novel Armageddon 2419 A.D. (1928), the enemy airships used "repellor beams" for support and propulsion, similar to the "eighth ray" beams used for support and propulsion of Martian airships in the Barsoom/John Carter of Mars series (first published 1912–1943) by Edgar Rice Burroughs.
• Tom Swift – In the Tom Swift Jr. book Tom Swift and The Deep-Sea Hydrodome (1958), Tom invents the "repellatron". The device can be set to repel specific chemical elements. It was used to create a bubble habitat on the ocean floor, and as the propulsion system for his spacecraft Challenger.
• The Sector General books by James White: The 1963 novel Star Surgeon is the source of the combined tractor/pressor beam weapon called the Rattler. The weapon attracts then repels the target (an entire ship or a segment of the ship's hull) at 80 gs, several times a minute. The novel also featured a type of force field called a "repulsion screen".
• The Trigger by Arthur C. Clarke involves the development of tractor beams in the early part of the novel.
• Sixth Column by Robert A. Heinlein describes tractor/pressor beams as a product of the physics of a "newly-discovered magneto-gravitic or electro-gravitic spectra" featured in the novel.

Comics

• Buck Rogers comic strip – originally just repulsor-beams; tractors appeared by the 1970s
• Iron Man's various armor suits usually feature repulsor beam projectors mounted in the palms as one of the main weapon systems.

Movies and television series

Star Trek (TV series, films, books and games). One of the most visible and iconic uses of the concept. One of the few prominent fictitious depictions which used such beams repeatedly and referred to them consistently as tractor beams.