Markov decision process

From Wikipedia, the free encyclopedia

A Markov decision process (MDP) is a discrete time stochastic control process. It provides a mathematical framework for modeling decision making in situations where outcomes are partly random and partly under the control of a decision maker. MDPs are useful for studying optimization problems solved via dynamic programming and reinforcement learning. MDPs were known at least as early as the 1950s; a core body of research on Markov decision processes resulted from Howard's 1960 book, Dynamic Programming and Markov Processes. They are used in many disciplines, including robotics, automatic control, economics and manufacturing. The name of MDPs comes from the Russian mathematician Andrey Markov.

At each time step, the process is in some state ${\displaystyle s}$, and the decision maker may choose any action ${\displaystyle a}$ that is available in state ${\displaystyle s}$. The process responds at the next time step by randomly moving into a new state ${\displaystyle s'}$, and giving the decision maker a corresponding reward ${\displaystyle R_{a}(s,s')}$.

The probability that the process moves into its new state ${\displaystyle s'}$ is influenced by the chosen action. Specifically, it is given by the state transition function ${\displaystyle P_{a}(s,s')}$. Thus, the next state ${\displaystyle s'}$ depends on the current state ${\displaystyle s}$ and the decision maker's action ${\displaystyle a}$. But given ${\displaystyle s}$ and ${\displaystyle a}$, it is conditionally independent of all previous states and actions; in other words, the state transitions of an MDP satisfies the Markov property.

Markov decision processes are an extension of Markov chains; the difference is the addition of actions (allowing choice) and rewards (giving motivation). Conversely, if only one action exists for each state (e.g. "wait") and all rewards are the same (e.g. "zero"), a Markov decision process reduces to a Markov chain.

Definition

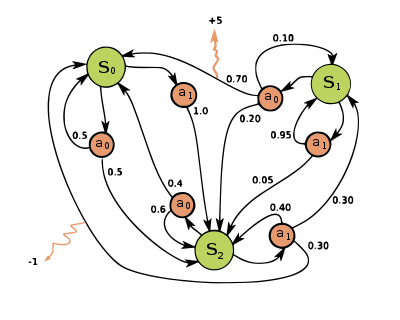
Example of a simple MDP with three states (green circles) and two actions (orange circles), with two rewards (orange arrows).

A Markov decision process is a 4-tuple ${\displaystyle (S,A,P_{a},R_{a})}$, where:

• ${\displaystyle S}$ is a finite set of states;
• ${\displaystyle A}$ is a finite set of actions (alternatively, ${\displaystyle A_{s}}$ is the finite set of actions available from state ${\displaystyle s}$);
• ${\displaystyle P_{a}(s,s')=\Pr(s_{t+1}=s'\mid s_{t}=s,a_{t}=a)}$ is the probability that action ${\displaystyle a}$ in state ${\displaystyle s}$ at time ${\displaystyle t}$ will lead to state ${\displaystyle s'}$ at time ${\displaystyle t+1}$;
• ${\displaystyle R_{a}(s,s')}$ is the immediate reward (or expected immediate reward) received after transitioning from state ${\displaystyle s}$ to state ${\displaystyle s'}$, due to action ${\displaystyle a}$.

(Note: The theory of Markov decision processes does not state that ${\displaystyle S}$ or ${\displaystyle A}$ are finite, but the basic algorithms below assume that they are finite.

Definition

Example of a simple MDP with three states (green circles) and two actions (orange circles), with two rewards (orange arrows).

A Markov decision process is a 4-tuple ${\displaystyle (S,A,P_{a},R_{a})}$, where:

1. ${\displaystyle S}$ is a finite set of states;
2. ${\displaystyle A}$ is a finite set of actions (alternatively, ${\displaystyle A_{s}}$ is the finite set of actions available from state ${\displaystyle s}$);
3. ${\displaystyle P_{a}(s,s')=\Pr(s_{t+1}=s'\mid s_{t}=s,a_{t}=a)}$ is the probability that action ${\displaystyle a}$ in state ${\displaystyle s}$ at time ${\displaystyle t}$ will lead to state ${\displaystyle s'}$ at time ${\displaystyle t+1}$;
4. ${\displaystyle R_{a}(s,s')}$ is the immediate reward (or expected immediate reward) received after transitioning from state ${\displaystyle s}$ to state ${\displaystyle s'}$, due to action ${\displaystyle a}$.

(Note: The theory of Markov decision processes does not state that ${\displaystyle S}$ or ${\displaystyle A}$ are finite, but the basic algorithms below assume that they are finite.)

Problem

The core problem of MDPs is to find a "policy" for the decision maker: a function ${\displaystyle \pi }$ that specifies the action ${\displaystyle \pi (s)}$ that the decision maker will choose when in state ${\displaystyle s}$. Once a Markov decision process is combined with a policy in this way, this fixes the action for each state and the resulting combination behaves like a Markov chain (since the action chosen in state ${\displaystyle s}$ is completely determined by ${\displaystyle \pi (s)}$ and ${\displaystyle \Pr(s_{t+1}=s'\mid s_{t}=s,a_{t}=a)}$ reduces to ${\displaystyle \Pr(s_{t+1}=s'\mid s_{t}=s)}$, a Markov transition matrix).

The goal is to choose a policy ${\displaystyle \pi }$ that will maximize some cumulative function of the random rewards, typically the expected discounted sum over a potentially infinite horizon:

${\displaystyle \sum _{t=0}^{\infty }{\gamma ^{t}R_{a_{t}}(s_{t},s_{t+1})}}$ (where we choose ${\displaystyle a_{t}=\pi (s_{t})}$, i.e. actions given by the policy),

where ${\displaystyle \ \gamma \ }$ is the discount factor and satisfies ${\displaystyle 0\leq \ \gamma \ <1 annotation="">$. (For example, ${\displaystyle \gamma =1/(1+r)}$ when the discount rate is r.) ${\displaystyle \gamma }$ is typically close to 1.

Because of the Markov property, the optimal policy for this particular problem can indeed be written as a function of ${\displaystyle s}$ only, as assumed above.

Algorithms

The solution for an MDP is a policy which describes the best action for each state in the MDP, known as the optimal policy. This optimal policy can be found through a variety of methods, like dynamic programming.

Some dynamic programming solutions require knowledge of the state transition function ${\displaystyle P}$ and the reward function ${\displaystyle R}$. Others can solve for the optimal policy of an MDP using experimentation alone.

Consider the case in which there is a given the state transition function ${\displaystyle P}$ and reward function ${\displaystyle R}$ for an MDP, and we seek the optimal policy ${\displaystyle \pi ^{*}}$ that maximizes the expected discounted reward.

The standard family of algorithms to calculate this optimal policy requires storage for two arrays indexed by state: value ${\displaystyle V}$, which contains real values, and policy ${\displaystyle \pi }$ which contains actions. At the end of the algorithm, ${\displaystyle \pi }$ will contain the solution and ${\displaystyle V(s)}$ will contain the discounted sum of the rewards to be earned (on average) by following that solution from state ${\displaystyle s}$.

The algorithm has two kinds of steps, a value update and a policy update, which are repeated in some order for all the states until no further changes take place. Both recursively update a new estimation of the optimal policy and state value using an older estimation of those values.

${\displaystyle \pi (s):={\arg \max }_{a}\left\{\sum _{s'}P(s'|s,a)\left(R(s'|s,a)+\gamma V(s')\right)\right\}}$

${\displaystyle V(s):=\sum _{s'}P_{\pi (s)}(s,s')\left(R_{\pi (s)}(s,s')+\gamma V(s')\right)}$

Their order depends on the variant of the algorithm; one can also do them for all states at once or state by state, and more often to some states than others. As long as no state is permanently excluded from either of the steps, the algorithm will eventually arrive at the correct solution.

Notable variants

Value iteration

In value iteration (Bellman 1957), which is also called backward induction, the ${\displaystyle \pi }$ function is not used; instead, the value of ${\displaystyle \pi (s)}$ is calculated within ${\displaystyle V(s)}$ whenever it is needed. Substituting the calculation of ${\displaystyle \pi (s)}$ into the calculation of ${\displaystyle V(s)}$ gives the combined step:

${\displaystyle V_{i+1}(s):=\max _{a}\left\{\sum _{s'}P_{a}(s,s')\left(R_{a}(s,s')+\gamma V_{i}(s')\right)\right\},}$

where ${\displaystyle i}$ is the iteration number. Value iteration starts at ${\displaystyle i=0}$ and ${\displaystyle V_{0}}$ as a guess of the value function. It then iterates, repeatedly computing ${\displaystyle V_{i+1}}$ for all states ${\displaystyle s}$, until ${\displaystyle V}$ converges with the left-hand side equal to the right-hand side (which is the "Bellman equation" for this problem). Lloyd Shapley's 1953 paper on stochastic games included as a special case the value iteration method for MDPs, but this was recognized only later on.

Policy iteration

In policy iteration (Howard 1960), step one is performed once, and then step two is repeated until it converges. Then step one is again performed once and so on.

Instead of repeating step two to convergence, it may be formulated and solved as a set of linear equations. These equations are merely obtained by making ${\displaystyle s=s'}$ in the step two equation. Thus, repeating step two to convergence can be interpreted as solving the linear equations by Relaxation (iterative method).
 
This variant has the advantage that there is a definite stopping condition: when the array ${\displaystyle \pi }$ does not change in the course of applying step 1 to all states, the algorithm is completed.

Policy iteration is usually slower than value iteration for a large number of possible states.

Modified policy iteration

In modified policy iteration (van Nunen 1976; Puterman & Shin 1978), step one is performed once, and then step two is repeated several times. Then step one is again performed once and so on.

Prioritized sweeping

In this variant, the steps are preferentially applied to states which are in some way important – whether based on the algorithm (there were large changes in ${\displaystyle V}$ or ${\displaystyle \pi }$ around those states recently) or based on use (those states are near the starting state, or otherwise of interest to the person or program using the algorithm).

Extensions and generalizations

A Markov decision process is a stochastic game with only one player.

Partial observability

The solution above assumes that the state ${\displaystyle s}$ is known when action is to be taken; otherwise ${\displaystyle \pi (s)}$ cannot be calculated. When this assumption is not true, the problem is called a partially observable Markov decision process or POMDP.

A major advance in this area was provided by Burnetas and Katehakis in "Optimal adaptive policies for Markov decision processes". In this work, a class of adaptive policies that possess uniformly maximum convergence rate properties for the total expected finite horizon reward were constructed under the assumptions of finite state-action spaces and irreducibility of the transition law. These policies prescribe that the choice of actions, at each state and time period, should be based on indices that are inflations of the right-hand side of the estimated average reward optimality equations.

Reinforcement learning

If the probabilities or rewards are unknown, the problem is one of reinforcement learning.

For this purpose it is useful to define a further function, which corresponds to taking the action ${\displaystyle a}$ and then continuing optimally (or according to whatever policy one currently has):

${\displaystyle \ Q(s,a)=\sum _{s'}P_{a}(s,s')(R_{a}(s,s')+\gamma V(s')).\ }$

While this function is also unknown, experience during learning is based on ${\displaystyle (s,a)}$ pairs (together with the outcome ${\displaystyle s'}$; that is, "I was in state ${\displaystyle s}$ and I tried doing ${\displaystyle a}$ and ${\displaystyle s'}$ happened"). Thus, one has an array ${\displaystyle Q}$ and uses experience to update it directly. This is known as Q-learning.

Reinforcement learning can solve Markov decision processes without explicit specification of the transition probabilities; the values of the transition probabilities are needed in value and policy iteration. In reinforcement learning, instead of explicit specification of the transition probabilities, the transition probabilities are accessed through a simulator that is typically restarted many times from a uniformly random initial state. Reinforcement learning can also be combined with function approximation to address problems with a very large number of states.

Learning automata

Another application of MDP process in machine learning theory is called learning automata. This is also one type of reinforcement learning if the environment is stochastic. The first detail learning automata paper is surveyed by Narendra and Thathachar (1974), which were originally described explicitly as finite state automata. Similar to reinforcement learning, learning automata algorithm also has the advantage of solving the problem when probability or rewards are unknown. The difference between learning automata and Q-learning is that they omit the memory of Q-values, but update the action probability directly to find the learning result. Learning automata is a learning scheme with a rigorous proof of convergence.

In learning automata theory, a stochastic automaton consists of:

• a set x of possible inputs,
• a set Φ = { Φ₁, ..., Φ_s } of possible internal states,
• a set α = { α₁, ..., α_r } of possible outputs, or actions, with r≤s,
• an initial state probability vector p(0) = ≪ p₁(0), ..., p_s(0) ≫,
• a computable function A which after each time step t generates p(t+1) from p(t), the current input, and the current state, and
• a function G: Φ → α which generates the output at each time step.

The states of such an automaton correspond to the states of a "discrete-state discrete-parameter Markov process". At each time step t=0,1,2,3,..., the automaton reads an input from its environment, updates P(t) to P(t+1) by A, randomly chooses a successor state according to the probabilities P(t+1) and outputs the corresponding action. The automaton's environment, in turn, reads the action and sends the next input to the automaton.

Category theoretic interpretation

Other than the rewards, a Markov decision process ${\displaystyle (S,A,P)}$ can be understood in terms of Category theory. Namely, let ${\displaystyle {\mathcal {A}}}$ denote the free monoid with generating set A. Let Dist denote the Kleisli category of the Giry monad. Then a functor ${\displaystyle {\mathcal {A}}\to \mathbf {Dist} }$ encodes both the set S of states and the probability function P.

In this way, Markov decision processes could be generalized from monoids (categories with one object) to arbitrary categories. One can call the result ${\displaystyle ({\mathcal {C}},F:{\mathcal {C}}\to \mathbf {Dist} )}$ a context-dependent Markov decision process, because moving from one object to another in ${\displaystyle {\mathcal {C}}}$ changes the set of available actions and the set of possible states.

Fuzzy Markov decision processes (FMDPs)

In the MDPs, an optimal policy is a policy which maximizes the probability-weighted summation of future rewards. Therefore, an optimal policy consists of several actions which belong to a finite set of actions. In fuzzy Markov decision processes (FMDPs), first, the value function is computed as regular MDPs (i.e., with a finite set of actions); then, the policy is extracted by a fuzzy inference system. In other words, the value function is utilized as an input for the fuzzy inference system, and the policy is the output of the fuzzy inference system.

Continuous-time Markov decision process

In discrete-time Markov Decision Processes, decisions are made at discrete time intervals. However, for continuous-time Markov decision processes, decisions can be made at any time the decision maker chooses. In comparison to discrete-time Markov decision processes, continuous-time Markov decision processes can better model the decision making process for a system that has continuous dynamics, i.e., the system dynamics is defined by partial differential equations (PDEs).

Definition

In order to discuss the continuous-time Markov decision process, we introduce two sets of notations:
If the state space and action space are finite,

• ${\displaystyle {\mathcal {S}}}$: State space;
• ${\displaystyle {\mathcal {A}}}$: Action space;
• ${\displaystyle q(i|j,a)}$: ${\displaystyle {\mathcal {S}}\times {\mathcal {A}}\rightarrow \triangle {\mathcal {S}}}$, transition rate function;
• ${\displaystyle R(i,a)}$: ${\displaystyle {\mathcal {S}}\times {\mathcal {A}}\rightarrow \mathbb {R} }$, a reward function.

If the state space and action space are continuous,

• ${\displaystyle {\mathcal {X}}}$: state space;
• ${\displaystyle {\mathcal {U}}}$: space of possible control;
• ${\displaystyle f(x,u)}$: ${\displaystyle {\mathcal {X}}\times {\mathcal {U}}\rightarrow \triangle {\mathcal {X}}}$, a transition rate function;
• ${\displaystyle r(x,u)}$: ${\displaystyle {\mathcal {X}}\times {\mathcal {U}}\rightarrow \mathbb {R} }$, a reward rate function such that ${\displaystyle r(x(t),u(t))dt=dR(x(t),u(t))}$, where ${\displaystyle R(x,u)}$ is the reward function we discussed in previous case.

Problem

Like the discrete-time Markov decision processes, in continuous-time Markov decision processes we want to find the optimal policy or control which could give us the optimal expected integrated reward:

${\displaystyle \max \quad \mathbb {E} _{u}\left[\left.\int _{0}^{\infty }\gamma ^{t}r(x(t),u(t)))dt\;\right|x_{0}\right]}$

Where ${\displaystyle 0\leq \gamma <1 annotation="">$

Linear programming formulation

If the state space and action space are finite, we could use linear programming to find the optimal policy, which was one of the earliest approaches applied. Here we only consider the ergodic model, which means our continuous-time MDP becomes an ergodic continuous-time Markov chain under a stationary policy. Under this assumption, although the decision maker can make a decision at any time at the current state, he could not benefit more by taking more than one action. It is better for him to take an action only at the time when system is transitioning from the current state to another state. Under some conditions, if our optimal value function ${\displaystyle V^{*}}$ is independent of state ${\displaystyle i}$, we will have the following inequality:

${\displaystyle g\geq R(i,a)+\sum _{j\in S}q(j\mid i,a)h(j)\quad \forall i\in S{\text{ and }}a\in A(i)}$

If there exists a function ${\displaystyle h}$, then ${\displaystyle {\bar {V}}^{*}}$ will be the smallest ${\displaystyle g}$ satisfying the above equation. In order to find ${\displaystyle {\bar {V}}^{*}}$, we could use the following linear programming model:

• Primal linear program(P-LP);

${\displaystyle {\begin{aligned}{\text{Minimize}}\quad &g\\{\text{s.t}}\quad &g-\sum _{j\in S}q(j\mid i,a)h(j)\geq R(i,a)\,\,\forall i\in S,\,a\in A(i)\end{aligned}}}$

• Dual linear program(D-LP);

${\displaystyle {\begin{aligned}{\text{Maximize}}&\sum _{i\in S}\sum _{a\in A(i)}R(i,a)y(i,a)\\{\text{s.t.}}&\sum _{i\in S}\sum _{a\in A(i)}q(j\mid i,a)y(i,a)=0\quad \forall j\in S,\\&\sum _{i\in S}\sum _{a\in A(i)}y(i,a)=1,\\&y(i,a)\geq 0\qquad \forall a\in A(i){\text{ and }}\forall i\in S\end{aligned}}}$

${\displaystyle y(i,a)}$ is a feasible solution to the D-LP if ${\displaystyle y(i,a)}$ is nonnative and satisfied the constraints in the D-LP problem. A feasible solution ${\displaystyle y^{*}(i,a)}$ to the D-LP is said to be an optimal solution if:

${\displaystyle {\begin{aligned}\sum _{i\in S}\sum _{a\in A(i)}R(i,a)y^{*}(i,a)\geq \sum _{i\in S}\sum _{a\in A(i)}R(i,a)y(i,a)\end{aligned}}}$

for all feasible solution ${\displaystyle y(i,a)}$ to the D-LP. Once we have found the optimal solution ${\displaystyle y^{*}(i,a)}$, we can use it to establish the optimal policies.

Hamilton–Jacobi–Bellman equation

In continuous-time MDP, if the state space and action space are continuous, the optimal criterion could be found by solving Hamilton–Jacobi–Bellman (HJB) partial differential equation. In order to discuss the HJB equation, we need to reformulate our problem

${\displaystyle {\begin{aligned}V(x(0),0)={}&\max _{u}\int _{0}^{T}r(x(t),u(t))\,dt+D[x(T)]\\{\text{s.t.}}\quad &{\frac {dx(t)}{dt}}=f[t,x(t),u(t)]\end{aligned}}}$

${\displaystyle D(\cdot )}$ is the terminal reward function, ${\displaystyle x(t)}$ is the system state vector, ${\displaystyle u(t)}$ is the system control vector we try to find. ${\displaystyle f(\cdot )}$ shows how the state vector changes over time. The Hamilton–Jacobi–Bellman equation is as follows:

${\displaystyle 0=\max _{u}(r(t,x,u)+{\frac {\partial V(t,x)}{\partial x}}f(t,x,u))}$

We could solve the equation to find the optimal control ${\displaystyle u(t)}$, which could give us the optimal value ${\displaystyle V^{*}}$

Application

Continuous-time Markov decision processes have applications in queueing systems, epidemic processes, and population processes.

Alternative notations

The terminology and notation for MDPs are not entirely settled. There are two main streams — one focuses on maximization problems from contexts like economics, using the terms action, reward, value, and calling the discount factor ${\displaystyle \beta }$ or ${\displaystyle \gamma }$, while the other focuses on minimization problems from engineering and navigation, using the terms control, cost, cost-to-go, and calling the discount factor ${\displaystyle \alpha }$. In addition, the notation for the transition probability varies.

in this article	alternative	comment
action ${\displaystyle a}$	control ${\displaystyle u}$
reward ${\displaystyle R}$	cost ${\displaystyle g}$	${\displaystyle g}$ is the negative of ${\displaystyle R}$
value ${\displaystyle V}$	cost-to-go ${\displaystyle J}$	${\displaystyle J}$ is the negative of ${\displaystyle V}$
policy ${\displaystyle \pi }$	policy ${\displaystyle \mu }$
discounting factor ${\displaystyle \ \gamma \ }$	discounting factor ${\displaystyle \alpha }$
transition probability ${\displaystyle P_{a}(s,s')}$	transition probability ${\displaystyle p_{ss'}(a)}$

In addition, transition probability is sometimes written ${\displaystyle Pr(s,a,s')}$, ${\displaystyle Pr(s'|s,a)}$ or, rarely, ${\displaystyle p_{s's}(a).}$

Constrained Markov decision processes

Constrained Markov decision processes (CMDPs) are extensions to Markov decision process (MDPs). There are three fundamental differences between MDPs and CMDPs^:

1. There are multiple costs incurred after applying an action instead of one.
2. CMDPs are solved with linear programs only, and dynamic programming does not work.
3. The final policy depends on the starting state.

There are a number of applications for CMDPs. It has recently been used in motion planning scenarios in robotics.