Kerr metric

From Wikipedia, the free encyclopedia

The Kerr metric or Kerr geometry describes the geometry of empty spacetime around a rotating uncharged axially-symmetric black hole with a quasispherical event horizon. The Kerr metric is an exact solution of the Einstein field equations of general relativity; these equations are highly non-linear, which makes exact solutions very difficult to find.

Overview

The Kerr metric is a generalization of the Schwarzschild metric, discovered by Karl Schwarzschild in 1915, which described the geometry of spacetime around an uncharged, spherically-symmetric, and non-rotating body. The corresponding solution for a charged, spherical, non-rotating body, the Reissner–Nordström metric, was discovered soon afterwards (1916–1918). However, the exact solution for an uncharged, rotating black-hole, the Kerr metric, remained unsolved until 1963, when it was discovered by Roy Kerr. The natural extension to a charged, rotating black-hole, the Kerr–Newman metric, was discovered shortly thereafter in 1965. These four related solutions may be summarized by the following table:

	Non-rotating (J = 0)	Rotating (J ≠ 0)
Uncharged (Q = 0)	Schwarzschild	Kerr
Charged (Q ≠ 0)	Reissner–Nordström	Kerr–Newman

where Q represents the body's electric charge and J represents its spin angular momentum.

According to the Kerr metric, such rotating black-holes should exhibit frame-dragging (also known as Lense–Thirring precession), a distinctive prediction of general relativity. Measurement of this frame dragging effect was a major goal of the Gravity Probe B experiment. Roughly speaking, this effect predicts that objects coming close to a rotating mass will be entrained to participate in its rotation, not because of any applied force or torque that can be felt, but rather because of the swirling curvature of spacetime itself associated with rotating bodies. At close enough distances, all objects – even light – must rotate with the black-hole; the region where this holds is called the ergosphere.

Rotating black holes have surfaces where the metric appears to have a singularity; the size and shape of these surfaces depends on the black hole's mass and angular momentum. The outer surface encloses the ergosphere and has a shape similar to a flattened sphere. The inner surface marks the "radius of no return" also called the "event horizon"; objects passing through this radius can never again communicate with the world outside that radius. However, neither surface is a true singularity, since their apparent singularity can be eliminated in a different coordinate system. Objects between these two horizons must co-rotate with the rotating body, as noted above; this feature can be used to extract energy from a rotating black hole, up to its invariant mass energy, Mc².

The LIGO experiment which detected gravitational waves also provided the first direct observation of a pair of Kerr black holes.

Mathematical form

in Boyer–Lindquist coordinates

The Kerr metric describes the geometry of spacetime in the vicinity of a mass M rotating with angular momentum J. The line element in Boyer–Lindquist coordinates is

${\displaystyle {\begin{aligned}-c^{2}d\tau ^{2}=ds^{2}=&-\left(1-{\frac {r_{s}r}{\Sigma }}\right)c^{2}dt^{2}+{\frac {\Sigma }{\Delta }}dr^{2}+\Sigma d\theta ^{2}\\&+\left(r^{2}+a^{2}+{\frac {r_{s}ra^{2}}{\Sigma }}\sin ^{2}\theta \right)\sin ^{2}\theta \ d\phi ^{2}-{\frac {2r_{s}ra\sin ^{2}\theta }{\Sigma }}\,c\,dt\,d\phi \end{aligned}}}$

where the coordinates ${\displaystyle r,\theta ,\phi }$ are standard spherical coordinate system, which are equivalent to the cartesian coordinates

${\displaystyle {x}={\sqrt {r^{2}+a^{2}}}\sin \theta \cos \phi }$

${\displaystyle {y}={\sqrt {r^{2}+a^{2}}}\sin \theta \sin \phi }$

${\displaystyle {z}=r\cos \theta }$

and r_s is the Schwarzschild radius

${\displaystyle r_{s}={\frac {2GM}{c^{2}}}}$

and where the length-scales a, Σ and Δ have been introduced for brevity

${\displaystyle a={\frac {J}{Mc}}}$

${\displaystyle \Sigma =r^{2}+a^{2}\cos ^{2}\theta }$

${\displaystyle \Delta =r^{2}-r_{s}r+a^{2}}$

A key feature to note in the above metric is the cross product ${\displaystyle {\begin{aligned}dt\,d\phi \end{aligned}}}$ term. There is coupling between time and motion in the plane of rotation that disappears when the black hole's angular momentum goes to zero.

In the non-relativistic limit where M (or, equivalently, r_s) goes to zero, the Kerr metric becomes the orthogonal metric for the oblate spheroidal coordinates

${\displaystyle c^{2}d\tau ^{2}=c^{2}dt^{2}-{\frac {\Sigma }{r^{2}+a^{2}}}dr^{2}-\Sigma d\theta ^{2}-\left(r^{2}+a^{2}\right)\sin ^{2}\theta d\phi ^{2}}$

The total mass equivalent M (the gravitating mass) of the body (including its rotational energy) and its irreducible mass M_irr are related by

${\displaystyle M_{\rm {irr}}={\sqrt {\frac {{\sqrt {M^{4}-a^{2}M^{2}}}+M^{2}}{2}}}\ \to \ M=2{\sqrt {\frac {M_{\rm {irr}}^{4}}{4M_{\rm {irr}}^{2}-a^{2}}}}}$.

If the complete rotational energy E_rot=c²(M-M_irr) of a black hole is extracted, for example with the Penrose process, the remaining mass cannot shrink below the irreducible mass. Therefore, if a black hole rotates with the spin a=M, its total mass-equivalent M is higher by a factor of √2 in comparison with a corresponding Schwarzschild black hole where M is equal to M_irr. The reason for this is that in order to get a static body to spin, energy needs to be applied to the system. Because of the mass–energy equivalence this energy also has a mass-equivalent, which adds to the total mass-energy of the system, M.

In Kerr–Schild coordinates

The Kerr metric can be expressed in "Kerr–Schild" form, using a particular set of Cartesian coordinates as follows. These solutions were proposed by Kerr and Schild in 1965.

${\displaystyle g_{\mu \nu }=\eta _{\mu \nu }+fk_{\mu }k_{\nu }\!}$

${\displaystyle f={\frac {Gr^{2}}{r^{4}+a^{2}z^{2}}}\left[2Mr\right]}$

${\displaystyle \mathbf {k} =(k_{x},k_{y},k_{z})=\left({\frac {rx+ay}{r^{2}+a^{2}}},{\frac {ry-ax}{r^{2}+a^{2}}},{\frac {z}{r}}\right)}$

${\displaystyle k_{0}=1.\!}$

Notice that k is a unit vector. Here M is the constant mass of the spinning object, η is the Minkowski tensor, and a is a constant rotational parameter of the spinning object. It is understood that the vector ${\displaystyle {\vec {a}}}$ is directed along the positive z-axis. The quantity r is not the radius, but rather is implicitly defined like this:

${\displaystyle 1={\frac {x^{2}+y^{2}}{r^{2}+a^{2}}}+{\frac {z^{2}}{r^{2}}}}$

Notice that the quantity r becomes the usual radius R

${\displaystyle r\to R={\sqrt {x^{2}+y^{2}+z^{2}}}}$

when the rotational parameter a approaches zero. In this form of solution, units are selected so that the speed of light is unity (c = 1). At large distances from the source (R >> a), these equations reduce to the Eddington–Finkelstein form of the Schwarzschild metric.

In the Kerr–Schild form of the Kerr metric, the determinant of the metric tensor is everywhere equal to negative one, even near the source.

Wave operator

Since even a direct check on the Kerr metric involves cumbersome calculations, the contravariant components ${\displaystyle g^{ik}}$ of the metric tensor in Boyer–Lindquist coordinates are shown below in the expression for the square of the four-gradient operator:

${\displaystyle {\begin{aligned}g^{\mu \nu }{\frac {\partial }{\partial {x^{\mu }}}}{\frac {\partial }{\partial {x^{\nu }}}}=&{\frac {1}{c^{2}\Delta }}\left(r^{2}+a^{2}+{\frac {r_{s}ra^{2}}{\Sigma }}\sin ^{2}\theta \right)\left({\frac {\partial }{\partial {t}}}\right)^{2}+{\frac {2r_{s}ra}{c\Sigma \Delta }}{\frac {\partial }{\partial {\phi }}}{\frac {\partial }{\partial {t}}}\\&-{\frac {1}{\Delta \sin ^{2}\theta }}\left(1-{\frac {r_{s}r}{\Sigma }}\right)\left({\frac {\partial }{\partial {\phi }}}\right)^{2}-{\frac {\Delta }{\Sigma }}\left({\frac {\partial }{\partial {r}}}\right)^{2}-{\frac {1}{\Sigma }}\left({\frac {\partial }{\partial {\theta }}}\right)^{2}\end{aligned}}}$

Frame dragging

We may rewrite the Kerr metric (1) in the following form:

${\displaystyle c^{2}d\tau ^{2}=\left(g_{tt}-{\frac {g_{t\phi }^{2}}{g_{\phi \phi }}}\right)dt^{2}+g_{rr}dr^{2}+g_{\theta \theta }d\theta ^{2}+g_{\phi \phi }\left(d\phi +{\frac {g_{t\phi }}{g_{\phi \phi }}}dt\right)^{2}.}$

This metric is equivalent to a co-rotating reference frame that is rotating with angular speed Ω that depends on both the radius r and the colatitude θ, where Ω is called the Killing horizon.

${\displaystyle \Omega =-{\frac {g_{t\phi }}{g_{\phi \phi }}}={\frac {r_{s}rac}{\Sigma \left(r^{2}+a^{2}\right)+r_{s}ra^{2}\sin ^{2}\theta }}.}$

Thus, an inertial reference frame is entrained by the rotating central mass to participate in the latter's rotation; this is called frame-dragging, and has been tested experimentally. Qualitatively, frame-dragging can be viewed as the gravitational analog of electromagnetic induction. An "ice skater", in orbit over the equator and rotationally at rest with respect to the stars, extends her arms. The arm extended toward the black hole will be torqued spinward. The arm extended away from the black hole will be torqued anti-spinward. She will therefore be rotationally sped up, in a counter-rotating sense to the black hole. This is the opposite of what happens in everyday experience. If she is already rotating at a certain speed when she extends her arms, inertial effects and frame-dragging effects will balance and her spin will not change. Due to the Principle of Equivalence gravitational effects are locally indistinguishable from inertial effects, so this rotation rate, at which when she extends her arms nothing happens, is her local reference for non-rotation. This frame is rotating with respect to the fixed stars and counter-rotating with respect to the black hole. A useful metaphor is a planetary gear system with the black hole being the sun gear, the ice skater being a planetary gear and the outside universe being the ring gear. This can be also be interpreted through Mach's principle.

Important surfaces

Location of the horizons, ergospheres and the ring singularity of the Kerr spacetime in Cartesian Kerr-Schild coordinates.

Comparison of the shadow (black) and the important surfaces (white) of a black hole. The spin parameter a is animated from 0 to M, while the left side of the black hole is rotating towards the observer.

The Kerr metric has two physical relevant surfaces on which it appears to be singular. The inner surface corresponds to an event horizon similar to that observed in the Schwarzschild metric; this occurs where the purely radial component g_rr of the metric goes to infinity. Solving the quadratic equation 1/g_rr = 0 yields the solution:

${\displaystyle r_{\rm {H}}^{\pm }={\frac {r_{s}\pm {\sqrt {r_{s}^{2}-4a^{2}}}}{2}}\ }$ which is in natural units of G=M=c=1: ${\displaystyle \ r_{\rm {H}}^{\pm }=1\pm {\sqrt {1-a^{2}}}}$.

Another singularity occurs where the purely temporal component g_tt of the metric changes sign from positive to negative. Again solving a quadratic equation g_tt=0 yields the solution:

${\displaystyle r_{\rm {E}}^{\pm }={\frac {r_{s}\pm {\sqrt {r_{s}^{2}-4a^{2}\cos ^{2}\theta }}}{2}}\ }$ or in natural units: ${\displaystyle \ r_{\rm {E}}^{\pm }=1\pm {\sqrt {1-a^{2}\cos ^{2}(\theta )}}}$.

Due to the cos²θ term in the square root, this outer surface resembles a flattened sphere that touches the inner surface at the poles of the rotation axis, where the colatitude θ equals 0 or π; the space between these two surfaces is called the ergosphere. Within this volume, the purely temporal component g_tt is negative, i.e., acts like a purely spatial metric component. Consequently, particles within this ergosphere must co-rotate with the inner mass, if they are to retain their time-like character. A moving particle experiences a positive proper time along its worldline, its path through spacetime. However, this is impossible within the ergosphere, where g_tt is negative, unless the particle is co-rotating with the interior mass M with an angular speed at least of Ω. Thus, no particle can rotate opposite to the central mass within the ergosphere.

As with the event horizon in the Schwarzschild metric the apparent singularities at r_H and r_E are an illusion created by the choice of coordinates (i.e., they are coordinate singularities). In fact, the space-time can be smoothly continued through them by an appropriate choice of coordinates.

Ergosphere and the Penrose process

A black hole in general is surrounded by a surface, called the event horizon and situated at the Schwarzschild radius for a nonrotating black hole, where the escape velocity is equal to the velocity of light. Within this surface, no observer/particle can maintain itself at a constant radius. It is forced to fall inwards, and so this is sometimes called the static limit.

A rotating black hole has the same static limit at its event horizon but there is an additional surface outside the event horizon named the "ergosurface" given by ${\displaystyle (r-M)^{2}=M^{2}-J^{2}\cos ^{2}\theta }$ in Boyer–Lindquist coordinates, which can be intuitively characterized as the sphere where "the rotational velocity of the surrounding space" is dragged along with the velocity of light. Within this sphere the dragging is greater than the speed of light, and any observer/particle is forced to co-rotate.

The region outside the event horizon but inside the surface where the rotational velocity is the speed of light, is called the ergosphere (from Greek ergon meaning work). Particles falling within the ergosphere are forced to rotate faster and thereby gain energy. Because they are still outside the event horizon, they may escape the black hole. The net process is that the rotating black hole emits energetic particles at the cost of its own total energy. The possibility of extracting spin energy from a rotating black hole was first proposed by the mathematician Roger Penrose in 1969 and is thus called the Penrose process. Rotating black holes in astrophysics are a potential source of large amounts of energy and are used to explain energetic phenomena, such as gamma-ray bursts.

Features of the Kerr geometry

The Kerr geometry exhibits many noteworthy features: the maximal analytic extension includes a sequence of asymptotically flat exterior regions, each associated with an ergosphere, stationary limit surfaces, event horizons, Cauchy horizons, closed timelike curves, and a ring-shaped curvature singularity. The geodesic equation can be solved exactly in closed form. In addition to two Killing vector fields (corresponding to time translation and axisymmetry), the Kerr geometry admits a remarkable Killing tensor. There is a pair of principal null congruences (one ingoing and one outgoing). The Weyl tensor is algebraically special, in fact it has Petrov type D. The global structure is known. Topologically, the homotopy type of the Kerr spacetime can be simply characterized as a line with circles attached at each integer point.

Note that the inner Kerr geometry is unstable with regard to perturbations in the interior region. This instability means that although the Kerr metric is axis-symmetric, a black hole created through gravitational collapse may not be so. This instability also implies that many of the features of the Kerr geometry described above may not be present inside such a black hole.

A surface on which light can orbit a black hole is called a photon sphere. The Kerr solution has infinitely many photon spheres, lying between an inner one and an outer one. In the nonrotating, Schwarzschild solution, with a=0, the inner and outer photon spheres degenerate, so that there is only one photon sphere at a single radius. The greater the spin of a black hole, the farther from each other the inner and outer photon spheres move. A beam of light traveling in a direction opposite to the spin of the black hole will circularly orbit the hole at the outer photon sphere. A beam of light traveling in the same direction as the black hole's spin will circularly orbit at the inner photon sphere. Orbiting geodesics with some angular momentum perpendicular to the axis of rotation of the black hole will orbit on photon spheres between these two extremes. Because the space-time is rotating, such orbits exhibit a precession, since there is a shift in the ${\displaystyle \phi \,}$ variable after completing one period in the ${\displaystyle \theta \,}$ variable.

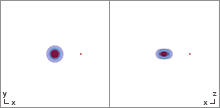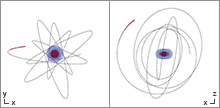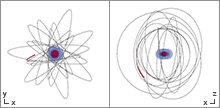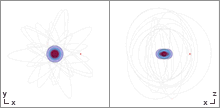
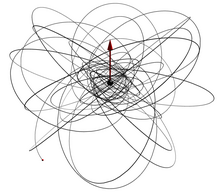
Trajectory equations

Animation of a test-particle's orbit around a spinning black hole. Left: top view, right: side view.

Another trajectory of a test mass around a spinning (Kerr) black hole. Unlike orbits around a Schwarzschild black hole, the orbit is not confined to a single plane, but will ergodically fill a toruslike region around the equator.

The equations of motion for test particles in the Kerr spacetime are governed by four constants of motion. The first is the invariant mass ${\displaystyle \mu }$ of the test particle, defined by the relation

${\displaystyle -\mu ^{2}=p^{\alpha }g_{\alpha \beta }p^{\beta },}$

where ${\displaystyle p^{\alpha }}$ is the four-momentum of the particle. Furthermore, there are two constants of motion given by the time translation and rotation symmetries of Kerr spacetime, the energy ${\displaystyle E}$, and the component of the orbital angular momentum parallel to spin of the black hole ${\displaystyle L_{z}}$:

${\displaystyle E=-p_{t}}$, and .

Using Hamilton–Jacobi theory, Brandon Carter showed that there exists a fourth constant of motion, ${\displaystyle Q}$, now referred to as the Carter constant. It is related to the total angular momentum of the particle and is given by

${\displaystyle Q=p_{\theta }^{2}+\cos ^{2}\theta {\Bigg (}a^{2}(\mu ^{2}-E^{2})+\left({\frac {L_{z}}{\sin \theta }}\right)^{2}{\Bigg )}}$.

Since there are four (independent) constants of motion for degrees of freedom the equations of motion for a test particle in Kerr spacetime are integrable.

Using these constants of motion, the trajectory equations for a test particle can be written (using natural units of G=M=c=1),

${\displaystyle \Sigma {\frac {dr}{d\lambda }}=\pm {\sqrt {R(r)}}}$

${\displaystyle \Sigma {\frac {d\theta }{d\lambda }}=\pm {\sqrt {\Theta (\theta )}}}$

${\displaystyle \Sigma {\frac {d\phi }{d\lambda }}=-\left(aE-{\frac {L_{z}}{\sin ^{2}\theta }}\right)+{\frac {a}{\Delta }}P(r)}$

${\displaystyle \Sigma {\frac {dt}{d\lambda }}=-a(aE\sin ^{2}\theta -L_{z})+{\frac {r^{2}+a^{2}}{\Delta }}P(r)}$

with

${\displaystyle \Theta (\theta )=Q-\cos ^{2}\theta \left(a^{2}(\mu ^{2}-E^{2})+{\frac {L_{z}^{2}}{\sin ^{2}\theta }}\right)}$

${\displaystyle P(r)=E(r^{2}+a^{2})-aL_{z}}$

${\displaystyle R(r)=P(r)^{2}-\Delta \left(r^{2}+(L_{z}-aE)^{2}+Q\right)}$

Where, ${\displaystyle \lambda }$ is an affine parameter such that ${\displaystyle {\frac {dx^{\alpha }}{d\lambda }}=p^{\alpha }}$. In particular, when ${\displaystyle \mu >0}$ the affine parameter ${\displaystyle \lambda }$, is related to the proper time ${\displaystyle \tau }$ through ${\displaystyle \lambda =\tau /\mu }$.

Because of the Frame-dragging-effect a zero angular momentum observer (ZAMO) is corotating with the angular velocity ${\displaystyle \Omega }$ which is defined with respect to the bookkeeper's coordinate time ${\displaystyle t}$. The local velocity ${\displaystyle v}$ of the test-particle is measured relative to a probe corotating with ${\displaystyle \Omega }$. The gravitational time-dilation between a ZAMO at fixed ${\displaystyle r}$ and a stationary observer far away from the mass is

${\displaystyle {\frac {t}{\tau }}={\sqrt {\frac {(a^{2}+r^{2})^{2}-a^{2}\ \Delta \ \sin ^{2}\theta }{\Delta \ \Sigma }}}}$.

Symmetries

The group of isometries of the Kerr metric is the subgroup of the ten-dimensional Poincaré group which takes the two-dimensional locus of the singularity to itself. It retains the time translations (one dimension) and rotations around its axis of rotation (one dimension). Thus it has two dimensions. Like the Poincaré group, it has four connected components: the component of the identity; the component which reverses time and longitude; the component which reflects through the equatorial plane; and the component that does both.

In physics, symmetries are typically associated with conserved constants of motion, in accordance with Noether's theorem. As shown above, the geodesic equations have four conserved quantities: one of which comes from the definition of a geodesic, and two of which arise from the time translation and rotation symmetry of the Kerr geometry. The fourth conserved quantity does not arise from a symmetry in the standard sense and is commonly referred to as a hidden symmetry.

Overextreme Kerr solutions

The location of the event horizon is determined by the larger root of ${\displaystyle \Delta =0}$. When ${\displaystyle {r_{s}/2}$ (i.e. ${\displaystyle GM^{2}$), there are no (real valued) solutions to this equation, and there is no event horizon. With no event horizons to hide it from the rest of the universe, the black hole ceases to be a black hole and will instead be a naked singularity.

Kerr black holes as wormholes

Although the Kerr solution appears to be singular at the roots of Δ = 0, these are actually coordinate singularities, and, with an appropriate choice of new coordinates, the Kerr solution can be smoothly extended through the values of ${\displaystyle r}$ corresponding to these roots. The larger of these roots determines the location of the event horizon, and the smaller determines the location of a Cauchy horizon. A (future-directed, time-like) curve can start in the exterior and pass through the event horizon. Once having passed through the event horizon, the ${\displaystyle r}$ coordinate now behaves like a time coordinate, so it must decrease until the curve passes through the Cauchy horizon.

The region beyond the Cauchy horizon has several surprising features. The ${\displaystyle r}$ coordinate again behaves like a spatial coordinate and can vary freely. The interior region has a reflection symmetry, so that a (future-directed time-like) curve may continue along a symmetric path, which continues through a second Cauchy horizon, through a second event horizon, and out into a new exterior region which is isometric to the original exterior region of the Kerr solution. The curve could then escape to infinity in the new region or enter the future event horizon of the new exterior region and repeat the process. This second exterior is sometimes thought of as another universe. On the other hand, in the Kerr solution, the singularity is a ring, and the curve may pass through the center of this ring. The region beyond permits closed time-like curves. Since the trajectory of observers and particles in general relativity are described by time-like curves, it is possible for observers in this region to return to their past. This interior solution is not likely to be physical and considered as a purely mathematical artifact.

While it is expected that the exterior region of the Kerr solution is stable, and that all rotating black holes will eventually approach a Kerr metric, the interior region of the solution appears to be unstable, much like a pencil balanced on its point. This is related to the idea of cosmic censorship.

Relation to other exact solutions

The Kerr geometry is a particular example of a stationary axially symmetric vacuum solution to the Einstein field equation. The family of all stationary axially symmetric vacuum solutions to the Einstein field equation are the Ernst vacuums.

The Kerr solution is also related to various non-vacuum solutions which model black holes. For example, the Kerr–Newman electrovacuum models a (rotating) black hole endowed with an electric charge, while the Kerr–Vaidya null dust models a (rotating) hole with infalling electromagnetic radiation.

The special case ${\displaystyle a=0\,}$ of the Kerr metric yields the Schwarzschild metric, which models a nonrotating black hole which is static and spherically symmetric, in the Schwarzschild coordinates. (In this case, every Geroch moment but the mass vanishes.)

The interior of the Kerr geometry, or rather a portion of it, is locally isometric to the Chandrasekhar–Ferrari CPW vacuum, an example of a colliding plane wave model. This is particularly interesting, because the global structure of this CPW solution is quite different from that of the Kerr geometry, and in principle, an experimenter could hope to study the geometry of (the outer portion of) the Kerr interior by arranging the collision of two suitable gravitational plane waves.

Multipole moments

Each asymptotically flat Ernst vacuum can be characterized by giving the infinite sequence of relativistic multipole moments, the first two of which can be interpreted as the mass and angular momentum of the source of the field. There are alternative formulations of relativistic multipole moments due to Hansen, Thorne, and Geroch, which turn out to agree with each other. The relativistic multipole moments of the Kerr geometry were computed by Hansen; they turn out to be

${\displaystyle M_{n}=M\,(i\,a)^{n}}$.

Thus, the special case of the Schwarzschild vacuum (a=0) gives the "monopole point source" of general relativity.

Warning: do not confuse these relativistic multipole moments with the Weyl multipole moments, which arise from treating a certain metric function (formally corresponding to Newtonian gravitational potential) which appears the Weyl-Papapetrou chart for the Ernst family of all stationary axisymmetric vacuum solutions using the standard euclidean scalar multipole moments. In a sense, the Weyl moments only (indirectly) characterize the "mass distribution" of an isolated source, and they turn out to depend only on the even order relativistic moments. In the case of solutions symmetric across the equatorial plane the odd order Weyl moments vanish. For the Kerr vacuum solutions, the first few Weyl moments are given by

${\displaystyle a_{0}=M,\;\;a_{1}=0,\;\;a_{2}=M\,\left({\frac {M^{2}}{3}}-a^{2}\right)}$.

In particular, we see that the Schwarzschild vacuum has nonzero second order Weyl moment, corresponding to the fact that the "Weyl monopole" is the Chazy–Curzon vacuum solution, not the Schwarzschild vacuum solution, which arises from the Newtonian potential of a certain finite length uniform density thin rod.

In weak field general relativity, it is convenient to treat isolated sources using another type of multipole, which generalize the Weyl moments to mass multipole moments and momentum multipole moments, characterizing respectively the distribution of mass and of momentum of the source. These are multi-indexed quantities whose suitably symmetrized (anti-symmetrized) parts can be related to the real and imaginary parts of the relativistic moments for the full nonlinear theory in a rather complicated manner.

Perez and Moreschi have given an alternative notion of "monopole solutions" by expanding the standard NP tetrad of the Ernst vacuums in powers of r (the radial coordinate in the Weyl-Papapetrou chart). According to this formulation:

• the isolated mass monopole source with zero angular momentum is the Schwarzschild vacuum family (one parameter),
• the isolated mass monopole source with radial angular momentum is the Taub–NUT vacuum family (two parameters; not quite asymptotically flat),
• the isolated mass monopole source with axial angular momentum is the Kerr vacuum family (two parameters).

In this sense, the Kerr vacuums are the simplest stationary axisymmetric asymptotically flat vacuum solutions in general relativity.

Open problems

The Kerr geometry is often used as a model of a rotating black hole. But if we hold the solution to be valid only outside some compact region (subject to certain restrictions), in principle we should be able to use it as an exterior solution to model the gravitational field around a rotating massive object other than a black hole, such as a neutron star, or the Earth. This works out very nicely for the non-rotating case, where we can match the Schwarzschild vacuum exterior to a Schwarzschild fluid interior, and indeed to more general static spherically symmetric perfect fluid solutions. However, the problem of finding a rotating perfect-fluid interior which can be matched to a Kerr exterior, or indeed to any asymptotically flat vacuum exterior solution, has proven very difficult. In particular, the Wahlquist fluid, which was once thought to be a candidate for matching to a Kerr exterior, is now known not to admit any such matching. At present it seems that only approximate solutions modeling slowly rotating fluid balls are known. (Slowly rotating fluid balls are the relativistic analog of oblate spheroidal balls with nonzero mass and angular momentum but vanishing higher multipole moments.) However, the exterior of the Neugebauer–Meinel disk, an exact dust solution which models a rotating thin disk, approaches in a limiting case the ${\displaystyle GM^{2}=cJ}$ Kerr geometry. Physical thin-disk solutions obtained by identifying parts of the Kerr space-time are also known.