Higgs boson

From Wikipedia, the free encyclopedia

Higgs boson

Candidate Higgs boson events from collisions between protons in the LHC. The top event in the CMS experiment shows a decay into two photons (dashed yellow lines and green towers). The lower event in the ATLAS experiment shows a decay into four muons (red tracks).
Composition	Elementary particle
Statistics	Bosonic
Status	A new particle with a mass of 125 GeV was discovered in 2012 and later confirmed to be the Higgs boson with more precise measurements. (See: Current status)
Symbol	H0
Theorised	R. Brout, F. Englert, P. Higgs, G. S. Guralnik, C. R. Hagen, and T. W. B. Kibble (1964)
Discovered	Large Hadron Collider (2011–2013)
Mass	125.18 ± 0.16 GeV/c2
Mean lifetime	1.56×10−22 s (predicted)
Decays into	Bottom-antibottom pair (observed) Two W bosons (observed) Two gluons (predicted) Tau-antitau pair (observed) Two Z bosons (observed) Two photons (observed) Various other decays (predicted)
Electric charge	0 e
Colour charge	0
Spin	0
Weak isospin	−1/2
Weak hypercharge	+1
Parity	+1

The Higgs boson is an elementary particle in the Standard Model of particle physics, produced by the quantum excitation of the Higgs field, one of the fields in particle physics theory. It is named after physicist Peter Higgs, who in 1964, along with five other scientists, proposed the mechanism which suggested the existence of such a particle. Its existence was confirmed in 2012 by the ATLAS and CMS collaborations based on collisions in the LHC at CERN.

On December 10, 2013, two of the physicists, Peter Higgs and François Englert, were awarded the Nobel Prize in Physics for their theoretical predictions. Although Higgs's name has come to be associated with this theory (the Higgs mechanism), several researchers between about 1960 and 1972 independently developed different parts of it.

In mainstream media the Higgs boson has often been called the "God particle", from a 1993 book on the topic, although the nickname is strongly disliked by many physicists, including Higgs himself, who regard it as sensationalism.

Introduction

The Standard Model

Physicists explain the properties of forces between elementary particles in terms of the Standard Model – a widely accepted framework for understanding almost everything in the known universe, other than gravity. (A separate theory, general relativity, is used for gravity.) In this model, the fundamental forces in nature arise from properties of our universe called gauge invariance and symmetries. The forces are transmitted by particles known as gauge bosons.

In the Standard Model, the Higgs particle is a boson with spin zero, no electric charge and no colour charge. It is also very unstable, decaying into other particles almost immediately. The Higgs field is a scalar field, with two neutral and two electrically charged components that form a complex doublet of the weak isospin SU(2) symmetry. The Higgs field has a "Mexican hat-shaped" potential. In its ground state, this causes the field to have a nonzero value everywhere (including otherwise empty space), and as a result, below a very high energy it breaks the weak isospin symmetry of the electroweak interaction. (Technically the non-zero expectation value converts the Lagrangian's Yukawa coupling terms into mass terms.) When this happens, three components of the Higgs field are "absorbed" by the SU(2) and U(1) gauge bosons (the "Higgs mechanism") to become the longitudinal components of the now-massive W and Z bosons of the weak force. The remaining electrically neutral component either manifests as a Higgs particle, or may couple separately to other particles known as fermions (via Yukawa couplings), causing these to acquire mass as well.

The problem of gauge boson mass

Field theories had been used with great success in understanding the electromagnetic field and the strong force, but by around 1960 all attempts to create a gauge invariant theory for the weak force (and its combination with fundamental force electromagnetism, the electroweak interaction) had consistently failed, with gauge theories thereby starting to fall into disrepute as a result. The problem was that the symmetry requirements in gauge theory predicted that both electromagnetism's gauge boson (the photon) and the weak force's gauge bosons (W and Z) should have zero mass. Although the photon is indeed massless, experiments show that the weak force's bosons have mass. This meant that either gauge invariance was an incorrect approach, or something else – unknown – was giving these particles their mass, but all attempts to suggest a theory able to solve this problem just seemed to create new theoretical issues.

By the late 1950s, physicists had not resolved these issues, which were significant obstacles to developing a full-fledged theory for particle physics.

Symmetry breaking

By the early 1960s, physicists had realised that a given symmetry law might not always be followed under certain conditions, at least in some areas of physics. This is called symmetry breaking and was recognised in the late 1950s by Yoichiro Nambu. Symmetry breaking can lead to surprising and unexpected results. In 1962 physicist Philip Anderson – an expert in superconductivity – wrote a paper that considered symmetry breaking in particle physics, and suggested that perhaps symmetry breaking might be the missing piece needed to solve the problems of gauge invariance in particle physics. If electroweak symmetry was somehow being broken, it might explain why electromagnetism's boson is massless, yet the weak force bosons have mass, and solve the problems. Shortly afterwards, in 1963, this was shown to be theoretically possible, at least for some limited (non-relativistic) cases.

Higgs mechanism

Following the 1962 and 1963 papers, three groups of researchers independently published the 1964 PRL symmetry breaking papers with similar conclusions and for all cases, not just some limited cases. They showed that the conditions for electroweak symmetry would be "broken" if an unusual type of field existed throughout the universe, and indeed, some fundamental particles would acquire mass. The field required for this to happen (which was purely hypothetical at the time) became known as the Higgs field (after Peter Higgs, one of the researchers) and the mechanism by which it led to symmetry breaking, known as the Higgs mechanism. A key feature of the necessary field is that it would take less energy for the field to have a non-zero value than a zero value, unlike all other known fields, therefore, the Higgs field has a non-zero value (or vacuum expectation) everywhere. It was the first proposal capable of showing how the weak force gauge bosons could have mass despite their governing symmetry, within a gauge invariant theory. 

Although these ideas did not gain much initial support or attention, by 1972 they had been developed into a comprehensive theory and proved capable of giving "sensible" results that accurately described particles known at the time, and which, with exceptional accuracy, predicted several other particles discovered during the following years. During the 1970s these theories rapidly became the Standard Model of particle physics. There was not yet any direct evidence that the Higgs field existed, but even without proof of the field, the accuracy of its predictions led scientists to believe the theory might be true. By the 1980s the question of whether or not the Higgs field existed, and therefore whether or not the entire Standard Model was correct, had come to be regarded as one of the most important unanswered questions in particle physics.

Higgs field

According to the Standard Model, a field of the necessary kind (the Higgs field) exists throughout space and breaks certain symmetry laws of the electroweak interaction. Via the Higgs mechanism, this field causes the gauge bosons of the weak force to be massive at all temperatures below an extreme high value. When the weak force bosons acquire mass, this affects their range, which becomes very small. Furthermore, it was later realised that the same field would also explain, in a different way, why other fundamental constituents of matter (including electrons and quarks) have mass. 

For many decades, scientists had no way to determine whether or not the Higgs field existed, because the technology needed for its detection did not exist at that time. If the Higgs field did exist, then it would be unlike any other known fundamental field, but it also was possible that these key ideas, or even the entire Standard Model, were somehow incorrect. Only discovering that the Higgs boson and therefore the Higgs field existed solved the problem. 

Unlike other known fields such as the electromagnetic field, the Higgs field is scalar and has a non-zero constant value in vacuum. The existence of the Higgs field became the last unverified part of the Standard Model of particle physics, and for several decades was considered "the central problem in particle physics".

The presence of the field, now confirmed by experimental investigation, explains why some fundamental particles have mass, despite the symmetries controlling their interactions implying that they should be massless. It also resolves several other long-standing puzzles, such as the reason for the extremely short range of the weak force. 

Although the Higgs field is non-zero everywhere and its effects are ubiquitous, proving its existence was far from easy. In principle, it can be proved to exist by detecting its excitations, which manifest as Higgs particles (the Higgs boson), but these are extremely difficult to produce and detect. The importance of this fundamental question led to a 40-year search, and the construction of one of the world's most expensive and complex experimental facilities to date, CERN's Large Hadron Collider, in an attempt to create Higgs bosons and other particles for observation and study. On 4 July 2012, the discovery of a new particle with a mass between 125 and 127 GeV/c² was announced; physicists suspected that it was the Higgs boson. Since then, the particle has been shown to behave, interact, and decay in many of the ways predicted for Higgs particles by the Standard Model, as well as having even parity and zero spin, two fundamental attributes of a Higgs boson. This also means it is the first elementary scalar particle discovered in nature. As of 2018, in-depth research shows the particle continuing to behave in line with predictions for the Standard Model Higgs boson. More studies are needed to verify with higher precision that the discovered particle has all of the properties predicted, or whether, as described by some theories, multiple Higgs bosons exist.

Higgs boson

The hypothesised Higgs mechanism made several accurate predictions, however to confirm its existence there was an extensive search for a matching particle associated with it – the "Higgs boson". Detecting Higgs bosons was difficult due to the energy required to produce them and their very rare production even if the energy is sufficient. It was therefore several decades before the first evidence of the Higgs boson was found. Particle colliders, detectors, and computers capable of looking for Higgs bosons took more than 30 years (c. 1980–2010) to develop.

By March 2013, the existence of the Higgs boson was confirmed, and therefore, the concept of some type of Higgs field throughout space is strongly supported. The nature and properties of this field are now being investigated further, using more data collected at the LHC.

Interpretation

Various analogies have been used to describe the Higgs field and boson, including analogies with well-known symmetry-breaking effects such as the rainbow and prism, electric fields, ripples, and resistance of macro objects moving through media (such as people moving through crowds or some objects moving through syrup or molasses). However, analogies based on simple resistance to motion are inaccurate, as the Higgs field does not work by resisting motion.

Significance

Evidence of the Higgs field and its properties has been extremely significant for many reasons. The importance of the Higgs boson is largely that it is able to be examined using existing knowledge and experimental technology, as a way to confirm and study the entire Higgs field theory. Conversely, proof that the Higgs field and boson do not exist would have also been significant.

Particle physics

Validation of the Standard Model

The Higgs boson validates the Standard Model through the mechanism of mass generation. As more precise measurements of its properties are made, more advanced extensions may be suggested or excluded. As experimental means to measure the field's behaviours and interactions are developed, this fundamental field may be better understood. If the Higgs field had not been discovered, the Standard Model would have needed to be modified or superseded.

Related to this, a belief generally exists among physicists that there is likely to be "new" physics beyond the Standard Model, and the Standard Model will at some point be extended or superseded. The Higgs discovery, as well as the many measured collisions occurring at the LHC, provide physicists a sensitive tool to parse data for where the Standard Model fails, and could provide considerable evidence guiding researchers into future theoretical developments.

Symmetry breaking of the electroweak interaction

Below an extremely high temperature, electroweak symmetry breaking causes the electroweak interaction to manifest in part as the short-ranged weak force, which is carried by massive gauge bosons. This symmetry breaking is required for atoms and other structures to form, as well as for nuclear reactions in stars, such as our Sun. The Higgs field is responsible for this symmetry breaking.

Particle mass acquisition

The Higgs field is pivotal in generating the masses of quarks and charged leptons (through Yukawa coupling) and the W and Z gauge bosons (through the Higgs mechanism).

It is worth noting that the Higgs field does not "create" mass out of nothing (which would violate the law of conservation of energy), nor is the Higgs field responsible for the mass of all particles. For example, approximately 99% of the mass of baryons (composite particles such as the proton and neutron), is due instead to quantum chromodynamic binding energy, which is the sum of the kinetic energies of quarks and the energies of the massless gluons mediating the strong interaction inside the baryons. In Higgs-based theories, the property of "mass" is a manifestation of potential energy transferred to fundamental particles when they interact ("couple") with the Higgs field, which had contained that mass in the form of energy.

Scalar fields and extension of the Standard Model

The Higgs field is the only scalar (spin 0) field to be detected; all the other fields in the Standard Model are spin ½ fermions or spin 1 bosons. According to Rolf-Dieter Heuer, director general of CERN when the Higgs boson was discovered, this existence proof of a scalar field is almost as important as the Higgs's role in determining the mass of other particles. It suggests that other hypothetical scalar fields suggested by other theories, from the inflaton to quintessence, could perhaps exist as well.

Cosmology

Inflaton

There has been considerable scientific research on possible links between the Higgs field and the inflaton – a hypothetical field suggested as the explanation for the expansion of space during the first fraction of a second of the universe (known as the "inflationary epoch"). Some theories suggest that a fundamental scalar field might be responsible for this phenomenon; the Higgs field is such a field, and its existence has led to papers analysing whether it could also be the inflaton responsible for this exponential expansion of the universe during the Big Bang. Such theories are highly tentative and face significant problems related to unitarity, but may be viable if combined with additional features such as large non-minimal coupling, a Brans–Dicke scalar, or other "new" physics, and they have received treatments suggesting that Higgs inflation models are still of interest theoretically.

Nature of the universe, and its possible fates

Diagram showing the Higgs boson and top quark masses, which could indicate whether our universe is stable, or a long-lived 'bubble'. As of 2012, the 2σ ellipse based on Tevatron and LHC data still allows for both possibilities.

 

In the Standard Model, there exists the possibility that the underlying state of our universe – known as the "vacuum" – is long-lived, but not completely stable. In this scenario, the universe as we know it could effectively be destroyed by collapsing into a more stable vacuum state. This was sometimes misreported as the Higgs boson "ending" the universe. If the masses of the Higgs boson and top quark are known more precisely, and the Standard Model provides an accurate description of particle physics up to extreme energies of the Planck scale, then it is possible to calculate whether the vacuum is stable or merely long-lived. A 125 – 127 GeV Higgs mass seems to be extremely close to the boundary for stability, but a definitive answer requires much more precise measurements of the pole mass of the top quark. New physics can change this picture.

If measurements of the Higgs boson suggest that our universe lies within a false vacuum of this kind, then it would imply – more than likely in many billions of years – that the universe's forces, particles, and structures could cease to exist as we know them (and be replaced by different ones), if a true vacuum happened to nucleate. It also suggests that the Higgs self-coupling λ and its β_λ function could be very close to zero at the Planck scale, with "intriguing" implications, including theories of gravity and Higgs-based inflation. A future electron–positron collider would be able to provide the precise measurements of the top quark needed for such calculations.

Vacuum energy and the cosmological constant

More speculatively, the Higgs field has also been proposed as the energy of the vacuum, which at the extreme energies of the first moments of the Big Bang caused the universe to be a kind of featureless symmetry of undifferentiated, extremely high energy. In this kind of speculation, the single unified field of a Grand Unified Theory is identified as (or modelled upon) the Higgs field, and it is through successive symmetry breakings of the Higgs field, or some similar field, at phase transitions that the presently known forces and fields of the universe arise.

The relationship (if any) between the Higgs field and the presently observed vacuum energy density of the universe has also come under scientific study. As observed, the present vacuum energy density is extremely close to zero, but the energy density expected from the Higgs field, supersymmetry, and other current theories are typically many orders of magnitude larger. It is unclear how these should be reconciled. This cosmological constant problem remains a further major unanswered problem in physics.

Practical and technological impact

As yet, there are no known immediate technological benefits of finding the Higgs particle. However, a common pattern for fundamental discoveries is for practical applications to follow later, and once the discovery has been explored further, perhaps becoming the basis for new technologies of importance to society.

The challenges in particle physics have furthered major technological progress of widespread importance. For example, the World Wide Web began as a project to improve CERN's communication system. CERN's requirement to process massive amounts of data produced by the Large Hadron Collider also led to contributions to the fields of distributed and cloud computing.

History

Theorization

The six authors of the 1964 PRL papers, who received the 2010 J. J. Sakurai Prize for their work; from left to right: Kibble, Guralnik, Hagen, Englert, Brout; right: Higgs.

Nobel Prize Laureate Peter Higgs in Stockholm, December 2013

 

Particle physicists study matter made from fundamental particles whose interactions are mediated by exchange particles – gauge bosons – acting as force carriers. At the beginning of the 1960s a number of these particles had been discovered or proposed, along with theories suggesting how they relate to each other, some of which had already been reformulated as field theories in which the objects of study are not particles and forces, but quantum fields and their symmetries. However, attempts to produce quantum field models for two of the four known fundamental forces – the electromagnetic force and the weak nuclear force – and then to unify these interactions, were still unsuccessful. 

One known problem was that gauge invariant approaches, including non-abelian models such as Yang–Mills theory (1954), which held great promise for unified theories, also seemed to predict known massive particles as massless. Goldstone's theorem, relating to continuous symmetries within some theories, also appeared to rule out many obvious solutions, since it appeared to show that zero-mass particles also would have to exist that simply were "not seen". According to Guralnik, physicists had "no understanding" how these problems could be overcome.

Particle physicist and mathematician Peter Woit summarised the state of research at the time:

Yang and Mills work on non-abelian gauge theory had one huge problem: in perturbation theory it has massless particles which don’t correspond to anything we see. One way of getting rid of this problem is now fairly well understood, the phenomenon of confinement realized in QCD, where the strong interactions get rid of the massless “gluon” states at long distances. By the very early sixties, people had begun to understand another source of massless particles: spontaneous symmetry breaking of a continuous symmetry. What Philip Anderson realized and worked out in the summer of 1962 was that, when you have both gauge symmetry and spontaneous symmetry breaking, the Nambu–Goldstone massless mode can combine with the massless gauge field modes to produce a physical massive vector field. This is what happens in superconductivity, a subject about which Anderson was (and is) one of the leading experts. [text condensed]

The Higgs mechanism is a process by which vector bosons can acquire rest mass without explicitly breaking gauge invariance, as a byproduct of spontaneous symmetry breaking. Initially, the mathematical theory behind spontaneous symmetry breaking was conceived and published within particle physics by Yoichiro Nambu in 1960, and the concept that such a mechanism could offer a possible solution for the "mass problem" was originally suggested in 1962 by Philip Anderson (who had previously written papers on broken symmetry and its outcomes in superconductivity. Anderson concluded in his 1963 paper on the Yang-Mills theory, that "considering the superconducting analog... [t]hese two types of bosons seem capable of canceling each other out... leaving finite mass bosons"), and in March 1964, Abraham Klein and Benjamin Lee showed that Goldstone's theorem could be avoided this way in at least some non-relativistic cases, and speculated it might be possible in truly relativistic cases.

These approaches were quickly developed into a full relativistic model, independently and almost simultaneously, by three groups of physicists: by François Englert and Robert Brout in August 1964; by Peter Higgs in October 1964; and by Gerald Guralnik, Carl Hagen, and Tom Kibble (GHK) in November 1964. Higgs also wrote a short, but important, response published in September 1964 to an objection by Gilbert, which showed that if calculating within the radiation gauge, Goldstone's theorem and Gilbert's objection would become inapplicable. (Higgs later described Gilbert's objection as prompting his own paper.) Properties of the model were further considered by Guralnik in 1965, by Higgs in 1966, by Kibble in 1967, and further by GHK in 1967. The original three 1964 papers demonstrated that when a gauge theory is combined with an additional field that spontaneously breaks the symmetry, the gauge bosons may consistently acquire a finite mass. In 1967, Steven Weinberg  and Abdus Salam independently showed how a Higgs mechanism could be used to break the electroweak symmetry of Sheldon Glashow's unified model for the weak and electromagnetic interactions, (itself an extension of work by Schwinger), forming what became the Standard Model of particle physics. Weinberg was the first to observe that this would also provide mass terms for the fermions.

At first, these seminal papers on spontaneous breaking of gauge symmetries were largely ignored, because it was widely believed that the (non-Abelian gauge) theories in question were a dead-end, and in particular that they could not be renormalised. In 1971–72, Martinus Veltman and Gerard 't Hooft proved renormalisation of Yang–Mills was possible in two papers covering massless, and then massive, fields. Their contribution, and the work of others on the renormalisation group – including "substantial" theoretical work by Russian physicists Ludvig Faddeev, Andrei Slavnov, Efim Fradkin, and Igor Tyutin – was eventually "enormously profound and influential", but even with all key elements of the eventual theory published there was still almost no wider interest. For example, Coleman found in a study that "essentially no-one paid any attention" to Weinberg's paper prior to 1971 and discussed by David Politzer in his 2004 Nobel speech. – now the most cited in particle physics – and even in 1970 according to Politzer, Glashow's teaching of the weak interaction contained no mention of Weinberg's, Salam's, or Glashow's own work. In practice, Politzer states, almost everyone learned of the theory due to physicist Benjamin Lee, who combined the work of Veltman and 't Hooft with insights by others, and popularised the completed theory. In this way, from 1971, interest and acceptance "exploded" and the ideas were quickly absorbed in the mainstream.

The resulting electroweak theory and Standard Model have accurately predicted (among other things) weak neutral currents, three bosons, the top and charm quarks, and with great precision, the mass and other properties of some of these. Many of those involved eventually won Nobel Prizes or other renowned awards. A 1974 paper and comprehensive review in Reviews of Modern Physics commented that "while no one doubted the [mathematical] correctness of these arguments, no one quite believed that nature was diabolically clever enough to take advantage of them", adding that the theory had so far produced accurate answers that accorded with experiment, but it was unknown whether the theory was fundamentally correct. By 1986 and again in the 1990s it became possible to write that understanding and proving the Higgs sector of the Standard Model was "the central problem today in particle physics".

Summary and impact of the PRL papers

The three papers written in 1964 were each recognised as milestone papers during Physical Review Letters's 50th anniversary celebration. Their six authors were also awarded the 2010 J. J. Sakurai Prize for Theoretical Particle Physics for this work. (A controversy also arose the same year, because in the event of a Nobel Prize only up to three scientists could be recognised, with six being credited for the papers.) Two of the three PRL papers (by Higgs and by GHK) contained equations for the hypothetical field that eventually would become known as the Higgs field and its hypothetical quantum, the Higgs boson. Higgs' subsequent 1966 paper showed the decay mechanism of the boson; only a massive boson can decay and the decays can prove the mechanism.

In the paper by Higgs the boson is massive, and in a closing sentence Higgs writes that "an essential feature" of the theory "is the prediction of incomplete multiplets of scalar and vector bosons". (Frank Close comments that 1960s gauge theorists were focused on the problem of massless vector bosons, and the implied existence of a massive scalar boson was not seen as important; only Higgs directly addressed it.) In the paper by GHK the boson is massless and decoupled from the massive states. In reviews dated 2009 and 2011, Guralnik states that in the GHK model the boson is massless only in a lowest-order approximation, but it is not subject to any constraint and acquires mass at higher orders, and adds that the GHK paper was the only one to show that there are no massless Goldstone bosons in the model and to give a complete analysis of the general Higgs mechanism. All three reached similar conclusions, despite their very different approaches: Higgs' paper essentially used classical techniques, Englert and Brout's involved calculating vacuum polarisation in perturbation theory around an assumed symmetry-breaking vacuum state, and GHK used operator formalism and conservation laws to explore in depth the ways in which Goldstone's theorem may be worked around. Some versions of the theory predicted more than one kind of Higgs fields and bosons, and alternative "Higgsless" models were considered until the discovery of the Higgs boson.

Experimental search

To produce Higgs bosons, two beams of particles are accelerated to very high energies and allowed to collide within a particle detector. Occasionally, although rarely, a Higgs boson will be created fleetingly as part of the collision byproducts. Because the Higgs boson decays very quickly, particle detectors cannot detect it directly. Instead the detectors register all the decay products (the decay signature) and from the data the decay process is reconstructed. If the observed decay products match a possible decay process (known as a decay channel) of a Higgs boson, this indicates that a Higgs boson may have been created. In practice, many processes may produce similar decay signatures. Fortunately, the Standard Model precisely predicts the likelihood of each of these, and each known process, occurring. So, if the detector detects more decay signatures consistently matching a Higgs boson than would otherwise be expected if Higgs bosons did not exist, then this would be strong evidence that the Higgs boson exists. 

Because Higgs boson production in a particle collision is likely to be very rare (1 in 10 billion at the LHC), and many other possible collision events can have similar decay signatures, the data of hundreds of trillions of collisions needs to be analysed and must "show the same picture" before a conclusion about the existence of the Higgs boson can be reached. To conclude that a new particle has been found, particle physicists require that the statistical analysis of two independent particle detectors each indicate that there is lesser than a one-in-a-million chance that the observed decay signatures are due to just background random Standard Model events – i.e., that the observed number of events is more than 5 standard deviations (sigma) different from that expected if there was no new particle. More collision data allows better confirmation of the physical properties of any new particle observed, and allows physicists to decide whether it is indeed a Higgs boson as described by the Standard Model or some other hypothetical new particle. 

To find the Higgs boson, a powerful particle accelerator was needed, because Higgs bosons might not be seen in lower-energy experiments. The collider needed to have a high luminosity in order to ensure enough collisions were seen for conclusions to be drawn. Finally, advanced computing facilities were needed to process the vast amount of data (25 petabytes per year as of 2012) produced by the collisions. For the announcement of 4 July 2012, a new collider known as the Large Hadron Collider was constructed at CERN with a planned eventual collision energy of 14 TeV – over seven times any previous collider – and over 300 trillion (3×10¹⁴) LHC proton–proton collisions were analysed by the LHC Computing Grid, the world's largest computing grid (as of 2012), comprising over 170 computing facilities in a worldwide network across 36 countries.

Search before 4 July 2012

The first extensive search for the Higgs boson was conducted at the Large Electron–Positron Collider (LEP) at CERN in the 1990s. At the end of its service in 2000, LEP had found no conclusive evidence for the Higgs. This implied that if the Higgs boson were to exist it would have to be heavier than 114.4 GeV/c².

The search continued at Fermilab in the United States, where the Tevatron – the collider that discovered the top quark in 1995 – had been upgraded for this purpose. There was no guarantee that the Tevatron would be able to find the Higgs, but it was the only supercollider that was operational since the Large Hadron Collider (LHC) was still under construction and the planned Superconducting Super Collider had been cancelled in 1993 and never completed. The Tevatron was only able to exclude further ranges for the Higgs mass, and was shut down on 30 September 2011 because it no longer could keep up with the LHC. The final analysis of the data excluded the possibility of a Higgs boson with a mass between 147 GeV/c² and 180 GeV/c². In addition, there was a small (but not significant) excess of events possibly indicating a Higgs boson with a mass between 115 GeV/c² and 140 GeV/c².

The Large Hadron Collider at CERN in Switzerland, was designed specifically to be able to either confirm or exclude the existence of the Higgs boson. Built in a 27 km tunnel under the ground near Geneva originally inhabited by LEP, it was designed to collide two beams of protons, initially at energies of 3.5 TeV per beam (7 TeV total), or almost 3.6 times that of the Tevatron, and upgradeable to 2 × 7 TeV (14 TeV total) in future. Theory suggested if the Higgs boson existed, collisions at these energy levels should be able to reveal it. As one of the most complicated scientific instruments ever built, its operational readiness was delayed for 14 months by a magnet quench event nine days after its inaugural tests, caused by a faulty electrical connection that damaged over 50 superconducting magnets and contaminated the vacuum system.

Data collection at the LHC finally commenced in March 2010. By December 2011 the two main particle detectors at the LHC, ATLAS and CMS, had narrowed down the mass range where the Higgs could exist to around 116-130 GeV (ATLAS) and 115-127 GeV (CMS). There had also already been a number of promising event excesses that had "evaporated" and proven to be nothing but random fluctuations. However, from around May 2011, both experiments had seen among their results, the slow emergence of a small yet consistent excess of gamma and 4-lepton decay signatures and several other particle decays, all hinting at a new particle at a mass around 125 GeV. By around November 2011, the anomalous data at 125 GeV was becoming "too large to ignore" (although still far from conclusive), and the team leaders at both ATLAS and CMS each privately suspected they might have found the Higgs. On November 28, 2011, at an internal meeting of the two team leaders and the director general of CERN, the latest analyses were discussed outside their teams for the first time, suggesting both ATLAS and CMS might be converging on a possible shared result at 125 GeV, and initial preparations commenced in case of a successful finding. While this information was not known publicly at the time, the narrowing of the possible Higgs range to around 115–130 GeV and the repeated observation of small but consistent event excesses across multiple channels at both ATLAS and CMS in the 124-126 GeV region (described as "tantalising hints" of around 2-3 sigma) were public knowledge with "a lot of interest". It was therefore widely anticipated around the end of 2011, that the LHC would provide sufficient data to either exclude or confirm the finding of a Higgs boson by the end of 2012, when their 2012 collision data (with slightly higher 8 TeV collision energy) had been examined.

Discovery of candidate boson at CERN

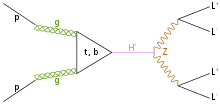
Feynman diagrams showing the cleanest channels associated with the low-mass (~125 GeV) Higgs boson candidate observed by ATLAS and CMS at the LHC. The dominant production mechanism at this mass involves two gluons from each proton fusing to a Top-quark Loop, which couples strongly to the Higgs field to produce a Higgs boson. Left: Diphoton channel: Boson subsequently decays into 2 gamma ray photons by virtual interaction with a W boson loop or top quark loop. Right: 4-Lepton "golden channel": Boson emits 2 Z bosons, which each decay into 2 leptons (electrons, muons). Experimental analysis of these channels reached a significance of more than 5 sigma in both experiments.

On 22 June 2012 CERN announced an upcoming seminar covering tentative findings for 2012, and shortly afterwards (from around 1 July 2012 according to an analysis of the spreading rumour in social media) rumours began to spread in the media that this would include a major announcement, but it was unclear whether this would be a stronger signal or a formal discovery. Speculation escalated to a "fevered" pitch when reports emerged that Peter Higgs, who proposed the particle, was to be attending the seminar, and that "five leading physicists" had been invited – generally believed to signify the five living 1964 authors – with Higgs, Englert, Guralnik, Hagen attending and Kibble confirming his invitation (Brout having died in 2011).

On 4 July 2012 both of the CERN experiments announced they had independently made the same discovery: CMS of a previously unknown boson with mass 125.3 ± 0.6 GeV/c² and ATLAS of a boson with mass 126.0 ± 0.6 GeV/c². Using the combined analysis of two interaction types (known as 'channels'), both experiments independently reached a local significance of 5 sigma – implying that the probability of getting at least as strong a result by chance alone is less than 1 in 3 million. When additional channels were taken into account, the CMS significance was reduced to 4.9 sigma.

The two teams had been working 'blinded' from each other from around late 2011 or early 2012, meaning they did not discuss their results with each other, providing additional certainty that any common finding was genuine validation of a particle. This level of evidence, confirmed independently by two separate teams and experiments, meets the formal level of proof required to announce a confirmed discovery. 

On 31 July 2012, the ATLAS collaboration presented additional data analysis on the "observation of a new particle", including data from a third channel, which improved the significance to 5.9 sigma (1 in 588 million chance of obtaining at least as strong evidence by random background effects alone) and mass 126.0 ± 0.4 (stat) ± 0.4 (sys) GeV/c², and CMS improved the significance to 5-sigma and mass 125.3 ± 0.4 (stat) ± 0.5 (sys) GeV/c².

The new particle tested as a possible Higgs boson

Following the 2012 discovery, it was still unconfirmed whether or not the 125 GeV/c² particle was a Higgs boson. On one hand, observations remained consistent with the observed particle being the Standard Model Higgs boson, and the particle decayed into at least some of the predicted channels. Moreover, the production rates and branching ratios for the observed channels broadly matched the predictions by the Standard Model within the experimental uncertainties. However, the experimental uncertainties currently still left room for alternative explanations, meaning an announcement of the discovery of a Higgs boson would have been premature. To allow more opportunity for data collection, the LHC's proposed 2012 shutdown and 2013–14 upgrade were postponed by 7 weeks into 2013.

In November 2012, in a conference in Kyoto researchers said evidence gathered since July was falling into line with the basic Standard Model more than its alternatives, with a range of results for several interactions matching that theory's predictions. Physicist Matt Strassler highlighted "considerable" evidence that the new particle is not a pseudoscalar negative parity particle (consistent with this required finding for a Higgs boson), "evaporation" or lack of increased significance for previous hints of non-Standard Model findings, expected Standard Model interactions with W and Z bosons, absence of "significant new implications" for or against supersymmetry, and in general no significant deviations to date from the results expected of a Standard Model Higgs boson. However some kinds of extensions to the Standard Model would also show very similar results; so commentators noted that based on other particles that are still being understood long after their discovery, it may take years to be sure, and decades to fully understand the particle that has been found.

These findings meant that as of January 2013, scientists were very sure they had found an unknown particle of mass ~ 125 GeV/c², and had not been misled by experimental error or a chance result. They were also sure, from initial observations, that the new particle was some kind of boson. The behaviours and properties of the particle, so far as examined since July 2012, also seemed quite close to the behaviours expected of a Higgs boson. Even so, it could still have been a Higgs boson or some other unknown boson, since future tests could show behaviours that do not match a Higgs boson, so as of December 2012 CERN still only stated that the new particle was "consistent with" the Higgs boson, and scientists did not yet positively say it was the Higgs boson. Despite this, in late 2012, widespread media reports announced (incorrectly) that a Higgs boson had been confirmed during the year.

In January 2013, CERN director-general Rolf-Dieter Heuer stated that based on data analysis to date, an answer could be possible 'towards' mid-2013, and the deputy chair of physics at Brookhaven National Laboratory stated in February 2013 that a "definitive" answer might require "another few years" after the collider's 2015 restart. In early March 2013, CERN Research Director Sergio Bertolucci stated that confirming spin-0 was the major remaining requirement to determine whether the particle is at least some kind of Higgs boson.

Confirmation of existence and current status

On 14 March 2013 CERN confirmed that:

"CMS and ATLAS have compared a number of options for the spin-parity of this particle, and these all prefer no spin and even parity [two fundamental criteria of a Higgs boson consistent with the Standard Model]. This, coupled with the measured interactions of the new particle with other particles, strongly indicates that it is a Higgs boson."

This also makes the particle the first elementary scalar particle to be discovered in nature.

Examples of tests used to validate that the discovered particle is the Higgs boson:

Requirement	How tested / explanation	Current status (As of July 2017)
Zero spin	Examining decay patterns. Spin-1 had been ruled out at the time of initial discovery by the observed decay to two photons (γ γ), leaving spin-0 and spin-2 as remaining candidates.	Spin-0 confirmed. The spin-2 hypothesis is excluded with a confidence level exceeding 99.9%.
Even (Positive) parity	Studying the angles at which decay products fly apart. Negative parity was also disfavoured if spin-0 was confirmed.	Even parity tentatively confirmed. The spin-0 negative parity hypothesis is excluded with a confidence level exceeding 99.9%.
Decay channels (outcomes of particle decaying) are as predicted	The Standard Model predicts the decay patterns of a 125 GeV Higgs boson. Are these all being seen, and at the right rates? Particularly significant, we should observe decays into pairs of photons (γ γ), W and Z bosons (WW and ZZ), bottom quarks (bb), and tau leptons (τ τ), among the possible outcomes.	bb, γ γ, τ τ, WW and ZZ observed. All observed signal strengths are consistent with the Standard Model prediction.
Couples to mass (i.e., strength of interaction with Standard Model particles proportional to their mass)	Particle physicist Adam Falkowski states that the essential qualities of a Higgs boson are that it is a spin-0 (scalar) particle which also couples to mass (W and Z bosons); proving spin-0 alone is insufficient.	Couplings to mass strongly evidenced ("At 95% confidence level cV is within 15% of the standard model value cV=1").
Higher energy results remain consistent	After the LHC's 2015 restart at the higher energy of 13 TeV, searches for multiple Higgs particles (as predicted in some theories) and tests targeting other versions of particle theory continued. These higher energy results must continue to give results consistent with Higgs theories.	Analysis of collisions up to July 2017 do not show deviations from the Standard Model, with experimental precisions better than results at lower energies.

Findings since 2013

In July 2017, CERN confirmed that all measurements still agree with the predictions of the Standard Model, and called the discovered particle simply "the Higgs boson". As of 2019, the Large Hadron Collider has continued to produce findings that confirm the 2013 understanding of the Higgs field and particle.

The LHC's experimental work since restarting in 2015 has included probing the Higgs field and boson to a greater level of detail, and confirming whether or not less common predictions were correct. In particular, exploration since 2015 has provided strong evidence of the predicted direct decay into fermions such as pairs of bottom quarks (3.6 σ) – described as an "important milestone" in understanding its short lifetime and other rare decays – and also to confirm decay into pairs of tau leptons (5.9 σ). This was described by CERN as being "of paramount importance to establishing the coupling of the Higgs boson to leptons and represents an important step towards measuring its couplings to third generation fermions, the very heavy copies of the electrons and quarks, whose role in nature is a profound mystery". Published results as of 19 Mar 2018 at 13 TeV for ATLAS and CMS had their measurements of the Higgs mass at 124.98±0.28 GeV and 125.26±0.21 GeV respectively. 

In July 2018, the ATLAS and CMS experiments reported observing the Higgs boson decay into a pair of bottom quarks, which makes up approximately 60% of all of its decays.

Theoretical properties

Theoretical need for the Higgs

"Symmetry breaking illustrated": – At high energy levels (left) the ball settles in the centre, and the result is symmetrical. At lower energy levels (right), the overall "rules" remain symmetrical, but the "Mexican hat" potential comes into effect: "local" symmetry inevitably becomes broken since eventually the ball must at random roll one way or another.

 

Gauge invariance is an important property of modern particle theories such as the Standard Model, partly due to its success in other areas of fundamental physics such as electromagnetism and the strong interaction (quantum chromodynamics). However, there were great difficulties in developing gauge theories for the weak nuclear force or a possible unified electroweak interaction. Fermions with a mass term would violate gauge symmetry and therefore cannot be gauge invariant. (This can be seen by examining the Dirac Lagrangian for a fermion in terms of left and right handed components; we find none of the spin-half particles could ever flip helicity as required for mass, so they must be massless.) W and Z bosons are observed to have mass, but a boson mass term contains terms which clearly depend on the choice of gauge, and therefore these masses too cannot be gauge invariant. Therefore, it seems that none of the standard model fermions or bosons could "begin" with mass as an inbuilt property except by abandoning gauge invariance. If gauge invariance were to be retained, then these particles had to be acquiring their mass by some other mechanism or interaction. Additionally, whatever was giving these particles their mass had to not "break" gauge invariance as the basis for other parts of the theories where it worked well, and had to not require or predict unexpected massless particles or long-range forces (seemingly an inevitable consequence of Goldstone's theorem) which did not actually seem to exist in nature. 

A solution to all of these overlapping problems came from the discovery of a previously unnoticed borderline case hidden in the mathematics of Goldstone's theorem, that under certain conditions it might theoretically be possible for a symmetry to be broken without disrupting gauge invariance and without any new massless particles or forces, and having "sensible" (renormalisable) results mathematically. This became known as the Higgs mechanism. 

Summary of interactions between certain particles described by the Standard Model.

 

The Standard Model hypothesises a field which is responsible for this effect, called the Higgs field (symbol: ${\displaystyle \phi }$), which has the unusual property of a non-zero amplitude in its ground state; i.e., a non-zero vacuum expectation value. It can have this effect because of its unusual "Mexican hat" shaped potential whose lowest "point" is not at its "centre". In simple terms, unlike all other known fields, the Higgs field requires less energy to have a non-zero value than a zero value, so it ends up having a non-zero value everywhere. Below a certain extremely high energy level the existence of this non-zero vacuum expectation spontaneously breaks electroweak gauge symmetry which in turn gives rise to the Higgs mechanism and triggers the acquisition of mass by those particles interacting with the field. This effect occurs because scalar field components of the Higgs field are "absorbed" by the massive bosons as degrees of freedom, and couple to the fermions via Yukawa coupling, thereby producing the expected mass terms. When symmetry breaks under these conditions, the Goldstone bosons that arise interact with the Higgs field (and with other particles capable of interacting with the Higgs field) instead of becoming new massless particles. The intractable problems of both underlying theories "neutralise" each other, and the residual outcome is that elementary particles acquire a consistent mass based on how strongly they interact with the Higgs field. It is the simplest known process capable of giving mass to the gauge bosons while remaining compatible with gauge theories. Its quantum would be a scalar boson, known as the Higgs boson.

Properties of the Higgs field

In the Standard Model, the Higgs field is a scalar tachyonic field – scalar meaning it does not transform under Lorentz transformations, and tachyonic meaning the field (but not the particle) has imaginary mass, and in certain configurations must undergo symmetry breaking. It consists of four components: two neutral ones and two charged component fields. Both of the charged components and one of the neutral fields are Goldstone bosons, which act as the longitudinal third-polarisation components of the massive W⁺, W⁻, and Z bosons. The quantum of the remaining neutral component corresponds to (and is theoretically realised as) the massive Higgs boson, this component can also interact with fermions via Yukawa coupling to give them mass, as well. 

Mathematically, the Higgs field has imaginary mass and is therefore a tachyonic field. While tachyons (particles that move faster than light) are a purely hypothetical concept, fields with imaginary mass have come to play an important role in modern physics. Under no circumstances do any excitations ever propagate faster than light in such theories – the presence or absence of a tachyonic mass has no effect whatsoever on the maximum velocity of signals (there is no violation of causality). Instead of faster-than-light particles, the imaginary mass creates an instability: Any configuration in which one or more field excitations are tachyonic must spontaneously decay, and the resulting configuration contains no physical tachyons. This process is known as tachyon condensation, and is now believed to be the explanation for how the Higgs mechanism itself arises in nature, and therefore the reason behind electroweak symmetry breaking. 

Although the notion of imaginary mass might seem troubling, it is only the field, and not the mass itself, that is quantised. Therefore, the field operators at spacelike separated points still commute (or anticommute), and information and particles still do not propagate faster than light. Tachyon condensation drives a physical system that has reached a local limit – and might naively be expected to produce physical tachyons – to an alternate stable state where no physical tachyons exist. Once a tachyonic field such as the Higgs field reaches the minimum of the potential, its quanta are not tachyons any more but rather are ordinary particles such as the Higgs boson.

Properties of the Higgs boson

Since the Higgs field is scalar, the Higgs boson has no spin. The Higgs boson is also its own antiparticle and is CP-even, and has zero electric and colour charge.

The Standard Model does not predict the mass of the Higgs boson. If that mass is between 115 and 180 GeV/c² (consistent with empirical observations of 125 GeV/c²), then the Standard Model can be valid at energy scales all the way up to the Planck scale (10¹⁹ GeV). Many theorists expect new physics beyond the Standard Model to emerge at the TeV-scale, based on unsatisfactory properties of the Standard Model. The highest possible mass scale allowed for the Higgs boson (or some other electroweak symmetry breaking mechanism) is 1.4 TeV; beyond this point, the Standard Model becomes inconsistent without such a mechanism, because unitarity is violated in certain scattering processes.

It is also possible, although experimentally difficult, to estimate the mass of the Higgs boson indirectly. In the Standard Model, the Higgs boson has a number of indirect effects; most notably, Higgs loops result in tiny corrections to masses of W and Z bosons. Precision measurements of electroweak parameters, such as the Fermi constant and masses of W/Z bosons, can be used to calculate constraints on the mass of the Higgs. As of July 2011, the precision electroweak measurements tell us that the mass of the Higgs boson is likely to be less than about 161 GeV/c² at 95% confidence level (this upper limit would increase to 185 GeV/c² if the lower bound of 114.4 GeV/c² from the LEP-2 direct search is allowed for). These indirect constraints rely on the assumption that the Standard Model is correct. It may still be possible to discover a Higgs boson above these masses if it is accompanied by other particles beyond those predicted by the Standard Model.

Production

Feynman diagrams for Higgs production

Gluon fusion	Higgs Strahlung
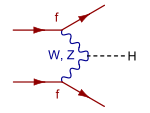Vector boson fusion	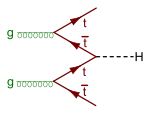Top fusion

If Higgs particle theories are valid, then a Higgs particle can be produced much like other particles that are studied, in a particle collider. This involves accelerating a large number of particles to extremely high energies and extremely close to the speed of light, then allowing them to smash together. Protons and lead ions (the bare nuclei of lead atoms) are used at the LHC. In the extreme energies of these collisions, the desired esoteric particles will occasionally be produced and this can be detected and studied; any absence or difference from theoretical expectations can also be used to improve the theory. The relevant particle theory (in this case the Standard Model) will determine the necessary kinds of collisions and detectors. The Standard Model predicts that Higgs bosons could be formed in a number of ways, although the probability of producing a Higgs boson in any collision is always expected to be very small – for example, only 1 Higgs boson per 10 billion collisions in the Large Hadron Collider. The most common expected processes for Higgs boson production are:

• Gluon fusion. If the collided particles are hadrons such as the proton or antiproton – as is the case in the LHC and Tevatron – then it is most likely that two of the gluons binding the hadron together collide. The easiest way to produce a Higgs particle is if the two gluons combine to form a loop of virtual quarks. Since the coupling of particles to the Higgs boson is proportional to their mass, this process is more likely for heavy particles. In practice it is enough to consider the contributions of virtual top and bottom quarks (the heaviest quarks). This process is the dominant contribution at the LHC and Tevatron being about ten times more likely than any of the other processes.
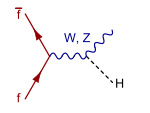
• Higgs Strahlung. If an elementary fermion collides with an anti-fermion – e.g., a quark with an anti-quark or an electron with a positron – the two can merge to form a virtual W or Z boson which, if it carries sufficient energy, can then emit a Higgs boson. This process was the dominant production mode at the LEP, where an electron and a positron collided to form a virtual Z boson, and it was the second largest contribution for Higgs production at the Tevatron. At the LHC this process is only the third largest, because the LHC collides protons with protons, making a quark-antiquark collision less likely than at the Tevatron. Higgs Strahlung is also known as associated production.
• Weak boson fusion. Another possibility when two (anti-)fermions collide is that the two exchange a virtual W or Z boson, which emits a Higgs boson. The colliding fermions do not need to be the same type. So, for example, an up quark may exchange a Z boson with an anti-down quark. This process is the second most important for the production of Higgs particle at the LHC and LEP.
• Top fusion. The final process that is commonly considered is by far the least likely (by two orders of magnitude). This process involves two colliding gluons, which each decay into a heavy quark–antiquark pair. A quark and antiquark from each pair can then combine to form a Higgs particle.

Decay

The Standard Model prediction for the decay width of the Higgs particle depends on the value of its mass.

 

Quantum mechanics predicts that if it is possible for a particle to decay into a set of lighter particles, then it will eventually do so. This is also true for the Higgs boson. The likelihood with which this happens depends on a variety of factors including: the difference in mass, the strength of the interactions, etc. Most of these factors are fixed by the Standard Model, except for the mass of the Higgs boson itself. For a Higgs boson with a mass of 125 GeV/c² the SM predicts a mean life time of about 1.6×10⁻²² s.

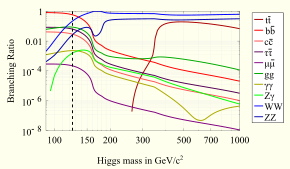
The Standard Model prediction for the branching ratios of the different decay modes of the Higgs particle depends on the value of its mass.

 

Since it interacts with all the massive elementary particles of the SM, the Higgs boson has many different processes through which it can decay. Each of these possible processes has its own probability, expressed as the branching ratio; the fraction of the total number decays that follows that process. The SM predicts these branching ratios as a function of the Higgs mass (see plot). 

One way that the Higgs can decay is by splitting into a fermion–antifermion pair. As general rule, the Higgs is more likely to decay into heavy fermions than light fermions, because the mass of a fermion is proportional to the strength of its interaction with the Higgs. By this logic the most common decay should be into a top–antitop quark pair. However, such a decay would only be possible if the Higgs were heavier than ~346 GeV/c², twice the mass of the top quark. For a Higgs mass of 125 GeV/c² the SM predicts that the most common decay is into a bottom–antibottom quark pair, which happens 57.7% of the time. The second most common fermion decay at that mass is a tau–antitau pair, which happens only about 6.3% of the time.

Another possibility is for the Higgs to split into a pair of massive gauge bosons. The most likely possibility is for the Higgs to decay into a pair of W bosons (the light blue line in the plot), which happens about 21.5% of the time for a Higgs boson with a mass of 125 GeV/c². The W bosons can subsequently decay either into a quark and an antiquark or into a charged lepton and a neutrino. The decays of W bosons into quarks are difficult to distinguish from the background, and the decays into leptons cannot be fully reconstructed (because neutrinos are impossible to detect in particle collision experiments). A cleaner signal is given by decay into a pair of Z-bosons (which happens about 2.6% of the time for a Higgs with a mass of 125 GeV/c²), if each of the bosons subsequently decays into a pair of easy-to-detect charged leptons (electrons or muons).

Decay into massless gauge bosons (i.e., gluons or photons) is also possible, but requires intermediate loop of virtual heavy quarks (top or bottom) or massive gauge bosons. The most common such process is the decay into a pair of gluons through a loop of virtual heavy quarks. This process, which is the reverse of the gluon fusion process mentioned above, happens approximately 8.6% of the time for a Higgs boson with a mass of 125 GeV/c². Much rarer is the decay into a pair of photons mediated by a loop of W bosons or heavy quarks, which happens only twice for every thousand decays. However, this process is very relevant for experimental searches for the Higgs boson, because the energy and momentum of the photons can be measured very precisely, giving an accurate reconstruction of the mass of the decaying particle.

Alternative models

The Minimal Standard Model as described above is the simplest known model for the Higgs mechanism with just one Higgs field. However, an extended Higgs sector with additional Higgs particle doublets or triplets is also possible, and many extensions of the Standard Model have this feature. The non-minimal Higgs sector favoured by theory are the two-Higgs-doublet models (2HDM), which predict the existence of a quintet of scalar particles: two CP-even neutral Higgs bosons h⁰ and H⁰, a CP-odd neutral Higgs boson A⁰, and two charged Higgs particles H^±. Supersymmetry ("SUSY") also predicts relations between the Higgs-boson masses and the masses of the gauge bosons, and could accommodate a 125 GeV/c² neutral Higgs boson. 

The key method to distinguish between these different models involves study of the particles' interactions ("coupling") and exact decay processes ("branching ratios"), which can be measured and tested experimentally in particle collisions. In the Type-I 2HDM model one Higgs doublet couples to up and down quarks, while the second doublet does not couple to quarks. This model has two interesting limits, in which the lightest Higgs couples to just fermions ("gauge-phobic") or just gauge bosons ("fermiophobic"), but not both. In the Type-II 2HDM model, one Higgs doublet only couples to up-type quarks, the other only couples to down-type quarks. The heavily researched Minimal Supersymmetric Standard Model (MSSM) includes a Type-II 2HDM Higgs sector, so it could be disproven by evidence of a Type-I 2HDM Higgs.

In other models the Higgs scalar is a composite particle. For example, in technicolor the role of the Higgs field is played by strongly bound pairs of fermions called techniquarks. Other models, feature pairs of top quarks (see top quark condensate). In yet other models, there is no Higgs field at all and the electroweak symmetry is broken using extra dimensions.

Further theoretical issues and hierarchy problem

A one-loop Feynman diagram of the first-order correction to the Higgs mass. In the Standard Model the effects of these corrections are potentially enormous, giving rise to the so-called hierarchy problem.

 

The Standard Model leaves the mass of the Higgs boson as a parameter to be measured, rather than a value to be calculated. This is seen as theoretically unsatisfactory, particularly as quantum corrections (related to interactions with virtual particles) should apparently cause the Higgs particle to have a mass immensely higher than that observed, but at the same time the Standard Model requires a mass of the order of 100 to 1000 GeV to ensure unitarity (in this case, to unitarise longitudinal vector boson scattering). Reconciling these points appears to require explaining why there is an almost-perfect cancellation resulting in the visible mass of ~ 125 GeV, and it is not clear how to do this. Because the weak force is about 10³² times stronger than gravity, and (linked to this) the Higgs boson's mass is so much less than the Planck mass or the grand unification energy, it appears that either there is some underlying connection or reason for these observations which is unknown and not described by the Standard Model, or some unexplained and extremely precise fine-tuning of parameters – however at present neither of these explanations is proven. This is known as a hierarchy problem. More broadly, the hierarchy problem amounts to the worry that a future theory of fundamental particles and interactions should not have excessive fine-tunings or unduly delicate cancellations, and should allow masses of particles such as the Higgs boson to be calculable. The problem is in some ways unique to spin-0 particles (such as the Higgs boson), which can give rise to issues related to quantum corrections that do not affect particles with spin. A number of solutions have been proposed, including supersymmetry, conformal solutions and solutions via extra dimensions such as braneworld models. 

There are also issues of quantum triviality, which suggests that it may not be possible to create a consistent quantum field theory involving elementary scalar particles. However, if quantum triviality is avoided, triviality constraints may set bounds on the Higgs Boson mass.

Public discussion

Naming

Names used by physicists

The name most strongly associated with the particle and field is the Higgs boson and Higgs field. For some time the particle was known by a combination of its PRL author names (including at times Anderson), for example the Brout–Englert–Higgs particle, the Anderson-Higgs particle, or the Englert–Brout–Higgs–Guralnik–Hagen–Kibble mechanism, and these are still used at times. Fuelled in part by the issue of recognition and a potential shared Nobel Prize, the most appropriate name was still occasionally a topic of debate until 2013. Higgs himself prefers to call the particle either by an acronym of all those involved, or "the scalar boson", or "the so-called Higgs particle".

A considerable amount has been written on how Higgs' name came to be exclusively used. Two main explanations are offered. The first is that Higgs undertook a step which was either unique, clearer or more explicit in his paper in formally predicting and examining the particle. Of the PRL papers' authors, only the paper by Higgs explicitly offered as a prediction that a massive particle would exist and calculated some of its properties; he was therefore "the first to postulate the existence of a massive particle" according to Nature. Physicist and author Frank Close and physicist-blogger Peter Woit both comment that the paper by GHK was also completed after Higgs and Brout–Englert were submitted to Physical Review Letters. and that Higgs alone had drawn attention to a predicted massive scalar boson, while all others had focused on the massive vector bosons; In this way, Higgs' contribution also provided experimentalists with a crucial "concrete target" needed to test the theory. However, in Higgs' view, Brout and Englert did not explicitly mention the boson since its existence is plainly obvious in their work, while according to Guralnik the GHK paper was a complete analysis of the entire symmetry breaking mechanism whose mathematical rigour is absent from the other two papers, and a massive particle may exist in some solutions. Higgs' paper also provided an "especially sharp" statement of the challenge and its solution according to science historian David Kaiser.

The alternative explanation is that the name was popularised in the 1970s due to its use as a convenient shorthand or because of a mistake in citing. Many accounts (including Higgs' own) credit the "Higgs" name to physicist Benjamin Lee (in Korean: Lee Whi-soh). Lee was a significant populist for the theory in its early stages, and habitually attached the name "Higgs" as a "convenient shorthand" for its components from 1972 and in at least one instance from as early as 1966. Although Lee clarified in his footnotes that "'Higgs' is an abbreviation for Higgs, Kibble, Guralnik, Hagen, Brout, Englert", his use of the term (and perhaps also Steven Weinberg's mistaken cite of Higgs' paper as the first in his seminal 1967 paper) meant that by around 1975–76 others had also begun to use the name 'Higgs' exclusively as a shorthand.

Nickname

The Higgs boson is often referred to as the "God particle" in popular media outside the scientific community. The nickname comes from the title of the 1993 book on the Higgs boson and particle physics, The God Particle: If the Universe Is the Answer, What Is the Question? by Physics Nobel Prize winner and Fermilab director Leon Lederman. Lederman wrote it in the context of failing US government support for the Superconducting Super Collider, a part-constructed titanic competitor to the Large Hadron Collider with planned collision energies of 2 × 20 TeV that was championed by Lederman since its 1983 inception and shut down in 1993. The book sought in part to promote awareness of the significance and need for such a project in the face of its possible loss of funding. Lederman, a leading researcher in the field, writes that he wanted to title his book The Goddamn Particle: If the Universe is the Answer, What is the Question? Lederman's editor decided that the title was too controversial and convinced him to change the title to The God Particle: If the Universe is the Answer, What is the Question? 

While media use of this term may have contributed to wider awareness and interest, many scientists feel the name is inappropriate since it is sensational hyperbole and misleads readers; the particle also has nothing to do with God, leaves open numerous questions in fundamental physics, and does not explain the ultimate origin of the universe. Higgs, an atheist, was reported to be displeased and stated in a 2008 interview that he found it "embarrassing" because it was "the kind of misuse... which I think might offend some people". The nickname has been satirised in mainstream media as well. Science writer Ian Sample stated in his 2010 book on the search that the nickname is "universally hate[d]" by physicists and perhaps the "worst derided" in the history of physics, but that (according to Lederman) the publisher rejected all titles mentioning "Higgs" as unimaginative and too unknown.

Lederman begins with a review of the long human search for knowledge, and explains that his tongue-in-cheek title draws an analogy between the impact of the Higgs field on the fundamental symmetries at the Big Bang, and the apparent chaos of structures, particles, forces and interactions that resulted and shaped our present universe, with the biblical story of Babel in which the primordial single language of early Genesis was fragmented into many disparate languages and cultures.

Today ... we have the standard model, which reduces all of reality to a dozen or so particles and four forces. ... It's a hard-won simplicity [...and...] remarkably accurate. But it is also incomplete and, in fact, internally inconsistent... This boson is so central to the state of physics today, so crucial to our final understanding of the structure of matter, yet so elusive, that I have given it a nickname: the God Particle. Why God Particle? Two reasons. One, the publisher wouldn't let us call it the Goddamn Particle, though that might be a more appropriate title, given its villainous nature and the expense it is causing. And two, there is a connection, of sorts, to another book, a much older one...

— Leon M. Lederman and Dick Teresi, The God Particle: If the Universe is the Answer, What is the Question p. 22

Lederman asks whether the Higgs boson was added just to perplex and confound those seeking knowledge of the universe, and whether physicists will be confounded by it as recounted in that story, or ultimately surmount the challenge and understand "how beautiful is the universe [God has] made".

Other proposals

A renaming competition by British newspaper The Guardian in 2009 resulted in their science correspondent choosing the name "the champagne bottle boson" as the best submission: "The bottom of a champagne bottle is in the shape of the Higgs potential and is often used as an illustration in physics lectures. So it's not an embarrassingly grandiose name, it is memorable, and [it] has some physics connection too." The name Higgson was suggested as well, in an opinion piece in the Institute of Physics' online publication physicsworld.com.

Educational explanations and analogies

There has been considerable public discussion of analogies and explanations for the Higgs particle and how the field creates mass, including coverage of explanatory attempts in their own right and a competition in 1993 for the best popular explanation by then-UK Minister for Science Sir William Waldegrave and articles in newspapers worldwide.

Photograph of light passing through a dispersive prism: the rainbow effect arises because photons are not all affected to the same degree by the dispersive material of the prism.

 

An educational collaboration involving an LHC physicist and a High School Teachers at CERN educator suggests that dispersion of light – responsible for the rainbow and dispersive prism – is a useful analogy for the Higgs field's symmetry breaking and mass-causing effect.

Symmetry breaking in optics	In a vacuum, light of all colours (or photons of all wavelengths) travels at the same velocity, a symmetrical situation. In some substances such as glass, water or air, this symmetry is broken (See: Photons in matter). The result is that light of different wavelengths have different velocities.
Symmetry breaking in particle physics	In 'naive' gauge theories, gauge bosons and other fundamental particles are all massless – also a symmetrical situation. In the presence of the Higgs field this symmetry is broken. The result is that particles of different types will have different masses.

Matt Strassler uses electric fields as an analogy:

Some particles interact with the Higgs field while others don’t. Those particles that feel the Higgs field act as if they have mass. Something similar happens in an electric field – charged objects are pulled around and neutral objects can sail through unaffected. So you can think of the Higgs search as an attempt to make waves in the Higgs field [create Higgs bosons] to prove it’s really there.

A similar explanation was offered by The Guardian:

The Higgs boson is essentially a ripple in a field said to have emerged at the birth of the universe and to span the cosmos to this day ... The particle is crucial however: It is the smoking gun, the evidence required to show the theory is right.

The Higgs field's effect on particles was famously described by physicist David Miller as akin to a room full of political party workers spread evenly throughout a room: the crowd gravitates to and slows down famous people but does not slow down others. He also drew attention to well-known effects in solid state physics where an electron's effective mass can be much greater than usual in the presence of a crystal lattice.

Analogies based on drag effects, including analogies of "syrup" or "molasses" are also well known, but can be somewhat misleading since they may be understood (incorrectly) as saying that the Higgs field simply resists some particles' motion but not others' – a simple resistive effect could also conflict with Newton's third law.

Recognition and awards

There was considerable discussion prior to late 2013 of how to allocate the credit if the Higgs boson is proven, made more pointed as a Nobel prize had been expected, and the very wide basis of people entitled to consideration. These include a range of theoreticians who made the Higgs mechanism theory possible, the theoreticians of the 1964 PRL papers (including Higgs himself), the theoreticians who derived from these a working electroweak theory and the Standard Model itself, and also the experimentalists at CERN and other institutions who made possible the proof of the Higgs field and boson in reality. The Nobel prize has a limit of 3 persons to share an award, and some possible winners are already prize holders for other work, or are deceased (the prize is only awarded to persons in their lifetime). Existing prizes for works relating to the Higgs field, boson, or mechanism include:

• Nobel Prize in Physics (1979) – Glashow, Salam, and Weinberg, for contributions to the theory of the unified weak and electromagnetic interaction between elementary particles
• Nobel Prize in Physics (1999) – 't Hooft and Veltman, for elucidating the quantum structure of electroweak interactions in physics
• J. J. Sakurai Prize for Theoretical Particle Physics (2010) – Hagen, Englert, Guralnik, Higgs, Brout, and Kibble, for elucidation of the properties of spontaneous symmetry breaking in four-dimensional relativistic gauge theory and of the mechanism for the consistent generation of vector boson masses (for the 1964 papers described above)
• Wolf Prize (2004) – Englert, Brout, and Higgs
• Breakthrough Prize in Fundamental Physics (2012) – Fabiola Gianotti and Peter Jenni, at that time spokespersons of the ATLAS and CMS collaborations, respectively, "For [their] leadership role in the scientific endeavour that led to the discovery of the new Higgs-like particle by the ATLAS and CMS collaborations at CERN's Large Hadron Collider."
• Nobel Prize in Physics (2013) – Peter Higgs and François Englert, for the theoretical discovery of a mechanism that contributes to our understanding of the origin of mass of subatomic particles, and which recently was confirmed through the discovery of the predicted fundamental particle, by the ATLAS and CMS experiments at CERN's Large Hadron Collider Englert's co-researcher Robert Brout had died in 2011 and the Nobel Prize is not ordinarily given posthumously.

Additionally Physical Review Letters' 50-year review (2008) recognised the 1964 PRL symmetry breaking papers and Weinberg's 1967 paper A model of Leptons (the most cited paper in particle physics, as of 2012) "milestone Letters".

Following reported observation of the Higgs-like particle in July 2012, several Indian media outlets reported on the supposed neglect of credit to Indian physicist Satyendra Nath Bose after whose work in the 1920s the class of particles "bosons" is named (although physicists have described Bose's connection to the discovery as tenuous).

Technical aspects and mathematical formulation

In the Standard Model, the Higgs field is a four-component scalar field that forms a complex doublet of the weak isospin SU(2) symmetry:

${\displaystyle \phi ={\frac {1}{\sqrt {2}}}\left({\begin{array}{c}\phi ^{1}+i\phi ^{2}\\\phi ^{0}+i\phi ^{3}\end{array}}\right)\;,}$

(1)

while the field has charge +½ under the weak hypercharge U(1) symmetry.

Note: This article uses the scaling convention where the electric charge, Q, the weak isospin, T₃, and the weak hypercharge, Y_W, are related by Q = T₃ + Y_W. A different convention used in most other Wikipedia articles is Q = T₃ + ½ Y_W.

The potential for the Higgs field, plotted as function of ${\displaystyle \phi ^{0}}$ and ${\displaystyle \phi ^{3}}$. It has a Mexican-hat or champagne-bottle profile at the ground.

 

The Higgs part of the Lagrangian is

${\displaystyle {\mathcal {L}}_{H}=\left|\left(\partial _{\mu }-igW_{\mu }^{a}\tau ^{a}-i{\frac {1}{2}}g'B_{\mu }\right)\phi \right|^{2}+\mu ^{2}\phi ^{\dagger }\phi -\lambda (\phi ^{\dagger }\phi )^{2},}$

(2)

where ${\displaystyle W_{\mu }^{a}}$ and ${\displaystyle B_{\mu }}$ are the gauge bosons of the SU(2) and U(1) symmetries, ${\displaystyle g}$ and ${\displaystyle g'}$ their respective coupling constants, ${\displaystyle \tau ^{a}={\frac {1}{2}}\sigma ^{a}}$ (where ${\displaystyle \sigma ^{a}}$ are the Pauli matrices) a complete set generators of the SU(2) symmetry, and ${\displaystyle \lambda >0}$ and ${\displaystyle \mu ^{2}>0}$, so that the ground state breaks the SU(2) symmetry (see figure). The ground state of the Higgs field (the bottom of the potential) is degenerate with different ground states related to each other by a SU(2) gauge transformation. It is always possible to pick a gauge such that in the ground state ${\displaystyle \phi ^{1}=\phi ^{2}=\phi ^{3}=0}$. The expectation value of ${\displaystyle \phi ^{0}}$ in the ground state (the vacuum expectation value or VEV) is then ${\displaystyle \langle \phi ^{0}\rangle ={\tfrac {1}{{\sqrt {2}}\ }}v}$, where ${\displaystyle v={\tfrac {1}{{\sqrt {\lambda }}\ }}\left|\mu \right|}$. The measured value of this parameter is ~246 GeV/c². It has units of mass, and is the only free parameter of the Standard Model that is not a dimensionless number. Quadratic terms in ${\displaystyle W_{\mu }}$ and ${\displaystyle B_{\mu }}$ arise, which give masses to the W and Z bosons:

${\displaystyle m_{W}={\tfrac {1}{2}}v\left|g\right|,}$

(3)

${\displaystyle m_{Z}={\tfrac {1}{2}}v{\sqrt {g^{2}+{g'}^{2}}},}$

(4)

with their ratio determining the Weinberg angle, ${\displaystyle \cos \theta _{W}={\frac {m_{W}}{m_{Z}}}={\frac {|g|}{\sqrt {g^{2}+{g'}^{2}}}}}$, and leave a massless U(1) photon, ${\displaystyle \gamma }$. The mass of the Higgs boson itself is given by

${\displaystyle m_{H}={\sqrt {2\mu ^{2}}}\equiv {\sqrt {2\lambda v^{2}}}.}$

(5)

The quarks and the leptons interact with the Higgs field through Yukawa interaction terms:

${\displaystyle {\begin{aligned}{\mathcal {L}}_{Y}=&-\lambda _{u}^{ij}{\frac {\phi ^{0}-i\phi ^{3}}{\sqrt {2}}}{\overline {u}}_{L}^{i}u_{R}^{j}+\lambda _{u}^{ij}{\frac {\phi ^{1}-i\phi ^{2}}{\sqrt {2}}}{\overline {d}}_{L}^{i}u_{R}^{j}\\&-\lambda _{d}^{ij}{\frac {\phi ^{0}+i\phi ^{3}}{\sqrt {2}}}{\overline {d}}_{L}^{i}d_{R}^{j}-\lambda _{d}^{ij}{\frac {\phi ^{1}+i\phi ^{2}}{\sqrt {2}}}{\overline {u}}_{L}^{i}d_{R}^{j}\\&-\lambda _{e}^{ij}{\frac {\phi ^{0}+i\phi ^{3}}{\sqrt {2}}}{\overline {e}}_{L}^{i}e_{R}^{j}-\lambda _{e}^{ij}{\frac {\phi ^{1}+i\phi ^{2}}{\sqrt {2}}}{\overline {\nu }}_{L}^{i}e_{R}^{j}+{\textrm {h.c.}},\end{aligned}}}$

(6)

where ${\displaystyle (d,u,e,\nu )_{L,R}^{i}}$ are left-handed and right-handed quarks and leptons of the ith generation, ${\displaystyle \lambda _{u,d,e}^{ij}}$ are matrices of Yukawa couplings where h.c. denotes the hermitian conjugate of all the preceding terms. In the symmetry breaking ground state, only the terms containing ${\displaystyle \phi ^{0}}$ remain, giving rise to mass terms for the fermions. Rotating the quark and lepton fields to the basis where the matrices of Yukawa couplings are diagonal, one gets

${\displaystyle {\mathcal {L}}_{m}=-m_{u}^{i}{\overline {u}}_{L}^{i}u_{R}^{i}-m_{d}^{i}{\overline {d}}_{L}^{i}d_{R}^{i}-m_{e}^{i}{\overline {e}}_{L}^{i}e_{R}^{i}+{\textrm {h.c.}},}$

(7)

where the masses of the fermions are ${\displaystyle m_{u,d,e}^{i}={\tfrac {1}{{\sqrt {2}}\ }}\lambda _{u,d,e}^{i}v}$, and ${\displaystyle \lambda _{u,d,e}^{i}}$ denote the eigenvalues of the Yukawa matrices.