Delta-v budget

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Delta-v_budget 

Delta-v in feet per second, and fuel requirements for a typical Apollo Lunar Landing mission.

In astrodynamics and aerospace, a delta-v budget is an estimate of the total change in velocity (delta-v) required for a space mission. It is calculated as the sum of the delta-v required to perform each propulsive maneuver needed during the mission. As input to the Tsiolkovsky rocket equation, it determines how much propellant is required for a vehicle of given empty mass and propulsion system.

Delta-v is a scalar quantity dependent only on the desired trajectory and not on the mass of the space vehicle. For example, although more fuel is needed to transfer a heavier communication satellite from low Earth orbit to geosynchronous orbit than for a lighter one, the delta-v required is the same. Delta-v is also additive, as contrasted to rocket burn time, the latter having greater effect later in the mission when more fuel has been used up.

Tables of the delta-v required to move between different space regime are useful in the conceptual planning of space missions. In the absence of an atmosphere, the delta-v is typically the same for changes in orbit in either direction; in particular, gaining and losing speed cost an equal effort. An atmosphere can be used to slow a spacecraft by aerobraking.

A typical delta-v budget might enumerate various classes of maneuvers, delta-v per maneuver, and number of each maneuver required over the life of the mission, then simply sum the total delta-v, much like a typical financial budget. Because the delta-v needed to achieve the mission usually varies with the relative position of the gravitating bodies, launch windows are often calculated from porkchop plots that show delta-v plotted against the launch time.

General principles

The Tsiolkovsky rocket equation shows that the delta-v of a rocket (stage) is proportional to the logarithm of the fuelled-to-empty mass ratio of the vehicle, and to the specific impulse of the rocket engine. A key goal in designing space-mission trajectories is to minimize the required delta-v to reduce the size and expense of the rocket that would be needed to successfully deliver any particular payload to its destination.

The simplest delta-v budget can be calculated with Hohmann transfer, which moves from one circular orbit to another coplanar circular orbit via an elliptical transfer orbit. In some cases a bi-elliptic transfer can give a lower delta-v.

Hohmann transfer orbit, labelled 2, from an orbit (1) to a higher orbit (3). This is a very commonly used maneuver between orbits.

A more complex transfer occurs when the orbits are not coplanar. In that case there is an additional delta-v necessary to change the plane of the orbit. The velocity of the vehicle needs substantial burns at the intersection of the two orbital planes and the delta-v is usually extremely high. However, these plane changes can be almost free in some cases if the gravity and mass of a planetary body are used to perform the deflection. In other cases, boosting up to a relatively high altitude apoapsis gives low speed before performing the plane change, thus requiring lower total delta-v.

The slingshot effect can be used to give a boost of speed/energy; if a vehicle goes past a planetary or lunar body, it is possible to pick up (or lose) some of that body's orbital velocity relative to the Sun or another planet.

Another effect is the Oberth effect—this can be used to greatly decrease the delta-v needed, because using propellant at low potential energy/high speed multiplies the effect of a burn. Thus for example the delta-v for a Hohmann transfer from Earth's orbital radius to Mars's orbital radius (to overcome the Sun's gravity) is many kilometres per second, but the incremental burn from low Earth orbit (LEO) over and above the burn to overcome Earth's gravity is far less if the burn is done close to Earth than if the burn to reach a Mars transfer orbit is performed at Earth's orbit, but far away from Earth.

A less used effect is low energy transfers. These are highly nonlinear effects that work by orbital resonances and by choosing trajectories close to Lagrange points. They can be very slow, but use very little delta-v.

Because delta-v depends on the position and motion of celestial bodies, particularly when using the slingshot effect and Oberth effect, the delta-v budget changes with launch time. These can be plotted on a porkchop plot.

Course corrections usually also require some propellant budget. Propulsion systems never provide precisely the right propulsion in precisely the right direction at all times, and navigation also introduces some uncertainty. Some propellant needs to be reserved to correct variations from the optimum trajectory.

Budget

Delta-v map of selected bodies in the Solar System, assuming burns are at periapsis, and gravity assist and inclination changes are ignored (full size)

Launch/landing

The delta-v requirements for sub-orbital spaceflight are much lower than for orbital spaceflight. For the Ansari X Prize altitude of 100 km, Space Ship One required a delta-v of roughly 1.4 km/s. To reach the initial low Earth orbit of the International Space Station of 300 km (now 400 km), the delta-v is over six times higher, about 9.4 km/s. Because of the exponential nature of the rocket equation the orbital rocket needs to be considerably bigger.

• Launch to LEO—this not only requires an increase of velocity from 0 to 7.8 km/s, but also typically 1.5–2 km/s for atmospheric drag and gravity drag
• Re-entry from LEO—the delta-v required is the orbital maneuvering burn to lower perigee into the atmosphere, atmospheric drag takes care of the rest.

Earth–Moon space—high thrust

Delta-v needed to move inside the Earth–Moon system (speeds lower than escape velocity) are given in km/s. This table assumes that the Oberth effect is being used—this is possible with high thrust chemical propulsion but not with current (as of 2018) electrical propulsion.

The return to LEO figures assume that a heat shield and aerobraking/aerocapture are used to reduce the speed by up to 3.2 km/s. The heat shield increases the mass, possibly by 15%. Where a heat shield is not used the higher "from LEO" Delta-v figure applies. The extra propellant needed to replace the aerobraking is likely to be heavier than a heat shield. LEO-Ken refers to a low Earth orbit with an inclination to the equator of 28 degrees, corresponding to a launch from Kennedy Space Center. LEO-Eq is an equatorial orbit.

q	LEO-Ken	LEO-Eq	GEO	EML-1	EML-2	EML-4/5	LLO	Moon	C3=0
Earth	9.3–10
Low Earth orbit (LEO-Ken)		4.24	4.33	3.77	3.43	3.97	4.04	5.93	3.22
Low Earth orbit (LEO-Eq)	4.24		3.90	3.77	3.43	3.99	4.04	5.93	3.22
Geostationary orbit (GEO)	2.06	1.63		1.38	1.47	1.71	2.05	3.92	1.30
Lagrangian point 1 (EML-1)	0.77	0.77	1.38		0.14	0.33	0.64	2.52	0.14
Lagrangian point 2 (EML-2)	0.33	0.33	1.47	0.14		0.34	0.64	2.52	0.14
Lagrangian point 4/5 (EML-4/5)	0.84	0.98	1.71	0.33	0.34		0.98	2.58	0.43
Low lunar orbit (LLO)	0.90	0.90	2.05	0.64	0.65	0.98		1.87	1.40
Moon surface	2.74	2.74	3.92	2.52	2.53	2.58	1.87		2.80
Earth escape velocity (C3=0)	0	0	1.30	0.14	0.14	0.43	1.40	2.80

Earth–Moon space—low thrust

Current electric ion thrusters produce a very low thrust (milli-newtons, yielding a small fraction of a g), so the Oberth effect cannot normally be used. This results in the journey requiring a higher delta-v and frequently a large increase in time compared to a high thrust chemical rocket. Nonetheless, the high specific impulse of electrical thrusters may significantly reduce the cost of the flight. For missions in the Earth–Moon system, an increase in journey time from days to months could be unacceptable for human space flight, but differences in flight time for interplanetary flights are less significant and could be favorable.

The table below presents delta-v's in km/s, normally accurate to 2 significant figures and will be the same in both directions, unless aerobraking is used as described in the high thrust section above.

From	To	Delta-v (km/s)
Low Earth orbit (LEO)	Earth–Moon Lagrangian 1 (EML-1)	7.0
Low Earth orbit (LEO)	Geostationary Earth orbit (GEO)	6.0
Low Earth orbit (LEO)	Low Lunar orbit (LLO)	8.0
Low Earth orbit (LEO)	Sun–Earth Lagrangian 1 (SEL-1)	7.4
Low Earth orbit (LEO)	Sun–Earth Lagrangian 2 (SEL-2)	7.4
Earth–Moon Lagrangian 1 (EML-1)	Low Lunar orbit (LLO)	0.60–0.80
Earth–Moon Lagrangian 1 (EML-1)	Geostationary Earth orbit (GEO)	1.4–1.75
Earth–Moon Lagrangian 1 (EML-1)	Sun-Earth Lagrangian 2 (SEL-2)	0.30–0.40

Earth Lunar Gateway—high thrust

The Lunar Gateway space station is planned to be deployed in a highly elliptical seven-day near-rectilinear halo orbit (NRHO) around the Moon. Spacecraft launched from Earth would perform a powered flyby of the Moon followed by a NRHO orbit insertion burn to dock with the Gateway as it approaches the apoapsis point of its orbit.

From	To	Delta-v (km/s)
Low Earth orbit (LEO)	Trans-Lunar Injection (TLI)	3.20
Trans-Lunar Injection (TLI)	Low (polar) lunar orbit (LLO)	0.90
Trans-Lunar Injection (TLI)	Lunar Gateway	0.43
Lunar Gateway	Low (polar) lunar orbit	0.73
Low (polar) lunar orbit	Lunar Gateway	0.73
Lunar Gateway	Earth Interface (EI)	0.41

Interplanetary

The spacecraft is assumed to be using chemical propulsion and the Oberth effect.

From	To	Delta-v (km/s)
LEO	Mars transfer orbit	4.3 ("typical", not minimal)
Earth escape velocity (C3=0)	Mars transfer orbit	0.6
Mars transfer orbit	Mars capture orbit	0.9
Mars capture orbit	Deimos transfer orbit	0.2
Deimos transfer orbit	Deimos surface	0.7
Deimos transfer orbit	Phobos transfer orbit	0.3
Phobos transfer orbit	Phobos surface	0.5
Mars capture orbit	Low Mars orbit	1.4
Low Mars orbit	Mars surface	4.1
Earth–Moon Lagrange point 2	Mars transfer orbit	<1.0
Mars transfer orbit	Low Mars orbit	2.7 (not minimal)
Earth escape velocity (C3=0)	Closest NEO	0.8–2.0

According to Marsden and Ross, "The energy levels of the Sun–Earth L₁ and L₂ points differ from those of the Earth–Moon system by only 50 m/s (as measured by maneuver velocity)."

We may apply the formula

${\displaystyle \mathrm{\Delta }v=\sqrt{\frac{\mu }{r_1}}\left(\sqrt{\frac{2r_2}{r_1+r_2}}-1\right)}$

(where μ = GM is the standard gravitational parameter of the sun, see Hohmann transfer orbit) to calculate the Δv in km/s needed to arrive at various destinations from Earth (assuming circular orbits for the planets, and using perihelion distance for Pluto). In this table, the column labeled "Δv to enter Hohmann orbit from Earth's orbit" gives the change from Earth's velocity to the velocity needed to get on a Hohmann ellipse whose other end will be at the desired distance from the Sun. The column labeled "v exiting LEO" gives the velocity needed (in a non-rotating frame of reference centred on Earth) when 300 km above Earth's surface. This is obtained by adding to the specific kinetic energy the square of the speed (7.73 km/s) of this low Earth orbit (that is, the depth of Earth's gravity well at this LEO). The column "Δv from LEO" is simply the previous speed minus 7.73 km/s. The transit time is calculated as ${\displaystyle ((1+\text{orbital radius})/2{)}^{3/2}/2}$ years.

Note that the values in the table only give the Δv needed to get to the orbital distance of the planet. The speed relative to the planet will still be considerable, and in order to go into orbit around the planet either aerocapture is needed using the planet's atmosphere, or more Δv is needed.

Destination	Orbital radius (AU)	Δv to enter Hohmann orbit from Earth's orbit	Δv exiting LEO	Δv from LEO	Transit time
Sun	0	29.8	31.7	24.0	2.1 months
Mercury	0.39	7.5	13.3	5.5	3.5 months
Venus	0.72	2.5	11.2	3.5	4.8 months
Mars	1.52	2.9	11.3	3.6	8.5 months
Jupiter	5.2	8.8	14.0	6.3	2.7 years
Saturn	9.54	10.3	15.0	7.3	6.0 years
Uranus	19.19	11.3	15.7	8.0	16.0 years
Neptune	30.07	11.7	16.0	8.2	30.6 years
Pluto	29.66 (perih.)	11.6	16.0	8.2	45.5 years
1 light-year	63,241	12.3	16.5	8.8	2.8 million years

The New Horizons space probe to Pluto achieved a near-Earth speed of over 16 km/s which was enough to escape from the Sun. (It also got a boost from a fly-by of Jupiter.)

To get to the Sun, it is actually not necessary to use a Δv of 24 km/s. One can use 8.8 km/s to go very far away from the Sun, then use a negligible Δv to bring the angular momentum to zero, and then fall into the Sun. This can be considered a sequence of two Hohmann transfers, one up and one down. Also, the table does not give the values that would apply when using the Moon for a gravity assist. There are also possibilities of using one planet, like Venus which is the easiest to get to, to assist getting to other planets or the Sun. The Galileo spacecraft used Venus once and Earth twice in order to reach Jupiter. The Ulysses solar probe used Jupiter to attain polar orbit around the Sun.

Delta-vs between Earth, Moon and Mars

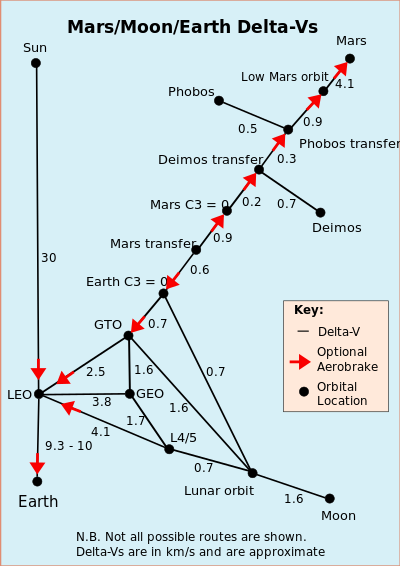
Delta-v needed for various orbital manoeuvers using conventional rockets.

Abbreviations key

• Escape orbits with low pericentre – C3 = 0
• Geostationary orbit – GEO
• Geostationary transfer orbit – GTO
• Earth–Moon L₅ Lagrangian point – L5
• Low Earth orbit – LEO
• Lunar orbit means low lunar orbit
• Red arrows show where optional aerobraking/aerocapture can be performed in that particular direction, black numbers give delta-v in km/s that apply in either direction. Lower-delta-v transfers than shown can often be achieved, but involve rare transfer windows or take significantly longer, see: fuzzy orbital transfers.
• Electric propulsion vehicles going from Mars C3 = 0 to Earth C3 = 0 without using the Oberth effect need a larger Delta-v of between 2.6 km/s and 3.15 km/s. Not all possible links are shown.
• The Delta-v for C3 = 0 to Mars transfer must be applied at pericentre, i.e. immediately after accelerating to the escape trajectory, and do not agree with the formula above which gives 0.4 from Earth escape and 0.65 from Mars escape.
• The figures for LEO to GTO, GTO to GEO, and LEO to GEO are inconsistent. The figure of 30 for LEO to the Sun is also too high.

Near-Earth objects

Near-Earth objects are asteroids whose orbits can bring them within about 0.3 astronomical units of the Earth. There are thousands of such objects that are easier to reach than the Moon or Mars. Their one-way delta-v budgets from LEO range upwards from 3.8 km/s (12,000 ft/s), which is less than 2/3 of the delta-v needed to reach the Moon's surface. But NEOs with low delta-v budgets have long synodic periods, and the intervals between times of closest approach to the Earth (and thus most efficient missions) can be decades long.

The delta-v required to return from Near-Earth objects is usually quite small, sometimes as low as 60 m/s (200 ft/s), with aerocapture using Earth's atmosphere. However, heat shields are required for this, which add mass and constrain spacecraft geometry. The orbital phasing can be problematic; once rendezvous has been achieved, low delta-v return windows can be fairly far apart (more than a year, often many years), depending on the body.

In general, bodies that are much further away or closer to the Sun than Earth, have more frequent windows for travel, but usually require larger delta-vs.

Perturbation (astronomy)

From Wikipedia, the free encyclopedia
https://en.wikipedia.org/wiki/Perturbation_(astronomy)

The perturbing forces of the Sun on the Moon at two places in its orbit. The blue arrows represent the direction and magnitude of the gravitational force on the Earth. Applying this to both the Earth's and the Moon's position does not disturb the positions relative to each other. When it is subtracted from the force on the Moon (black arrows), what is left is the perturbing force (red arrows) on the Moon relative to the Earth. Because the perturbing force is different in direction and magnitude on opposite sides of the orbit, it produces a change in the shape of the orbit.

In astronomy, perturbation is the complex motion of a massive body subjected to forces other than the gravitational attraction of a single other massive body. The other forces can include a third (fourth, fifth, etc.) body, resistance, as from an atmosphere, and the off-center attraction of an oblate or otherwise misshapen body.

Introduction

The study of perturbations began with the first attempts to predict planetary motions in the sky. In ancient times the causes were unknown. Isaac Newton, at the time he formulated his laws of motion and of gravitation, applied them to the first analysis of perturbations, recognizing the complex difficulties of their calculation. Many of the great mathematicians since then have given attention to the various problems involved; throughout the 18th and 19th centuries there was demand for accurate tables of the position of the Moon and planets for marine navigation.

The complex motions of gravitational perturbations can be broken down. The hypothetical motion that the body follows under the gravitational effect of one other body only is a conic section, and can be described in geometrical terms. This is called a two-body problem, or an unperturbed Keplerian orbit. The differences between that and the actual motion of the body are perturbations due to the additional gravitational effects of the remaining body or bodies. If there is only one other significant body then the perturbed motion is a three-body problem; if there are multiple other bodies it is an n-body problem. A general analytical solution (a mathematical expression to predict the positions and motions at any future time) exists for the two-body problem; when more than two bodies are considered analytic solutions exist only for special cases. Even the two-body problem becomes insoluble if one of the bodies is irregular in shape.

Mercury's orbital longitude and latitude, as perturbed by Venus, Jupiter and all of the planets of the Solar System, at intervals of 2.5 days. Mercury would remain centered on the crosshairs if there were no perturbations.

Most systems that involve multiple gravitational attractions present one primary body which is dominant in its effects (for example, a star, in the case of the star and its planet, or a planet, in the case of the planet and its satellite). The gravitational effects of the other bodies can be treated as perturbations of the hypothetical unperturbed motion of the planet or satellite around its primary body.

Mathematical analysis

General perturbations

In methods of general perturbations, general differential equations, either of motion or of change in the orbital elements, are solved analytically, usually by series expansions. The result is usually expressed in terms of algebraic and trigonometric functions of the orbital elements of the body in question and the perturbing bodies. This can be applied generally to many different sets of conditions, and is not specific to any particular set of gravitating objects. Historically, general perturbations were investigated first. The classical methods are known as variation of the elements, variation of parameters or variation of the constants of integration. In these methods, it is considered that the body is always moving in a conic section, however the conic section is constantly changing due to the perturbations. If all perturbations were to cease at any particular instant, the body would continue in this (now unchanging) conic section indefinitely; this conic is known as the osculating orbit and its orbital elements at any particular time are what are sought by the methods of general perturbations.

General perturbations takes advantage of the fact that in many problems of celestial mechanics, the two-body orbit changes rather slowly due to the perturbations; the two-body orbit is a good first approximation. General perturbations is applicable only if the perturbing forces are about one order of magnitude smaller, or less, than the gravitational force of the primary body. In the Solar System, this is usually the case; Jupiter, the second largest body, has a mass of about 1/1000 that of the Sun.

General perturbation methods are preferred for some types of problems, as the source of certain observed motions are readily found. This is not necessarily so for special perturbations; the motions would be predicted with similar accuracy, but no information on the configurations of the perturbing bodies (for instance, an orbital resonance) which caused them would be available.

Special perturbations

In methods of special perturbations, numerical datasets, representing values for the positions, velocities and accelerative forces on the bodies of interest, are made the basis of numerical integration of the differential equations of motion. In effect, the positions and velocities are perturbed directly, and no attempt is made to calculate the curves of the orbits or the orbital elements.

Special perturbations can be applied to any problem in celestial mechanics, as it is not limited to cases where the perturbing forces are small. Once applied only to comets and minor planets, special perturbation methods are now the basis of the most accurate machine-generated planetary ephemerides of the great astronomical almanacs. Special perturbations are also used for modeling an orbit with computers.

Cowell's formulation

Cowell's method. Forces from all perturbing bodies (black and gray) are summed to form the total force on body ${\displaystyle i}$ (red), and this is numerically integrated starting from the initial position (the epoch of osculation).

Cowell's formulation (so named for Philip H. Cowell, who, with A.C.D. Cromellin, used a similar method to predict the return of Halley's comet) is perhaps the simplest of the special perturbation methods. In a system of ${\displaystyle n}$ mutually interacting bodies, this method mathematically solves for the Newtonian forces on body ${\displaystyle i}$ by summing the individual interactions from the other ${\displaystyle j}$ bodies:

${\displaystyle {\ddot{\mathbf{r}}}_i=\sum _{\underset{j\ne i}{j=1}}^{n}G{m}_j\frac{({\mathbf{r}}_j-{\mathbf{r}}_i)}{\Vert {\mathbf{r}}_j-{\mathbf{r}}_i{\Vert }^3}}$

where ${\displaystyle {\ddot{\mathbf{r}}}_i}$ is the acceleration vector of body ${\displaystyle i}$, ${\displaystyle G}$ is the gravitational constant, ${\displaystyle m_j}$ is the mass of body ${\displaystyle j}$, ${\displaystyle {\mathbf{r}}_i}$ and ${\displaystyle {\mathbf{r}}_j}$ are the position vectors of objects ${\displaystyle i}$ and ${\displaystyle j}$ respectively, and ${\displaystyle r_{ij}\equiv \Vert {\mathbf{r}}_j-{\mathbf{r}}_i\Vert }$ is the distance from object ${\displaystyle i}$ to object ${\displaystyle j}$, all vectors being referred to the barycenter of the system. This equation is resolved into components in ${\displaystyle x,}$ ${\displaystyle y,}$ and ${\displaystyle z,}$ and these are integrated numerically to form the new velocity and position vectors. This process is repeated as many times as necessary. The advantage of Cowell's method is ease of application and programming. A disadvantage is that when perturbations become large in magnitude (as when an object makes a close approach to another) the errors of the method also become large. However, for many problems in celestial mechanics, this is never the case. Another disadvantage is that in systems with a dominant central body, such as the Sun, it is necessary to carry many significant digits in the arithmetic because of the large difference in the forces of the central body and the perturbing bodies, although with high precision numbers built into modern computers this is not as much of a limitation as it once was.

Encke's method

Encke's method. Greatly exaggerated here, the small difference δr (blue) between the osculating, unperturbed orbit (black) and the perturbed orbit (red), is numerically integrated starting from the initial position (the epoch of osculation).

Encke's method begins with the osculating orbit as a reference and integrates numerically to solve for the variation from the reference as a function of time. Its advantages are that perturbations are generally small in magnitude, so the integration can proceed in larger steps (with resulting lesser errors), and the method is much less affected by extreme perturbations. Its disadvantage is complexity; it cannot be used indefinitely without occasionally updating the osculating orbit and continuing from there, a process known as rectification. Encke's method is similar to the general perturbation method of variation of the elements, except the rectification is performed at discrete intervals rather than continuously.

Letting ${\displaystyle \mathit{\rho }}$ be the radius vector of the osculating orbit, ${\displaystyle \mathbf{r}}$ the radius vector of the perturbed orbit, and ${\displaystyle \delta \mathbf{r}}$ the variation from the osculating orbit,

${\displaystyle \delta \mathbf{r}=\mathbf{r}-\mathit{\rho }}$, and the equation of motion of ${\displaystyle \delta \mathbf{r}}$ is simply

(1)

${\displaystyle \ddot{\delta \mathbf{r}}=\ddot{\mathbf{r}}-\ddot{\mathit{\rho }}}$.

(2)

${\displaystyle \ddot{\mathbf{r}}}$ and ${\displaystyle \ddot{\mathit{\rho }}}$ are just the equations of motion of ${\displaystyle \mathbf{r}}$ and ${\displaystyle \mathit{\rho },}$

${\displaystyle \ddot{\mathbf{r}}={\mathbf{a}}_{\text{per}}-\frac{\mu }{r^3}\mathbf{r}}$ for the perturbed orbit and

(3)

${\displaystyle \ddot{\mathit{\rho }}=-\frac{\mu }{{\rho }^3}\mathit{\rho }}$ for the unperturbed orbit,

(4)

where ${\displaystyle \mu =G(M+m)}$ is the gravitational parameter with ${\displaystyle M}$ and ${\displaystyle m}$ the masses of the central body and the perturbed body, ${\displaystyle {\mathbf{a}}_{\text{per}}}$ is the perturbing acceleration, and ${\displaystyle r}$ and ${\displaystyle \rho }$ are the magnitudes of ${\displaystyle \mathbf{r}}$ and ${\displaystyle \mathit{\rho }}$.

Substituting from equations (3) and (4) into equation (2),

${\displaystyle \ddot{\delta \mathbf{r}}={\mathbf{a}}_{\text{per}}+\mu \left(\frac{\mathit{\rho }}{{\rho }^3}-\frac{\mathbf{r}}{r^3}\right),}$

(5)

which, in theory, could be integrated twice to find ${\displaystyle \delta \mathbf{r}}$. Since the osculating orbit is easily calculated by two-body methods, ${\displaystyle \mathit{\rho }}$ and ${\displaystyle \delta \mathbf{r}}$ are accounted for and ${\displaystyle \mathbf{r}}$ can be solved. In practice, the quantity in the brackets, ${\displaystyle \frac{\mathit{\rho }}{{\rho }^3}-\frac{\mathbf{r}}{r^3}}$, is the difference of two nearly equal vectors, and further manipulation is necessary to avoid the need for extra significant digits. Encke's method was more widely used before the advent of modern computers, when much orbit computation was performed on mechanical calculating machines.

Periodic nature

Gravity Simulator plot of the changing orbital eccentricity of Mercury, Venus, Earth, and Mars over the next 50,000 years. The 0 point on this plot is the year 2007.

In the Solar System, many of the disturbances of one planet by another are periodic, consisting of small impulses each time a planet passes another in its orbit. This causes the bodies to follow motions that are periodic or quasi-periodic – such as the Moon in its strongly perturbed orbit, which is the subject of lunar theory. This periodic nature led to the discovery of Neptune in 1846 as a result of its perturbations of the orbit of Uranus.

On-going mutual perturbations of the planets cause long-term quasi-periodic variations in their orbital elements, most apparent when two planets' orbital periods are nearly in sync. For instance, five orbits of Jupiter (59.31 years) is nearly equal to two of Saturn (58.91 years). This causes large perturbations of both, with a period of 918 years, the time required for the small difference in their positions at conjunction to make one complete circle, first discovered by Laplace. Venus currently has the orbit with the least eccentricity, i.e. it is the closest to circular, of all the planetary orbits. In 25,000 years' time, Earth will have a more circular (less eccentric) orbit than Venus. It has been shown that long-term periodic disturbances within the Solar System can become chaotic over very long time scales; under some circumstances one or more planets can cross the orbit of another, leading to collisions.

The orbits of many of the minor bodies of the Solar System, such as comets, are often heavily perturbed, particularly by the gravitational fields of the gas giants. While many of these perturbations are periodic, others are not, and these in particular may represent aspects of chaotic motion. For example, in April 1996, Jupiter's gravitational influence caused the period of Comet Hale–Bopp's orbit to decrease from 4,206 to 2,380 years, a change that will not revert on any periodic basis.