Koinophilia

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Koinophilia 

 

This leucistic Indian peacock, Pavo cristatus, is unlikely to find a mate and reproduce in a natural setting due to its unusual coloration. However, its striking colour is appreciated by humans, and may be included in artificial selective breeding to produce more individuals with the leucistic phenotype.

Koinophilia is an evolutionary hypothesis proposing that during sexual selection, animals preferentially seek mates with a minimum of unusual or mutant features, including functionality, appearance and behavior. Koinophilia intends to explain the clustering of sexual organisms into species and other issues described by Darwin's Dilemma. The term derives from the Greek, koinos, "common", "that which is shared", and philia, "fondness".

Natural selection causes beneficial inherited features to become more common at the expense of their disadvantageous counterparts. The koinophilia hypothesis proposes that a sexually-reproducing animal would therefore be expected to avoid individuals with rare or unusual features, and to prefer to mate with individuals displaying a predominance of common or average features. Mutants with strange, odd or peculiar features would be avoided because most mutations that manifest themselves as changes in appearance, functionality or behavior are disadvantageous. Because it is impossible to judge whether a new mutation is beneficial (or might be advantageous in the unforeseeable future) or not, koinophilic animals avoid them all, at the cost of avoiding the very occasional potentially beneficial mutation. Thus, koinophilia, although not infallible in its ability to distinguish fit from unfit mates, is a good strategy when choosing a mate. A koinophilic choice ensures that offspring are likely to inherit a suite of features and attributes that have served all the members of the species well in the past.

Koinophilia differs from the "like prefers like" mating pattern of assortative mating. If like preferred like, leucistic animals (such as white peacocks) would be sexually attracted to one another, and a leucistic subspecies would come into being. Koinophilia predicts that this is unlikely because leucistic animals are attracted to the average in the same way as are all the other members of its species. Since non-leucistic animals are not attracted by leucism, few leucistic individuals find mates, and leucistic lineages will rarely form.

Koinophilia provides simple explanations for the almost universal canalization of sexual creatures into species, the rarity of transitional forms between species (between both extant and fossil species), evolutionary stasis, punctuated equilibria, and the evolution of cooperation. Koinophilia might also contribute to the maintenance of sexual reproduction, preventing its reversion to the much simpler asexual form of reproduction.

The koinophilia hypothesis is supported by the findings of Judith Langlois and her co-workers. They found that the average of two human faces was more attractive than either of the faces from which that average was derived. The more faces (of the same gender and age) that were used in the averaging process the more attractive and appealing the average face became. This work into averageness supports koinophilia as an explanation of what constitutes a beautiful face.

Speciation and punctuated equilibria

Main articles: Speciation § Darwin's dilemma: Why do species exist?, and Punctuated equilibrium

Biologists from Darwin onwards have puzzled over how evolution produces species whose adult members look extraordinarily alike, and distinctively different from the members of other species. Lions and leopards are, for instance, both large carnivores that inhabit the same general environment, and hunt much the same prey, but look quite different. The question is why intermediates do not exist.

The overwhelming impression of strict uniformity, involving all the external features of the adult members of a species, is illustrated by this herd of Springbok, Antidorcas marsupialis, in the Kalahari Desert. This homogeneity in appearance is typical, and virtually diagnostic, of almost all species, and a great evolutionary mystery. Darwin emphasized individual variation, which is unquestionably present in any herd such as this, but is extraordinarily difficult to discern, even after long-term familiarity with the herd. Each individual needs to be uniquely and prominently tagged to follow its life history and interactions with the other (tagged) members of the population.

This is the "horizontal" dimension of a two-dimensional problem, referring to the almost complete absence of transitional or intermediate forms between present-day species (e.g. between lions, leopards, and cheetahs).

Speciation poses a "2-dimensional" problem. The discontinuities in appearance between existing species represent the "horizontal dimension" of the problem. The succession of fossil species represent the "vertical dimension".

The "vertical" dimension concerns the fossil record. Fossil species are frequently remarkably stable over extremely long periods of geological time, despite continental drift, major climate changes, and mass extinctions. When a change in form occurs, it tends to be abrupt in geological terms, again producing phenotypic gaps (i.e. an absence of intermediate forms), but now between successive species, which then often co-exist for long periods of time. Thus the fossil record suggests that evolution occurs in bursts, interspersed by long periods of evolutionary stagnation in so-called punctuated equilibria. Why this is so has been an evolutionary enigma ever since Darwin first recognized the problem.

Koinophilia could explain both the horizontal and vertical manifestations of speciation, and why it, as a general rule, involves the entire external appearance of the animals concerned. Since koinophilia affects the entire external appearance, the members of an interbreeding group are driven to look alike in every detail. Each interbreeding group will rapidly develop its own characteristic appearance. An individual from one group which wanders into another group will consequently be recognized as different, and will be discriminated against during the mating season. Reproductive isolation induced by koinophilia might thus be the first crucial step in the development of, ultimately, physiological, anatomical and behavioral barriers to hybridization, and thus, ultimately, full specieshood. Koinophilia will thereafter defend that species' appearance and behavior against invasion by unusual or unfamiliar forms (which might arise by immigration or mutation), and thus be a paradigm of punctuated equilibria (or the "vertical" aspect of the speciation problem).

Evolution under koinophilic conditions

Plants and domestic animals and can differ markedly from their wild ancestors

 

Top: wild teosinte; middle: maize-teosinte hybrid; bottom: maize

 

Ancestral wild cabbage

 

Domesticated cauliflower

 

Ancestral prussian carp

 

Domestic gold fish

 

Ancestral mouflon

 

Domestic sheep

 

More detailed version of diagram on left by geographical area.

Background

Evolution can be extremely rapid, as shown by the creation of domesticated animals and plants in a very short period of geological time, spanning only a few tens of thousands of years, by humans with little or no knowledge of genetics. Maize, Zea mays, for instance, was created in Mexico in only a few thousand years, starting about 7 000 to 12 000 years ago. This raises the question of why the long term rate of evolution is far slower than is theoretically possible.

Evolution is imposed on species or groups. It is not planned or striven for in some Lamarckist way. The mutations on which the process depends are random events, and, except for the "silent mutations" which do not affect the functionality or appearance of the carrier, are thus usually disadvantageous, and their chance of proving to be useful in the future is vanishingly small. Therefore, while a species or group might benefit by being able to adapt to a new environment through the accumulation of a wide range of genetic variation, this is to the detriment of the individuals who have to carry these mutations until a small, unpredictable minority of them ultimately contributes to such an adaptation. Thus, the capability to evolve is a group adaptation, which has been discredited by, among others, George C. Williams, John Maynard Smith and Richard Dawkins. because it is not to the benefit of the individual.

Consequently, sexual individuals would be expected to avoid transmitting mutations to their progeny by avoiding mates with strange or unusual characteristics. Mutations that therefore affect the external appearance and habits of their carriers will seldom be passed on to the next and subsequent generations. They will therefore seldom be tested by natural selection. Evolutionary change in a large population with a wide choice of mates, will, therefore, come to a virtual standstill. The only mutations that can accumulate in a population are ones that have no noticeable effect on the outward appearance and functionality of their bearers (they are thus termed "silent" or "neutral mutations").

Evolutionary process

The restraint koinophilia exerts on phenotypic change suggests that evolution can only occur if mutant mates cannot be avoided as a result of a severe scarcity of potential mates. This is most likely to occur in small restricted communities, such as on small islands, in remote valleys, lakes, river systems, caves, or during periods of glaciation, or following mass extinctions, when sudden bursts of evolution can be expected. Under these circumstances, not only is the choice of mates severely restricted, but population bottlenecks, founder effects, genetic drift and inbreeding cause rapid, random changes in the isolated population's genetic composition. Furthermore, hybridization with a related species trapped in the same isolate might introduce additional genetic changes. If an isolated population such as this survives its genetic upheavals, and subsequently expands into an unoccupied niche, or into a niche in which it has an advantage over its competitors, a new species, or subspecies, will have come in being. In geological terms this will be an abrupt event. A resumption of avoiding mutant mates will, thereafter, result, once again, in evolutionary stagnation.

Thus the fossil record of an evolutionary progression typically consists of species that suddenly appear, and ultimately disappear hundreds of thousands or millions of years later, without any change in external appearance. Graphically, these fossil species are represented by horizontal lines, whose lengths depict how long each of them existed. The horizontality of the lines illustrates the unchanging appearance of each of the fossil species depicted on the graph. During each species' existence new species appear at random intervals, each also lasting many hundreds of thousands of years before disappearing without a change in appearance. The degree of relatedness and the lines of descent of these concurrent species is generally impossible to determine. This is illustrated in the following diagram depicting the evolution of modern humans from the time that the hominins separated from the line that led to the evolution of our closest living primate relatives, the chimpanzees.

Distribution of Hominin species over time. For examples of similar evolutionary timelines see the paleontological list of African dinosaurs, Asian dinosaurs, the Lampriformes and the Amiiformes.

Phenotypic implications

This proposal, that population bottlenecks are possibly the primary generators of the variation that fuels evolution, predicts that evolution will usually occur in intermittent, relatively large scale morphological steps, interspersed with prolonged periods of evolutionary stagnation,nstead of in a continuous series of finely graded changes. However, it makes a further prediction. Darwin emphasized that the shared biologically useless oddities and incongruities that characterize a species are signs of an evolutionary history – something that would not be expected if a bird's wing, for instance, was engineered de novo, as argued by his detractors. The present model predicts that, in addition to vestiges which reflect an organism's evolutionary heritage, all the members of a given species will also bear the stamp of their isolationary past – arbitrary, random features, accumulated through founder effects, genetic drift and the other genetic consequences of sexual reproduction in small, isolated communities. Thus all lions, African and Asian, have a highly characteristic black tuft of fur at the end of their tails, which is difficult to explain in terms of an adaptation, or as a vestige from an early feline, or more ancient ancestor. The unique, often color- and pattern-rich plumage of each of today's wide variety of bird species presents a similar evolutionary enigma. This richly varied array of phenotypes is more easily explained as the products of isolates, subsequently defended by koinophilia, than as assemblies of very diverse evolutionary relics, or as sets of uniquely evolved adaptations.

• 

  The black tuft of fur at the end of this Asiatic lion's tail is difficult to explain as an evolutionary vestige, or adaptation. Yet it occurs in all lions.

• 

  The “spectacles” of the spectacled petrel, Procellaria conspicillata, represent an unexplained peculiarity of this species.

• 

  The unique plumage of the common chaffinch, Fringilla coelebs, unmistakably identifies the species, but its adaptive role is enigmatic.

Evolution of co-operation

Main articles: Co-operation (evolution) and Altruism (biology)

Co-operation is any group behavior that benefits the individuals more than if they were to act as independent agents.

Co-operative hunting by wolves allows them to tackle much larger and more nutritious prey than any individual wolf could handle. However, such co-operation could be exploited by selfish individuals which do not expose themselves to the dangers of the hunt, but nevertheless share in the spoils.

However selfish individuals can exploit the co-operativeness of others by not taking part in the group activity, but still enjoying its benefits. For instance, a selfish individual which does not join the hunting pack and share in its risks, but nevertheless shares in the spoils, has a fitness advantage over the other members of the pack. Thus, although a group of co-operative individuals is fitter than an equivalent group of selfish individuals, selfish individuals interspersed among a community of co-operators are always fitter than their hosts. They will raise, on average, more offspring than their hosts, and will ultimately replace them.

If, however, the selfish individuals are ostracized, and rejected as mates, because of their deviant and unusual behavior, then their evolutionary advantage becomes an evolutionary liability. Co-operation then becomes evolutionarily stable.

Effects of diets and environmental conditions

Male Drosophila pseudoobscura

The best-documented creations of new species in the laboratory were performed in the late 1980s. William Rice and G.W. Salt bred fruit flies, Drosophila melanogaster, using a maze with three different choices of habitat, such as light/dark and wet/dry. Each generation was placed into the maze, and the groups of flies that came out of two of the eight exits were set apart to breed with each other in their respective groups. After thirty-five generations, the two groups and their offspring were isolated reproductively because of their strong habitat preferences: they mated only within the areas they preferred, and so did not mate with flies that preferred the other areas. The history of such attempts is described in Rice and Hostert (1993).

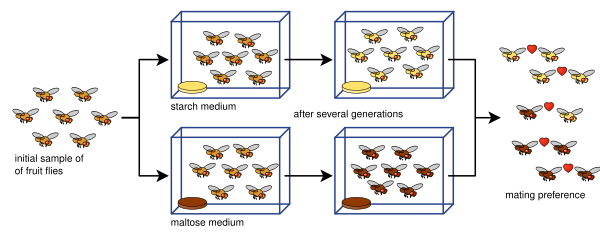
Diane Dodd used a laboratory experiment to show how reproductive isolation can evolve in Drosophila pseudoobscura fruit flies after several generations by placing them in different media, starch- or maltose-based media.

Dodd's experiment has been easy for many others to replicate, including with other kinds of fruit flies and foods.

A map of Europe indicating the distribution of the carrion and hooded crows on either side of a contact zone (white line) separating the two species.

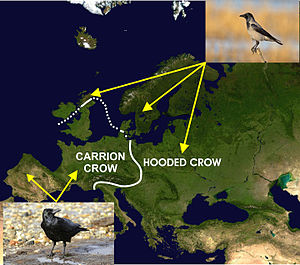
The carrion crow (Corvus corone) and hooded crow (Corvus cornix) are two closely related species whose geographical distribution across Europe is illustrated in the accompanying diagram. It is believed that this distribution might have resulted from the glaciation cycles during the Pleistocene, which caused the parent population to split into isolates which subsequently re-expanded their ranges when the climate warmed causing secondary contact. Jelmer W. Poelstra and coworkers sequenced almost the entire genomes of both species in populations at varying distances from the contact zone to find that the two species were genetically identical, both in their DNA and in its expression (in the form of RNA), except for the lack of expression of a small portion (<0.28%) of the genome (situated on avian chromosome 18) in the hooded crow, which imparts the lighter plumage coloration on its torso. Thus the two species can viably hybridize, and occasionally do so at the contact zone, but the all-black carrion crows on the one side of the contact zone mate almost exclusively with other all-black carrion crows, while the same occurs among the hooded crows on the other side of the contact zone. It is therefore clear that it is only the outward appearance of the two species that inhibits hybridization. The authors attribute this to assortative mating, the advantage of which is not clear, and it would lead to the rapid appearance of streams of new lineages, and possibly even species, through mutual attraction between mutants. Unnikrishnan and Akhila propose, instead, that koinophilia is a more precise explanation for the resistance to hybridization across the contact zone, despite the absence of physiological, anatomical or genetic barriers to such hybridization.

Reception

William B. Miller, in an extensive recent (2013) review of koinophilia theory, notes that while it provides precise explanations for the grouping of sexual animals into species, their unchanging persistence in the fossil record over long periods of time, and the phenotypic gaps between species, both fossil and extant, it represents a major departure from the widely accepted view that beneficial mutations spread, ultimately, to the whole, or some portion of the population (causing it to evolve gene by gene). Darwin recognized that this process had no inherent, or inevitable propensity to produce species. Instead populations would be in a perpetual state of transition both in time and space. They would, at any given moment, consist of individuals with varying numbers of beneficial characteristics that may or may not have reached them from their various points of origin in the population, and neutral features will have a scattering determined by random mechanisms such as genetic drift.

He also notes that koinophilia provides no explanation as to how the physiological, anatomical and genetic causes of reproductive isolation come about. It is only the behavioral reproductive isolation that is addressed by koinophilia. It is furthermore difficult to see how koinophilia might apply to plants, and certain marine creatures that discharge their gametes into the environment to meet up and fuse, it seems, entirely randomly (within conspecific confines). However, when pollen from several compatible donors is used to pollinate stigmata, the donors typically do not sire equal numbers of seeds. Marshall and Diggle state that the existence of some kind of non-random seed paternity is, in fact, not in question in flowering plants. How this occurs remains unknown. Pollen choice is one of the possibilities, taking into account that 50% of the pollen grain's haploid genome is expressed during its tube's growth towards the ovule.

The apparent preference of the females of certain, particularly bird, species for exaggerated male ornaments, such as the peacock's tail, is not easily reconciled with the concept of koinophilia.

Animals in Islam

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Animals_in_Islam 

According to Islam, animals are conscious of God. According to the Quran, they praise Him, even if this praise is not expressed in human language. Baiting animals for entertainment or gambling is prohibited. It is forbidden to kill any animal except for food or to prevent it from harming people.

The Quran explicitly allows the consumption of the meat of certain halal (lawful) animals. Although some Sufis have practised vegetarianism, there has been no serious discourse on the possibility of interpretations of scripture that require vegetarianism. Certain animals can be eaten under the condition that they are slaughtered in a specified way.

Pre-7th century

In the Arabian Peninsula before the advent of Islam in the 7th century CE, Arabs, like other people, attributed the qualities and the faults of humans to animals. Virility, for example, was attributed to the cock; perfidy to the monkey; stupidity to the lizard; and baldness to the elephant.

Based on the facts that the names of certain tribes bear the names of animals, survivals of animal cults, prohibitions of certain foods and other indications, W.  R. Smith argued for the practice of totemism by certain pre-Islamic tribes of Arabia. Others have argued that this evidence may only imply practice of a form of animalism. In support of this, for example, it was believed that upon one's death, the soul departs from the body in the form of a bird (usually a sort of owl); the soul-as-bird then flies about the tomb for some time, occasionally crying out (for vengeance).

Human duties in utilizing animals

According to Islam, human beings are allowed to use animals, but only if the rights of the animals are respected. The owner of an animal must do everything to benefit the animal. If the owner fails to perform their duties for the animal, the animal goes to someone else. The duties humans have to animals in Islam are based in the Quran, Sunnah and traditions.

Protection of animal lives

Animal protection is more important than the fulfillment of religious obligations in special circumstances. (... that whoever kills a soul unless for a soul or for corruption [done] in the land - it is as if he had slain mankind entirely. And whoever saves one - it is as if he had saved mankind entirely...)

Protection of animals' physical health

Harming, disabling, injuring, or cutting out the organs from any animal is strongly prohibited. Muslims may not cut the forelock, mane, or tail of a horse, because it is believed there is goodness in its forelock; its mane provides it warmth and it swats insects away with its tail.

Protection of animals' sexual health

Muslims are not allowed to perform acts such as the interbreeding (as in inbreeding) of animals. Muhammad forbade people from castrating animals.

Preventing cruelty and maltreatment to animals

Muslims are not allowed to harass and misuse animals, which includes snatching a leaf from an ant's mouth. Muslims have no right to brand animals, hamstring or crucify animals before killing, or burn animals even if they cause harm to humans. Humans should obtain animal meat by a swift slaughter and avoid cutting lengthwise. In Islamic slaughter, the spinal cord cannot be broken. Removing wool from animals is prohibited because it causes them vulnerability.

Avoiding punishment of animals

Muslims cannot use any equipment that injures an animal, (i.e., beating them in a circus show, forcing them to carry heavy loads, or running at extreme speeds in races) even to train them. Exposure to sound is also regulated.

Providing food

Muslims are obliged to provide food and water for any animal they see, even if the animal does not belong to them. In providing food and water considerations are the quality of the provisions and the amount of the provision based on the animal's condition and location.

Providing sanitation

Animals' health must be respected, along with food, water, and shelter.

Providing medication

In the event of illness, Muslims are expected to pay for the care and medication.

Providing dwelling

From an Islamic view, the appropriate shelter for an animal has three characteristics:

• Fits the animal's needs and they should not be placed in an unsanitary condition on the pretext that they do not understand.
• Fits the physical needs of the animal and its health and protect it from cold and heat.
• The dwelling of animals should not pollute the environment or spread disease to other organisms.

Respecting animal of status

In Islam, the rights of animals are respected in both life and death. Animal bodies may never be used for malicious purposes.

Qur'an

Quran

See also: List of characters and names mentioned in the Quran § Relate animals

Although over two hundred verses in the Qur'an deal with animals and six Quranic chapters (surah) are named after animals, animal life is not a predominant theme in the Qur'an. The Qur'an teaches that God created animals from water. God cares for all his creatures and provides for them. All creation praises God, even if this praise is not expressed in human language. God has prescribed laws for each species (laws of nature). Since animals follow the laws God has ordained for them, they are to be regarded as "Muslim", just as a human who obeys the laws prescribed for humans (Islamic law) is a Muslim. Just like humans, animals form "communities". In verse 6:38, the Qur'an applies the term ummah, generally used to mean "a human religious community", for genera of animals. The Encyclopaedia of the Qur'an states that this verse has been "far reaching in its moral and ecological implications."

There is not an animal (that lives) on the earth, nor a being that flies on its wings, but (forms part of) communities like you. Nothing have we omitted from the Book, and they (all) shall be gathered to their Lord in the end.

The Qur'an says that animals benefit humans in many ways and that they are aesthetically pleasing to look at. This is used as proof of God's benevolence towards humans. Animals that are slaughtered in accordance with sharia may be consumed. According to many verses of the Qur'an, the consumption of pork is sinful, unless there is no alternative other than starving to death (in times, for example, of war or famine). Surat Yusuf of the Quran mentions that a reason why Ya'qub was reluctant to let his son Yusuf to play in the open, even in the presence of his brothers, was that a dhiʾb (Arabic: ذِئْب, lit. 'wolf') could eat him.

The Quran contains three mentions of dogs:

• Verse 5:4 says "Lawful for you are all good things, and [the prey] that trained [hunting] dogs and falcons catch for you."
• Verse 18:18 describes the Companions of the Cave, a group of saintly young men presented in the Qurʼan as exemplars of religion, sleeping with "their dog stretching out its forelegs at the threshold." Further on, in verse 22, the dog is always counted as one of their numbers, no matter how they are numbered. In Muslim folklore, affectionate legends have grown around the loyal and protective qualities of this dog, whose name in legend is Qiṭmīr.

The above verses are seen as portraying dogs positively. An alleged hadith which regards black dogs as "evil" has been rejected by majority of Islamic scholars as fabricated. Nevertheless, Islamic scholars have tended to regard dogs' saliva as impure; practically, this means anything licked by a dog necessitates washing. Many Islamic jurists allowed owning dogs for herding, farming, hunting, or protection, but prohibited ownership for reasons they regarded as "frivolous".

There is a whole chapter in the Quran named "The Ants." As a result, the killing of ants in Sunni Islam is prohibited. Within the aforementioned chapter of "The Ant," there is an account of Sulaymaan (Solomon) talking to the eponymous ant as well as birds, most famously the hoopoe.

The Quran talks about a miraculous She-Camel of God (Arabic: نَـاقَـة, 'she-camel') that came from stone, in the context of the Prophet Salih, Thamudi people and Al-Hijr.

Pork is haram (forbidden) to eat, because its essence is considered impure, this is based on the verse of the Qur'an where it is described as being rijs (Arabic: رِجْس, impure) (Quran 6:145).

Forbidden (haram) is also the meat of domesticated donkeys, mules, any predatory animal with canine teeth and birds with talons.

Verses 50 and 51 of Surat al-Muddaththir in the Quran talk about ḥumur ('asses' or 'donkeys') fleeing from a qaswarah ('lion', 'beast of prey' or 'hunter'), in its criticism of people who were averse to Muhammad's teachings, such as donating wealth to the less wealthy.

The Arabic word meaning "animal" (hayawān/haywān (Arabic: حَيَوَان \ حَيْوَان; plural haywānāt (Arabic: حَيَوَانَات))) appears only once in the Qur'an but in the sense of everlasting life (personal). On the other hand, the term dābbah (Arabic: دَابَّة; plural dawābb), usually translated as "beast" or "creature" to sometimes differentiate from flying birds while surprisingly including humans, occurs a number of times in the Qur'an, while remaining rare in medieval Arabic works on zoology. Animals in the Qur'an and early Muslim thought may usually (though not necessarily) be seen in terms of their relation to human beings, producing a tendency toward anthropocentrism.

Sunnah

Sunnah refers to the traditional biographies of Muhammad wherein examples of sayings attributed to him and his conduct have been recorded. Sunnah consists of hadith (anecdotes about Muhammad).

Animals must not be mutilated while they are alive. Muhammad is also reported (by Ibn Omar and Abdallah bin Al-As) to have said: "there is no man who kills [even] a sparrow or anything smaller, without its deserving it, but God will question him about it [on the judgment day]" and "Whoever is kind to the creatures of God is kind to himself."

Muhammad issued advice to kill animals that were Fawāsiq (Arabic: فَوَاسِق "Harmful ones"), such as the rat and the scorpion, within the haram (holy area) of Mecca. Killing other non-domesticated animals in this area, such as equids and birds, is forbidden.

Muslims are required to sharpen the blade when slaughtering animals to ensure that no pain is felt. Muhammad is said to have said: "For [charity showed to] each creature which has a wet liver [i.e. is alive], there is a reward."

There is a hadith in Muwatta' Imam Malik about Muslim Pilgrims having to beware of the wolf, besides other animals.

Muhammad is also reported as having reprimanded some men who were sitting idly on their camels in a marketplace, saying "either ride them or leave them alone". Apart from that, the camel has significance in Islam. Al Qaswa (Arabic: ٱلْقَصْوَاء) was a female Arabian camel that belonged to Muhammad, and was dear to him. Muhammad rode on Qaswa during the Hijrah ('Migration') from Mecca to Medina, his Hajj in 629 CE, and the Conquest of Mecca in 630. The camel was also present during the Battle of Badr in 624. After the death of the Prophet, the camel is reported to have starved herself to death, refusing to take food from anyone.

In the Nahj al-Balagha, the Shi'a book of the sayings of Ali, an entire sermon is dedicated to praising peacocks. Bees are highly revered in Islam. The structural genius of a bee is thought as due to divine inspiration. Their product honey is also revered as medicine. Killing a bee is considered a great sin.

In Shi'ite ahadith, bats are praised as a miracle of nature.

The wolf may symbolize ferocity. As for the kalb (Arabic: كَلْب, dog), there are different views regarding it. The Sunni Maliki school of Islamic jurisprudence distinguishes between wild dogs and pet dogs, only considering the saliva of the former to be impure; on the other hand, some schools of Islamic law consider dogs as unclean (najis). The historian William Montgomery Watt states that Muhammad's kindness to animals was remarkable, citing an instance of Muhammad while traveling with his army to Mecca in 630 AD, posting sentries to ensure that a female dog and her newborn puppies were not disturbed. Muhammad himself prayed in the presence of dogs and many of his cousins and companions, who were the first Muslims, owned dogs; the Mosque of the Prophet in Medina allowed dogs to frolic about in Muhammad's time and for several centuries afterwards. In "two separate narrations by Abu Hurayrah, the Prophet told his companions of the virtue of saving the life of a dog by giving it water and quenching its thirst. One story referred to a man who was blessed by Allah for giving water to a thirsty dog, the other was a prostitute who filled her shoe with water and gave it to a dog, who had its tongue rolling out from thirst. For this deed she was granted the ultimate reward, the eternal Paradise under which rivers flow, to live therein forever." The Qur'an (Surah 18, verse 9-26) praises the dog for guarding the Seven Sleepers fleeing religious persecution; Islamic scholar Ingrid Mattson thus notes that "This tender description of the dog guarding the cave makes it clear that the animal is good company for believers." Umar, the second Caliph of Islam, said that if a dog was hungry in his kingdom, he would be derelict of his duty. According to the Qur'an the use of hunting dogs is permitted, which is a reason the Maliki school draws a distinction between feral and domesticated dogs―since Muslims can eat game that has been caught in a domesticated dog's mouth, the saliva of a domesticated dog cannot be impure. Abou El Fadl "found it hard to believe that the same God who created such companionable creatures would have his prophet declare them 'unclean'", stating that animosity towards dogs in folk Islam "reflected views far more consistent with pre-Islamic Arab customs and attitudes". Furthermore, "he found that a hadith from one of the most trustworthy sources tells how the Prophet himself had prayed in the presence of his playfully cavorting dogs." According to a story by Muslim ibn al-Hajjaj, black dogs are a manifestation of evil in animal form and the company of dogs voids a portion of a Muslim's good deeds; however, according to Khaled Abou El Fadl, the majority of scholars regard this to be "pre-Islamic Arab mythology" and "a tradition to be falsely attributed to the Prophet". Mattson teaches that for followers of other schools, "there are many other impurities present in our homes, mostly in the form of human waste, blood, and other bodily fluids" and that since it is common for these impurities to come in contact with a Muslim's clothes, they are simply washed or changed before prayer. However, this is not necessary for adherents of the Sunni Maliki school as "jurists from the Sunni Maliki School disagree with the idea that dogs are unclean." Individual fatāwā ("rulings") have indicated that dogs be treated kindly or otherwise released, and earlier Islamic literature often portrayed dogs as symbols of highly esteemed virtues such as self-sacrifice and loyalty, which, in the hands of despotic and unjust rulers, become oppressive instruments.

Domestic cats have a special place in Islamic culture. Muhammad is said to have loved his cat Muezzah to the extent that "he would go without his cloak rather than disturb Muezza that was sleeping on it."

Big cats like the asad (lion), namir (نَمِر, leopard), and namur (نَمُر, Tiger), can symbolize ferocity, similar to the wolf. Apart from ferocity, the lion has an important position in Islam and Arab culture. Men noted for their bravery, like Ali, Hamzah ibn Abdul-Muttalib and Omar Mukhtar, were given titles like "Asad Allāh" ("Lion of God") and "Asad aṣ-Ṣaḥrāʾ" ("Lion of the Desert").

A spider is told to have saved Muhammad and Abu Bakr by spinning a web over the entrance of the cave in which they hid. Because of the spider web, their persecutors thought the cave must be empty; otherwise, there would not have been a web. Therefore, Muslims consider killing spiders ('ankabūt) a sin.

Muslim cultures

Usually, in Muslim majority cultures, animals have names (one animal may be given several names), which are often interchangeable with names of people. Muslim names or titles like asad and ghadanfar (Arabic for lion), shir and arslan (Persian and Turkish for lion, respectively) and fahad (Could mean either a cheetah or leopard, however "nimr" is more common for the latter) are common in the Muslim world. Prominent Muslims with animal names include: Hamzah, Abd al-Rahman ibn Sakhr Al-Dawsi Al-Zahrani (more commonly known by his kunya "Abu Hurairah" or the Father of the kitten), Abdul-Qadir Gilani (called al-baz al-ashhab, the wise falcon) and Lal Shahbaz Qalander of Sehwan (called "red falcon").

Islamic literature has many stories of animals. Arabic and Persian literature boast many animal fables. The most famous, Kalilah wa-Dimnah or Panchatantra, translated into Arabic by Abd-Allāh Ibn al-Muqaffaʿ in the 8th century, was also known in Europe. In the 12th century, Shihab al-Din al-Suhrawadi wrote many short stories of animals. At about the same time, in north-eastern Iran, Attar Neyshapuri (Farid al-Din Attar) composed the epic poem Mantiq al-Tayr (meaning The Conference of the Birds).

In Malaysia in 2016, the Malaysian Islamic Development Department, a religious governing body, prohibited the use of the term hot dog to refer to the food of that name. It asked food outlets selling them to rename their products or risk refusal of halal certification. Per local media, Malaysian halal food guidelines prohibit naming halal products after non-halal products. Islamist organization Hamas which controls the Gaza Strip, banned public dog walking in May 2017, stating it was to "protect our women and children". Hamas officials stated that the ban was in response to rise in dog walking on the streets which they stated was "against culture and traditions in Gaza".

Ritual slaughter

Main article: Halal

UK animal welfare organizations have decried some ritual methods of slaughter practiced in Islam (dhabihah) and Judaism (shechita) as inhumane and causing "severe suffering". According to Judy MacArthur Clark, Chairperson of the Farm Animal Welfare Council, cattle require up to two minutes to bleed to death when halal or kosher means of slaughter are used on cattle: "This is a major incision into the animal and to say that it doesn't suffer is quite ridiculous." In response, Majid Katme of the Muslim Council of Britain stated that "[i]t's a sudden and quick haemorrhage. A quick loss of blood pressure and the brain is instantaneously starved of blood and there is no time to start feeling any pain."

In permitting dhabiha, the German Constitutional Court cited the 1978 study led by Professor Wilhelm Schulze at the University of Veterinary Medicine Hanover which concluded that "[t]he slaughter in the form of ritual cut is, if carried out properly, painless in sheep and calves according to the EEG recordings and the missing defensive actions." Muslims and Jews have also argued that traditional British methods of slaughter have meant that "animals are sometimes rendered physically immobile, although with full consciousness and sensation. Applying a sharp knife in shechita and dhabh, by contrast, ensures that no pain is felt: the wound inflicted is clean, and the loss of blood causes the animal to lose consciousness within seconds."

Animals in Islamic art

Title: Double-face textile with a tree of life & a winged lion Description: Rayy (Iran). Early Islamic Period. Silk

 

Title: Tree of Life, Khirbat al-Mafjar. Description: Jordan. Early Islamic Period, 8th century. Mosaic.

 

Title: Pyxis of al Mughira Description: Made at the Royal Workshop at Madinat al-Zahra, Spain for Prince al-Mughira. Hispano Umayyad, 968 CE.

The depiction of animals serve numerous functions in Islamic art. Various animal motifs may work to serve as symbolic metaphors for human beings in a variety objects but their use may vary a great degree from object to object ultimately dependent upon context in which these figures are situated in. The depiction of animals may also serve the purpose of being decorative motifs, examples of the use of animals for decorative purposes can be found in textiles, ceramics, metal work, mosaics, and in general, a wide spectrum of Islamic artistic mediums. Furthermore, depictions of animals in Islam can potentially be a combination of both decorative and symbolic in their respective usage, e.g. royal tapestries with animal motifs used to cover furniture such as the "Double-Face Textile with a Tree of Life & a Winged Lion," hailing from Rayy, Iran circa the Early Islamic Period. In the instance of the "Double-Face Textile with a Tree of Life and a Winged Lion," the use of lions can serve as a great study for reoccurring animal motifs which are used as a representational link between the symbolic power of the lion in nature and the sultan's power. Which in term demonstrates a dual use in visually portraying a lions.

Many animals are often represented alongside "vegetal" (Arabesque) patterns and are often found in an adorsed position (represented twice, symmetrically, and often side by side). Often we can find these adorsed or flanking animals surrounding an actual visual representation of a tree, this seems to be a common motif. The "Tree of Life" mosaic found at the desert palace of Khirbat al-Mafjar built under Caliph Walid II's rule during the Umayyad period, is perhaps one of the most well known mosaics depicting animals in figural form in the Islamic world. This particular mosaic was found in a private room of the desert palace which served as a bathhouse complex for the purpose of leisure. There is no religious context to this particular mosaic which explains the figural depictions of animals, under a religious context we would not see such figural depictions due to aniconism in the Islamic faith. In this mosaic we see a lion attacking a gazelle on the right side of the mosaic, and on the left side we see a depiction of two other gazelles casually grazing. Although there are multiple interpretations of this mosaic, one major interpretation seems to be that the actual physical depiction of the tree of life is a metaphor for the great and vast knowledge growing from the Islamic world. The lion attacking the gazelle is a borrowed motif from previous civilizations that is meant to represent Islam and the Islamic caliphates power as continuing the legacy of the great civilizations the preceded them (e.g. Mesopotamia). Another main interpretation is that this mosaic was a private erotic piece of art that depicted the caliphates sexual prowess, seeing as it was located in a private room of the bath complex. The entanglement of branches on the trees bearing fruit, the female gazelles grazing by the tree, and of course the lion (a stand in for the sultan) taking down his "prey" (a sole female gazelle), are all a testament to the sultan's (Walid II) reputation and exploits, which were well documented in the sultan's own writings.

Live animals or trophy pieces of deceased animals would sometimes be gifted to royal courts from one sultan to another sultan in the Islamic world. In some instances, this exchange of animals as gifts would come from outside the Islamic world as well. There is a documented instance for example of Charlemagne gifting a sultan a live animal (a living, breathing elephant to be exact). In many instances, we can observe these acquired pieces of animals such as ivory tusks, being repurposed, not only as a trophies but as a decorations. A great example of the aforementioned is "The Pyxis of al-Mughira," made at the Royal Workshop at Madinat al-Zahra, Spain, This Ivory Casket was gifted to the prince for the purpose of serving as a decorative piece with a nefarious political connotation behind it. Perhaps most interesting is that these caskets would be intricately carved from ivory, and depict various animal motifs, in various relations to pleasure, power, etc. Once again these pieces were not anionic for they were meant to be displayed in palaces or in private quarters. They did not have religious connotations behind them. Upon viewing "The Pyxis of al-Mughira" we see the adorned animals figures depicted time and time again in Islamic art. We can observe, two bulls, two men on horses, and of course two lions attacking stags. This ivory casket also depicts numerous birds, two men engaged in wrestling, what is presumed to be the sultan and his sons, musicians, the vegetal or arabesque pattern we have previously seen in other examples of Islamic art carved throughout the entirety of this casket, and a tiraz band across the upper area of the casket which serves as the aforementioned political warning.

The general overarching Idea of the examples given above are that the use of animals as symbolic representations of humans, royal accoutrements, symbolic representations of power, etc. were not necessarily exclusive in their use. Instead, they could cross the entire gamut in terms of art and culture. There is a multitude of usage and meanings in the depiction of animals in Islamic art. The context could range from political, religious, decorative, etc. These animal representations in the Islamic are not static and tell countless stories.

Probability space

From Wikipedia, the free encyclopedia

https://en.wikipedia.org/wiki/Probability_space

In probability theory, a probability space or a probability triple ${\displaystyle (\Omega ,{\mathcal {F}},P)}$ is a mathematical construct that provides a formal model of a random process or "experiment". For example, one can define a probability space which models the throwing of a die.

A probability space consists of three elements:

1. A sample space, ${\displaystyle \Omega }$, which is the set of all possible outcomes.
2. An event space, which is a set of events ${\displaystyle {\mathcal {F}}}$, an event being a set of outcomes in the sample space.
3. A probability function, which assigns each event in the event space a probability, which is a number between 0 and 1.

In order to provide a sensible model of probability, these elements must satisfy a number of axioms, detailed in this article.

In the example of the throw of a standard die, we would take the sample space to be ${\displaystyle \{1,2,3,4,5,6\}}$. For the event space, we could simply use the set of all subsets of the sample space, which would then contain simple events such as ${\displaystyle \{5\}}$ ("the die lands on 5"), as well as complex events such as ${\displaystyle \{2,4,6\}}$ ("the die lands on an even number"). Finally, for the probability function, we would map each event to the number of outcomes in that event divided by 6 — so for example, ${\displaystyle \{5\}}$ would be mapped to ${\displaystyle 1/6}$, and ${\displaystyle \{2,4,6\}}$ would be mapped to ${\displaystyle 3/6=1/2}$.

When an experiment is conducted, we imagine that "nature" "selects" a single outcome, ${\displaystyle \omega }$, from the sample space ${\displaystyle \Omega }$. All the events in the event space ${\displaystyle {\mathcal {F}}}$ that contain the selected outcome ${\displaystyle \omega }$ are said to "have occurred". This "selection" happens in such a way that if the experiment were repeated many times, the number of occurrences of each event, as a fraction of the total number of experiments, would most likely tend towards the probability assigned to that event by the probability function ${\displaystyle P}$.

The Soviet mathematician Andrey Kolmogorov introduced the notion of probability space, together with other axioms of probability, in the 1930s. In modern probability theory there are a number of alternative approaches for axiomatization — for example, algebra of random variables.

Introduction

Probability space for throwing a die twice in succession: The sample space ${\displaystyle \Omega }$ consists of all 36 possible outcomes; three different events (colored polygons) are shown, with their respective probabilities (assuming a discrete uniform distribution).

A probability space is a mathematical triplet ${\displaystyle (\Omega ,{\mathcal {F}},P)}$ that presents a model for a particular class of real-world situations. As with other models, its author ultimately defines which elements ${\displaystyle \Omega }$, ${\displaystyle {\mathcal {F}}}$, and ${\displaystyle P}$ will contain.

• The sample space ${\displaystyle \Omega }$ is the set of all possible outcomes. An outcome is the result of a single execution of the model. Outcomes may be states of nature, possibilities, experimental results and the like. Every instance of the real-world situation (or run of the experiment) must produce exactly one outcome. If outcomes of different runs of an experiment differ in any way that matters, they are distinct outcomes. Which differences matter depends on the kind of analysis we want to do. This leads to different choices of sample space.
• The σ-algebra ${\displaystyle {\mathcal {F}}}$ is a collection of all the events we would like to consider. This collection may or may not include each of the elementary events. Here, an "event" is a set of zero or more outcomes; that is, a subset of the sample space. An event is considered to have "happened" during an experiment when the outcome of the latter is an element of the event. Since the same outcome may be a member of many events, it is possible for many events to have happened given a single outcome. For example, when the trial consists of throwing two dice, the set of all outcomes with a sum of 7 pips may constitute an event, whereas outcomes with an odd number of pips may constitute another event. If the outcome is the element of the elementary event of two pips on the first die and five on the second, then both of the events, "7 pips" and "odd number of pips", are said to have happened.
• The probability measure ${\displaystyle P}$ is a set function returning an event's probability. A probability is a real number between zero (impossible events have probability zero, though probability-zero events are not necessarily impossible) and one (the event happens almost surely, with almost total certainty). Thus ${\displaystyle P}$ is a function ${\displaystyle P:{\mathcal {F}}\to [0,1].}$ The probability measure function must satisfy two simple requirements: First, the probability of a countable union of mutually exclusive events must be equal to the countable sum of the probabilities of each of these events. For example, the probability of the union of the mutually exclusive events ${\displaystyle {\text{Head}}}$ and ${\displaystyle {\text{Tail}}}$ in the random experiment of one coin toss, ${\displaystyle P({\text{Head}}\cup {\text{Tail}})}$, is the sum of probability for ${\displaystyle {\text{Head}}}$ and the probability for ${\displaystyle {\text{Tail}}}$, ${\displaystyle P({\text{Head}})+P({\text{Tail}})}$. Second, the probability of the sample space ${\displaystyle \Omega }$ must be equal to 1 (which accounts for the fact that, given an execution of the model, some outcome must occur). In the previous example the probability of the set of outcomes ${\displaystyle P(\{{\text{Head}},{\text{Tail}}\})}$ must be equal to one, because it is entirely certain that the outcome will be either ${\displaystyle {\text{Head}}}$ or ${\displaystyle {\text{Tail}}}$ (the model neglects any other possibility) in a single coin toss.

Not every subset of the sample space ${\displaystyle \Omega }$ must necessarily be considered an event: some of the subsets are simply not of interest, others cannot be "measured". This is not so obvious in a case like a coin toss. In a different example, one could consider javelin throw lengths, where the events typically are intervals like "between 60 and 65 meters" and unions of such intervals, but not sets like the "irrational numbers between 60 and 65 meters".

Definition

In short, a probability space is a measure space such that the measure of the whole space is equal to one.

The expanded definition is the following: a probability space is a triple ${\displaystyle (\Omega ,{\mathcal {F}},P)}$ consisting of:

• the sample space ${\displaystyle \Omega }$ — an arbitrary non-empty set,
• the σ-algebra ${\displaystyle {\mathcal {F}}\subseteq 2^{\Omega }}$ (also called σ-field) — a set of subsets of ${\displaystyle \Omega }$, called events, such that:
  • ${\displaystyle {\mathcal {F}}}$ contains the sample space: ${\displaystyle \Omega \in {\mathcal {F}}}$,
  • ${\displaystyle {\mathcal {F}}}$ is closed under complements: if ${\displaystyle A\in {\mathcal {F}}}$, then also ${\displaystyle (\Omega \setminus A)\in {\mathcal {F}}}$,
  • ${\displaystyle {\mathcal {F}}}$ is closed under countable unions: if ${\displaystyle A_{i}\in {\mathcal {F}}}$ for ${\displaystyle i=1,2,\dots }$, then also ${\textstyle (\bigcup _{i=1}^{\infty }A_{i})\in {\mathcal {F}}}$
    • The corollary from the previous two properties and De Morgan’s law is that ${\displaystyle {\mathcal {F}}}$ is also closed under countable intersections: if ${\displaystyle A_{i}\in {\mathcal {F}}}$ for ${\displaystyle i=1,2,\dots }$, then also ${\textstyle (\bigcap _{i=1}^{\infty }A_{i})\in {\mathcal {F}}}$
• the probability measure ${\displaystyle P:{\mathcal {F}}\to [0,1]}$ — a function on ${\displaystyle {\mathcal {F}}}$ such that:
  • P is countably additive (also called σ-additive): if ${\displaystyle \{A_{i}\}_{i=1}^{\infty }\subseteq {\mathcal {F}}}$ is a countable collection of pairwise disjoint sets, then ${\textstyle P(\bigcup _{i=1}^{\infty }A_{i})=\sum _{i=1}^{\infty }P(A_{i}),}$
  • the measure of entire sample space is equal to one: ${\displaystyle P(\Omega )=1}$.

Discrete case

Discrete probability theory needs only at most countable sample spaces ${\displaystyle \Omega }$. Probabilities can be ascribed to points of ${\displaystyle \Omega }$ by the probability mass function ${\displaystyle p:\Omega \to [0,1]}$ such that ${\textstyle \sum _{\omega \in \Omega }p(\omega )=1}$. All subsets of ${\displaystyle \Omega }$ can be treated as events (thus, ${\displaystyle {\mathcal {F}}=2^{\Omega }}$ is the power set). The probability measure takes the simple form

$${\displaystyle P(A)=\sum _{\omega \in A}p(\omega )\quad {\text{for all }}A\subseteq \Omega .}$$

(⁎)

The greatest σ-algebra ${\displaystyle {\mathcal {F}}=2^{\Omega }}$ describes the complete information. In general, a σ-algebra ${\displaystyle {\mathcal {F}}\subseteq 2^{\Omega }}$ corresponds to a finite or countable partition ${\displaystyle \Omega =B_{1}\cup B_{2}\cup \dots }$, the general form of an event ${\displaystyle A\in {\mathcal {F}}}$ being ${\displaystyle A=B_{k_{1}}\cup B_{k_{2}}\cup \dots }$. See also the examples.

The case ${\displaystyle p(\omega )=0}$ is permitted by the definition, but rarely used, since such ${\displaystyle \omega }$ can safely be excluded from the sample space.

General case

If Ω is uncountable, still, it may happen that p(ω) ≠ 0 for some ω; such ω are called atoms. They are an at most countable (maybe empty) set, whose probability is the sum of probabilities of all atoms. If this sum is equal to 1 then all other points can safely be excluded from the sample space, returning us to the discrete case. Otherwise, if the sum of probabilities of all atoms is between 0 and 1, then the probability space decomposes into a discrete (atomic) part (maybe empty) and a non-atomic part.

Non-atomic case

If p(ω) = 0 for all ω ∈ Ω (in this case, Ω must be uncountable, because otherwise P(Ω) = 1 could not be satisfied), then equation (⁎) fails: the probability of a set is not necessarily the sum over the probabilities of its elements, as summation is only defined for countable numbers of elements. This makes the probability space theory much more technical. A formulation stronger than summation, measure theory is applicable. Initially the probabilities are ascribed to some "generator" sets (see the examples). Then a limiting procedure allows assigning probabilities to sets that are limits of sequences of generator sets, or limits of limits, and so on. All these sets are the σ-algebra ${\displaystyle {\mathcal {F}}}$. For technical details see Carathéodory's extension theorem. Sets belonging to ${\displaystyle {\mathcal {F}}}$ are called measurable. In general they are much more complicated than generator sets, but much better than non-measurable sets.

Complete probability space

A probability space ${\displaystyle (\Omega ,\;{\mathcal {F}},\;P)}$ is said to be a complete probability space if for all ${\displaystyle B\in {\mathcal {F}}}$ with ${\displaystyle P(B)=0}$ and all ${\displaystyle A\;\subset \;B}$ one has ${\displaystyle A\in {\mathcal {F}}}$. Often, the study of probability spaces is restricted to complete probability spaces.

Examples

Discrete examples

Example 1

If the experiment consists of just one flip of a fair coin, then the outcome is either heads or tails: ${\displaystyle \Omega =\{{\text{H}},{\text{T}}\}}$. The σ-algebra ${\displaystyle {\mathcal {F}}=2^{\Omega }}$ contains ${\displaystyle 2^{2}=4}$ events, namely: ${\displaystyle \{{\text{H}}\}}$ ("heads"), ${\displaystyle \{{\text{T}}\}}$ ("tails"), ${\displaystyle \{\}}$ ("neither heads nor tails"), and ${\displaystyle \{{\text{H}},{\text{T}}\}}$ ("either heads or tails"); in other words, ${\displaystyle {\mathcal {F}}=\{\{\},\{{\text{H}}\},\{{\text{T}}\},\{{\text{H}},{\text{T}}\}\}}$. There is a fifty percent chance of tossing heads and fifty percent for tails, so the probability measure in this example is ${\displaystyle P(\{\})=0}$, ${\displaystyle P(\{{\text{H}}\})=0.5}$, ${\displaystyle P(\{{\text{T}}\})=0.5}$, ${\displaystyle P(\{{\text{H}},{\text{T}}\})=1}$.

Example 2

The fair coin is tossed three times. There are 8 possible outcomes: Ω = {HHH, HHT, HTH, HTT, THH, THT, TTH, TTT} (here "HTH" for example means that first time the coin landed heads, the second time tails, and the last time heads again). The complete information is described by the σ-algebra ${\displaystyle {\mathcal {F}}=2^{\Omega }}$ of 2⁸ = 256 events, where each of the events is a subset of Ω.

Alice knows the outcome of the second toss only. Thus her incomplete information is described by the partition Ω = A₁ ⊔ A₂ = {HHH, HHT, THH, THT} ⊔ {HTH, HTT, TTH, TTT}, where ⊔ is the disjoint union, and the corresponding σ-algebra ${\displaystyle {\mathcal {F}}_{\text{Alice}}=\{\{\},A_{1},A_{2},\Omega \}}$. Bryan knows only the total number of tails. His partition contains four parts: Ω = B₀ ⊔ B₁ ⊔ B₂ ⊔ B₃ = {HHH} ⊔ {HHT, HTH, THH} ⊔ {TTH, THT, HTT} ⊔ {TTT}; accordingly, his σ-algebra ${\displaystyle {\mathcal {F}}_{\text{Bryan}}}$ contains 2⁴ = 16 events.

The two σ-algebras are incomparable: neither ${\displaystyle {\mathcal {F}}_{\text{Alice}}\subseteq {\mathcal {F}}_{\text{Bryan}}}$ nor ${\displaystyle {\mathcal {F}}_{\text{Bryan}}\subseteq {\mathcal {F}}_{\text{Alice}}}$; both are sub-σ-algebras of 2^Ω.

Example 3

If 100 voters are to be drawn randomly from among all voters in California and asked whom they will vote for governor, then the set of all sequences of 100 Californian voters would be the sample space Ω. We assume that sampling without replacement is used: only sequences of 100 different voters are allowed. For simplicity an ordered sample is considered, that is a sequence {Alice, Bryan} is different from {Bryan, Alice}. We also take for granted that each potential voter knows exactly his/her future choice, that is he/she doesn’t choose randomly.

Alice knows only whether or not Arnold Schwarzenegger has received at least 60 votes. Her incomplete information is described by the σ-algebra ${\displaystyle {\mathcal {F}}_{\text{Alice}}}$ that contains: (1) the set of all sequences in Ω where at least 60 people vote for Schwarzenegger; (2) the set of all sequences where fewer than 60 vote for Schwarzenegger; (3) the whole sample space Ω; and (4) the empty set ∅.

Bryan knows the exact number of voters who are going to vote for Schwarzenegger. His incomplete information is described by the corresponding partition Ω = B₀ ⊔ B₁ ⊔ ⋯ ⊔ B₁₀₀ and the σ-algebra ${\displaystyle {\mathcal {F}}_{\text{Bryan}}}$ consists of 2¹⁰¹ events.

In this case Alice’s σ-algebra is a subset of Bryan’s: ${\displaystyle {\mathcal {F}}_{\text{Alice}}\subset {\mathcal {F}}_{\text{Bryan}}}$. Bryan’s σ-algebra is in turn a subset of the much larger "complete information" σ-algebra 2^Ω consisting of 2^{n(n−1)⋯(n−99)} events, where n is the number of all potential voters in California.

Non-atomic examples

Example 4

A number between 0 and 1 is chosen at random, uniformly. Here Ω = [0,1], ${\displaystyle {\mathcal {F}}}$ is the σ-algebra of Borel sets on Ω, and P is the Lebesgue measure on [0,1].

In this case the open intervals of the form (a,b), where 0 < a < b < 1, could be taken as the generator sets. Each such set can be ascribed the probability of P((a,b)) = (b − a), which generates the Lebesgue measure on [0,1], and the Borel σ-algebra on Ω.

Example 5

A fair coin is tossed endlessly. Here one can take Ω = {0,1}^∞, the set of all infinite sequences of numbers 0 and 1. Cylinder sets {(x₁, x₂, ...) ∈ Ω : x₁ = a₁, ..., x_n = a_n} may be used as the generator sets. Each such set describes an event in which the first n tosses have resulted in a fixed sequence (a₁, ..., a_n), and the rest of the sequence may be arbitrary. Each such event can be naturally given the probability of 2⁻ⁿ.

These two non-atomic examples are closely related: a sequence (x₁, x₂, ...) ∈ {0,1}^∞ leads to the number 2⁻¹x₁ + 2⁻²x₂ + ⋯ ∈ [0,1]. This is not a one-to-one correspondence between {0,1}^∞ and [0,1] however: it is an isomorphism modulo zero, which allows for treating the two probability spaces as two forms of the same probability space. In fact, all non-pathological non-atomic probability spaces are the same in this sense. They are so-called standard probability spaces. Basic applications of probability spaces are insensitive to standardness. However, non-discrete conditioning is easy and natural on standard probability spaces, otherwise it becomes obscure.

Related concepts

Probability distribution

Any probability distribution defines a probability measure.

Random variables

A random variable X is a measurable function X: Ω → S from the sample space Ω to another measurable space S called the state space.

If A ⊂ S, the notation Pr(X ∈ A) is a commonly used shorthand for ${\displaystyle \Pr(\{\omega \in \Omega :X(\omega )\in A\})}$.

Defining the events in terms of the sample space

If Ω is countable we almost always define ${\displaystyle {\mathcal {F}}}$ as the power set of Ω, i.e. ${\displaystyle {\mathcal {F}}=2^{\Omega }}$ which is trivially a σ-algebra and the biggest one we can create using Ω. We can therefore omit ${\displaystyle {\mathcal {F}}}$ and just write (Ω,P) to define the probability space.

On the other hand, if Ω is uncountable and we use ${\displaystyle {\mathcal {F}}=2^{\Omega }}$ we get into trouble defining our probability measure P because ${\displaystyle {\mathcal {F}}}$ is too "large", i.e. there will often be sets to which it will be impossible to assign a unique measure. In this case, we have to use a smaller σ-algebra ${\displaystyle {\mathcal {F}}}$, for example the Borel algebra of Ω, which is the smallest σ-algebra that makes all open sets measurable.

Conditional probability

Kolmogorov’s definition of probability spaces gives rise to the natural concept of conditional probability. Every set A with non-zero probability (that is, P(A) > 0) defines another probability measure

$${\displaystyle P(B|A)={P(B\cap A) \over P(A)}}$$

on the space. This is usually pronounced as the "probability of B given A".

For any event B such that P(B) > 0 the function Q defined by Q(A) = P(A|B) for all events A is itself a probability measure.

Independence

Two events, A and B are said to be independent if P(A ∩ B) = P(A) P(B).

Two random variables, X and Y, are said to be independent if any event defined in terms of X is independent of any event defined in terms of Y. Formally, they generate independent σ-algebras, where two σ-algebras G and H, which are subsets of F are said to be independent if any element of G is independent of any element of H.

Mutual exclusivity

Two events, A and B are said to be mutually exclusive or disjoint if the occurrence of one implies the non-occurrence of the other, i.e., their intersection is empty. This is a stronger condition than the probability of their intersection being zero.

If A and B are disjoint events, then P(A ∪ B) = P(A) + P(B). This extends to a (finite or countably infinite) sequence of events. However, the probability of the union of an uncountable set of events is not the sum of their probabilities. For example, if Z is a normally distributed random variable, then P(Z = x) is 0 for any x, but P(Z ∈ R) = 1.

The event A ∩ B is referred to as "A and B", and the event A ∪ B as "A or B".