Theoretical and experimental justification for the Schrödinger equation

From Wikipedia, the free encyclopedia

The theoretical and experimental justification for the Schrödinger equation motivates the discovery of the Schrödinger equation, the equation that describes the dynamics of nonrelativistic particles. The motivation uses photons, which are relativistic particles with dynamics determined by Maxwell's equations, as an analogue for all types of particles.

This article is at a postgraduate level. For a more general introduction to the topic see Introduction to quantum mechanics.

Classical electromagnetic waves

Nature of light

The quantum particle of light is called a photon. Light has both a wave-like and a particle-like nature. In other words, light can appear to be made of photons (particles) in some experiments and light can act like waves in other experiments. The dynamics of classical electromagnetic waves are completely determined by Maxwell's equations, the classical description of electrodynamics. In the absence of sources, Maxwell's equations can be written as wave equations in the electric and magnetic field vectors. Maxwell's equations thus describe, among other things, the wave-like properties of light. When "classical" (coherent or thermal) light is incident on a photographic plate or CCD, the average number of "hits", "dots", or "clicks" per unit time that result is approximately proportional to the square of the electromagnetic fields of the light. By formal analogy, the wavefunction of a material particle can be used to find the probability density by taking its absolute-value squared. Unlike electromagnetic fields, quantum-mechanical wavefunctions are complex. (Often in the case of EM fields complex notation is used for convenience, but it is understood that in fact the fields are real. On the contrary, wavefunctions are genuinely complex.)

Maxwell's equations were completely known by the latter part of the nineteenth century. The dynamical equations for light were, therefore, well-known long before the discovery of the photon. This is not true for other particles such as the electron. It was surmised from the interaction of light with atoms that electrons also had both a particle-like and a wave-like nature. Newtonian mechanics, a description of the particle-like behavior of macroscopic objects, failed to describe very small objects such as electrons. Abductive reasoning was performed to obtain the dynamics of massive objects (particles with mass) such as electrons. The electromagnetic wave equation, the equation that described the dynamics of light, was used as a prototype for discovering the Schrödinger equation, the equation that describes the wave-like and particle-like dynamics of nonrelativistic massive particles.

Plane sinusoidal waves

Electromagnetic wave equation

The electromagnetic wave equation describes the propagation of electromagnetic waves through a medium or in a vacuum. The homogeneous form of the equation, written in terms of either the electric field E or the magnetic field B, takes the form:

${\displaystyle \nabla ^{2}\mathbf {E} \ -\ {1 \over c^{2}}{\partial ^{2}\mathbf {E} \over \partial t^{2}}\ \ =\ \ 0}$

${\displaystyle \nabla ^{2}\mathbf {B} \ -\ {1 \over c^{2}}{\partial ^{2}\mathbf {B} \over \partial t^{2}}\ \ =\ \ 0}$

where c is the speed of light in the medium. In a vacuum, c = 2.998 × 10⁸ meters per second, which is the speed of light in free space.

The magnetic field is related to the electric field through Faraday's law (cgs units)

${\displaystyle \nabla \times \mathbf {E} =-{1 \over c}{\frac {\partial \mathbf {B} }{\partial t}}}$.

Plane wave solution of the electromagnetic wave equation

The plane sinusoidal solution for an electromagnetic wave traveling in the z direction is (cgs units and SI units)

${\displaystyle \mathbf {E} (\mathbf {r} ,t)=\mid \mathbf {E} \mid \mathrm {Re} \left\{|\zeta \rangle \exp \left[i\left(kz-\omega t\right)\right]\right\}\equiv \mid \mathbf {E} \mid \mathrm {Re} \left\{|\phi \rangle \right\}}$

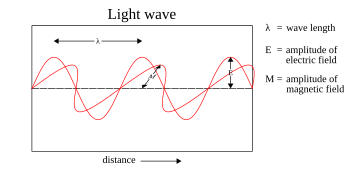
Electromagnetic radiation can be imagined as a self-propagating transverse oscillating wave of electric and magnetic fields. This diagram shows a plane linearly polarised wave propagating from left to right.

for the electric field and

${\displaystyle \mathbf {B} (\mathbf {r} ,t)={\hat {\mathbf {z} }}\times \mathbf {E} (\mathbf {r} ,t)}$

for the magnetic field, where k is the wavenumber,

${\displaystyle \omega _{}^{}=ck}$

is the angular frequency of the wave, and ${\displaystyle c}$ is the speed of light. The hats on the vectors indicate unit vectors in the x, y, and z directions. In complex notation, the quantity ${\displaystyle \mid \mathbf {E} \mid }$ is the amplitude of the wave.

Here

${\displaystyle |\zeta \rangle \equiv {\begin{pmatrix}\zeta _{x}\\\zeta _{y}\end{pmatrix}}={\begin{pmatrix}\cos \theta \exp \left(i\alpha _{x}\right)\\\sin \theta \exp \left(i\alpha _{y}\right)\end{pmatrix}}}$

is the Jones vector in the x-y plane. The notation for this vector is the bra–ket notation of Dirac, which is normally used in a quantum context. The quantum notation is used here in anticipation of the interpretation of the Jones vector as a quantum state vector. The angles ${\displaystyle \theta ,\;\alpha _{x},\;{\mbox{and}}\;\alpha _{y}}$ are the angle the electric field makes with the x axis and the two initial phases of the wave, respectively.

The quantity

${\displaystyle |\phi \rangle =\exp \left[i\left(kz-\omega t\right)\right]|\zeta \rangle }$

is the state vector of the wave. It describes the polarization of the wave and the spatial and temporal functionality of the wave. For a coherent state light beam so dim that its average photon number is much less than 1, this is approximately equivalent to the quantum state of a single photon.

Energy, momentum, and angular momentum of electromagnetic waves

Energy density of classical electromagnetic waves

Energy in a plane wave

The energy per unit volume in classical electromagnetic fields is (cgs units)

${\displaystyle {\mathcal {E}}_{c}={\frac {1}{8\pi }}\left[\mathbf {E} ^{2}(\mathbf {r} ,t)+\mathbf {B} ^{2}(\mathbf {r} ,t)\right]}$.

For a plane wave, converting to complex notation (and hence dividing by a factor of 2), this becomes

${\displaystyle {\mathcal {E}}_{c}={\frac {\mid \mathbf {E} \mid ^{2}}{8\pi }}}$

where the energy has been averaged over a wavelength of the wave.

Fraction of energy in each component

The fraction of energy in the x component of the plane wave (assuming linear polarization) is

${\displaystyle f_{x}={\frac {\mid \mathbf {E} \mid ^{2}\cos ^{2}\theta }{\mid \mathbf {E} \mid ^{2}}}=\phi _{x}^{*}\phi _{x}}$

with a similar expression for the y component.

The fraction in both components is

${\displaystyle \phi _{x}^{*}\phi _{x}+\phi _{y}^{*}\phi _{y}=\langle \phi |\phi \rangle =1}$.

Momentum density of classical electromagnetic waves

The momentum density is given by the Poynting vector

${\displaystyle {\boldsymbol {\mathcal {P}}}={1 \over 4\pi c}\mathbf {E} (\mathbf {r} ,t)\times \mathbf {B} (\mathbf {r} ,t)}$.

For a sinusoidal plane wave traveling in the z direction, the momentum is in the z direction and is related to the energy density:

${\displaystyle {\mathcal {P}}c={\mathcal {E}}_{c}}$.

The momentum density has been averaged over a wavelength.

Angular momentum density of classical electromagnetic waves

The angular momentum density is

${\displaystyle {\boldsymbol {\mathcal {L}}}=\mathbf {r} \times {\boldsymbol {\mathcal {P}}}={1 \over 4\pi c}\mathbf {r} \times \left[\mathbf {E} (\mathbf {r} ,t)\times \mathbf {B} (\mathbf {r} ,t)\right]}$.

For a sinusoidal plane wave the angular momentum is in the z direction and is given by (going over to complex notation)

${\displaystyle {\mathcal {L}}={{\mid \mathbf {E} \mid ^{2}} \over {8\pi \omega }}\left(\mid \langle R|\phi \rangle \mid ^{2}-\mid \langle L|\phi \rangle \mid ^{2}\right)={1 \over \omega }{\mathcal {E}}_{c}\left(\mid \phi _{R}\mid ^{2}-\mid \phi _{L}\mid ^{2}\right)}$

where again the density is averaged over a wavelength. Here right and left circularly polarized unit vectors are defined as

${\displaystyle |R\rangle \equiv {1 \over {\sqrt {2}}}{\begin{pmatrix}1\\i\end{pmatrix}}}$

and

${\displaystyle |L\rangle \equiv {1 \over {\sqrt {2}}}{\begin{pmatrix}1\\-i\end{pmatrix}}}$.

Unitary operators and energy conservation

A wave can be transformed by, for example, passing through a birefringent crystal or through slits in a diffraction grating. We can define the transformation of the state from the state at time t to the state at time ${\displaystyle (t+\tau )}$ as

${\displaystyle |\phi (t+\tau )\rangle ={\hat {U}}(\tau )|\phi (t)\rangle }$.

To conserve energy in the wave we require

${\displaystyle \langle \phi (t+\tau )|\phi (t+\tau )\rangle =\langle \phi (t)|{\hat {U}}^{\dagger }(\tau ){\hat {U}}(\tau )|\phi (t)\rangle =\langle \phi (t)|\phi (t)\rangle =1}$

where ${\displaystyle U^{\dagger }}$ is the adjoint of U, the complex conjugate transpose of the matrix.

This implies that a transformation that conserves energy must obey

${\displaystyle {\hat {U}}^{\dagger }{\hat {U}}=I}$

where I is the identity operator and U is called a unitary operator. The unitary property is necessary to ensure energy conservation in state transformations.

Hermitian operators and energy conservation

If ${\displaystyle \tau }$ is an infinitesimal real quantity ${\displaystyle dt}$, then the unitary transformation is very close to the identity matrix (the final state is very close to the initial state) and can be written

${\displaystyle {\hat {U}}\approx I-i{\hat {H}}\tau }$

and the adjoint by

${\displaystyle {\hat {U}}^{\dagger }\approx I+i{\hat {H}}^{\dagger }\tau }$.

The factor of i is introduced for convenience. With this convention, it will be shown that energy conservation requires H to be a Hermitian operator and that H is related to the energy of a particle.

Energy conservation requires

${\displaystyle I={\hat {U}}^{\dagger }{\hat {U}}\approx \left(I+i{\hat {H}}^{\dagger }\tau \right)\left(I-i{\hat {H}}\tau \right)\approx I+i{\hat {H}}^{\dagger }\tau -i{\hat {H}}\tau +{\hat {H}}^{\dagger }{\hat {H}}\tau ^{2}}$.

Since ${\displaystyle \tau }$ is infinitesimal, which means that ${\displaystyle \tau ^{2}}$ may be neglected with respect to ${\displaystyle \tau }$, the last term can be omitted. Further, if H is equal to its adjoint:

${\displaystyle {\hat {H}}={\hat {H}}^{\dagger }}$,

it follows that (for infinitesimal translations in time ${\displaystyle \tau =dt\,}$)

${\displaystyle {\hat {U}}^{\dagger }{\hat {U}}=I}$,

so that, indeed, energy is conserved.

Operators that are equal to their adjoints are called Hermitian or self-adjoint.

The infinitesimal translation of the polarization state is

${\displaystyle |\phi (t+dt)\rangle -|\phi (t)\rangle =-i{\hat {H}}dt|\phi (t)\rangle }$.

Thus, energy conservation requires that infinitesimal transformations of a polarization state occur through the action of a Hermitian operator. While this derivation is classical, the concept of a Hermitian operator generating energy-conserving infinitesimal transformations forms an important basis for quantum mechanics. The derivation of the Schrödinger equation follows directly from this concept.

Quantum analogy of classical electrodynamics

The treatment to this point has been classical. However, the quantum mechanical treatment of particles follows along lines formally analogous however, to Maxwell's equations for electrodynamics. The analog of the classical "state vectors"

${\displaystyle \mid \phi \rangle }$

in the classical description is quantum state vectors in the description of photons.

Energy, momentum, and angular momentum of photons

Energy

The early interpretation is based on the experiments of Max Planck and the interpretation of those experiments by Albert Einstein, which was that electromagnetic radiation is composed of irreducible packets of energy, known as photons. The energy of each packet is related to the angular frequency of the wave by the relation

${\displaystyle \epsilon =\hbar \omega }$

where ${\displaystyle \hbar }$ is an experimentally determined quantity known as the reduced Planck's constant. If there are ${\displaystyle N}$ photons in a box of volume ${\displaystyle V}$, the energy (neglecting zero point energy) in the electromagnetic field is

${\displaystyle N\hbar \omega }$

and the energy density is

${\displaystyle {N\hbar \omega \over V}}$

The energy of a photon can be related to classical fields through the correspondence principle which states that for a large number of photons, the quantum and classical treatments must agree. Thus, for very large ${\displaystyle N}$, the quantum energy density must be the same as the classical energy density

${\displaystyle {N\hbar \omega \over V}={\mathcal {E}}_{c}={\frac {\mid \mathbf {E} \mid ^{2}}{8\pi }}}$.

The average number of photons in the box in a coherent state is then

${\displaystyle N={\frac {V}{8\pi \hbar \omega }}\mid \mathbf {E} \mid ^{2}}$.

Momentum

The correspondence principle also determines the momentum and angular momentum of the photon. For momentum

${\displaystyle {\mathcal {P}}_{c}={N\hbar \omega \over cV}={N\hbar k \over V}}$

which implies that the momentum of a photon is

${\displaystyle \hbar k}$ (or equivalently ${\displaystyle h \over \lambda }$).

Angular momentum and spin

Similarly for the angular momentum

${\displaystyle {\mathcal {L}}={1 \over \omega }{\mathcal {E}}_{c}\left(\mid \psi _{R}\mid ^{2}-\mid \psi _{L}\mid ^{2}\right)={\hbar \over V}\left(\mid \psi _{R}\mid ^{2}-\mid \psi _{L}\mid ^{2}\right)}$

which implies that the angular momentum of the photon is

${\displaystyle l_{z}=\hbar \left(\mid \psi _{R}\mid ^{2}-\mid \psi _{L}\mid ^{2}\right)}$.

the quantum interpretation of this expression is that the photon has a probability of ${\displaystyle \mid \psi _{R}\mid ^{2}}$ of having an angular momentum of ${\displaystyle \hbar }$ and a probability of ${\displaystyle \mid \psi _{L}\mid ^{2}}$ of having an angular momentum of ${\displaystyle -\hbar }$. We can therefore think of the angular momentum of the photon being quantized as well as the energy. This has indeed been experimentally verified. Photons have only been observed to have angular momenta of ${\displaystyle \pm \hbar }$.

Spin operator

The spin of the photon is defined as the coefficient of ${\displaystyle \hbar }$ in the angular momentum calculation. A photon has spin 1 if it is in the ${\displaystyle |R\rangle }$ state and -1 if it is in the ${\displaystyle |L\rangle }$ state. The spin operator is defined as the outer product

${\displaystyle {\hat {S}}\equiv |R\rangle \langle R|-|L\rangle \langle L|={\begin{pmatrix}0&-i\\i&0\end{pmatrix}}}$.

The eigenvectors of the spin operator are ${\displaystyle |R\rangle }$ and ${\displaystyle |L\rangle }$ with eigenvalues 1 and -1, respectively.
The expected value of a spin measurement on a photon is then

${\displaystyle \langle \psi |{\hat {S}}|\psi \rangle =\mid \psi _{R}\mid ^{2}-\mid \psi _{L}\mid ^{2}}$.

An operator S has been associated with an observable quantity, the angular momentum. The eigenvalues of the operator are the allowed observable values. This has been demonstrated for angular momentum, but it is in general true for any observable quantity.

Probability for a single photon

There are two ways in which probability can be applied to the behavior of photons; probability can be used to calculate the probable number of photons in a particular state, or probability can be used to calculate the likelihood of a single photon to be in a particular state. The former interpretation is applicable to thermal or to coherent light (see Quantum optics). The latter interpretation is the option for a single-photon Fock state. Dirac explains this ^{[Note 1]} in the context of the double-slit experiment:

Some time before the discovery of quantum mechanics people realized that the connection between light waves and photons must be of a statistical character. What they did not clearly realize, however, was that the "wave function" gives information about the probability of one photon being in a particular place and not the probable number of photons in that place. The importance of the distinction can be made clear in the following way. Suppose we have a beam of light consisting of a large number of photons split up into two components of equal intensity. On the assumption that the beam is connected with the probable number of photons in it, we should have half the total number going into each component. If the two components are now made to interfere, we should require a photon in one component to be able to interfere with one in the other. Sometimes these two photons would have to annihilate one another and other times they would have to produce four photons. This would contradict the conservation of energy. The new theory, which connects the wave function with probabilities for one photon gets over the difficulty by making each photon go partly into each of the two components. Each photon then interferes only with itself. Interference between two different photons never occurs.

— Paul Dirac, The Principles of Quantum Mechanics, Fourth Edition, Chapter 1

Probability amplitudes

The probability for a photon to be in a particular polarization state depends on the probability distribution over the fields as calculated by the classical Maxwell's equations (in the Glauber-Sudarshan P-representation of a one-photon Fock state.) The expectation value of the photon number in a coherent state in a limited region of space is quadratic in the fields. In quantum mechanics, by analogy, the state or probability amplitude of a single particle contains the basic probability information. In general, the rules for combining probability amplitudes look very much like the classical rules for composition of probabilities: (The following quote is from Baym, Chapter 1)

1. The probability amplitude for two successive probabilities is the product of amplitudes for the individual possibilities. ...
2. The amplitude for a process that can take place in one of several indistinguishable ways is the sum of amplitudes for each of the individual ways. ...
3. The total probability for the process to occur is the absolute value squared of the total amplitude calculated by 1 and 2.

de Broglie waves

Louis de Broglie. De Broglie received the Nobel Prize in Physics in 1929 for his identification of waves with particles.

In 1923 Louis de Broglie addressed the question of whether all particles can have both a wave and a particle nature similar to the photon. Photons differ from many other particles in that they are massless and travel at the speed of light. Specifically de Broglie asked the question of whether a particle that has both a wave and a particle associated with it is consistent with Einstein's two great 1905 contributions, the special theory of relativity and the quantization of energy and momentum. The answer turned out to be positive. The wave and particle nature of electrons was experimentally observed in 1927, two years after the discovery of the Schrödinger equation.

de Broglie hypothesis

De Broglie supposed that every particle was associated with both a particle and a wave. The angular frequency ${\displaystyle \omega }$ and wavenumber ${\displaystyle k}$ of the wave was related to the energy E and momentum p of the particle by

${\displaystyle E=\hbar \omega }$

and

${\displaystyle p=\hbar k}$.

The question reduces to whether every observer in every inertial reference frame can agree on the phase of the wave. If so, then a wave-like description of particles may be consistent with special relativity.

Rest frame

First consider the rest frame of the particle. In that case the frequency and wavenumber of the wave are related to the energy and momentum of the particles properties by

${\displaystyle E_{0}=mc^{2}=\hbar \omega _{0}}$

and

${\displaystyle p_{0}=0=\hbar k_{0}}$

where m is the rest mass of the particle.

This describes a wave of infinite wavelength and infinite phase velocity

${\displaystyle v_{\phi }={\omega _{0} \over k_{0}}}$.

The wave may be written as proportional to

${\displaystyle \cos(\omega _{0}^{}t)}$.

This, however, is also the solution for a simple harmonic oscillator, which can be thought of as a clock in the rest frame of the particle. We can imagine a clock ticking at the same frequency as the wave is oscillating. The phases of the wave and the clock can be synchronized.

Frame of the observer

It is shown that the phase of the wave in an observer frame is the same as the phase of the wave in a particle frame, and also the same as clocks in the two frames. There is, therefore, consistency of both a wave-like and a particle-like picture in special relativity.

Phase of the observer clock

In the frame of an observer moving at relative speed v with respect to the particle, the particle clock is observed to tick at a frequency

${\displaystyle \omega _{c}={\omega _{0} \over \gamma }}$

where

${\displaystyle \gamma ={1 \over {\sqrt {1-{v^{2} \over c^{2}}}}}}$

is a Lorentz factor that describes time dilation of the particle clock as observed by the observer.

The phase of the observer clock is

${\displaystyle \omega _{c}t={\omega _{0} \over \gamma }(\gamma t_{0})=\omega _{0}t_{0}}$

where ${\displaystyle t_{0}}$ is time measured in the particle frame. Both the observer clock and the particle clock agree on the phase.

Phase of the observer wave

The frequency and wavenumber of the wave in the observer frame is given by

${\displaystyle E=\gamma m_{o}c^{2}=\hbar \omega =\gamma \hbar \omega _{o}}$

and

${\displaystyle {\vec {p}}=\gamma m_{o}{\vec {v}}=\hbar {\vec {k}}={\frac {\gamma \hbar \omega _{o}{\vec {v}}}{c^{2}}}}$

with a phase velocity

${\displaystyle v_{\phi }={\omega \over k}={E \over p}={c^{2} \over v}}$.

The phase of the wave in the observer frame is

${\displaystyle \omega t-kx=\omega t-{\omega \over v_{\phi }}vt=\omega t\left(1-{v^{2} \over c^{2}}\right)={\omega t \over \gamma ^{2}}={1 \over \gamma ^{2}}{\gamma m_{o}c^{2} \over \hbar }(\gamma t_{o})=\omega _{o}t_{o}=\omega _{c}t}$.

The phase of the wave in the observer frame is the same as the phase in the particle frame, as the clock in the particle frame, and the clock in the observer frame. A wave-like picture of particles is thus consistent with special relativity.

In fact, we now know that these relations can be succinctly written using special relativistic 4-vector notation:

The relevant four-vectors are:

Four-position ${\displaystyle \mathbf {X} =(ct,{\vec {x}})}$

Four-velocity ${\displaystyle \mathbf {U} =\gamma (c,{\vec {u}})}$

Four-momentum ${\displaystyle \mathbf {P} =\left({\frac {E}{c}},{\vec {p}}\right)}$

Four-wavevector ${\displaystyle \mathbf {K} =\left({\frac {\omega }{c}},{\vec {k}}\right)=\left({\frac {\omega }{c}},{\frac {\omega }{v_{\phi }}}{\hat {n}}\right)}$

The relations between the four-vectors are as follows:

${\displaystyle \mathbf {U} ={\frac {d\mathbf {X} }{d\tau }}}$

${\displaystyle \mathbf {P} =\hbar \mathbf {K} =m_{o}\mathbf {U} }$

${\displaystyle \mathbf {K} =\left({\frac {m_{o}}{\hbar }}\right)\mathbf {U} =\left({\frac {\omega _{o}}{c^{2}}}\right)\mathbf {U} }$

The phase of the wave is the relativistic invariant:

${\displaystyle \mathbf {K} \cdot \mathbf {X} =\omega t-{\vec {k}}\cdot {\vec {x}}=\omega _{o}t_{o}=\omega _{o}\tau }$

Bohr atom

Niels Bohr. In 1922 the Nobel Prize in Physics was awarded to Niels Bohr for his contributions to the understanding of quantum mechanics.

Inconsistency of observation with classical physics

The de Broglie hypothesis helped resolve outstanding issues in atomic physics. Classical physics was unable to explain the observed behaviour of electrons in atoms. Specifically, accelerating electrons emit electromagnetic radiation according to the Larmor formula. Electrons orbiting a nucleus should lose energy to radiation and eventually spiral into the nucleus. This is not observed. Atoms are stable on timescales much longer than predicted by the classical Larmor formula.

Also, it was noted that excited atoms emit radiation with discrete frequencies. Einstein used this fact to interpret discrete energy packets of light as, in fact, real particles. If these real particles are emitted from atoms in discrete energy packets, however, must the emitters, the electrons, also change energy in discrete energy packets? There is nothing in Newtonian mechanics that explains this.

The de Broglie hypothesis helped explain these phenomena by noting that the only allowed states for an electron orbiting an atom are those that allow for standing waves associated with each electron.

Balmer series

The Balmer series identifies those frequencies of light that can be emitted from an excited hydrogen atom:

${\displaystyle \hbar \omega _{n}=R\left({\frac {1}{2^{2}}}-{\frac {1}{n^{2}}}\right)\quad n=3,4,5,...}$

where R is known at the Rydberg constant and is equal to 13.6 electron volts.

Assumptions of the Bohr model

The Bohr model, introduced in 1913, was an attempt to provide a theoretical basis for the Balmer series. The assumptions of the model are:

1. The orbiting electrons existed in circular orbits that had discrete quantized energies. That is, not every orbit is possible but only certain specific ones.
2. The laws of classical mechanics do not apply when electrons make the jump from one allowed orbit to another.
3. When an electron makes a jump from one orbit to another the energy difference is carried off (or supplied) by a single quantum of light (called a photon) which has an energy equal to the energy difference between the two orbitals.
4. The allowed orbits depend on quantized (discrete) values of orbital angular momentum, L according to the equation
   ${\displaystyle {L}=n\hbar }$
   Where n = 1,2,3,… and is called the principal quantum number.

Implications of the Bohr model

In a circular orbit the centrifugal force balances the attractive force of the electron

${\displaystyle {mv^{2} \over r}={{e_{M}}^{2} \over r^{2}}}$

where m is the mass of the electron, v is the speed of the electron, r is the radius of the orbit and

${\displaystyle {e_{M}}={e \over {4\pi \epsilon _{0}}}}$

where e is the charge on the electron or proton.

The energy of the orbiting electron is

${\displaystyle E={1 \over 2}mv^{2}-{{e_{M}}^{2} \over r}=-{1 \over 2}{{e_{M}}^{2} \over r}}$

which follows from the centrifugal force expression.

The angular momentum assumption of the Bohr model implies

${\displaystyle L=mvr=n\hbar }$

which implies that, when combined with the centrifugal force equation, the radius of the orbit is given by

${\displaystyle r={n^{2}\hbar ^{2} \over m{e_{M}}^{2}}}$.

This implies, from the energy equation,

${\displaystyle E_{n}=-{1 \over 2}{{e_{M}}^{2} \over r}=-{1 \over 2}\left({m{e_{M}}^{4} \over \hbar ^{2}}\right){1 \over n^{2}}}$.

The difference between energy levels recovers the Balmer series.

De Broglie's contribution to the Bohr model

The Bohr assumptions recover the observed Balmer series. The Bohr assumptions themselves, however, are not based on any more general theory. Why, for instance, should the allowed orbits depend on the angular momentum? The de Broglie hypothesis provides some insight.

If we assume that the electron has a momentum given by

${\displaystyle p=mv=\hbar k}$

as postulated by the de Broglie hypothesis, then the angular momentum is given by

${\displaystyle L=mvr=\hbar kr=\hbar \left({2\pi \over \lambda }\right)r}$

where ${\displaystyle \lambda }$ is the wavelength of the electron wave.

If only standing electron waves are permitted in the atom then only orbits with perimeters equal to integral numbers of wavelengths are allowed:

${\displaystyle \lambda ={2\pi r \over n}}$.

This implies that allowed orbits have angular momentum

${\displaystyle L=n\hbar }$

which is Bohr's fourth assumption.

Assumptions one and two immediately follow. Assumption three follows from energy conservation, which de Broglie showed was consistent with the wave interpretation of particles.

Need for dynamical equations

The problem with the de Broglie hypothesis as applied to the Bohr atom is that we have forced a plane wave solution valid in empty space to a situation in which there is a strong attractive potential. We have not yet discovered the general dynamic equation for the evolution of electron waves. The Schrödinger equation is the immediate generalization of the de Broglie hypothesis and the dynamics of the photon.

Schrödinger equation

Analogy with photon dynamics

The dynamics of a photon are given by

${\displaystyle |\phi (t+dt)\rangle -|\phi (t)\rangle =-i{\hat {H}}dt|\phi (t)\rangle }$

where H is a Hermitian operator determined by Maxwell's equations. The Hermiticity of the operator ensures that energy is conserved.

Erwin Schrödinger assumed that the dynamics for massive particles were of the same form as the energy-conserving photon dynamics.

${\displaystyle |\psi (t+dt)\rangle -|\psi (t)\rangle =-i{\hat {H}}dt|\psi (t)\rangle }$

where ${\displaystyle |\psi (t)\rangle }$ is the state vector for the particle and H is now an unknown Hermitian operator to be determined.

Particle state vector

Rather than polarization states as in the photon case, Schrödinger assumed the state of the vector depended on the position of the particle. If a particle lives in one spatial dimension, then he divided the line up into an infinite number of small bins of length ${\displaystyle \lambda }$ and assigned a component of the state vector to each bin

${\displaystyle |\psi (t)\rangle \equiv {\begin{pmatrix}\vdots \\\psi _{j-1}(t)\\\psi _{j}(t)\\\psi _{j+1}(t)\\\vdots \end{pmatrix}}}$.

The subscript j identifies the bin.

Matrix form and transition amplitudes

The transition equation can be written in matrix form as

${\displaystyle \psi _{j}(t+dt)^{}-\psi _{j}(t)=-i\sum _{k}^{}H_{jk}\,dt\,\psi _{k}(t)}$.

The Hermitian condition requires

${\displaystyle H_{jk}=H_{kj}^{*}}$.

Schrödinger assumed that probability could only leak into adjacent bins during the small time step dt. In other words, all components of H are zero except for transitions between neighboring bins

${\displaystyle H_{j\pm 1,j}^{}\neq 0}$,

${\displaystyle H_{j,j}^{}\neq 0}$.

Moreover, it is assumed that space is uniform in that all transitions to the right are equal

${\displaystyle H_{j+1,j}^{}=H_{j,j-1}^{}\equiv H_{R}}$.

The same is true for transitions to the left

${\displaystyle H_{j-1,j}^{}=H_{j,j+1}^{}\equiv H_{L}}$.

The transition equation becomes

${\displaystyle i{\partial \psi _{j}(t) \over \partial t}=H_{L}\psi _{j+1}(t)-H_{R}\psi _{j}(t)+H_{R}\psi _{j-1}(t)-H_{L}\psi _{j}(t)+H_{jj}\psi _{j}(t)}$.

The first term on the right side represents the movement of probability amplitude into bin j from the right. The second term represents leakage of probability from bin j to the right. The third term represents leakage of probability into bin j from the left. The fourth term represents leakage from bin j to the left. The final term represents any change of phase in the probability amplitude in bin j.

If we expand the probability amplitude to second order in the bin size ${\displaystyle \lambda }$ and assume space is isotropic, ${\displaystyle H_{R}=H_{L}\equiv H_{0}}$ the transition equation reduces to

${\displaystyle i{\partial \psi _{j}(t) \over \partial t}=H_{0}{\lambda ^{2}}{\partial ^{2}\psi _{j}(t) \over \partial x^{2}}+H_{jj}\psi _{j}(t)}$.

Schrödinger equation in one dimension

Probability densities for the electron at different quantum numbers in the hydrogen atom.

The transition equation must be consistent with the de Broglie hypothesis. In free space the probability amplitude for the de Broglie wave is proportional to

${\displaystyle \exp \left[i\left(kx-\omega t\right)\right]}$

where

${\displaystyle E=\hbar \omega ={p^{2} \over 2m}={\hbar ^{2}k^{2} \over 2m}}$

in the non-relativistic limit.

The de Broglie solution for free space is a solution of the transition equation if we require

${\displaystyle H_{0}\lambda ^{2}=-{\hbar \over 2m}}$

and

${\displaystyle H_{jj}^{}=0^{}}$.

The time derivative term in the transition equation can be identified with the energy of the de Broglie wave. The spatial derivative term can be identified with the kinetic energy. This suggests that the term containing ${\displaystyle H_{jj}}$ is proportional to the potential energy. This yields the Schrödinger equation

${\displaystyle i\hbar {\partial \psi (x,t) \over \partial t}=-{\frac {\hbar ^{2}}{2m}}{\frac {\partial ^{2}\psi (x,t)}{\partial x^{2}}}+U(x)\psi (x,t)}$

where U is the classical potential energy and

${\displaystyle \psi (x,t)\equiv {1 \over {\sqrt {\lambda }}}\psi _{j}(t)}$

and

${\displaystyle 1=\int _{-\infty }^{\infty }\psi ^{*}(x,t)\psi (x,t)dx}$.

Schrödinger equation in three dimensions

In three dimensions the Schrödinger equation becomes

${\displaystyle -{\frac {\hbar ^{2}}{2m}}{\nabla ^{2}\psi }+U\psi =i\hbar {\partial \over \partial t}\psi }$

Hydrogen atom

The solution for the hydrogen atom describes standing waves of energy exactly given by the Balmer series. This was a spectacular validation of the Schrödinger equation and of the wave-like behaviour of matter.