Electroweak interaction

From Wikipedia, the free encyclopedia

In particle physics, the electroweak interaction is the unified description of two of the four known fundamental interactions of nature: electromagnetism and the weak interaction. Although these two forces appear very different at everyday low energies, the theory models them as two different aspects of the same force. Above the unification energy, on the order of 246 GeV, they would merge into a single electroweak force. Thus, if the universe is hot enough (approximately 10¹⁵ K, a temperature not exceeded since shortly after the Big Bang), then the electromagnetic force and weak force merge into a combined electroweak force. During the quark epoch, the electroweak force split into the electromagnetic and weak force.

Sheldon Glashow, Abdus Salam, and Steven Weinberg were awarded the 1979 Nobel Prize in Physics for their contributions to the unification of the weak and electromagnetic interaction between elementary particles. The existence of the electroweak interactions was experimentally established in two stages, the first being the discovery of neutral currents in neutrino scattering by the Gargamelle collaboration in 1973, and the second in 1983 by the UA1 and the UA2 collaborations that involved the discovery of the W and Z gauge bosons in proton–antiproton collisions at the converted Super Proton Synchrotron. In 1999, Gerardus 't Hooft and Martinus Veltman were awarded the Nobel prize for showing that the electroweak theory is renormalizable.

Formulation

Weinberg's weak mixing angle θ_W, and relation between coupling constants g, g', and e. Adapted from T D Lee's book Particle Physics and Introduction to Field Theory (1981).

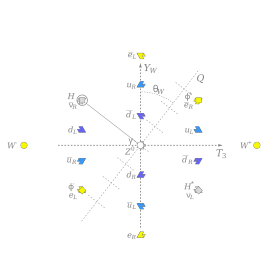
The pattern of weak isospin, T₃, and weak hypercharge, Y_W, of the known elementary particles, showing the electric charge, Q, along the weak mixing angle. The neutral Higgs field (circled) breaks the electroweak symmetry and interacts with other particles to give them mass. Three components of the Higgs field become part of the massive W and Z bosons.

Mathematically, the unification is accomplished under an SU(2) × U(1) gauge group. The corresponding gauge bosons are the three W bosons of weak isospin from SU(2) (W₁, W₂, and W₃), and the B boson of weak hypercharge from U(1), respectively, all of which are massless.

In the Standard Model, the
W^± and
Z⁰ bosons, and the photon, are produced by the spontaneous symmetry breaking of the electroweak symmetry from SU(2) × U(1)_Y to U(1)_em, caused by the Higgs mechanism. U(1)_Y and U(1)_em are different copies of U(1); the generator of U(1)_em is given by Q = Y/2 + T₃, where Y is the generator of U(1)_Y (called the weak hypercharge), and T₃ is one of the SU(2) generators (a component of weak isospin).

The spontaneous symmetry breaking makes the W₃ and B bosons coalesce into two different bosons – the
Z⁰ boson, and the photon (γ),

${\displaystyle {\begin{pmatrix}\gamma \\Z^{0}\end{pmatrix}}={\begin{pmatrix}\cos \theta _{W}&\sin \theta _{W}\\-\sin \theta _{W}&\cos \theta _{W}\end{pmatrix}}{\begin{pmatrix}B\\W_{3}\end{pmatrix}}}$

where θ_W is the weak mixing angle. The axes representing the particles have essentially just been rotated, in the (W₃, B) plane, by the angle θ_W. This also introduces a mismatch between the mass of the
Z⁰ and the mass of the
W^± particles (denoted as M_Z and M_W, respectively),

${\displaystyle M_{Z}={\frac {M_{W}}{\cos \theta _{W}}}.}$

The W₁ and W₂ bosons, in turn, combine to give massive charged bosons

${\displaystyle W^{\pm }={\frac {1}{\sqrt {2}}}(W_{1}\mp iW_{2}).}$

The distinction between electromagnetism and the weak force arises because there is a (nontrivial) linear combination of Y and T₃ that vanishes for the Higgs boson (it is an eigenstate of both Y and T₃, so the coefficients may be taken as −T₃ and Y): U(1)_em is defined to be the group generated by this linear combination, and is unbroken because it does not interact with the Higgs.

Lagrangian

Before electroweak symmetry breaking

The Lagrangian for the electroweak interactions is divided into four parts before electroweak symmetry breaking becomes manifest,

${\displaystyle {\mathcal {L}}_{\text{EW}}={\mathcal {L}}_{g}+{\mathcal {L}}_{f}+{\mathcal {L}}_{h}+{\mathcal {L}}_{y}~.}$

The ${\displaystyle {\mathcal {L}}_{g}}$ term describes the interaction between the three W vector bosons and the B vector boson,

${\displaystyle {\mathcal {L}}_{g}=-{\tfrac {1}{4}}W_{a}^{\mu \nu }W_{\mu \nu }^{a}-{\tfrac {1}{4}}B^{\mu \nu }B_{\mu \nu }}$,

where ${\displaystyle W^{a\mu \nu }}$ (${\displaystyle a=1,2,3}$) and ${\displaystyle B^{\mu \nu }}$ are the field strength tensors for the weak isospin and weak hypercharge gauge fields.

${\displaystyle {\mathcal {L}}_{f}}$ is the kinetic term for the Standard Model fermions. The interaction of the gauge bosons and the fermions are through the gauge covariant derivative,

${\displaystyle {\mathcal {L}}_{f}={\overline {Q}}_{i}iD\!\!\!\!/\;Q_{i}+{\overline {u}}_{i}iD\!\!\!\!/\;u_{i}+{\overline {d}}_{i}iD\!\!\!\!/\;d_{i}+{\overline {L}}_{i}iD\!\!\!\!/\;L_{i}+{\overline {e}}_{i}iD\!\!\!\!/\;e_{i}}$,

where the subscript i runs over the three generations of fermions; Q, u, and d are the left-handed doublet, right-handed singlet up, and right handed singlet down quark fields; and L and e are the left-handed doublet and right-handed singlet electron fields.

The h term describes the Higgs field and its interactions with itself and the gauge bosons,

${\displaystyle {\mathcal {L}}_{h}=|D_{\mu }h|^{2}-\lambda \left(|h|^{2}-{\frac {v^{2}}{2}}\right)^{2}}$

The y term displays the Yukawa interaction with the fermions,

${\displaystyle {\mathcal {L}}_{y}=-y_{u\,ij}\epsilon ^{ab}\,h_{b}^{\dagger }\,{\overline {Q}}_{ia}u_{j}^{c}-y_{d\,ij}\,h\,{\overline {Q}}_{i}d_{j}^{c}-y_{e\,ij}\,h\,{\overline {L}}_{i}e_{j}^{c}+h.c.~,}$

and generates their masses, manifest when the Higgs field acquires a nonzero vacuum expectation value, discussed next.

After electroweak symmetry breaking

The Lagrangian reorganizes itself as the Higgs boson acquires a non-vanishing vacuum expectation value dictated by the potential of the previous section. As a result of this rewriting, the symmetry breaking becomes manifest.

Due to its complexity, this Lagrangian is best described by breaking it up into several parts as follows.

${\displaystyle {\mathcal {L}}_{\text{EW}}={\mathcal {L}}_{\text{K}}+{\mathcal {L}}_{\text{N}}+{\mathcal {L}}_{\text{C}}+{\mathcal {L}}_{\text{H}}+{\mathcal {L}}_{\text{HV}}+{\mathcal {L}}_{\text{WWV}}+{\mathcal {L}}_{\text{WWVV}}+{\mathcal {L}}_{\text{Y}}.}$

The kinetic term ${\displaystyle {\mathcal {L}}_{K}}$ contains all the quadratic terms of the Lagrangian, which include the dynamic terms (the partial derivatives) and the mass terms (conspicuously absent from the Lagrangian before symmetry breaking)

${\displaystyle {\begin{aligned}{\mathcal {L}}_{\text{K}}=\sum _{f}{\overline {f}}(i\partial \!\!\!/\!\;-m_{f})f-{\frac {1}{4}}A_{\mu \nu }A^{\mu \nu }-{\frac {1}{2}}W_{\mu \nu }^{+}W^{-\mu \nu }+m_{W}^{2}W_{\mu }^{+}W^{-\mu }\\\qquad -{\frac {1}{4}}Z_{\mu \nu }Z^{\mu \nu }+{\frac {1}{2}}m_{Z}^{2}Z_{\mu }Z^{\mu }+{\frac {1}{2}}(\partial ^{\mu }H)(\partial _{\mu }H)-{\frac {1}{2}}m_{H}^{2}H^{2}~,\end{aligned}}}$

where the sum runs over all the fermions of the theory (quarks and leptons), and the fields ${\displaystyle A_{\mu \nu }^{}}$, ${\displaystyle Z_{\mu \nu }^{}}$, ${\displaystyle W_{\mu \nu }^{-}}$, and ${\displaystyle W_{\mu \nu }^{+}\equiv (W_{\mu \nu }^{-})^{\dagger }}$ are given as

${\displaystyle X_{\mu \nu }^{a}=\partial _{\mu }X_{\nu }^{a}-\partial _{\nu }X_{\mu }^{a}+gf^{abc}X_{\mu }^{b}X_{\nu }^{c}~,}$

with X to be replaced by the relevant field, and f ^abc by the structure constants of the appropriate gauge group.

The neutral current ${\displaystyle {\mathcal {L}}_{\text{N}}}$ and charged current ${\displaystyle {\mathcal {L}}_{\text{C}}}$ components of the Lagrangian contain the interactions between the fermions and gauge bosons,

${\displaystyle {\mathcal {L}}_{\text{N}}=eJ_{\mu }^{\text{em}}A^{\mu }+{\frac {g}{\cos \theta _{W}}}(J_{\mu }^{3}-\sin ^{2}\theta _{W}J_{\mu }^{\text{em}})Z^{\mu }}$,

where e= g sin θ_W= g' cos θ_W; while the electromagnetic current ${\displaystyle J_{\mu }^{\text{em}}}$ and the neutral weak current ${\displaystyle J_{\mu }^{3}}$ are

${\displaystyle J_{\mu }^{\text{em}}=\sum _{f}q_{f}{\overline {f}}\gamma _{\mu }f}$,

and

${\displaystyle J_{\mu }^{3}=\sum _{f}I_{f}^{3}{\overline {f}}\gamma _{\mu }{\frac {1-\gamma ^{5}}{2}}f}$

where ${\displaystyle q_{f}^{}}$ and ${\displaystyle I_{f}^{3}}$ are the fermions' electric charges and weak isospin.

The charged current part of the Lagrangian is given by

${\displaystyle {\mathcal {L}}_{\text{C}}=-{\frac {g}{\sqrt {2}}}\left[{\overline {u}}_{i}\gamma ^{\mu }{\frac {1-\gamma ^{5}}{2}}M_{ij}^{\text{CKM}}d_{j}+{\overline {\nu }}_{i}\gamma ^{\mu }{\frac {1-\gamma ^{5}}{2}}e_{i}\right]W_{\mu }^{+}+{\text{h.c.}}~,}$

where ${\displaystyle {\mathcal {L}}_{\text{H}}}$ contains the Higgs three-point and four-point self interaction terms,

${\displaystyle {\mathcal {L}}_{\text{H}}=-{\frac {gm_{H}^{2}}{4m_{W}}}H^{3}-{\frac {g^{2}m_{H}^{2}}{32m_{W}^{2}}}H^{4}~.}$

${\displaystyle {\mathcal {L}}_{\text{HV}}}$ contains the Higgs interactions with gauge vector bosons,

${\displaystyle {\mathcal {L}}_{\text{HV}}=\left(gm_{W}H+{\frac {g^{2}}{4}}H^{2}\right)\left(W_{\mu }^{+}W^{-\mu }+{\frac {1}{2\cos ^{2}\theta _{W}}}Z_{\mu }Z^{\mu }\right).}$

${\displaystyle {\mathcal {L}}_{\text{WWV}}}$ contains the gauge three-point self interactions,

${\displaystyle {\mathcal {L}}_{\text{WWV}}=-ig[(W_{\mu \nu }^{+}W^{-\mu }-W^{+\mu }W_{\mu \nu }^{-})(A^{\nu }\sin \theta _{W}-Z^{\nu }\cos \theta _{W})+W_{\nu }^{-}W_{\mu }^{+}(A^{\mu \nu }\sin \theta _{W}-Z^{\mu \nu }\cos \theta _{W})].}$

${\displaystyle {\mathcal {L}}_{\text{WWVV}}}$ contains the gauge four-point self interactions,

${\displaystyle {\begin{aligned}{\mathcal {L}}_{\text{WWVV}}=-{\frac {g^{2}}{4}}{\Big \{}&[2W_{\mu }^{+}W^{-\mu }+(A_{\mu }\sin \theta _{W}-Z_{\mu }\cos \theta _{W})^{2}]^{2}\\&-[W_{\mu }^{+}W_{\nu }^{-}+W_{\nu }^{+}W_{\mu }^{-}+(A_{\mu }\sin \theta _{W}-Z_{\mu }\cos \theta _{W})(A_{\nu }\sin \theta _{W}-Z_{\nu }\cos \theta _{W})]^{2}{\Big \}}.\end{aligned}}}$

${\displaystyle {\mathcal {L}}_{\text{Y}}}$ contains the Yukawa interactions between the fermions and the Higgs field,

${\displaystyle {\mathcal {L}}_{\text{Y}}=-\sum _{f}{\frac {gm_{f}}{2m_{W}}}{\overline {f}}fH.}$

Note the ${\displaystyle {\tfrac {1}{2}}(1-\gamma ^{5})}$ factors in the weak couplings: these factors project out the left handed components of the spinor fields. This is why electroweak theory is said to be a chiral theory.