Fermi gas

From Wikipedia, the free encyclopedia

An ideal Fermi gas is a phase of matter which is an ensemble of a large number of non-interacting fermions. Fermions are particles that obey Fermi–Dirac statistics, like electrons, protons and neutrons, and in general, particles with half-integer spin. These statistics determine the energy distribution of fermions in a Fermi gas in thermal equilibrium, and is characterized by their number density, temperature, and the set of available energy states. The model is named after the Italian physicist Enrico Fermi.

This physical model can be accurately applied to many systems with a large number of fermions. Some key examples are the behaviour of charge carriers in a metal, nucleons in an atomic nucleus, neutrons in a neutron star, and electrons in a white dwarf.

Description

Illustration of the energy states: Energy-occupation diagram for a system with 7 energy levels, the energy E_i is degenerate D_i times and has an occupancy given by N_i, with i=1,2,3,4,5,6,7. By the Pauli exclusion principle, up to D_i fermions can occupy a level of energy E_i of the system.

An ideal Fermi gas or free Fermi gas is a physical model assuming a collection of non-interacting fermions in a constant potential well. It is the quantum mechanical version of an ideal gas, for the case of fermionic particles.

By the Pauli exclusion principle, no quantum state can be occupied by more than one fermion with an identical set of quantum numbers. Thus a non-interacting Fermi gas, unlike a Bose gas, concentrates a small number of particles per energy. Thus a Fermi gas is prohibited from condensing into a Bose–Einstein condensate, although weakly-interacting Fermi gases might. The total energy of the Fermi gas at absolute zero is larger than the sum of the single-particle ground states because the Pauli principle implies a sort of interaction or pressure that keeps fermions separated and moving. For this reason, the pressure of a Fermi gas is non-zero even at zero temperature, in contrast to that of a classical ideal gas. For example, this so-called degeneracy pressure stabilizes a neutron star (a Fermi gas of neutrons) or a white dwarf star (a Fermi gas of electrons) against the inward pull of gravity, which would ostensibly collapse the star into a black hole. Only when a star is sufficiently massive to overcome the degeneracy pressure can it collapse into a singularity.

It is possible to define a Fermi temperature below which the gas can be considered degenerate (its pressure derives almost exclusively from the Pauli principle). This temperature depends on the mass of the fermions and the density of energy states.

The main assumption of the free electron model to describe the delocalized electrons in a metal can be derived from the Fermi gas. Since interactions are neglected due to screening effect, the problem of treating the equilibrium properties and dynamics of an ideal Fermi gas reduces to the study of the behaviour of single independent particles. In these systems the Fermi temperature is generally many thousands of kelvins, so in human applications the electron gas can be considered degenerate. The maximum energy of the fermions at zero temperature is called the Fermi energy. The Fermi energy surface in momentum space is known as the Fermi surface.

The nearly free electron model adapts the Fermi gas model to consider the crystal structure of metals and semiconductors. Where electrons in a crystal lattice are substituted by Bloch waves with a corresponding crystal momentum. As such, periodic systems are still relatively tractable and the model forms the starting point for more advanced theories that deal with interactions, e.g., using the perturbation theory.

Illustration of the Fermi energy for a one-dimensional well

The one-dimensional infinite square well of length L is a model for a one-dimensional box. It is a standard model-system in quantum mechanics for which the solution for a single particle is well known. The levels are labelled by a single quantum number n and the energies are given by

${\displaystyle E_{n}=E_{0}+{\frac {\hbar ^{2}\pi ^{2}}{2mL^{2}}}n^{2}.\,}$

where ${\displaystyle E_{0}}$ is the potential energy level inside the box, ${\displaystyle m}$ the mass of a single fermion, and ${\displaystyle \hbar }$ is the reduced Planck constant.

Suppose now that instead of one particle in this box we have N particles in the box and that these particles are fermions with spin-½. Then not more than two particles can have the same energy, i.e., two particles can have the energy of ${\textstyle E_{1}}$, two other particles can have energy ${\textstyle E_{2}}$ and so forth. The reason that two particles can have the same energy is that a particle can have a spin of ½ (spin up) or a spin of −½ (spin down), leading to two states for each energy level. In the configuration for which the total energy is lowest (the ground state), all the energy levels up to n = N/2 are occupied and all the higher levels are empty.

Defining the reference for the Fermi energy to be ${\displaystyle E_{0}}$, the Fermi energy is therefore given by

${\displaystyle E_{\mathrm {F} }^{({\text{1D}})}=E_{N^{*}/2}-E_{0}={\frac {\hbar ^{2}\pi ^{2}}{2mL^{2}}}(N^{*}/2)^{2},}$

where N* is equal to (N − 1) when the number of particles N is odd, and its equal to (N) for an even number of particles.

Three-dimensional case

A model of the atomic nucleus showing it as a compact bundle of the two types of nucleons: protons (red) and neutrons (blue). As a first approximation, the nucleus can be treated as composed of non-interacting proton and neutron gases.

The three-dimensional isotropic and non-relativistic case is known as the Fermi sphere.

Let us now consider a three-dimensional infinite square well, that is, a cubical box that has a side length L. The states are now labelled by three quantum numbers n_x, n_y, and n_z. The single particle energies are

${\displaystyle E_{n_{x},n_{y},n_{z}}=E_{0}+{\frac {\hbar ^{2}\pi ^{2}}{2mL^{2}}}\left(n_{x}^{2}+n_{y}^{2}+n_{z}^{2}\right)\,}$,

where n_x, n_y, n_z are positive integers. There are multiple states with the same energy, for example ${\displaystyle E_{211}=E_{121}=E_{112}}$. Now let's put N non-interacting fermions of spin ½ into this box. To calculate the Fermi energy, we look at the case where N is large.

If we introduce a vector ${\displaystyle \mathbf {n} =(n_{x},n_{y},n_{z})}$ then each quantum state corresponds to a point in 'n-space' with energy

${\displaystyle E_{\mathbf {n} }=E_{0}+{\frac {\hbar ^{2}\pi ^{2}}{2mL^{2}}}|\mathbf {n} |^{2}\,}$

With ${\displaystyle |\mathbf {n} |^{2}}$denoting the square of the usual Euclidean length ${\displaystyle |\mathbf {n} |={\sqrt {n_{x}^{2}+n_{y}^{2}+n_{z}^{2}}}}$. The number of states with energy less than E_F +  E₀ is equal to the number of states that lie within a sphere of radius ${\displaystyle |\mathbf {n} _{\mathrm {F} }|}$ in the region of n-space where n_x, n_y, n_z are positive. In the ground state this number equals the number of fermions in the system.

${\displaystyle N=2\times {\frac {1}{8}}\times {\frac {4}{3}}\pi n_{\mathrm {F} }^{3}\,}$

The free fermions that occupy the lowest energy states form a sphere in momentum space. The surface of this sphere is the Fermi surface.

The factor of two is found again because there are two spin states, while the factor of 1/8 is because only 1/8 of the sphere lies in the region where all n are positive. We find

${\displaystyle n_{\mathrm {F} }=\left({\frac {3N}{\pi }}\right)^{1/3}}$

so the Fermi energy is given by

${\displaystyle E_{\mathrm {F} }={\frac {\hbar ^{2}\pi ^{2}}{2mL^{2}}}n_{\mathrm {F} }^{2}={\frac {\hbar ^{2}\pi ^{2}}{2mL^{2}}}\left({\frac {3N}{\pi }}\right)^{2/3}}$

Which results in a relationship between the Fermi energy and the number of particles per volume (when we replace L² with V^2/3):

${\displaystyle E_{\mathrm {F} }={\frac {\hbar ^{2}}{2m}}\left({\frac {3\pi ^{2}N}{V}}\right)^{2/3}\,}$

The total energy of a Fermi sphere of ${\displaystyle N}$ fermions is given by

${\displaystyle E_{\rm {T}}=NE_{0}+\int _{0}^{N}E_{\mathrm {F} }\,\mathrm {d} N^{\prime }=\left({\frac {3}{5}}E_{\mathrm {F} }+E_{0}\right)N}$

Therefore, the average energy per particle is given by:

${\displaystyle E_{\mathrm {av} }=E_{0}+{\frac {3}{5}}E_{\mathrm {F} }}$

Related quantities

Using this definition of Fermi energy, various related quantities can be useful. The Fermi temperature is defined as:

${\displaystyle T_{\mathrm {F} }={\frac {E_{\mathrm {F} }}{k_{\rm {B}}}}}$

where ${\displaystyle k_{\rm {B}}}$ is the Boltzmann constant. The Fermi temperature can be thought of as the temperature at which thermal effects are comparable to quantum effects associated with Fermi statistics. The Fermi temperature for a metal is a couple of orders of magnitude above room temperature.

Other quantities defined in this context are Fermi momentum

${\displaystyle p_{\mathrm {F} }={\sqrt {2mE_{\mathrm {F} }}}}$,

and Fermi velocity

${\displaystyle v_{\mathrm {F} }={\frac {p_{\mathrm {F} }}{m}}}$.

These quantities are the momentum and group velocity, respectively, of a fermion at the Fermi surface. The Fermi momentum can also be described as ${\displaystyle p_{\mathrm {F} }=\hbar k_{\mathrm {F} }}$, where ${\displaystyle k_{\mathrm {F} }}$ is the radius of the Fermi sphere and is called the Fermi wave vector.

These quantities are not well-defined in cases where the Fermi surface is non-spherical.

Thermodynamic quantities

Degeneracy pressure

As we showed above, a Fermi gas has a non-zero total energy even at zero temperature. By using the first law of thermodynamics, we can associate a pressure to this internal energy, that is

${\displaystyle P=-{\frac {\partial E_{\rm {T}}}{\partial V}}={\frac {2}{5}}{\frac {N}{V}}E_{\mathrm {F} }={\frac {(3\pi ^{2})^{2/3}\hbar ^{2}}{5m}}\left({\frac {N}{V}}\right)^{5/3},}$

where the expression is only valid for temperatures much smaller than the Fermi temperature. This pressure is known as the degeneracy pressure. In this sense, systems composed of fermions are also referred as degenerate matter.

Standard stars avoid collapse by balancing thermal pressure (plasma and radiation) against gravitational forces. At the end of the star lifetime, when thermal processes are weaker, some stars may become white dwarfs, which are only sustained against gravity by electron degeneracy pressure. Using the Fermi gas as a model, it is possible to calculate the Chandrasekhar limit, i.e. the maximum mass any star may acquire (without significant thermally generated pressure) before collapsing into a black hole or a neutron star. The latter, is a star mainly composed of neutrons, where the collapse is also avoided by neutron degeneracy pressure.

For the case of metals, the electron degeneracy pressure contributes to the compressibility or bulk modulus of the material.

Chemical potential

Assuming that the concentration of fermions does not change with temperature, then the total chemical potential µ (Fermi level) of the three-dimensional ideal Fermi gas is related to the zero temperature Fermi energy E_F by a Sommerfeld expansion (assuming ${\displaystyle k_{\rm {B}}T\ll E_{\mathrm {F} }}$):

${\displaystyle \mu (T)=E_{0}+E_{\mathrm {F} }\left[1-{\frac {\pi ^{2}}{12}}\left({\frac {k_{\rm {B}}T}{E_{\mathrm {F} }}}\right)^{2}-{\frac {\pi ^{4}}{80}}\left({\frac {k_{\rm {B}}T}{E_{\mathrm {F} }}}\right)^{4}+\cdots \right]}$,

where T is the temperature.

Hence, the internal chemical potential, µ-E₀, is approximately equal to the Fermi energy at temperatures that are much lower than the characteristic Fermi temperature T_F. This characteristic temperature is on the order of 10⁵ K for a metal, hence at room temperature (300 K), the Fermi energy and internal chemical potential are essentially equivalent.

Density of states

Figure 3: Density of states (DOS) of a Fermi gas in 3-dimensions

For the three dimensional case, with fermions of spin-½, we can obtain the number of particles as a function of the energy ${\textstyle N(E)}$ by substituting the Fermi energy by a variable energy ${\textstyle (E-E_{0})}$:

${\displaystyle N(E)={\frac {V}{3\pi ^{2}}}\left[{\frac {2m}{\hbar ^{2}}}(E-E_{0})\right]^{3/2}}$,

which we can use to obtain the density of states (number of energy states per energy per volume) ${\displaystyle g(E)}$. It can be calculated by differentiating the number of particles with respect to the energy:

${\displaystyle g(E)={\frac {1}{V}}{\frac {\partial N(E)}{\partial E}}={\frac {1}{2\pi ^{2}}}\left({\frac {2m}{\hbar ^{2}}}\right)^{3/2}{\sqrt {E-E_{0}}}}$.

Arbitrary-dimensional case

Using a volume integral on ${\textstyle d}$ dimensions, we can find the state density:

${\displaystyle g^{(d)}(E)=g_{s}\int {\frac {\mathrm {d} ^{d}\mathbf {k} }{(2\pi )^{d}}}\delta \left(E-E_{0}-{\frac {\hbar ^{2}|\mathbf {k} |^{2}}{2m}}\right)=g_{s}\ {\frac {d}{2}}\left({\frac {m}{2\pi \hbar ^{2}}}\right)^{d/2}{\frac {(E-E_{0})^{d/2-1}}{\Gamma (d/2+1)}}}$

By then looking for the number density of particles, we can extract the Fermi energy:

${\displaystyle \rho ={\frac {N}{V}}=\int _{E_{0}}^{E_{0}+E_{\mathrm {F} }^{(d)}}g^{(d)}(E)\,\mathrm {d} E}$

To get:

${\displaystyle E_{\mathrm {F} }^{(d)}={\frac {2\pi \hbar ^{2}}{m}}\left({\tfrac {1}{g_{s}}}\Gamma \left({\tfrac {d}{2}}+1\right){\frac {N}{V}}\right)^{2/d}}$

where ${\textstyle V}$ is the corresponding d-dimensional volume, ${\textstyle g_{s}}$ is the dimension for the internal Hilbert space. For the case of spin-½, every energy is twice-degenerate, so in this case ${\textstyle g_{s}=2}$.

A particular result is obtained for ${\displaystyle d=2}$, where the density of states becomes a constant (does not depend on the energy):

${\displaystyle g^{(2\mathrm {D} )}(E)={\frac {g_{s}}{2}}{\frac {m}{\pi \hbar ^{2}}}}$.

Typical values

Metals

Under the free electron model, the electrons in a metal can be considered to form a Fermi gas. The number density ${\displaystyle N/V}$ of conduction electrons in metals ranges between approximately 10²⁸ and 10²⁹ electrons/m³, which is also the typical density of atoms in ordinary solid matter. This number density produces a Fermi energy of the order:

${\displaystyle E_{\mathrm {F} }={\frac {\hbar ^{2}}{2m_{e}}}\left(3\pi ^{2}\ 10^{28\ \sim \ 29}\ \mathrm {m} ^{-3}\right)^{2/3}\approx 2\ \sim \ 10\ \mathrm {eV} }$,

where m_e is the electron mass. This Fermi energy corresponds to a Fermi temperature of the order of 10⁶ kelvins, much higher than the temperature of the sun surface. Any metal will boil before reaching this temperature under atmospheric pressure. Thus for any practical purpose a metal, can be considered as a Fermi gas at zero temperature as a first approximation (normal temperatures are small compared to T_F).

White dwarfs

Stars known as white dwarfs have mass comparable to our Sun, but have about a hundredth of its radius. The high densities mean that the electrons are no longer bound to single nuclei and instead form a degenerate electron gas. The number density of electrons in a white dwarf is of the order of 10³⁶ electrons/m³. This means their Fermi energy is:

${\displaystyle E_{\mathrm {F} }={\frac {\hbar ^{2}}{2m_{e}}}\left({\frac {3\pi ^{2}(10^{36})}{1\ \mathrm {m} ^{3}}}\right)^{2/3}\approx 3\times 10^{5}\ \mathrm {eV} =0.3\ \mathrm {MeV} }$

Nucleus

Another typical example is that of the particles in a nucleus of an atom. The radius of the nucleus is roughly:

${\displaystyle R=\left(1.25\times 10^{-15}\mathrm {m} \right)\times A^{1/3}}$

where A is the number of nucleons.
The number density of nucleons in a nucleus is therefore:

${\displaystyle \rho ={\frac {A}{{\begin{matrix}{\frac {4}{3}}\end{matrix}}\pi R^{3}}}\approx 1.2\times 10^{44}\ \mathrm {m} ^{-3}}$

Now since the Fermi energy only applies to fermions of the same type, one must divide this density in two. This is because the presence of neutrons does not affect the Fermi energy of the protons in the nucleus, and vice versa.

So the Fermi energy of a nucleus is about:

${\displaystyle E_{\mathrm {F} }={\frac {\hbar ^{2}}{2m_{\rm {p}}}}\left({\frac {3\pi ^{2}(6\times 10^{43})}{1\ \mathrm {m} ^{3}}}\right)^{2/3}\approx 3\times 10^{7}\ \mathrm {eV} =30\ \mathrm {MeV} }$,

where m_p is the proton mass.

The radius of the nucleus admits deviations around the value mentioned above, so a typical value for the Fermi energy is usually given as 38 MeV.

Extensions to the model

Relativistic Fermi gas

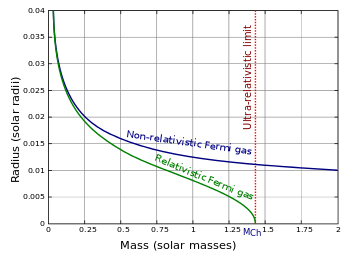
Radius–mass relations for a model white dwarf, relativistic relation vs non-relativistic. The Chandrasekhar limit is indicated as M_Ch.

For the whole article, we have only discussed the case where particles have a parabolic relation between energy and momentum, as is the case in non-relativistic mechanics. For particles with energies close to their respective rest mass, we have to use the equations of special relativity. Where single-particle energy is given by:

${\displaystyle E={\sqrt {(pc)^{2}+(mc^{2})^{2}}}}$.

For this system, the Fermi energy is given by:

${\displaystyle E_{\mathrm {F} }={\sqrt {(p_{\mathrm {F} }c)^{2}+(mc^{2})^{2}}}-mc^{2}\approx p_{\mathrm {F} }c}$ ,

where the ${\displaystyle \approx }$ equality is only valid in the ultrarelativistic limit, and

${\displaystyle p_{\mathrm {F} }=\hbar \left({\frac {1}{g_{s}}}6\pi ^{2}{\frac {N}{V}}\right)^{1/3}}$.

The relativistic Fermi gas model is also used for the description of large white dwarfs which are close to the Chandresekhar limit. For the ultrarelativistic case, the degeneracy pressure is proportional to ${\displaystyle (N/V)^{4/3}}$.

Fermi liquid

In 1956, Lev Landau developed the Fermi liquid theory, where he treated the case of a Fermi liquid, i.e., a system with repulsive, not necessarily small, interactions between fermions. The theory shows that the thermodynamic properties of an ideal Fermi gas and a Fermi liquid do not differ that much. It can be shown that the Fermi liquid is equivalent to a Fermi gas composed of collective excitations or quasiparticles, each with a different effective mass and magnetic moment.