Assuming that the standard model of cosmology is correct, the best current measurements indicate that dark energy contributes 68% of the total energy in the present-day observable universe. The mass–energy of dark matter and ordinary (baryonic) matter contribute 27% and 5%, respectively, and other components such as neutrinos and photons contribute a very small amount. The density of dark energy is very low (~ 7 × 10−30 g/cm3)
much less than the density of ordinary matter or dark matter within
galaxies. However, it dominates the mass–energy of the universe because
it is uniform across space.
Two proposed forms for dark energy are the cosmological constant, representing a constant energy density filling space homogeneously, and scalar fields such as quintessence or moduli, dynamic quantities whose energy density can vary in time and space. Contributions from scalar fields that are constant in space are usually also included in the cosmological constant. The cosmological constant can be formulated to be equivalent to the zero-point radiation of space i.e. the vacuum energy. Scalar fields that change in space can be difficult to distinguish from a cosmological constant because the change may be extremely slow.
Two proposed forms for dark energy are the cosmological constant, representing a constant energy density filling space homogeneously, and scalar fields such as quintessence or moduli, dynamic quantities whose energy density can vary in time and space. Contributions from scalar fields that are constant in space are usually also included in the cosmological constant. The cosmological constant can be formulated to be equivalent to the zero-point radiation of space i.e. the vacuum energy. Scalar fields that change in space can be difficult to distinguish from a cosmological constant because the change may be extremely slow.
History of discovery and previous speculation
Einstein's cosmological constant
The "cosmological constant" is a constant term that can be added to Einstein's field equation
of general relativity. If considered as a "source term" in the field
equation, it can be viewed as equivalent to the mass of empty space
(which conceptually could be either positive or negative), or "vacuum energy".
The cosmological constant was first proposed by Einstein as a mechanism to obtain a solution of the gravitational field equation that would lead to a static universe, effectively using dark energy to balance gravity.
Einstein gave the cosmological constant the symbol Λ (capital lambda).
Einstein stated that the cosmological constant required that `empty
space takes the role of gravitating negative masses which are distributed all over the interstellar space'.
The mechanism was an example of fine-tuning,
and it was later realized that Einstein's static universe would not be
stable: local inhomogeneities would ultimately lead to either the
runaway expansion or contraction of the universe. The equilibrium
is unstable: if the universe expands slightly, then the expansion
releases vacuum energy, which causes yet more expansion. Likewise, a
universe which contracts slightly will continue contracting. These sorts
of disturbances are inevitable, due to the uneven distribution of
matter throughout the universe. Further, observations made by Edwin Hubble
in 1929 showed that the universe appears to be expanding and not static
at all. Einstein reportedly referred to his failure to predict the idea
of a dynamic universe, in contrast to a static universe, as his
greatest blunder.
Inflationary dark energy
Alan Guth and Alexei Starobinsky proposed in 1980 that a negative pressure field, similar in concept to dark energy, could drive cosmic inflation
in the very early universe. Inflation postulates that some repulsive
force, qualitatively similar to dark energy, resulted in an enormous and
exponential expansion of the universe slightly after the Big Bang.
Such expansion is an essential feature of most current models of the
Big Bang. However, inflation must have occurred at a much higher energy
density than the dark energy we observe today and is thought to have
completely ended when the universe was just a fraction of a second old.
It is unclear what relation, if any, exists between dark energy and
inflation. Even after inflationary models became accepted, the
cosmological constant was thought to be irrelevant to the current
universe.
Nearly all inflation models predict that the total (matter+energy) density of the universe should be very close to the critical density. During the 1980s, most cosmological research focused on models with critical density in matter only, usually 95% cold dark matter
and 5% ordinary matter (baryons). These models were found to be
successful at forming realistic galaxies and clusters, but some problems
appeared in the late 1980s: in particular, the model required a value
for the Hubble constant
lower than preferred by observations, and the model under-predicted
observations of large-scale galaxy clustering. These difficulties became
stronger after the discovery of anisotropy in the cosmic microwave background by the COBE spacecraft in 1992, and several modified CDM models came under active study through the mid-1990s: these included the Lambda-CDM model and a mixed cold/hot dark matter model. The first direct evidence for dark energy came from supernova observations in 1998 of accelerated expansion in Riess et al. and in Perlmutter et al.,
and the Lambda-CDM model then became the leading model. Soon after,
dark energy was supported by independent observations: in 2000, the BOOMERanG and Maxima cosmic microwave background experiments observed the first acoustic peak in the CMB, showing that the total (matter+energy) density is close to 100% of critical density. Then in 2001, the 2dF Galaxy Redshift Survey
gave strong evidence that the matter density is around 30% of critical.
The large difference between these two supports a smooth component of
dark energy making up the difference. Much more precise measurements
from WMAP in 2003–2010 have continued to support the standard model and give more accurate measurements of the key parameters.
The term "dark energy", echoing Fritz Zwicky's "dark matter" from the 1930s, was coined by Michael Turner in 1998.
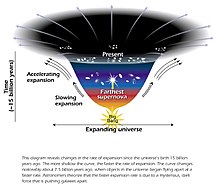
Change in expansion over time
Diagram representing the accelerated expansion of the universe due to dark energy.
High-precision measurements of the expansion of the universe are required to understand how the expansion rate changes over time and space. In general relativity, the evolution of the expansion rate is estimated from the curvature of the universe and the cosmological equation of state
(the relationship between temperature, pressure, and combined matter,
energy, and vacuum energy density for any region of space). Measuring
the equation of state for dark energy is one of the biggest efforts in
observational cosmology today. Adding the cosmological constant to
cosmology's standard FLRW metric leads to the Lambda-CDM model, which has been referred to as the "standard model of cosmology" because of its precise agreement with observations.
As of 2013, the Lambda-CDM model is consistent with a series of increasingly rigorous cosmological observations, including the Planck spacecraft
and the Supernova Legacy Survey. First results from the SNLS reveal
that the average behavior (i.e., equation of state) of dark energy
behaves like Einstein's cosmological constant to a precision of 10%.
Recent results from the Hubble Space Telescope Higher-Z Team indicate
that dark energy has been present for at least 9 billion years and
during the period preceding cosmic acceleration.
Nature
The nature of dark energy is more hypothetical than that of dark matter, and many things about it remain matters of speculation. Dark energy is thought to be very homogeneous and not very dense, and is not known to interact through any of the fundamental forces other than gravity. Since it is quite rarefied and un-massive — roughly 10−27 kg/m3
— it is unlikely to be detectable in laboratory experiments. The reason
dark energy can have such a profound effect on the universe, making up
68% of universal density in spite of being so dilute, is that it
uniformly fills otherwise empty space.
Independently of its actual nature, dark energy would need to have a strong negative pressure (repulsive action), like radiation pressure in a metamaterial, to explain the observed acceleration of the expansion of the universe.
According to general relativity, the pressure within a substance
contributes to its gravitational attraction for other objects just as
its mass density does. This happens because the physical quantity that
causes matter to generate gravitational effects is the stress–energy tensor, which contains both the energy (or matter) density of a substance and its pressure and viscosity. In the Friedmann–Lemaître–Robertson–Walker metric,
it can be shown that a strong constant negative pressure in all the
universe causes an acceleration in the expansion if the universe is
already expanding, or a deceleration in contraction if the universe is
already contracting. This accelerating expansion effect is sometimes
labeled "gravitational repulsion".
Technical definition
In standard cosmology, there are three components of the universe:
matter, radiation, and dark energy. Matter is anything whose energy
density scales with the inverse cube of the scale factor, i.e., ρ ∝ a−3, while radiation is anything which scales to the inverse fourth power of the scale factor (ρ ∝ a−4).
This can be understood intuitively: for an ordinary particle in a
square box, doubling the length of a side of the box decreases the
density (and hence energy density) by a factor of eight (23). For radiation, the decrease in energy density is greater, because an increase in spatial distance also causes a redshift.
The final component, dark energy, is an intrinsic property of
space, and so has a constant energy density regardless of the volume
under consideration (ρ ∝ a0). Thus, unlike ordinary matter, it does not get diluted with the expansion of space.
Evidence of existence
The evidence for dark energy is indirect but comes from three independent sources:
- Distance measurements and their relation to redshift, which suggest the universe has expanded more in the last half of its life.
- The theoretical need for a type of additional energy that is not matter or dark matter to form the observationally flat universe (absence of any detectable global curvature).
- Measures of large-scale wave-patterns of mass density in the universe.
Supernovae
A Type Ia supernova (bright spot on the bottom-left) near a galaxy
In 1998, the High-Z Supernova Search Team published observations of Type Ia ("one-A") supernovae. In 1999, the Supernova Cosmology Project followed by suggesting that the expansion of the universe is accelerating. The 2011 Nobel Prize in Physics was awarded to Saul Perlmutter, Brian P. Schmidt, and Adam G. Riess for their leadership in the discovery.
Since then, these observations have been corroborated by several independent sources. Measurements of the cosmic microwave background, gravitational lensing, and the large-scale structure of the cosmos, as well as improved measurements of supernovae, have been consistent with the Lambda-CDM model.
Some people argue that the only indications for the existence of dark
energy are observations of distance measurements and their associated
redshifts. Cosmic microwave background anisotropies and baryon acoustic
oscillations serve only to demonstrate that distances to a given
redshift are larger than would be expected from a "dusty"
Friedmann–Lemaître universe and the local measured Hubble constant.
Supernovae are useful for cosmology because they are excellent standard candles
across cosmological distances. They allow researchers to measure the
expansion history of the universe by looking at the relationship between
the distance to an object and its redshift, which gives how fast it is receding from us. The relationship is roughly linear, according to Hubble's law.
It is relatively easy to measure redshift, but finding the distance to
an object is more difficult. Usually, astronomers use standard candles:
objects for which the intrinsic brightness, or absolute magnitude, is known. This allows the object's distance to be measured from its actual observed brightness, or apparent magnitude. Type Ia supernovae are the best-known standard candles across cosmological distances because of their extreme and consistent luminosity.
Recent observations of supernovae are consistent with a universe made up 71.3% of dark energy and 27.4% of a combination of dark matter and baryonic matter.
Cosmic microwave background
Estimated division of total energy in the universe into matter, dark matter and dark energy based on five years of WMAP data.
The existence of dark energy, in whatever form, is needed to
reconcile the measured geometry of space with the total amount of matter
in the universe. Measurements of cosmic microwave background (CMB) anisotropies indicate that the universe is close to flat. For the shape of the universe to be flat, the mass-energy density of the universe must be equal to the critical density. The total amount of matter in the universe (including baryons and dark matter),
as measured from the CMB spectrum, accounts for only about 30% of the
critical density. This implies the existence of an additional form of
energy to account for the remaining 70%. The Wilkinson Microwave Anisotropy Probe (WMAP) spacecraft seven-year analysis estimated a universe made up of 72.8% dark energy, 22.7% dark matter, and 4.5% ordinary matter.
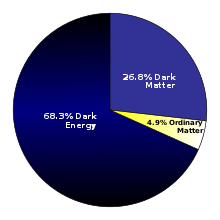
Work done in 2013 based on the Planck spacecraft observations of the CMB gave a more accurate estimate of 68.3% dark energy, 26.8% dark matter, and 4.9% ordinary matter.
Large-scale structure
The theory of large-scale structure, which governs the formation of structures in the universe (stars, quasars, galaxies and galaxy groups and clusters), also suggests that the density of matter in the universe is only 30% of the critical density.
A 2011 survey, the WiggleZ galaxy survey of more than 200,000
galaxies, provided further evidence towards the existence of dark
energy, although the exact physics behind it remains unknown. The WiggleZ survey from the Australian Astronomical Observatory scanned the galaxies to determine their redshift. Then, by exploiting the fact that baryon acoustic oscillations have left voids
regularly of ~150 Mpc diameter, surrounded by the galaxies, the voids
were used as standard rulers to estimate distances to galaxies as far as
2,000 Mpc (redshift 0.6), allowing for accurate estimate of the speeds
of galaxies from their redshift and distance. The data confirmed cosmic acceleration up to half of the age of the universe (7 billion years) and constrain its inhomogeneity to 1 part in 10. This provides a confirmation to cosmic acceleration independent of supernovae.
Late-time integrated Sachs-Wolfe effect
Accelerated cosmic expansion causes gravitational potential wells and hills to flatten as photons
pass through them, producing cold spots and hot spots on the CMB
aligned with vast supervoids and superclusters. This so-called late-time
Integrated Sachs–Wolfe effect (ISW) is a direct signal of dark energy in a flat universe. It was reported at high significance in 2008 by Ho et al. and Giannantonio et al.
Observational Hubble constant data
A new approach to test evidence of dark energy through observational Hubble constant data (OHD) has gained significant attention in recent years. The Hubble constant, H(z), is measured as a function of cosmological redshift.
OHD directly tracks the expansion history of the universe by taking
passively evolving early-type galaxies as “cosmic chronometers”.
From this point, this approach provides standard clocks in the
universe. The core of this idea is the measurement of the differential
age evolution as a function of redshift of these cosmic chronometers.
Thus, it provides a direct estimate of the Hubble parameter
The reliance on a differential quantity, Δz/Δt,
can minimize many common issues and systematic effects; and as a direct
measurement of the Hubble parameter instead of its integral, like supernovae and baryon acoustic oscillations
(BAO), it brings more information and is appealing in computation. For
these reasons, it has been widely used to examine the accelerated cosmic
expansion and study properties of dark energy.
Theories of dark energy
Dark
energy's status as a hypothetical force with unknown properties makes
it a very active target of research. The problem is attacked from a
great variety of angles, such as modifying the prevailing theory of
gravity (general relativity), attempting to pin down the properties of
dark energy, and finding alternative ways to explain the observational
data.
The equation of state of Dark Energy for 4 common models by Redshift.
A: CPL Model,
B: Jassal Model,
C: Barboza & Alcaniz Model,
D: Wetterich Model
A: CPL Model,
B: Jassal Model,
C: Barboza & Alcaniz Model,
D: Wetterich Model
Cosmological constant
The simplest explanation for dark energy is that it is an intrinsic,
fundamental energy of space. This is the cosmological constant, usually
represented by the Greek letter Λ (Lambda, hence Lambda-CDM model). Since energy and mass are related according to the equation E = mc2, Einstein's theory of general relativity predicts that this energy will have a gravitational effect. It is sometimes called a vacuum energy because it is the energy density of empty vacuum.
The cosmological constant has negative pressure equal to its energy density and so causes the expansion of the universe to accelerate.
The reason a cosmological constant has negative pressure can be seen
from classical thermodynamics. In general, energy must be lost from
inside a container (the container must do work on its environment) in
order for the volume to increase. Specifically, a change in volume dV requires work done equal to a change of energy −P dV, where P
is the pressure. But the amount of energy in a container full of vacuum
actually increases when the volume increases, because the energy is
equal to ρV, where ρ is the energy density of the cosmological constant. Therefore, P is negative and, in fact, P = −ρ.
There are two major advantages for the cosmological constant. The
first is that it is simple. Einstein had in fact introduced this term
in his original formulation of general relativity such as to get a
static universe. Although he later discarded the term after Hubble
found that the universe is expanding, a nonzero cosmological constant
can act as dark energy, without otherwise changing the Einstein field
equations. The other advantage is that there is a natural explanation
for its origin. Most quantum field theories predict vacuum fluctuations that would give the vacuum this sort of energy. This is related to the Casimir effect,
in which there is a small suction into regions where virtual particles
are geometrically inhibited from forming (e.g. between plates with tiny
separation).
A major outstanding problem is that the same quantum field theories predict a huge cosmological constant, more than 100 orders of magnitude too large. This would need to be almost, but not exactly, cancelled by an equally large term of the opposite sign. Some supersymmetric theories require a cosmological constant that is exactly zero, which does not help because supersymmetry must be broken.
Nonetheless, the cosmological constant is the most economical solution to the problem of cosmic acceleration.
Thus, the current standard model of cosmology, the Lambda-CDM model,
includes the cosmological constant as an essential feature.
Quintessence
In quintessence models of dark energy, the observed acceleration of the scale factor is caused by the potential energy of a dynamical field,
referred to as quintessence field. Quintessence differs from the
cosmological constant in that it can vary in space and time. In order
for it not to clump and form structure like matter, the field must be very light so that it has a large Compton wavelength.
No evidence of quintessence is yet available, but it has not been
ruled out either. It generally predicts a slightly slower acceleration
of the expansion of the universe than the cosmological constant. Some
scientists think that the best evidence for quintessence would come from
violations of Einstein's equivalence principle and variation of the fundamental constants in space or time. Scalar fields are predicted by the Standard Model of particle physics and string theory, but an analogous problem to the cosmological constant problem (or the problem of constructing models of cosmological inflation) occurs: renormalization theory predicts that scalar fields should acquire large masses.
The coincidence problem asks why the acceleration of the Universe began when it did. If acceleration began earlier in the universe, structures such as galaxies would never have had time to form, and life, at least as we know it, would never have had a chance to exist. Proponents of the anthropic principle
view this as support for their arguments. However, many models of
quintessence have a so-called "tracker" behavior, which solves this
problem. In these models, the quintessence field has a density which
closely tracks (but is less than) the radiation density until matter-radiation equality, which triggers quintessence to start behaving as dark energy, eventually dominating the universe. This naturally sets the low energy scale of the dark energy.
In 2004, when scientists fit the evolution of dark energy with
the cosmological data, they found that the equation of state had
possibly crossed the cosmological constant boundary (w = −1) from above
to below. A No-Go theorem has been proved that gives this scenario at
least two degrees of freedom as required for dark energy models. This
scenario is so-called Quintom scenario.
Some special cases of quintessence are phantom energy,
in which the energy density of quintessence actually increases with
time, and k-essence (short for kinetic quintessence) which has a
non-standard form of kinetic energy such as a negative kinetic energy. They can have unusual properties: phantom energy, for example, can cause a Big Rip.
Interacting dark energy
This
class of theories attempts to come up with an all-encompassing theory
of both dark matter and dark energy as a single phenomenon that modifies
the laws of gravity at various scales. This could, for example, treat
dark energy and dark matter as different facets of the same unknown
substance, or postulate that cold dark matter decays into dark energy.
Another class of theories that unifies dark matter and dark energy are
suggested to be covariant theories of modified gravity. These theories
alter the dynamics of the space-time such that the modified dynamic
stems what have been assigned to the presence of dark energy and dark
matter.
Variable dark energy models
The
density of dark energy might have varied in time over the history of
the universe. Modern observational data allow for estimates of the
present density. Using baryon acoustic oscillations, it is possible to investigate the effect of dark energy in the history of the Universe, and constrain parameters of the equation of state
of dark energy. To that end, several models have been proposed. One of
the most popular models is the Chevallier–Polarski–Linder model (CPL). Some other common models are, (Barboza & Alcaniz. 2008), (Jassal et al. 2005), (Wetterich. 2004), (Oztas et al. 2018).
Observational skepticism
Some
alternatives to dark energy aim to explain the observational data by a
more refined use of established theories. In this scenario, dark energy
doesn't actually exist, and is merely a measurement artifact. For
example, if we are located in an emptier-than-average region of space,
the observed cosmic expansion rate could be mistaken for a variation in
time, or acceleration. A different approach uses a cosmological extension of the equivalence principle
to show how space might appear to be expanding more rapidly in the
voids surrounding our local cluster. While weak, such effects considered
cumulatively over billions of years could become significant, creating
the illusion of cosmic acceleration, and making it appear as if we live
in a Hubble bubble.
Yet other possibilities are that the accelerated expansion of the
universe is an illusion caused by the relative motion of us to the rest
of the universe, or that the supernovae sample size used wasn't large enough.
Other mechanism driving acceleration
Modified gravity
The
evidence for dark energy is heavily dependent on the theory of general
relativity. Therefore, it is conceivable that a modification to general
relativity also eliminates the need for dark energy. There are very many
such theories, and research is ongoing. The measurement of the speed of gravity in the first gravitational wave measured by non-gravitational means (GW170817) ruled out many modified gravity theories as explanations to dark energy.
Astrophysicist Ethan Siegel
states that, while such alternatives gain a lot of mainstream press
coverage, almost all professional astrophysicists are confident that
dark energy exists, and that none of the competing theories successfully
explain observations to the same level of precision as standard dark
energy.
Implications for the fate of the universe
Cosmologists estimate that the acceleration began roughly 5 billion years ago.
Before that, it is thought that the expansion was decelerating, due to
the attractive influence of matter. The density of dark matter in an
expanding universe decreases more quickly than dark energy, and
eventually the dark energy dominates. Specifically, when the volume of
the universe doubles, the density of dark matter is halved, but the density of dark energy is nearly unchanged (it is exactly constant in the case of a cosmological constant).
Projections into the future can differ radically for different
models of dark energy. For a cosmological constant, or any other model
that predicts that the acceleration will continue indefinitely, the
ultimate result will be that galaxies outside the Local Group will have a line-of-sight velocity that continually increases with time, eventually far exceeding the speed of light. This is not a violation of special relativity because the notion of "velocity" used here is different from that of velocity in a local inertial frame of reference, which is still constrained to be less than the speed of light for any massive object. Because the Hubble parameter
is decreasing with time, there can actually be cases where a galaxy
that is receding from us faster than light does manage to emit a signal
which reaches us eventually.
However, because of the accelerating expansion, it is projected that
most galaxies will eventually cross a type of cosmological event horizon where any light they emit past that point will never be able to reach us at any time in the infinite future
because the light never reaches a point where its "peculiar velocity"
toward us exceeds the expansion velocity away from us. Assuming the dark energy is constant (a cosmological constant),
the current distance to this cosmological event horizon is about 16
billion light years, meaning that a signal from an event happening at present
would eventually be able to reach us in the future if the event were
less than 16 billion light years away, but the signal would never reach
us if the event were more than 16 billion light years away.
As galaxies approach the point of crossing this cosmological event horizon, the light from them will become more and more redshifted, to the point where the wavelength becomes too large to detect in practice and the galaxies appear to vanish completely. Planet Earth, the Milky Way,
and the Local Group of which the Milky way is a part, would all remain
virtually undisturbed as the rest of the universe recedes and disappears
from view. In this scenario, the Local Group would ultimately suffer heat death, just as was hypothesized for the flat, matter-dominated universe before measurements of cosmic acceleration.
There are other, more speculative ideas about the future of the universe. The phantom energy model of dark energy results in divergent
expansion, which would imply that the effective force of dark energy
continues growing until it dominates all other forces in the universe.
Under this scenario, dark energy would ultimately tear apart all
gravitationally bound structures, including galaxies and solar systems,
and eventually overcome the electrical and nuclear forces to tear apart atoms themselves, ending the universe in a "Big Rip". It is also possible the universe may never have an end and continue in its present state forever.
On the other hand, dark energy might dissipate with time or even become
attractive. Such uncertainties leave open the possibility that gravity
might yet rule the day and lead to a universe that contracts in on
itself in a "Big Crunch", or that there may even be a dark energy cycle, which implies a cyclic model of the universe in which every iteration (Big Bang then eventually a Big Crunch) takes about a trillion (1012) years. While none of these are supported by observations, they are not ruled out.
In philosophy of science
In philosophy of science, dark energy is an example of an "auxiliary hypothesis", an ad hoc postulate that is added to a theory in response to observations that falsify it. It has been argued that the dark energy hypothesis is a conventionalist hypothesis, that is, a hypothesis that adds no empirical content and hence is unfalsifiable in the sense defined by Karl Popper.