Introduction
The
nervous system consists networks made up of neurons and synapses
connected to and controlling tissues as well as impacting human thoughts
and behavior. In modeling neural networks of the nervous system one has
to consider many factors. The brain and the neural network should be
considered as an integrated and self-contained firmware system that
includes hardware (organs), software (programs), memory (short term and
long term), database (centralized and distributed), and a complex
network of active elements (such as neurons, synapses, and tissues) and
passive elements (such as parts of visual and auditory system) that
carry information within and in-and-out of the body.
Why does one want to model the brain and neural network? Although
highly sophisticated computer systems have been developed and used in
all walks of life, they are nowhere close to the human system in
hardware and software capabilities. So, scientists have been at work to
understand the human operation system and try to simulate its
functionalities. In order to accomplish this, one needs to model its
components and functions and validate its performance with real life.
Computational models of a well simulated nervous system enable learning
the nervous system and apply it to real life problem solutions.
What is brain and what is neural network? "Network connectivity and models" below addresses
the former question from an evolutionary perspective. The answer to the
second question is based on the neural doctrine proposed by Ramon y
Cajal (1894).
He hypothesized that the elementary biological unit is an active cell,
called neuron, and the human machine is run by a vast network that
connects these neurons, called neural (or neuronal) network. The neural
network is integrated with the human organs to form the human machine
comprising the nervous system.
Innumerable number of models of various aspects of the nervous
system has been developed and there are several Wikipedia articles
identified above that have been generated on the subject. The purpose of
this article is to present a comprehensive view of all the models and
provide the reader, especially a novice, to the neuroscience, with
reference to the various sources.
Network characteristics
The basic structural unit of the neural network is connectivity of
one neuron to another via an active junction, called synapse. Neurons of
widely divergent characteristics are connected to each other via
synapses, whose characteristics are also of diverse chemical and
electrical properties. In presenting a comprehensive view of all
possible modeling of the brain and neural network, an approach is to
organize the material based on the characteristics of the networks and
the goals that need to be accomplished. The latter could be either for
understanding the brain and the nervous system better or to apply the
knowledge gained from the total or partial nervous system to real world
applications such as artificial intelligence, Neuroethics or improvements in medical science for society.
Network connectivity and models
On
a high level representation, the neurons can be viewed as connected to
other neurons to form a neural network in one of three ways. A specific
network can be represented as a physiologically (or anatomically)
connected network and modeled that way. There are several approaches to
this (see Ascoli, G.A. (2002) Sporns, O. (2007), Connectionism, Rumelhart, J. L., McClelland, J. L., and PDP Research Group (1986), Arbib, M. A. (2007)).
Or, it can form a functional network that serves a certain function and
modeled accordingly (Honey, C. J., Kotter, R., Breakspear, R., &
Sporns, O. (2007), Arbib, M. A. (2007)).
A third way is to hypothesize a theory of the functioning of the
biological components of the neural system by a mathematical model, in
the form of a set of mathematical equations. The variables of the
equation are some or all of the neurobiological properties of the entity
being modeled, such as the dimensions of the dendrite or the
stimulation rate of action potential along the axon in a neuron. The
mathematical equations are solved using computational techniques and the
results are validated with either simulation or experimental processes.
This approach to modeling is called computational neuroscience. This
methodology is used to model components from the ionic level to system
level of the brain. This method is applicable for modeling integrated
system of biological components that carry information signal from one
neuron to another via intermediate active neurons that can pass the
signal through or create new or additional signals. The computational
neuroscience approach is extensively used and is based on two generic
models, one of cell membrane potential Goldman (1943) and Hodgkin and Katz (1949), and the other based on Hodgkin-Huxley model of action potential (information signal).
Modeling levels
Sterratt, D., Graham, B., Gillies, A., & Willshaw, D. (2011)
classify the biological model of neuroscience into nine levels from ion
channels to nervous system level based on size and function. Table 1 is
based on this for neuronal networks.
| Level | Size | Description and Functions |
|---|---|---|
| Nervous system | > 1 m | Total system controlling thought, behavior, and sensory & motor functions |
| Subsystem | 10 cm | Subsystem associated with one or more functions |
| Neural network | 1 cm | Neural networks for system, subsystem, and functions |
| Microcircuit | 1 mm | Networks of multilevel neurons, e.g., visual subsystem |
| Neuron | 100 µm | Elementary biological unit of neuronal network |
| Dendric subunit | 10 µm | Arbor of receptors in neuron |
| Synapse | 1 µm | Junction or connectivity between neurons |
| Signalling pathway | 1 nm | Link between connecting neurons |
| Ion channels | 1 pm | Channels that act as gateway causing voltage change |
Sporns, O. (2007)
presents in his article on brain connectivity, modeling based on
structural and functional types. A network that connects at neuron and
synaptic level falls into the microscale. If the neurons are grouped
into population of columns and minicolumns, the level is defined as
mesoscale. The macroscale representation considers the network as
regions of the brain connected by inter-regional pathways.
Arbib, M. A. (2007) considers in the modular model, a hierarchical formulation of the system into modules and sub-modules.
Signaling modes
The
neuronal signal comprises a stream of short electrical pulses of about
100 millivolt amplitude and about 1 to 2 millisecond duration (Gerstner,
W., & Kistler, W. (2002)
Chapter 1). The individual pulses are action potentials or spikes and
the chain of pulses is called spike train. The action potential does not
contain any information. A combination of the timing of the start of
the spike train, the rate or frequency of the spikes, and the number and
pattern of spikes in the spike train determine the coding of the
information content or the signal message.
The neuron cell has three components – dendrites, soma, and axon
as shown in Figure 1. Dendrites, which have the shape of a tree with
branches, called arbor, receive the message from other neurons with
which the neuron is connected via synapses. The action potential
received by each dendrite from the synapse is called the postsynaptic
potential. The cumulative sum of the postsynaptic potentials is fed to
the soma. The ionic components of the fluid inside and outside maintain
the cell membrane at a resting potential of about 65 millivolts. When
the cumulative postsynaptic potential exceeds the resting potential, an
action potential is generated by the cell body or soma and propagated
along the axon. The axon may have one or more terminals and these
terminals transmit neurotransmitters to the synapses with which the
neuron is connected. Depending on the stimulus received by the
dendrites, soma may generate one or more well-separated action
potentials or spike train. If the stimulus drives the membrane to a
positive potential, it is an excitatory neuron; and if it drives the
resting potential further in the negative direction, it is an inhibitory
neuron.
Figure 1. Neuron anatomy for network model
The generation of the action potential is called the “firing.” The
firing neuron described above is called a spiking neuron. We will model
the electrical circuit of the neuron in Section 3.6. There are two types
of spiking neurons. If the stimulus remains above the threshold level
and the output is a spike train, it is called the Integrate-and-Fire
(IF) neuron model. If output is modeled as dependent on the impulse
response of the circuit, then it is called the Spike Response Model
(SRM) (Gestner, W. (1995)).
The spiking neuron model assumes that frequency (inverse of the
rate at which spikes are generated) of spiking train starts at 0 and
increases with the stimulus current. There is another hypothetical model
that formulates the firing to happen at the threshold, but there is a
quantum jump in frequency in contrast to smooth rise in frequency as in
the spiking neuron model. This model is called the rate model. Gerstner,
W., & Kistler, W. (2002), and Sterratt, D., Graham, B., Gillies, A., & Willshaw, D. (2011) are good sources for a detailed treatment of spiking neuron models and rate neuron models.
Biological vs. artificial neural network
The concept of artificial neural network (ANN) was introduced by McColloch, W. S. & Pitts, W. (1943) for models based on behavior of biological neurons. Norbert Wiener (1961) gave this new field the popular name of cybernetics,
whose principle is the interdisciplinary relationship among
engineering, biology, control systems, brain functions, and computer
science. With the computer science field advancing, the von Neumann-type
computer was introduced early in the neuroscience study. But it was not
suitable for symbolic processing, nondeterministic computations,
dynamic executions, parallel distributed processing, and management of
extensive knowledge bases, which are needed for biological neural
network applications; and the direction of mind-like machine development
changed to a learning machine. Computing technology has since advanced
extensively and computational neuroscience is now able to handle
mathematical models developed for biological neural network. Research
and development are progressing in both artificial and biological neural
networks including efforts to merge the two.
Nervous system models
Evolutionary brain model
The “triune theory of the brain” McLean, P. (2003)
is one of several models used to theorize the organizational structure
of the brain. The most ancient neural structure of the brain is the
brain stem or “lizard brain.” The second phase is limbic or
paleo-mammalian brain and performs the four functions needed for animal
survival – fighting, feeding, fleeing, and fornicating. The third phase
is the neocortex or the neo-mammalian brain. The higher cognitive
functions which distinguish humans from other animals are primarily in
the cortex. The reptilian brain controls muscles, balance, and autonomic
functions, such as breathing and heartbeat. This part of the brain is
active, even in deep sleep. The limbic system includes the hypothalamus,
hippocampus, and amygdala. The neocortex includes the cortex and the
cerebrum. It corresponds to the brain of primates and, specifically, the
human species. Each of the three brains is connected by nerves to the
other two, but each seems to operate as its own brain system with
distinct capacities.
PDP / connectionist model
The connectionist model evolved out of Parallel Distributed
Processing framework that formulates a metatheory from which specific
models can be generated for specific applications. PDP approach
(Rumelhart, J. L., McClelland, J. L., and PDP Research Group (1986))
is a distributed parallel processing of many inter-related operations,
somewhat similar to what’s happening in the human nervous system. The
individual entities are defined as units and the units are connected to
form a network. Thus, in the application to nervous system, one
representation could be such that the units are the neurons and the
links are the synapses.
Brain connectivity model
There are three types of brain connectivity models of a network (Sporns, O. (2007)).
“Anatomical (or structural) connectivity” describes a network with
anatomical links having specified relationship between connected
“units.” If the dependent properties are stochastic, it is defined as
“functional connectivity.” “Effective connectivity” has causal
interactions between distinct units in the system. As stated earlier,
brain connectivity can be described at three levels. At microlevel, it
connects neurons through electrical or chemical synapses. A column of
neurons can be considered as a unit in the mesolevel and regions of the
brain comprising a large number of neurons and neuron populations as
units in the macrolevel. The links in the latter case are the
inter-regional pathways, forming large-scale connectivity.
Figure 2 Types of brain connectivity
Figure 2 shows the three types of connectivity. The analysis is done using the directed graphs (see Sporns, O. (2007) and Hilgetag, C. C. (2002)).
In the structural brain connectivity type, the connectivity is a sparse
and directed graph. The functional brain connectivity has bidirectional
graphs. The effective brain connectivity is bidirectional with
interactive cause and effect relationships. Another representation of
the connectivity is by matrix representation (See Sporns, O. (2007)). Hilgetag, C. C. (2002) describes the computational analysis of brain connectivity.
Modular models of brain function
Arbib, M. A. (2007)
describes the modular models as follows. “Modular models of the brain
aid the understanding of a complex system by decomposing it into
structural modules (e.g., brain regions, layers, columns) or functional
modules (schemas) and exploring the patterns of competition and
cooperation that yield the overall function.” This definition is not the
same as that defined in functional connectivity. The modular approach
is intended to build cognitive models and is, in complexity, between the
anatomically defined brain regions (defined as macrolevel in brain
connectivity) and the computational model at the neuron level.
There are three views of modules for modeling. They are (1)
modules for brain structures, (2) modules as schemas, and (3) modules as
interfaces. Figure 3 presents the modular design of a model for reflex
control of saccades (Arbib, M. A. (2007)).
It involves two main modules, one for superior colliculus (SC), and one
for brain stem. Each of these is decomposed into sub-modules, with each
sub-module defining an array of physiologically defined neurons. In
Figure 3(b) the model of Figure 3(a) is embedded into a far larger model
which embraces various regions of cerebral cortex (represented by the
modules Pre-LIP Vis, Ctx., LIP, PFC, and FEF), thalamus, and basal
ganglia. While the model may indeed be analyzed at this top level of
modular decomposition, we need to further decompose basal ganglia, BG,
as shown in Figure 3(c) if we are to tease apart the role of dopamine in
differentially modulating (the 2 arrows shown arising from SNc) the
direct and indirect pathways within the basal ganglia (Crowley, M.
(1997)).
Neural Simulation Language (NSL) has been developed to provide a
simulation system for large-scale general neural networks. It provides
an environment to develop an object-oriented approach to brain modeling.
NSL supports neural models having as basic data structure neural layers
with similar properties and similar connection patterns. Models
developed using NSL are documented in Brain Operation Database (BODB) as
hierarchically organized modules that can be decomposed into lower
levels.
Artificial neural networks
As mentioned in Section 2.4, development of artificial neural network
(ANN), or neural network as it is now called, started as simulation of
biological neuron network and ended up using artificial neurons. Major
development work has gone into industrial applications with learning
process. Complex problems were addressed by simplifying the assumptions.
Algorithms were developed to achieve a neurological related
performance, such as learning from experience. Since the background and
overview have been covered in the other internal references, the
discussion here is limited to the types of models. The models are at the
system or network level.
The four main features of an ANN are topology, data flow, types
of input values, and forms of activation (Meireles, M. R. G. (2003), Munakata, T. (1998)).
Topology can be multilayered, single-layered, or recurrent. Data flow
can be recurrent with feedback or non-recurrent with feedforward model.
The inputs are binary, bipolar, or continuous. The activation is linear,
step, or sigmoid. Multilayer Perceptron (MLP) is the most popular of
all the types, which is generally trained with back-propagation of error
algorithm. Each neuron output is connected to every neuron in
subsequent layers connected in cascade and with no connections between
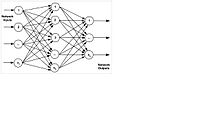
neurons in the same layer. Figure 4 shows a basic MLP topology
(Meireles, M. R. G. (2003)), and a basic telecommunication network (Subramanian, M. (2010))
that most are familiar with. We can equate the routers at the nodes in
telecommunication network to neurons in MLP technology and the links to
synapses.
Figure 4(a) Basic telecommunication network
Figure 4(b) Basic MLP technology model Figure 4. Telecommunication network and neural network topologies
Computational neuron models
Computational science is an interdisciplinary field that combines
engineering, biology, control systems, brain functions, physical
sciences, and computer science. It has fundamental development models
done at the lower levels of ions, neurons, and synapses, as well as
information propagation between neurons. These models have established
the enabling technology for higher-level models to be developed. They
are based on chemical and electrical activities in the neurons for which
electrical equivalent circuits are generated. A simple model for the
neuron with predominantly potassium ions inside the cell and sodium ions
outside establishes an electric potential on the membrane under
equilibrium, i.e., no external activity, condition. This is called the
resting membrane potential, which can be determined by Nernst Equation
(Nernst, W. (1888)). An equivalent electrical circuit for a patch of membrane, for example an axon or dendrite, is shown in Figure 5. EK and ENa are the potentials associated with the potassium and sodium channels respectively and RK and RNa
are the resistances associated with them. C is the capacitance of the
membrane and I is the source current, which could be the test source or
the signal source (action potential). The resting potential for
potassium-sodium channels in a neuron is about -65 millivolts.
Figure 5 Membrane model
The membrane model is for a small section of the cell membrane; for
larger sections it can be extended by adding similar sections, called
compartments, with the parameter values being the same or different. The
compartments are cascaded by a resistance, called axial resistance.
Figure 6 shows a compartmental model of a neuron that is developed over
the membrane model. Dendrites are the postsynaptic receptors receiving
inputs from other neurons; and the axon with one or more axon terminals
transmits neurotransmitters to other neurons.
Figure 6 Neuron model
The second building block is the Hodgkin-Huxley (HH) model of the
action potential. When the membrane potential from the dendrites exceeds
the resting membrane potential, a pulse is generated by the neuron cell
and propagated along the axon. This pulse is called the action
potential and HH model is a set of equations that is made to fit the
experimental data by the design of the model and the choice of the
parameter values.
Models for more complex neurons containing other types of ions
can be derived by adding to the equivalent circuit additional battery
and resistance pairs for each ionic channel. The ionic channel could be
passive or active as they could be gated by voltage or be ligands. The
extended HH model has been developed to handle the active channel
situation.
Although there are neurons that are physiologically connected to
each other, information is transmitted at most of the synapses by
chemical process across a cleft. Synapses are also computationally
modeled. The next level of complexity is that of stream of action
potentials, which are generated, whose pattern contains the coding
information of the signal being transmitted. There are basically two
types of action potentials, or spikes as they are called, that are
generated. One is “integrate-and-fire” (the one we have so far
addressed) and the other which is rate based. The latter is a stream
whose rate varies. The signal going across the synapses could be modeled
either as a deterministic or a stochastic process based on the
application (See Section 3.7). Another anatomical complication is when a
population of neurons, such as a column of neurons in visionary system,
needs to be handled. This is done by considering the collective
behavior of the group (Kotter, R., Nielson, P., Dyhrfjeld-Johnson, J.,
Sommer, F. T., & Northoff, G. (2002)).
Spiking neuron models
The action potential or the spike does not itself carry any
information. It is the stream of spikes, called spike train, that carry
the information in its number and pattern of spikes and timing of
spikes. The postsynaptic potential can be either positive, the
excitatory synapse or negative, inhibitory synapse. In modeling, the
postsynaptic potentials received by the dendrites in the postsynaptic
neuron are integrated and when the integrated potential exceeds the
resting potential, the neuron fires an action potential along its axon.
This model is the Integrate-and-Fire (IF) model that was mentioned in
Section 2.3. Closely related to IF model is a model called Spike
Response Model (SRM) (Gerstner, W. (1995)
Pages 738-758) that is dependent on impulse function response
convoluted with the input stimulus signal. This forms a base for a large
number of models developed for spiking neural networks.
The IF and SR model of spike train occurs in Type I neurons, in
which the spike rate or spike frequency of the occurrence increases
smoothly with the increase in stimulus current starting from zero.
Another phenomenon of spike train generation happens in Type II neurons,
where firing occurs at the resting potential threshold, but with a
quantum jump to a non-zero frequency. Models have been developed using
the rate (frequency) of the spike train and are called rate-based
models.
What is important for understanding the functions of the nervous
system is how the message is coded and transported by the action
potential in the neuron. There are two theories on how the signal that
is being propagated is coded in the spikes as to whether it is pulse
code or rate code. In the former, it is the time delay of the first
spike from the time of stimulus as seen by the postsynaptic receiver
that determines the coding. In the rate code, it is average rate of the
spike that influences the coding. It is not certain as to which is
really the actual physiological phenomenon in each case. However, both
cases can be modeled computationally and the parameters varied to match
the experimental result. The pulse mode is more complex to model and
numerous detailed neuron models and population models are described by
Gerstner and Kistler in Parts I and II of Gerstner, W., & Kistler,
W. (2002) and Chapter 8 of Sterratt, D., Graham, B., Gillies, A., & Willshaw, D. (2011).
Another important characteristic associated with SR model is the
spike-time-dependent-plasticity. It is based on Hebb’s postulate on
plasticity of synapse, which states that “the neurons that fire together
wire together.” This causes the synapse to be a long-term potentiation
(LTP) or long-term depression (LTD). The former is the strengthening of
the synapse between two neurons if the postsynaptic spike temporally
follows immediately after the presynaptic spike. Latter is the case if
it is reverse, i.e., the presynaptic spike occurs after the postsynaptic
spike. Gerstner, W. & Kistler, W. (2002) in Chapter 10 and Sterratt, D., Graham, B., Gillies, A., & Willshaw, D. (2011) in Chapter 7 discuss the various models related to Hebbian models on plasticity and coding.
Nervous system network models
The
challenge involved in developing models for small, medium, and large
networks is one of reducing the complexity by making valid simplifying
assumptions in and extending the Hodgkin-Huxley neuronal model
appropriately to design those models ( see Chapter 9 of Sterratt, D.,
Graham, B., Gillies, A., & Willshaw, D. (2011), Kotter, R., Nielson, P., Dyhrfjeld-Johnson, J., Sommer, F. T., & Northoff, G. (2002), and Chapter 9 of Gerstner, W., & Kistler, W. (2002)).
Network models can be classified as either network of neurons
propagating through different levels of cortex or neuron populations
interconnected as multilevel neurons. The spatial positioning of neuron
could be 1-, 2- or 3-dimensional; the latter ones are called small-world networks
as they are related to local region. The neuron could be either
excitatory or inhibitory, but not both. Modeling design depends on
whether it is artificial neuron or biological neuron of neuronal model.
Type I or Type II choice needs to be made for the firing mode. Signaling
in neurons could be rate-based neurons, spiking response neurons, or
deep-brain stimulated. The network can be designed as feedforward or
recurrent type. The network needs to be scaled for the computational
resource capabilities. Large-scale thalamocortical systems are handled
in the manner of the Blue Brain project (Markam, H. (2006)).
Nervous system development models
No
generalized modeling concepts exist for modeling the development of
anatomical physiology and morphology similar to the one of behavior of
neuronal network, which is based on HH model. Shankle, W. R., Hara, J.,
Fallon, J. H., and Landing, B. H. (2002)
describe the application of neuroanatomical data of the developing
human cerebral cortex to computational models. Sterratt, D., Graham, B.,
Gillies, A., & Willshaw, D. (2011)
discuss aspects of the nervous system of computational modeling in the
development of nerve cell morphology, cell physiology, cell patterning,
patterns of ocular dominance, and connection between nerve cell and
muscle, and retinotopic maps. Carreira-Perpinan, M. A. & Goodhill,
G. J. (2002) deal with the optimization of the computerized models of the visual cortex.
Modeling tools
With
the enormous number of models that have been created, tools have been
developed for dissemination of the information, as well as platforms to
develop models. Several generalized tools, such as GENESIS, NEURON, XPP,
and NEOSIM are available and are discussed by Hucka, M. (2002).