Gut–brain axis

From Wikipedia, the free encyclopedia

 

The gut-brain axis is the relationship between the GI tract and brain function and development

The gut–brain axis is the biochemical signaling that takes place between the gastrointestinal tract (GI tract) and the central nervous system (CNS). The term "gut–brain axis" is occasionally used to refer to the role of the gut flora in the interplay as well, whereas the term "microbiome–gut–brain axis" explicitly includes the role of gut flora in the biochemical signaling events that take place between the GI tract and CNS.

Broadly defined, the gut-brain axis includes the central nervous system, neuroendocrine and neuroimmune systems, including the hypothalamic–pituitary–adrenal axis (HPA axis), sympathetic and parasympathetic arms of the autonomic nervous system, including the enteric nervous system and the vagus nerve, and the gut microbiota. The first of the brain-gut interactions shown, was the cephalic phase of digestion, in the release of gastric and pancreatic secretions in response to sensory signals, such as the smell and sight of food. This was first demonstrated by pavlov.

Interest in the field was sparked by a 2004 study showing that germ-free mice showed an exaggerated HPA axis response to stress compared to non-GF laboratory mice.

As of October 2016, most of the work that had been done on the role of gut flora in the gut-brain axis had been conducted in animals, or on characterizing the various neuroactive compounds that gut flora can produce. Studies with humans – measuring variations in gut flora between people with various psychiatric and neurological conditions or when stressed, or measuring effects of various probiotics (dubbed "psychobiotics" in this context) – had generally been small and were just beginning to be generalized. Whether changes to gut flora are a result of disease, a cause of disease, or both in any number of possible feedback loops in the gut-brain axis, remained unclear.

Gut flora

Bifidobacterium adolescentis Gram

 

Lactobacillus sp 01

The gut flora is the complex community of microorganisms that live in the digestive tracts of humans and other animals. The gut metagenome is the aggregate of all the genomes of gut microbiota. The gut is one niche that human microbiota inhabit.

In humans, the gut microbiota has the largest numbers of bacteria and the greatest number of species compared to other areas of the body. In humans the gut flora is established at one to two years after birth, and by that time the intestinal epithelium and the intestinal mucosal barrier that it secretes have co-developed in a way that is tolerant to, and even supportive of, the gut flora and that also provides a barrier to pathogenic organisms.

The relationship between gut flora and humans is not merely commensal (a non-harmful coexistence), but rather a mutualistic relationship. Human gut microorganisms benefit the host by collecting the energy from the fermentation of undigested carbohydrates and the subsequent absorption of short-chain fatty acids (SCFAs), acetate, butyrate, and propionate. Intestinal bacteria also play a role in synthesizing vitamin B and vitamin K as well as metabolizing bile acids, sterols, and xenobiotics. The systemic importance of the SCFAs and other compounds they produce are like hormones and the gut flora itself appears to function like an endocrine organ, and dysregulation of the gut flora has been correlated with a host of inflammatory and autoimmune conditions.

The composition of human gut flora changes over time, when the diet changes, and as overall health changes.

Enteric nervous system

The enteric nervous system is one of the main divisions of the nervous system and consists of a mesh-like system of neurons that governs the function of the gastrointestinal system; it has been described as a "second brain" for several reasons. The enteric nervous system can operate autonomously. It normally communicates with the central nervous system (CNS) through the parasympathetic (e.g., via the vagus nerve) and sympathetic (e.g., via the prevertebral ganglia) nervous systems. However, vertebrate studies show that when the vagus nerve is severed, the enteric nervous system continues to function.

In vertebrates, the enteric nervous system includes efferent neurons, afferent neurons, and interneurons, all of which make the enteric nervous system capable of carrying reflexes in the absence of CNS input. The sensory neurons report on mechanical and chemical conditions. Through intestinal muscles, the motor neurons control peristalsis and churning of intestinal contents. Other neurons control the secretion of enzymes. The enteric nervous system also makes use of more than 30 neurotransmitters, most of which are identical to the ones found in CNS, such as acetylcholine, dopamine, and serotonin. More than 90% of the body's serotonin lies in the gut, as well as about 50% of the body's dopamine and the dual function of these neurotransmitters is an active part of gut-brain research.

The first of the gut-brain interactions was shown to be between the sight and smell of food and the release of gastric secretions, known as the cephalic phase, or cephalic response of digestion.^[4][5]

Gut-brain integration

The gut–brain axis, a bidirectional neurohumoral communication system, is important for maintaining homeostasis and is regulated through the central and enteric nervous systems and the neural, endocrine, immune, and metabolic pathways, and especially including the hypothalamic–pituitary–adrenal axis (HPA axis). That term has been expanded to include the role of the gut flora as part of the "microbiome-gut-brain axis", a linkage of functions including the gut flora.

Interest in the field was sparked by a 2004 study (Nobuyuki Sudo and Yoichi Chida) showing that germ-free mice (genetically homogeneous laboratory mice, birthed and raised in an antiseptic environment) showed an exaggerated HPA axis response to stress compared to non-GF laboratory mice.

The gut flora can produce a range of neuroactive molecules, such as acetylcholine, catecholamines, γ-aminobutyric acid, histamine, melatonin, and serotonin, which is essential for regulating peristalsis and sensation in the gut. Changes in the composition of the gut flora due to diet, drugs, or disease correlate with changes in levels of circulating cytokines, some of which can affect brain function. The gut flora also release molecules that can directly activate the vagus nerve which transmits information about the state of the intestines to the brain.

Likewise, chronic or acutely stressful situations activate the hypothalamic–pituitary–adrenal axis, causing changes in the gut flora and intestinal epithelium, and possibly having systemic effects. Additionally, the cholinergic anti-inflammatory pathway, signaling through the vagus nerve, affects the gut epithelium and flora. Hunger and satiety are integrated in the brain, and the presence or absence of food in the gut and types of food present, also affect the composition and activity of gut flora.

That said, most of the work that has been done on the role of gut flora in the gut-brain axis has been conducted in animals, including the highly artificial germ-free mice. As of 2016 studies with humans measuring changes to gut flora in response to stress, or measuring effects of various probiotics, have generally been small and cannot be generalized; whether changes to gut flora are a result of disease, a cause of disease, or both in any number of possible feedback loops in the gut-brain axis, remains unclear.

Research

Probiotics

A 2016 systematic review of laboratory animal studies and preliminary human clinical trials using commercially available strains of probiotic bacteria found that certain species of the Bifidobacterium and Lactobacillus genera (i.e., B. longum, B. breve, B. infantis, L. helveticus, L. rhamnosus, L. plantarum, and L. casei) had the most potential to be useful for certain central nervous system disorders.

Anxiety and mood disorders

As of 2018 work on the relationship between gut flora and anxiety disorders and mood disorders, as well as trying to influence that relationship using probiotics or prebiotics (called "psychobiotics"), was at an early stage, with insufficient evidence to draw conclusions about a causal role for gut flora changes in these conditions, or about the efficacy of any probiotic or prebiotic treatment.

People with anxiety and mood disorders tend to have gastrointestinal problems; small studies have been conducted to compare the gut flora of people with major depressive disorder and healthy people, but those studies have had contradictory results.

Much interest was generated in the potential role of gut flora in anxiety disorders, and more generally in the role of gut flora in the gut-brain axis, by studies published in 2004 showing that germ-free mice have an exaggerated HPA axis response to stress caused by being restrained, which was reversed by colonizing their gut with a Bifidobacterium species. Studies looking at maternal separation for rats shows neonatal stress leads to long-term changes in the gut microbiota such as its diversity and composition, which also led to stress and anxiety-like behavior. Additionally, while much work had been done as of 2016 to characterize various neurotransmitters known to be involved in anxiety and mood disorders that gut flora can produce (for example, Escherichia, Bacillus, and Saccharomyces species can produce noradrenalin; Candida, Streptococcus, and Escherichia species can produce serotonin, etc) the inter-relationships and pathways by which the gut flora might affect anxiety in humans were unclear.

Autism

Around 70% of people with autism also have gastrointestinal problems, and autism is often diagnosed at the time that the gut flora becomes established, indicating that there may be a connection between autism and gut flora. Some studies have found differences in the gut flora of children with autism compared with children without autism – most notably elevations in the amount of Clostridium in the stools of children with autism compared with the stools of the children without – but these results have not been consistently replicated. Many of the environmental factors thought to be relevant to the development of autism would also affect the gut flora, leaving open the question whether specific developments in the gut flora drive the development of autism or whether those developments happen concurrently. As of 2016, studies with probiotics had only been conducted with animals; studies of other dietary changes to treat autism have been inconclusive.

Parkinson's disease

As of 2015 one study had been conducted comparing the gut flora of people with Parkinson's disease to healthy controls; in that study people with Parkinsons had lower levels of Prevotellaceae and people with Parkinsons who had higher levels of Enterobacteriaceae had more clinically severe symptoms; the authors of the study drew no conclusions about whether gut flora changes were driving the disease or vice versa.

Models of neural computation

From Wikipedia, the free encyclopedia

 

Models of neural computation are attempts to elucidate, in an abstract and mathematical fashion, the core principles that underlie information processing in biological nervous systems, or functional components thereof. This article aims to provide an overview of the most definitive models of neuro-biological computation as well as the tools commonly used to construct and analyze them.

Introduction

Due to the complexity of nervous system behavior, the associated experimental error bounds are ill-defined, but the relative merit of the different models of a particular subsystem can be compared according to how closely they reproduce real-world behaviors or respond to specific input signals. In the closely related field of computational neuroethology, the practice is to include the environment in the model in such a way that the loop is closed. In the cases where competing models are unavailable, or where only gross responses have been measured or quantified, a clearly formulated model can guide the scientist in designing experiments to probe biochemical mechanisms or network connectivity.

In all but the simplest cases, the mathematical equations that form the basis of a model cannot be solved exactly. Nevertheless, computer technology, sometimes in the form of specialized software or hardware architectures, allow scientists to perform iterative calculations and search for plausible solutions. A computer chip or a robot that can interact with the natural environment in ways akin to the original organism is one embodiment of a useful model. The ultimate measure of success is however the ability to make testable predictions.

General criteria for evaluating models

Speed of information processing

The rate of information processing in biological neural systems are constrained by the speed at which an action potential can propagate down a nerve fibre. This conduction velocity ranges from 1 m/s to over 100 m/s, and generally increases with the diameter of the neuronal process. Slow in the timescales of biologically-relevant events dictated by the speed of sound or the force of gravity, the nervous system overwhelmingly prefers parallel computations over serial ones in time-critical applications.

Robustness

A model is robust if it continues to produce the same computational results under variations in inputs or operating parameters introduced by noise. For example, the direction of motion as computed by a robust motion detector would not change under small changes of luminance, contrast or velocity jitter.

Gain control

This refers to the principle that the response of a nervous system should stay within certain bounds even as the inputs from the environment change drastically. For example, when adjusting between a sunny day and a moonless night, the retina changes the relationship between light level and neuronal output by a factor of more than ${\displaystyle 10^{6}}$ so that the signals sent to later stages of the visual system always remain within a much narrower range of amplitudes.

Linearity versus nonlinearity

A linear system is one whose response in a specified unit of measure, to a set of inputs considered at once, is the sum of its responses due to the inputs considered individually.

Linear systems are easier to analyze mathematically and are a persuasive assumption in many models including the McCulloch and Pitts neuron, population coding models, and the simple neurons often used in Artificial neural networks. Linearity may occur in the basic elements of a neural circuit such as the response of a postsynaptic neuron, or as an emergent property of a combination of nonlinear subcircuits. Though linearity is often seen as incorrect, there has been recent work suggesting it may, in fact, be biophysically plausible in some cases.

Examples

A computational neural model may be constrained to the level of biochemical signalling in individual neurons or it may describe an entire organism in its environment. The examples here are grouped according to their scope.

Models of information transfer in neurons

The most widely used models of information transfer in biological neurons are based on analogies with electrical circuits. The equations to be solved are time-dependent differential equations with electro-dynamical variables such as current, conductance or resistance, capacitance and voltage.

Hodgkin–Huxley model and its derivatives

The Hodgkin–Huxley model, widely regarded as one of the great achievements of 20th-century biophysics, describes how action potentials in neurons are initiated and propagated in axons via voltage-gated ion channels. It is a set of nonlinear ordinary differential equations that were introduced by Alan Lloyd Hodgkin and Andrew Huxley in 1952 to explain the results of voltage clamp experiments on the squid giant axon. Analytic solutions do not exist, but the Levenberg–Marquardt algorithm, a modified Gauss–Newton algorithm, is often used to fit these equations to voltage-clamp data.

The FitzHugh–Nagumo model is a simplication of the Hodgkin–Huxley model. The Hindmarsh–Rose model is an extension which describes neuronal spike bursts. The Morris–Lecar model is a modification which does not generate spikes, but describes slow-wave propagation, which is implicated in the inhibitory synaptic mechanisms of central pattern generators.

Transfer functions and linear filters

This approach, influenced by control theory and signal processing, treats neurons and synapses as time-invariant entities that produce outputs that are linear combinations of input signals, often depicted as sine waves with a well-defined temporal or spatial frequencies.

The entire behavior of a neuron or synapse are encoded in a transfer function, lack of knowledge concerning the exact underlying mechanism notwithstanding. This brings a highly developed mathematics to bear on the problem of information transfer.

The accompanying taxonomy of linear filters turns out to be useful in characterizing neural circuitry. Both low- and high-pass filters are postulated to exist in some form in sensory systems, as they act to prevent information loss in high and low contrast environments, respectively.

Indeed, measurements of the transfer functions of neurons in the horseshoe crab retina according to linear systems analysis show that they remove short-term fluctuations in input signals leaving only the long-term trends, in the manner of low-pass filters. These animals are unable to see low-contrast objects without the help of optical distortions caused by underwater currents.

Models of computations in sensory systems

Lateral inhibition in the retina: Hartline–Ratliff equations

In the retina, an excited neural receptor can suppress the activity of surrounding neurons within an area called the inhibitory field. This effect, known as lateral inhibition, increases the contrast and sharpness in visual response, but leads to the epiphenomenon of Mach bands. This is often illustrated by the optical illusion of light or dark stripes next to a sharp boundary between two regions in an image of different luminance.

The Hartline-Ratliff model describes interactions within a group of p photoreceptor cells. Assuming these interactions to be linear, they proposed the following relationship for the steady-state response rate ${\displaystyle r_{p}}$ of the given p-th photoreceptor in terms of the steady-state response rates ${\displaystyle r_{j}}$ of the j surrounding receptors:

${\displaystyle r_{p}=\left|\left[e_{p}-\sum _{j=1,j\neq p}^{n}k_{pj}\left|r_{j}-r_{pj}^{o}\right|\right]\right|}$.

Here,
${\displaystyle e_{p}}$ is the excitation of the target p-th receptor from sensory transduction
${\displaystyle r_{pj}^{o}}$ is the associated threshold of the firing cell, and
${\displaystyle k_{pj}}$ is the coefficient of inhibitory interaction between the p-th and the jth receptor. The inhibitory interaction decreases with distance from the target p-th receptor.

Cross-correlation in sound localization: Jeffress model

According to Jeffress, in order to compute the location of a sound source in space from interaural time differences, an auditory system relies on delay lines: the induced signal from an ipsilateral auditory receptor to a particular neuron is delayed for the same time as it takes for the original sound to go in space from that ear to the other. Each postsynaptic cell is differently delayed and thus specific for a particular inter-aural time difference. This theory is equivalent to the mathematical procedure of cross-correlation.

Following Fischer and Anderson, the response of the postsynaptic neuron to the signals from the left and right ears is given by

${\displaystyle y_{R}\left(t\right)-y_{L}\left(t\right)}$

where

${\displaystyle y_{L}\left(t\right)=\int _{0}^{\tau }u_{L}\left(\sigma \right)w\left(t-\sigma \right)d\sigma }$
${\displaystyle y_{R}\left(t\right)=\int _{0}^{\tau }u_{R}\left(\sigma \right)w\left(t-\sigma \right)d\sigma }$

and

${\displaystyle w\left(t-\sigma \right)}$ represents the delay function. This is not entirely correct and a clear eye is needed to put the symbols in order.

Structures have been located in the barn owl which are consistent with Jeffress-type mechanisms.

Cross-correlation for motion detection: Hassenstein–Reichardt model

A motion detector needs to satisfy three general requirements: pair-inputs, asymmetry and nonlinearity. The cross-correlation operation implemented asymmetrically on the responses from a pair of photoreceptors satisfies these minimal criteria, and furthermore, predicts features which have been observed in the response of neurons of the lobula plate in bi-wing insects.

The master equation for response is

${\displaystyle R=A_{1}(t-\tau )B_{2}(t)-A_{2}(t-\tau )B_{1}(t)}$

The HR model predicts a peaking of the response at a particular input temporal frequency. The conceptually similar Barlow–Levick model is deficient in the sense that a stimulus presented to only one receptor of the pair is sufficient to generate a response. This is unlike the HR model, which requires two correlated signals delivered in a time ordered fashion. However the HR model does not show a saturation of response at high contrasts, which is observed in experiment. Extensions of the Barlow-Levick model can provide for this discrepancy.

Watson–Ahumada model for motion estimation in humans

This uses a cross-correlation in both the spatial and temporal directions, and is related to the concept of optical flow.

Neurophysiological metronomes: neural circuits for pattern generation

Mutually inhibitory processes are a unifying motif of all central pattern generators. This has been demonstrated in the stomatogastric (STG) nervous system of crayfish and lobsters. Two and three-cell oscillating networks based on the STG have been constructed which are amenable to mathematical analysis, and which depend in a simple way on synaptic strengths and overall activity, presumably the knobs on these things. The mathematics involved is the theory of dynamical systems.

Feedback and control: models of flight control in the fly

Flight control in the fly is believed to be mediated by inputs from the visual system and also the halteres, a pair of knob-like organs which measure angular velocity. Integrated computer models of Drosophila, short on neuronal circuitry but based on the general guidelines given by control theory and data from the tethered flights of flies, have been constructed to investigate the details of flight control.

Software modelling approaches and tools

Neural networks

In this approach the strength and type, excitatory or inhibitory, of synaptic connections are represented by the magnitude and sign of weights, that is, numerical coefficients ${\displaystyle w'}$ in front of the inputs ${\displaystyle x}$ to a particular neuron. The response of the ${\displaystyle j}$-th neuron is given by a sum of nonlinear, usually "sigmoidal" functions ${\displaystyle g}$ of the inputs as:

${\displaystyle f_{j}=\sum _{i}g\left(w_{ji}'x_{i}+b_{j}\right)}$.

This response is then fed as input into other neurons and so on. The goal is to optimize the weights of the neurons to output a desired response at the output layer respective to a set given inputs at the input layer. This optimization of the neuron weights is often performed using the backpropagation algorithm and an optimization method such as gradient descent or Newton's method of optimization. Backpropagation compares the output of the network with the expected output from the training data, then updates the weights of each neuron to minimize the contribution of that individual neuron to the total error of the network.

Genetic algorithms

Genetic algorithms are used to evolve neural (and sometimes body) properties in a model brain-body-environment system so as to exhibit some desired behavioral performance. The evolved agents can then be subjected to a detailed analysis to uncover their principles of operation. Evolutionary approaches are particularly useful for exploring spaces of possible solutions to a given behavioral task because these approaches minimize a priori assumptions about how a given behavior ought to be instantiated. They can also be useful for exploring different ways to complete a computational neuroethology model when only partial neural circuitry is available for a biological system of interest.

NEURON

The NEURON software, developed at Duke University, is a simulation environment for modeling individual neurons and networks of neurons. The NEURON environment is a self-contained environment allowing interface through its GUI or via scripting with hoc or python. The NEURON simulation engine is based on a Hodgkin–Huxley type model using a Borg–Graham formulation. Several examples of models written in NEURON are available from the online database ModelDB.

Embodiment in electronic hardware

Conductance-based silicon neurons

Nervous systems differ from the majority of silicon-based computing devices in that they resemble analog computers (not digital data processors) and massively parallel processors, not sequential processors. To model nervous systems accurately, in real-time, alternative hardware is required.
The most realistic circuits to date make use of analog properties of existing digital electronics (operated under non-standard conditions) to realize Hodgkin–Huxley-type models in silico.

Neural coding

From Wikipedia, the free encyclopedia

 

Neural coding is a neuroscience field concerned with characterising the hypothetical relationship between the stimulus and the individual or ensemble neuronal responses and the relationship among the electrical activity of the neurons in the ensemble. Based on the theory that sensory and other information is represented in the brain by networks of neurons, it is thought that neurons can encode both digital and analog information.

Overview

Neurons are remarkable among the cells of the body in their ability to propagate signals rapidly over large distances. They do this by generating characteristic electrical pulses called action potentials: voltage spikes that can travel down nerve fibers. Sensory neurons change their activities by firing sequences of action potentials in various temporal patterns, with the presence of external sensory stimuli, such as light, sound, taste, smell and touch. It is known that information about the stimulus is encoded in this pattern of action potentials and transmitted into and around the brain.

Although action potentials can vary somewhat in duration, amplitude and shape, they are typically treated as identical stereotyped events in neural coding studies. If the brief duration of an action potential (about 1ms) is ignored, an action potential sequence, or spike train, can be characterized simply by a series of all-or-none point events in time. The lengths of interspike intervals (ISIs) between two successive spikes in a spike train often vary, apparently randomly. The study of neural coding involves measuring and characterizing how stimulus attributes, such as light or sound intensity, or motor actions, such as the direction of an arm movement, are represented by neuron action potentials or spikes. In order to describe and analyze neuronal firing, statistical methods and methods of probability theory and stochastic point processes have been widely applied.

With the development of large-scale neural recording and decoding technologies, researchers have begun to crack the neural code and have already provided the first glimpse into the real-time neural code as memory is formed and recalled in the hippocampus, a brain region known to be central for memory formation. Neuroscientists have initiated several large-scale brain decoding projects.

Encoding and decoding

The link between stimulus and response can be studied from two opposite points of view. Neural encoding refers to the map from stimulus to response. The main focus is to understand how neurons respond to a wide variety of stimuli, and to construct models that attempt to predict responses to other stimuli. Neural decoding refers to the reverse map, from response to stimulus, and the challenge is to reconstruct a stimulus, or certain aspects of that stimulus, from the spike sequences it evokes.

Hypothesized coding schemes

A sequence, or 'train', of spikes may contain information based on different coding schemes. In motor neurons, for example, the strength at which an innervated muscle is contracted depends solely on the 'firing rate', the average number of spikes per unit time (a 'rate code'). At the other end, a complex 'temporal code' is based on the precise timing of single spikes. They may be locked to an external stimulus such as in the visual and auditory system or be generated intrinsically by the neural circuitry.

Whether neurons use rate coding or temporal coding is a topic of intense debate within the neuroscience community, even though there is no clear definition of what these terms mean. In one theory, termed "neuroelectrodynamics", the following coding schemes are all considered to be epiphenomena, replaced instead by molecular changes reflecting the spatial distribution of electric fields within neurons as a result of the broad electromagnetic spectrum of action potentials, and manifested in information as spike directivity.

Rate coding

The rate coding model of neuronal firing communication states that as the intensity of a stimulus increases, the frequency or rate of action potentials, or "spike firing", increases. Rate coding is sometimes called frequency coding.

Rate coding is a traditional coding scheme, assuming that most, if not all, information about the stimulus is contained in the firing rate of the neuron. Because the sequence of action potentials generated by a given stimulus varies from trial to trial, neuronal responses are typically treated statistically or probabilistically. They may be characterized by firing rates, rather than as specific spike sequences. In most sensory systems, the firing rate increases, generally non-linearly, with increasing stimulus intensity. Any information possibly encoded in the temporal structure of the spike train is ignored. Consequently, rate coding is inefficient but highly robust with respect to the ISI 'noise'.

During rate coding, precisely calculating firing rate is very important. In fact, the term "firing rate" has a few different definitions, which refer to different averaging procedures, such as an average over time or an average over several repetitions of experiment.

In rate coding, learning is based on activity-dependent synaptic weight modifications.
Rate coding was originally shown by ED Adrian and Y Zotterman in 1926. In this simple experiment different weights were hung from a muscle. As the weight of the stimulus increased, the number of spikes recorded from sensory nerves innervating the muscle also increased. From these original experiments, Adrian and Zotterman concluded that action potentials were unitary events, and that the frequency of events, and not individual event magnitude, was the basis for most inter-neuronal communication.

In the following decades, measurement of firing rates became a standard tool for describing the properties of all types of sensory or cortical neurons, partly due to the relative ease of measuring rates experimentally. However, this approach neglects all the information possibly contained in the exact timing of the spikes. During recent years, more and more experimental evidence has suggested that a straightforward firing rate concept based on temporal averaging may be too simplistic to describe brain activity.

Spike-count rate

The spike-count rate, also referred to as temporal average, is obtained by counting the number of spikes that appear during a trial and dividing by the duration of trial. The length T of the time window is set by the experimenter and depends on the type of neuron recorded from and to the stimulus. In practice, to get sensible averages, several spikes should occur within the time window. Typical values are T = 100 ms or T = 500 ms, but the duration may also be longer or shorter.

The spike-count rate can be determined from a single trial, but at the expense of losing all temporal resolution about variations in neural response during the course of the trial. Temporal averaging can work well in cases where the stimulus is constant or slowly varying and does not require a fast reaction of the organism — and this is the situation usually encountered in experimental protocols. Real-world input, however, is hardly stationary, but often changing on a fast time scale. For example, even when viewing a static image, humans perform saccades, rapid changes of the direction of gaze. The image projected onto the retinal photoreceptors changes therefore every few hundred milliseconds.

Despite its shortcomings, the concept of a spike-count rate code is widely used not only in experiments, but also in models of neural networks. It has led to the idea that a neuron transforms information about a single input variable (the stimulus strength) into a single continuous output variable (the firing rate).

There is a growing body of evidence that in Purkinje neurons, at least, information is not simply encoded in firing but also in the timing and duration of non-firing, quiescent periods.

Time-dependent firing rate

The time-dependent firing rate is defined as the average number of spikes (averaged over trials) appearing during a short interval between times t and t+Δt, divided by the duration of the interval. It works for stationary as well as for time-dependent stimuli. To experimentally measure the time-dependent firing rate, the experimenter records from a neuron while stimulating with some input sequence. The same stimulation sequence is repeated several times and the neuronal response is reported in a Peri-Stimulus-Time Histogram (PSTH). The time t is measured with respect to the start of the stimulation sequence. The Δt must be large enough (typically in the range of one or a few milliseconds) so there are sufficient number of spikes within the interval to obtain a reliable estimate of the average. The number of occurrences of spikes n_K(t;t+Δt) summed over all repetitions of the experiment divided by the number K of repetitions is a measure of the typical activity of the neuron between time t and t+Δt. A further division by the interval length Δt yields time-dependent firing rate r(t) of the neuron, which is equivalent to the spike density of PSTH.

For sufficiently small Δt, r(t)Δt is the average number of spikes occurring between times t and t+Δt over multiple trials. If Δt is small, there will never be more than one spike within the interval between t and t+Δt on any given trial. This means that r(t)Δt is also the fraction of trials on which a spike occurred between those times. Equivalently, r(t)Δt is the probability that a spike occurs during this time interval.

As an experimental procedure, the time-dependent firing rate measure is a useful method to evaluate neuronal activity, in particular in the case of time-dependent stimuli. The obvious problem with this approach is that it can not be the coding scheme used by neurons in the brain. Neurons can not wait for the stimuli to repeatedly present in an exactly same manner before generating response.

Nevertheless, the experimental time-dependent firing rate measure can make sense, if there are large populations of independent neurons that receive the same stimulus. Instead of recording from a population of N neurons in a single run, it is experimentally easier to record from a single neuron and average over N repeated runs. Thus, the time-dependent firing rate coding relies on the implicit assumption that there are always populations of neurons.

Temporal coding

When precise spike timing or high-frequency firing-rate fluctuations are found to carry information, the neural code is often identified as a temporal code. A number of studies have found that the temporal resolution of the neural code is on a millisecond time scale, indicating that precise spike timing is a significant element in neural coding. Such codes, that communicate via the time between spikes are referred to as interpulse interval codes, and have been supported by recent studies.

Neurons exhibit high-frequency fluctuations of firing-rates which could be noise or could carry information. Rate coding models suggest that these irregularities are noise, while temporal coding models suggest that they encode information. If the nervous system only used rate codes to convey information, a more consistent, regular firing rate would have been evolutionarily advantageous, and neurons would have utilized this code over other less robust options. Temporal coding supplies an alternate explanation for the “noise," suggesting that it actually encodes information and affects neural processing. To model this idea, binary symbols can be used to mark the spikes: 1 for a spike, 0 for no spike. Temporal coding allows the sequence 000111000111 to mean something different from 001100110011, even though the mean firing rate is the same for both sequences, at 6 spikes/10 ms. Until recently, scientists had put the most emphasis on rate encoding as an explanation for post-synaptic potential patterns. However, functions of the brain are more temporally precise than the use of only rate encoding seems to allow^{[citation needed]}. In other words, essential information could be lost due to the inability of the rate code to capture all the available information of the spike train. In addition, responses are different enough between similar (but not identical) stimuli to suggest that the distinct patterns of spikes contain a higher volume of information than is possible to include in a rate code.

Temporal codes employ those features of the spiking activity that cannot be described by the firing rate. For example, time to first spike after the stimulus onset, characteristics based on the second and higher statistical moments of the ISI probability distribution, spike randomness, or precisely timed groups of spikes (temporal patterns) are candidates for temporal codes. As there is no absolute time reference in the nervous system, the information is carried either in terms of the relative timing of spikes in a population of neurons or with respect to an ongoing brain oscillation. One way in which temporal codes are decoded, in presence of neural oscillations, is that spikes occurring at specific phases of an oscillatory cycle are more effective in depolarizing the post-synaptic neuron.

The temporal structure of a spike train or firing rate evoked by a stimulus is determined both by the dynamics of the stimulus and by the nature of the neural encoding process. Stimuli that change rapidly tend to generate precisely timed spikes and rapidly changing firing rates no matter what neural coding strategy is being used. Temporal coding refers to temporal precision in the response that does not arise solely from the dynamics of the stimulus, but that nevertheless relates to properties of the stimulus. The interplay between stimulus and encoding dynamics makes the identification of a temporal code difficult.

In temporal coding, learning can be explained by activity-dependent synaptic delay modifications. The modifications can themselves depend not only on spike rates (rate coding) but also on spike timing patterns (temporal coding), i.e., can be a special case of spike-timing-dependent plasticity.

The issue of temporal coding is distinct and independent from the issue of independent-spike coding. If each spike is independent of all the other spikes in the train, the temporal character of the neural code is determined by the behavior of time-dependent firing rate r(t). If r(t) varies slowly with time, the code is typically called a rate code, and if it varies rapidly, the code is called temporal.

Temporal coding in sensory systems

For very brief stimuli, a neuron's maximum firing rate may not be fast enough to produce more than a single spike. Due to the density of information about the abbreviated stimulus contained in this single spike, it would seem that the timing of the spike itself would have to convey more information than simply the average frequency of action potentials over a given period of time. This model is especially important for sound localization, which occurs within the brain on the order of milliseconds. The brain must obtain a large quantity of information based on a relatively short neural response. Additionally, if low firing rates on the order of ten spikes per second must be distinguished from arbitrarily close rate coding for different stimuli, then a neuron trying to discriminate these two stimuli may need to wait for a second or more to accumulate enough information. This is not consistent with numerous organisms which are able to discriminate between stimuli in the time frame of milliseconds, suggesting that a rate code is not the only model at work.

To account for the fast encoding of visual stimuli, it has been suggested that neurons of the retina encode visual information in the latency time between stimulus onset and first action potential, also called latency to first spike. This type of temporal coding has been shown also in the auditory and somato-sensory system. The main drawback of such a coding scheme is its sensitivity to intrinsic neuronal fluctuations. In the primary visual cortex of macaques, the timing of the first spike relative to the start of the stimulus was found to provide more information than the interval between spikes. However, the interspike interval could be used to encode additional information, which is especially important when the spike rate reaches its limit, as in high-contrast situations. For this reason, temporal coding may play a part in coding defined edges rather than gradual transitions.

The mammalian gustatory system is useful for studying temporal coding because of its fairly distinct stimuli and the easily discernible responses of the organism. Temporally encoded information may help an organism discriminate between different tastants of the same category (sweet, bitter, sour, salty, umami) that elicit very similar responses in terms of spike count. The temporal component of the pattern elicited by each tastant may be used to determine its identity (e.g., the difference between two bitter tastants, such as quinine and denatonium). In this way, both rate coding and temporal coding may be used in the gustatory system – rate for basic tastant type, temporal for more specific differentiation. Research on mammalian gustatory system has shown that there is an abundance of information present in temporal patterns across populations of neurons, and this information is different from that which is determined by rate coding schemes. Groups of neurons may synchronize in response to a stimulus. In studies dealing with the front cortical portion of the brain in primates, precise patterns with short time scales only a few milliseconds in length were found across small populations of neurons which correlated with certain information processing behaviors. However, little information could be determined from the patterns; one possible theory is they represented the higher-order processing taking place in the brain.

As with the visual system, in mitral/tufted cells in the olfactory bulb of mice, first-spike latency relative to the start of a sniffing action seemed to encode much of the information about an odor. This strategy of using spike latency allows for rapid identification of and reaction to an odorant. In addition, some mitral/tufted cells have specific firing patterns for given odorants. This type of extra information could help in recognizing a certain odor, but is not completely necessary, as average spike count over the course of the animal's sniffing was also a good identifier. Along the same lines, experiments done with the olfactory system of rabbits showed distinct patterns which correlated with different subsets of odorants, and a similar result was obtained in experiments with the locust olfactory system.

Temporal coding applications

The specificity of temporal coding requires highly refined technology to measure informative, reliable, experimental data. Advances made in optogenetics allow neurologists to control spikes in individual neurons, offering electrical and spatial single-cell resolution. For example, blue light causes the light-gated ion channel channelrhodopsin to open, depolarizing the cell and producing a spike. When blue light is not sensed by the cell, the channel closes, and the neuron ceases to spike. The pattern of the spikes matches the pattern of the blue light stimuli. By inserting channelrhodopsin gene sequences into mouse DNA, researchers can control spikes and therefore certain behaviors of the mouse (e.g., making the mouse turn left). Researchers, through optogenetics, have the tools to effect different temporal codes in a neuron while maintaining the same mean firing rate, and thereby can test whether or not temporal coding occurs in specific neural circuits.

Optogenetic technology also has the potential to enable the correction of spike abnormalities at the root of several neurological and psychological disorders. If neurons do encode information in individual spike timing patterns, key signals could be missed by attempting to crack the code while looking only at mean firing rates. Understanding any temporally encoded aspects of the neural code and replicating these sequences in neurons could allow for greater control and treatment of neurological disorders such as depression, schizophrenia, and Parkinson's disease. Regulation of spike intervals in single cells more precisely controls brain activity than the addition of pharmacological agents intravenously.

Phase-of-firing code

Phase-of-firing code is a neural coding scheme that combines the spike count code with a time reference based on oscillations. This type of code takes into account a time label for each spike according to a time reference based on phase of local ongoing oscillations at low or high frequencies.

It has been shown that neurons in some cortical sensory areas encode rich naturalistic stimuli in terms of their spike times relative to the phase of ongoing network oscillatory fluctuations, rather than only in terms of their spike count. The local field potential signals reflect population (network) oscillations. The phase-of-firing code is often categorized as a temporal code although the time label used for spikes (i.e. the network oscillation phase) is a low-resolution (coarse-grained) reference for time. As a result, often only four discrete values for the phase are enough to represent all the information content in this kind of code with respect to the phase of oscillations in low frequencies. Phase-of-firing code is loosely based on the phase precession phenomena observed in place cells of the hippocampus. Another feature of this code is that neurons adhere to a preferred order of spiking between a group of sensory neurons, resulting in firing sequence.

Phase code has been shown in visual cortex to involve also high-frequency oscillations. Within a cycle of gamma oscillation, each neuron has its own preferred relative firing time. As a result, an entire population of neurons generates a firing sequence that has a duration of up to about 15 ms.

Population coding

Population coding is a method to represent stimuli by using the joint activities of a number of neurons. In population coding, each neuron has a distribution of responses over some set of inputs, and the responses of many neurons may be combined to determine some value about the inputs.
From the theoretical point of view, population coding is one of a few mathematically well-formulated problems in neuroscience. It grasps the essential features of neural coding and yet is simple enough for theoretic analysis. Experimental studies have revealed that this coding paradigm is widely used in the sensor and motor areas of the brain. For example, in the visual area medial temporal (MT), neurons are tuned to the moving direction. In response to an object moving in a particular direction, many neurons in MT fire with a noise-corrupted and bell-shaped activity pattern across the population. The moving direction of the object is retrieved from the population activity, to be immune from the fluctuation existing in a single neuron’s signal. In one classic example in the primary motor cortex, Apostolos Georgopoulos and colleagues trained monkeys to move a joystick towards a lit target. They found that a single neuron would fire for multiple target directions. However it would fire fastest for one direction and more slowly depending on how close the target was to the neuron's 'preferred' direction.

Kenneth Johnson originally derived that if each neuron represents movement in its preferred direction, and the vector sum of all neurons is calculated (each neuron has a firing rate and a preferred direction), the sum points in the direction of motion. In this manner, the population of neurons codes the signal for the motion. This particular population code is referred to as population vector coding. This particular study divided the field of motor physiologists between Evarts' "upper motor neuron" group, which followed the hypothesis that motor cortex neurons contributed to control of single muscles, and the Georgopoulos group studying the representation of movement directions in cortex.

The Johns Hopkins University Neural Encoding laboratory led by Murray Sachs and Eric Young developed place-time population codes, termed the Averaged-Localized-Synchronized-Response (ALSR) code for neural representation of auditory acoustic stimuli. This exploits both the place or tuning within the auditory nerve, as well as the phase-locking within each nerve fiber Auditory nerve. The first ALSR representation was for steady-state vowels; ALSR representations of pitch and formant frequencies in complex, non-steady state stimuli were demonstrated for voiced-pitch and formant representations in consonant-vowel syllables. The advantage of such representations is that global features such as pitch or formant transition profiles can be represented as global features across the entire nerve simultaneously via both rate and place coding.

Population coding has a number of other advantages as well, including reduction of uncertainty due to neuronal variability and the ability to represent a number of different stimulus attributes simultaneously. Population coding is also much faster than rate coding and can reflect changes in the stimulus conditions nearly instantaneously. Individual neurons in such a population typically have different but overlapping selectivities, so that many neurons, but not necessarily all, respond to a given stimulus.

Typically an encoding function has a peak value such that activity of the neuron is greatest if the perceptual value is close to the peak value, and becomes reduced accordingly for values less close to the peak value.

It follows that the actual perceived value can be reconstructed from the overall pattern of activity in the set of neurons. The Johnson/Georgopoulos vector coding is an example of simple averaging. A more sophisticated mathematical technique for performing such a reconstruction is the method of maximum likelihood based on a multivariate distribution of the neuronal responses. These models can assume independence, second order correlations, or even more detailed dependencies such as higher order maximum entropy models or copulas.

Correlation coding

The correlation coding model of neuronal firing claims that correlations between action potentials, or "spikes", within a spike train may carry additional information above and beyond the simple timing of the spikes. Early work suggested that correlation between spike trains can only reduce, and never increase, the total mutual information present in the two spike trains about a stimulus feature. However, this was later demonstrated to be incorrect. Correlation structure can increase information content if noise and signal correlations are of opposite sign. Correlations can also carry information not present in the average firing rate of two pairs of neurons. A good example of this exists in the pentobarbital-anesthetized marmoset auditory cortex, in which a pure tone causes an increase in the number of correlated spikes, but not an increase in the mean firing rate, of pairs of neurons.

Independent-spike coding

The independent-spike coding model of neuronal firing claims that each individual action potential, or "spike", is independent of each other spike within the spike train.

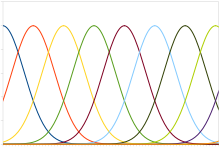
Position coding

Plot of typical position coding

A typical population code involves neurons with a Gaussian tuning curve whose means vary linearly with the stimulus intensity, meaning that the neuron responds most strongly (in terms of spikes per second) to a stimulus near the mean. The actual intensity could be recovered as the stimulus level corresponding to the mean of the neuron with the greatest response. However, the noise inherent in neural responses means that a maximum likelihood estimation function is more accurate.

Neural responses are noisy and unreliable.

This type of code is used to encode continuous variables such as joint position, eye position, color, or sound frequency. Any individual neuron is too noisy to faithfully encode the variable using rate coding, but an entire population ensures greater fidelity and precision. For a population of unimodal tuning curves, i.e. with a single peak, the precision typically scales linearly with the number of neurons. Hence, for half the precision, half as many neurons are required. In contrast, when the tuning curves have multiple peaks, as in grid cells that represent space, the precision of the population can scale exponentially with the number of neurons. This greatly reduces the number of neurons required for the same precision.

Sparse coding

The sparse code is when each item is encoded by the strong activation of a relatively small set of neurons. For each item to be encoded, this is a different subset of all available neurons. In contrast to sensor-sparse coding, sensor-dense coding implies that all information from possible sensor locations is known.

As a consequence, sparseness may be focused on temporal sparseness ("a relatively small number of time periods are active") or on the sparseness in an activated population of neurons. In this latter case, this may be defined in one time period as the number of activated neurons relative to the total number of neurons in the population. This seems to be a hallmark of neural computations since compared to traditional computers, information is massively distributed across neurons. A major result in neural coding from Olshausen and Field is that sparse coding of natural images produces wavelet-like oriented filters that resemble the receptive fields of simple cells in the visual cortex. The capacity of sparse codes may be increased by simultaneous use of temporal coding, as found in the locust olfactory system.

Given a potentially large set of input patterns, sparse coding algorithms (e.g. Sparse Autoencoder) attempt to automatically find a small number of representative patterns which, when combined in the right proportions, reproduce the original input patterns. The sparse coding for the input then consists of those representative patterns. For example, the very large set of English sentences can be encoded by a small number of symbols (i.e. letters, numbers, punctuation, and spaces) combined in a particular order for a particular sentence, and so a sparse coding for English would be those symbols.

Linear generative model

Most models of sparse coding are based on the linear generative model. In this model, the symbols are combined in a linear fashion to approximate the input.

More formally, given a k-dimensional set of real-numbered input vectors ${\displaystyle {\vec {\xi }}\in \mathbb {R} ^{k}}$, the goal of sparse coding is to determine n k-dimensional basis vectors ${\displaystyle {\vec {b_{1}}},\ldots ,{\vec {b_{n}}}\in \mathbb {R} ^{k}}$ along with a sparse n-dimensional vector of weights or coefficients ${\displaystyle {\vec {s}}\in \mathbb {R} ^{n}}$ for each input vector, so that a linear combination of the basis vectors with proportions given by the coefficients results in a close approximation to the input vector: ${\displaystyle {\vec {\xi }}\approx \sum _{j=1}^{n}s_{j}{\vec {b}}_{j}}$.

The codings generated by algorithms implementing a linear generative model can be classified into codings with soft sparseness and those with hard sparseness. These refer to the distribution of basis vector coefficients for typical inputs. A coding with soft sparseness has a smooth Gaussian-like distribution, but peakier than Gaussian, with many zero values, some small absolute values, fewer larger absolute values, and very few very large absolute values. Thus, many of the basis vectors are active. Hard sparseness, on the other hand, indicates that there are many zero values, no or hardly any small absolute values, fewer larger absolute values, and very few very large absolute values, and thus few of the basis vectors are active. This is appealing from a metabolic perspective: less energy is used when fewer neurons are firing.

Another measure of coding is whether it is critically complete or overcomplete. If the number of basis vectors n is equal to the dimensionality k of the input set, the coding is said to be critically complete. In this case, smooth changes in the input vector result in abrupt changes in the coefficients, and the coding is not able to gracefully handle small scalings, small translations, or noise in the inputs. If, however, the number of basis vectors is larger than the dimensionality of the input set, the coding is overcomplete. Overcomplete codings smoothly interpolate between input vectors and are robust under input noise. The human primary visual cortex is estimated to be overcomplete by a factor of 500, so that, for example, a 14 x 14 patch of input (a 196-dimensional space) is coded by roughly 100,000 neurons.

Biological evidence

Sparse coding may be a general strategy of neural systems to augment memory capacity. To adapt to their environments, animals must learn which stimuli are associated with rewards or punishments and distinguish these reinforced stimuli from similar but irrelevant ones. Such task requires implementing stimulus-specific associative memories in which only a few neurons out of a population respond to any given stimulus and each neuron responds to only a few stimuli out of all possible stimuli.
Theoretical work on Sparse distributed memory has suggested that sparse coding increases the capacity of associative memory by reducing overlap between representations. Experimentally, sparse representations of sensory information have been observed in many systems, including vision, audition, touch, and olfaction. However, despite the accumulating evidence for widespread sparse coding and theoretical arguments for its importance, a demonstration that sparse coding improves the stimulus-specificity of associative memory has been lacking until recently.

Some progress has been made in 2014 by Gero Miesenböck's lab at the University of Oxford analyzing Drosophila Olfactory system. In Drosophila, sparse odor coding by the Kenyon cells of the mushroom body is thought to generate a large number of precisely addressable locations for the storage of odor-specific memories. Lin et al. demonstrated that sparseness is controlled by a negative feedback circuit between Kenyon cells and the GABAergic anterior paired lateral (APL) neuron. Systematic activation and blockade of each leg of this feedback circuit show that Kenyon cells activate APL and APL inhibits Kenyon cells. Disrupting the Kenyon cell-APL feedback loop decreases the sparseness of Kenyon cell odor responses, increases inter-odor correlations, and prevents flies from learning to discriminate similar, but not dissimilar, odors. These results suggest that feedback inhibition suppresses Kenyon cell activity to maintain sparse, decorrelated odor coding and thus the odor-specificity of memories.